| 1. |
• La résistance est :
.
• L'estimation rudimentaire de l'incertitude est
:
. • Si on suppose que les incertitudes sont de nature
uniquement aléatoire, on peut proposer aussi l'estimation
:
. |
|
|
2.a.
|
• Si on impose une valeur de plus
grande, la droite la mieux ajustée bascule pour passer au
mieux par le barycentre (pondéré) des points mesurés ; cela
correspond à une diminution de
(intersection avec l'axe des abscisse).
|
|
|
| 2.b. |
• Dans un plan de coordonnées et
, les
courbes d'égales valeur de sont
des droites passant par l'origine et de pente
:
. |
|
|
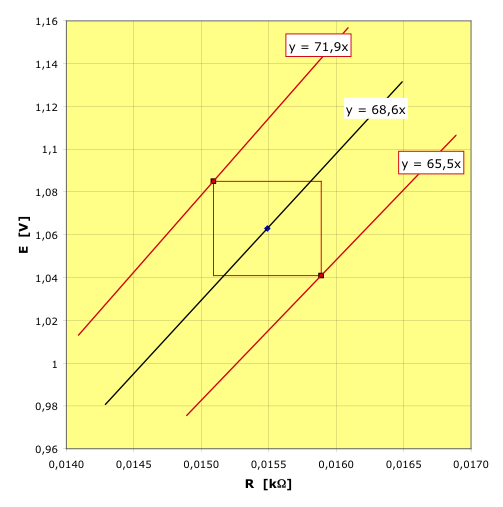
2.c.
|
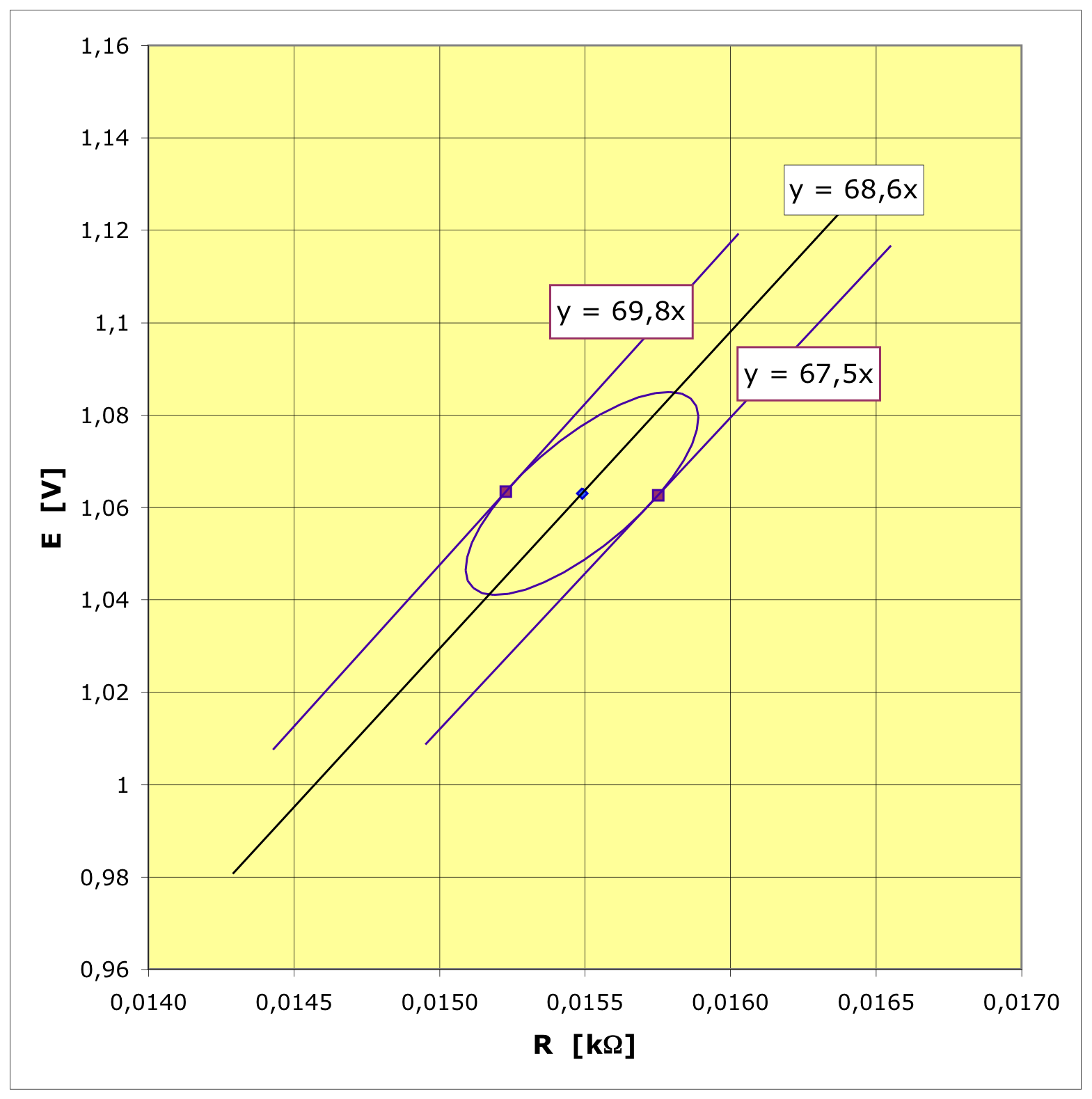
• Pour le mode de calcul (sans
corrélation) , la zone
d'incertitude correspond au rectangle de largeur et
de hauteur
.
L'intervalle de valeurs
peut être retrouvé en traçant les droites limites.
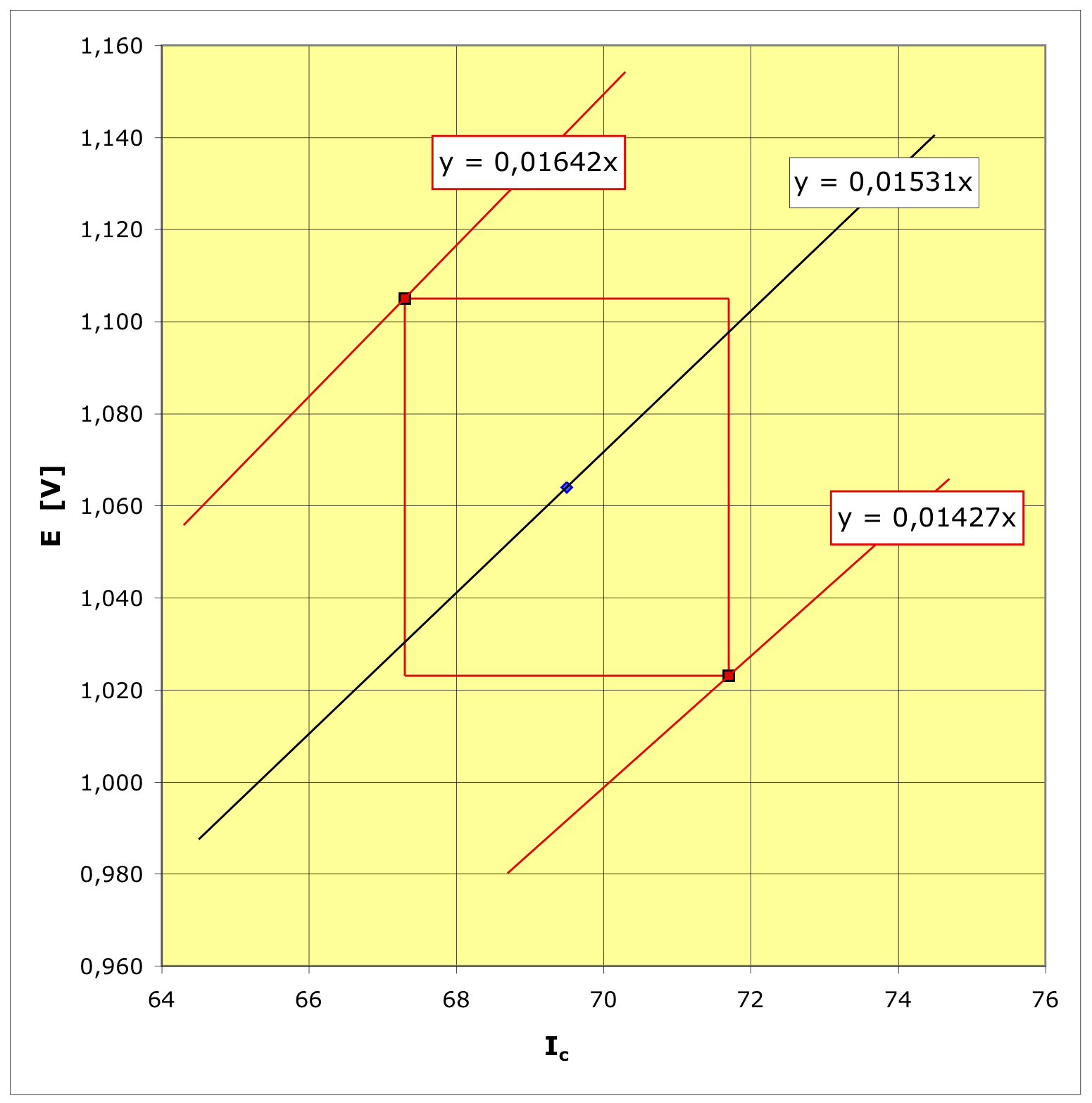
• Pour le mode de calcul (sans corrélation)
, la zone d'incertitude correspond l'ellipse “droite”
de largeur et
de hauteur
. On
peut la tracer sous forme paramétrique en
considérant
et
. L'intervalle de valeurs
peut être retrouvé en traçant les droites limites.
|
|
|
| 2.d. |
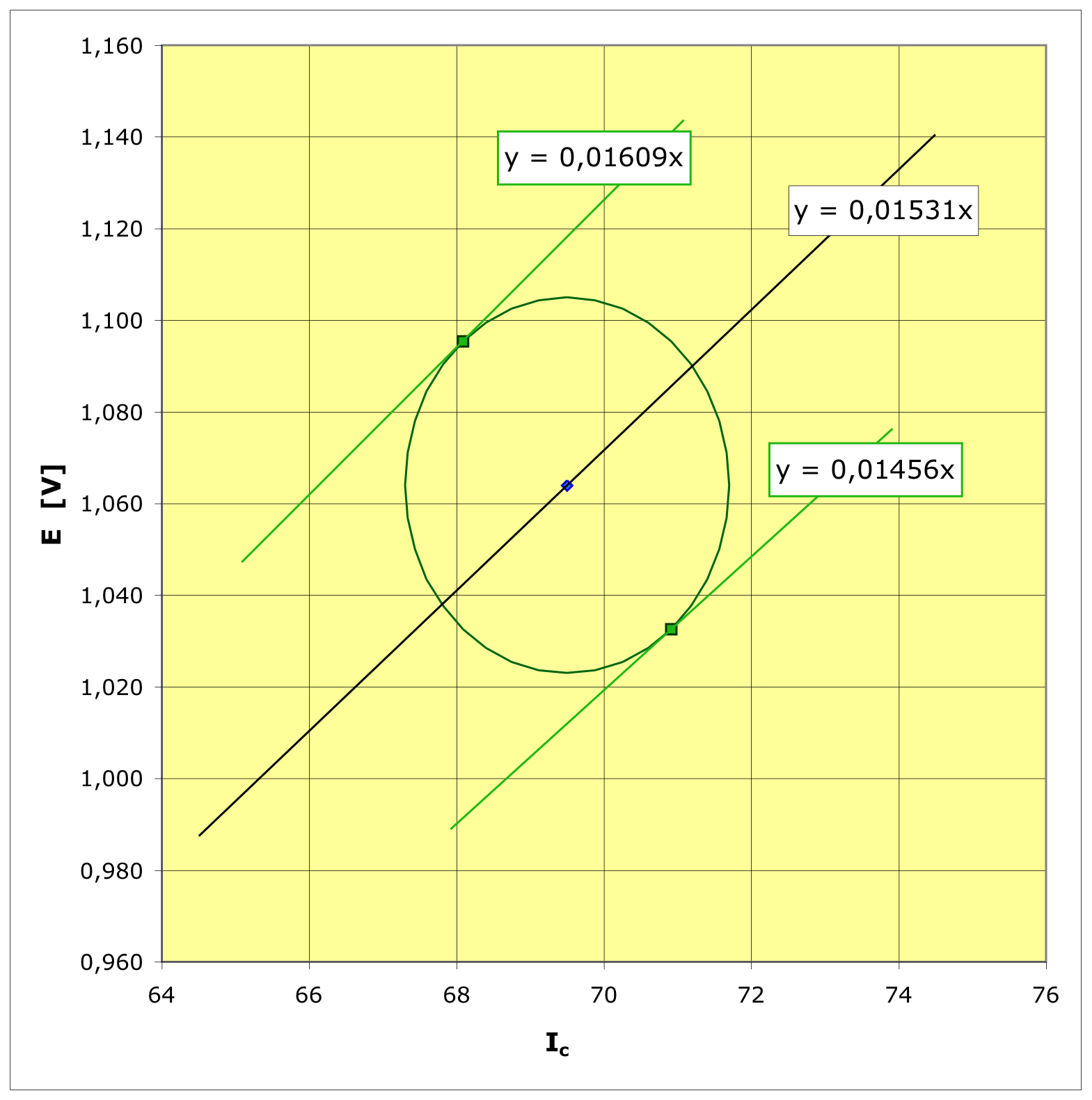
• Pour le mode de calcul avec
corrélation . |
|
|
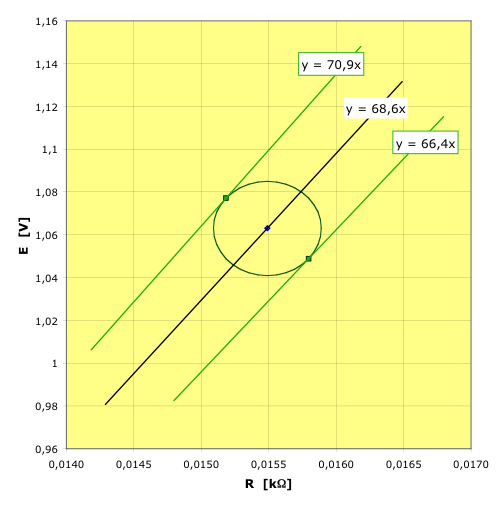
2.e.
|
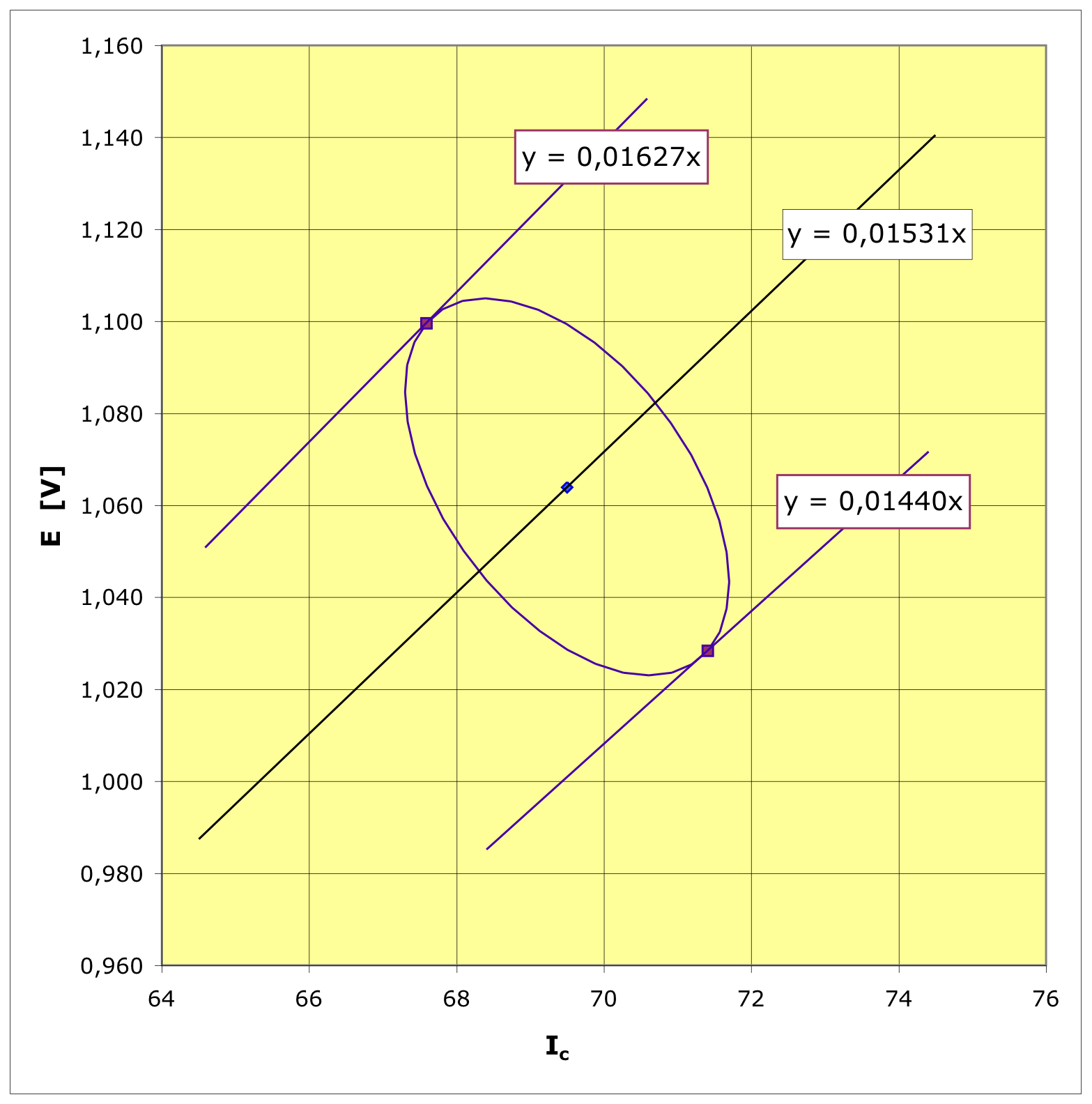
• La zone d'incertitude correspond l'ellipse
“oblique” ; on peut la tracer sous forme paramétrique à
l'aide d'un changement de notations.
• Dans le cas précédent, on pouvait écrire l'équation de
l'ellipse sous la forme
en considérant
et
.
• Dans le cas étudié ici, l'équation est de la
forme
avec . On
peut alors utiliser
et
donnant
.
◊ remarque : le choix du changement de variables le plus
efficace peut se déduire de la diagonalisation de la
matrice
.
• En posant par ailleurs :
et
, ceci donne :
et
.
L'intervalle de valeurs
peut être retrouvé en traçant les droites limites.
◊ remarque : on retrouve une projection horizontale de
l'ellipse correspondant à
et une projection verticale correspondant à
. |
|
|
| 3. |
• De façon générale, le résultat de
l'expression quadratique est inférieur à celui de
l'expression linéaire. Il est ainsi souvent considéré que la
seconde est trop approximative et conduit à une
surestimation systématique.
• En fait, lorsque la corrélation est positive,
l'incertitude est encore plus petite que le résultat de
l'expression quadratique ; ceci peut donner l'impression de
confirmer le jugement précédent.
• Toutefois, au contraire, lorsque la corrélation est
négative (cas étudié ici), l'incertitude est souvent plus
proche du résultat de l'expression linéaire que de celui de
l'expression quadratique.
• Si on ignore la corrélation et qu'on veut éviter de
sous-estimer les incertitudes, il est alors parfois prudent
d'utiliser l'expression linéaire. |