INCERTITUDES DE MESURE - exercices

A. EXERCICES DE BASE

I. “Propagation” des incertitudes

        • Un prisme de verre d’angle $A$ est utilisé pour dévier les rayons lumineux. L'angle de déviation dépend de l'orientation du dispositif ; il prend une valeur minimum $D$ pour la disposition symétrique.
        • L’indice de réfraction du verre constituant le prisme peut s'exprimer en fonction l’angle $A$ et de l’angle de déviation minimum $D$ des rayons lumineux :  $n=\frac{\sin⁡\left(\frac{D+A}{2}\right)}{\sin⁡\left(\frac{A}{2}\right)}$ .
        • À l’aide d’un goniomètre, on a mesuré séparément :   $D=40°±1'$   et   $A=60°±1'$ .
        • Calculer $n$ et $∆n$ (avec le nombre de chiffres significatifs convenable).

II. “Propagation” des incertitudes

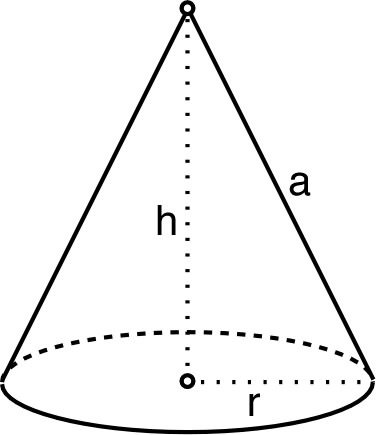
1.     • On considère un cône droit de hauteur $h$ et dont la base a pour rayon $r$.

        • Montrer que l’aire de la surface latérale est :   $A=π \:r \:\sqrt{r^2+h^2}$ .

2.     • On a mesuré  :   $r=30,0±0,2 \:\mathrm{mm}$   et  $h=50,0±0,2 \:\mathrm{mm}$.
        • Calculer $A$ et $∆A$ (avec le nombre de chiffres significatifs convenable).

III. “Propagation” des incertitudes

        • Calculer   $f\left(x,y\right)=\frac{x-y}{x+y}$   et  $∆f$  pour :  $x=200±3$   et  y=$100±1$.

B. EXERCICES D'APPROFONDISSEMENT

IV. “Corrélation” des incertitudes

        • On considère une série de mesure de la tension $U$ aux bornes d'une pile Daniell, en fonction du courant $I$ qui la traverse. Un logiciel spécialisé est utilisé pour ajuster un modèle théorique :  $U\left(I\right)=E-R \:I$ .
        • L'ajustement donne :  $E=1,063±0,022 \:\mathrm{V}$   et   $R=15,49±0,40 \:\mathrm{Ω}$  ;  il indique de plus le coefficient de covariance :  $c\left(E, R\right)=0,006554 \:\mathrm{V}.\mathrm{Ω}$ .

1.     • Calculer le courant de court-circuit $I_c$ et estimer son incertitude sans tenir compte de la corrélation.

2.     a) Quelle est la cause de la corrélation positive ?
        b) Pour comprendre l'effet de la corrélation, on veut représenter graphiquement les courbes d'égales valeur de $I_c$ dans un plan de coordonnées $R$ (en abscisse) et $E$ (en ordonnée). Décrire ces courbes.
        c) Représenter sur un tel graphique le point expérimental et la zone d'incertitude associée.
        d) Calculer l'incertitude en tenant compte de la corrélation.
        e) Représenter sur le graphique la zone d'incertitude correspondante.

3.     • En utilisant le même logiciel pour ajuster un modèle théorique :  $U\left(I\right)=R.\left(I_c-I\right)$  on obtient de façon analogue :  $R=15,49±0,40 \:\mathrm{Ω}$   et   $I_c=68,6±1,2 \:\mathrm{mA}$ .  Que peut-on en conclure ?

V. “Corrélation” des incertitudes

        • On considère une série de mesure de la tension $U$ aux bornes d'une pile Daniell, en fonction du courant $I$ qui la traverse. Un logiciel spécialisé est utilisé pour ajuster un modèle théorique de la forme :  $U\left(I\right)=E .\left(1-\frac{I}{I_c} \right)$ .
        • L'ajustement donne :  $E=1,064±0,041\:\mathrm{V}$   et   $I_c=69,5±2,2 \:\mathrm{mA}$  ;  il indique de plus le coefficient de covariance :  $c\left(E, I_c \right)=-0,0400 \:\mathrm{V}.\mathrm{mA}$ .

1.     • Calculer la résistance $R$ et estimer son incertitude sans tenir compte de la corrélation.

2.     a) Quelle est la cause de la corrélation négative ?
        b) Pour comprendre l'effet de la corrélation, on veut représenter graphiquement les courbes d'égales valeur de $R$ dans un plan de coordonnées $I_c$ (en abscisse) et $E$ (en ordonnée). Décrire ces courbes.
        c) Représenter sur un tel graphique le point expérimental et la zone d'incertitude associée.
        d) Calculer l'incertitude en tenant compte de la corrélation.
        e) Représenter sur le graphique la zone d'incertitude correspondante.

3.     • Lorsqu'on ne connaît pas la corrélation des variables, est-il préférable de propager les incertitudes par l'approximation :  $∆R≈\left|\frac{∂R}{∂I_c}\right| \:∆I_c+\left|\frac{∂R}{∂E}\right| \:∆E$ ,   ou par l'approximation :  $∆R≈\sqrt{\left(\frac{∂R}{∂I_c}\:∆I_c \right)^2+\left(\frac{∂R}{∂E}\:∆E\right)^2}$  ?