TRIÈDRE DE FRÉNET - corrigé des exercices


Centre instantané de rotation

1.        • Les coordonnées de AA peuvent s’écrire (xA;0)(x_A \,; 0) . Par ailleurs, les coordonnées du vecteur AM⟶\overset{⟶}{AM} sont  (bcos(ϕ);bsin(ϕ))\left(b \;\cos(ϕ) \,; b \:\sin(ϕ) \right) . Les coordonnées du point MM sont donc :  (xA+bcos(ϕ);bsin⁡(ϕ))\left(x_A+b \;\cos(ϕ) \,; b \;\sin⁡(ϕ) \right) .
• De même pour les coordonnées de BB :  (xA+𝓁cos(ϕ);𝓁sin(ϕ))\left(x_A+𝓁 \;\cos(ϕ) \,; 𝓁 \;\sin(ϕ) \right)  ; mais BB doit rester sur l’axe OyOy et ses coordonnées sont de la forme  (0;yB)(0 \,;y_B ) .  Par conséquent :  xA=−𝓁cos(ϕ)x_A=-𝓁 \; \cos(ϕ)  et on peut écrire les coordonnées du point MM :  ((b−𝓁)cos(ϕ);bsin(ϕ))\left((b-𝓁) \; \cos(ϕ) \,; b \;\sin(ϕ) \right) .
• Ceci correspond à une trajectoire elliptique, d’axes OxOx et OyOy , de demi-diamètre horizontal  𝓁−b𝓁-b  et de demi-diamètre vertical bb .  L’équation de cette trajectoire peut s’écrire :  x2(𝓁−b)2+y2b2=1\displaystyle \frac{x^2}{(𝓁-b)^2} +\frac{y^2}{b^2} =1 .
◊ remarque : si on n’étudie que l’aspect cinématique, on ne sait pas de quelle façon (en fonction du temps) est parcourue cette trajectoire.

2.
• Les coordonnées du vecteur vitesse peuvent s’obtenir symboliquement en dérivant par rapport à tt :
vx=x˙=(𝓁−b)ϕ˙sin(ϕ)v_x=\dot{x}=(𝓁-b) \:\dot{ϕ} \; \sin(ϕ)  ;  vy=y˙=bϕ˙cos(ϕ)v_y=\dot{y}=b \:\dot{ϕ} \; \cos(ϕ) .
◊ remarque :  ceci ne détermine pas la façon dont est parcourue la trajectoire car on ne connaît pas  ϕ(t)ϕ(t) .
• D’après l’énoncé, II a pour coordonnées :
(xA;yB)=(−𝓁cos(ϕ);𝓁sin(ϕ))(x_A \,;y_B )=\left(-𝓁 \;\cos(ϕ) \,; 𝓁 \;\sin(ϕ) \right)  ;
donc  OI=AB=𝓁OI=AB=𝓁  et  II  décrit un cercle de centre OO et de rayon 𝓁𝓁 .
• Le vecteur IM⟶\overset{⟶}{IM} a pour coordonnées :  (bcos(ϕ);(b−𝓁)sin(ϕ))\left(b \;\cos(ϕ) \,; (b-𝓁) \; \sin(ϕ) \right)  et l’orthogonalité au vecteur vitesse se déduit du produit scalaire :
v→∙IM⟶=b.[(𝓁−b)+(b−𝓁)]ϕ˙cos(ϕ)sin(ϕ)=0\overset{→}{v}∙\overset{⟶}{IM}=b.[(𝓁-b)+(b-𝓁)] \: \dot{ϕ} \; \cos(ϕ) \: \sin(ϕ)=0 .
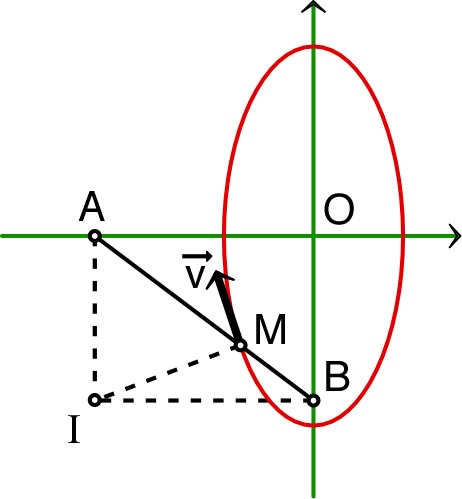Frenet_cor_Im/Frenet_cor_Im1.jpg
• D’après les coordonnées :
IM=b2cos2(ϕ)+(b−𝓁)2sin2(ϕ)IM=\sqrt{b^2 \; \cos^2(ϕ)+(b-𝓁)^2 \; \sin^2(ϕ)}   et   v=|ϕ˙|(𝓁−b)2sin2(ϕ)+b2cos2(ϕ)=|ϕ˙|IMv=|\dot{ϕ}| \: \sqrt{(𝓁-b)^2 \; \sin^2(ϕ)+b^2 \; \cos^2(ϕ)}=|\dot{ϕ}| \: IM .
◊ remarque : avec  ω→=ϕ˙u→z\overset{→}{ω}=\dot{ϕ} \;\overset{→}{u}_z  (vecteur rotation perpendiculaire au plan) on peut écrire :  v→=ω→×IM⟶\overset{→}{v}=\overset{→}{ω} × \overset{⟶}{IM}  ;  cela découle du fait que tout déplacement peut être décomposé en une rotation autour d’un axe instantané de rotation et une translation parallèle à cet axe ; or ici la translation est nulle puisque le mouvement reste dans le plan, or II est le centre instantané de rotation (intersection de l’axe orthogonal au plan avec celui ci) ; en effet : une rotation qui donne à AA un mouvement parallèle à OxOx a forcément son centre instantané sur la perpendiculaire en AA à OxOx (rayon perpendiculaire à la tangente) ; de même pour BB ,  d’où la position de II ; on retrouve alors que  v→\overset{→}{v}  est perpendiculaire au rayon (instantané) IMIM .