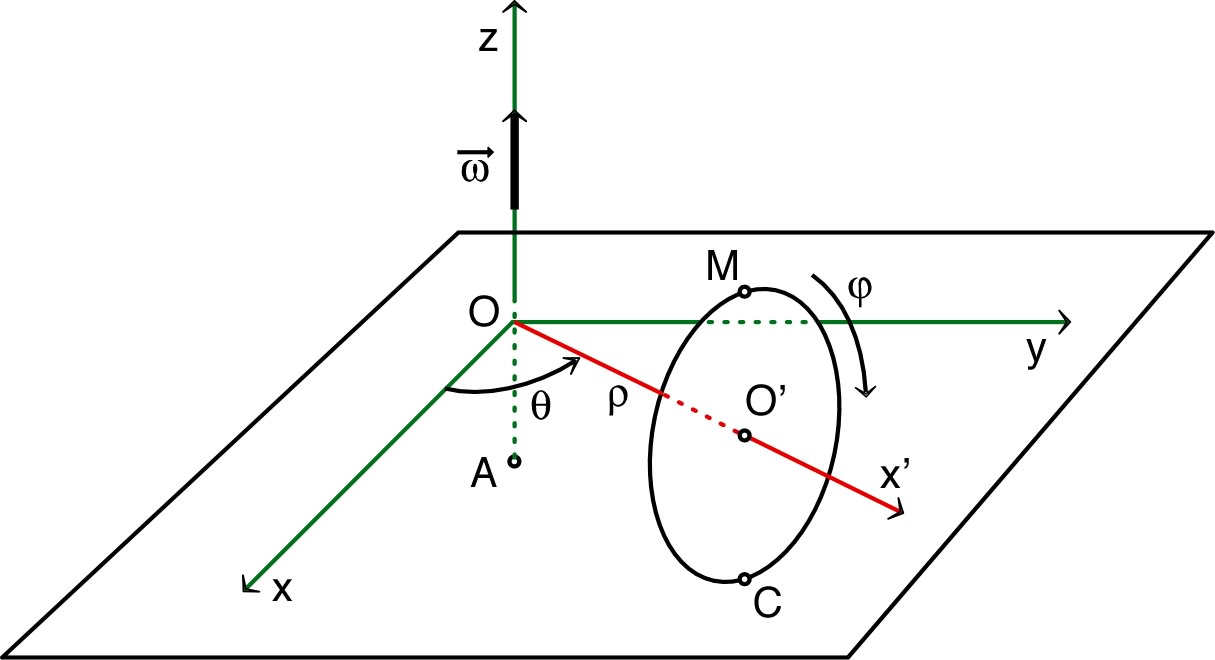
;
.
“vitesse d’entraînement” ;
“vitesse relative” (par rapport à ).
(translation de ) ;
(rotation autour de ).
;
.
accélération d’entraînement ;
accélération relative (par rapport à ) ;
accélération “complémentaire”.
(translation de ) ;
(rotation).
.

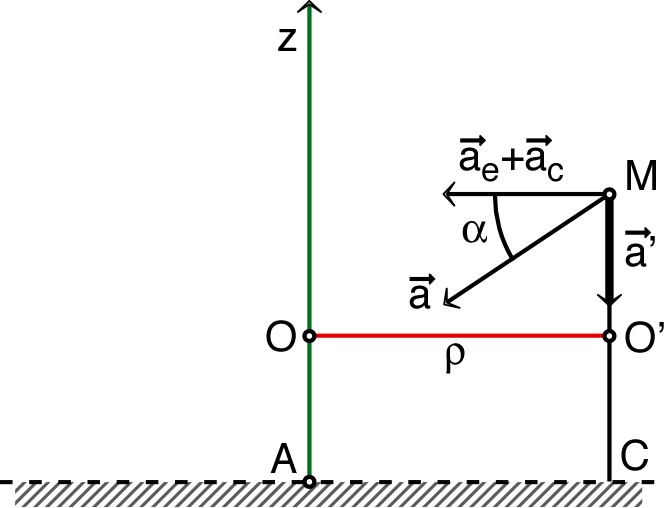
.