AC. III - COORDONNÉES  CYLINDRIQUES ET SPHÉRIQUES


Coordonnées cylindriques

Description générale

• Pour définir des coordonnées cylindriques, on choisit un “axe cylindrique”, par exemple (Oz)(Oz) , puis on repère le point HH projeté orthogonal de MM sur le plan passant par OO et orthogonal à (Oz)(Oz) . Dans ce plan, on repère HH par ses coordonnées polaires, ce qui repère MM par ses coordonnées (r,θ,z)(r \,, \,θ \,, \,z) .

• Les vecteurs sont alors exprimés selon la base (u→r,u→θ,u→z)\left(\overset{→}{u}_r \,,\,\overset{→}{u}_θ \,,\,\overset{→}{u}_z \right) dépendant du point MM :
u→r=u→r(θ)=cos(θ)u→x+sin(θ)u→y\overset{→}{u}_r=\overset{→}{u}_r (θ)=\cos(θ) \; \overset{→}{u}_x+\sin(θ) \; \overset{→}{u}_y  ;
u→θ=u→θ(θ)=−sin(θ)u→x+cos(θ)u→y\overset{→}{u}_θ=\overset{→}{u}_θ (θ)=-\sin(θ) \; \overset{→}{u}_x+\cos(θ) \; \overset{→}{u}_y .

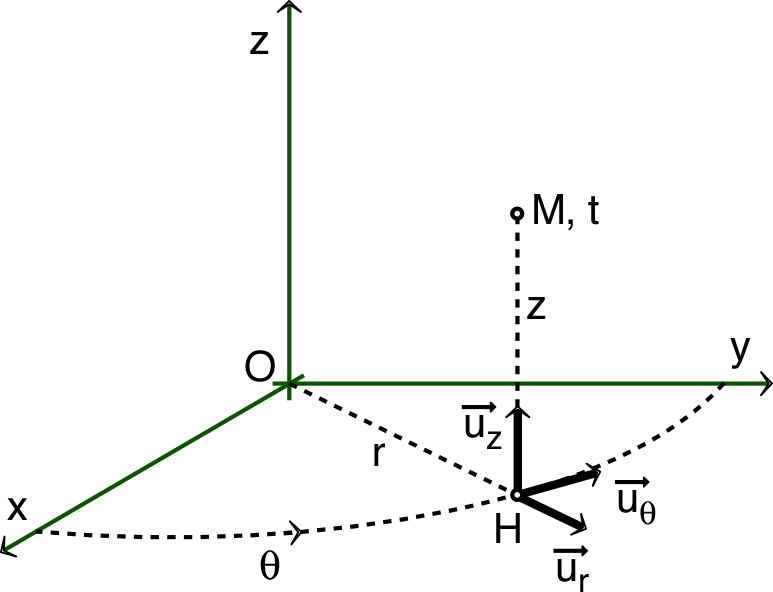
Ces vecteurs unitaires sont définis de façon “standard” : selon la direction et le sens des déplacements de MM résultant des augmentations respectives de rr , θθ  et  zz .

On constate alors que :
du→rdθ=u→θ\displaystyle \frac{d\overset{→}{u}_r}{dθ}=\overset{→}{u}_θ  ;  du→θdθ=−u→r\displaystyle \frac{d\overset{→}{u}_θ}{dθ}=-\overset{→}{u}_r .

◊ remarque : contrairement aux coordonnées sphériques, ici le vecteur u→r\overset{→}{u}_r est selon OH⟶\overset{⟶}{OH} .
coordonnees_Im/coordonnees_Im1.jpg

• Avec ces notations :
OM⟶=ru→r+zu→z\overset{⟶}{OM}=r \:\overset{→}{u}_r+z \:\overset{→}{u}_z  ;
v→=OM⟶˙=r˙u→r+rθ˙u→θ+z˙u→z\overset{→}{v}=\dot{\overset{⟶}{OM}}=\dot{r} \: \overset{→}{u}_r+r \:\dot{θ} \: \overset{→}{u}_θ+\dot{z} \: \overset{→}{u}_z  ;
a→=v→˙=(r̈−rθ˙2)u→r+(2r˙θ˙+rθ̈)u→θ+z̈u→z\overset{→}{a}=\dot{\overset{→}{v}}=\left(\ddot{r}-r \:\dot{θ}^2 \right) \: \overset{→}{u}_r+\left(2 \,\dot{r} \: \dot{θ}+r \:\ddot{θ} \right) \: \overset{→}{u}_θ+z ̈ \: \overset{→}{u}_z .

◊ remarque : on constate entre autres que (contrairement aux repères cartésiens) les coordonnées de OM⟶\overset{⟶}{OM} sont différentes des coordonnées de MM ; en particulier, OM⟶\overset{⟶}{OM} peut sembler ne dépendre que des deux coordonnées rr et zz , mais il dépend de θθ par la direction de u→r\overset{→}{u}_r (il faut trois coordonnées).

◊ remarque : il s’agit de v→\overset{→}{v} et a→\overset{→}{a} par rapport à  (O,u→x,u→y,u→z)\left(O\,,\,\overset{→}{u}_x \,,\,\overset{→}{u}_y \,,\,\overset{→}{u}_z \right) ,  réexprimés sur la base (u→r,u→θ,u→z)\left(\overset{→}{u}_r \,,\,\overset{→}{u}_θ \,,\,\overset{→}{u}_z \right)  (sinon il n’y aurait pas les termes de rotation en θ˙\dot{θ} et θ̈\ddot{θ} ).

Mouvement hélicoïdal

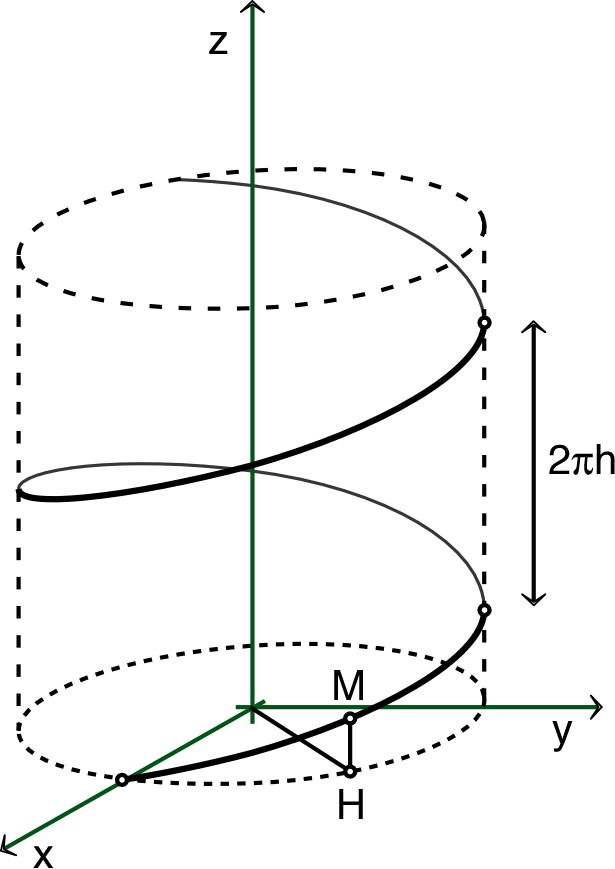
• On considère le mouvement hélicoïdal d’un point MM sur un cylindre de rayon rr :
OM⟶=ru→r+zu→z\overset{⟶}{OM}=r \:\overset{→}{u}_r+z \:\overset{→}{u}_z
avec  z(t)=hθ(t)z(t)=h \:θ(t)  et  h=Csteh=Cste  (le “pas” de l'hélice est  2πh2π \:h ).

D’après la symétrie, le plus simple est d’utiliser des coordonnées cylindriques.

• La vitesse est alors :
v→=rθ˙u→θ+hθ˙u→z\overset{→}{v}=r \:\dot{θ} \: \overset{→}{u}_θ+h \:\dot{θ} \: \overset{→}{u}_z  ;
v¯=ρθ˙\widebar{v}= ρ \:\dot{θ}   avec   ρ=r2+h2>rρ=\sqrt{r^2+h^2}>r .

D’une façon analogue :
a→=−rθ˙2u→r+rθ̈u→θ+hθ̈u→z\overset{→}{a}=-r \:\dot{θ}^2 \: \overset{→}{u}_r+r \:\ddot{θ} \: \overset{→}{u}_θ+h \:\ddot{θ} \: \overset{→}{u}_z .
coordonnees_Im/coordonnees_Im2.jpg

◊ remarque : la vitesse v→\overset{→}{v} fait un angle αα constant avec l’axe cylindrique (vecteur u→z\overset{→}{u}_z ) car :  cos(α)=v→v∙u→z=hρsgn(θ˙)\displaystyle \cos(α)=\frac{\overset{→}{v}}{v}∙\overset{→}{u}_z=\frac{h}{ρ} \: \mathrm{sgn}(\dot{θ} ) .

📖 exercice n° I.

Coordonnées sphériques

• Pour définir des coordonnées sphériques, on choisit un “axe des pôles”, par exemple (Oz)(Oz) , puis on repère un “plan méridien” défini par (Oz)(Oz) et le point MM . Dans ce plan, on y repère MM par ses coordonnées polaires (r,θ)(r, θ) .

Enfin, on choisit un plan contenant (Oz)(Oz) comme référence des rotations autour de (Oz)(Oz) ; ceci permet de repérer le plan méridien précédent par un angle φφ , ce qui repère MM par ses coordonnées  (r,θ,φ)(r, θ,φ) .

• Les vecteurs sont alors exprimés selon la base (u→r,u→θ,u→φ)\left(\overset{→}{u}_r \,,\,\overset{→}{u}_θ \,,\,\overset{→}{u}_φ \right) dépendant du point MM . Ces vecteurs unitaires sont définis de façon standard :
u→r=u→r(θ,φ)=sin(θ).[cos(φ)u→x+sin(φ)u→y]+cos(θ)u→z\overset{→}{u}_r=\overset{→}{u}_r (θ,φ)=\sin(θ).\left[\cos(φ) \: \overset{→}{u}_x+\sin(φ) \: \overset{→}{u}_y \right]+\cos(θ) \: \overset{→}{u}_z  ;
u→θ=u→θ(θ,φ)=cos(θ).[cos(φ)u→x+sin(φ)u→y]−sin(θ)u→z\overset{→}{u}_θ=\overset{→}{u}_θ (θ,φ)=\cos(θ).\left[\cos(φ) \: \overset{→}{u}_x+\sin(φ) \: \overset{→}{u}_y \right]-\sin(θ) \: \overset{→}{u}_z  ;
u→φ=u→φ(φ)=−sin(φ)u→x+cos(φ)u→y\overset{→}{u}_φ=\overset{→}{u}_φ (φ)=-\sin(φ) \: \overset{→}{u}_x+\cos(φ) \: \overset{→}{u}_y .

◊ remarque : ici rr et θθ (et de même u→r\overset{→}{u}_r et u→θ\overset{→}{u}_θ ) n’ont pas la même signification qu'en coordonnées cylindriques ; en particulier θθ est limité à [0,π][0 \,,π] et u→r\overset{→}{u}_r est parallèle à OM⟶\overset{⟶}{OM} .

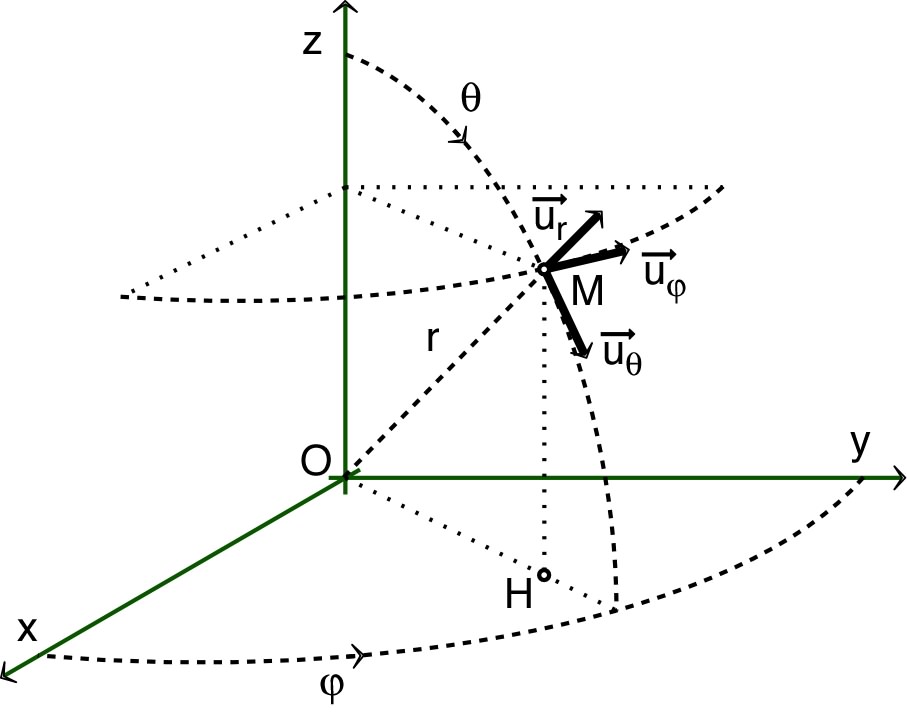
coordonnees_Im/coordonnees_Im3.jpg

• On constate alors que :
∂u→r∂θ=u→θ\displaystyle \frac{∂\overset{→}{u}_r}{∂θ}=\overset{→}{u}_θ   et    ∂u→θ∂θ=−u→r\displaystyle \frac{∂\overset{→}{u}_θ}{∂θ}=-\overset{→}{u}_r  (semblable aux coordonnées polaires) ;
∂u→r∂φ=sin(θ)u→φ\displaystyle \frac{∂\overset{→}{u}_r}{∂φ}=\sin(θ) \: \overset{→}{u}_φ   et   ∂u→θ∂φ=cos(θ)u→φ\displaystyle \frac{∂\overset{→}{u}_θ}{∂φ}=\cos(θ) \: \overset{→}{u}_φ
(seules les projections sur (Oxy)(Oxy) dépendent de φφ ) ;
∂u→φ∂φ=u→z×u→φ=−cos(φ)u→x−sin(φ)u→y=−sin(θ)u→r−cos(θ)u→θ\displaystyle \frac{∂\overset{→}{u}_φ}{∂φ}=\overset{→}{u}_z × \overset{→}{u}_φ=-\cos(φ) \: \overset{→}{u}_x-\sin(φ) \: \overset{→}{u}_y=-\sin(θ) \: \overset{→}{u}_r-\cos(θ) \: \overset{→}{u}_θ .

☞ remarque : de façon générale, la dérivée d'un vecteur unitaire par rapport à un angle de rotation est le produit vectoriel du vecteur unitaire de l'axe de rotation par le vecteur unitaire qu'on dérive.

• On obtient ainsi :
OM⟶=ru→r\overset{⟶}{OM}=r \:\overset{→}{u}_r   et   v→=r˙u→r+ru→˙r=r˙u→r+rθ˙u→θ+rsin(θ)φ˙u→φ\overset{→}{v}=\dot{r} \: \overset{→}{u}_r+r \:\dot{\overset{→}{u}}_r=\dot{r} \: \overset{→}{u}_r+r \:\dot{θ} \: \overset{→}{u}_θ+r \: \sin(θ) \: \dot{φ} \: \overset{→}{u}_φ .

◊ remarque : on constate ici encore que les coordonnées de OM⟶\overset{⟶}{OM} sont différentes des coordonnées de MM ; en particulier, OM⟶\overset{⟶}{OM} peut sembler ne dépendre que de la coordonnée rr , mais il dépend de θθ et φφ par l’intermédiaire de la direction de u→r\overset{→}{u}_r (il faut trois coordonnées).

◊ remarque : l’expression générale de l’accélération est ici plus compliquée, or elle est en pratique moins utilisée à ce niveau.

📖 exercices n° II et III.