COORDONNÉES  CYLINDRIQUES ET SPHÉRIQUES - corrigé des exercices


Coordonnées cylindriques et frottement solide

1.a.     • En coordonnées cylindriques :  u→r=cos(θ)u→x+sin(θ)u→y\overset{→}{u}_r=\cos(θ) \: \overset{→}{u}_x+\sin(θ) \: \overset{→}{u}_y  et  u→θ=−sin(θ)u→x+cos(θ)u→y\overset{→}{u}_θ=-\sin(θ) \: \overset{→}{u}_x+\cos(θ) \: \overset{→}{u}_y , par conséquent :  du→rdθ=u→θ\displaystyle \frac{d\overset{→}{u}_r}{dθ}=\overset{→}{u}_θ   et   du→θdθ=−u→r\displaystyle\frac{ d\overset{→}{u}_θ}{dθ}=-\overset{→}{u}_r .
• On en déduit pour le cas général :
OM⟶=ru→r+zu→z\overset{⟶}{OM}=r \:\overset{→}{u}_r+z \:\overset{→}{u}_z  ;   v→=OM⟶˙=r˙u→r+ru→˙r+z˙u→z=r˙u→r+rθ˙u→θ+z˙u→z\overset{→}{v}=\dot{\overset{⟶}{OM}}=\dot{r} \: \overset{→}{u}_r+r \:\dot{\overset{→}{u}}_r+\dot{z} \: \overset{→}{u}_z=\dot{r} \: \overset{→}{u}_r+r \:\dot{θ} \: \overset{→}{u}_θ+\dot{z} \: \overset{→}{u}_z  ;
a→=v→˙=OM⟶̈=(r̈−rθ˙2)u→r+(2r˙θ˙+rθ̈)u→θ+z̈u→z\overset{→}{a}=\dot{\overset{→}{v}}=\ddot{\overset{⟶}{OM}}=\left(\ddot{r}-r \:\dot{θ}^2 \right) \: \overset{→}{u}_r+\left(2 \,\dot{r} \: \dot{θ}+r \:\ddot{θ} \right) \: \overset{→}{u}_θ+\ddot{z} \: \overset{→}{u}_z .


1.b. • Dans le cas étudié, rr est constant et  z=hθz = h\:θ  donc :
v→=rθ˙u→θ+z˙u→z=z˙.(rhu→θ+u→z)\displaystyle \overset{→}{v}=r \:\dot{θ} \: \overset{→}{u}_θ+\dot{z} \: \overset{→}{u}_z=\dot{z} .\left(\frac{r}{h} \, \overset{→}{u}_θ+\overset{→}{u}_z \right)  ;
a→=−rθ˙2u→r+rθ̈u→θ+z̈u→z=−rh2z˙2u→r+z̈.(rhu→θ+u→z)\displaystyle \overset{→}{a}=-r \:\dot{θ}^2 \: \overset{→}{u}_r+r \:\ddot{θ} \: \overset{→}{u}_θ+\ddot{z} \: \overset{→}{u}_z=-\frac{r}{h^2} \, \dot{z}^2 \: \overset{→}{u}_r+\ddot{z} .\left(\frac{r}{h} \, \overset{→}{u}_θ+ \overset{→}{u}_z \right).


2.a.     • Le principe fondamental de la dynamique correspond à :  ma→=P→+R→+f→m \:\overset{→}{a}=\overset{→}{P}+\overset{→}{R}+\overset{→}{f}  avec  P→=mg→\overset{→}{P}=m \:\overset{→}{g} .  On en déduit les trois équations différentielles :
−mrh2z˙2=Rr+fr\displaystyle -m \, \frac{r}{h^2} \, \dot{z}^2=R_r+f_r  ;   mrhz̈=Rθ+fθ\displaystyle m \, \frac{r}{h} \, \ddot{z}=R_θ+f_θ  ;   mz̈=−mg+Rz+fzm \:\ddot{z} = - m \:g+R_z+f_z .


2.b. • La réaction normale est perpendiculaire à la vitesse :  R→∙v→=rRθ+hRz=0\overset{→}{R}∙\overset{→}{v}=r \:R_θ+h \:R_z=0 .
• Le frottement est parallèle à la vitesse, donc en particulier  fr=0f_r=0  ;  mais on peut écrire plus généralement :  f→×v→=(z˙fθ−rθ˙fz)u→r=0→\overset{→}{f} × \overset{→}{v}=(\dot{z} \: f_θ-r \:\dot{θ} \: f_z ) \: \overset{→}{u}_r=\overset{→}{0}  ;  on en déduit :  hfθ−rfz=0h \:f_θ-r \:f_z=0 .


2.c. • En simplifiant les équations différentielles, on peut écrire :
−mrh2z˙2=Rr\displaystyle -m \, \frac{r}{h^2} \: \dot{z}^2=R_r  ;   mz̈=hrRθ+fz\displaystyle m \:\ddot{z}=\frac{h}{r} \, R_θ+f_z  ;   mz̈=−mg−rhRθ+fz\displaystyle m \:\ddot{z} = - m \:g- \frac{r}{h} \, R_θ+f_z .
• La différence des deux dernières équations donne :  Rθ=−mgrhr2+h2\displaystyle R_θ=-m \:g \, \frac{r \:h}{r^2+h^2} .


2.d. • La condition de glissement  f=λRf=λ \:R  donne :  fθ2+fz2=λ2.(Rr2+Rθ2+Rz2)f_θ^{\:2}+f_z^{\:2}=λ^2.\left(R_r^{\:2}+R_θ^{\:2}+R_z^{\:2} \right) .
• En utilisant  fθ=rhfz\displaystyle f_θ=\frac{r}{h} \, f_z  et  Rz=−rhRθ\displaystyle R_z=-\frac{r}{h} \, R_θ ,  on obtient (après simplification et compte tenu de  fz>0f_z>0  pour la descente) :  fz=λh2Rr2r2+h2+Rθ2\displaystyle f_z=λ \;\sqrt{\frac{h^2 \: R_r^{\:2}}{r^2+h^2}+R_θ^{\:2}} .


2.e. • En éliminant fzf_z , puis RrR_r et RθR_θ , dans les équations précédentes, on obtient une équation différentielle sur la variable zz uniquement (qu'on peut envisager d'intégrer numériquement) :
z̈=−gh2r2+h2+λrhr2+h2r2+h2h4z˙4+g2\displaystyle \ddot{z}=-\frac{g \:h^2}{r^2+h^2}+\frac{λ \:r \:h}{r^2+h^2} \, \sqrt{\frac{r^2+h^2}{h^4} \: \dot{z}^4+g^2} .


3.a.     • Pour chaque tour, la distance parcourue horizontalement est  2πr2π \:r  et la distance parcourue verticalement est  2πh2π \:h  (pas de l'hélice) ; la tangente de l'angle de la pente est donc constante :  tan(α)=hr\displaystyle \tan(α)=\frac{h}{r} .
◊ remarque : avec   z˙=vz=v→∙u→z=v¯sin(α)\dot{z}=v_z=\overset{→}{v}∙\overset{→}{u}_z=\widebar{v} \; \sin(α)   et   v¯=z˙r2h2+1\displaystyle \widebar{v}=\dot{z} \; \sqrt{\frac{r^2}{h^2} +1}   on obtient :  sin(α)=hr2+h2=Cste\displaystyle \sin(α)=\frac{h}{\sqrt{r^2+h^2}}=Cste .


3.b. • En considérant que le cylindre est un “plan enroulé”, on peut le “dérouler” en passant à la limite  r→∞ r→∞  à condition de conserver constant :  tan(α)=hr\displaystyle \tan(α)=\frac{h}{r}  (donc aussi le sinus et le cosinus), ce qui implique en même temps  h→∞h→∞ .
• L'équation différentielle peut ainsi s'écrire :  z̈=−gsin2(α)+λsin(α)cos(α)z˙4h2sin2(α)+g2\displaystyle \ddot{z}=-g \; \sin^2(α)+λ \; \sin(α) \: \cos(α) \; \sqrt{\frac{\dot{z}^4}{h^2 \; \sin^2(α)}+g^2} .  Sa limite correspond à :  z̈=−gsin2(α)+λgsin(α)cos(α)\ddot{z}=-g \; \sin^2(α)+λ \:g \; \sin(α) \: \cos(α) .


4.a.     • Sur le fil hélicoïdal, la rotation nécessite une accélération radiale en permanence orientée vers l'axe ; celle-ci est associée à une composante RrR_r supplémentaire de la réaction normale.
• Les relations entre les autres composantes de R→\overset{→}{R} et f→\overset{→}{f} restant inchangées, du fait de leurs orientations par rapport à v→\overset{→}{v} , cela impose (dans des conditions de mouvement par ailleurs analogues) à une norme plus grande de la réaction normale dans le cas de l'hélice. Ceci impose alors un frottement plus grand et une accélération vers le bas plus faible (accélération algébrique plus grande car moins négative).


4.b. • On retrouve effectivement une accélération algébrique plus grande puisque :  z˙4h2sin2(α)+g2>g\displaystyle \sqrt{\frac{\dot{z}^4}{h^2 \; \sin^2(α)}+g^2}\:>g .


Coordonnées sphériques ; loxodromie

          
 • Avec les coordonnées sphériques :  OM⟶=Ru→r\overset{⟶}{OM}=R \:\overset{→}{u}_r  donc  v→=OM⟶˙=Ru→˙r=Rθ˙u→θ+Rsin(θ)φ˙u→φ\overset{→}{v}=\dot{\overset{⟶}{OM}}=R \:\dot{\overset{→}{u}}_r=R \:\dot{θ}\: \overset{→}{u}_θ+R \; \sin(θ) \: \dot{φ} \: \overset{→}{u}_φ  où u→φ\overset{→}{u}_φ a la direction des “parallèles” et le sens des φφ croissants (de l’ouest vers l’est) ; où u→θ\overset{→}{u}_θ a la direction des “méridiens” et le sens des θθ croissants (du nord vers le sud).

• Pour que la trajectoire fasse toujours le même angle α0α_0 avec le parallèle terrestre, il faut donc que :  tan(α0)=−Rθ˙Rsin(θ)φ˙\displaystyle \tan(α_0)=-\frac{R \:\dot{θ}}{R \;\sin(θ) \: \dot{φ}}   soit constant. On en déduit :  θ˙sin(θ)=x˙x=−tan(α0)φ˙\displaystyle \frac{\dot{θ}}{\sin(θ)}=\frac{\dot{x}}{x}=-\tan(α_0) \: \dot{φ}  dont l’intégration donne :  ln(|x|)=−tan(α0)φ+Cste\ln(\,|x|\,)=-\tan(α_0) \: φ+Cste   où la constante d’intégration dépend de la position initiale.
• En notant θ0θ_0 et φ0φ_0 les coordonnées initiales, on peut finalement écrire la relation sous la forme :
tan(θ2)=tan(θ02)exp[−tan(α0).(φ−φ0)]\displaystyle \tan\left(\frac{θ}{2}\right)=\tan\left(\frac{θ_0}{2}\right) \; \exp\left[-\tan(α_0).(φ-φ_0 )\right] .


Coordonnées sphériques ; base locale et transport parallèle

1.a.     • Puisque la porte ouvre vers le sud et que la fenêtre est sur le côté droit, on risquerait d'être tenté de penser qu'elle est orientée vers l'est. Mais en partant du pôle nord (intersection des méridiens) tout éloignement rapproche du sud : la fenêtre est orientée au sud (tout ce qui s'écarte du pôle nord est orienté “au sud”).
• Par contre, pour un observateur en face de la porte (donc décalé vers le sud), la zone en face de la fenêtre est par rapport à lui vers l'est. Ceci montre que l'utilisation d'un repérage local peut causer des ambiguïtés si on ne précise pas suffisamment le système étudié.


1.b. • Pour s'écarter du pôle, l'avion doit augmenter l'angle θθ ; juste après avoir quitté le pôle, il part donc dans la direction du vecteur u→θ\overset{→}{u}_θ local (quel que soit l'angle φφ ). En se déplaçant “droit devant”, il se déplace le plus droit possible en suivant la surface courbe de la Terre ; par symétrie ce mouvement est dans un plan passant par le centre de la Terre, le long d'un “grand cercle” nommé “géodésique”. Ceci revient dans ce cas à continuer son déplacement selon le vecteur u→θ\overset{→}{u}_θ local, ce qui ne fait varier que la coordonnée θθ en suivant un méridien (qui est un géodésique).


1.c. • Dans une durée  ∆t=1h∆t=1 \:\mathrm{h}  l'avion a parcouru une distance  ∆𝓁=v∆t=5000km∆𝓁=v \:∆t=5000 \:\mathrm{km}  correspondant à la moitié de la distance qui sépare le pôle de l'équateur ; il se trouve donc à une colatitude  θ=π4θ=\frac{π}{4}  et à la longitude  φ=0φ=0  (constante) du méridien qu'il a suivi.


2.a.
• En tournant d'un quart de tour, l'avion se déplace initialement dans la direction du vecteur u→φ\overset{→}{u}_φ local. En se déplaçant “droit devant”, il se déplace le plus droit possible en suivant la surface courbe de la Terre, donc selon un grand cercle géodésique. Or, les parallèles terrestres sont centrés en des points différents sur l'axe nord-sud ; seul l'équateur est un géodésique.
• Le géodésique passant par le point de redépart est donc un géodésique incliné d'un angle π4\frac{π}{4} par rapport à l'équateur. Ce géodésique recoupe l'équateur en deux points symétriques A′A' et A″A'' décalés d'un quart de tour par rapport au point de redépart  (donc pour  φ=±π2φ=±\frac{π}{2} ).
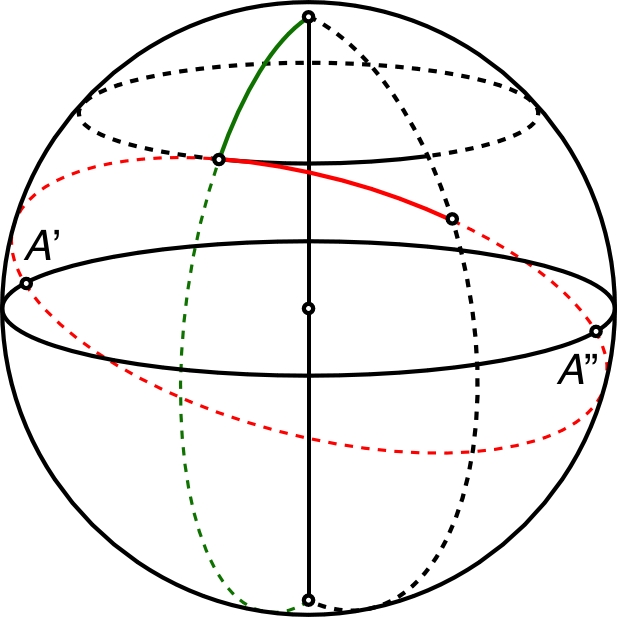
coordonnees_cor_Im/coordonnees_cor_Im1.jpg


2.b. • L'avion a parcouru une distance  ∆𝓁=v∆t=5000km∆𝓁=v \:∆t=5000 \:\mathrm{km}  correspondant à la moitié de la distance qui sépare le redépart de l'équateur (jusqu'en A″A'' le long du géodésique parcouru). On peut retrouver ce point en considérant un point placé sur l'équateur à  φ=π4φ=\frac{π}{4} ,  puis en lui faisant subir une rotation de π4\frac{π}{4} selon l'axe A′A″A'A'' (comme si le géodésique initial était un équateur et A″A'' un pôle).
• L'axe A′A″A'A'' étant l'axe (Oy)(Oy) cartésien correspondant, on peut par exemple considérer les coordonnées cartésiennes du point sur l'équateur :  OM⟶=ru→r\overset{⟶}{OM}=r \:\overset{→}{u}_r  ;  x=r2\displaystyle x=\frac{r}{\sqrt{2}}  ;  y=r2\displaystyle y=\frac{r}{\sqrt{2}}  ;  z=0z=0 .
• L'application de la rotation de π4\frac{π}{4} donne :
x1=cos(π4)x−sin(π4)z=r2\displaystyle x_1=\cos\left(\frac{π}{4}\right) \; x-\sin\left(\frac{π}{4}\right) \; z=\frac{r}{2}  ;   y1=y=r2\displaystyle y_1=y=\frac{r}{\sqrt{2}}  ;   z1=sin(π4)x+cos(π4)z=r2\displaystyle z_1=\sin\left(\frac{π}{4}\right) \; x+\cos\left(\frac{π}{4}\right) \; z=\frac{r}{2} .
• Les angles θθ et φφ cherchés correspondent donc à :
x1=rsin(θ)cos(φ)=r2\displaystyle x_1=r \; \sin(θ) \: \cos(φ)=\frac{r}{2}  ;   y1=rsin(θ)sin⁡(φ)=r2\displaystyle y_1=r \; \sin(θ) \: \sin⁡(φ)=\frac{r}{\sqrt{2}}  ;   z1=rcos(θ)=r2\displaystyle z_1=r \; \cos(θ)=\frac{r}{2} .
• On en déduit :  θ1=arccos(12)=π3=60°θ_1=\arccos\left(\frac{1}{2}\right)=\frac{π}{3}=60\,°  ;   φ1=arctan(2)=arccos(13)≈π3,29≈54,7°φ_1=\arctan\left(\sqrt{2}\,\right)=\arccos\left(\frac{1}{\sqrt{3}}\right)≈\frac{π}{3\text{,}29}≈54\text{,}7\,° .
◊ remarque : on obtient  θ1>π4θ_1>\frac{π}{4}  car plus on se déplace sur le géodésique, plus on se rapproche de l'équateur (rejoint en A″A'' ) ; on obtient  φ1>π4φ_1>\frac{π}{4}  car un arc de même longueur correspond qualitativement (puisque le déplacement ne s'effectue pas selon un parallèle terrestre) à une variation de longitude d'autant plus grande qu'on est proche du pôle.


3.a.     • Au lieu de terminer le trajet selon les deux côtés du “pseudo-carré” précédemment commencé, on peut imaginer que le pôle était le milieu d'un trajet analogue dont on considère alors la première moitié. Le second côté d'un tel trajet est un quart du méridien correspondant à  φ=π2φ=\frac{π}{2}  et le départ est symétrique de l'arrivée (point (1)(1) précédemment calculé) par rapport à  φ=π4φ=\frac{π}{4} .
• La distance infinitésimale associée à un déplacement élémentaire  OM⟶=rdθu→θ+rsin(θ)dφu→φ\overset{⟶}{OM}=r \:dθ \:\overset{→}{u}_θ+r \; \sin(θ) \:dφ\: \overset{→}{u}_φ  peut s'écrire :  d𝓁=r(dθdφ)2+sin2(θ)dφ\displaystyle d𝓁=r \;\sqrt{\left(\frac{dθ}{dφ}\right)^2+\sin^2(θ)} \;\: dφ ,  mais cela nécessite d'établir la relation  θ=θ(φ)θ=θ(φ)  décrivant le grand cercle reliant le point (1)(1) à son symétrique.
• Si l'arc de cercle n'est pas trop grand, on peut supposer que le terme en  dθdφ\displaystyle \frac{dθ}{dφ}  est négligeable (il intervient dans une correction du second ordre) et proposer l'approximation correspondant à l'arc de parallèle :  ∆𝓁≈rsin(θ1)∆φ=2rsin(θ1)(φ1−π4)≈1870km∆𝓁≈r \; \sin(θ_1 ) \: ∆φ=2 \,r \; \sin(θ_1 ) \: \left(φ_1-\frac{π}{4}\right)≈1870 \:\mathrm{km}  ;  ceci est nettement inférieur aux distances considérées, de l'ordre de 50005000 à 10000km10000 \:\mathrm{km} ,  mais ce n'est pas vraiment négligeable.
• Pour tester simplement l'ordre de grandeur, on peut alors chercher la distance (en ligne droite) entre le point (1)(1) et son symétrique (2′)(2') :
x2′=y1x'_2=y_1  ;  y2′=x1y'_2=x_1  ;  z2′=z1z'_2=z_1  ;
D=(x2′−x1)2+(y2′−y1)2+(z2′−z1)2=r.(1−12)≈1865kmD=\sqrt{(x'_2-x_1 )^2+(y'_2-y_1 )^2+(z'_2-z_1 )^2}=r.\left(1-\frac{1}{\sqrt{2}}\right)≈1865 \:\mathrm{km}  ;
ce résultat très peu différent confirme que la courbure n'intervient qu'au second ordre.
• On peut enfin calculer la longueur de l'arc de grand cercle sous-tendu par une telle corde :
∆𝓁≈2rarcsin(D2r)≈1870km\displaystyle ∆𝓁≈2 \,r \; \arcsin\left(\frac{D}{2 \,r}\right)≈1870 \:\mathrm{km}  ;  ainsi l'arc de parallèle était une très bonne estimation.


3.b.
• D'après la symétrie précédente, avec un point (1)(1) tel que  φ1=54,7°>45°φ_1=54\text{,}7 \,°>45 \,° ,  on peut conclure que l'autre moitié du trajet est telle que le quatrième côté recoupe le premier côté : en prenant le pôle au milieu du trajet, on obtient l'autre extrémité à  φ2′=π2−φ1≈35,3°<45°φ'_2=\frac{π}{2}-φ_1≈35\text{,}3 \,°<45 \,°  donc “avant” l'axe de symétrie de l'ensemble.
• En partant du pôle, on peut donc conclure que la seconde moitié du trajet aboutit du côté opposé à la fenêtre de la base : à gauche de la porte ; un peu à l'ouest pour un observateur situé un peu au sud.
• La direction du point d'arrivée n'étant pas très éloignée de la perpendiculaire au méridien selon φ1φ_1 (il faudrait considérer la perpendiculaire au grand cercle passant par le point (1)(1) et par le point d'intersection des premier et quatrième côtés), l'ordre de grandeur est donc  φ2≈φ1−π2≈−35°φ_2≈φ_1-\frac{π}{2}≈-35 \,°  (décalage à gauche de la porte).
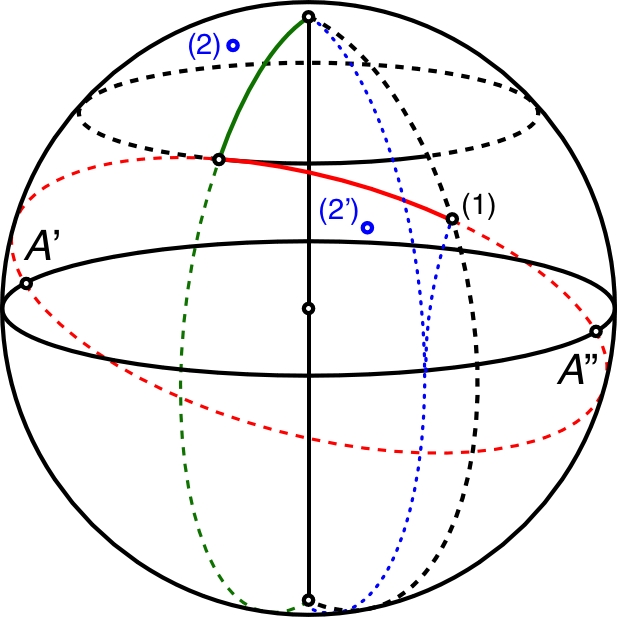
coordonnees_cor_Im/coordonnees_cor_Im2.jpg

• Si on souhaite approfondir, on peut (par exemple) considérer que le trajet réel  [(N)→(1)→(2)][(N)→(1)→(2)]  est symétrique du trajet  [(2′)→(N)→(1)][(2')→(N)→(1)]  par rapport au plan médiateur du segment [(N)(1)][(N)(1)] .  Sachant que (N)(N) est sur (Oz)(Oz) à la distance rr , en écrivant l'égalité des distances par rapport aux extrémités du segment, on obtient l'équation du plan :  x+2y−z=0x+\sqrt{2} \; y-z=0 .  Cela caractérise le fait que les points de ce plan (passant par OO )  sont tels que  OM⟶\overset{⟶}{OM}  est perpendiculaire au vecteur  (a=1;b=2;c=−1)\left(a=1\,;\,b=\sqrt{2}\,;\,c=-1\right) .  En se ramenant à un vecteur unitaire avec  λ=rax′+by′+cz′a2+b2+c2\displaystyle λ=r \: \frac{a \:x'+b \:y'+c \:z'}{a^2+b^2+c^2}  on peut retrouver les coordonnées de (2)(2) d'après celles de (2′)(2') selon :  x=x′−2λax=x'-2 \,λ \:a  ;  y=y′−2λby=y'-2 \,λ \:b  ;  z=z′−2λcz=z'-2 \,λ \:c .
• On obtient ainsi :
x2=r4\displaystyle x_2=\frac{r}{4}  ;  y2=(2−2)r4\displaystyle y_2=\left(\sqrt{2}-2\right) \, \frac{r}{4}  ;  z2=(22+1)r4\displaystyle z_2=\left(2 \,\sqrt{2}+1\right) \, \frac{r}{4}  ;
φ2=arctan(y2x2)≈−π5,93≈−30,4°\displaystyle φ_2=\arctan\left(\frac{y_2}{x_2} \right)≈-\frac{π}{5\text{,}93}≈-30\text{,}4 \,°  ; l'approximation ci-dessus était grossière mais acceptable.