COORDONNÉES CYLINDRIQUES ET SPHÉRIQUES

COORDONNÉES CYLINDRIQUES ET SPHÉRIQUES - exercices

Coordonnées cylindriques et frottement solide

• On considère un fil fin rigide, enroulé en hélice d'équation :

z=h \:θ

(où

h

est une constante), sur un cylindre d’axe

Oz

, de rayon

r

et de hauteur totale

L

.
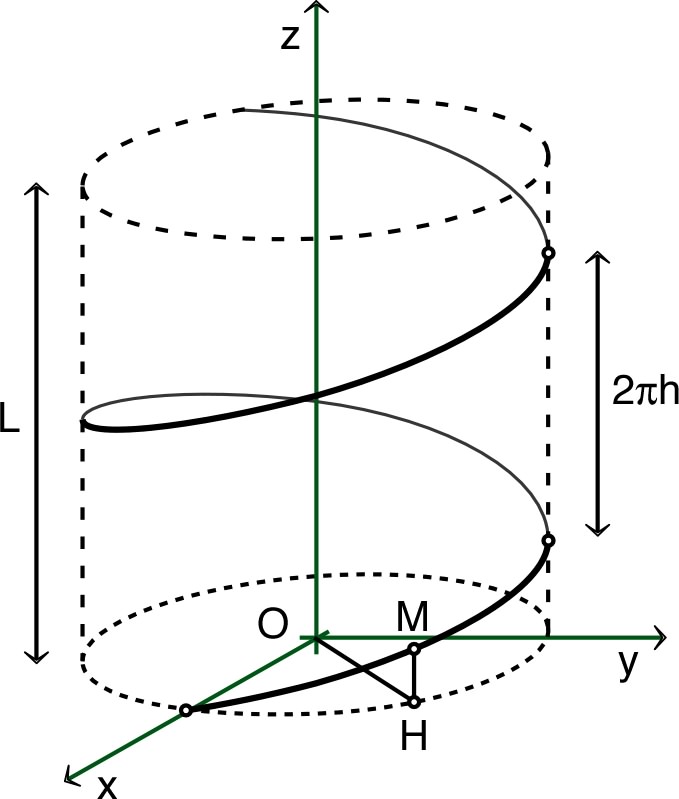
• Un petit anneau, considéré comme un point matériel

M

de masse

m

, peut glisser le long du fil avec un frottement solide de coefficient

λ

. À l’instant initial, cet anneau est lâché en haut du fil avec une vitesse nulle.
• On note

\overset{→}{R}=R_r \: \overset{→}{u}_r+R_θ \: \overset{→}{u}_θ+R_z \: \overset{→}{u}_z

la réaction normale et

\overset{→}{f}=f_r \: \overset{→}{u}_r+f_θ \: \overset{→}{u}_θ+f_z \: \overset{→}{u}_z

le frottement.

1. a) Établir les expressions générales de la vitesse et de l’accélération en coordonnées cylindriques (indépendamment de la forme du fil envisagé ici).
b) Simplifier ces expressions dans le cas particulier étudié ici.

coordonnees_ex_Im/coordonnees_ex_Im1.jpg

2. a) À l’aide du principe fondamental de la dynamique, établir trois équations différentielles décrivant le mouvement de l’anneau

M

.
b) Montrer que les angles respectifs de

\overset{→}{R}

\overset{→}{f}

par rapport à la vitesse

\overset{→}{v}

imposent respectivement :

$r \:R_θ+h \:R_z=0$ ; $f_r=0$ ; $h \:f_θ-r \:f_z=0$ .

c) Montrer que ces conditions imposent :

\displaystyle R_θ=-m \:g \: \frac{r \:h}{r^2+h^2}

.
d) Justifier que la condition de glissement impose :

\displaystyle f_z=λ \;\sqrt{\frac{h^2 \: R_r^{\:2}}{r^2+h^2}+R_θ^{\:2}}

.
e) En déduire que la variable

z

vérifie l'équation différentielle :

$\displaystyle \ddot{z}=-\frac{g \:h^2}{r^2+h^2}+\frac{λ \:r \:h}{r^2+h^2} \; \sqrt{\frac{r^2+h^2}{h^4} \; \dot{z}^4+g^2}$ .

3. a) Justifier (en montrant par exemple que :

\displaystyle \tan(α)=\frac{h}{r}

) que l'angle

α

du fil par rapport à l'horizontale est constant.
        b) Compte tenu de cette propriété, on désire comparer le mouvement précédent à celui qui serait analogue sur un plan incliné de même pente. Montrer qu'on peut obtenir l'équation différentielle décrivant ce cas par un judicieux passage à la limite dans l'équation différentielle précédente.

4.     a) Sans calcul (et en particulier sans intégrer les équations différentielles), justifier que la descente est plus lente sur le fil enroulé en hélice que sur le plan incliné.
        b) Vérifier que cela est cohérent avec les équations différentielles précédentes.

Coordonnées sphériques ; loxodromie

• Un bateau se déplace de façon telle que la tangente à sa trajectoire fasse toujours le même angle

α_0

avec le parallèle terrestre. Établir la relation entre

φ

θ

(longitude et colatitude) caractérisant cette trajectoire (appelée loxodromie).
◊ remarque : on peut utiliser la variable

\displaystyle x=\tan\left(\frac{θ}{2}\right)

Coordonnées sphériques ; base locale et transport parallèle

• Une expédition scientifique dispose d'une base au pôle nord, constituée d'un local carré et d'une piste d'atterrissage. Le local dispose d'une porte sur l'un des murs et d'une fenêtre sur le mur perpendiculaire, du côté droit de la porte (ces commentaires peuvent être utiles pour le repérage visuel de l'orientation). La piste est alignée face à la porte d'entrée, selon le méridien

φ=0

.

1. a) La base étant juste au pôle nord, on peut dire que la porte d'entrée s'ouvre “vers le sud” ; que peut-on dire de l'orientation de la fenêtre ?
b) Partant du pôle nord, un avion décolle de la base puis se déplace “droit devant” à la vitesse constante

v=500 \:\mathrm{km.h^{-1}}

. Justifier que la tangente à sa trajectoire reste ainsi parallèle à un méridien terrestre.
c) Après dix heures de vol, l'avion s'arrête dans un aérodrome (ou sur un porte-avions) pour faire le plein des réservoirs. Calculer ses coordonnées (colatitude

θ

et longitude

φ

).

2. a) L'avion repart à angle droit, vers la gauche de sa direction d'arrivée, puis se déplace à nouveau “droit devant” à la vitesse

v

. Justifier que la tangente à sa trajectoire ne reste ainsi pas parallèle à un parallèle terrestre.
b) Après dix heures de vol, l'avion s'arrête à nouveau dans un aérodrome (ou sur un porte-avions) pour faire le plein des réservoirs. Calculer ses coordonnées (colatitude

θ

et longitude

φ

).

3. • L'avion repart encore à angle droit, vers la gauche de sa direction d'arrivée, puis se déplace à nouveau “droit devant” à la vitesse

v

. Après dix heures de vol, l'avion effectue un nouvel arrêt, suivi d'un nouveau départ à angle droit, vers la gauche ; il se déplace encore “droit devant” à la vitesse

v

, pendant dix heures, puis s'arrête enfin.
a) Justifier que l'avion n'est ainsi pas retourné à la base ; montrer qu'une symétrie judicieuse permet de calculer simplement la distance qui le sépare de cette dernière.
b) Sans effectuer tout les calculs, estimer l'orientation de sa position par rapport à la base.