AC. I - REPÉRAGE DU MOUVEMENT


Espace et temps d’un observateur

• Certains objets semblent expérimentalement “rigides” (indéformables) ; ces objets peuvent alors servir d’étalons de longueur.

◊ remarque : le mètre étalon de 1789 en platine iridié mesurait  1/(40.106)1/(40.{10}^6 \,)  du méridien terrestre (précision relative 10−5{10}^{-5} ) ; depuis 1983, la définition découle de la célérité de la lumière dans le vide (c=299792458m.s−1c=299 \,792 \,458 \:\mathrm{m.s^{-1}} ) considérée comme une valeur exacte (précision relative 10−14{10}^{-14} ).
 
• Le temps n’est “défini” que de manière très relative : il semble qu’on peut classer des événements dans un ordre dans lequel ils paraissent se produire.

Par ailleurs, il semble exister des phénomènes cycliques se reproduisant “régulièrement” ; ces phénomènes peuvent alors servir d’étalons de temps.

◊ remarque : avant 1960, la seconde était définie comme  1⁄(24×3600)1⁄(24 × 3600)  du jour solaire moyen, mais la rotation de la Terre ralentit (à cause des frottements associés aux marées) ; depuis 1967, la définition se réfère à la période d’une raie spectrale hyperfine de 133Cs{}^{133}\mathrm{Cs} (précision relative 10−14{10}^{-14} ).

Notion de point matériel

• On considère comme “point matériel” tout système dont l’étude se ramène à celle d’un point (associé ensuite à une masse, dans l'étude dynamique).

Ainsi, dans tout calcul sans rotation ni de déformation, un système complexe peut être décrit par le point matériel qu’est son centre d’inertie.

◊ remarque : un objet en rotation, même très petit, ne peut pas être traité comme un point matériel si l’énergie cinétique de rotation sur lui même n’est pas négligeable (un point ne peut pas avoir de rotation sur lui même).

Notations vectorielles

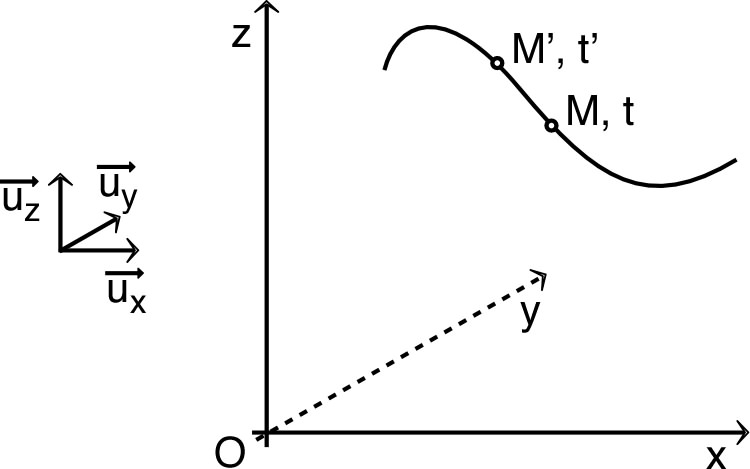
• Les axes des repères cartésiens portent l'indication du nom des coordonnées et du sens positif (ce ne sont pas des vecteurs).

Les vecteur unitaires sont désignés par le symbole u→\overset{→}{u} avec en indice le nom de la coordonnée.

Ces vecteurs sont souvent représentés à côté du repère, pour ne pas encombrer les schémas.
repMouv_Im/repMouv_Im1.jpg

Vitesse et accélération

• La vitesse d’un point MM peut être définie par la dérivée vectorielle :
v→(t)=limt′→tMM⟶′t′−t=dOM⟶dt=OM⟶˙\displaystyle \overset{→}{v}(t)=\lim_{t'→t}\:\:\frac{\overset{⟶}{MM}{}'}{t'-t}=\frac{d\overset{⟶}{OM}}{dt}=\dot{\overset{⟶}{OM}} .

De même en dérivant la vitesse :
a→(t)=limt′→tv→(t′)−v→(t)t′−t=dv→(t)dt=v→˙=OM⟶̈\displaystyle \overset{→}{a}(t)=\lim_{t'→t}\:\: \frac{\overset{→}{v}(t')-\overset{→}{v}(t)}{t'-t}=\frac{d\overset{→}{v}(t)}{dt}=\dot{\overset{→}{v}}=\ddot{\overset{⟶}{OM}} .

☞ remarque : les “points de dérivation”, comme pour  OM⟶˙\dot{\overset{⟶}{OM}}  et  OM⟶̈\ddot{\overset{⟶}{OM}} ,  sont réservés pour les dérivations par rapport à la variable temps ( tt ).

• Dans un repère  (O,u→x,u→y,u→z)(O \,, \overset{→}{u}_x \,, \overset{→}{u}_y \,, \overset{→}{u}_z \,)  (parfois noté en abrégé OxyzOxyz ) :
OM⟶=xu→x+yu→y+zu→z\overset{⟶}{OM}=x \:\overset{→}{u}_x+y \:\overset{→}{u}_y+z \:\overset{→}{u}_z  ;
v→=x˙u→x+y˙u→y+z˙u→z\overset{→}{v}=\dot{x} \: \overset{→}{u}_x+\dot{y} \: \overset{→}{u}_y+\dot{z} \: \overset{→}{u}_z   ;   a→=ẍu→x+ÿu→y+z̈u→z\overset{→}{a}=\ddot{x} \: \overset{→}{u}_x+\ddot{y} \: \overset{→}{u}_y+\ddot{z} \: \overset{→}{u}_z .

☞ remarque : lors du calcul des dérivées, on considère ici comme fixes l’origine OO et les vecteurs de la base  (u→x,u→y,u→z)(\,\overset{→}{u}_x \,, \overset{→}{u}_y \,, \overset{→}{u}_z \,) .

📖 exercices n° I et II.

Coordonnées polaires (dans un plan)

Description générale

• En coordonnées polaires, on repère MM par la norme et la direction de OM⟶\overset{⟶}{OM} .

On définit u→r\overset{→}{u}_r unitaire selon rr croissant et de même u→θ\overset{→}{u}_θ selon θθ croissant :
u→r=u→r(θ)=cos(θ)u→x+sin(θ)u→y\overset{→}{u}_r=\overset{→}{u}_r (θ)=\cos(θ) \; \overset{→}{u}_x+\sin(θ) \; \overset{→}{u}_y  ;
u→θ=u→θ(θ)=−sin(θ)u→x+cos(θ)u→y\overset{→}{u}_θ=\overset{→}{u}_θ (θ)=-\sin(θ) \; \overset{→}{u}_x+\cos(θ) \; \overset{→}{u}_y .

Ainsi :  du→r(θ)dθ=u→θ \displaystyle \frac{d\overset{→}{u}_r (θ)}{dθ}=\overset{→}{u}_θ    ;   du→θ(θ)dθ=−u→r\displaystyle \frac{d\overset{→}{u}_θ (θ)}{dθ}=-\overset{→}{u}_r .
repMouv_Im/repMouv_Im2.jpg

• Avec ces notations :  OM⟶=ru→r\overset{⟶}{OM}=r \:\overset{→}{u}_r  peut sembler ne dépendre que de rr , mais il dépend de θθ par la direction de u→r\overset{→}{u}_r (il faut deux coordonnées dans le plan).

◊ remarque : les coordonnées de OM⟶\overset{⟶}{OM} (r,0)(r,0) diffèrent de celles de MM (r,θ)(r,θ\,) .

• En dérivant :  v→=r˙u→r+ru→˙r\overset{→}{v}=\dot{r} \: \overset{→}{u}_r+r \:\dot{\overset{→}{u}}_r  ;   u→˙r=du→r(θ(t))dt=du→r(θ)dθdθ(t)dt=θ˙u→θ\displaystyle \dot{\overset{→}{u}}_r=\frac{d\overset{→}{u}_r (θ(t))}{dt}=\frac{d\overset{→}{u}_r (θ)}{dθ} \, \frac{dθ(t)}{dt}=\dot{θ} \: \overset{→}{u}_θ  ;

Ainsi :
v→=r˙u→r+rθ˙u→θ\overset{→}{v}=\dot{r} \: \overset{→}{u}_r+r \:\dot{θ} \: \overset{→}{u}_θ  ;
a→=(r̈−rθ˙2)u→r+(2r˙θ˙+rθ̈)u→θ\overset{→}{a}=\left(\ddot{r}-r \:\dot{θ}^2 \,\right) \: \overset{→}{u}_r+(2 \,\dot{r} \: \dot{θ}+r \:\ddot{θ} \,) \: \overset{→}{u}_θ  .

☞ remarque : il s’agit de v→\overset{→}{v} et a→\overset{→}{a} par rapport à  (O,u→x,u→y)(O \,, \overset{→}{u}_x \,, \overset{→}{u}_y \,) ,  ré-exprimés sur la base locale  (u→r,u→θ)(\,\overset{→}{u}_r \,, \overset{→}{u}_θ \,)  (sinon il n’y aurait pas les termes en θ˙\dot{θ} et θ̈\ddot{θ} ).

◊ remarque : avec la vitesse angulaire algébrique  ω=θ˙ω=\dot{θ}  et le vecteur rotation  ω→=ωu→z\overset{→}{ω}=ω \:\overset{→}{u}_z ,  on obtient :  u→˙r=θ˙u→θ=ω→×u→r\dot{\overset{→}{u}}_r=\dot{θ} \: \overset{→}{u}_θ=\overset{→}{ω} × \overset{→}{u}_r   et  u→˙θ=−θ˙u→r=ω→×u→θ\dot{\overset{→}{u}}_θ=-\dot{θ} \: \overset{→}{u}_r=\overset{→}{ω} × \overset{→}{u}_θ .

Mouvement circulaire

• La géométrie du mouvement conduit ici à utiliser des coordonnées polaires.

• Pour un point MM sur un cercle de centre OO et de rayon rr :  OM⟶=ru→r\overset{⟶}{OM}=r \:\overset{→}{u}_r  et l’évolution dans le temps est liée à l’orientation du vecteur  u→r(θ(t))\overset{→}{u}_r (θ(t)) .

• On obtient la vitesse :  v→=rθ˙u→θ\overset{→}{v}=r \:\dot{θ} \: \overset{→}{u}_θ  (tangente au cercle)  et l’accélération :  a→=−rθ˙2u→r+rθ̈u→θ\overset{→}{a}=-r \:\dot{θ}^2 \: \overset{→}{u}_r+r \:\ddot{θ} \: \overset{→}{u}_θ .

☞ remarque : la composante radiale de l'accélération est non nulle même si le mouvement est “uniforme” : le changement de direction du vecteur vitesse constitue une accélération.

◊ remarque : en utilisant le vecteur rotation  ω→=ωu→z\overset{→}{ω}=ω \:\overset{→}{u}_z  on obtient :
v→(t)=OM⟶˙=ω→×OM⟶\overset{→}{v}(t)=\dot{\overset{⟶}{OM}}=\overset{→}{ω} × \overset{⟶}{OM}  (dans la mesure où  OM=‖OM⟶‖=CteOM=\left‖ \overset{⟶}{OM} \right‖=Cte )  ;
et de même, si  ‖v→‖=rθ˙=Cte\left‖\, \overset{→}{v} \,\right‖=r \:\dot{θ}=Cte :  a→=v→˙=ω→×(ω→×OM⟶)\overset{→}{a}=\dot{\overset{→}{v}}=\overset{→}{ω} × \left(\,\overset{→}{ω} × \overset{⟶}{OM} \right) .

📖 exercices n° III et IV.

Notion de référentiel

• On appelle “référentiel” un “objet de référence”, considéré comme fixe, par rapport auquel on étudie le mouvement d'autres objets.

Pour décrire les mouvements, on associe au référentiel un repère mathématique (fixe). Le choix d'un autre repère (fixe) pour le même référentiel modifie l'expression mathématique des coordonnées, mais ne modifie pas l’allure du mouvement constaté par l’observateur.

Plus même : le fait de réexprimer sur la base locale mobile  (u→r,u→θ)(\,\overset{→}{u}_r \,, \overset{→}{u}_θ \,)  la vitesse et l'accélération de MM par rapport à un référentiel de repère  (O,u→x,u→y)(O \,, \overset{→}{u}_x \,, \overset{→}{u}_y \,)  ne change en rien le référentiel auquel sont associées ces grandeurs.