Interaction probability ; symmetry of the time direction


• One may consider that the wave does not completely describe the physical process but only a kind of convolution between the sender's offer and the receiver's “retroactive” demand, which would be filtered in a global way by those symmetries of apparatus that are contained in interaction hamiltonian.

Thus the fundamental property of a particle with respect to quantum mechanics may be its interaction probability and not its presence probability (the ambiguousness comes from the fact that in order to detect the presence of a particle one must interact with it). But as we know nothing of the world apart from interactions that we have with it, the quantum description is sufficient for us to predict (statistically) the results of all the measures.

This may cause some difficulties (or even impossibilities) for experimental verification. The existence of free particles asymptotic states may thus be questioned back : if the Universe would contain some matter only “in one side” of a given particle sender, who can say if this apparatus would emit symmetrically ? Do the eventual particles leaving the apparatus to the “empty” side and never reinteracting exist ?

A sender isolated in an “empty” space would it be able to emit a photon (if it already “knows” where it is coming to as early as it starts, where would it go ?) ? Then, if the sender does not emit, is it not possible to consider that its “time” does not elapse ? All this may lead to experimental situations showing new phenomena (similarly to Casimir's effect [1]).

It would be necessary for that to be able to produce (as example) an isolated atom in such an excited state that it could desexcite only by emitting photons with a precise frequency (at a temperature necessarily very close to 0 K), placed in a cavity “totally” anti-resonant for the frequency in question, and then to test its ability to desexcite in these conditions.

In practice, this kind of situation does not clearly appear since it is certain that the particles involved in experiments are finally doomed to reinteract ; but nothing forbids to assert that if one sets a receiver in a given configuration, one forces (through the wave and the associated instantaneousness) the particles reaching this one to be in some states that it is able to detect. In the absence of any receiver, the particles going this way would not necessarily have been in one of these states, but they would nevertheless have been in similar states since they would necessarily travel within the course to another interaction.

Moreover, in the case of a Young's fringes experiment with hyperboloid-shaped interference sheets, nothing forbids on principle the particles to go through the dark regions without interacting (their interaction probability vanishing with the wave) to reach an interaction in a light region located behind.  The knowledge that we can have about particles trajectories thus becomes very hazy since we only have access to the interaction probability (more especially as some physicists even consider interaction in further space-time dimensions).

• From another point of view, beside the sender-receiver symmetry appears a macroscopic dissymmetry between past and future : if one places two identical sources of light in front of a receiver, this one detects twice more photons, whereas if one places two receivers in front of a source, the source does not emit twice more.

But this may be explained, while keeping the microscopic influence of the receiver on the source, by the fact that we live in a world where energy is rare, bounded on the under side and not on the upper one. The receivers demand is very large (every system able to interact behaves as a receiver) and they detect all that is offered to them, thus twice more if one doubles the source (linear behavior). On the other hand, the sources offer is very weak (little available energy) and they have a saturated behavior, apparently independent of the very large number of receivers (nothing seems changed if one modifies a few receivers among a very large number). This dissymmetry is thus fully compatible with the microphysical symmetry between sender and receiver.

Inversely (accordingly to the temporal symmetry for interactions), some effects like induced absorption would they not be considered (“inverse Laser” effect for which it might be considered the phase coherence, but unlikely the amplification, according to the previous remark) ? It may be considered for that to reinterpret in reverse direction (within the relativistic instantaneousness approach) the “usual” diagrams, while being careful to respect the direction of interactions ; thus, it is usually considered that spontaneous absorption and induced absorption are “naturally” proportional to the flow of incident photons, therefore it is noticed that spontaneous emission is independent of the incident flow, whereas it would be more consistent to consider that it is proportional to the emitted flow (in the same way as spontaneous absorption is independent to the emitted flow...), and then to think about a possible effect of induced absorption, proportional to the emitted flow (within hypothetical conditions where there would not be “saturation” of emittors by limitation of the available energy) [2].

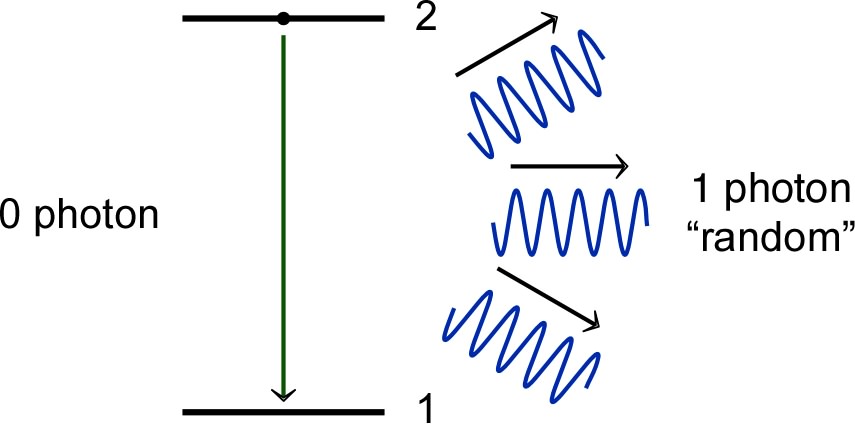
emspont

spontaneous emission reveals a photon, emitted with “random” direction and phase

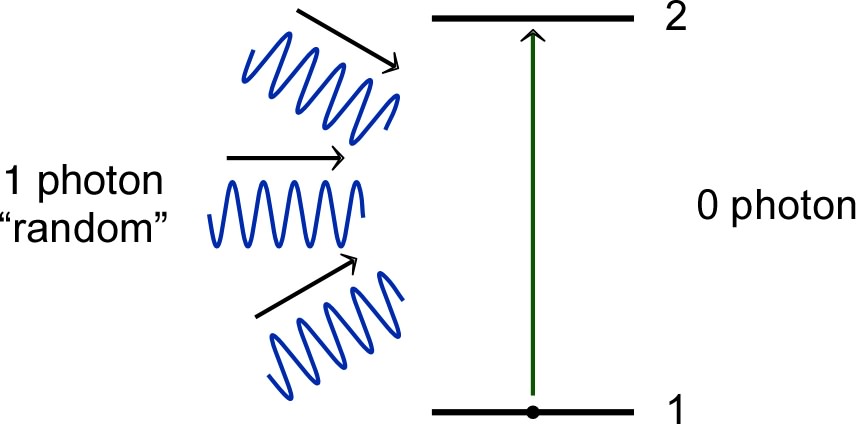
 absspont

spontaneous absorption removes a photon, absorbed with “random” direction and phase
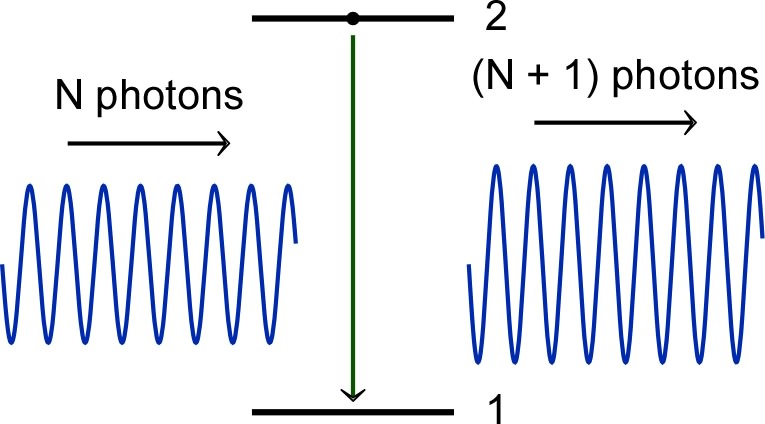
emind

induced emission produces a photon in the same mode that the incident wave (the emission is amplified)
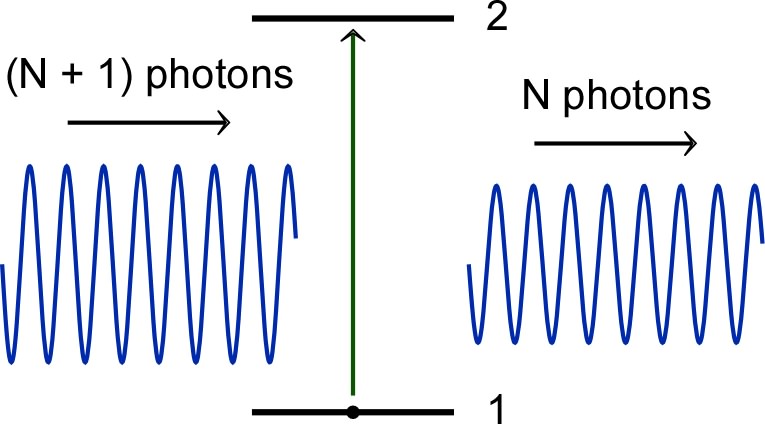
 absind

induced absorption removes a photon in the same mode as the outgoing wave (absorption is amplified) ; however, under usual conditions, we do not distinguish the difference between the two kinds of absorption, failing to perceive the reciprocal causality of receptors (associated with the relativistic instantaneousness)

If such effects don't appear in usual situations, they might occur in extreme situations, as example in very high energy ions collisions [3]. But moreover, it would seem rather logic that this kind of effect might participate in the explanation of photons coalescence. In the case of two photons coming from two independent sources of single photons and joining together at the time of passing through a semi-reflecting plate : while increasing the indiscernibility of the photons, one reduces the relative probability for them to be accepted by uncorrelated detectors and favours the induced absorption [4].

• Elsemore, through the permanent contact imposed by the generalized instantness between senders and receivers, one can rejoin statistical aspects assignable to a hidden thermodynamics for particles. As an example, if a source of light is confronted with the demand of many receivers, the state of some receivers may be modified, among other things by the arrival of a photon coming from another source. Thus, because of the large number of the receivers, the demand is unceasingly fluctuating (although stationary on an average) and one may consider that a train of waves is nothing but the state which takes place between two fluctuations ; the equations of quantum mechanics then representing a kind of thermodynamical flow between a hot source (sender) and a cold source (receiver) [5].

• What does happen therefore in the experimental case of the Einstein-Podolski-Rosen paradox ? Let us thus consider a source S emitting correlated particles pairs in the direction to two receivers R1 and R2 ; it may be asked if the wave packet reduction allows a superluminary communication between the receivers R1 and R2.

The answer is double. Yes in a certain way at the microphysical level, since when modifying R1 one influences the detection at the level of R2 ; no in any way at the macrophysical level, since the modification of the only receiver R1 among the very large number able to interact with the source cannot modify with appreciable change the global demand received by the source, and thus cannot modify the statistical detection at the level of R2.

__________________
References :

1. see as example :
        “L'infiniment vide n'existe pas”, T. Boyer, Pour la Science n° 278, december 2000 ;
        “La force qui vient du vide”, A. Lambrecht, La Recherche n° 376, june 2004.

2.  see as example :
       “Du GPS au DVD”, P. Yam, Pour la Science n° 326, december 2004 ;
       “Les fluctuations d'Einstein”, S. Reynaud, Pour la Science n° 326, december 2004.

3.  see as example :
“Le big bang en laboratoire”, C. Roy, La Recherche n° 395, march 2006 ;
“Les premières microsecondes de l'Univers”, Pour la Science n° 344, june 2006.

4. see as example : “Photons indiscernables : qui se ressemble s'assemble”, I. Robert-Philip et al., Images de la Physique 2006, p. 106.

5. by this aspect, the quantum mechnics is perhaps not independent of the methods used to describe the flows in production lines ; see as example : “L'algèbre des sandwichs”, G. Cohen, S. Gaubert and J.P. Quadrat, Pour la Science n° 328, february 2005.


Return to the beginning