Photon lifetime ; relativistic instantaneousness and
localeousness of interactions
• One of the tests for relativity is connected to particles lifetime.
If one considers a muon coming from cosmic rays and reaching the Earth
with a speed close to the speed of light, one finds out that its
lifetime is larger than the one for a muon at rest. This comes from the
fact that the duration with physical meaning for the muon is the one
connected to its proper reference frame
; it is thus necessary to found upon the proper time interval 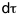 (or upon the relativistic invariant metric element ds = c
(or upon the relativistic invariant metric element ds = c 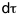 )
rather than upon the time interval dt measured within our
reference frame.
)
rather than upon the time interval dt measured within our
reference frame.
If one takes interest in the similar case for a photon, which mass is
null, one may consider a massive particle,
and afterwards get the massless limit with constant momentum. For a
muon moving with the speed v from a point A to a point B
separated by a distance D, the journey duration is T = D/v.
In the reference frame where the
muon is at rest, the journey duration is T’ = T . 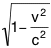 , duration
while which the points A and B (mooving with the speed -v) travel
through a distance
D’ = D .
, duration
while which the points A and B (mooving with the speed -v) travel
through a distance
D’ = D . 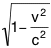 .
.
When one gets the massless limit with a constant momentum, the speed v
tends to c and then T’ and D’
tend to zero. This consists to say that, with respect to its “proper
reference frame”, the photon travel through no
distance within no duration.
One is thus leaded to the notion of a photon “arriving in the same time
as it starts” (not with respect to our vision of things, but with
respect to the interaction to which it is participating), which does
not forbid to
distinguish the start point and the end point since there is an energy
transfer from the one to the other.
• This manner of “instantaneous” flashing rejoins the idea, previously
used by Newton, of
particles interacting instantaneously at a distance. Although it is
certain that the light “starts from the source” and “goes towards the
detector”, the propagation which follows from the newtonian
representation of interactions is in a manner instantaneous (which is a
language misuse since the word
“propagation” evokes a spatial distance but also a time difference).
Then, if one replaces (according to the introduction by Einstein of the
relativistic light propagation) the instantaneousness corresponding
to dt = 0 by its analoguous corresponding to 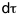 = 0, one finds out that the
propagation with the speed of light may rightly be considered as the
relativistic instantaneousness of the light interaction.
= 0, one finds out that the
propagation with the speed of light may rightly be considered as the
relativistic instantaneousness of the light interaction.
All this leads to a non
local model, or rather to one having a relativistic “localeousness”
connected to the property ds = 0, where the path of a wave
packet describing a
particle must be considered globally (I
prefer to use the neologism “localeousness” rather than the expression
“locality”, which have several meanings, in order to emphasize the same
difference as between the words “instant” and
“instantaneousness”).
This interpretation of phenomena contains some hardly deterministic
aspects in the way that, being
considered as a whole, the wave shows some
correlations with informations about its end point as early as it
starts. This global manner to consider interactions may run counter to
intuition, particularly in some cases of
distant correlations where it becomes
difficult to
separate causes from effects without contradict quantum
mechanics. However, when one studies an elctromagnetic field in the
Coulomb jauge, one is lead to use the non delayed scalar potential of
electrostatics, which seems to have nothing like relativistic ;
one is still lead to the same result as in the Lorentz jauge where the
delayed potential is used. This is indeed coherent with the determinist
principle qui saying that present can be deduced from past and is thus
partly equivalent to it with respect to the contained information ;
this moreover shows that the spatio-temporal correlations of the
physical world may seem stange when they are expressed in the
appropriate reference frame or jauge.
• Moreover, this is not independent of the interpretation that Feynman
had proposed in order to attempt to eliminate from some computations
the divergences caused by electrons autointeraction : with Wheeler, he
considered a distant interaction connected to a superposition of equal
contributions of delayed and advanced waves [1]. A frequent reproach to
this work was that it replaced the difficulty
of a divergence by the difficulty of a violation of the causality
principle. Now, this kind of argument is not appropriate in the
relativistic instantaneousness approach : not only an electron can
interact by advanced potentials as source, but (in so far as is
respected the symmetry between the two directions of time) it do that
logically as much as it interacts by delayed potentials as detector.
• A complication may seem to appear if one comes back to the muon case
in order to
treat, in the way evoked at the beginning, the case of massive
particles, moving with a speed inferior to the light one. Indeed, there
is no longer ds = 0 along the path and it is thus not
possible to use directely the relativistic instantaneousness.
Several hypotheses may be considered in order to
generalize this notion. But the
generalization is direct if one considers that “naked” particles are
massless and that the mass of
particles “dressed” by interactions comes from a
renormalization.
__________________
References :
1. see as example : “vous voulez rire”, Pour la Science -
les génies de la science, n° 19 (“Feynman, génie
magicien”), may 2004.
Return to the beginning
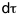 (or upon the relativistic invariant metric element ds = c
(or upon the relativistic invariant metric element ds = c 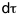 )
rather than upon the time interval dt measured within our
reference frame.
)
rather than upon the time interval dt measured within our
reference frame.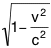 , duration
while which the points A and B (mooving with the speed -v) travel
through a distance
D’ = D .
, duration
while which the points A and B (mooving with the speed -v) travel
through a distance
D’ = D . 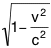 .
.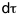 = 0, one finds out that the
propagation with the speed of light may rightly be considered as the
relativistic instantaneousness of the light interaction.
= 0, one finds out that the
propagation with the speed of light may rightly be considered as the
relativistic instantaneousness of the light interaction.