RG V - CHAMP CENTRAL SYMÉTRIQUE EXTÉRIEUR

Conditions supplémentaires imposées à la métrique

• Les dix équations du champ de gravitation (

R^{αβ}-\frac{1}{2} g^{αβ} \:R=χ \:T^{αβ}

) ne sont pas indépendantes, car elles sont liées par les quatre identités de Bianchi :

D_α (R^{αβ}-\frac{1}{2} g^{αβ} \:R)=0

.

Les dix composantes indépendantes de la métrique

g^{αβ}

ne sont donc pas totalement déterminées : pour un champ de gravitation donné, il est toujours possible d'effectuer un changement de coordonnées, ce qui correspond à quatre équations arbitraires.

◊ remarque : cette situation est analogue à celle de l'électromagnétisme, pour lequel les équations de Maxwell ne déterminent pas totalement le quadri-potentiel

A^α

, mais laissent la liberté d'imposer une condition de jauge arbitraire (par exemple la jauge de Lorentz, pour laquelle

∂_α A^α=0

).

• Il est parfois pratique d'utiliser un système de coordonnées “harmoniques”, telles que :

∂_α \left(\sqrt{|g|} \:g^{αβ} \right)=0

, ce qui peut aussi s'écrire :

Γ^β=g^{μν} \:Γ_{\phantom{.}μν}^β=0

.

Cette condition, non invariante car la connexion affine n'est pas un tenseur, privilégie un type de repérage particulier qui simplifie certains calculs.

Compte tenu de la transformation de la connexion dans un changement de coordonnées :

x^α→\underline{x}^β

tel que :

dx^α=\underline{∂}_β x^α \:d\underline{x}^β

d\underline{x}^β=∂_α \underline{x}^β \:dx^α

, on obtient :

\underline{Γ}^ρ=∂_κ \underline{x}^ρ \:Γ^κ-g^{αβ} \:∂_{αβ} \underline{x}^ρ

. Il est ainsi toujours possible de trouver une transformation qui aboutit à des coordonnées “harmoniques”.

Cette condition n'impose pas totalement le repérage : tout changement de coordonnées tel que

g^{αβ} \:∂_{αβ} \underline{x}^ρ=0

conserve le caractère “harmonique”.

📖 exercices n° I, II, III, IV et V.

Forme générale de la métrique à symétrie sphérique

• La métrique doit s'écrire en fonction des invariants spatiaux par rotation :

\overset{→}{X}^2

\overset{→}{X}∙\overset{⟶}{dX}

\overset{⟶}{dX}^2

. Il est généralement plus pratique de noter en coordonnées de type sphérique :

x^1=r\;\sin(θ)\: \cos(φ)

x^2=r\;\sin(θ) \:\sin(φ)

x^3=r\;\cos(θ)

, mais sans préjuger la signification de la variable radiale

r=\sqrt{\,\overset{→}{X}^2}

.

• La forme la plus générale peut s'écrire :

$ds^2=A(r,t)\:c^2 \,dt^2+B(r,t) \:c \,dt \,dr-C(r,t) \:dr^2-D(r,t) \:[dθ^2+\sin^2(θ) \:dφ^2]$ .

Il reste possible d'imposer deux transformations simplificatrices aux coordonnées

r

t

. On utilise souvent :

B=0

D=r^2

, mais on peut préférer

D=C \:r^2

(coordonnées “isotropes”), ou imposer une condition d'harmonicité.

Étude du cas statique dans le vide

Métrique “classique” de Schwarzschild

• Dans le vide, on peut montrer que la métrique précédente est forcément statique ; ainsi :

ds^2=A(r)\:c^2 \,dt^2-C(r) \:dr^2-r^2 \:[dθ^2+\sin^2(θ) \:dφ^2]

.

On obtient alors :

$g_{00}=A$ ; $g_{11}=-C$ ; $g_{22}=-r^2$ ; $g_{33}=-r^2 \:\sin^2⁡(θ)$ ;
$\displaystyle g^{00}=\frac{1}{A}$ ; $\displaystyle g^{11}=-\frac{1}{C}$ ; $\displaystyle g^{22}=-\frac{1}{r^2}$ ; $\displaystyle g^{33}=-\frac{1}{r^2 \:\sin^2⁡(θ)}$ ;
$\displaystyle Γ_{001}=-Γ_{100}=\frac{A'}{2\,}$ ; $\displaystyle Γ_{111}=-\frac{C'}{2\,}$ ; $Γ_{221}=-Γ_{122}=-r$ ;
$Γ_{331}=-Γ_{133}=-r \;\sin^2⁡(θ)$ ; $Γ_{332}=-Γ_{233}=-r^2\:\sin⁡(θ)\: \cos⁡(θ)$ ;
$\displaystyle Γ_{\phantom{.}01}^0=\frac{A'}{2\,A}$ ; $\displaystyle Γ_{\phantom{.}00}^1=\frac{A'}{2\,C}$ ; $\displaystyle Γ_{\phantom{.}11}^1=\frac{C'}{2\,C}$ ;
$\displaystyle Γ_{\phantom{.}21}^2=Γ_{\phantom{.}31}^3=\frac{1}{r}$ ; $\displaystyle Γ_{\phantom{.}22}^1=-\frac{r}{C}$ ; $\displaystyle Γ_{\phantom{.}33}^1=-\frac{r}{C} \:\sin^2(θ)$ ;
$Γ_{\phantom{.}32}^3=\mathrm{cotan}(θ)$ ; $Γ_{\phantom{.}33}^2=-\sin(θ)\:\cos(θ)$ .

• Dans le vide entourant un astre à symétrie sphérique, les équations du champ (correspondant à

R_{μν}=0

) donnent en simplifiant :

$r \:A \:A' \:C'-2 \:r \:A \:C \:A''+r \:C \:{A'}^2-4 \:A \:C \:A'=0$ ( $R_{00}$ ) ;
$r \:A \:A' \:C'-2 \:r\:A \:C \:A''+r\:C\:{A'}^2+4 \:A^2 \:C'=0$ ( $R_{11}$ ) ;
$-r \:C \:A'+r \:A \:C'+2 \:A \:C^2-2 \:A \:C=0$ ( $R_{22}$ et $R_{33}$ ).

On en déduit :

A' \:C+A \:C'=0

donc

A \:C=Cste

; puis

A \:C=1

puisque la limite à l'infini est

A→1

C→1

.

On obtient ensuite (en simplifiant) :

r \:A'+A-1=0

(

R_{22}

R_{33}

), dont la solution est de la forme :

\displaystyle A=1-\frac{r_s}{r}

. La constante

r_s

est imposée par la limite des champs faibles :

\displaystyle A≈1+\frac{2 \,𝒱}{c^2} ≈1-\frac{2 \,G \,M}{c^2 \,r}

.

Il est alors utile de s'assurer que l'autre équation est vérifiée. Compte tenu de

A \:C=1

, la simplification donne :

r \:A''+2 \:A'=0

(

R_{11}

) ; or ceci peut se mettre sous la forme :

(r \:A'+A-1)'=0

, qui est automatiquement vérifiée.

☞ remarque : cette solution laisse apparaître une “singularité” de ces coordonnées dans le cas où l'astre central créant le champ a un rayon

r<r_s

; il existe alors, dans le vide environnant, une région où

A<0

C<0

; les particularités correspondantes ne seront pas abordées dans ce qui suit, mais seulement dans des parties ultérieures.

Métrique “isotrope”

• On peut aussi chercher sous la forme “isotrope” :

$ds^2=A(\underline{r})\:c^2\,dt^2-\underline{C} (\underline{r}) \:\{d\underline{r}^2+\underline{r}^2 \:dΩ^2\}$ ; $dΩ^2=dθ^2+\sin^2(θ) \:dφ^2$ .

Le changement de notation correspond à :

$C(r)\:dr^2+r^2\:dΩ^2=C(r)\:\{dr^2+A(r) \:r^2\:dΩ^2 \}=\underline{C}(\underline{r}) \:\{d\underline{r}^2+\underline{r}^2\:dΩ^2 \}$ .

Les deux expressions devant s'annuler dans les mêmes conditions, cela impose la relation :

\displaystyle \frac{d\underline{r}^2}{\underline{r}^2} =\frac{dr^2}{A \:r^2}

donc :

\displaystyle \frac{d\underline{r}}{\underline{r}}=±\frac{dr}{\sqrt{r.(r-r_s)}}

.

L'intégration donne :

\displaystyle \underline{r}=\frac{r}{2} \:\left[\left(1-\frac{r_s}{2 \:r}\right)±\sqrt{1-\frac{r_s}{r}} \right]

c'est à dire :

\displaystyle r=\underline{r} .\left(1+\frac{\underline{r}_s}{\underline{r}}\right)^2

avec

\displaystyle \underline{r}_s=\frac{r_s}{4}

. On en déduit :

\displaystyle \underline{C}(\underline{r})=\left(1+\frac{\underline{r}_s}{\underline{r}}\right)^4

\displaystyle A(\underline{r})=\frac{(\underline{r}-\underline{r}_s )^2}{(\underline{r}+\underline{r}_s )^2}

Métrique “harmonique”

• On peut encore chercher sous forme nommée “harmonique”, en notant bien que par cela, on ne désigne pas ici des coordonnées

(\underline{r},θ,φ)

telles que :

❑\underline{x}^{(ρ)}=g^{αβ} \:D_α (D_β \underline{x}^{(ρ)} )=g^{αβ} \:∂_{αβ} \underline{x}^{(ρ)}-Γ^γ \:∂_γ \underline{x}^{(ρ)}=0

; on considère des coordonnées, vérifiant ces relations, mais de type “pseudo-cartésien” :

$\underline{x}^{(1)}=\underline{r}\;\sin(θ) \:\cos(φ)\, , \;\underline{x}^{(2)}=\underline{r} \;\sin(θ) \:\sin(φ)\, , \;\underline{x}^{(3)}=\underline{r} \;\cos(θ)$ .

◊ remarque : les indices entre parenthèses signifient que, pour chaque valeur fixée de l'indice, on raisonne comme si la quantité correspondante était un scalaire (vis à vis de cet indice).

• Partant de la forme “classique” :

ds^2=A(r) \:c^2 \,dt^2-C(r) \:dr^2-r^2 \:dΩ^2

, on recherche une expression

\underline{r}(r)

donnant ainsi :

$\displaystyle Γ^1=\frac{1}{C} \: \left(\frac{A'}{2 \,A}-\frac{C'}{2 \,C}+\frac{2}{r}\right)$ ; $\displaystyle Γ^2=\frac{\cos(θ)}{r^2 \:\sin(θ)}$ ; $❑ct=0$ ;
$\displaystyle ❑\underline{x}^{(i)}=-\frac{1}{C} \: \frac{\underline{r}''}{\underline{r}\;} \underline{x}^{(i)}-\frac{1}{C} \:\left(\frac{A'}{2 \,A}-\frac{C'}{2 \,C}+\frac{2}{r}\right) \: \frac{\underline{r}'}{\underline{r}\,} \underline{x}^{(i)}+\frac{2}{r^2} \:\underline{x}^{(i)}=0$ .

La condition se limite donc à :

\displaystyle \frac{\underline{r}''}{\underline{r}\;}+\left(\frac{A'}{2 \,A}-\frac{C'}{2 \,C}+\frac{2}{r}\right) \: \frac{\underline{r}'}{\underline{r}\,}-\frac{2 \:C}{r^2} =0

.

Compte tenu de

A \,C=1

\displaystyle A=1-\frac{r_s}{r}

, on obtient :

$\displaystyle A \:\underline{r}'' \:\left(A'+\frac{2 \,A}{r}\right) \:\underline{r}'-\frac{2}{r^2} \:\underline{r}=0$ ; $r.(r-r_s) \:\underline{r}''+(2\,r-r_s) \:\underline{r}'-2 \,\underline{r}=0$ .

Les solutions s'écrivent :

\displaystyle \underline{r}=K_1 .\left(r-\frac{r_s}{2}\right)+K_2 .\left(\left(r-\frac{r_s}{2}\right) \;\ln⁡\left(1-\frac{r_s}{r}\right)+r_s \right)

; on choisit en général simplement :

K_1=1

;

K_2=0

;

\displaystyle \underline{r}=r-\frac{r_s}{2}

.

• On obtient ainsi une métrique de la forme :

ds^2=A \:c^2 \,dt^2-C \:dr^2-D \:dΩ^2

, avec :

\displaystyle A=\frac{\underline{r}-\underline{r}_s}{\underline{r}+\underline{r}_s}

;

\displaystyle \underline{r}_s=\frac{r_s}{2}

;

\displaystyle C=\frac{\underline{r}+\underline{r}_s}{\underline{r}-\underline{r}_s}

;

D=(\underline{r}+\underline{r}_s )^2

.

◊ remarque : on peut noter

\underline{A}=A

car

\underline{A}(\underline{r}(r))=A(r)

(idem pour

C

D

).

📖 exercices n° VI, VII, VIII, IX et X.

Équations du mouvement

Étude générale

• La métrique peut s'écrire :

ds^2=A(r) \:c^2 \,dt^2-C(r) \:dr^2-D(r) \:\left[dθ^2+\sin^2(θ) \:dφ^2\right]

.

En l'absence d'effet électromagnétique, l'équation générale du mouvement d'une particule test correspond aux géodésiques ; on peut l'écrire (en fonction d'un paramètre

σ

à préciser) :

\displaystyle \frac{d^2 x^λ}{dσ^2} +Γ_{\phantom{.}μν}^λ \:\frac{dx^μ}{dσ} \,\frac{dx^ν}{dσ}=0

.

Pour une particule massive, on utilise dans cette partie

σ=s

(dans la suite plutôt le temps propre

τ

). C'est impossible pour les photons, pour lesquels

ds=0

; on est alors amené à utiliser un paramètre

ς

tel que

dς=g_{00} \:c \,dt

.

• La symétrie sphérique permet de se limiter au plan

θ=\frac{π}{2}

(on peut vérifier que l'équation correspondante donne alors

θ=Cste

).

On obtient les équations du mouvement géodésique :

$\displaystyle c \,\frac{d^2 t}{dσ^2} +\frac{A'}{A} c \,\frac{dt}{dσ} \,\frac{dr}{dσ}=0$   ;
$\displaystyle \frac{d^2 r}{dσ^2} +\frac{A'}{2 \,C} \:\left(c \,\frac{dt}{dσ}\right)^2+\frac{C'}{2 \,C} \:\left(\frac{dr}{dσ}\right)^2-\frac{D'}{2 \,C} \:\left(\frac{dφ}{dσ}\right)^2=0$   ;
$\displaystyle \frac{d^2 θ}{dσ^2} +\frac{D'}{D} \frac{dr}{dσ} \frac{dθ}{dσ}-\sin(θ) \:\cos⁡(θ) \:\left(\frac{dφ}{dσ}\right)^2=0$   ;
$\displaystyle \frac{d^2 φ}{dσ^2} +\frac{D'}{D} \frac{dr}{dσ} \frac{dφ}{dσ}=0$ .

• En posant

\displaystyle T=\frac{dt}{dσ}

, l'équation temporelle peut s'écrire :

\displaystyle A \:\frac{dT}{dσ}+T \:\frac{dA}{dσ}=0

; on en déduit :

\displaystyle A \:c \,\frac{dt}{dσ}=𝓀=Cste

.

◊ remarque : ceci est lié à la conservation de l'énergie ; pour un photon on obtient

𝓀=1

(imposant

dς=g_{00} \:c \,dt

) ; pour une particule massive on peut montrer que

\displaystyle 𝓀=\frac{ℰ}{m \,c^2}

) où

ℰ

est une “énergie” constante incluant l'effet de la gravitation (analogue relativiste de l'énergie mécanique).

• En posant

\displaystyle Φ=\frac{dφ}{dσ}

, l'équation angulaire s'écrit :

\displaystyle D \:\frac{dΦ}{dσ}+Φ \:\frac{dD}{dσ}=0

; ainsi :

\displaystyle D \:\frac{dφ}{dσ}=\frac{𝒽}{c}=Cste

(ceci est lié à la conservation du moment cinétique).

• Le résultat de l'équation radiale peut être obtenu plus simplement en reportant les expressions de

T

Φ

dans la métrique :

\displaystyle ds^2=\frac{𝓀^2}{A\,} \:dσ^2-C \:dr^2-\frac{𝒽^2}{c^2 \:D} \:dσ^2

.

En posant

\displaystyle R=\frac{dr}{dσ}

, on obtient :

pour un photon $ds^2=0$ ; $\displaystyle R^2=\frac{𝓀^2}{A \,C}-\frac{𝒽^2}{c^2 \,C \,D}$ ;
pour une particule matérielle : $ds^2=dσ^2$ ; $\displaystyle R^2=\frac{𝓀^2}{A \,C}-\frac{𝒽^2}{c^2 \,C \,D}-\frac{1}{C}$ .

• Les cas étudiés dans cette partie étant limités aux distances supérieures au rayon de Schwarzschild

r_s

; peu importe le choix de coordonnées parmi les précédentes : on utilisera les coordonnées “classiques” :

D=r^2

;

\displaystyle A=1-\frac{r_s}{r}

;

\displaystyle C=\frac{1}{A}

.

📖 exercices n° XI et XII.

Trajectoires des particules matérielles

• On peut étudier les types de trajectoires en s'aidant de la comparaison avec le cas non relativiste.

La loi angulaire peut s'écrire

\displaystyle r^2 \, \frac{dφ}{dτ}=𝒽

; elle joue ici un rôle analogue à la “loi des aires”

\displaystyle r^2 \,\frac{dφ}{dt}=\frac{L}{m}

(associée au moment cinétique

L

).

La loi radiale peut s'écrire

\displaystyle \left(\frac{dr}{dτ}\right)^2=c^2 \:(𝓀^2-1)+\frac{2 \,𝒢 \,M}{r}-\frac{𝒽^2}{r^2} \:\left(1-\frac{r_s}{r}\right)

; elle joue ici un rôle analogue à la loi déduite du théorème de l'énergie mécanique :

\displaystyle \left(\frac{dr}{dt}\right)^2=\frac{2 \,E_m}{m}+\frac{2 \,𝒢 \,M}{r}-\frac{L^2}{m^2\:r^2}

.

◊ remarque : ici l'énergie

E_m

n'est pas au carré (comme

𝓀

) parce qu'on y utilise l'expression non relativiste de l'énergie cinétique (qui est quadratique) ; en outre on n'écrit pas

E_m-m \,c^2

(qui correspondrait à

𝓀^2-1

) car on y omet l'énergie de masse.

• En mécanique non relativiste, on considère

E_m=E_{cr}+E_{pr}

avec l'énergie cinétique radiale

E_{cr}=\frac{1}{2} m \:\dot{r}^2

et l'énergie potentielle radiale

E_{pr}=m \:𝒱_r

où

\displaystyle 𝒱_r=-\frac{𝒢\,M}{r}+\frac{L^2}{2 \,m^2 \:r^2}

est un “potentiel radial”.

Les types de trajectoires se déduisent de la représentation graphique (analogue pour tout moment cinétique

L≠0

) :

pour $E_m≥0$ les trajectoires possèdent un minimum d'approche $r_m$ mais ne sont pas bornées (paraboles ou hyperboles) ;
pour $E_m<0$ les trajectoires sont bornées et alternent entre un minimum $r_m$ et un maximum $r_M$ (ellipses ; les trajectoires circulaires correspondent au cas particulier du rayon $r_0$ au minimum de la courbe).

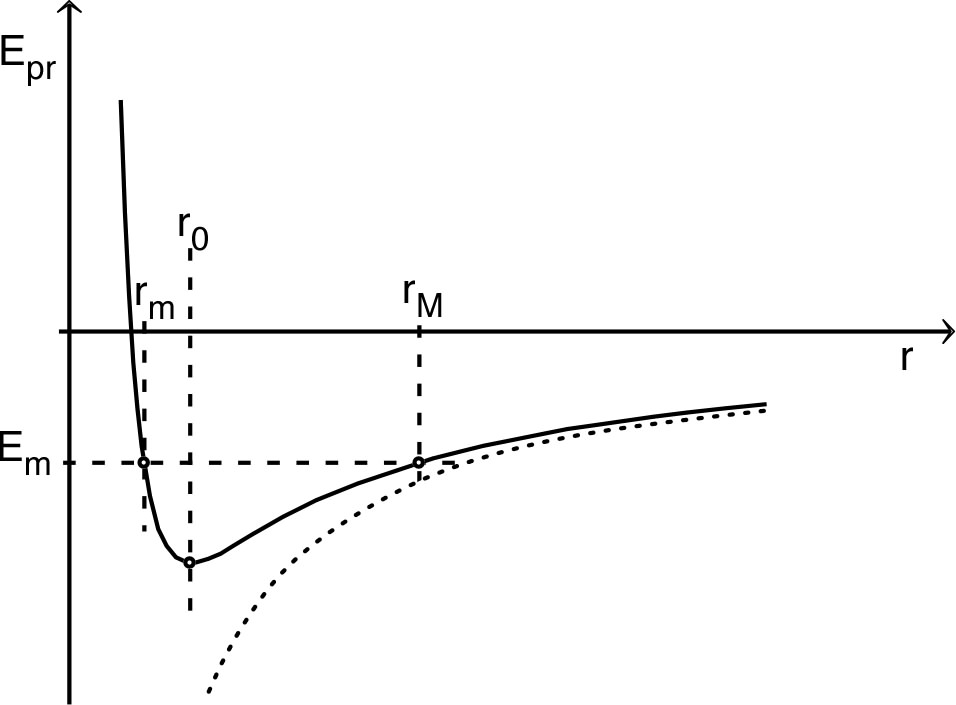
• La loi relativiste peut être traitée de même par analogie avec un pseudo “potentiel radial”

\displaystyle 𝒱_r=-\frac{c^2 \:r_s}{2 \,r}+\frac{𝒽^2}{2 \,r^2} \:\left(1-\frac{r_s}{r}\right)

représenté ci-après pour plusieurs valeurs de h.

◊ remarque : pour ce “potentiel”, l'analogie est “seulement” mathématique, puisque

ℰ

n'intervient pas de la même façon que

E_m

, mais tout à fait utilisable puisque ces deux énergies ne sont ici que des valeurs constantes de paramètres analogues.

• Le comportement est, dans de nombreux cas, semblable au cas non relativiste (qui doit être retrouvé dans certaines limites) ; on constate toutefois d'importantes différences.

Ainsi, la divergence est négative vers

r=0

(à cause du terme en

\displaystyle -\frac{r_s}{r^3}

). La conséquence est qu'il existe une énergie

ℰ

(une valeur de

𝓀

pour

𝒽

donné) maximum au dessus de laquelle la trajectoire n'a pas de minimum d'approche (la rotation décrite par

𝒽

doit être suffisante par rapport au mouvement radial).

• On peut préciser les courbes en étudiant le lieu des extrémums, caractérisés par :

\displaystyle \frac{d𝒱_r}{dr}=\frac{c^2 \:r_s}{2 \,r^2}-\frac{𝒽^2}{r^3} \:\left(1-\frac{3 \,r_s}{2 \,r}\right)=0

.

Ceci impose

\displaystyle \frac{r_e}{r_s} =\frac{𝒽^2}{c^2 \:r_s^{\,2}}±\sqrt{\frac{𝒽^2}{c^2 \:r_s^{\,2}} \left(\frac{𝒽^2}{c^2 \:r_s^{\,2}}-3\right)}

puis

\displaystyle 𝒱_r (r_e )=-\frac{c^2\:r_s}{2 \,r_e} \left(\frac{r_e-2 \,r_s}{2 \,r_e-3 \,r_s}\right)

en reportant la condition d'extrémum (cette courbe est reportée en tirets).

La conséquence est qu'il existe une rotation (valeur de

𝒽

) minimum au dessous de laquelle la trajectoire ne peut pas avoir de minimum d'approche (quelle que soit la valeur de

𝓀

).

• De façon générale, on retrouve donc des trajectoires bornées entre deux valeurs

r_m

r_M

(mais elles ne sont pas elliptiques) ; des trajectoires non bornées allant jusqu'à l'infini (ni paraboliques, ni hyperboliques) ; des trajectoires rejoignant forcément la singularité en

r=r_s

Trajectoires des photons

• Les photons étant forcément relativistes, une étude analogue à la précédente semblerait nécessiter une approche “newtonienne” (sans effet gravitationnel) avec la relativité restreinte.

Il se trouve qu'on peut déduire des caractéristiques intéressantes par une simple comparaison mathématique des équations pour les photons en relativité générale avec celles des particules massives en mécanique newtonienne.

• La loi angulaire peut s'écrire

\displaystyle r^2 \:\frac{dφ}{dς}=𝒽

; sa forme est analogue à la “loi des aires”

\displaystyle r^2 \:\frac{dφ}{dt}=\frac{L}{m}

(associée au moment cinétique

L

).

Avec

𝓀=1

, la loi radiale peut s'écrire

\displaystyle \left(\frac{dr}{dς}\right)^2=1-\frac{𝒽^2}{c^2 \:r^2} \:\left(1-\frac{r_s}{r}\right)

; sa forme est analogue à la loi déduite du théorème de l'énergie mécanique, mais où serait omis le terme gravitationnel (les photons “newtoniens” n'y sont pas soumis) :

\displaystyle \left(\frac{dr}{dt}\right)^2=\frac{2 \,E_m}{m}+\textcolor{"LightGrey"}{\left[\frac{2 \,𝒢 \,M}{r}\right]}-\frac{L^2}{m^2\:r^2}

.

◊ remarque : bien qu'on n'utilise ici qu'une analogie mathématique, il se trouve ici qu'en l'absence d'effet gravitationnel un photon non dévié respecte la loi des aires, avec une constante où la masse

m

est remplacée par

\displaystyle \frac{h \,ν}{c^2}

.

• En mécanique non relativiste, sans terme gravitationnel, cela peut être décrit par l'énergie potentielle radiale

E_{pr}=m \:𝒱_r

, où

\displaystyle 𝒱_r=\frac{L^2}{2 \,m^2 \:r^2}

est un “potentiel radial” (uniquement “centrifuge”).

La représentation graphique met en évidence que les trajectoires, ici rectilignes, possèdent un minimum d'approche

r_m

mais ne sont pas bornées.

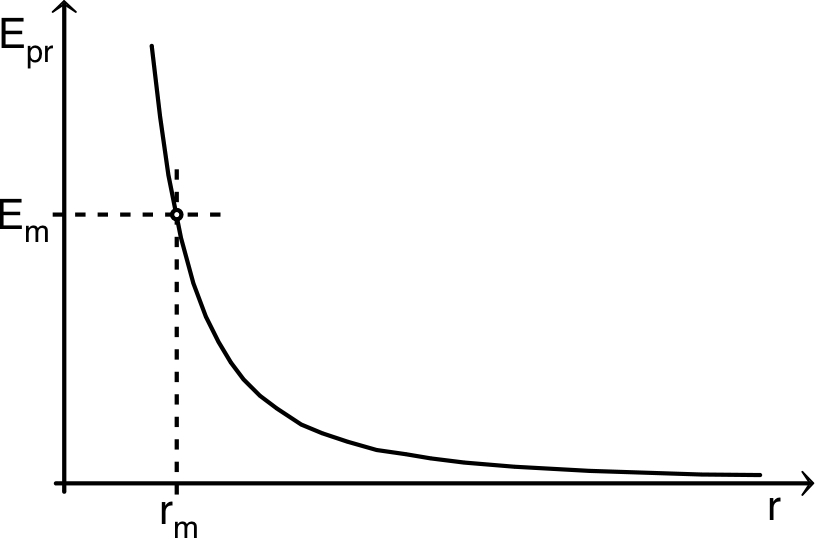
• La loi relativiste peut être traitée de même par analogie avec un pseudo “potentiel radial”

\displaystyle 𝒱_r=\frac{𝒽^2}{2 \,c^2 \:r^2} \:\left(1-\frac{r_s}{r}\right)

, représenté ci-après (la forme ne dépend pas de la valeur de

𝒽

• Le comportement est, dans de nombreux cas, semblable au cas non relativiste (qui doit être retrouvé dans certaines limites).

Mais ici encore la divergence est négative vers

r=0

. Ainsi, les trajectoires passant trop près de l'astre n'ont pas de minimum d'approche (la rotation décrite par

𝒽

doit être suffisante par rapport au mouvement radial).

• On peut préciser les courbes en étudiant le maximum, caractérisé par :

\displaystyle \frac{d𝒱_r}{dr}=-\frac{𝒽^2}{c^2 \:r^3} \:\left(1-\frac{3 \,r_s}{2 \,r}\right)=0

. Ceci impose

\displaystyle \frac{r_e}{r_s} =\frac{3}{2}

;

\displaystyle 𝒱_r≤𝒱_r (r_e )=\frac{2 \,𝒽^2}{27 \,c^2 \:r_s^{\,2}}

.

La condition d'extremum

\displaystyle \left(\frac{dr}{dς}\right)^2=1-2 \:𝒱_r=0

nécessite

\displaystyle \frac{𝒽}{c}≥\frac{\sqrt{27}}{2} \:r_s

(sinon

r_m

n'exixte pas et la trajectoire rejoint forcément la singularité en

r=r_s

).

📖 exercices n° XIII, XIV et XV.

Tests classiques

Effet Einstein

• Cet effet correspond au décalage gravitationnel des fréquences, dû à la “dilatation” des durées “locales” (durées propres des observateurs immobiles) :

∆t_{loc}=\sqrt{A(r)} \;∆t

;

\displaystyle T_{réc}=\frac{\sqrt{A(r_{réc})}}{\sqrt{A(r_{ém})}} \;T_{ém}

;

\displaystyle λ_{réc}=\frac{\sqrt{A(r_{réc})}}{\sqrt{A(r_{ém})}} \;λ_{ém}

;

\displaystyle ν_{réc}=\frac{\sqrt{A(r_{ém})}}{\sqrt{A(r_{réc})}} \;ν_{ém}

.

• Ceci peut aussi être décrit avec les équations d'Euler-Lagrange, ou à l'aide du “vecteur de Killing”

\overset{↔}{ξ}_{(t)}=\overset{↔}{e_0}=∂_0\overset{↔}{M}=(1;0;0;0)

puisque la métrique est indépendante du temps. Ceci correspond à

ξ_{(t)α}=g_{αβ}\:ξ_{(t)}^{\;\;β}=(A;0;0;0)

.

Pour une particule massive, on peut considérer le vecteur

\displaystyle U^α=\frac{dx^α}{dτ}

tangent à sa trajectoire géodésique, ou le vecteur énergie-impulsion

p^α=m \:U^α

.

Les propriétés des vecteurs de Killing permettent d'en déduire une constante du mouvement :

\displaystyle p^α \:ξ_{(t)α}=A \:p^0=A \,m \,c \,\frac{dt}{dτ}=Cste

.

L'énergie de la particule (non compris l'effet de la gravitation) correspond alors à :

E=γ \,m \:c^2=\sqrt{A} \:c \,p^0

; on en déduit donc la loi :

ℰ=E \;\sqrt{A}=Cste

.

◊ remarque : ceci peut s'interpréter en considérant que cette quantité

ℰ

décrit une “énergie” incluant l'effet de la gravitation.

• Le cas des photons peut être traité de façon analogue avec

\displaystyle υ^α=\frac{dx^α}{dς}

\displaystyle p^α=\frac{h \,ν_∞}{c} \,\frac{dx^α}{dς}

. On obtient dans ce cas :

E=h \,ν=\sqrt{A} \:c \,p^0

et la loi est la même ; en particulier :

ν \:\sqrt{A}=Cste

.

• Ce décalage des fréquences (généralement très petit) est souvent étudié par l'intermédiaire de la quantité

\displaystyle z=\frac{λ_{réc}-λ_{ém}}{λ_{ém}} =\frac{\sqrt{A(r_{réc})}}{\sqrt{A(r_{ém})}}-1

.

• L'effet mesuré sur Terre est

z≈{10}^{-14}

; il est en bon accord avec la relativité générale.

Bien qu'il soit très faible, l'effet sur Terre doit être pris en compte dans les calculs nécessaires au repérage GPS ; en effet, les satellites sont en mouvement (ce qui fait intervenir la relativité restreinte), mais ils sont aussi accélérés (puisqu'en mouvement orbital) et dans le champ gravitationnel.

• L'effet mesuré pour des étoiles peut être nettement plus grand, mais il doit être soigneusement distingué de l'effet Doppler dû au mouvement de ces dernières. En outre, l'interprétation nécessite des hypothèses sur l'émission des photons en surface ou en profondeur.

📖 exercices n° XVI et XVII.

Avance du péri-astre des satellites

• Avec des trajectoires bornées entre

r_m

r_M

, les satellites ont généralement des orbites quasi-elliptiques ; on peut les étudier par une approximation de faible correction.

• Avec

\displaystyle \frac{ds}{dφ}=\frac{c \;r^2}{𝒽}

on obtient :

\displaystyle \left(\frac{dr}{dφ}\right)^2=\frac{k^2 \:c^2 \:r^4}{𝒽^2} -r .(r-r_s)-\frac{c^2 \:r^3.\,(r-r_s)}{𝒽^2}

.

Avec une variable de Binet

𝓊=\frac{1}{r}

on peut écrire :

$\displaystyle \left(\frac{d𝓊}{dφ}\right)^2=\frac{1}{r^4} \left(\frac{dr}{dφ}\right)^2=\frac{𝓀^2 \:c^2}{𝒽^2} -𝓊^2+r_s \:𝓊^3-\frac{c^2 .(1-r_s \:𝓊)}{𝒽^2}$ .

En dérivant par rapport à

φ

on obtient ensuite :

\displaystyle \frac{d^2 𝓊}{dφ^2} +𝓊=\frac{c^2 \:r_s}{2 \,𝒽^2}+\frac{3 \,r_s \:𝓊^2}{2}

.

• L'équation a une forme semblable à celle obtenue en mécanique non relativiste, avec en plus un terme correctif

\displaystyle \frac{3 \,r_s \:𝓊^2}{2}

où

r_s \:𝓊≪1

.

La solution non relativiste est :

\displaystyle 𝓊=\frac{1}{𝓅} \:[1+ℯ \:\cos(φ)]

; avec un “paramètre”

\displaystyle 𝓅=\frac{𝒽^2}{𝒢 \,M}

et une “excentricité”

ℯ

dépendant des conditions initiales (l'autre constante d'intégration est ici éliminée par le choix de l'origine de

φ

).

On peut chercher des solutions de la forme :

\displaystyle 𝓊=\frac{1}{𝓅'} \:[1+ℯ' \:\cos(φ')]

en posant :

φ'≈φ.(1-ε)

ε≪1

.

On en déduit :

𝓅'≈𝓅.(1-ε)

\displaystyle ε=\frac{3 \,𝒢 \,M}{c^2 \,𝓅}

; ainsi, entre deux maximums successifs de

𝓊

, l'angle

φ

varie de

2π .(1+ε)

, d'où une avance du péri-astre.

◊ remarque : pour des conditions initiales données, l'excentricité

ℯ'

est en outre aussi un peu différente car la trajectoire est un peu déformée.

• Expérimentalement, pour la planète Mercure, on observe depuis la Terre un décalage par siècle

∆φ=5600,73''±0,41''

.

La théorie newtonienne prévoit

∆φ=5557,62''±0,20''

dont environ

5025''

dues au fait qu'on observe depuis la Terre, auxquelles s'ajoutent environ

532''

dues à l'aplatissement du Soleil et aux perturbations par les autres planètes (Venus et la Terre sont proches ; Jupiter est très massif). Au total, il manque

∆φ=43,11''±0,45''

.

La correction relativiste prévoit

∆φ=0,1038''

par révolution, avec

415

révolutions par siècle, donc

∆φ=43,03''

par siècle, en excellent accord.

📖 exercice n° XVIII.

Déviation des rayons lumineux par un astre

• Avec des trajectoires bornées inférieurement par

r_m

, les photons ont généralement des trajectoires quasi-rectilignes ; on peut les étudier par une approximation de faible correction.

• Avec

\displaystyle \frac{dς}{dφ}=\frac{c \:r^2}{𝒽}

on peut écrire :

\displaystyle \left(\frac{dr}{dφ}\right)^2=\frac{𝓀^2 \:c^2 \:r^4}{𝒽^2} -r .(r-r_s)

.

Avec une variable de Binet

\displaystyle 𝓊=\frac{1}{r}

on obtient :

\displaystyle \left(\frac{d𝓊}{dφ}\right)^2=\frac{1}{r^4} \left(\frac{dr}{dφ}\right)^2=\frac{𝓀^2 \:c^2}{𝒽^2} -𝓊^2+r_s \:𝓊^3

.

En dérivant par rapport à

φ

on obtient ensuite :

\displaystyle \frac{d^2 𝓊}{dφ^2} +𝓊=\frac{3 \,r_s \:𝓊^2}{2}

.

• L'équation a une forme semblable à celle obtenue en mécanique non relativiste, avec en plus un terme correctif

\displaystyle \frac{3 \,r_s \:𝓊^2}{2}

où

r_s \:𝓊≪1

.

La solution non relativiste est :

\displaystyle 𝓊=\frac{1}{r_m} \:\cos(φ)

(l'autre constante d'intégration est ici éliminée par le choix de l'origine de

φ

).

On peut utiliser cette expression comme approximation pour estimer le terme correctif et chercher des solutions de l'équation :

\displaystyle \frac{d^2 𝓊}{dφ^2} +𝓊≈\frac{3 \,r_s}{2 \,r_m^{\:2}} \:\cos^2(φ)

.

La solution s'écrit :

\displaystyle 𝓊≈\frac{1}{r_m} \:\cos(φ)+\frac{r_s}{2 \,r_m^{\:2}} \:[\cos^2(φ)+2 \:\sin^2(φ) ]

; puis avec des coordonnées asymptotiquement cartésiennes :

$x=r \:\cos(φ)$ ; $y=r \:\sin(φ)$ ; $\displaystyle r_m≈x+\frac{r_s}{2 \,r_m} \,\frac{x^2+2 \,y^2}{\sqrt{x^2+y^2}}$ .

• Dans la limite

y≫x

, on obtient :

\displaystyle r_m≈x±\frac{r_s}{r_m} \:y

; ceci correspond à :

$\displaystyle \frac{∆φ}{2}≈\tan⁡\left(\frac{∆φ}{2}\right)≈\frac{r_m-x}{y}≈\frac{r_s}{r_m}$ ; $\displaystyle ∆φ≈\frac{2 \,r_s}{r_m}$ .

• Expérimentalement, on peut comparer des étoiles à la limite d'être éclipsées par le Soleil (

r_m=R_S

) avec des observations analogues des mêmes étoiles nettement éloignées de la situation d'éclipse. On constate depuis la Terre un décalage :

∆φ=1,70''±0,10''

.

La correction relativiste prévoit

∆φ=1,75''

, en excellent accord.

📖 exercice n° XIX.

Effet Shapiro (retard des échos radar)

• Puisque l'écoulement du temps est différent à proximité d'un astre, on peut tester la relativité générale en mesurant la durée d'aller-retour d'un signal radar entre la Terre et un satellite passant de l'autre côté du Soleil.

• La loi radiale peut s'écrire

\displaystyle \frac{1}{c^2\:A^2} \,\left(\frac{dr}{dt}\right)^2=1-\frac{𝒽^2}{c^2 \:r^2}\,A

, avec

\displaystyle A=1-\frac{r_s}{r}

.

Pour qu'un signal radar passant près d'un astre n'y “tombe” pas irrémédiablement, il faut qu'il existe une distance minimale d'approche

r_m

avec

\displaystyle \frac{dr}{dt}=0

. Ceci correspond à :

\displaystyle 𝒽^2=\frac{c^2 \:r_m^{\:2}}{A_m}

avec

A_m=A(r_m)

.

On obtient ainsi :

\displaystyle \frac{1}{c^2 \:A^2} \:\left(\frac{dr}{dt}\right)^2=1-\frac{r_m^{\:2}}{r^2} \frac{A}{A_m}

puis la durée :

$\displaystyle T(r_m,r)=\frac{1}{c} \,∫_{r_m}^r \,\frac{1}{A \,\sqrt{1-\frac{r_m^{\:2}}{{r'}^2} \frac{A}{A_m}} } dr'$ .

◊ remarque : puisque la Terre et le satellite sont loin de l'astre, on confond ici la durée et l'intervalle de la variable

t

(sans multiplier par

\sqrt{A(r)}

).

• Puisque les cas expérimentaux correspondent à

r≫r_s

, on peut utiliser un développement au premier ordre :

\displaystyle \frac{dt}{dr}≈±\frac{1}{c} \frac{r}{\sqrt{r^2-r_m^{\:2}}}\:\left(1+\frac{r_s}{r}+\frac{r_s \:r_m}{2 \,r.(r+r_m)}\right)

.

Ceci donne :

\displaystyle T(r_m,r)≈\frac{1}{c} \:\left[\sqrt{r^2-r_m^{\:2}}+r_s \:\ln⁡\left(\frac{r}{r_m} +\sqrt{\frac{r^2}{r_m^{\:2}}-1}\right)+\frac{r_s}{2} \:\sqrt{\frac{r-r_m}{r+r_m}}\right]

.

Or, le premier terme correspond au trajet rectiligne d'un photon newtonien. Le retard est donc :

\displaystyle ΔT(r_m,r)≈\frac{r_s}{c} \:\left[\,\ln⁡\left(\frac{r}{r_m} +\sqrt{\frac{r^2}{r_m^{\:2}}-1}\right)+\frac{1}{2} \:\sqrt{\frac{r-r_m}{r+r_m}}\right]

.

En outre, les études entre la Terre et un satellite correspondent généralement à

r_T≫r_m

r_{sat}≫r_m

; ainsi :

\displaystyle ∆T(r_m,r)≈\frac{r_s}{c} \:\left[\,\ln⁡\left(\frac{2 \,r}{r_m} \right)+\frac{1}{2}\right]

.

Compte tenu de l'aller-retour, le retard pour un trajet Terre-satellite est finalement :

∆T(r_T,r_{sat},r_T)=2\,∆T(r_m,r_T)+2 \,∆T(r_m,r_{sat})

.

• Les premières séries de mesures, effectuées avec la planète Mercure (satellite naturel du Soleil) ont donné

218±44 \:\mathrm{μs}

pour les photons rasants (le trajet aller-retour dure environ

20 \:\mathrm{min}

).

La principale difficulté était l'analyse détaillée du signal pour réduire l'incertitude due à une réflexion sur une surface irrégulière. Une autre difficulté était de connaitre assez précisément les positions de la Terre et de Mercure en fonction du temps.

La théorie prévoit un retard maximum

∆T=240 \:\mathrm{μs}

, en excellent accord (des mesures ultérieures, avec d'autres satellites, ont par ailleurs permis d'améliorer la précision).

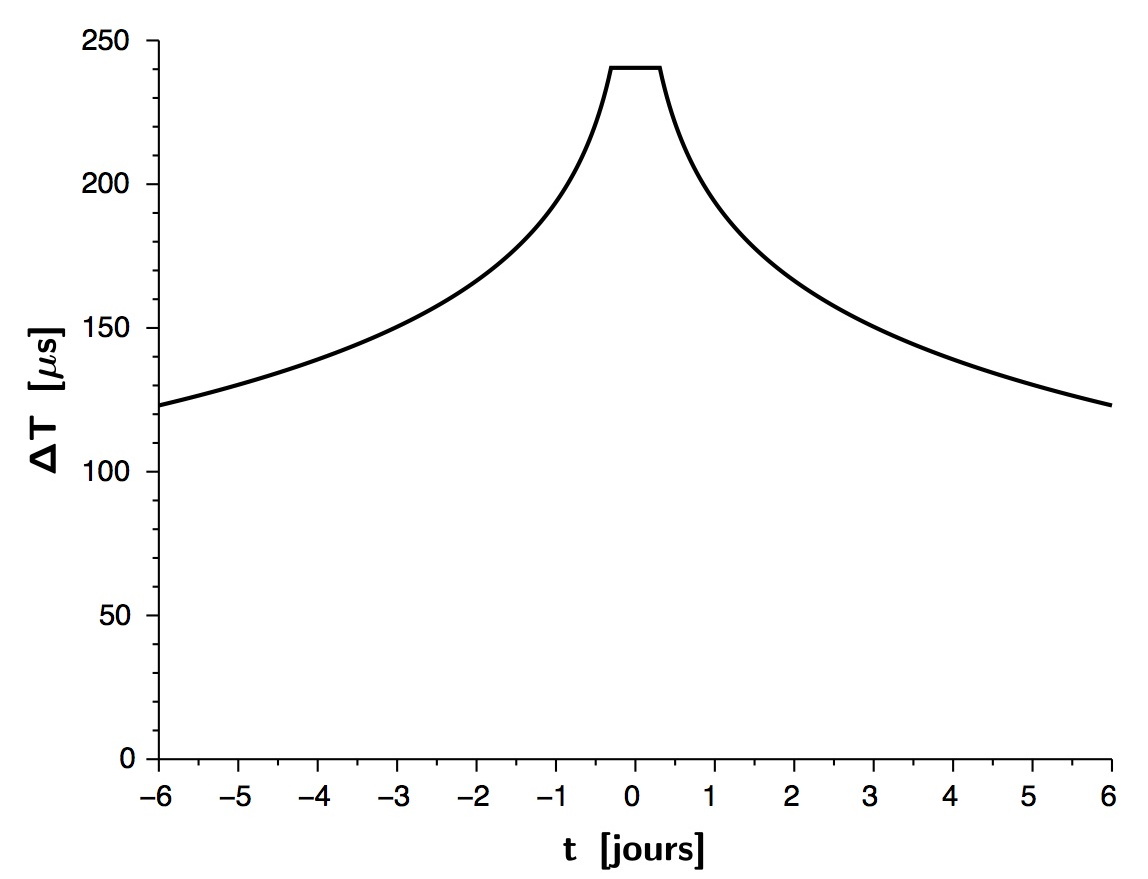
• Il est possible de préciser en étudiant les variations du retard en fonction du temps. Sur une durée limitée à

± 6 \:\mathrm{jours}

(faible en comparaison de la période), on peut considérer

r_T

r_{sat}

quasi constants et décrire le mouvement apparent (synodique) en projection selon un axe passant par le centre du Soleil. La vitesse correspondante est

v≈3,26 \:R_S/\mathrm{jour}

.

Ceci nécessite de borner le calcul au niveau du rayon

R_S

du Soleil. On peut pour cela utiliser

r_m≈max(|x|,R_S)

où

x

est une variable de position sur l'axe considéré. On obtient ainsi l'allure suivante.

• Une étude sur une durée plus longue nécessite une prise en compte plus détaillée du mouvement. On peut utiliser la distance

𝓁

parcourue par Mercure sur son orbite, donc correspondant à un angle

\displaystyle φ=\frac{𝓁}{r_{Mer}}

.

Ensuite, la simplification de

∆T(r_m,r)

supposant

r_T≫r_m

r_{Mer}≫r_m

ne peut plus être utilisée (

r_m

passe même par un maximum égal à

r_{Mer}

).

Enfin, il n'y a plus passage par

r_m

\displaystyle φ>φ_m=\frac{π}{2}+\arcsin⁡\left(\frac{r_{Mer}}{r_T} \right)

; dans ce cas on obtient :

∆T(r_T,r_{Mer},r_T)=2 ∆T(r_m,r_T)-2 ∆T(r_m,r_{Mer})

.

◊ remarque :

φ_m

correspond à

r_m=r_{Mer}

∆T(r_m,r_{Mer})=0

.

• En calculant la distance

d=MT=\sqrt{(r_{Mer} \:\sin(φ) )^2+(r_T+r_{Mer} \:\cos(φ) )^2}

, on peut en déduire (en bornant inférieurement par

R_S

) :

\displaystyle r_m=\frac{r_T \:r_{Mer} \:\sin(φ)}{d}

.

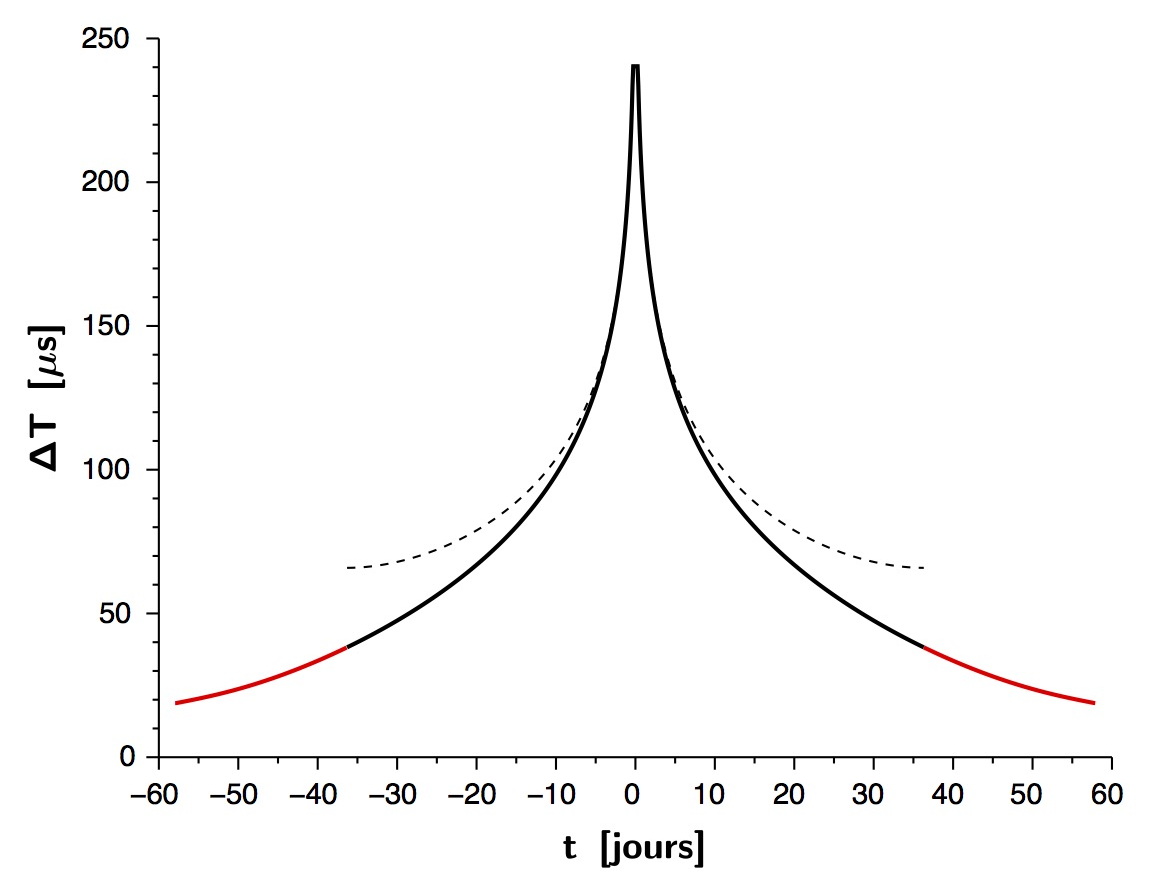
On obtient l'allure suivante ; on y constate que le retard minimum, pour la conjonction inférieure, n'est pas nul.

◊ remarque : l'approximation supposant

r_T≫r_m

r_{Mer}≫r_m

est reportée en pointillés.

📖 exercices n° XX et XXI.

Précession géodésique (effet Einstein - de Sitter)

• En relativité restreinte comme en mécanique newtonienne, un gyroscope effectuant une révolution circulaire autour d'un astre conserve une orientation constante. En relativité générale, la courbure de l'espace-temps cause une précession.

• On considère un gyroscope (quasi-ponctuel) de “spin”

S^μ

, en rotation sur une orbite circulaire de rayon

r

autour d'un astre décrit par la métrique “classique”. L'évolution du spin correspond à :

\displaystyle \frac{DS^μ}{dτ}=\frac{dS^μ}{dτ}+Γ_{\phantom{.}αβ}^μ \:S^α \:U^β=0

.

• En considérant que la trajectoire est dans le plan

θ=\frac{π}{2}

, les équations du mouvement montrent que la 4-vitesse peut s'écrire :

U^β=\dot{t} .(c,0,0,Ω)

avec

\displaystyle \dot{t}=\frac{𝓀}{A}=\frac{1}{\sqrt{1-\frac{3 \,r_s}{2 \,r}}}

\displaystyle Ω=\frac{dφ}{dt}=\frac{\dot{φ}}{\dot{t}} =\frac{A}{r^2} \frac{𝒽}{𝓀}=\sqrt{\frac{c^2 \:r_s}{2 \,r^3}}

.

• En supposant pour simplifier que le spin est dans le plan équatorial (

S^2=0

), on obtient :

$\displaystyle \dot{S^0}+\frac{A'}{2 \,A} \:S^1 \:U^0=0$ ;
$\displaystyle \dot{S^1}+\frac{A'}{2 \,C} \:S^0 \:U^0-\frac{r}{C} \,S^3 \:U^3=0$ ;
$\displaystyle \dot{S^3}+\frac{1}{r}\,S^1 \:U^3=0$ .

• Dans un référentiel où le gyroscope est en mouvement, on peut utiliser l'orthogonalité :

g_{αβ} \:S^α \:U^β=A \:S^0 \:U^0-r^2 \:S^3 \:U^3=0

; ainsi :

\displaystyle S^0=\frac{r^2}{A} \frac{Ω}{c} \:S^3

.

La première équation équivaut donc à la troisième et, en notant

\displaystyle ϖ=\frac{Ω}{\dot{t}}

, on se ramène au système simplifié :

\displaystyle \frac{dS^1}{dt\,}-\frac{r}{Ω}\, ϖ^2 \:S^3=0

;

\displaystyle \frac{dS^3}{dt\,}+\frac{r}{Ω} \,S^1=0

.

En choisissant l'origine du temps à l'instant où

S^1

est maximum, on obtient (le spin est ainsi initialement orienté dans la direction radiale) :

$S^1(t)=S^1 (0) \:\cos(-ϖ \,t)$ ; $\displaystyle S^3 (t)=\frac{Ω}{r \,ϖ} \,S^1 (0) \:\sin(-ϖ \,t)$ .

• Le gyroscope est en orbite à la vitesse angulaire

Ω

; par rapport à la direction radiale locale (tournant comme le mouvement orbital), le spin précesse à la vitesse angulaire

-ϖ

avec

\displaystyle ϖ=Ω \:\sqrt{1-\frac{3 \,r_s}{2 \,r}}<Ω

.

Si l'effet était négligeable (

ϖ≈Ω

), la direction du gyroscope resterait fixe par rapport à un observateur “à l'infini”. Plus la correction est importante, plus le gyroscope prend de retard dans la “compensation” de

Ω

par rapport à l'infini, donc il précesse légèrement dans le sens de

Ω

.
Pour un tour, le décalage angulaire est :

\displaystyle α=2π \:\left(1-\sqrt{1-\frac{3 \,r_s}{2 \,r}}\right)≈2π \,\frac{3 \,r_s}{4 \,r}

(généralement faible car

r≫r_s

).

La vitesse de précession est :

$\displaystyle ω=Ω-ϖ=Ω .\left(1-\sqrt{1-\frac{3 \,r_s}{2 \,r}}\right)≈\frac{3 \,r_s}{4 \,r} \sqrt{\frac{c^2 \:r_s}{2 \,r^3}}=\frac{3 \,c}{2 \,r} \:\left(\frac{r_s}{2 \,r}\right)^{3/2}$ .

• Le rayon de Schwarzschild de la Terre est

r_s≈8,9 \:\mathrm{mm}

. Pour une orbite de faible altitude (

r≈7000 \:\mathrm{km}

) on obtient :

ω≈1,03.{10}^{-12} \:\mathrm{rad.s^{-1}}≈6,7''/\mathrm{an}

.

Cela a été bien vérifié par le satellite “gravity probe B”, mais les incertitudes dues aux blindages électrostatique et magnétique nécessitent de grandes précautions.

📖 exercices n° XXII et XXIII.