CHAMP CENTRAL SYMÉTRIQUE EXTÉRIEUR - corrigé des exercices

I. Coordonnées “harmoniques”

• On peut considérer :

Γ^β=g^{μν} \:g^{βγ} \:Γ_{γμν}=\frac{1}{2} g^{μν} \:g^{βγ} \:(∂_μ g_{νγ}+∂_ν g_{μγ}-∂_γ g_{μν} )=0

.
• Par ailleurs :

0=∂_ν \left(δ_μ^β \right)=∂_ν \left(g^{βγ} \,g_{μγ} \right)

donc

g^{βγ} \:∂_ν g_{μγ}=-g_{μγ} \:∂_ν g^{βγ}

;

\frac{1}{2} g^{μν} \:g^{βγ} \:\left(∂_μ g_{νγ}+∂_ν g_{μγ} \right)=-\frac{1}{2} g^{μν} \:\left(g_{νγ} \:∂_μ g^{βγ}+g_{μγ} \:∂_ν g^{βγ} \right)

=-\frac{1}{2} \left(δ_γ^μ \:∂_μ g^{βγ}+δ_γ^ν \:∂_ν g^{βγ} \right)=-∂_γ g^{βγ}

• En outre, la matrice inverse de

g_{μν}

peut s'écrire

\displaystyle g^{μν}=\frac{γ^{μν}}{g}

en fonction du déterminant

g

et des mineurs

γ^{μν}

des

g_{μν}

; ainsi :

∂_γ g=γ^{μν} \:∂_γ g_{μν}=g \:g^{μν} \:∂_γ g_{μν}

;

\displaystyle -\frac{1}{2} g^{μν} \:g^{βγ} \:∂_γ g_{μν}=-\frac{1}{2} g^{βγ} \,\frac{∂_γ g}{g}=-g^{βγ} \,\frac{∂_γ \left(\sqrt{|g|}\right)}{\sqrt{|g|}}

;

\displaystyle Γ^β=-∂_γ g^{βγ}-g^{βγ} \:\frac{∂_γ \left(\sqrt{|g|}\right)}{\sqrt{|g|}}=-\frac{∂_γ \left(\sqrt{|g|} \:g^{βγ} \right)}{\sqrt{|g|}}

• Par conséquent

Γ^β=0

correspond à :

∂_γ \left(\sqrt{|g|} \:g^{βγ} \right)=0

II. Coordonnées “harmoniques”

• La transformation de la connexion peut s'écrire :

Γ_{\phantom{.}αβ}^κ=∂_α \underline{x}^μ \:∂_β \underline{x}^ν \:\underline{∂}_ρ x^κ \:\underline{Γ}_{\phantom{.}μν}^ρ+∂_{αβ} \underline{x}^μ \:\underline{∂}_μ x^κ

; ainsi :

Γ^κ=∂_α \underline{x}^μ \:∂_β \underline{x}^ν \:g^{αβ} \: \underline{∂}_ρ x^κ \:\underline{Γ}_{\phantom{.}μν}^ρ+g^{αβ} \:∂_{αβ} \underline{x}^μ \:\underline{∂}_μ x^κ=\underline{∂}_ρ x^κ \:\underline{Γ}^ρ+g^{αβ} \:∂_{αβ} \underline{x}^μ \:\underline{∂}_μ x^κ

.
• Ceci peut aussi s'écrire inversement :

\underline{Γ}^ρ=∂_κ \underline{x}^ρ \:Γ^κ-g^{αβ} \:∂_{αβ} \underline{x}^ρ

2.a.

• Le d'alembertien correspond à :

❑φ=g^{αβ} \:D_α (D_β φ)=g^{αβ} \:D_α (∂_β φ)=g^{αβ} \:[∂_α (∂_β φ)-Γ_{\phantom{.}βα}^γ \:∂_γ φ]

;

❑φ=g^{αβ} \:∂_{αβ} φ-Γ^γ \:∂_γ φ

2.b.

• En partant de coordonnées quelconques (

Γ^β≠0

), la recherche d'un changement de repérage pour obtenir des coordonnées “harmoniques” correspond à la condition :

\underline{Γ}^ρ=∂_κ \underline{x}^ρ \:Γ^κ-g^{αβ} \:∂_{αβ} \underline{x}^ρ=0

.
• Or, pour chaque

ρ

fixé, en considérant

\underline{x}^{(ρ)}

comme si c'était une fonction scalaire, l'équation précédente peut s'écrire :

❑\underline{x}^{(ρ)}=g^{αβ} \:∂_{αβ} \underline{x}^{(ρ)}-Γ^γ \:∂_γ \underline{x}^{(ρ)}=0

.
◊ remarque : il s'agit évidemment d'un abus de langage, puisqu'au sens du calcul tensoriel les composantes d'un vecteur ne se comportent pas comme des “scalaires” (c'est à dire ne sont pas invariantes) lors des changements de coordonnées ; ce sont des scalaires au sens algébrique, mais non des “scalaires purs” au sens tensoriel.

III. Coordonnées “harmoniques” et limite newtonienne

1.a.

• La condition d'harmonicité correspond à :

Γ^β=g^{μν} \:Γ_{\phantom{.}μν}^β=\frac{1}{2} g^{μν} \:g^{βγ} \:\left(∂_μ g_{νγ}+∂_ν g_{μγ}-∂_γ g_{μν} \right)=0

.
• Dans l'approximation du champ faible, en négligeant les termes du second ordre :

g^{μν} =η^{μν}-h^{μν}

(pour respecter la condition :

δ_ρ^μ=g^{μν} \:g_{νρ}=δ_ρ^μ+h_{\;\:ρ}^μ-h_{\;\:ρ}^μ

) ;

Γ^β=\frac{1}{2} η^{μν} \:η^{βγ} \:\left(∂_μ h_{νγ}+∂_ν h_{μγ}-∂_γ h_{μν} \right)=∂_μ \left(h^{μβ}-\frac{1}{2} η^{μβ} \:h\right)=0

1.b.

• Le tenseur de Ricci :

R_{μν}=R_{\phantom{.}μλν}^λ=∂_λ Γ_{\phantom{.}μν}^λ-∂_ν Γ_{\phantom{.}μλ}^λ+Γ_{\phantom{.}μν}^ρ \:Γ_{\phantom{.}ρλ}^λ-Γ_{\phantom{.}μλ}^ρ \:Γ_{\phantom{.}νρ}^λ

peut aussi s'écrire :

R_{μν}=\frac{1}{2} g^{κλ} \:\left(∂_{μλ} g_{κν}+∂_{κν} g_{μλ}-∂_{κλ} g_{μν}-∂_{μν} g_{κλ} \right)+g^{κλ} \:g_{αβ} \:\left(Γ_{\phantom{.}μλ}^α \:Γ_{\phantom{.}κν}^β-Γ_{\phantom{.}κλ}^α \:Γ_{\phantom{.}μν}^β \right)

.
• Pour un champ faible :

R_{μν}=∂_λ Γ_{\phantom{.}μν}^λ-∂_ν Γ_{\phantom{.}μλ}^λ=\frac{1}{2} η^{κλ} \:\left(∂_{μλ} h_{κν}+∂_{κν} h_{μλ}-∂_{κλ} h_{μν}-∂_{μν} h_{κλ} \right)

;

R_{μν}=-\frac{1}{2}❑h_{μν}+\frac{1}{2} η^{κλ} \:\left(∂_{μλ} h_{κν}+∂_{κν} h_{μλ}-∂_{μν} h_{κλ} \right)

;

R_{μν}=-\frac{1}{2}❑h_{μν}+\frac{1}{2} \left(η_{κν} \:∂_{μλ} h^{λκ}+η_{κμ} \:∂_{νλ} h^{λκ}-∂_{μν}\:h\right)

• En utilisant les coordonnées “harmoniques” :

R_{μν}=-\frac{1}{2}❑h_{μν}+\frac{1}{2} \left(\frac{1}{2} η_{κν} \:η^{λκ} \:∂_{μλ}h+\frac{1}{2} η_{κμ} \:η^{λκ} \:∂_{νλ}h-∂_{μν}h\right)

;

R_{μν}=-\frac{1}{2}❑h_{μν}+\frac{1}{2} \left(\frac{1}{2} ∂_{μν}h+\frac{1}{2} ∂_{νμ}h-∂_{μν}h\right)=-\frac{1}{2}❑h_{μν}

• On peut remarquer que, dans l'espace sans matière, les équations du champ de gravitation correspondent à :

R_{μν}=-\frac{1}{2}❑h_{μν}=0

. Ceci revient à dire (conformément aux propriétés usuelles de l'équation de d'Alembert) que les perturbations du champ se propagent à la vitesse de la lumière.

• Les équations du mouvement correspondent aux géodésiques :

\displaystyle \frac{d^2 x^i}{{ds}^2} +Γ_{\phantom{.}μν}^i \,\frac{dx^μ}{ds} \frac{dx^ν}{ds}=0

.
• Pour les mouvements lents,

dx^k

est négligeable en comparaison de

dx^0=c \,dt≈ds

, donc les équations se limitent à :

\displaystyle \frac{d^2 x^i}{{dt}^2} ≈-c^2 \:Γ_{\phantom{.}00}^i

.
• Puisque les dérivées temporelles du champ sont négligeables :

Γ_{\phantom{.}00}^i≈-\frac{1}{2} η^{ik}\:∂_k g_{00}≈-\frac{1}{2} ∂^i h_{00}

; les équations peuvent donc s'écrire :

\displaystyle \frac{d^2 x^i}{{dt}^2} ≈\frac{1}{2} c^2 \:∂^i h_{00}

.
• Dans l'exemple “matière pure” :

T_{μν}=μ \:U_μ \,U_ν

; pour des mouvements lents, les équations de la gravitation peuvent s'écrire :

R_{00}=χ .(T_{00}-\frac{1}{2} η_{00} \:T)≈\frac{1}{2} χ \,μ \,c^2

.
• Pour les champs faibles en coordonnées “harmoniques” :

R_{μν}=-\frac{1}{2}❑h_{μν}

; on obtient donc ainsi :

❑h_{00}≈-χ \,μ \,c^2

, puis dans l'espace autour d'une masse

m

“ponctuelle” :

\displaystyle h_{00}≈-\frac{χ \,m \,c^2}{4π \,r}

.
• Cela donne pour les équations du mouvement :

\displaystyle \frac{d^2 x^i}{{dt}^2} ≈-\frac{χ \,m \,c^4}{8π} \,∂^i \left(\frac{1}{r}\right)

. La comparaison avec la loi de Newton :

\displaystyle \frac{d^2 x^i}{{dt}^2} ≈-𝒢 \,m \:∂^i \left(\frac{1}{r}\right)

conduit à la correspondance :

\displaystyle χ=\frac{8π \,𝒢}{c^4}

IV. Coordonnées “harmoniques”

1.a.	• La métrique correspond à : ${ds}^2=R^2 \:{dθ}^2+R^2 \:\sin^2⁡(θ) \:{dφ}^2$ ; $g_{22}=R^2$ et $g_{33}=R^2 \: \sin^2⁡(θ)$ . ◊ remarque : on réserve l'indice 1 pour la coordonnée radiale utilisée dans la suite. • Ainsi : $\displaystyle g^{22}=\frac{1}{R^2}$ et $\displaystyle g^{33}=\frac{1}{R^2\:\sin^2⁡(θ)}$ .

1.b.	• La connexion correspond à : $Γ_{233}=-R^2 \: \sin⁡(θ) \: \cos⁡(θ)$ et $Γ_{323}=Γ_{332}=R^2 \: \sin⁡(θ) \: \cos⁡(θ)$ . • Ainsi : $Γ_{\phantom{.}33}^2=-\sin⁡(θ) \: \cos⁡(θ)$ et $\displaystyle Γ_{\phantom{.}23}^3=Γ_{\phantom{.}32}^3=\frac{\cos⁡(θ)}{\sin⁡(θ)}$ .

1.c.	• Ces coordonnées ne sont pas “harmoniques” : $Γ^3=0$ mais $\displaystyle Γ^2=g^{33} \:Γ_{\phantom{.}33}^2=-\frac{\cos⁡(θ)}{R^2 \: \sin⁡(θ)}≠0$ .

2.a.

• Puisque la métrique et la connexion ne font pas intervenir

φ

, on peut chercher des coordonnées “harmoniques” en conservant

φ

(on conserve ainsi

Γ^3=0

2.b.

• Si on recherche une expression

ζ(θ)

telle que les coordonnées

(ζ \:; φ)

soient “harmoniques”, il faut et il suffit (selon la loi de changement de coordonnées) qu'elle respecte :

\underline{Γ}^2=∂_2 ζ \:\:Γ^2-g^{22} \:∂_{22} ζ=0

.
• En notant

\displaystyle Ζ=\frac{dζ}{dθ}

, ceci donne :

\displaystyle \cos⁡(θ) \:Ζ+\sin⁡(θ) \:\frac{dΖ}{dθ}=0

;

\sin⁡(θ) \:Ζ=Cste

.
• On recherche alors

ζ

telle que :

\displaystyle \frac{dζ}{dθ}=\frac{Cste}{\sin⁡(θ)}

. On peut choisir la solution

ζ=\mathrm{arctanh}⁡(\cos⁡(θ))

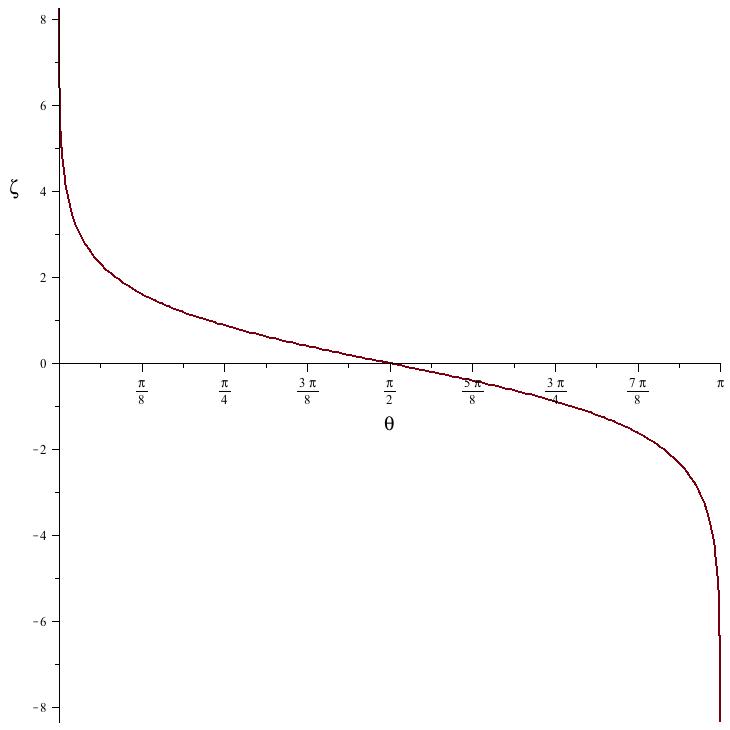
2.c.

• La représentation graphique a l'allure ci-après. On y constate que la quantité

ζ

ressemble à une “coordonnée axiale” telle que les pôles de la sphère soient à l'infini.

2.d.

• Avec ces coordonnées, la métrique correspond à :

\displaystyle {ds}^2=R^2 \:\sin^2⁡(θ) \:({dζ}^2+{dφ}^2 )=\frac{R^2}{\cosh^2⁡(ζ)} \:({dζ}^2+{dφ}^2 )

;

\displaystyle g_{22}=g_{33}=\frac{R^2}{\cosh^2⁡(ζ)}

;

\displaystyle g^{22}=g^{33}=\frac{\cosh^2⁡(ζ)}{R^2}

• La connexion correspond à :

\displaystyle Γ_{233}=\frac{\sinh⁡(ζ)}{R^2 \:\cosh^3⁡(ζ)}

\displaystyle Γ_{222}=Γ_{323}=Γ_{332}=-\frac{\sinh⁡(ζ)}{R^2 \:\cosh^3⁡(ζ)}

.
• Ainsi :

\displaystyle Γ_{\phantom{.}33}^2=\frac{\sinh⁡(ζ)}{\cosh⁡(ζ)}

\displaystyle Γ_{\phantom{.}22}^2=Γ_{\phantom{.}23}^3=Γ_{\phantom{.}32}^3=-\frac{\sinh⁡(ζ)}{\cosh⁡(ζ)}

.
◊ remarque : on vérifie que

Γ^2=g^{22} \:Γ_{\phantom{.}22}^2+g^{33} \:Γ_{\phantom{.}33}^2=0

3.a.

• La métrique correspond à :

{ds}^2={dr}^2+r^2 \:{dθ}^2+r^2 \: \sin^2⁡(θ) \:{dφ}^2

• Ainsi :

g_{11}=1

;

g_{22}=r^2

;

g_{33}=r^2 \: \sin^2⁡(θ)

;

g^{11}=1

;

\displaystyle g^{22}=\frac{1}{r^2}

;

\displaystyle g^{33}=\frac{1}{r^2 \:\sin^2⁡(θ)}

• La connexion correspond à :

Γ_{122}=-r

Γ_{212}=r

;

Γ_{133}=-r \:\sin^2⁡(θ)

Γ_{313}=r \:\sin^2⁡(θ)

;

Γ_{233}=-r^2 \: \sin⁡(θ) \: \cos⁡(θ)

Γ_{323}=r^2 \: \sin⁡(θ) \: \cos⁡(θ)

• Ainsi :

Γ_{\phantom{.}22}^1=-r

\displaystyle Γ_{\phantom{.}12}^2=Γ_{\phantom{.}13}^3=\frac{1}{r}

;

Γ_{\phantom{.}33}^1=-r \:\sin^2⁡(θ)

;

Γ_{\phantom{.}33}^2=-\sin⁡(θ) \: \cos⁡(θ)

\displaystyle Γ_{\phantom{.}23}^3=\frac{\cos⁡(θ)}{\sin⁡(θ)}

.
• Ces coordonnées ne sont pas “harmoniques” :

Γ^3=0

mais

\displaystyle Γ^1=g^{22} \:Γ_{\phantom{.}22}^1+g^{33} \:Γ_{\phantom{.}33}^1=-\frac{2}{r}≠0

\displaystyle Γ^2=g^{33} \:Γ_{\phantom{.}33}^2=-\frac{\cos⁡(θ)}{r^2 \:\sin⁡(θ)}≠0

.
• Si on recherche une expression

ζ(θ)

on obtient la même équation que précédemment (

r

se simplifie de même que

R

) ; on peut choisir la solution

ζ=\mathrm{arctanh⁡}(\cos⁡(θ) )

.
• Si on recherche de même une expression

ρ(r)

on obtient l'équation :

\underline{Γ}^1=∂_1 ρ \:\:Γ^1-g^{11} \:∂_{11} ρ=0

, c'est-à-dire :

\displaystyle \frac{2}{r} \,∂_1 ρ+∂_{11} ρ=0

.
• En notant

Ρ=\frac{dρ}{dr}

, ceci donne :

\displaystyle 2 \,r \:Ρ+r^2 \,\frac{dΡ}{dr}=0

;

r^2 \:Ρ=Cste

.
• On recherche alors

ρ

telle que :

\displaystyle \frac{dρ}{dr}=\frac{Cste}{r^2}

. On peut choisir la solution

\displaystyle ρ=\frac{1}{r}

.
◊ remarque : on constate que les coordonnées harmoniques (en général), bien que simplifiant certains calculs (ici on retrouve la variable

𝓊

de Binet), n'ont pas forcément une compréhension intuitive évidente.

3.b.

• Avec ces coordonnées, la métrique correspond à :

\displaystyle {ds}^2=\frac{1}{ρ^4} \:{dρ}^2+\frac{1}{ρ^2\: \cosh^2⁡(ζ)} \:({dζ}^2+{dφ}^2 )

;

\displaystyle g_{11}=\frac{1}{ρ^4}

;

\displaystyle g_{22}=g_{33}=\frac{1}{ρ^2 \:\cosh^2⁡(ζ)}

;

g^{11}=ρ^4

;

g^{22}=g^{33}=ρ^2 \: \cosh^2⁡(ζ)

• La connexion correspond à :

\displaystyle Γ_{111}=-\frac{2}{ρ^5}

;

\displaystyle Γ_{122}=Γ_{133}=\frac{1}{ρ^3 \:\cosh^2⁡(ζ)}

\displaystyle Γ_{212}=Γ_{313}=-\frac{1}{ρ^3 \: \cosh^2⁡(ζ)}

;

\displaystyle Γ_{233}=\frac{\sinh⁡(ζ)}{ρ^2 \:\cosh^3⁡(ζ)}

\displaystyle Γ_{222}=Γ_{323}=-\frac{\sinh⁡(ζ)}{ρ^2 \:\cosh^3⁡(ζ)}

• Ainsi :

\displaystyle Γ_{\phantom{.}11}^1=-\frac{2}{ρ}

;

\displaystyle Γ_{\phantom{.}22}^1=Γ_{\phantom{.}33}^1=\frac{ρ}{\cosh^2⁡(ζ)}

\displaystyle Γ_{\phantom{.}12}^2=Γ_{\phantom{.}13}^3=-\frac{1}{ρ}

;

\displaystyle Γ_{\phantom{.}33}^2=\frac{\sinh⁡(ζ)}{\cosh⁡(ζ)}

\displaystyle Γ_{\phantom{.}22}^2=Γ_{\phantom{.}23}^3=-\frac{\sinh⁡(ζ)}{\cosh⁡(ζ)}

◊ remarque : on obtient comme précédemment

Γ^2=g^{22} \:Γ_{\phantom{.}22}^2+g^{33} \:Γ_{\phantom{.}33}^2=0

; on vérifie que de plus

Γ^1=g^{11} \:Γ_{\phantom{.}11}^1+g^{22} \:Γ_{\phantom{.}22}^1+g^{33} \:Γ_{\phantom{.}33}^1=0

V. Coordonnées “harmoniques”

1.a.

• La métrique correspond à :

{ds}^2={dr}^2+r^2 \:{dθ}^2+{dz}^2

• Ainsi :

g_{11}=1

;

g_{22}=r^2

;

g_{33}=1

;

g^{11}=1

;

\displaystyle g^{22}=\frac{1}{r^2}

;

g^{33}=1

1.b.

• La connexion correspond à :

Γ_{122}=-r

Γ_{212}=r

.
• Ainsi :

Γ_{\phantom{.}22}^1=-r

\displaystyle Γ_{\phantom{.}12}^2=\frac{1}{r}

1.c.

• Ces coordonnées ne sont pas “harmoniques” :

Γ^2=0

Γ^3=0

mais

\displaystyle Γ^1=g^{22} \:Γ_{\phantom{.}22}^1=-\frac{1}{r}≠0

2.a.

• Si on cherche

ρ(r)

qui soit harmonique, on obtient l'équation :

\underline{Γ}^1=∂_1 ρ \:\:Γ^1-g^{11} \:∂_{11} ρ=0

, c'est-à-dire :

\displaystyle \frac{1}{r} \:∂_1 ρ+∂_{11} ρ=0

.
• En notant

\displaystyle Ρ=\frac{dρ}{dr}

, ceci donne :

\displaystyle Ρ+r \:\frac{dΡ}{dr}=0

;

r \:Ρ=Cste

.
• On recherche alors

ρ

telle que :

\displaystyle \frac{dρ}{dr}=\frac{Cste}{r}

. On peut choisir la solution

ρ=\ln(r)

2.b.

• Avec ces coordonnées, la métrique correspond à :

{ds}^2=\mathrm{e}^{2ρ} \:({dρ}^2+{dθ}^2 )+{dz}^2

;

g_{11}=g_{22}=\mathrm{e}^{2ρ}

;

g_{33}=1

;

g^{11}=g^{22}=\mathrm{e}^{-2ρ}

;

g^{33}=1

• La connexion correspond à :

Γ_{111}=Γ_{212}=\mathrm{e}^{2ρ}

;

Γ_{122}=\mathrm{e}^{-2ρ}

.
• Ainsi :

Γ_{\phantom{.}11}^1=Γ_{\phantom{.}12}^2=1

;

Γ_{\phantom{.}22}^1=-1

.
◊ remarque : on vérifie qu'on obtient

Γ^1=g^{11} \:Γ_{\phantom{.}11}^1+g^{22} \:Γ_{\phantom{.}22}^1=0

VI. Champ statique à symétrie sphérique

• On obtient ainsi :

g_{00}=\mathrm{e}^{2α}

;

g_{11}=-\mathrm{e}^{2β}

;

g_{22}=-r^2

;

g_{33}=-r^2 \:\sin^2⁡(θ)

;

g^{00}=\mathrm{e}^{-2α}

;

g^{11}=-\mathrm{e}^{-2β}

;

\displaystyle g^22=-\frac{1}{r^2}

;

\displaystyle g^{33}=-\frac{1}{r^2 \:\sin^2⁡(θ)}

;

Γ_{001}=-Γ_{100}=α' \:\mathrm{e}^{2α}

;

Γ_{111}=-β' \:\mathrm{e}^{2β}

;

Γ_{221}=-Γ_{122}=-r

;

Γ_{331}=-Γ_{133}=-r \: \sin^2⁡(θ)

;

Γ_{332}=-Γ_{233}=-r^2 \: \sin⁡(θ) \: \cos⁡(θ)

;

Γ_{\phantom{.}01}^0=α'

;

Γ_{\phantom{.}00}^1=α' \:\mathrm{e}^{2α-2β}

;

Γ_{\phantom{.}11}^1=β'

;

\displaystyle Γ_{\phantom{.}12}^2=Γ_{\phantom{.}13}^3=\frac{1}{r}

;

Γ_{\phantom{.}22}^1=-r \:\mathrm{e}^{-2β}

;

Γ_{\phantom{.}33}^1=-r \: \sin^2⁡(θ) \:\mathrm{e}^{-2β}

;

Γ_{\phantom{.}23}^3=\mathrm{cotan}(θ)

;

Γ_{\phantom{.}33}^2=-\sin⁡(θ) \: \cos⁡(θ)

• Si on cherche la métrique dans le vide entourant l'astre, les équations du champ correspondent à :

R_{μν}=0

; en simplifiant :

\displaystyle α''-α' \:β'+{α'}^2+\frac{2}{r}\,α'=0

(

R_{00}

) ;

\displaystyle α''-α' \:β'+{α'}^2-\frac{2}{r}\,β'=0

(

R_{11}

) ;

r \:α'-r \:β'-\mathrm{e}^{2β}+1=0

(

R_{22}

R_{33}

• On en déduit :

α'=-β'

(

R_{00}

R_{11}

) et

2 \,r \:β'+\mathrm{e}^{2β}-1=0

(report dans la troisième).

• La résolution donne :

α=-β

(puisque la limite à l'infini est

0

) ;

r .(-2 \,β' \:\mathrm{e}^{-2β} )+\mathrm{e}^{-2β}=1

;

r \:\mathrm{e}^{-2β}=r+Cste

;

\displaystyle \mathrm{e}^{-2β}=\mathrm{e}^{2α}=1-\frac{r_s}{r}

• La constante

r_s

est imposée par l'équivalence des champs faibles :

\displaystyle \mathrm{e}^{2α}≈1+\frac{2 \,𝒱}{c^2} ≈1-\frac{2 \,𝒢 \,M}{c^2 \:r}

.
• On doit aussi s'assurer que l'autre équation (

R_{00}

R_{11}

) est vérifiée. D'après ce qui précède, la simplification donne :

\displaystyle \frac{α''}{α'}+2 \,α'+\frac{2}{r}=0

;

\ln⁡(α')+\ln⁡(\mathrm{e}^{2α} )+2 \:\ln⁡(r)=Cste

;

\displaystyle 2 \,α' \:\mathrm{e}^{2α}=(\mathrm{e}^{2α} \,)'=\frac{Cste}{r^2}

; or, ceci correspond à la dérivée de l'équation précédente.

VII. Champ à symétrie sphérique

• Pour un champ à symétrie sphérique, la forme la plus générale peut s'écrire :

{ds}^2=A(r,t) \:c^2 \,{dt}^2+B(r,t) \:c \,dt \:dr-C(r,t) \:{dr}^2-D(r,t).[{dθ}^2+\sin^2⁡(θ) \:{dφ}^2]

• On peut alors effectuer un changement de coordonnées :

\underline{r}(r,t)

\underline{t}(r,t)

de façon à simplifier deux des quatre coefficients, par exemple

B

D

. Plus précisément, la condition

D=r^2

impose

\underline{r}(r,t)

puis la condition

B=0

impose

\underline{t}(r,t)

2.a.

• Pour une métrique de la forme :

{ds}^2=A(r,t) \:c^2 \,{dt}^2-C(r,t) \:{dr}^2-r^2.[{dθ}^2+\sin^2⁡(θ) \:{dφ}^2]

, on obtient :

g_{00}=A

;

g_{11}=-C

;

g_{22}=-r^2

;

g_{33}=-r^2 \: \sin^2⁡(θ)

;

\displaystyle g^{00}=\frac{1}{A}

;

\displaystyle g^{11}=-\frac{1}{C}

;

\displaystyle g^{22}=-\frac{1}{r^2}

;

\displaystyle g^{33}=-\frac{1}{r^2 \:\sin^2⁡(θ)}

;

\displaystyle Γ_{000}=\frac{\dot{A}}{2}

;

\displaystyle Γ_{001}=-Γ_{100}=\frac{A'}{2\:}

;

\displaystyle Γ_{011}=-Γ_{110}=\frac{\dot{C}}{2}

;

\displaystyle Γ_{111}=-\frac{C'}{2\,}

;

Γ_{221}=-Γ_{122}=-r

;

Γ_{331}=-Γ_{133}=-r \: \sin^2⁡(θ)

;

Γ_{332}=-Γ_{233}=-r^2 \: \sin⁡(θ) \: \cos⁡(θ)

;

\displaystyle Γ_{\phantom{.}00}^0=\frac{\dot{A}}{2\,A}

;

\displaystyle Γ_{\phantom{.}01}^0=\frac{A'}{2\,A}

;

\displaystyle Γ_{\phantom{.}00}^1=\frac{A'}{2\,C}

;

\displaystyle Γ_{\phantom{.}11}^0=\frac{\dot{C}}{2\,A}

;

\displaystyle Γ_{\phantom{.}10}^1=\frac{\dot{C}}{2\,C}

;

\displaystyle Γ_{\phantom{.}11}^1=\frac{C'}{2\,C}

;

\displaystyle Γ_{\phantom{.}21}^2=Γ_{\phantom{.}31}^3=\frac{1}{r}

;

\displaystyle Γ_{\phantom{.}22}^1=-\frac{r}{C}

;

\displaystyle Γ_{\phantom{.}33}^1=-\frac{r}{C} \,\sin^2⁡(θ)

;

Γ_{\phantom{.}23}^3=\mathrm{cotan}(θ)

;

Γ_{\phantom{.}33}^2=-\sin⁡(θ) \: \cos⁡(θ)

2.b.

• Si on cherche la métrique dans le vide entourant l'astre, les équations du champ correspondent à :

R_{μν}=0

; en simplifiant :

\displaystyle \frac{4}{r} \,A \,C \,A'-A \,A' \,C'+2 \,A \,C \,A''+A \,\dot{C}^2-2 \,A \,C \,\ddot{C}+C \,\dot{A} \,\dot{C}-C \,{A'}^2=0

(

R_{00}

) ;

\dot{C}=0

(

R_{01}

) ;

\displaystyle -\frac{4}{r} \,A^2 \,C'-A \,A' \,C'+2 \,A \,C \,A''+A \,\dot{C}^2-2 \,A \,C \,\ddot{C}+C \,\dot{A} \,\dot{C}-C\,{A'}^2=0

(

R_{11}

) ;

\displaystyle -C \,A'+A \,C'+\frac{2}{r} \,A \,C .(C-1)=0

(

R_{22}

R_{33}

• On constate que

C=C(r)

ne dépend pas du temps ; ainsi en combinant et simplifiant :

-C \,A'=A \,C'

;

\displaystyle \frac{2}{r}\,A'+A''=0

;

\displaystyle C'+\frac{1}{r} \,C .(C-1)=0

2.c.

• La première équation donne

A \,C=Cste

; puis

A \,C=1

car la limite à l'infini est

A→1

C→1

. Ceci signifie que la métrique est forcément statique (dès lors qu'on a imposé

D=r^2

indépendant du temps).
◊ remarque : en particulier, un astre à symétrie sphérique ne peut pas émettre d'ondes gravitationnelles strictement sphériques (donc monopolaires) dans l'espace environnant.
• La seconde équation donne

\displaystyle A'=\frac{r_s}{r^2}

puis

\displaystyle A=1-\frac{r_s}{r}

; la constante est imposée par la limite des champs faibles :

\displaystyle A≈1+\frac{2 \,𝒱}{c^2} ≈1-\frac{2 \,𝒢 \,M}{c^2 \:r}

.
• Il faut alors s'assurer que la troisième équation est vérifiée. Compte tenu de

A \,C=1

, la simplification donne :

\displaystyle A \,C'+\frac{1}{r} \,(C-1)=0

; or ceci peut se mettre sous la forme :

-r \,A'+1=A

, qui est automatiquement vérifiée.
◊ remarque : il peut être intéressant de constater que la métrique ainsi obtenue ne dépend pas de ce qu'il advient de la répartition de masse de l'astre (explosion, effondrement...), pourvu qu'elle respecte la symétrie sphérique ; ceci (correspondant au “théorème de Birkhoff”) généralise d'une certaine façon une conséquence connue du théorème de Gauss en gravitation non relativiste : le champ “extérieur” ne dépend pas dans ce cas de la répartition de la masse.

3.a.

• Dans la mesure où un astre sphérique ne peut pas émettre d'ondes à symétrie sphériques, on peut se demander comment il peut exercer un champ extérieur.

3.b.

• La situation est analogue pour l'électromagnétisme (conformément au théorème de Gauss). En fait il n'existe pas d'ondes sphériques (ondes “monopolaires”) dans le vide car les ondes électromagnétiques sont transversales. Les ondes usuellement nommées “sphériques” (par abus de langage) ne sont que l'approximation à grande distance d'ondes dipolaires.
• Bien que le champ à symétrie rigoureusement sphérique soit une très bonne approximation pour un système qui ne respecte pas exactement cette symétrie, des petites oscillations d'un tel système permettent l'émission d'ondes, par exemple dipolaires (par oscillation d'un noyau plus dense) ou quadripolaires (par allongement/aplatissement).

• L'impossibilité d'ondes sphériques transversales vient de l'impossibilité de “peigner” les vecteurs tangents à la surface d'une sphère sans avoir au moins un “épi”. Par exemple, si on les “peigne” selon les méridiens (comme

\overset{→}{u_θ}

) ou selon les parallèles (comme

\overset{→}{u_φ}

) il y a dans l'un ou l'autre cas un épi à chaque pôle (la direction de

\overset{→}{u_θ}

\overset{→}{u_φ}

y est indéterminée).
• La situation est en fait simplement analogue pour le champ de gravitation ; un astre “à peu près” sphérique peut émettre des ondes gravitationnelles.

VIII. Coordonnées “isotropes”

1.a.

• On obtient ainsi :

g_{00}=\mathrm{e}^{2α}

;

g_{11}=-\mathrm{e}^{2β}

;

g_{22}=-\mathrm{e}^{2β} \:\underline{r}^2

;

g_{33}=-\mathrm{e}^{2β} \: \underline{r}^2 \: \sin^2⁡(θ)

;

g^{00}=\mathrm{e}^{-2α}

;

g^{11}=-\mathrm{e}^{-2β}

;

\displaystyle g^{22}=-\mathrm{e}^{2β} \: \frac{1}{\underline{r}^2}

;

\displaystyle g^{33}=-\mathrm{e}^{2β} \: \frac{1}{\underline{r}^2 \: \sin^2⁡(θ)}

;

Γ_{001}=-Γ_{100}=α' \:\mathrm{e}^{2α}

;

Γ_{111}=-β' \:\mathrm{e}^{2β}

;

Γ_{221}=-Γ_{122}=-\underline{r} \:\mathrm{e}^{2β} \:(1+\underline{r} \:β')

;

Γ_{331}=-Γ_{133}=-\underline{r} \: \sin^2⁡(θ) \: \mathrm{e}^{2β} \: (1+\underline{r} \: β')

;

Γ_{332}=-Γ_{233}=-\underline{r}^2 \: \mathrm{e}^{2β} \: \sin⁡(θ) \: \cos⁡(θ)

;

Γ_{\phantom{.}01}^0=α'

;

Γ_{\phantom{.}00}^1=α' \:\mathrm{e}^{2α-2β}

;

Γ_{\phantom{.}11}^1=β'

;

\displaystyle Γ_{\phantom{.}12}^2=Γ_{\phantom{.}13}^3=\frac{1}{\underline{r}} \,(1+\underline{r} \:β')

;

Γ_{\phantom{.}22}^1=-\underline{r} .(1+\underline{r} \: β')

;

Γ_{\phantom{.}33}^1=-\underline{r} \: \sin^2⁡(θ) \: (1+\underline{r} \: β')

;

Γ_{\phantom{.}23}^3=\mathrm{cotan}(θ)

;

Γ_{\phantom{.}33}^2=-\sin⁡(θ) \: \cos⁡(θ)

1.b.

• Si on cherche la métrique dans le vide entourant l'astre, les équations du champ correspondent à :

R_{μν}=0

; en simplifiant :

\displaystyle α''+α' \:β'+{α'}^2-\frac{2}{\underline{r}} \:α'=0

(

R_{00}

) ;

\displaystyle α''-α' \:β'+{α'}^2+\frac{2}{\underline{r}} \,β'+2 \,β''=0

(

R_{11}

) ;

\displaystyle β''+{β'}^2+α' \:β'+\frac{3}{\underline{r}} \,β'+\frac{1}{\underline{r}} \,α'=0

(

R_{22}

R_{33}

• On en déduit :

\displaystyle β''-α' \:β'+\frac{1}{\underline{r}} \,(β'-α')=0

\left\{\frac{(1)-(0)}{2}\right\}

;

\displaystyle 2 \,β''+{β'}^2+\frac{4}{\underline{r}} \, β'=0

\left\{(2,3)+\frac{(1)-(0)}{2}\right\}

1.c.

• La seconde des deux équations précédentes peut s'écrire :

2 \,\underline{r}^2 \: β''+4 \: \underline{r} \: β'+\underline{r}^2 \:{β'}^2=0

. En posant

γ=\underline{r}^2 \: β'

, on obtient :

\displaystyle \frac{2\: γ'}{γ^2} =-\frac{1}{\underline{r}^2}

; on en déduit alors :

\displaystyle γ=-\frac{2 \,\underline{r}}{1+K \:\underline{r}}

puis

\displaystyle β'=-\frac{2}{\underline{r} .(1+K \:\underline{r})}

où

K

est une constante d'intégration. Finalement :

\mathrm{e}^{2β}=\left(1+\frac{\underline{r}_s}{\underline{r}}\right)^4

(puisque la limite à l'infini est

1

) ; avec

\displaystyle \underline{r}_s=\frac{1}{K}

.
• L'autre équation donne :

\displaystyle α'=\frac{\underline{r} \: β''+β'}{\underline{r} \: β'+1}=-\frac{2 \,K}{1-K^2 \: \underline{r}^2}

. Ainsi :

\displaystyle \mathrm{e}^{2α}=\frac{(\underline{r}-\underline{r}_s )^2}{(\underline{r}+\underline{r}_s )^2}

(la limite à l'infini est

1

).
• La constante

\underline{r}_s

se déduit de la limite des champs faibles :

\displaystyle \mathrm{e}^{2α}≈1-\frac{4 \,\underline{r}_s}{\underline{r}}≈1+\frac{2 \,𝒱}{c^2} ≈1-\frac{2 \,𝒢 \,M}{c^2 \:\underline{r}}

.
• Il faut alors s'assurer que les trois équations initiales sont vérifiées (on n'a utilisé qu'une combinaison des deux premières). En reportant dans la première, on vérifie que :

\displaystyle α''+α' \:β'+{α'}^2-\frac{2}{\underline{r}}\, α'=0

2.a.

• La comparaison est plus facile en notant :

A(\underline{r})=\mathrm{e}^{2α(\underline{r})}

\underline{C}(\underline{r})=\mathrm{e}^{2β(\underline{r})}

.
• L'équivalence des deux métriques impose (entre autres) :

\displaystyle r^2=\underline{C}(\underline{r}) \;\underline{r}^2=\left(1+\frac{\underline{r}_s}{\underline{r}}\right)^4 \underline{r}^2

.
• Compte tenu de l'équivalence

r≈\underline{r}

à l'infini, on en déduit :

\displaystyle r=\underline{r} .\left(1+\frac{\underline{r}_s}{\underline{r}}\right)^2

.
• En inversant la relation précédente (non bijective), on obtient :

\displaystyle \underline{r}=\frac{r}{2} \left(\left(1-\frac{r_s}{2 \,r}\right)±\sqrt{1-\frac{r_s}{r}}\right)

;

\displaystyle \underline{r}_s=\frac{r_s}{4}

2.b.

• L'équivalence des deux métriques impose aussi :

C(r) \:dr^2=\underline{C}(\underline{r}) \:{d\underline{r}}^2

.
• Compte tenu de

r^2=\underline{C}(\underline{r}) \;\underline{r}^2

, on obtient ainsi :

\displaystyle \frac{d\underline{r}}{\underline{r}}=±\sqrt{C(r)} \;\frac{dr}{r}=±\frac{dr}{\sqrt{r .(r-r_s)}}

.
• Cette équation peut s'écrire plus simplement avec la variable

\displaystyle υ=\frac{2 \,r}{r_s} -1

; ainsi :

\displaystyle \frac{d\underline{r}}{\underline{r}}=± \frac{dυ}{\sqrt{υ^2-1}}

.
• Ceci donne :

\ln(\underline{r})=± \mathrm{arccosh}(υ)+Cste

, mais il est plus efficace d'utiliser l'expression logarithmique :

\ln(\underline{r})=± \ln\left(υ+\sqrt{υ^2-1}\right)+Cste

.
• La constante peut être déterminée d'après la limite à l'infini :

C→1

;

\underline{C}→1

;

r→∞

;

υ→∞

;

\underline{r}→∞

;

\underline{r}≈r

;

\displaystyle υ≈\frac{2 \,r}{r_s}

;

\ln\left(υ+\sqrt{υ^2-1}\right)≈\ln(2 \,υ)≈\ln(r)-\ln(\underline{r}_s)

• Dans cette limite le signe

±

correspond donc au signe

+

et la constante d'intégration est

\ln(\underline{r}_s)

\displaystyle \underline{r}=\underline{r}_s .\left(υ+\sqrt{υ^2-1}\right)=\frac{r}{2} \,\left(\left(1-\frac{r_s}{2 \,r}\right)+\sqrt{1-\frac{r_s}{r}}\right)

• En inversant la relation on retrouve :

\displaystyle r=\underline{r} .\left(1+\frac{\underline{r}_s}{\underline{r}}\right)^2

, mais cette forme est plus générale puisqu'elle correspond au signe

±

dans la relation précédente.
• On constate alors que l'option avec le signe

-

correspond à la limite :

r→∞

;

υ→∞

;

\underline{r}→0

;

\displaystyle r≈\frac{r_s^{\;2}}{\underline{r}}

;

\displaystyle υ≈\frac{2 \,r}{r_s}

;

\ln\left(υ+\sqrt{υ^2-1}\right)≈\ln(r)-\ln(\underline{r}_s)

;

\ln(\underline{r})≈-\ln(r)+\ln(\underline{r}_s)+Cste

, où la constante d'intégration est aussi

\ln(\underline{r}_s)

par comparaison.

• On retrouve bien ainsi la solution complète de l'équation différentielle.

IX. Coordonnées “isochrones”

• On obtient ainsi :

g_{00}=1

;

g_{11}=-\mathrm{e}^{2β}

;

g_{22}=-\mathrm{e}^{2δ} \:r^2

;

g_{33}=-\mathrm{e}^{2δ} \:r^2 \: \sin^2⁡(θ)

;

g^{00}=1

;

g^{11}=-\mathrm{e}^{-2β}

;

\displaystyle g^{22}=-\frac{\mathrm{e}^{-2δ}}{r^2}

;

\displaystyle g^{33}=-\frac{\mathrm{e}^{-2δ}}{r^2 \:\sin^2⁡(θ)}

;

Γ_{111}=-β' \:\mathrm{e}^{2β}

;

Γ_{221}=-Γ_{122}=-r \:\mathrm{e}^{2δ} \:(1+r \:δ')

;

Γ_{331}=-Γ_{133}=-r \: \sin^2⁡(θ) \: \mathrm{e}^{2δ} \: (1+r \:δ')

;

Γ_{332}=-Γ_{233}=-r^2 \: \mathrm{e}^{2δ} \: \sin⁡(θ) \: \cos⁡(θ)

;

Γ_{\phantom{.}11}^1=β'

;

\displaystyle Γ_{\phantom{.}12}^2=Γ_{\phantom{.}13}^3=\frac{1}{r} \, (1+r \:δ')

;

Γ_{\phantom{.}22}^1=-r \:\mathrm{e}^{2δ} \: \mathrm{e}^{-2β} \: (1+r \,δ')

;

Γ_{\phantom{.}33}^1=-r \:\mathrm{e}^{2δ} \: \sin^2⁡(θ) \: \mathrm{e}^{-2β} \: (1+r \,δ')

;

Γ_{\phantom{.}23}^3=\mathrm{cotan}⁡(θ)

;

Γ_{\phantom{.}33}^2=-\sin⁡(θ) \: \cos⁡(θ)

• Si on cherche la métrique dans le vide entourant l'astre, les équations du champ correspondent à :

R_{μν}=0

; en simplifiant :

\displaystyle δ''-\frac{1}{r} \,β'-β' \,δ'+\frac{2}{r} \,δ'+{δ'}^2=0

(

R_{11}

) ;

\displaystyle δ''-\frac{1}{r} \, β'-β' \,δ'+\frac{4}{r} \, δ'+2 \,{δ'}^2+\frac{1}{r^2} -\frac{1}{r^2} \, \mathrm{e}^{2β} \: \mathrm{e}^{-2δ}=0

(

R_{22}

R_{33}

• Par différence, on en déduit :

\displaystyle \frac{1}{r^2} +\frac{2}{r} \, δ'+{δ'}^2=\frac{\mathrm{e}^{2β} \: \mathrm{e}^{-2δ}}{r^2}

et donc

1+r \:δ'=±\mathrm{e}^{β-δ}

; la limite à l'infini impose en fait :

1+r \:δ'=\mathrm{e}^{β-δ}

.
• En notant

\displaystyle υ=\frac{1}{r}+δ'=\frac{1}{r} \, \mathrm{e}^{β-δ}

la première équation donne alors :

υ'-β' \,υ+υ^2=0

. Ceci peut s'écrire :

β'=\frac{υ'}{υ}+υ

ou encore :

\displaystyle β'-δ'=\frac{υ'}{υ}+\frac{1}{r}

; l'intégration donne :

\displaystyle \frac{\mathrm{e}^{β-δ}}{1+r \,δ'}=Cste

(ce qui n'apporte rien de plus).

• La métrique “isochrone” la plus générale peut s'écrire :

{ds}^2=c^2 \,{dt}^2-\mathrm{e}^{2δ} \: \left\{(1+r \,δ')^2 \:{dr}^2+r^2 \:{dΩ}^2 \right\}

.
• En posant

\tilde{r}=r \:e^δ

, on obtient :

d\tilde{r}=(1+r \,δ') \: \mathrm{e}^δ \: dr

;

{ds}^2=c^2 \, {dt}^2-{d\tilde{r}}^2-\tilde{r}^2 \: {dΩ}^2

; ceci ne peut donc décrire qu'un espace plat (dès lors qu'on suppose a priori que la métrique est statique).
◊ remarque : les métriques à symétrie sphérique de Lemaître sont isochrones, mais non statiques.

X. Composantes angulaires de la métrique

• On obtient ainsi :

g_{00}=\mathrm{e}^{2α}

;

g_{11}=-\mathrm{e}^{2β}

;

g_{22}=-\mathrm{e}^{2δ} \; r^2

;

g_{33}=-\mathrm{e}^{2δ} \; r^2 \: F^2

;

g^{00}=\mathrm{e}^{-2α}

;

g^{11}=-\mathrm{e}^{-2β}

;

\displaystyle g^{22}=-\frac{\mathrm{e}^{-2δ}}{r^2}

;

\displaystyle g^{33}=-\frac{\mathrm{e}^{-2δ}}{r^2 \: F^2}

;

Γ_{001}=-Γ_{100}=α' \:\mathrm{e}^{2α}

;

Γ_{111}=-β' \:\mathrm{e}^{2β}

;

Γ_{221}=-Γ_{122}=-r \:\mathrm{e}^{2δ} \: (1+r \,δ')

;

Γ_{331}=-Γ_{133}=-r \:F^2 \: \mathrm{e}^{2δ} \: (1+r \,δ')

;

Γ_{332}=-Γ_{233}=-r^2 \: \mathrm{e}^{2δ} \: F \,F'

;

Γ_{\phantom{.}01}^0=α'

;

Γ_{\phantom{.}00}^1=α' \:\mathrm{e}^{2α-2β}

;

Γ_{\phantom{.}11}^1=β'

;

\displaystyle Γ_{\phantom{.}12}^2=Γ_{\phantom{.}13}^3=\frac{1}{r} \, (1+r \,δ')

;

Γ_{\phantom{.}22}^1=-r \:\mathrm{e}^{2δ-2β} \: (1+r \,δ')

;

Γ_{\phantom{.}33}^1=-r \:\mathrm{e}^{2δ-2β} \: F^2 \: (1+r \,δ')

;

\displaystyle Γ_{\phantom{.}23}^3=\frac{F'}{F}

;

Γ_{\phantom{.}33}^2=-F \,F'

• Dans le vide entourant l'astre, les équations du champ correspondent à :

R_{μν}=0

; en simplifiant, la seule relation concernant

F

est :

\displaystyle (1+r \:δ')\: \left[r \:β'-r \:α'-2 \,(1+r \:δ')\right]+1-r^2 \: δ''-\mathrm{e}^{2β-2δ} \: \frac{F''}{F\,}=0

(

R_{22}

R_{33}

• La limite à l'infini correspond à :

\displaystyle α=𝒪\left(\frac{1}{r}\right)

;

\displaystyle α'=𝒪\left(\frac{1}{r^2}\right)

... et ainsi de même pour

β

δ

; or

F

ne dépend pas de

r

, donc ceci impose finalement :

\displaystyle 1+\frac{F''}{F\,}=0

.
• L'équation

F''+F=0

doit redonner à l'infini

F(θ)≈\sin⁡(θ)

; la seule possibilité est

F(θ)=\sin⁡(θ)

. On retrouve donc l'expression “classique” pour

{dΩ}^2

XI. Analogue relativiste de l'énergie mécanique

• La relation

δ\left(∫ ds\right)=0

peut s'écrire

\displaystyle δ\left(∫ \sqrt{g_{μν} \:\dot{x}^μ \:\dot{x}^ν} \;ds\right)=δ\left(∫ ℒ\left(x^α,\dot{x}^β \right) \;ds\right)=0

, avec le lagrangien

\displaystyle ℒ=\frac{ds}{ds}=1

(on peut préférer

\displaystyle ℒ=m \,c \,\frac{ds}{ds}

mais l'action

𝒮=m \,c \,∫ ds

est ici simplifiée).
• On en déduit les équations des mouvements géodésiques :

\displaystyle \frac{d}{ds} \left(\frac{∂ℒ}{∂\dot{x}^α}\right)=\frac{∂ℒ}{∂x^α}

. Par ailleurs, l'énergie-impulsion correspond à :

\displaystyle p_α=\frac{∂ℒ}{∂\dot{x}^α}

; ainsi, si le lagrangien ne dépend pas explicitement du temps, la quantité

p_0

est une constante du mouvement :

\displaystyle \frac{dp_0}{ds}=\frac{d}{ds} \left(\frac{∂ℒ}{∂\dot{x}^0}\right)=\frac{∂ℒ}{∂x^0}=0

.
• Pour une métrique statique, on peut donc considérer que la quantité “énergie” (analogue relativiste de l'énergie mécanique, incluant l'effet gravitationnel) est constante :

\displaystyle \frac{ℰ}{c}=p_0=g_{00} \: m \,c \: \frac{dx^0}{ds}=A \:m \,c \,\frac{dt}{ds}=Cste

;

\displaystyle A \:c \,\frac{dt}{ds}=𝓀=\frac{ℰ}{m \,c^2}

◊ remarque : pour un point matériel immobile (

ds=c \,dt

) à l'infini (

A=1

), la relation précédente donne effectivement

𝓀=1

en accord avec

ℰ=E=m \,c^2

XII. Invariance angulaire

• Les coefficients de la métrique ne dépendent que de

r

θ

.
◊ remarque : la dérivée de Lie nulle

ℒ_\overset{⟷}{e_0} g_{μν}=∂_0 g_{μν}=0

indique que

\overset{⟷}{e_0}

est un vecteur de Killing ; une constante du mouvement lui correspond, associée à l'énergie (mais cela n'est pas demandé).
• La dérivée de Lie non nulle

\displaystyle ℒ_\overset{⟷}{e_1} g_{μν}=\frac{∂g_{μν}}{∂r}≠0

(toutes les composantes dépendent de

r

) indique que

\overset{⟷}{e_1}

n'est pas un vecteur de Killing.
• La dérivée de Lie non nulle

\displaystyle ℒ_\overset{⟷}{e_2} g_{μν}=\frac{∂g_{μν}}{∂θ}≠0

(la composante

g_{33}

dépend de

θ

) indique que

\overset{⟷}{e_2}

n'est pas un vecteur de Killing.
• La dérivée de Lie nulle

\displaystyle ℒ_\overset{⟷}{e_3} g_{μν}=\frac{∂g_{μν}}{∂φ}=0

indique que

\overset{⟷}{e_3}

est un vecteur de Killing ; une constante du mouvement lui correspond, associée au moment cinétique.

• Ceci peut aussi être décrit à l'aide du “vecteur de Killing”

\overset{⟷}{ξ}_{(φ)}=\overset{⟷}{e_3}=∂_3 \overset{⟷}{M}=(0\,;0\,;0\,;1)

puisque la métrique est indépendante de

φ

. Ceci correspond à

ξ_{(φ)α}=g_{αβ} \:ξ_{(φ)}^{\phantom{φ}β}=(0\,;0\,;0\,;-r^2 \:\sin^2⁡(θ) )

.
• Pour une particule massive, on peut considérer le vecteur

\displaystyle U^α=\frac{dx^α}{dτ}

tangent à sa trajectoire géodésique, ou le vecteur énergie-impulsion

p^α=m \:U^α

. Les propriétés des vecteurs de Killing permettent d'en déduire une constante du mouvement :

\displaystyle p^α \: ξ_{(φ)α}=-m \:r^2 \: \sin^2(θ) \, \frac{dφ}{dτ}=Cste

.
• Le cas des photons peut être traité de façon analogue avec

\displaystyle υ^α=\frac{dx^α}{dς}

\displaystyle p^α=\frac{h \,ν_∞}{c}\,υ^α

. On obtient dans ce cas :

\displaystyle p^α\: ξ_{(φ)α}=-\frac{h \,ν_∞}{c} \: r^2 \: \sin^2(θ) \,\frac{dφ}{dς}=Cste

XIII. Point matériel en orbite circulaire

1.a.

• Avec

\displaystyle A=\frac{r-r_s}{r}=\frac{1}{C}

on obtient :

\displaystyle \left(\frac{dr}{ds}\right)^2=𝓀^2-\frac{𝒽^2}{c^2}\, \frac{r-r_s}{r^3} -\frac{r-r_s}{r}

1.b.

• Avec

\displaystyle \frac{ds}{dφ}=\frac{c \:r^2}{𝒽}

on peut écrire :

\displaystyle \left(\frac{dr}{dφ}\right)^2=\frac{𝓀^2 \:c^2 \:r^4}{𝒽^2} -r .(r-r_s )-\frac{c^2 \:r^3.(r-r_s )}{𝒽^2}

.
• Avec une variable de Binet

\displaystyle 𝓊=\frac{1}{r}

on obtient :

\displaystyle \left(\frac{d𝓊}{dφ}\right)^2=\frac{1}{r^4}\, \left(\frac{dr}{dφ}\right)^2=\frac{𝓀^2 \,c^2}{𝒽^2} -𝓊^2+r_s \:𝓊^3-\frac{c^2.(1-r_s \:𝓊)}{𝒽^2}

• En dérivant par rapport à

φ

on obtient ensuite :

\displaystyle \frac{d^2 𝓊}{{dφ}^2} +𝓊=\frac{3 \,r_s \:𝓊^2}{2}+\frac{c^2 \:r_s}{2 \,𝒽^2}

2.a.

• Pour les trajectoires circulaires

\displaystyle \frac{d𝓊}{dφ}=0

\displaystyle \frac{d^2 𝓊}{{dφ}^2} =0

donc :

\displaystyle 𝓊^2=\frac{𝓀^2 \,c^2}{𝒽^2.(1-r_s\:𝓊)}-\frac{c^2}{𝒽^2}

;

\displaystyle 𝓊^2=\frac{c^2}{𝒽^2} \,\frac{r_s \:𝓊}{2-3 \,r_s \:𝓊}

• On obtient en reportant :

\displaystyle 𝒽^2=\frac{c^2 \:r_s}{𝓊.(2-3 \,r_s \:𝓊)}

;

\displaystyle 𝓀^2=\frac{2 \,(1-r_s \:𝓊)^2}{2-3 \,r_s \:𝓊}

2.b.

• Les orbites circulaires sont possibles si et seulement si

2-3 \,r_s \:𝓊>0

. Ceci correspond à

\displaystyle \frac{r}{r_s} >\frac{3}{2}

; aucune orbite circulaire n'est possible à proximité de la singularité.
• Mais en outre, la propriété

\displaystyle 𝓀=\frac{ℰ}{m \,c^2}

indique que les orbites circulaires correspondent à des état liés si et seulement si

𝓀<1

(équivalent de

E_m<0

en mécanique newtonienne). Ceci correspond à

\displaystyle \frac{r}{r_s} >2

; les orbites mathématiquement possibles mais trop proches de la singularité ne seraient pas liées : une perturbation de la particule pourrait la faire éjecter jusqu'à l'origine ou jusqu'à l'infini.

2.c.

• Pour une orbite circulaire, la vitesse du point matériel est :

\displaystyle v=\frac{d𝓁}{dt_{𝓁oc}}=\frac{r \:dφ}{\sqrt{A} \:dt}=\frac{𝒽}{𝓀} \frac{\sqrt{A}}{r}

.
• La limite correspond à :

r_s \:𝓊→\frac{2}{3}

;

2-3 \,r_s \:𝓊→0

;

𝒽→∞

;

𝓀→∞

(ce qui indique en fait un moment cinétique et une énergie infinis).
• On peut par contre utiliser :

\displaystyle \frac{𝒽^2}{𝓀^2} =\frac{c^2 \:r_s}{2 \,𝓊.(1-r_s \:𝓊)^2}→\frac{27 \,c^2 \:r_s^{\:2}}{4}

;

\sqrt{A}=\sqrt{1-r_s \:𝓊}→\frac{1}{\sqrt{3}}

;

\displaystyle r→\frac{3 \,r_s}{2}

. On obtient ainsi :

\displaystyle v=\frac{𝒽}{𝓀} \frac{\sqrt{A}}{r}→c

. Ceci correspond effectivement à un moment cinétique et une énergie infinis, justifiant clairement la limite physique.
• On constate en fait qu'il n'y a pas d'orbite stable pour

r<3 \,r_s

, correspondant à

𝒽>\sqrt{3} \:c \:r_s

(sur une telle orbite, la particule aurait une vitesse

v≈0,58 \:c

). Ceci fixe la limite des disques d'accrétion.
• Cela tient au fait que

𝒱_r (r_e )

a un minimum pour

r_e=3 \,r_s

; en deça, l'extremum de

𝒱_r (r)

pour

r=r_e

correspond à un maximum. Ainsi les orbites circulaires pour

\displaystyle \frac{3 \,r_s}{2}<r<3 \,r_s

sont instables (comme pour une bille oscillant dans le plan de symétrie longitudinal d'une selle de cheval) : toute perturbation fait tomber la particule sur l'astre ou l'éjecte vers l'extérieur.
◊ remarque : le plus singulier concerne les orbites circulaires instables avec

\displaystyle \frac{3 \,r_s}{2}<r<2 \,r_s

, pour lesquelles tout écart éjecte la particule jusqu'à l'infini (cela provoque probablement d'importantes turbulences au niveau des disques d'accrétion).

• Pour un mouvement circulaire, la troisième loi de Kepler relie la période, le rayon de l'orbite et la masse de l'astre attracteur. L'équivalent à considérer ici, d'un point de vue astronomique, correspond à une période apparente mesurée de loin : par rapport à la variable temporelle

t

“à l'infini”.
• D'après ce qui précède, la vitesse angulaire est ainsi :

\displaystyle ω=\frac{dφ}{dt}=\frac{𝒽}{𝓀} \,\frac{A}{r^2}

avec

\displaystyle \frac{𝒽^2}{𝓀^2} =\frac{c^2 \:r_s}{2 u.(1-r_s \:𝓊)^2}

; ceci donne en simplifiant :

\displaystyle \frac{2π}{T}=ω=\sqrt{\frac{𝒢 M}{r^3}}

.
• Cette expression est, plus ou moins fortuitement, la même que dans le cas non relativiste. Une différence est toutefois que cela n'est valable que si on observe de loin.
• Une autre différence est qu'en mécanique newtonienne la variable

r

est à la fois le rayon “périphérique” (comme pour l'étude relativiste) mais aussi le rayon “intérieur” (distance au centre). La correspondance est toutefois possible dans la mesure où, en astronomie, la “taille” de la trajectoire est mesurée de loin d'après le rayon périphérique (à condition de tenir compte de la déviation des rayons lumineux).
◊ remarque : il n'y a par contre pas ici de généralisation simple pour les orbites pseudo-elliptiques ; outre le fait que ces orbites ne sont pas fermées, cela est assez logique puisque l'expression newtonienne est d'après le demi-grand-axe seulement, alors que l'aspect “périphérique” de l'ellipse dépend aussi du demi-petit-axe.

XIV. Photon en orbite circulaire

1.a.	• Avec $\displaystyle A=\frac{r-r_s}{r}=\frac{1}{C}$ on obtient : $\displaystyle \left(\frac{dr}{dς}\right)^2=𝓀^2-\frac{𝒽^2}{c^2} \,\frac{r-r_s}{r^3}$ .

1.b.	• Avec $\displaystyle \frac{dς}{dφ}=\frac{c \:r^2}{𝒽}$ on peut écrire : $\displaystyle \left(\frac{dr}{dφ}\right)^2=\frac{𝓀^2 \:c^2 \:r^4}{𝒽^2} -r .(r-r_s )$ . • Avec une variable de Binet $\displaystyle 𝓊=\frac{1}{r}$ on obtient : $\displaystyle \left(\frac{d𝓊}{dφ}\right)^2=\frac{1}{r^4} \,\left(\frac{dr}{dφ}\right)^2=\frac{𝓀^2 \,c^2}{𝒽^2} -𝓊^2+r_s \:𝓊^3$ . • En dérivant par rapport à $φ$ on obtient ensuite : $\displaystyle \frac{d^2 𝓊}{{dφ}^2} +𝓊=\frac{3 \,r_s \:𝓊^2}{2}$ .

2.a.	• Pour les trajectoires circulaires $\displaystyle \frac{d𝓊}{dφ}=0$ et $\displaystyle \frac{d^2 𝓊}{{dφ}^2} =0$ donc : $\displaystyle r=\frac{1}{𝓊}=\frac{3 \,r_s}{2}$ ; $\displaystyle \frac{𝒽}{c \:𝓀}=r_s \:\sqrt{\frac{27}{8}}$ .

2.b.	• Pour les particules matérielles, pour compenser l'attraction gravitationnelle plus grande, la vitesse doit être d'autant plus grande que le rayon de l'orbite circulaire est petit. La limite possible correspond à la vitesse de la lumière, donc au cas analogue pour les photons.

2.c.	• Pour les particules matérielles, il y a plusieurs orbites circulaires et la relation entre $𝒽$ et $𝓀$ dépend de l'orbite considérée. Pour les photons, l'orbite est unique donc si $𝓀$ impose l'énergie, alors $𝒽$ est imposé et proportionnel à $𝓀$ .

XV. Photon au voisinage d'une singularité

1.a.

• Avec

\displaystyle A=\frac{r-r_s}{r}=\frac{1}{C}

on obtient :

\displaystyle \left(\frac{dr}{dς}\right)^2=𝓀^2-\frac{𝒽^2}{c^2} \,\frac{r-r_s}{r^3}

1.b.

• Avec

\displaystyle \frac{dς}{dφ}=\frac{c \:r^2}{𝒽}

on peut écrire :

\displaystyle \left(\frac{dr}{dφ}\right)^2=\frac{𝓀^2 \:c^2 \:r^4}{𝒽^2} -r .(r-r_s )

.
• Ainsi :

\displaystyle \frac{1}{r^2} \,\frac{dr}{dφ}=\sqrt{\frac{𝓀^2 \:c^2}{𝒽^2} -\frac{1}{r^2} \:(1-\frac{r_s}{r})}

; la limite est

\displaystyle \frac{𝓀 c}{𝒽}

1.c.

• Pour un mouvement plan en mécanique newtonienne, on peut considérer en coordonnées polaires :

\overset{⟶}{OM}=r \:\overset{→}{u_r}

;

\overset{→}{v}=\dot{r} \:\overset{→}{u_r}+r \:\dot{φ} \:\overset{⟶}{u_φ}

;

\overset{⟶}{OM} × \overset{→}{v}=r^2 \: \dot{φ} \: \overset{→}{u_z}

• Sous l'effet d'une force centrale, on en déduit :

r^2 \:\dot{φ}=Cste

(loi des aires).

• En notant

b

le paramètre d'impact et

v_∞

la vitesse asymptotique, la disposition géométrique montre que

r^2\: \dot{φ}=b \:v_∞

.
• À l'infini, le mouvement est tel que

\displaystyle \frac{dφ}{dr}→0

;

\dot{r}→v_∞

. Puisque

\displaystyle r^2 \:\dot{φ}=r^2 \:\frac{dφ}{dr} \: \dot{r}

la limite impose

\displaystyle r^2 \: \frac{dφ}{dr}→b

; par analogie, on peut donc préciser :

\displaystyle \frac{𝓀 \:c}{𝒽}=\frac{1}{b}

2.a.	• L'équation de la trajectoire montre que $\displaystyle \frac{dr}{dφ}=0$ correspond à $\displaystyle \frac{1}{b^2} =\frac{1}{r^2} \:\left(1-\frac{r_s}{r}\right)$ ; or le second membre a une valeur maximum $\displaystyle \frac{4}{27 \,r_s^{\:2}}$ pour $\displaystyle r=\frac{3 \,r_s}{2}$ ; ceci impose donc : $b>r_s \:\sqrt{\frac{27}{4}}$ .

2.b.	• L'intégration numérique permet de calculer $φ(r)$ en partant de $r≈∞$ pour $φ=0$ . Les tracés (ci-après) pour $\displaystyle \frac{b}{r_s} =5\, ; 4\, ; 3\, ; \text{2,603}$ montrent que pour $\displaystyle \frac{b}{r_s}$ approchant $\sqrt{\frac{27}{4}}≈\text{2,598}$ les trajectoires ont une allure d'autant plus “enroulée” autour du rayon limite $\displaystyle \frac{3 \,r_s}{2}$ . • Ce comportement optique caractéristique montre que tout astre sombre dont le rayon serait entre $r_s$ et $\displaystyle \frac{3 \,r_s}{2}$ aurait la même apparence extérieure qu'un “trou noir”. ◊ remarque : les photons avec $b$ plus petit que la limite “tombent” en spirale sur l'astre mais, contrairement à ce qui est parfois suggéré, l'existence d'une telle limite ne caractérise pas les trous noirs ; en mécanique newtonienne les photons tels que $b<R$ “tombent” aussi forcément sur l'astre.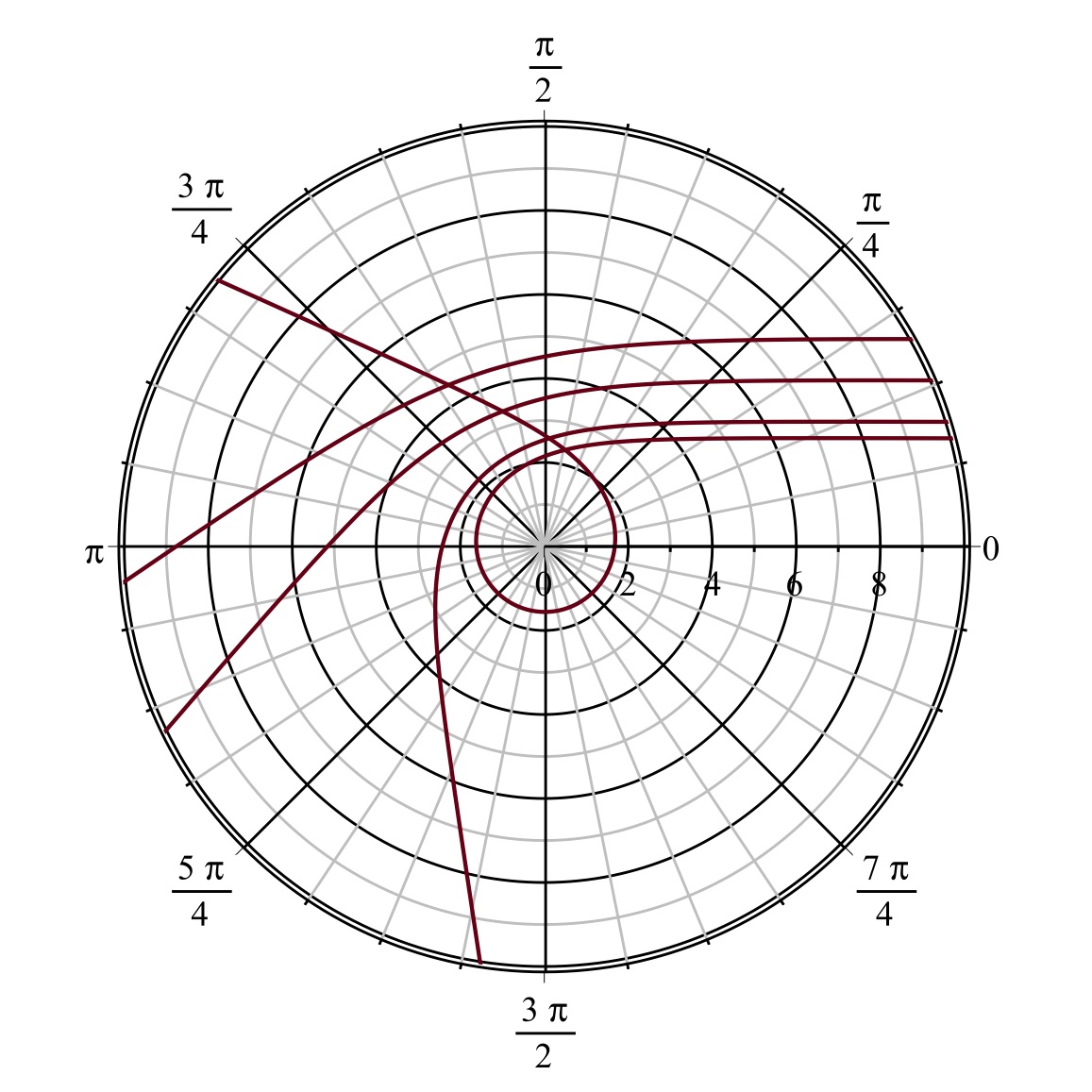

XVI. Effet Einstein

1.a.

• Par définition :

1 \:\mathrm{eV}=\text{1,6}.{10}^{-19} \: \mathrm{J}

; l'énergie des photons est donc :

E=\text{2,3}.{10}^{-15} \: \mathrm{J}

.
• La longueur d'onde est :

\displaystyle λ=\frac{c}{ν}=\frac{h \,c}{E}=87 \:\mathrm{pm}

1.b.

• Le rayon de Schwarzschild de la Terre est :

\displaystyle r_s=\frac{2 \,𝒢 \,M}{c^2} =\text{8,9} \:\mathrm{mm}

.
• En supposant le rayonnement émis en bas au niveau du sol terrestre :

\displaystyle A(r_{ém})=1-\frac{r_s}{R}

;

\displaystyle A(r_{réc})=1-\frac{r_s}{R+H}

;

\displaystyle \frac{λ_{réc}}{λ_{ém}} =\frac{\sqrt{A(r_{réc})}}{\sqrt{A(r_{ém})}}≈1-\frac{r_s}{2 \,(R+H)}+\frac{r_s}{2 \,R}≈1+\frac{r_s \,H}{2 \,R^2}

;

\displaystyle z≈\frac{r_s \,H}{2 \,R^2}=\text{2,5}.{10}^{-15}

1.c.

• Il peut sembler étrange d'utiliser une raie spectrale non usuelle pour obtenir un résultat qui, a priori, ne dépend pas de la longueur d'onde utilisée. Une cause possible pourrait être la discrimination de la lumière ambiante parasite.
• Pour mesurer un décalage spectral aussi faible, il faut par ailleurs utiliser une raie spectrale très fine (et en outre la “stabiliser” par effet Mössbauer). Le choix de Pound et Rebka peut avoir été induit par ce type de contraintes techniques.
◊ remarque : Pound et Snider ont repris le même dispositif en améliorant sa précision ; il est à noter qu'ils n'ont pas choisi d'augmenter la hauteur

H

, jugeant que le gain en précision serait perdu par l'augmentation d'autres types d'incertitudes sur le faisceau.

2.a.	• Le rayon de Schwarzschild d'une naine blanche est : $\displaystyle r_s'=\frac{2 \,𝒢 \,M'}{c^2} =\text{1,8} \:\mathrm{km}$ . • La gravitation en surface d'une naine blanche est très intense ; l'effet de la Terre est négligeable en comparaison : $\displaystyle \frac{r_s'}{R'}≈2.{10}^{-4}$ ; $\displaystyle \frac{r_s}{R}≈\text{1,4}.{10}^{-9}$ . • On peut ainsi considérer : $\displaystyle \frac{λ_{réc}}{λ_{ém}} =\frac{\sqrt{A(r_{réc})}}{\sqrt{A(r_{ém}})}≈1-\frac{r_s'}{2 \,R'}$ ; $\displaystyle z≈\frac{r_s'}{2 \,R'}=\text{1,0}.{10}^{-4}$ . ◊ remarque : les naines blanches sont composées essentiellement de carbone et d'oxygène, mais assez de traces d'hydrogène en surface pour émettre la (très fine) raie de Balmer $\mathrm{H_α}$ utilisée pour ceci.

2.b.	• L'effet Einstein se superpose à l'effet Doppler ; on ne peut en fait les séparer que si la naine blanche fait partie d'une paire (ou d'un groupe) d'étoiles dont on connait suffisamment de propriétés. Les incertitudes subsistant sont importantes.

XVII. Effet Einstein

1.a.	• Le rayon de Schwarzschild est : $\displaystyle r_s=\frac{2 \,𝒢 \,M}{c^2} =9 \:\mathrm{km}$ .

1.b.	• On obtient ainsi $R≈11 \:\mathrm{km}$ .

1.c.	• L'estimation du volume n'est pas évidente, car il dépend de la métrique intérieure. On peut proposer un ordre de grandeur en raisonnant avec $V≈\frac{4}{3} π \,R^3$ ; on obtient ainsi : $V≈6.{10}^{12} \:\mathrm{m^3}$ . • L'estimation de la masse volumique n'est pas plus évidente, car elle dépend de la métrique intérieure et de l'énergie gravitationnelle (la masse totale n'est pas la somme des masses). On peut proposer un ordre de grandeur en raisonnant avec $\displaystyle μ≈\frac{M}{V}$ ; on obtient ainsi : $μ≈{10}^{18} \:\mathrm{kg.m^{-3}}$ . Cette valeur est du même ordre que celle des neutrons : $μ_n≈4.{10}^{17} \:\mathrm{kg.m^{-3}}$ .

• À très grande distance, la longueur d'onde apparente peut s'écrire :

\displaystyle λ_{réc}≈λ_{ém} \, \sqrt{\frac{R}{R-r_s}}

(le champ terrestre a un effet négligeable) ; ainsi :

\displaystyle z=\frac{λ_{réc}}{λ_{ém}} -1≈4

(c'est une limite surestimée dont l'observation est peu probable).
◊ remarque : à cela s'ajoute (entre autres) un effet de l'expansion de l'univers, non décrit ici.

XVIII. Avance du péri-astre des satellites

• En reportant dans l'équation radiale, on obtient :

\displaystyle \frac{1}{𝓅'}+\frac{2 \,ε \:ℯ'}{𝓅'} \:\cos(φ')=\frac{1}{𝓅}+\frac{3 \,𝒢 \,M}{c^2 \:{𝓅'}^2} \:\left[1+2 \,ℯ' \:\cos(φ')+{ℯ'}^2 \:\cos^2⁡(φ') \right]

• La comparaison des termes constants ne dépend pas de l'amplitude des termes périodiques (qui reste limitée) ; on peut donc les comparer dans la limite

ℯ'≪1

.
• La comparaison des termes variables faibles donne alors :

\displaystyle ε=\frac{3 \,𝒢 \,M}{c^2 \:𝓅'}

; puis la comparaison des termes constants donne :

𝓅'≈𝓅 .(1-ε)

.
◊ remarque : à l'ordre le plus bas, on peut donc aussi écrire

\displaystyle ε=\frac{3 \,𝒢 \,M}{c^2 \:𝓅}

.
• Si la partie variable est plus importante, le terme en

\cos^2⁡(φ')

ne change que la forme de la courbe sans modifier la périodicité. On peut alors envisager un développement en série de Fourier, en supposant que les termes successifs sont d'amplitudes décroissantes.
• Si on se limite à l'ordre le plus bas :

\cos^2(φ')=\frac{1}{2}+\frac{1}{2} \,\cos(2 \,φ')

;

{ℯ'}^2 \:\cos^2(φ')≈\frac{1}{2} {ℯ'}^2

. La comparaison des termes variables donne de même

\displaystyle ε=\frac{3 \,𝒢 \,M}{c^2 \:𝓅}

à l'ordre le plus bas. La comparaison des constantes donne par contre un terme correctif :

𝓅'≈𝓅 .\left[1-ε .\left(1+\frac{1}{2} {ℯ'}^2 \right)\right]

.
• Si on veut ne limiter qu'à l'ordre suivant (de Fourier), il faut par contre chercher la solution sous la forme :

\displaystyle 𝓊≈\frac{1}{𝓅'} \:\left[1+ℯ' \:\cos(φ')+ℯ'' \:\cos(2 \,φ') \right]

; la symétrie fait qu'il n'y a pas de terme en

\sin(2 \,φ')

.
• En reportant dans l'équation radiale, on obtient (en gardant

2 \,φ'

mais sans

3 \,φ'

) :

\cos(φ') \: \cos(2 \,φ')=\frac{1}{2} \: \cos(φ')+\frac{1}{2} \: \cos(3 \,φ')≈\frac{1}{2} \: \cos(φ')

;

\displaystyle \frac{1}{𝓅'}-\frac{3 \,ℯ''}{𝓅'} \, \cos(2 \,φ')+\frac{2 \,ε \,ℯ'}{𝓅'} \, \cos(φ')-\frac{8 \,ε \,ℯ''}{𝓅'} \, \cos(2 \,φ')≈

\displaystyle ≈\frac{1}{𝓅}+\frac{3 \,𝒢 \,M}{c^2 \:{𝓅'}^2} \:\left[1+2 \,ℯ'\:\cos(φ')+2 \,ℯ''\:\cos(2 \,φ')+\frac{1}{2} {ℯ'}^2+\frac{1}{2} {ℯ'}^2 \: \cos(2 \,φ')+ℯ' \:ℯ''\:\cos(φ')\right]

• La comparaison des constantes donne le même terme correctif :

𝓅'≈𝓅 .\left[1-ε .\left(1+\frac{1}{2} {ℯ'}^2 \right)\right]

; la comparaison des termes en

φ'

donne à l'ordre le plus bas :

\displaystyle ε=\frac{3 \,𝒢 \,M}{c^2 \:𝓅} \left(1+\frac{ℯ''}{2} \right)

; la comparaison des termes en

2 \,φ'

donne :

\displaystyle ℯ''=-\frac{3 \,𝒢 \,M}{c^2 \: 𝓅} \,\frac{{ℯ'}^2}{6\:}

.

• Il peut être intéressant d'adapter les relations entre

ε

𝓅

et le demi grand axe

𝒶

. La mécanique newtonienne donne

\displaystyle 𝒶=\frac{1}{2} \,(r_m+r_M )=\frac{𝓅}{1-ℯ^2}

.
• Pour le calcul relativiste (au premier ordre) avec une quasi-ellipse de faible excentricité, ceci devient :

\displaystyle 𝒶≈\frac{𝓅'}{1-{ℯ'}^2}≈𝓅'≈𝓅 .(1-ε)

.
• Avec une excentricité moins faible (déformations en

2 \,φ'

), on peut utiliser l'analogie avec une pseudo-ellipse tournante ; on obtient ainsi (mais un calcul numérique direct d'après les équations relativistes exactes est souvent préférable) :

\displaystyle r_m≈\frac{𝓅'}{1+ℯ'+ℯ''}

;

\displaystyle r_M≈\frac{𝓅'}{1-ℯ'+ℯ''}

;

\displaystyle 𝒶≈\frac{𝓅'.(1+ℯ'')}{(1+ℯ'')^2-{ℯ'}^2}≈\frac{𝓅'.(1+ℯ'')}{1-{ℯ'}^2+2 \,ℯ''}≈𝓅 \:\frac{1-ε.\left(1+\frac{2}{3} {ℯ'}^2\right)}{1+{ℯ'}^2.\left(1+\frac{ε}{3}\right)}

XIX. Déviation des rayons lumineux par un astre

1.	• La taille des astres étant très nettement supérieure à la longueur d'onde lumineuse, il est tout à fait justifié d'utiliser une description corpusculaire.

• L'équation obtenue au premier ordre est :

\displaystyle \frac{d^2 𝓊}{{dφ}^2} +𝓊=\frac{3 \,r_s}{2 \,r_m^{\:2}} \, \cos^2⁡(φ)

.
• Cette équation étant linéaire, il suffit de rechercher une solution particulière, logiquement de forme analogue. Le plus simple est pour cela de linéariser :

\displaystyle \frac{d^2 𝓊}{{dφ}^2} +𝓊=\frac{3 \,r_s}{4 \,r_m^{\:2}}+\frac{3 \,r_s}{4 \,r_m^{\:2}} \: \cos⁡(2 \,φ)

.
• Il peut en principe apparaître deux constantes d'intégration (équation du second ordre), mais l'une correspond au choix d'une origine des phases, or la symétrie fait qu'il ne peut y avoir ici que des termes pairs. On cherche donc :

\displaystyle 𝓊=\frac{3 \,r_s}{4 \,r_m^{\:2}}+U\: \cos(2 \,φ)

.
• En reportant dans l'équation, on obtient :

\displaystyle \frac{d^2 𝓊}{{dφ}^2} +𝓊=\frac{3 \,r_s}{4 \,r_m^{\:2}}-3 \,U \:\cos(2 \,φ)

. Ainsi

\displaystyle U=-\frac{r_s}{4 \,r_m^{\:2}}

et la solution complète peut s'écrire :

\displaystyle 𝓊≈\frac{1}{r_m} \: \cos(φ)+\frac{3 \,r_s}{4 \,r_m^{\:2}}-\frac{r_s}{4 \,r_m^{\:2}} \: \cos(2 \,φ)

.
• On peut aussi écrire :

\displaystyle 𝓊≈\frac{1}{r_m}\: \cos(φ)+\frac{r_s}{r_m^{\:2}}-\frac{r_s}{2 \,r_m^{\:2}} \: \cos^2(φ)≈\frac{1}{r_m} \: \cos(φ)+\frac{r_s}{2 \,r_m^{\:2}}\: [\cos^2(φ)+2 \:\sin^2⁡(φ) ]

3.a.

• L'équation obtenue au second ordre peut s'écrire :

\displaystyle \frac{d^2 𝓊}{{dφ}^2} +𝓊≈\frac{3 \,r_s}{2 \,r_m^{\:2}} \:\left\{\cos(φ)+\frac{r_s}{4 \,r_m} [3-\cos(2 \,φ)]\right\}^2

.
• En limitant au second ordre, le développement s'écrit :

\displaystyle \frac{d^2 𝓊}{{dφ}^2} +𝓊≈\frac{3 \,r_s}{2 \,r_m^{\:2}} \:\left\{\cos^2(φ)+\frac{r_s}{2 \,r_m} \: \cos(φ) \:[3-\cos(2 \,φ)]\right\}

• Ceci donne en linéarisant le second membre :

\displaystyle \frac{d^2 𝓊}{{dφ}^2} +𝓊≈\frac{3 \,r_s}{4 \,r_m^{\:2}} \: \left\{1+\cos(2 \,φ)+\frac{r_s}{2 \,r_m} \,[5 \,\cos(φ)-\cos(3 \,φ)]\right\}

• On est donc ramené à ajouter des solutions particulières des équations :

\displaystyle \frac{d^2 𝓊}{{dφ}^2} +𝓊≈\frac{15 \,r_s^{\:2}}{8 \:r_m^{\:3}} \: \cos(φ)

;

\displaystyle \frac{d^2 𝓊}{{dφ}^2} +𝓊≈-\frac{3 \,r_s^{\:2}}{8 \,r_m^{\:3}} \: \cos(3 \,φ)

• Pour la seconde, on peut chercher sous la forme

𝓊=U \:\cos(3 \,φ)

. En reportant dans l'équation, on obtient :

\displaystyle \frac{d^2 𝓊}{{dφ}^2} +𝓊≈-8 \,U \:\cos(3 \,φ)

; ainsi

\displaystyle U=\frac{3 \,r_s^{\:2}}{64 \,r_m^{\:3}}

.
• Pour la première par contre, il y a dégénérescence : si on cherche

𝓊=U \:\cos(φ)

on obtient en reportant :

\displaystyle \frac{d^2 𝓊}{{dφ}^2} +𝓊≈0

. On peut utiliser la méthode de variation de la constante

U

, mais seulement à condition d'utiliser une combinaison laissant varier la phase :

𝓊=U(φ) \:\cos(φ-φ_0)

. En effet, cette dernière n'est alors plus imposée par la parité du cosinus, mais par celle du produit avec

U(φ)

.
• Le plus simple est alors de passer par les exponentielles complexes : on cherche une solution de la forme

𝓊=U(φ) \:\mathrm{e}^{jφ}

pour l'équation

\displaystyle \frac{d^2 𝓊}{{dφ}^2} +𝓊=α \:\mathrm{e}^{jφ}

.
• En reportant dans l'équation, on obtient :

\displaystyle \frac{d^2 𝓊}{{dφ}^2} +𝓊=(U''+2 \,j \:U') \: \mathrm{e}^{jφ}

. Puisqu'on cherche seulement une solution particulière, pour obtenir

U''+2 \,j \:U'=Cste

, il suffit de choisir

U'=Cste

U''=0

; ainsi

\displaystyle U=-j \,\frac{α}{2} \,φ

. Pour obtenir la solution de l'équation avec le second membre

\cos(φ)

, il suffit d'ajouter le conjugué complexe et de diviser par

2

\displaystyle 𝓊=\frac{15 \,r_s^{\:2}}{8 \,r_m^{\:3}} \, φ \: \sin(φ)

.
• On obtient donc au total :

\displaystyle 𝓊≈\frac{1}{r_m} \: \cos(φ)+\frac{r_s}{2 \,r_m^{\:2}} \:[\cos^2(φ)+2 \:\sin^2(φ) ]+\frac{3 \,r_s^{\:2}}{64 \,r_m^{\:3}}\:\cos(φ) \:[\cos^2(φ)-3 \,\sin^2(φ) ]+\frac{15 \,r_s^{\:2}}{8 \,r_m^{\:3}} \: φ \: \sin(φ)

3.b.

• Avec des coordonnées asymptotiquement cartésiennes :

x=r \: \cos(φ)

;

y=r \: \sin(φ)

;

\displaystyle r_m≈x+\frac{r_s}{2 \,r_m}\, \frac{x^2+2 \,y^2}{\sqrt{x^2+y^2}}+\frac{3 \,r_s^{\:2}}{64 \,r_m^{\:2}} \, x \, \frac{x^2-3 \,y^2}{x^2+y^2}+\frac{15 \,r_s^{\:2}}{8 \,r_m^{\:2}} \: φ \:y

• Dans la limite

y≫x

, on obtient :

\displaystyle r_m≈x±\frac{r_s}{r_m} \, y-\frac{9 \,r_s^{\:2}}{64 \,r_m^{\:2}} \, x+\frac{15 \,r_s^{\:2}}{8 \,r_m^{\:2}} \, φ \:y

; on peut en outre remplacer

φ

par la limite non relativiste

±\frac{π}{2}

(utiliser

\displaystyle ±\frac{π}{2}±\frac{r_s}{r_m}

ajouterait une correction à l'ordre suivant).
• Ceci correspond à :

\displaystyle \frac{∆φ}{2}≈\tan\left(\frac{∆φ}{2}\right)≈\frac{dx}{dy}≈\frac{r_s}{r_m} \, \frac{1+\frac{15 \,π}{16} \frac{r_s}{r_m}}{1-\frac{9 \,r_s^{\:2}}{64 \,r_m^{\:2}}}

; mais dans cette expression le terme correctif du dénominateur est à l'ordre suivant donc doit être négligé :

\displaystyle ∆φ≈\frac{2 \,r_s}{r_m} \:\left(1+\frac{15 \,π}{16} \frac{r_s}{r_m} \right)

3.c.

• Pour

\displaystyle \frac{r_s}{r_m} ≈\text{0,10}

on obtient à l'ordre le plus bas

∆φ≈\text{0,20} \:\mathrm{rad} ≈ 11°

; on obtient à l'ordre suivant

∆φ≈\text{0,26} \:\mathrm{rad} ≈ 15°

(au delà, un calcul de l'ordre suivant serait nécessaire, mais cette méthode n'est alors pas forcément la mieux adaptée).

XX. Effet Shapiro

• Pour

r_s≪r_m≤r

, on peut considérer :

\displaystyle ±c\,\frac{dt}{dr}=\left(1-\frac{r_s}{r}\right)^{-1} \:\left(1-\frac{r_m^{\:2}}{r^2}\, \frac{1-\frac{r_s}{r}}{1-\frac{r_s}{r_m}}\right)^{-\frac{1}{2}}≈\left(1+\frac{r_s}{r}\right) \left(1-\frac{r_m^{\:2}}{r^2} \, \left(1-\frac{r_s}{r}+\frac{r_s}{r_m} \right)\right)^{-\frac{1}{2}}

;

\displaystyle ±c\,\frac{dt}{dr}≈\left(1+\frac{r_s}{r}\right) \left(\left(1-\frac{r_m^{\:2}}{r^2} \right)\left(1+\frac{\frac{r_m^{\:2}}{r^2} \left(\frac{r_s}{r}-\frac{r_s}{r_m} \right)}{1-\frac{r_m^{\:2}}{r^2}}\right)\right)^{-\frac{1}{2}}≈\left(1+\frac{r_s}{r}\right) \left(1-\frac{r_m^{\:2}}{r^2} \right)^{-\frac{1}{2}} \;\left(1+\frac{r_s \:r_m^{\:2}.\left(\frac{r_m-r}{r \:r_m}\right)}{r^2-r_m^{\:2}}\right)^{-\frac{1}{2}}

;

\displaystyle ±c\,\frac{dt}{dr}≈\left(1+\frac{r_s}{r}\right) \left(1-\frac{r_m^{\:2}}{r^2} \right)^{-\frac{1}{2}} \;\left(1+\frac{r_s \,\frac{r_m}{r}}{r+r_m}\right)^{-\frac{1}{2}}≈\left(1+\frac{r_s}{r}\right) \left(1-\frac{r_m^{\:2}}{r^2} \right)^{-\frac{1}{2}} \;\left(1+\frac{r_s}{2\,r}\,\frac{r_m}{r+r_m}\right)

;

\displaystyle ±c\,\frac{dt}{dr}≈ \left(1-\frac{r_m^{\:2}}{r^2} \right)^{-\frac{1}{2}} \;\left(1+\frac{r_s}{r}+\frac{r_s}{2\,r}\,\frac{r_m}{r+r_m}\right)=\frac{r}{\sqrt{r^2-r_m^{\:2}}}\left(1+\frac{r_s}{r}+\frac{r_s}{2\,r}\,\frac{r_m}{r+r_m}\right)

• L'intégrale du second membre peut s'écrire :

\displaystyle \sqrt{r^2-r_m^{\:2}}+r_s \:\mathrm{arcosh}\left(\frac{r}{r_m}\right)+\frac{r_s}{2} \sqrt{\frac{r-r_m}{r+r_m}}

.
◊ remarque : pour trouver une primitive de la fonction

\left(u+1\right)^{-3/2} \;\left(u-1\right)^{-1/2}

, avant d'aborder une méthode plus systématique mais souvent plus longue, on peut (de façon opportuniste) chercher sous la forme

(u+1)^α \;(u-1)^β

; sinon, on peut poser

P(u)=u^2-1

\displaystyle v=\frac{\sqrt{P(u)}}{u+1}

, puis comparer

\displaystyle \frac{dv}{du}

\displaystyle \frac{1}{(u+1) \: \sqrt{P(u)}}

(la méthode plus générale est en fait simple dans ce cas).
• En utilisant

\displaystyle \mathrm{arcosh}\left(\frac{r}{r_m}\right)=\ln\left({\frac{r}{r_m} +\sqrt{\frac{r^2}{r_m^{\:2}}-1}}\right)

on obtient alors :

\displaystyle T(r_m \,, \,r)=\frac{1}{c} \:\left[\sqrt{r^2-r_m^{\:2}}+r_s \;\ln⁡\left(\frac{r}{r_m} +\sqrt{\frac{r^2}{r_m^{\:2}}-1}\right)+\frac{r_s}{2}\: \sqrt{\frac{r-r_m}{r+r_m}}\right]

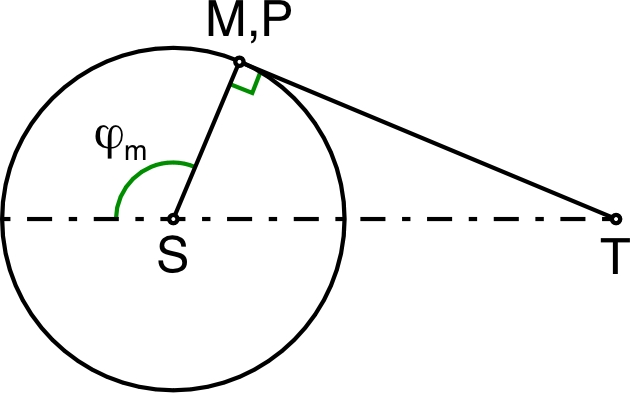
• On repère la position angulaire

φ

de Mercure, sur sa trajectoire apparente (synodique), à partir de la position de conjonction supérieure.
• Il faut alors distinguer deux cas, selon que

φ

dépasse ou non l'angle limite

φ_m

tel que

M

P

soient confondus (

r_m=r_{Mer}

) , donc tel que :

\displaystyle \sin⁡\left(φ_m-\frac{π}{2}\right)=\frac{r_{Mer}}{r_T}

;

◊	pour $φ<φ_m$ la durée est : $T(r_m \,, \,r_T)+T(r_m \,, \,r_{Mer})$ ;
◊	pour $φ≥φ_m$ la durée est : $T(r_m \,, \,r_T)-T(r_m \,, \,r_{Mer})$ .

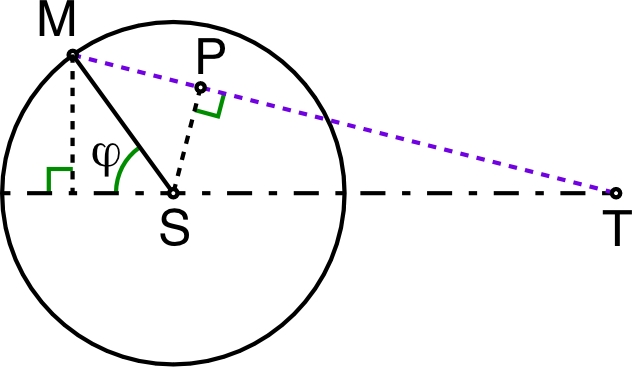
• Pour calculer

r_m=SP

, on peut considérer :

\displaystyle \sin⁡(\widehat{STM})=\frac{r_{Mer} \:\sin⁡(φ)}{TM}=\frac{SP}{r_T}

;

TM=\sqrt{[r_{Mer} \: \sin⁡(φ) ]^2+[r_{Mer} \: \cos⁡(φ)+r_T ]^2}

;

\displaystyle r_m=SP=r_T \: \sin⁡(\widehat{STM})=r_T \; \frac{r_{Mer} \; \sin⁡(φ)}{TM}

XXI. Mouvement apparent de Mercure

• La période de rotation de la Terre autour du Soleil est un an :

T_T=\text{31,5}.{10}^6 \:\mathrm{s}

. Sa vitesse angulaire est :

\displaystyle ω_T=\frac{2π}{T_T} =\text{1,99}.{10}^{-7} \: \mathrm{rad.s^{-1}}

.
• La période de rotation de Mercure autour du Soleil est :

\displaystyle T_M≈T_T .\left(\frac{r_{Mer}}{r_T} \right)^{\frac{3}{2}}≈\text{7,58}.{10}^6 \: \mathrm{s}

d'après la troisième loi de Kepler. Sa vitesse angulaire est :

\displaystyle ω_M=\frac{2π}{T_M} =\text{8,28}.{10}^{-7} \: \mathrm{rad.s^{-1}}

.
• Vue de la Terre, la vitesse angulaire apparente est :

ω_a≈ω_M-ω_T=\text{6,29}.{10}^{-7} \: \mathrm{rad.s^{-1}}

• La vitesse apparente (dans le référentiel tournant comme la Terre) est :

v_a=r_{Mer} \; ω_a=\text{36,4} \:\mathrm{km.s^{-1}}

.
• On peut alors raisonner en première approximation comme si la lumière se propageait en ligne droite. Avec la perspective, la vitesse apparente du point

P

est :

\displaystyle v≈v_a \:\frac{r_T}{r_T+r_{Mer}}=\text{26,2} \:\mathrm{km.s^{-1}}

. Cela peut aussi s'écrire :

v≈\text{3,26} \:R_S/\mathrm{jour}

.
◊ remarque : lors du passage devant le Soleil, la vitesse est

\displaystyle v≈v_a \:\frac{r_T}{r_T-r_{Mer}}=\text{7,37} \:R_S/\mathrm{jour}

; la durée de “traversée” est ainsi

\displaystyle t=\frac{2 \,R_S}{v}≈\text{6,5} \:\mathrm{heures}

(plusieurs comptes rendus d'observations indiquent que c'est plutôt

\text{7,5} \:\mathrm{heures}

, mais l'ordre de grandeur est correct pour les approximations utilisées).

XXII. Précession géodésique

1.	• Les variations du spin correspondent à : $\displaystyle \frac{DS^μ}{dτ}=\frac{dS^μ}{dτ}+Γ_{\phantom{.}αβ}^μ \:S^α \,U^β=0$ .

2.a.

• Le mouvement correspond à :

\displaystyle \frac{DU^μ}{dτ}=\frac{dU^μ}{dτ}+Γ_{\phantom{.}αβ}^μ \:U^α \,U^β=0

2.b.

• L'intégration donne :

\displaystyle A=\frac{dt}{dτ}=𝓀=Cste

;

θ=\frac{π}{2}=Cste

;

\displaystyle r^2 \:\frac{dφ}{dτ}=𝒽=Cste

2.c.

• L'équation pour r est obtenue plus facilement d'après l'expression de la métrique (en notant avec

\dot{⬚}

la dérivation par rapport à

τ

) :

c^2=A \:c^2 \,\dot{t}^2-C \:\dot{r}^2-r^2 \:\dot{φ}^2

;

\displaystyle \dot{r}^2=c^2.(𝓀^2-1)+\frac{c^2 \:r_s}{r}-\frac{𝒽^2}{r^2} \left(1-\frac{r_s}{r}\right)

2.d.

• Les trajectoires circulaires correspondent à

\dot{r}=0

mais nécessitent :

\ddot{r}=0

.
• On obtient en dérivant (et en simplifiant) :

\displaystyle 2 \,\ddot{r}=-\frac{c^2 \:r_s}{r^2} +\frac{𝒽^2}{r^3} \left(2-\frac{3 \,r_s}{r}\right)

. Cela impose une relation entre la rotation et le rayon :

\displaystyle 𝒽=\sqrt{\frac{r \:c^2 \:r_s}{2-\frac{3 \,r_s}{r}}}

.
• On en déduit en reportant :

\displaystyle 0=𝓀^2-1+\frac{r_s}{r}-\frac{𝒽^2}{c^2 \:r^2} \left(1-\frac{r_s}{r}\right)

;

\displaystyle 𝓀^2=1-\frac{r_s}{r}+\frac{h^2}{c^2 \:r^2} \left(1-\frac{r_s}{r}\right)=\left(1-\frac{r_s}{r}\right) \:\frac{2 \,(r-r_s )}{2 \,r-3 \,r_s}

;

\displaystyle 𝓀=\frac{r-r_s}{\sqrt{r.\left(r-\frac{3 r_s}{2}\right)}}

2.e.

• On peut calculer :

\displaystyle Ω=\frac{dφ}{dt}=\frac{\dot{φ}}{\dot{t}} =\frac{A}{r^2} \,\frac{𝒽}{𝓀}=\sqrt{\frac{c^2 \:r_s}{2 \,r^3}}

2.f.

• La 4-vitesse correspond à :

U^β=(c \,\dot{t}\,,0\,,0\,,\dot{φ})=\dot{t}.(c\,,0\,,0\,,Ω)

avec

\displaystyle \dot{t}=\frac{𝓀}{A}=\frac{1}{\sqrt{1-\frac{3 \,r_s}{2\,r}}}

3.a.

• Les variations du spin correspondent à :

\displaystyle \frac{DS^μ}{dτ}=\frac{dS^μ}{dτ}+Γ_{\phantom{.}αβ}^μ \:S^α \,U^β=0

; ainsi pour

θ=\frac{π}{2}

\displaystyle \dot{S^0}+Γ_{\phantom{.}10}^0 \:S^1 \,U^0=\dot{S^0}+\frac{A'}{2 \,A} \:S^1 \,U^0=0

;

\displaystyle \dot{S^1}+Γ_{\phantom{.}00}^1 \:S^0 \,U^0+Γ_{\phantom{.}33}^1 \:S^3 \,U^3=\dot{S^1}+\frac{A'}{2 \,C} \:S^0 \,U^0-\frac{r}{C} \:S^3 \,U^3=0

;

\dot{S^2}+Γ_{\phantom{.}33}^2 \:S^3 \,U^3=\dot{S^2}=0

; la composante

S^2

parallèle à l'axe de l'orbite reste constante ;

\displaystyle \dot{S^3}+Γ_{\phantom{.}13}^3 \:S^1 \,U^3+Γ_{\phantom{.}23}^3 \:S^2 \,U^3=\dot{S^3}+\frac{1}{r} \:S^1 \,U^3=0

3.b.

• Dans le référentiel de repos

S^0=0

; dans le référentiel où le gyroscope est en mouvement, on peut utiliser l'orthogonalité :

g_{αβ} \:S^α \:U^β=A \:S^0 \,U^0-r^2 \:S^3 \,U^3=0

.
• On en déduit :

\displaystyle S^0=\frac{r^2}{A} \frac{Ω}{c} \:S^3

3.c.

• Puisque

r=Cste

, la substitution dans la première équation montre qu'elle est équivalente à la dernière :

\displaystyle \frac{r^2}{A} \frac{Ω}{c} \:\dot{S^3}+\frac{r_s}{2\,r^2 \:A} \,\frac{c}{Ω} \:S^1 \,U^3=0

;

\displaystyle \dot{S^3}+\frac{r_s}{2 \,r^4} \,\frac{c^2}{Ω^2} \:S^1 \,U^3=\dot{S^3}+\frac{1}{r} \:S^1 \,U^3=0

3.d.

• La seconde équation se simplifie :

\displaystyle \frac{dS^1}{dt}+\frac{r_s}{2} Ω \:S^3-(r-r_s ) \:Ω \:S^3=\frac{dS^1}{dt}-r \:\frac{Ω\:}{\dot{t}^2} \:S^3=0

• On peut donc garder le système des deux équations sur

S^1

S^3

, écrit ici en notant

\displaystyle ϖ=\frac{Ω}{\dot{t}}

\displaystyle \frac{dS^1}{dt}-\frac{r}{Ω}\: ϖ^2\:S^3=0

;

\displaystyle \frac{dS^3}{dt}+\frac{Ω}{r} \:S^1=0

3.e.

• Pour résoudre, on peut substituer :

\displaystyle \frac{d^2 S^1}{{dt}^2} +ϖ^2 \:S^1=0

. En choisissant l'origine du temps à l'instant où

S^1

est maximum, on obtient :

S^1 (t)= S^1 (0) \:\cos⁡(ϖ \,t)

.
• On en déduit :

\displaystyle \frac{dS^1}{dt}=-ϖ \:S^1 (0) \: \sin⁡(ϖ \,t)

;

\displaystyle S^3=\frac{Ω}{r \:ϖ} \:S^1 (0) \: \sin⁡(-ϖ \,t)

; le spin est ainsi initialement orienté dans la direction radiale.
◊ remarque : d'après la parité du cosinus on peut alors aussi écrire :

S^1 (t)= S^1 (0) \: \cos⁡(-ϖ \,t)

.
◊ remarque : on peut vérifier que

\displaystyle ‖\;S‖^2=-\frac{r}{r-r_s} \:[S^1 (0)]^2=Cste

3.f.

• Le gyroscope est en orbite à la vitesse angulaire

Ω

. Le spin précesse à la vitesse angulaire

-ϖ

, avec

\displaystyle ϖ=\frac{Ω}{\dot{t}} =Ω \;\sqrt{1-\frac{3 \,r_s}{2 \,r}}<Ω

, par rapport à la direction radiale locale (tournant comme le mouvement orbital). Si l'effet était négligeable (

ϖ≈Ω

), la direction du gyroscope resterait fixe par rapport à un observateur “à l'infini”. Plus la correction est importante, plus le gyroscope prend de retard dans la “compensation” de

Ω

par rapport à l'infini, donc il précesse légèrement dans le sens de

Ω

4.a.	• Pour un tour complet, le décalage angulaire est : $\displaystyle ψ=2π \;\left(1-\sqrt{1-\frac{3 \,r_s}{2 \,r}}\right)≈2π \,\frac{3 \,r_s}{4 \,r}$ (généralement faible car $r≫r_s$ ). • La vitesse de précession est : $\displaystyle ω=Ω-ϖ=Ω .\left(1-\sqrt{1-\frac{3 \,r_s}{2 \,r}}\right)≈\frac{3 \,r_s}{4 \,r} \sqrt{\frac{c^2 \:r_s}{2 \,r^3}}=\frac{3 \,c}{2 \,r} \:\left(\frac{r_s}{2 r}\right)^{\frac{3}{2}}$ .

4.b.	• Le rayon de Schwarzschild de la Terre est $r_s≈\text{8,9} \:\mathrm{mm}$ . Pour une orbite terrestre de faible altitude ( $h≈640 \:\mathrm{km}$ ; $r≈7000 \:\mathrm{km}$ ) on obtient : $ω≈\text{1,03}.{10}^{-12} \: \mathrm{rad.s^{-1}}≈\text{6,7 "/an}$ . Cela a été bien vérifié par le satellite “gravity probe B”, mais les incertitudes dues aux blindages électrostatique et magnétique nécessitent de grandes précautions.

XXIII. Précession géodésique

1.a_α.

• La métrique de Minkowski

{ds}^2=c^2 \,{dt}^2-{dx}^2-{dy}^2-{dz}^2

peut aussi être adaptée aux coordonnées cylindriques ou sphériques selon les systèmes étudiés. Pour un satellite en orbite circulaire sous l'effet de la gravitation newtonienne (dans le cadre de la relativité restreinte), on peut supposer que le mouvement se fait dans le plan équatorial

θ=\frac{π}{2}

; on se limite alors à des coordonnées polaires :

{ds}^2=c^2 \,{dt}^2-{dr}^2-r^2 \:{dφ}^2

.
◊ remarque : ceci équivaut à utiliser des coordonnées cylindriques et à omettre le terme

-{dz}^2

.
• On choisit un repère en rotation correspondant à

ϕ=φ-ω \,t

; ceci donne :

{ds}^2=c^2 \,{dt}^2-{dr}^2-r^2 \:(dϕ+ω \:dt)^2=(c^2-r^2 \:ω^2 ) \:{dt}^2-2 \,r^2 \:ω \:dt \:dϕ-{dr}^2-r^2 \:{dϕ}^2

• À cause des termes croisés en

dt \:dϕ

, deux événements simultanés, en deux points voisins, sont séparés par un décalage des horloges :

\displaystyle {dt}_d=-\frac{g_{02}}{g_{00}} \: dϕ=\frac{r^2 \:ω}{c^2-r^2 \:ω^2} \: dϕ

. Or cette quantité dépendant de

r

ne donne pas toujours un décalage nul pour un déplacement le long d'un contour fermé (indépendamment du fait que

ϕ

est “périodique”) ; les horloges ne sont donc pas globalement synchronisables dans ce cas.
• On peut alors préférer regrouper les termes correspondants (la quantité entre crochets indique la variation de

t

à prendre en compte pour une particule se déplaçant de

dϕ

) :

\displaystyle {ds}^2=(c^2-r^2 \:ω^2 ) \:\left[dt-\frac{r^2\:ω}{c^2-r^2 \:ω^2} \:dϕ\right]^2-{dr}^2-\frac{c^2}{c^2-r^2 \:ω^2} \:r^2 \:{dϕ}^2

• La notion locale de distance est décrite par

{d𝓁}^2=g_{ij} \:dx^i \:dx^j

avec un tenseur métrique tridimensionnel

\displaystyle ℊ_{ij}=\frac{g_{0i} \:g_{0j}}{g_{00}} -g_{ij}

. Ainsi :

\displaystyle {d𝓁}^2={dr}^2+\frac{c^2}{c^2-r^2 \:ω^2} \:r^2 \:{dϕ}^2

1.b_α.

• Avec la métrique simplifiée, en utilisant

x^0=c \,t

\displaystyle w=\frac{ω}{c}

g_{00}=1-r^2 \:w^2

;

g_{02}=-r^2 \:w

;

g_{11}=-1

;

g_{22}=-r^2

;

g^{00}=1

;

g^{02}=-w

;

g^{11}=-1

;

\displaystyle g^{22}=-\frac{1-r^2 \:w^2}{r^2}

1.c_α.

• La connexion correspond à :

Γ_{100}=-Γ_{001}=r \:w^2

;

Γ_{102}=-Γ_{012}=-Γ_{201}=r \:w

;

Γ_{122}=-Γ_{212}=r

;

Γ_{\phantom{.}00}^1=-r \:w^2

;

Γ_{\phantom{.}02}^1=-r \:w

;

\displaystyle Γ_{\phantom{.}01}^2=\frac{w}{r}

;

Γ_{\phantom{.}22}^1=-r

;

\displaystyle Γ_{\phantom{.}12}^2=\frac{1}{r}

1.d_α.

• Les géodésiques correspondent à

\displaystyle \frac{d^2 t}{{dτ}^2} =0

; ainsi

\displaystyle \frac{dt}{dτ}=Cste

et on peut ramener les autres équations à des dérivées par rapport à

t

.
• On obtient ainsi :

\displaystyle \frac{d^2 r}{{dt}^2} -r \:\left(\frac{dϕ}{dt}\right)^2=r \:ω^2+2 \,r \:ω \:\frac{dϕ}{dt}

; le second terme du premier membre décrit un effet classique en coordonnées polaires ; le premier terme du second membre (en

ω^2

) est associé à la “force centrifuge”, le second terme (en

ω

et dépendant de la vitesse

\displaystyle \frac{dϕ}{dt}

) à la “force de Coriolis”.
• De même :

\displaystyle \frac{d^2 ϕ}{{dt}^2} +\frac{2}{r} \frac{dr}{dt} \frac{dϕ}{dt}=-\frac{2}{r} \:ω \:\frac{dr}{dt}

; le second terme du premier membre décrit un effet classique en coordonnées polaires ; le terme du second membre (en

ω

et dépendant de la vitesse

\displaystyle \frac{dr}{dt}

) est associé à la “force de Coriolis”.
◊ remarque : en coordonnées cylindriques on obtient en plus

\displaystyle \frac{d^2 z}{{dt}^2} =0

, justifiant que le mouvement initié avec

\displaystyle \frac{dz}{dt}=0

reste dans un même plan

z=Cste

1.a_β.

• Si on préfère utiliser des coordonnées sphériques, moins simples (d'autant plus que, contrairement à

z

θ

ne peut pas être omis), on considère :

{ds}^2=(c^2-r^2 \: \sin^2⁡(θ) \: ω^2 ) \:{dt}^2-2 \,r^2 \: \sin^2⁡(θ) \: ω \:dt \:dϕ-{dr}^2-r^2 \: {dθ}^2-r^2 \: \sin^2⁡(θ) \:{dϕ}^2

1.b_β.

• La métrique s'écrit :

g_{00}=1-r^2 \: \sin^2⁡(θ) \: w^2

;

g_{03}=-r^2 \: \sin^2⁡(θ) \: w

;

g_{11}=-1

;

g_{22}=-r^2

;

g_{33}=-r^2 \: \sin^2⁡(θ)

;

g^{00}=1

;

g^{03}=-w

;

g^{11}=-1

;

\displaystyle g^{22}=-\frac{1}{r^2}

;

\displaystyle g^{33}=-\frac{1-r^2 \: \sin^2⁡(θ) \: w^2}{r^2 \: \sin^2⁡(θ)}

1.c_β.

• La connexion (simplifiée) correspond à :

Γ_{100}=-Γ_{001}=r \:w^2

;

Γ_{103}=-Γ_{013}=-Γ_{301}=r \:w

;

Γ_{122}=-Γ_{212}=Γ_{133}=-Γ_{313}=r

;

Γ_{\phantom{.}00}^1=-r \:w^2

;

Γ_{\phantom{.}03}^1=-r \:w

;

\displaystyle Γ_{\phantom{.}01}^3=\frac{w}{r}

;

Γ_{\phantom{.}22}^1=Γ_{\phantom{.}33}^1=-r

;

\displaystyle Γ_{\phantom{.}12}^2=Γ_{\phantom{.}13}^3=\frac{1}{r}

1.d_β.

• Ici encore

\displaystyle \frac{d^2 t}{{dτ}^2} =0

; on peut se ramener aux dérivées par rapport à

t

.
• On obtient :

\displaystyle \frac{d^2 θ}{{dt}^2} +\frac{2}{r} \frac{dr}{dt} \frac{dθ}{dt}=0

; le mouvement initié dans le plan équatorial avec

\displaystyle \frac{dθ}{dt}=0

y reste par la suite. Les deux équations pour

r

ϕ

sont identiques à celles obtenues de façon simplifiée.

1.e.

• En l'absence de force exercée sur le système, son mouvement serait rectiligne uniforme dans le référentiel galiléen. Dans le référentiel en rotation, il a donc l'allure d'une spirale qui se rapproche puis s'éloigne de l'origine.

1.f.

• Pour étudier l'action sur un gyroscope en orbite circulaire, dans le référentiel galiléen, on suppose que ce mouvement est imposé par la gravitation “newtonienne”. En relativité restreinte, le centre d'inertie est barycentre des énergies

E=γ \:m \,c^2

; ceci suggère d'utiliser :

\displaystyle \frac{d\overset{→}{p}}{dt}=-γ \:m \, \frac{𝒢 \,M}{r^2} \overset{→}{u_r}

, avec

\overset{→}{p}=γ \:m \,\overset{→}{v}

. Pour un mouvement circulaire

γ=Cste

, donc on obtient

\displaystyle \frac{d\overset{→}{v}}{dt}=-\frac{𝒢 \,M}{r^2} \overset{→}{u_r}

comme en mécanique newtonienne (non relativiste).
◊ remarque : la vitesse du satellite restant faible, la correction relativiste serait surement négligeable.
• Ceci donne

\displaystyle \frac{v^2}{r}=\frac{𝒢 \,M}{r^2}

\displaystyle ω=\frac{v}{r}=\sqrt{\frac{𝒢 \,M}{r^3}}=\sqrt{\frac{c^2 \:r_s}{2 \,r^3}}

(loi de Kepler).
◊ remarque : il s'agit du même

ω

que précédemment puisque on souhaite étudier un référentiel où le gyroscope est au repos.

• On peut d'ailleurs aussi considérer, dans le référentiel tournant où le satellite est immobile (

γ=1

), la loi du mouvement complétée par l'effet gravitationnel newtonien :

\displaystyle \frac{d^2 r}{{dt}^2} =r \:ω^2-\frac{𝒢 \,M}{r^2} =0

1.g.

• Pour un gyroscope quasi-ponctuel, la force newtonienne n'influence pas son moment cinétique ; dans le référentiel tournant, elle ne fait que compenser la force centrifuge (pour un gyroscope initialement immobile, les lois du mouvement donnent :

\displaystyle \frac{d^2 r}{{dt}^2} =0

\displaystyle \frac{d^2 ϕ}{{dt}^2} =0

; le satellite reste immobile).
• On peut donc considérer pour le spin la même loi d'évolution qu'en l'absence de force extérieure :

\displaystyle \frac{DS^μ}{dτ}=\frac{dS^μ}{dτ}+Γ_{\phantom{.}αβ}^μ \:S^α \,U^β=0

, où la dérivation covariante ne décrit pas la gravitation relativiste, mais seulement la géométrie Riemannienne associée au repérage non cartésien. En outre

S^0=0

dans ce référentiel “de repos”.
• Pour

{dτ}^2=(1-r^2 \: w^2) \:{dt}^2

, la vitesse est :

U^β=(c \,\dot{t}\,,0\,,0\,,0)

avec

\displaystyle \dot{t}=\frac{1}{\sqrt{1-r^2 \: w^2}}=\frac{1}{\sqrt{1-\frac{r_s}{2 \,r}}}

.
• On obtient ainsi :

\dot{S^1}+Γ_{\phantom{.}30}^1 \:S^3 \,U^0=\dot{S^1}-r \:w \:S^3 \,U^0=0

;

\dot{S^2}=0

; la composante

S^2

parallèle à l'axe de l'orbite reste constante ;

\displaystyle \dot{S^3}+Γ_{\phantom{.}10}^3 \:S^1 \,U^0=\dot{S^3}+\frac{w}{r} \:S^1 \,U^0=0

1.h.

• Les équations sur

S^1

S^3

peuvent s'écrire :

\displaystyle \frac{dS^1}{dt}-r \:ω \:S^3=0

;

\displaystyle \frac{dS^3}{dt}+\frac{ω}{r} \:S^1=0

.
• Pour résoudre, on peut substituer :

\displaystyle \frac{d^2 S^1}{{dt}^2} +ω^2 \: S^1=0

. En choisissant l'origine du temps à l'instant où

S^1

est maximum, on obtient :

S^1 (t)= S^1 (0) \: \cos⁡(ω \,t)

.
• On en déduit :

\displaystyle \frac{dS^1}{dt}=- ω \:S^1 (0) \: \sin⁡(ω \,t)

;

\displaystyle S^3=\frac{1}{r}\:S^1 (0) \: \sin⁡(-ω \,t)

; le spin est ainsi initialement orienté dans la direction radiale.
◊ remarque : d'après la parité du cosinus on peut alors aussi écrire :

S^1 (t)= S^1 (0) \: \cos⁡(-ω \,t)

.
• Dans le référentiel tournant, les horloges ne sont pas synchronisées, mais le gyroscope ne se déplace pas. La variable

t

est la même que celle utilisée dans le référentiel galiléen. Un tour complet correspond donc à la “durée galiléenne”

\displaystyle ∆t=\frac{2π}{ω}

. Dans son référentiel de repos, la durée pour le satellite est

∆t_{𝓁oc}=\sqrt{1-r^2\:w^2} \:∆t<∆t

, mais c'est l'intervalle

∆t

qui repère un tour. Dans cet intervalle, la précession du spin lui a fait faire une rotation complète, donc par compensation il n'y a pas de précession dans le référentiel galiléen (comme en mécanique newtonienne).
◊ remarque : ce résultat est bien conforme à l'invariance des notations covariantes, puisqu'on aboutit à la même conclusion dans le référentiel galiléen, où

Γ_{\phantom{.}αβ}^μ=0

implique

\dot{S^μ}=0

2.a.

• Pour étudier le même problème avec la gravitation relativiste, on peut utiliser la métrique simplifiée (en conservant les notations

\displaystyle A=\frac{1}{C}=1-\frac{r_s}{r}

) :

{ds}^2=A \:c^2 \,{dt}^2-C \:{dr}^2-r^2 \: (dϕ+ω \:dt)^2=(A-r^2 \: w^2 ) \: c^2 \,{dt}^2-2 \,r^2 \: ω \:dt \:dϕ-C \:{dr}^2-r^2 \: {dϕ}^2

• Mais étant donné que la métrique de Schwarzschild est à symétrie sphérique, on peut juger prudent de passer par les coordonnées sphériques et de simplifier après :

{ds}^2=(A-r^2 \: \sin^2⁡(θ) \: w^2 ) \: c^2 \, {dt}^2-2 \,r^2 \: \sin^2⁡(θ) \: w\:c \:dt \:dϕ-C \:{dr}^2-r^2 \: {dθ}^2-r^2 \: \sin^2⁡(θ) \:{dϕ}^2

2.b.

• La métrique s'écrit :

g_{00}=A-r^2 \: \sin^2⁡(θ) \: w^2

;

g_{03}=-r^2 \: \sin^2⁡(θ) \: w

;

g_{11}=-C

;

g_{22}=-r^2

;

g_{33}=-r^2 \: \sin^2⁡(θ)

;

\displaystyle g^{00}=\frac{1}{A}

;

\displaystyle g^{03}=-\frac{w}{A}

;

\displaystyle g^{11}=-\frac{1}{C}

;

\displaystyle g^{22}=-\frac{1}{r^2}

;

\displaystyle g^{33}=-\frac{A-r^2 \: \sin^2⁡(θ) \: w^2}{A \:r^2 \: \sin^2⁡(θ)}

2.c.

• La connexion (simplifiée) correspond à :

\displaystyle Γ_{100}=-Γ_{001}=-\frac{A'}{2\,}+r \:w^2

;

Γ_{103}=-Γ_{013}=-Γ_{301}=r \:w

;

\displaystyle Γ_{111}=-\frac{C'}{2\,}

;

Γ_{122}=-Γ_{212}=Γ_{133}=-Γ_{313}=r

;

\displaystyle Γ_{\phantom{.}01}^0=\frac{A'}{2 \,A}

;

\displaystyle Γ_{\phantom{.}00}^1=\frac{A'}{2 \,C}-\frac{r}{C} \, w^2

;

\displaystyle Γ_{\phantom{.}03}^1=-\frac{r}{C}\, w

;

\displaystyle Γ_{\phantom{.}11}^1=\frac{C'}{2 \,C}

;

\displaystyle Γ_{\phantom{.}01}^3=\left(\frac{1}{r}-\frac{A'}{2 \,A}\right) \: w

;

\displaystyle Γ_{\phantom{.}22}^1=Γ_{\phantom{.}33}^1=-\frac{r}{C}

;

\displaystyle Γ_{\phantom{.}12}^2=Γ_{\phantom{.}13}^3=\frac{1}{r}

2.d.

• Les géodésiques correspondent à

\displaystyle \frac{d^2 t}{{dτ}^2} =0

; ainsi

\displaystyle \frac{dt}{dτ}=Cste

et on peut ramener les autres équations à des dérivées par rapport à

t

.
• On obtient ainsi :

\displaystyle \frac{d^2 θ}{{dt}^2} +\frac{2}{r} \frac{dr}{dt} \frac{dθ}{dt}=0

; le mouvement initié dans le plan équatorial avec

\displaystyle \frac{dθ}{dt}=0

y reste par la suite.
• De même :

\displaystyle \frac{d^2 ϕ}{{dt}^2} +\frac{2}{r} \frac{dr}{dt} \frac{dϕ}{dt}=-\frac{2}{r} \: ω \: \frac{dr}{dt}

; le satellite reste immobile s'il l'est initialement.
• Enfin (en simplifiant pour

θ

ϕ

) :

\displaystyle \frac{d^2 r}{{dt}^2} +\frac{C'}{2 \,C} \left(\frac{dr}{dt}\right)^2=\frac{1}{C} \:\left(r \:ω^2-\frac{A' \:c^2}{2}\right)=0

; pour un satellite initialement immobile, la condition d'équilibre peut s'écrire :

\displaystyle r \:ω^2-\frac{r_s \: c^2}{2 \,r^2}=0

, c'est à dire

\displaystyle ω=\sqrt{\frac{c^2 \:r_s}{2 \,r^3}}

2.e.

• On peut considérer pour le spin la loi d'évolution :

\displaystyle \frac{DS^μ}{dτ}=\frac{dS^μ}{dτ}+Γ_{\phantom{.}αβ}^μ \:S^α \,U^β=0

, incluant la gravitation relativiste, avec ici encore

S^0=0

dans ce référentiel “de repos”.
• Pour

{dτ}^2=(A-r^2 \: w^2) \:{dt}^2

, la vitesse est :

U^β=(c\,\dot{t}\,,0\,,0\,,0)

avec

\displaystyle \dot{t}=\frac{1}{\sqrt{A-r^2 \: w^2}}=\frac{1}{\sqrt{1-\frac{3 \,r_s}{2 \,r}}}

.
• On obtient ainsi :

\displaystyle \dot{S^1}+Γ_{\phantom{.}30}^1 \:S^3 \,U^0=\dot{S^1}-\frac{r}{C} \: ω \:S^3 \: \dot{t}=0

;

\dot{S^2}=0

; la composante

S^2

parallèle à l'axe de l'orbite reste constante ;

\displaystyle \dot{S^3}+Γ_{\phantom{.}10}^3 \:S^1\, U^0=\dot{S^3}+\left(\frac{1}{r}-\frac{A'}{2 \,A}\right) \:ω \:S^1 \: \dot{t}=0

• Les équations sur

S^1

S^3

peuvent s'écrire :

\displaystyle \frac{dS^1}{dt}-(r-r_s ) \: ω \:S^3=0

;

\displaystyle \frac{dS^3}{dt}+\frac{1-\frac{3 \,r_s}{2 \,r}}{r-r_s} \: ω \:S^1=0

• En notant

\displaystyle ϖ=\frac{ω}{\dot{t}}

la seconde équation peut s'écrire :

\displaystyle \frac{dS^3}{dt}+\frac{1}{(r-r_s ) \:ω} \: ϖ^2 \: S^1=0

2.f.

• Pour résoudre, on peut substituer :

\displaystyle \frac{d^2 S^1}{{dt}^2} +ϖ^2 \: S^1=0

. En choisissant l'origine du temps à l'instant où

S^1

est maximum, on obtient :

S^1 (t)= S^1 (0) \: \cos⁡(ϖ \,t)

.
• On en déduit :

\displaystyle \frac{dS^1}{dt}=- ϖ \:S^1 (0) \: \sin⁡(ϖ \,t)

;

\displaystyle S^3=\frac{ϖ}{(r-r_s ) \: ω} \: S^1 (0) \: \sin⁡(-ϖ \,t)

; le spin est ainsi initialement orienté dans la direction radiale.
◊ remarque : d'après la parité du cosinus on peut alors aussi écrire :

S^1 (t)= S^1 (0) \: \cos⁡(-ϖ \,t)

.
• Le gyroscope est en orbite à la vitesse angulaire

ω

par rapport au référentiel “galiléen” (à l'infini). Le spin précesse à la vitesse angulaire

-ϖ

, avec

\displaystyle ϖ=\frac{ω}{\dot{t}} =ω \;\sqrt{1-\frac{3 \,r_s}{2 \,r}}<ω

, par rapport au référentiel tournant. Si l'effet était négligeable (

ϖ≈ω

), la direction du gyroscope resterait fixe par rapport à un observateur “à l'infini”. Plus la correction est importante, plus le gyroscope prend de retard dans la “compensation” de

ω

par rapport à l'infini, donc il précesse légèrement dans le sens de

ω

.
• La vitesse de précession est :

\displaystyle Ω=ω-ϖ=ω.\left(1-\sqrt{1-\frac{3 \,r_s}{2 \,r}}\right)≈\frac{3 \,r_s}{4 \,r} \sqrt{\frac{c^2 \:r_s}{2 \,r^3}}=\frac{3 \,c}{2 \,r} \:\left(\frac{r_s}{2 \,r}\right)^{\frac{3}{2}}

.
• Ce résultat est bien identique à celui obtenu par raisonnement dans le référentiel “galiléen”. Conjointement avec ce qui précède, il montre que ce n'est pas le référentiel tournant qui cause cet effet, ni le mouvement accéléré dans le référentiel galiléen, mais bien le traitement relativiste de la gravitation.