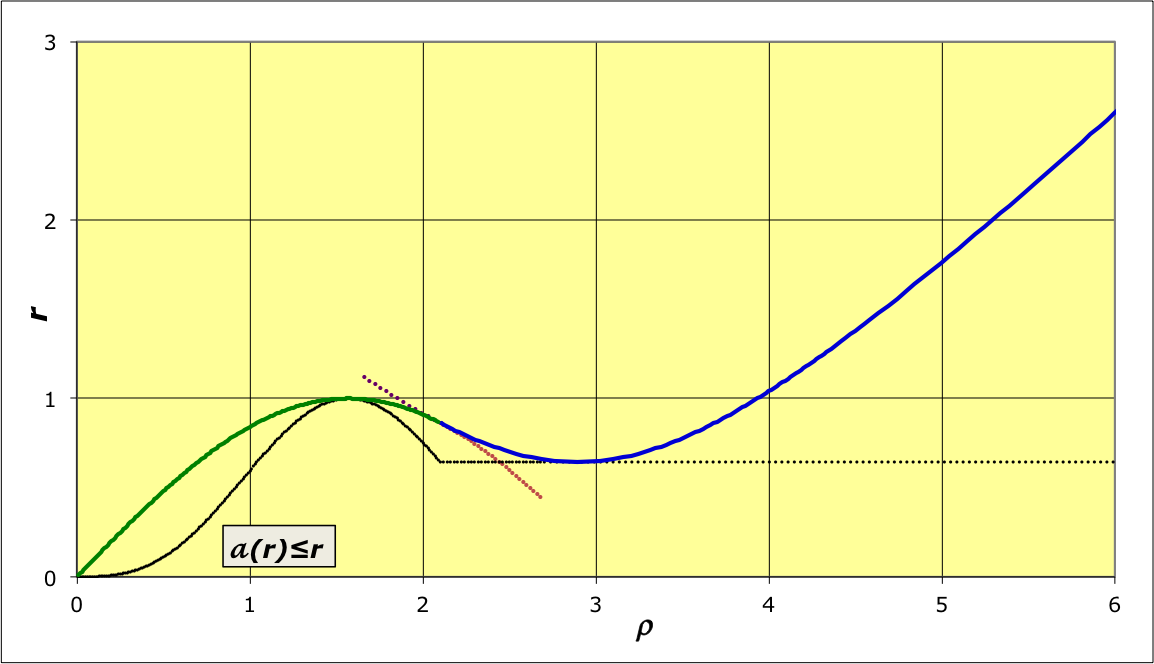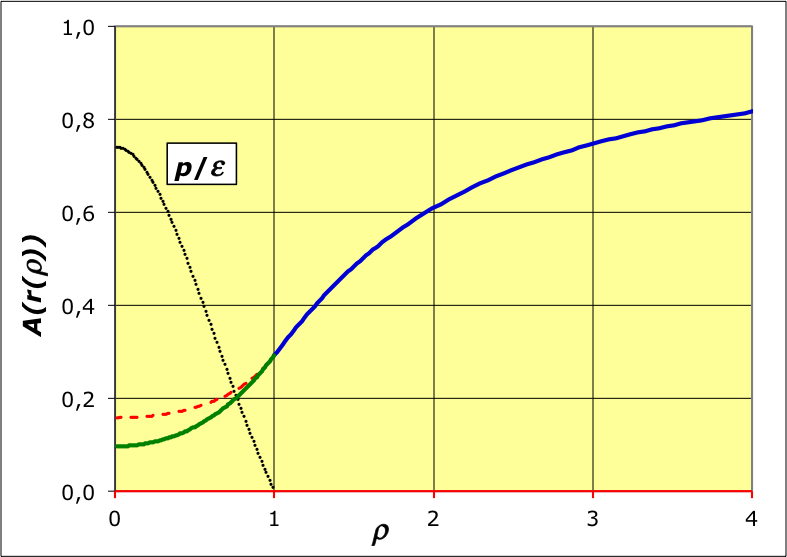
|
;
; ; . |
|
; ; . |
| ; . |
| ; . |
| . |
| . |
| . |

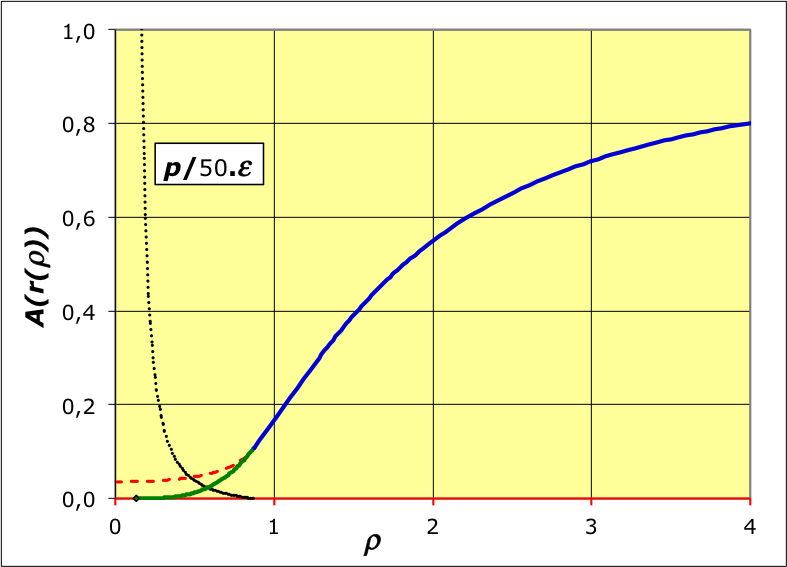
|
donc
; correspond à : . |
| . |
|
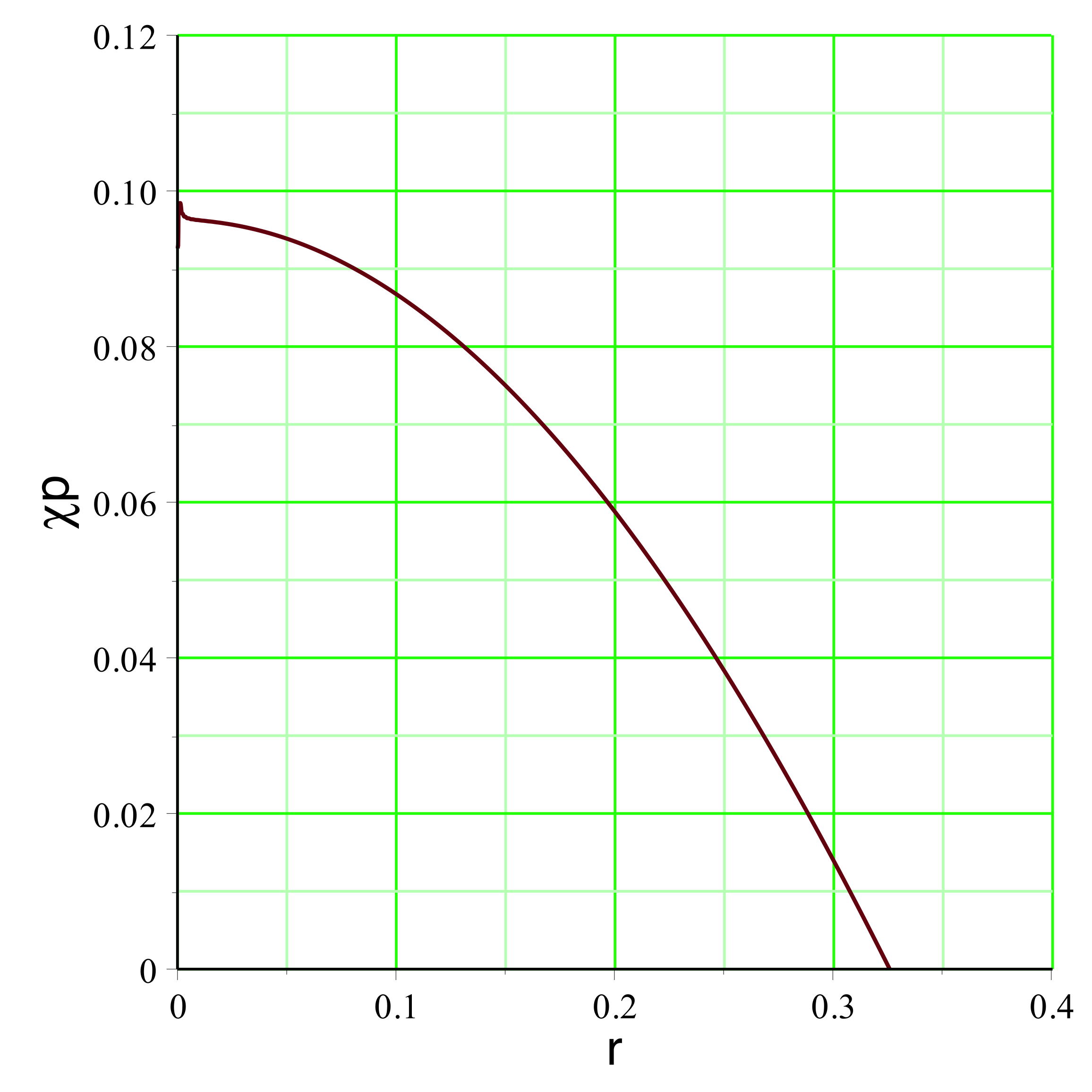 |
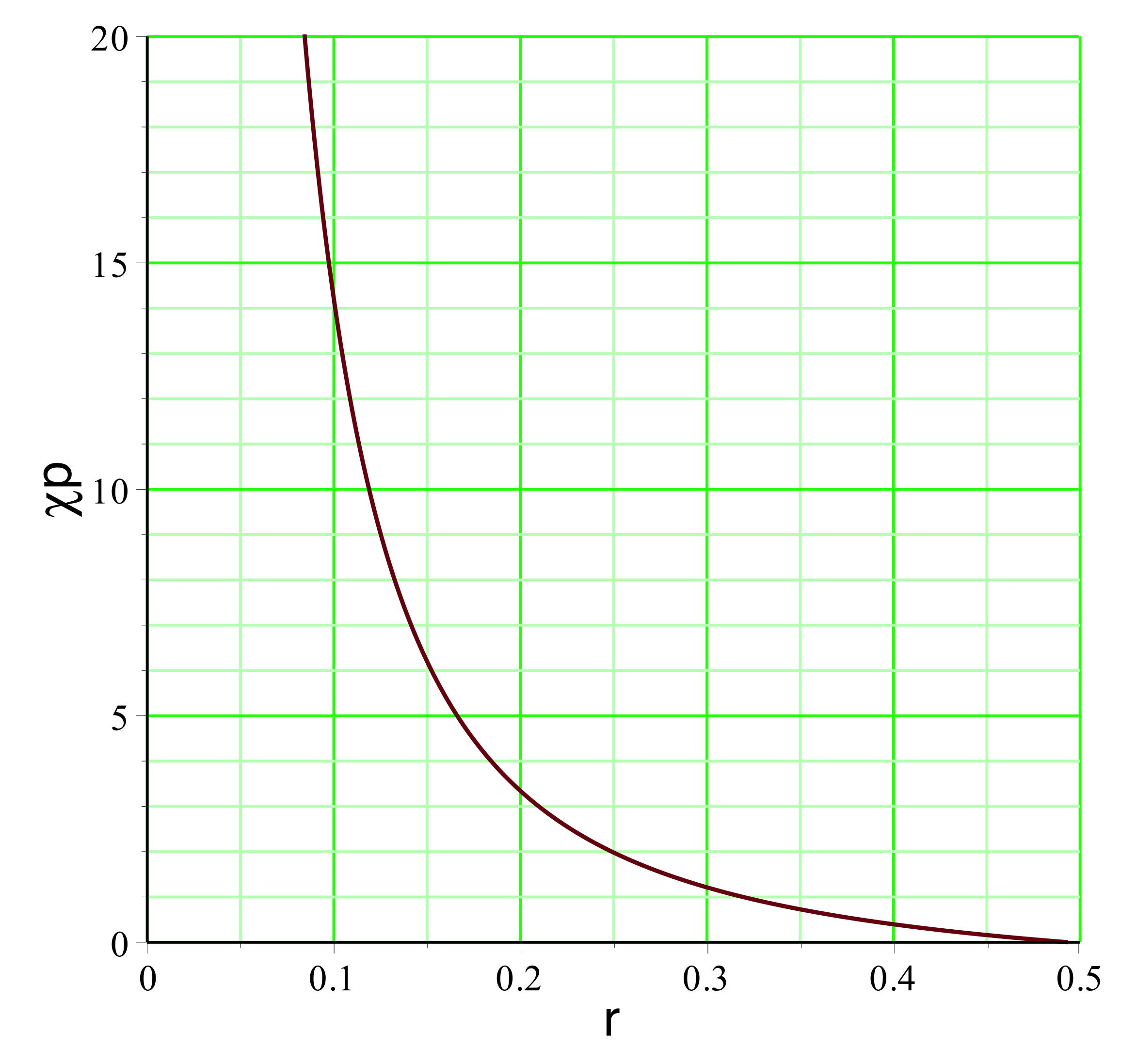 |
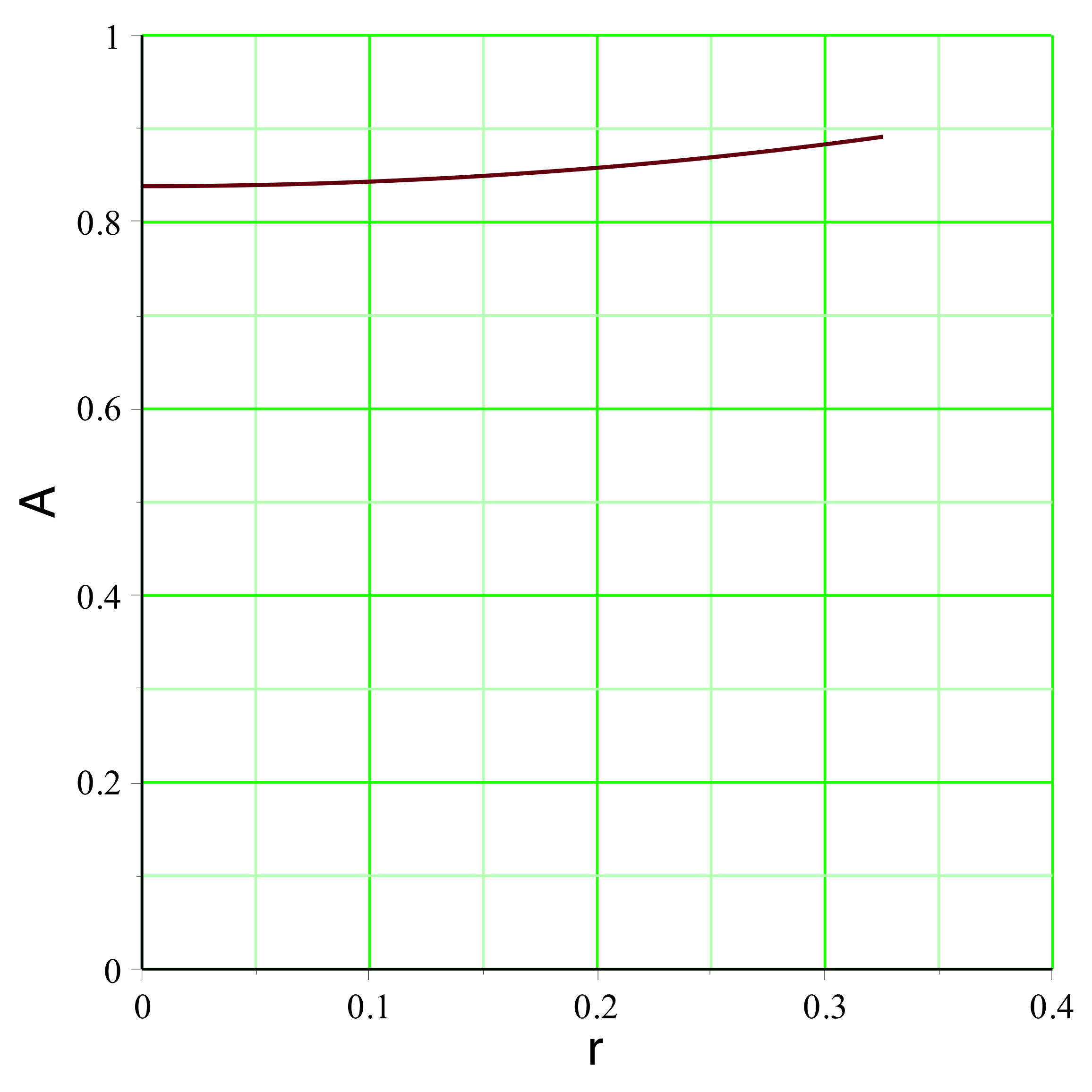 |
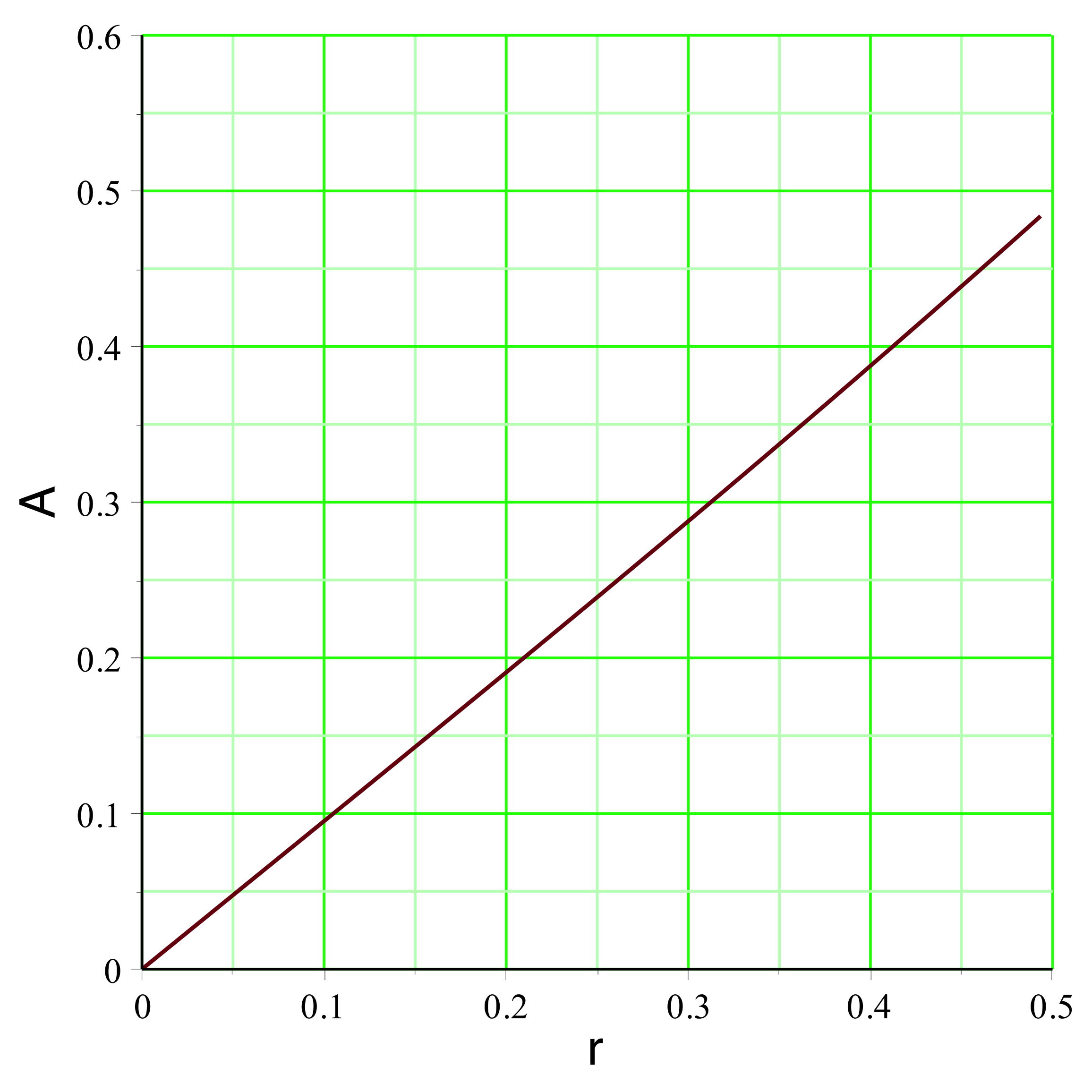 |
_hyp.jpg) |
_hyp.jpg) |
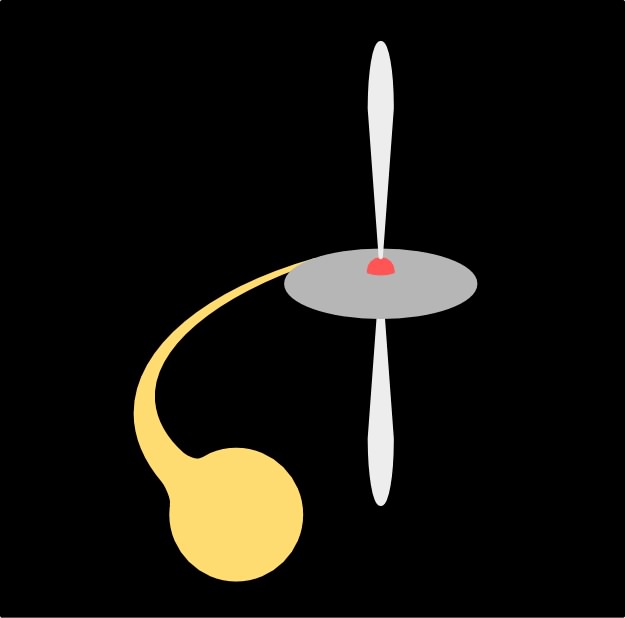
| • Dans certains cas, la limite peut être
dépassée “en douceur” : la matière provenant d'une étoile
compagnon binaire tombe progressivement en spirale de plus
en plus resserrée et forme un disque d'accrétion. Cette matière atteint le sol à une vitesse proche de celle de la lumière ; si elle ne peut s'accumuler car l'astre devient instable, alors sous l'effet de l'onde de choc elle peut être violemment éjectée selon l'axe polaire. |
 |
 |
 |