CHAMP CENTRAL SYMÉTRIQUE INTÉRIEUR “AVEC PRESSION” - corrigé des exercices


I. Astre solide “simple”

1. • Pour une métrique de la forme :  ds2=A(r)c2dt2−C(r)dr2−D(r)dΩ2{ds}^2=A(r) \:c^2 \,{dt}^2-C(r) \:{dr}^2-D(r) \:{dΩ}^2  on obtient :

 g00=Ag_{00}=A  ;  g11=−Cg_{11}=-C  ;  g22=−Dg_{22} = -D  ;  g33=−Dsin2(θ)g_{33}=-D \; \sin^2(θ)  ;
g00=1A\displaystyle g^{00}=\frac{1}{A}  ;  g11=−1C\displaystyle g^{11}=-\frac{1}{C}  ;  g22=−1D\displaystyle g^{22}=-\frac{1}{D}  ;  g33=−1Dsin2(θ)\displaystyle g^{33}=-\frac{1}{D \;\sin^2(θ)}  ;
Γ001=−Γ100=A′2\displaystyle Γ_{001}=-Γ_{100}=\frac{A'}{2}  ;  Γ111=−C′2\displaystyle Γ_{111}=-\frac{C'}{2}  ;  Γ221=−Γ122=−D′2\displaystyle Γ_{221}=-Γ_{122}=-\frac{D'}{2}  ;
Γ331=−Γ133=−D′2sin2(θ)\displaystyle Γ_{331}=-Γ_{133}=-\frac{D'}{2} \: \sin^2(θ)  ;  Γ332=−Γ233=−Dsin(θ)cos(θ)Γ_{332}=-Γ_{233}=-D \; \sin(θ) \; \cos(θ)  ;
Γ.010=A′2A\displaystyle Γ_{\phantom{.}01}^0=\frac{A'}{2 \,A}  ;  Γ.001=A′2C\displaystyle Γ_{\phantom{.}00}^1=\frac{A'}{2 \,C}  ;  Γ.111=C′2C\displaystyle Γ_{\phantom{.}11}^1=\frac{C'}{2 \,C}  ;
Γ.212=Γ.313=D′2D\displaystyle Γ_{\phantom{.}21}^2=Γ_{\phantom{.}31}^3=\frac{D'}{2 \,D}  ;  Γ.221=−D′2C\displaystyle Γ_{\phantom{.}22}^1=-\frac{D'}{2 \,C}  ;  Γ.331=−D′2Csin2(θ)\displaystyle Γ_{\phantom{.}33}^1=-\frac{D'}{2 \,C} \: \sin^2(θ)  ;
Γ.323=cot(θ)Γ_{\phantom{.}32}^3=\cot(θ)  ;  Γ.332=−sin(θ)cos(θ)Γ_{\phantom{.}33}^2=- \sin(θ) \;\cos(θ) .
• On en déduit :  R00=A″2C−A′2C(A′2A+C′2C−D′D)\displaystyle R_{00}=\frac{A''}{2 \,C}-\frac{A'}{2 \,C} \, \left(\frac{A'}{2 \,A}+\frac{C'}{2 \,C}-\frac{D'}{D}\right)  ;

 R11=−A″2A−D″D+A′2A(A′2A+C′2C)+D′D(C′2C+D′2D)\displaystyle R_{11}=-\frac{A''}{2 \,A}-\frac{D''}{D}+\frac{A'}{2 \,A} \, \left(\frac{A'}{2 \,A}+\frac{C'}{2 \,C}\right)+\frac{D'}{D} \, \left(\frac{C'}{2 \,C}+\frac{D'}{2 \,D}\right)  ;
R22=−D″2C−D′2C(A′2A−C′2C)+1\displaystyle R_{22}=-\frac{D''}{2 \,C}-\frac{D'}{2 \,C} \, \left(\frac{A'}{2 \,A}-\frac{C'}{2 \,C}\right)+1   ;   R33=R22sin2(θ)R_{33}=R_{22} \;\sin^2(θ) .
• Par ailleurs :   uμ=dxμds\displaystyle u^μ=\frac{dx^μ}{ds}  ;  u0=1A\displaystyle u^0=\frac{1}{\sqrt{A}}   et   uk=0u^k=0  ;

 T00=𝓅+εA−𝓅A=εA\displaystyle T^{00}=\frac{𝓅+ε}{A}-\frac{𝓅}{A}=\frac{ε}{A}  ;  T11=𝓅C\displaystyle T^{11}=\frac{𝓅}{C}  ;  T22=𝓅D\displaystyle T^{22}=\frac{𝓅}{D}  ;  T33=𝓅Dsin2(θ)\displaystyle T^{33}=\frac{𝓅}{D \;\sin^2(θ)}  ;
T=gαβTαβ=ε−3𝓅T=g_{αβ} \:T^{αβ}=ε-3 \,𝓅 .
• Ceci correspond à :  T00−12g00T=Aε+3𝓅2\displaystyle T_{00}-\frac{1}{2} g_{00} \: T=A \: \frac{ε+3 \,𝓅}{2}  ;  T11−12g11T=Cε−𝓅2\displaystyle T_{11}-\frac{1}{2} g_{11} \: T=C \: \frac{ε-𝓅}{2}  ;

 T22−12g22T=Dε−𝓅2\displaystyle T_{22}-\frac{1}{2} g_{22} \: T=D \: \frac{ε-𝓅}{2}  ;  T33−12g33T=Dsin2(θ)ε−𝓅2\displaystyle T_{33}-\frac{1}{2} g_{33} \: T=D \; \sin^2(θ) \: \frac{ε-𝓅}{2} .
• Les équations du champ peuvent donc s'écrire, avec  χ=8π𝒢c4\displaystyle χ=\frac{8π \:𝒢}{c^4}  :

 R00=A″2AC−A′2AC(A′2A+C′2C−D′D)=χε+3𝓅2\displaystyle R_0^{\,\,0}=\frac{A''}{2 \,A \:C}-\frac{A'}{2 \,A \:C} \, \left(\frac{A'}{2 \,A}+\frac{C'}{2 \,C}-\frac{D'}{D}\right)=χ \: \frac{ε+3 \,𝓅}{2}  ;
R11=A″2AC+D″CD−A′2AC(A′2A+C′2C)−D′CD(C′2C+D′2D)=−χε−𝓅2\displaystyle R_1^{\,\,1}=\frac{A''}{2 \,A \:C}+\frac{D''}{C \:D}-\frac{A'}{2 \,A \:C} \, \left(\frac{A'}{2 \,A}+\frac{C'}{2 \,C}\right)-\frac{D'}{C \:D} \, \left(\frac{C'}{2 \,C}+\frac{D'}{2 \,D}\right)=-χ \: \frac{ε-𝓅}{2}  ;
R22=R33=D″2CD+D′2CD(A′2A−C′2C)−1D=−χε−𝓅2\displaystyle R_2^{\,\,2}=R_3^{\,\,3}=\frac{D''}{2 \,C \:D}+\frac{D'}{2 \,C \:D} \, \left(\frac{A'}{2 \,A}-\frac{C'}{2 \,C}\right)-\frac{1}{D}=-χ \: \frac{ε-𝓅}{2}.

2. • On obtient par combinaison :

 R00−R11=−D″CD+D′CD(A′2A+C′2C+D′2D)=χ.(ε+𝓅)\displaystyle R_0^{\,\,0}-R_1^{\,\,1}=-\frac{D''}{C \:D}+\frac{D'}{C \:D} \, \left(\frac{A'}{2 \,A}+\frac{C'}{2 \,C}+\frac{D'}{2 \,D}\right)=χ .(ε+𝓅)  ;
R22+R33=D″CD+D′CD(A′2A−C′2C)−2D=−χ.(ε−𝓅)\displaystyle R_2^{\,\,2}+R_3^{\,\,3}=\frac{D''}{C \:D}+\frac{D'}{C \:D} \: \left(\frac{A'}{2 \,A}-\frac{C'}{2 \,C}\right)-\frac{2}{D}=-χ .(ε-𝓅) .
• La somme et la différence donnent ainsi respectivement :

 D′2CD(A′A+D′2D)−1D=χ𝓅\displaystyle \frac{D'}{2 \,C \:D} \: \left(\frac{A'}{A}+\frac{D'}{2 \,D}\right)-\frac{1}{D}=χ \:𝓅  ;   −D″CD+D′2CD(C′C+D′2D)+1D=χε\displaystyle -\frac{D''}{C \:D}+\frac{D'}{2 \,C \:D} \, \left(\frac{C'}{C}+\frac{D'}{2 \,D}\right)+\frac{1}{D}=χ \:ε .


II. Statique des fluides

1. • En notant zz la coordonnée verticale :  g→=−gu→z\overset{→}{g}=-g \:\overset{→}{u}_z  ;  la condition d'équilibre d'une tranche de fluide horizontale, de surface SS et d'épaisseur  dzdz  donc de masse  dm=μSdzdm=μ \:S \:dz ,  peut s'écrire :

 dmz̈=0=−S𝓅(z+dz)+S𝓅(z)−gdmdm \:\ddot{z}=0=- S \:𝓅(z+dz) + S \:𝓅(z)-g \:dm .
• On obtient ainsi :  d𝓅dz=−μg\displaystyle \frac{d𝓅}{dz}=-μ \:g  ;  𝓅(z)=𝓅(0)−μgz𝓅(z)=𝓅(0)-μ \:g \:z .


2.a. • La loi de conservation du tenseur d'énergie-impulsion peut s'écrire :  DβTαβ=0D_β T^{αβ}=0 ,  avec pour un fluide :  Tαβ=(𝓅+ε0)uαuβ−𝓅gαβT^{αβ}=(𝓅+ε_0 ) \: u^α \: u^β-𝓅 \:g^{αβ} .
• Ceci peut s'écrire :  ∂β(𝓅+ε0)uαuβ+(𝓅+ε0)Dβ(uαuβ)−∂β𝓅gαβ=0∂_β (𝓅+ε_0 ) \: u^α \: u^β+(𝓅+ε_0 ) \: D_β (u^α \: u^β )-∂_β 𝓅 \;g^{αβ}=0 .
• Puisque la seule composante non nulle de uβu^β est u0u^0 , l'indépendance du cas statique par rapport au temps permet de simplifier :  (𝓅+ε0)Dβ(uαuβ)−∂β𝓅gαβ=0(𝓅+ε_0 ) \: D_β (u^α \: u^β )-∂_β 𝓅 \; g^{αβ}=0 .
• On peut utiliser :

 Dβ(uαuβ)=∂β(uαuβ)+Γ.λβαuλuβ+Γ.λββuαuλD_β (u^α \: u^β )=∂_β (u^α \: u^β )+Γ_{\phantom{.}λβ}^α \: u^λ \: u^β+Γ_{\phantom{.}λβ}^β \: u^α \: u^λ  ;
Dβ(uαuβ)=Γ.λβαuλuβ+∂λ|g||g|uαuλ=Γ.λβαuλuβ=Γ.00αu0u0\displaystyle D_β (u^α \: u^β )=Γ_{\phantom{.}λβ}^α \: u^λ \: u^β+\frac{∂_λ \sqrt{|g|}}{\sqrt{|g|}} \: u^α \: u^λ=Γ_{\phantom{.}λβ}^α \: u^λ \: u^β=Γ_{\phantom{.}00}^α \: u^0 \: u^0  ;
(𝓅+ε0)Γμ00u0u0−∂μ𝓅=0  ;(𝓅+ε_0 ) \: Γ_{μ00} \: u^0 \: u^0-∂_μ 𝓅 =0
(𝓅+ε0)12∂μg00u0u0+∂μ𝓅=0(𝓅+ε_0 ) \, \frac{1}{2} ∂_μ g_{00} \: u^0 \: u^0+∂_μ 𝓅 =0 .
• Compte tenu de :  gαβuαuβ=g00u0u0=1g_{αβ} \: u^α \: u^β=g_{00} \: u^0 \: u^0=1 ,  on obtient (pour les composantes non nulles) :

 ∂i𝓅=−(𝓅+ε0)∂ig002g00=−(𝓅+ε0)∂iln(g00)\displaystyle ∂_i 𝓅 =-(𝓅+ε_0 ) \: \frac{∂_i g_{00}}{2 \:g_{00}}=-(𝓅+ε_0 ) \: ∂_i \ln\left(\sqrt{g_{00}}\right) .


2.b. • On obtient dans ce cas :  𝓅′=−(𝓅+ε0)A′2A\displaystyle 𝓅'=-(𝓅+ε_0 ) \: \frac{A'}{2 \,A} .


III. Astre solide “simple” en coordonnées “classiques”

1. • La loi de la statique peut s'écrire :  A′A=−2𝓅′ε+𝓅\displaystyle \frac{A'}{A}=-\frac{2 \,𝓅'}{ε+𝓅} .  L'intégration donne :  A.(ε+𝓅)2=CsteA .{(ε+𝓅)}^2=Cste .
• On obtient en outre :  C(r)=11−λr2\displaystyle C(r)=\frac{1}{1-λ \:r^2}  ;  ainsi par continuité avec l'extérieur :  A(R)=1C(R)=1−λR2\displaystyle A(R)=\frac{1}{C(R)}=1-λ \:R^2 .
• Avec  𝓅(R)=0𝓅(R)=0 ,  ceci donne finalement :  A.(ε+𝓅)2=(1−λR2)ε2A .{(ε+𝓅)}^2=(1-λ \:R^2 ) \: ε^2 .

2. • La loi de la statique peut s'écrire :  𝓅ε=βα−1\displaystyle \frac{𝓅}{ε}=\frac{β}{α}-1 .
• L'équation du champ sur AA peut s'écrire :  1−λr2r(2α′α+1r)−1r2=3λ𝓅ε\displaystyle \frac{1-λ \:r^2}{r} \, \left(\frac{2 \,α'}{α}+\frac{1}{r}\right)-\frac{1}{r^2} =3 \,λ \: \frac{𝓅}{ε} .
• En combinant on obtient :  1−λr2r2α′α=λ.(3βα−2)\displaystyle\frac{ 1-λ \:r^2}{r} \, \frac{2 \,α'}{α}=λ .\left(\frac{3 \,β}{α}-2\right)  où on peut substituer :  1−λr2r=−λxx′\displaystyle \frac{1-λ \:r^2}{r}=-λ \, \frac{x}{x'} .
• Ceci peut aussi s'écrire :  α′x=x′.(α−32β)α' \:x=x'.\left(α-\frac{3}{2} β\right)  ;  on en déduit  α−32β=kxα-\frac{3}{2} β=k \:x  avec une constante  k=−12k=-\frac{1}{2}  imposée par  α(R)=x(R)=βα(R)=x(R)=β .  Finalement en reportant :  A=14(31−λR2−1−λr2)2A=\frac{1}{4} \, \left(3 \,\sqrt{1-λ \:R^2}-\sqrt{1-λ \:r^2} \,\right)^2 .

3. • En reportant dans la loi de la statique :  𝓅ε=x−β3β−x\displaystyle \frac{𝓅}{ε}=\frac{x-β}{3 \:β-x}  c'est à dire :  𝓅=3λχ(1−λr2−1−λR231−λR2−1−λr2)\displaystyle 𝓅=\frac{3 \,λ}{χ} \, \left(\frac{\sqrt{1-λ \:r^2}-\sqrt{1-λ \:R^2}}{3\: \sqrt{1-λ \:R^2}-\sqrt{1-λ \:r^2}}\right) .


IV. Limite de stabilité d'un astre “simple”

1. • On peut obtenir par combinaison :

 R00−3R11=−A″AC+A′AC(A′2A+C′2C+1r)+3C′C2r=2χε\displaystyle R_0^{\,\,0}-3 \:R_1^{\,\,1}=-\frac{A''}{A \:C}+\frac{A'}{A \:C} \, \left(\frac{A'}{2 \,A}+\frac{C'}{2 \,C}+\frac{1}{r}\right)+ \frac{3 \,C'}{C^2 \: r}=2 \,χ \:ε .
• Ceci peut aussi s'écrire :

 A″−A′2(A′A+C′C+2r)=ArC(3C′−2rC2χε)\displaystyle A''-\frac{A'}{2} \, \left(\frac{A'}{A}+\frac{C'}{C}+\frac{2}{r}\right)=\frac{A}{r \:C} \:\left(3 \,C'-2 \,r \:C^2 \: χ \:ε\right) .


2. • Avec  A=α2A=α^2  on obtient :  2α″−α′.(C′C+2r)=αrC(3C′−2rC2χε)\displaystyle 2 \,α''-α' .\left(\frac{C'}{C}+\frac{2}{r}\right)=\frac{α}{r \:C} \, \left(3 \,C'-2 \,r \:C^2 \: χ \:ε\right) .
• Par ailleurs  C′C+2r=2ddr[ln(rC)]=−2rC(1rC)′\displaystyle \frac{C'}{C}+\frac{2}{r}=2 \,\frac{d}{dr} \left[\ln\left(r \:\sqrt{C}\right) \right]=-2 \,r \:\sqrt{C} \: \left(\frac{1}{r \:\sqrt{C}}\right)'  ;  on en déduit ainsi :

 2rC(α′rC)′=αrC(3C′−2rC2χε)\displaystyle 2 \,r \:\sqrt{C} \; \left(\frac{α'}{r \:\sqrt{C}}\right)'=\frac{α}{r \:C} \,\left(3 \,C'-2 \,r \:C^2 \: χ \:ε\right)  ;  (α′rC)′=αC21r2(3C′C2−2rχε)\displaystyle \left(\frac{α'}{r \:\sqrt{C}}\right)'=\frac{α \:\sqrt{C}}{2} \, \frac{1}{r^2} \: \left(3 \,\frac{C'}{C^2} -2 \,r \:χ \:ε\right) .
• D'autre part :  𝒶′=χεr2𝒶'=χ \:ε \:r^2   et   C′C2=𝒶′r−𝒶r2\displaystyle \frac{C'}{C^2} =\frac{𝒶'}{r}-\frac{𝒶}{r^2}  ;  finalement :

 1r2(3C′C2−2rχε)=𝒶′r3−3𝒶r4=(𝒶r3)′\displaystyle \frac{1}{r^2} \, \left(3 \,\frac{C'}{C^2} -2 \,r \:χ \:ε\right)=\frac{𝒶'}{r^3} -3\,\frac{𝒶}{r^4} =\left(\frac{𝒶}{r^3} \right)'  ;  (α′rC)′=αC2(𝒶r3)′\displaystyle \left(\frac{α'}{r \:\sqrt{C}}\right)'=\frac{α \:\sqrt{C}}{2} \, \left(\frac{𝒶}{r^3} \right)' .


3.a. • Si on veut éviter une singularité, la fonction αα ne peut pas s'annuler car  A=0A=0  correspond à une divergence de ln(A)\ln(A) qui se comporte comme un potentiel de gravitation : un champ infini correspondrait forcément à une pression infinie d'après la loi de la statique.
• La fonction αα doit donc être positive car elle l'est au niveau du raccordement avec l'extérieur et qu'elle est continue.
• Si la masse volumique μ(r)μ(r) est décroissante, la “masse volumique moyenne”  3M(r)4πr3\displaystyle \frac{3 \:M(r)}{4π \:r^3}  l'est forcément aussi, donc  (𝒶r3)′≤0\displaystyle \left(\frac{𝒶}{r^3} \right)'≤0   et   (α′rC)′≤0\displaystyle \left(\frac{α'}{r \:\sqrt{C}}\right)'≤0   (le cas avec masse volumique uniforme donne l'égalité).


3.b. • On obtient par intégration, compte tenu du raccordement pour  r=Rr=R  (continu, à dérivée continue) :  α′rC≥α′(R)RC(R)=rs2R3\displaystyle \frac{α'}{r \:\sqrt{C}}≥\frac{α'(R)}{R \:\sqrt{C(R)}}=\frac{r_s}{2 \,R^3} .
• Ainsi :  α′(r)≥rs2R3rC=rs2R3r1−𝒶(r)r\displaystyle α'(r)≥\frac{r_s}{2 \,R^3} \: r \:\sqrt{C}=\frac{r_s}{2 \,R^3} \, \frac{r}{\sqrt{1-\frac{𝒶(r)}{r}}} .


3.c. • On en déduit par intégration, compte tenu du raccordement pour  r=Rr=R :

 α(0)≤α(R)−rs2R3∫0Rr1−𝒶(r)rdr\displaystyle α(0)≤α(R)-\frac{r_s}{2 \,R^3} \, ∫_0^R \frac{r}{\sqrt{1-\frac{𝒶(r)}{r}}} \: dr   (le cas avec masse volumique uniforme donne l'égalité).
   
• On n'obtient ainsi  α(0)>0α(0)>0  (permettant la stabilité : absence de divergence) que dans des conditions qui ne peuvent pas être plus étendues que pour une masse volumique uniforme :  R<891λ\displaystyle R<\sqrt{\frac{8}{9}} \, \frac{1}{\sqrt{λ}} .


V. Limite d'un astre “ultra-relativiste”

1. • Dans le cas ultra-relativiste, la substitution de  𝓅=ε3\displaystyle 𝓅=\frac{ε}{3}  permet d'écrire l'équation sous la forme :

 3ε′(r)=−2ε(r)3𝒶(r)+χr3ε(r)r.(r−𝒶(r))\displaystyle 3 \,ε'(r)=-2 \,ε(r) \: \frac{3 \,𝒶(r)+χ \:r^3 \: ε(r)}{r.(r-𝒶(r))}   avec   𝒶′(r)=χr2ε(r)𝒶'(r)=χ \:r^2 \: ε(r) .
• On obtient ainsi :  3𝒶″(r)r.(r−𝒶(r))=2𝒶′(r)[3r−6𝒶(r)−r𝒶′(r)]3 \,𝒶''(r) \:r.(r-𝒶(r))=2 \,𝒶'(r) \:\left[3 \,r-6 \,𝒶(r)-r \:𝒶'(r)\right] .


2.a. • L'équation est invariante d'échelle : χχ se simplifie et aucun paramètre ne fixe une échelle particulière.
• La quantité 𝒶𝒶 correspond à une longueur ; 𝒶′𝒶' est sans unité et ne peut être qu'une constante ne dépendant que des coefficients numériques de l'équation : toute expression de rr ne pourrait être en fait qu'une expression de  rr0\displaystyle \frac{r}{r_0}  avec une constante r0r_0 fixant une échelle.


2.b. • La forme indiquée peut être notée :  𝒶′(r)=β𝒶'(r)=β  ;  on obtient ainsi :  0=2β.[3r−6βr−βr]0=2 \,β.[3 \,r - 6 \,β \:r - β \:r ] .
• Si on suppose  β≠0β≠0  on obtient :  β=37β=\frac{3}{7}  donc  𝒶(r)=37r𝒶(r)=\frac{3}{7} \, r .


VI. Approche de la limite d'un astre “ultra-relativiste”

1. • On peut éliminer la pression :  3𝓅=ε−εR3 \,𝓅=ε-ε_R  ;  3𝓅′=ε′=−16(4ε−εR)3𝒶+χr3.(ε−εR)r.(r−𝒶)\displaystyle 3 \,𝓅'=ε'=-\frac{1}{6} \, (4 \,ε-ε_R ) \,\frac{3 \,𝒶+χ \:r^3.(ε-ε_R)}{r.(r-𝒶 )} .
• Puis éliminer l'énergie volumique :  ε=𝒶′χr2\displaystyle ε=\frac{𝒶'}{χ \:r^2}  ;  𝒶″χr2−2𝒶′χr3=−16χr2(4𝒶′−χr2εR)3𝒶+r𝒶′−χr2εR)r.(r−𝒶)\displaystyle \frac{𝒶''}{χ \:r^2}-\frac{2 \,𝒶'}{χ \:r^3}=-\frac{1}{6 \,χ \:r^2} \, (4 \,𝒶'-χ \:r^2 \: ε_R ) \: \frac{3 \,𝒶+r \:𝒶'-χ \:r^2 \: ε_R)}{r.(r-𝒶)} .
• Ceci peut s'écrire :  6[𝒶″r−2𝒶′]=−(4𝒶′−3λr2)3𝒶+r𝒶′−3λr2r−𝒶\displaystyle 6 \,[𝒶'' \:r-2 \,𝒶']=-(4 \,𝒶'-3 \,λ \:r^2 ) \: \frac{3 \,𝒶+r \:𝒶'-3 \,λ \:r^2}{r-𝒶}  ou encore :

 6[𝒶″(r)r−2𝒶′(r)](r−𝒶(r))=(4𝒶′(r)−3λr2)[3λr3−3𝒶(r)−r𝒶′(r)]6 \,[𝒶''(r) \:r-2 \,𝒶'(r)] \: (r-𝒶(r))=(4 \,𝒶'(r)-3 \,λ \:r^2 ) \: [3 \,λ \:r^3-3 \,𝒶(r)-r \:𝒶'(r)] .


2. • Pour intégrer numériquement cette équation, on peut simplifier en prenant 1λ\displaystyle \frac{1}{\sqrt{λ}} comme unité de longueur ; c'est la valeur pour laquelle on obtiendrait  r=𝒶(r)r=𝒶(r)  pour une énergie volumique uniforme εRε_R . Avec cette notation :  6[𝒶″(r)r−2𝒶′(r)](r−𝒶(r))=(4𝒶′(r)−3r2)[3r3−3𝒶(r)−r𝒶′(r)]6 \,[𝒶''(r) \:r-2 \,𝒶'(r)] \: (r-𝒶(r))=(4 \,𝒶'(r)-3 \,r^2 ) \: [3 \, r^3-3 \,𝒶(r)-r \:𝒶'(r)] .
• On ne peut pas intégrer numériquement en partant de  r0=0r_0=0  car l'équation possède une singularité à l'origine. On peut par contre intégrer (par exemple avec la méthode d'Euler) en partant des conditions  {𝒶(r0)=37r0;𝒶′(r0)=37}\left\{𝒶(r_0)=\frac{3}{7} \, r_0\; ; \: 𝒶'(r_0)=\frac{3}{7} \, \right\}  pour  r0=10−3r_0={10}^{-3}  (unité relative). On obtient ainsi une solution dont le comportement au voisinage de l'origine est celui de la solution limite ultra-relativiste.

ChampSpherPres_cor_Im/a1_lin.jpg
 ChampSpherPres_cor_Im/a2_lin.jpg


ChampSpherPres_cor_Im/a3_lin.jpg
 ChampSpherPres_cor_Im/a4_lin.jpg


ChampSpherPres_cor_Im/a5_lin.jpg
 ChampSpherPres_cor_Im/a6_lin.jpg

• À l'autre limite, on peut partir de  {𝒶(r0)=1,2.10−6r0;𝒶′(r0)=3,5.10−6}\left \{𝒶(r_0)=\text{1,2}.{10}^{-6} \: r_0 \; ; \: 𝒶'(r_0)=\text{3,5}.{10}^{-6} \,\right \} :  on fixe 𝒶′(r0)𝒶'(r_0) et on ajuste 𝒶(r0)𝒶(r_0) de façon à obtenir la limite  𝒶″(0)=0𝒶''(0)=0 .  On obtient ainsi une solution dont le comportement est qualitativement le même que pour la solution avec masse volumique uniforme :  𝒶(r)≈λr3𝒶(r)≈λ \:r^3 .
◊ remarque : en pratique, à cause des incertitudes de calcul, il faut aussi surveiller  χ𝓅(0)χ \:𝓅(0)  et  C(0)C(0) .

ChampSpherPres_cor_Im/b1_lin.jpg
 ChampSpherPres_cor_Im/b2_lin.jpg


ChampSpherPres_cor_Im/b3_lin.jpg
 ChampSpherPres_cor_Im/b4_lin.jpg


ChampSpherPres_cor_Im/b5_lin.jpg
 ChampSpherPres_cor_Im/b6_lin.jpg

• Entre les deux, on peut partir des conditions  {𝒶(r0)=6,7.10−5r0;𝒶′(r0)=2,0.10−4}\left \{𝒶(r_0)=\text{6,7}.{10}^{-5} \: r_0 \; ; \: 𝒶'(r_0)=\text{2,0}.{10}^{-4} \,\right \} .  On obtient ainsi une solution dont le comportement est qualitativement intermédiaire.

ChampSpherPres_cor_Im/c3_lin.jpg
 ChampSpherPres_cor_Im/c4_lin.jpg


ChampSpherPres_cor_Im/c5_lin.jpg
 ChampSpherPres_cor_Im/c6_lin.jpg


3.
• Pour les “petits” astres (faible pression au centre) on retrouve logiquement que le rayon RR (valeur de rr pour laquelle la pression s'annule) augmente en fonction de 𝓅0𝓅_0 (et réciproquement).
• Par contre, pour les astres dont la pression centrale est plus grande, le rayon RR n'augmente plus (et diminue même un peu transitoirement). Cette propriété, qui peut surprendre, vient du fait que l'augmentation de pression cause une augmentation du “champ de gravitation”, ce qui modifie la métrique.
◊ remarque : on constate ainsi que RR reste inférieur à 1λ\displaystyle \frac{1}{\sqrt{λ}} , mais puisque ici la masse volumique n'est pas uniforme, cette valeur ne correspond pas à la limite des trous noirs :  rs=Rr_s=R .
ChampSpherPres_cor_Im/R(p0)_lin.jpg

• Il en est plus ou moins de même pour  rs=𝒶(R)r_s=𝒶(R) ,  pour les mêmes raisons. La principale différence est au contraire pour les faibles rayons :  𝒶(R)≈λR3𝒶(R)≈λ \:R^3 .

ChampSpherPres_cor_Im/rs(p0)_lin.jpg
 ChampSpherPres_cor_Im/rssR(p0)_lin.jpg

• L'évolution de rsR\displaystyle \frac{r_s}{R} montre de même une limite  ≈0,5<1≈\text{0,5}<1  ;  ceci signifie que la limite  rs=R r_s=R  correspondant à la formation des trous noirs n'est jamais atteinte.
◊ remarque : si on impose des conditions initiales qui “dépassent” la solution correspondant à la limite ultra-relativiste, on obtient des solutions tendant en périphérie vers la même limite que la solution égale au centre à la limite ultra-relativiste ; ces solutions aboutissent donc à des valeurs comparables de RR , rsr_s et 𝓅0𝓅_0 ; par contre, ces solutions “oscillent” de façon “instable” au voisinage de l'origine (très sensibles aux incertitudes du calcul numérique ; cela est dû à la singularité de l'équation à l'origine) ; ceci suggère que l'équilibre correspondant est plutôt instable au voisinage du centre : ainsi les astres proches de la limite des trous noirs, ultra-relativistes dans leur partie centrale, seraient instables.
◊ remarque : on peut en outre noter que cette limite s'approche de  R=32rsR=\frac{3}{2} \, r_s  correspondant à la trajectoire circulaire (instable) pour les photons, donc aussi pour les ondes gravitationnelles ; au delà il serait possible que l'énergie de l'astre interagisse avec elle même par émission/réabsorption d'ondes gravitationnelles ; on pourrait même se demander si les oscillations des courbes précédentes ne sont pas associées à des interférences, qui seraient éventuellement susceptibles de comporter des effets de quantification.


4.a. • On peut écrire :  T=3𝓅.(((εR3𝓅)2+1)−1)=εR26𝓅+𝒪(1𝓅3)→0\displaystyle T=3 \,𝓅 .\left(\left(\sqrt{\left(\frac{ε_R}{3 \,𝓅}\right)^2+1} \:\right)-1\right)=\frac{ε_R^{\:2}}{6 \,𝓅}+𝒪\,\left(\frac{1}{𝓅^3} \right)→0 .


4.b. • On obtient :  2εdε=18𝓅d𝓅2 \,ε \:dε=18 \,𝓅 \:d𝓅  ;  donc  dεd𝓅=9𝓅εR2+9𝓅2→0\displaystyle \frac{dε}{d𝓅}=\frac{9 \,𝓅}{\sqrt{ε_R^{\:2}+9 \,𝓅^2}}→0   et  vson=c∂𝓅∂ε→∞\displaystyle v_{son}=c\:\sqrt{\frac{∂𝓅}{∂ε}}→∞ .


4.c. • On peut écrire :  T=−εR2εR+𝓅→0\displaystyle T=-\frac{ε_R^{\:2}}{ε_R+𝓅}→0  pour  𝓅→∞𝓅→∞ .
• On obtient :  dεd𝓅=3−εR2(εR+𝓅)2→2\displaystyle \frac{dε}{d𝓅}=3-\frac{ε_R^{\:2}}{(ε_R+𝓅)^2} →2   et  vson=c∂𝓅∂ε→c2\displaystyle v_{son}=c\:\sqrt{\frac{∂𝓅}{∂ε}}→\frac{c}{\sqrt{2}}  pour  𝓅→0𝓅→0 .
◊ remarque : on aurait pu également proposer  ε(r)=3𝓅+εRe−𝓅/εRε(r)=3 \,𝓅+ε_R \: \mathrm{e}^{-𝓅/ε_R} .


4.d. • On peut utiliser une relation de la forme :  ε(r)=3𝓅+εR2εR+α𝓅\displaystyle ε(r)=3 \,𝓅+\frac{ε_R^{\:2}}{ε_R+α \:𝓅}  avec αα très petit, cela résout la difficulté théorique de la trace, pratiquement sans modifier les calculs numériques qui s'en déduisent.


4.e. • On peut éliminer de même la pression :

 3𝓅=12[(ε−3εR)+ε2+6εεR−3εR2]3 \,𝓅=\frac{1}{2} \, \left[(ε-3 \,ε_R )+\sqrt{ε^2+6 \,ε \:ε_R-3 \,ε_R^{\:2}} \, \right]  ;
3𝓅′=12ε′[(ε−3εR)+ε2+6εεR−3εR2]ε2+6εεR−3εR2=⋯\displaystyle 3 \,𝓅'=\frac{1}{2} \, ε' \: \frac{\left[(ε-3 \,ε_R )+\sqrt{ε^2+6 \,ε \:ε_R-3 \,ε_R^{\:2}} \, \right]}{\sqrt{ε^2+6 \,ε \:ε_R-3 \,ε_R^{\:2}}}=⋯

 124[(7ε−3εR)+ε2+6εεR−3εR2]6𝒶+χr3.[(ε−3εR)+ε2+6εεR−3εR2]r.(r−𝒶)\frac{1}{24} \, \left[(7 \,ε-3 \,ε_R )+\sqrt{ε^2+6 \,ε \:ε_R-3 \,ε_R^{\:2}}\,\right] \: \frac{6 \,𝒶+χ \:r^3.\left[(ε-3 \,ε_R )+\sqrt{ε^2+6 \,ε \:ε_R-3 \,ε_R^{\:2}} \, \right]}{r.(r-𝒶)} .

• En éliminant de même l'énergie volumique :  ε=𝒶′χr2\displaystyle ε=\frac{𝒶'}{χ \:r^2}  ;  les calculs sont plus longs, mais on obtient :

 (𝒶″r−2𝒶′)[(𝒶′+9λr2)+𝒶′2+18𝒶′λr2−27λ2r4]𝒶′2+18𝒶′λr2−27λ2r4=⋯\displaystyle (𝒶'' \:r-2 \,𝒶') \: \frac{\left[(𝒶'+9 \,λ \:r^2 )+\sqrt{{𝒶'}^2+18 \,𝒶' \:λ \:r^2-27 \:λ^2 \: r^4} \, \right]}{\sqrt{{𝒶'}^2+18 \,𝒶' \:λ \:r^2-27 \,λ^2 \: r^4} }=⋯

 −112[(7𝒶′−9λr2)+𝒶′2+18𝒶′λr2−27λ2r4)]6𝒶+r.[(a′−9λr2)+𝒶′2+18𝒶′λr2−27λ2r4]r−𝒶\displaystyle -\frac{1}{12} \, \left[(7 \,𝒶'-9 \,λ \:r^2 )+\sqrt{{𝒶'}^2+18 \,𝒶' \:λ \:r^2-27 \,λ^2 \: r^4 )} \, \right] \; \frac{6 \,𝒶+r.\left[(a'-9 \,λ \:r^2 )+\sqrt{{𝒶'}^2+18 \,𝒶' \:λ \:r^2-27 \,λ^2 \: r^4 } \, \right]}{r-𝒶} .
◊ remarque : la réécriture sans dénominateur est possible mais encombrante et peu utile.


5. • On peut simplifier en prenant 1λ\displaystyle \frac{1}{\sqrt{λ}} comme unité de longueur, puis intégrer en partant des conditions  {𝒶(r0)=37r0;𝒶′(r0)=37}\left\{𝒶(r_0)=\frac{3}{7} \, r_0\; ; \: 𝒶'(r_0)=\frac{3}{7} \, \right\}  pour  r0=10−3r_0={10}^{-3}  (unité relative). On obtient ainsi une solution dont le comportement au voisinage de l'origine est celui de la solution limite ultra-relativiste.

ChampSpherPres_cor_Im/a1_hyp.jpg
 ChampSpherPres_cor_Im/a2_hyp.jpg


ChampSpherPres_cor_Im/a3_hyp.jpg
 ChampSpherPres_cor_Im/a4_hyp.jpg


ChampSpherPres_cor_Im/a5_hyp.jpg
 ChampSpherPres_cor_Im/a6_hyp.jpg

◊ remarque : la transition entre le centre ultra-relativiste et la périphérie n'est que très légèrement différente de celle obtenue pour la modélisation “simple” précédente.

• À l'autre limite, on peut partir de  {𝒶(r0)=1,07.10−6r0;𝒶′(r0)=3,2.10−6}\left \{𝒶(r_0)=\text{1,07}.{10}^{-6} \: r_0 \; ; \: 𝒶'(r_0)=\text{3,2}.{10}^{-6} \,\right \} :  on fixe 𝒶′(r0)𝒶'(r_0) et on ajuste 𝒶(r0)𝒶(r_0) de façon à obtenir la limite  𝒶″(0)=0𝒶''(0)=0 .  On obtient ainsi une solution dont le comportement est qualitativement le même que pour la solution avec masse volumique uniforme :  𝒶(r)≈λr3𝒶(r)≈λ \:r^3 .

ChampSpherPres_cor_Im/b1_hyp.jpg
 ChampSpherPres_cor_Im/b2_hyp.jpg


ChampSpherPres_cor_Im/b3_hyp.jpg
 ChampSpherPres_cor_Im/b4_hyp.jpg


ChampSpherPres_cor_Im/b5_hyp.jpg
 ChampSpherPres_cor_Im/b6_hyp.jpg

◊ remarque : pour  r≈0r≈0  on voit ici des fluctuations de  χ𝓅χ \:𝓅  dues aux incertitudes de calcul ; pour RR petit le rôle de  χ𝓅χ \:𝓅  est peu important et on peut extrapoler paraboliquement les valeurs pour rr plus grand (la zone imprécise est très petite) ; une correction du second ordre serait négligeable.

• Entre les deux, on peut partir des conditions  {𝒶(r0)=3,33.10−5r0;𝒶′(r0)=1,0.10−4}\left \{𝒶(r_0)=\text{3,33}.{10}^{-5} \: r_0 \; ; \: 𝒶'(r_0)=\text{1,0}.{10}^{-4} \,\right \} .  On obtient ainsi une solution dont le comportement est qualitativement intermédiaire.

ChampSpherPres_cor_Im/c3_hyp.jpg
 ChampSpherPres_cor_Im/c4_hyp.jpg


ChampSpherPres_cor_Im/c5_hyp.jpg
 ChampSpherPres_cor_Im/c6_hyp.jpg

• L'évolution de RR ,  rsr_s  et  rsR\displaystyle \frac{r_s}{R}  en fonction de la pression centrale est tout à fait semblable à celle obtenue pour la modélisation “simple” précédente.

◊ remarque : cela est cohérent dans la mesure où l'utilisation d'une modélisation mathématique “simpliste” (sans justification physique) avait pour but de montrer que ce comportement est (seulement) caractéristique de l'approche de la limite ultra-relativiste.
ChampSpherPres_cor_Im/R(p0)_hyp.jpg

ChampSpherPres_cor_Im/rs(p0)_hyp.jpg
 ChampSpherPres_cor_Im/rssR(p0)_hyp.jpg


VII. Géométrie spatiale

1. • En notant   ε=μc2ε=μ \:c^2   et   λ=χε3\displaystyle λ=\frac{χ \:ε}{3}   on peut utiliser 1λ\displaystyle \frac{1}{\sqrt{λ}} comme unité de longueur pour simplifier les notations. On utilise le “rayon périphérique”  rr  comme paramètre ; on note  r=Rr=R  le rayon de l'astre.
• On obtient à l'intérieur (en notations réduites) :  A(r)=[A(R)]3/21−r2\displaystyle A(r)=\frac{[A(R)]^{3/2}}{\sqrt{1-r^2}}  ;  C(r)=11−r2\displaystyle C(r)=\frac{1}{1-r^2}  ;  ρ(r)=arcsin(r)ρ(r)=\arcsin(r)  ;  ρ(R)=arcsin(R)ρ(R)=\arcsin(R) .
• On obtient à l'extérieur :  A(r)=1−rsr\displaystyle A(r)=1-\frac{r_s}{r}  ;  C(r)=1A(r)\displaystyle C(r)=\frac{1}{A(r)}  ;  ρ(r)=rsartanh(1−rsr)+r1−rsr+ρR\displaystyle ρ(r)=r_s \: \mathrm{artanh}\left(\sqrt{1-\frac{r_s}{r}}\,\right)+r \:\sqrt{1-\frac{r_s}{r}}\, +ρ_R  avec  rs=R3r_s=R^3  et où ρRρ_R est une constante pour raccorder ρ(R)ρ(R)  ;  en outre  A(R)=1−R2A(R)=1-R^2  pour raccorder A(r)A(r) .
• Pour un astre “non relativiste”  ρ(R)≪π2ρ(R)≪\frac{π}{2}  ;  on peut choisir  rs=0,30r_s=\text{0,30}  (R=0,67R=\text{0,67}  et  ρ(R)=0,72ρ(R)=\text{0,72} )  ;  on obtient la représentation ci-après (l'intérieur est en marron).

ChampSpherPres_cor_Im/potSimple.jpg

2. • Avec les mêmes notations (réduites), on obtient à l'intérieur :  dρ2=dr2+dz2{dρ}^2={dr}^2+{dz}^2  ;  C(r)=11−r2\displaystyle C(r)=\frac{1}{1-r^2}  ;  dρ2=Cdr2{dρ}^2=C \:{dr}^2  ;  dz2=r2dr21−r2\displaystyle {dz}^2=\frac{r^2 \:{dr}^2}{1-r^2}  ;  z=1−1−r2z=1-\sqrt{1-r^2}  (compte tenu de  z(0)=0z(0)=0  ;  portion de sphère de centre 11 et de rayon 11 ).
• On obtient à l'extérieur :  A(r)=1−rsr\displaystyle A(r)=1-\frac{r_s}{r}  ;  C(r)=1A(r)\displaystyle C(r)=\frac{1}{A(r)}  ;  dz2=rsdr2r−rs\displaystyle {dz}^2=\frac{r_s \: {dr}^2}{r-r_s}  ;  z=z0+2rsrrs−1\displaystyle z=z_0+2 \,r_s \:\sqrt{\frac{r}{r_s} -1}  où z0z_0 est une constante pour raccorder z(R)z(R) .  Cela correspond à une portion de “paraboloïde” de révolution (selon un axe parallèle à sa directrice et non son axe de symétrie).

• Pour un astre “non relativiste”  ρ(R)≪π2ρ(R)≪\frac{π}{2}  ;  on peut choisir  rs=0,30r_s=\text{0,30}  (R=0,67R=\text{0,67}  et  ρ(R)=0,72ρ(R)=\text{0,72} )  ;  on obtient la représentation ci-dessous (l'intérieur est en marron).

ChampSpherPres_cor_Im/geomSimple.jpg

3. • Pour la partie intérieure, on peut éliminer la pression :

 3𝓅=12[(ε−3εR)+ε2+6εεR−3εR2]3 \,𝓅=\frac{1}{2} \, \left[(ε-3 \,ε_R )+\sqrt{ε^2+6 \,ε \:ε_R-3 \,ε_R^{\:2}} \, \right]  ;
3𝓅′=12ε′[(ε−3εR)+ε2+6εεR−3εR2]ε2+6εεR−3εR2=⋯\displaystyle 3 \,𝓅'=\frac{1}{2} \, ε' \: \frac{\left[(ε-3 \,ε_R )+\sqrt{ε^2+6 \,ε \:ε_R-3 \,ε_R^{\:2}} \, \right]}{\sqrt{ε^2+6 \,ε \:ε_R-3 \,ε_R^{\:2}}}=⋯

 124[(7ε−3εR)+ε2+6εεR−3εR2]6𝒶+χr3.[(ε−3εR)+ε2+6εεR−3εR2]r.(r−𝒶)\displaystyle \frac{1}{24} \, \left[(7 \,ε-3 \,ε_R )+\sqrt{ε^2+6 \,ε \:ε_R-3 \,ε_R^{\:2}} \,\right] \: \frac{6 \,𝒶+χ \:r^3.\left[(ε-3 \,ε_R )+\sqrt{ε^2+6 \,ε \:ε_R-3 \,ε_R^{\:2}} \, \right]}{r.(r-𝒶)} .
• Puis en éliminant l'énergie volumique :  ε=𝒶′χr2\displaystyle ε=\frac{𝒶'}{χ \:r^2}  on obtient :

 (𝒶″r−2𝒶′)[(𝒶′+9λr2)+𝒶′2+18𝒶′λr2−27λ2r4]𝒶′2+18𝒶′λr2−27λ2r4=⋯\displaystyle (𝒶'' \:r-2 \,𝒶') \, \frac{\left[(𝒶'+9 \,λ \:r^2 )+\sqrt{{𝒶'}^2+18 \,𝒶' \:λ \:r^2-27 \,λ^2 \:r^4}\, \right]}{\sqrt{{𝒶'}^2+18 \,𝒶' \:λ \:r^2-27 \,λ^2 \:r^4}}=⋯

 −112[(7𝒶′−9λr2)+𝒶′2+18𝒶′λr2−27λ2r4]6𝒶+r.[(𝒶′−9λr2)+𝒶′2+18𝒶′λr2−27λ2r4]r−𝒶\displaystyle -\frac{1}{12} \, \left[(7 \,𝒶'-9 \,λ \:r^2 )+\sqrt{{𝒶'}^2+18 \,𝒶' \:λ \:r^2-27 \,λ^2 \: r^4} \, \right] \: \frac{6 \,𝒶+r.\left[(𝒶'-9 \,λ \:r^2 )+\sqrt{{𝒶'}^2+18 \,𝒶' \:λ \:r^2-27 \,λ^2 \: r^4} \, \right]}{r-𝒶} .
◊ remarque : la réécriture sans dénominateur est possible mais encombrante et peu utile.

• On peut simplifier en prenant 1λ\displaystyle \frac{1}{\sqrt{λ}} comme unité de longueur, puis intégrer en partant des conditions  {𝒶(r0)=37r0;𝒶′(r0)=37}\left\{𝒶(r_0)=\frac{3}{7} \, r_0\; ; \: 𝒶'(r_0)=\frac{3}{7} \, \right\}  pour  r0=10−3r_0={10}^{-3}  (unité relative). On obtient ainsi une solution dont le comportement au voisinage de l'origine est celui de la solution limite ultra-relativiste.
• Connaissant 𝒶(r)𝒶(r) on en déduit  C(r)=rr−𝒶(r)\displaystyle C(r)=\frac{r}{r-𝒶(r)}  puis ρ(r)ρ(r) par intégration.
• Avec 𝒶′(r)𝒶'(r) on en déduit ε(r)ε(r) puis 𝓅(r)𝓅(r) ; ensuite on calcule  A′A=𝒶+χpr3r.(r−𝒶)\displaystyle \frac{A'}{A}=\frac{𝒶+χ \:p \:r^3}{r.(r-𝒶)}  puis  ln(A)\ln\left(\sqrt{A}\,\right)  par intégration.
• La partie extérieure est inchangée et se raccorde de façon analogue ; on obtient la représentation suivante, avec une divergence du potentiel à l'origine  (A→0A→0 ).

ChampSpherPres_cor_Im/potUltra.jpg

4. • Avec les mêmes notations (réduites), on obtient à l'intérieur :  dρ2=dr2+dz2{dρ}^2={dr}^2+{dz}^2  ;  C(r)=rr−𝒶(r)\displaystyle C(r)=\frac{r}{r-𝒶(r)}  ;  dρ2=Cdr2{dρ}^2=C \:{dr}^2  ;  dz2=𝒶(r)dr2r−𝒶(r)\displaystyle {dz}^2=\frac{𝒶(r) \:{dr}^2}{r-𝒶(r)}  ;  on en déduit z(r)z(r) par intégration, compte tenu de  z(0)=0z(0)=0  (portion d'allure conique).
• La partie extérieure est inchangée et se raccorde de façon analogue ; on obtient la représentation suivante. On peut remarquer à la périphérie de l'astre une courbure rappelant une portion de sphère, mais en se rapprochant du centre le comportement évolue vers une allure conique caractéristique de la limite ultra-relativiste.

ChampSpherPres_cor_Im/geomUltra.jpg


VIII. Pression dans un système en pré-expansion

1.a. • Pour une tranche de fluide incompressible l'équation du mouvement peut s'écrire :

 μSdzz̈=[𝓅(z)−𝓅(z+dz)]S+μSdzgμ \:S \:dz \:\ddot{z}=[𝓅(z)-𝓅(z + dz)] \:S+μ \:S \:dz \:g .
• Ceci correspond à :  d𝓅=μ.[g(z)−z̈]dzd𝓅=μ \,.[g(z)-\ddot{z} \, ] \:dz  où z̈\ddot{z} ne dépend pas de zz .
◊ remarque : cela correspond à la loi de la statique du fluide dans son référentiel propre, non galiléen, donc avec une force d'inertie d'entraînement associée à l'accélération.


1.b. • Pour l'ensemble de la tranche :  𝓅(0)=0𝓅(0)=0  et  𝓅(L)=0𝓅(L)=0 ,  donc :  z̈L=∫0Lg(z′)dz′=αln(L+ηη)\displaystyle \ddot{z} \: L=∫_0^L g(z') \:dz'=α \; \ln\left(\frac{L+η}{η}\right) .  On obtient ainsi :  z̈=αLln(L+ηη)\displaystyle \ddot{z}=\frac{α}{L} \: \ln\left(\frac{L+η}{η}\right) .


1.c. • On en déduit :  𝓅(z)=μ∫0zg(z′)dz′−μz̈∫0zdz′=μαln(z+ηη)−μαLln(L+ηη)z\displaystyle 𝓅(z)=μ \:∫_0^z g(z') \:dz'-μ \:\ddot{z} \: ∫_0^z dz'=μ \:α \; \ln\left(\frac{z+η}{η}\right)-μ \: \frac{α}{L} \: \ln\left(\frac{L+η}{η}\right) \:\: z .

ChampSpherPres_cor_Im/pression_z.png

• C'est le champ plus fort vers  z=0z=0  qui tend à entraîner le plus d'accélération, pour que l'ensemble du fluide incompressible accélère, forcément d'un même mouvement, il faut qu'une surpression apparaisse pour forcer l'accélération commune aux  zz  intermédiaires. Par contre la masse à pousser est d'autant plus faible qu'on se rapproche de  z=Lz=L  donc la surpression nécessaire diminue jusqu'à s'annuler.


2.a. • L'équation du mouvement peut s'écrire, initialement, selon la statique dans le référentiel non galiléen du fluide, où la force volumique inclut une force d'inertie d'entraînement :  ∇→𝓅=d𝓅dρu→ρ=μ.(g−ρ̈)u→ρ\displaystyle \overset{→}{∇}𝓅=\frac{d𝓅}{dρ} \: \overset{→}{u}_ρ=μ .(g-\ddot{ρ} \,) \: \overset{→}{u}_ρ .


2.b. • Ici  ρ̈=−r̈\ddot{ρ}=-\ddot{r}  dépend de rr par conservation du volume : à chaque instant le débit  𝒟(t)=πr2ρ˙(r,t)𝒟(t)=π \:r^2 \: \dot{ρ}(r,t)  est indépendant de rr .
• Ceci peut s'écrire :  ρ˙(r,t)=𝒟(t)πr2(t)\displaystyle \dot{ρ}(r,t)=\frac{𝒟(t)}{π \:r^2 (t)}  ;  ρ̈(r,t)=𝒟˙(t)πr2(t)−2𝒟(t)πr3(t)r˙(r,t)=𝒟˙(t)πr2(t)+2𝒟2(t)π2r5(t)\displaystyle \ddot{ρ}(r,t)=\frac{\dot{𝒟}(t)}{π \:r^2 (t)}-\frac{2 \,𝒟(t)}{π \:r^3 (t)} \: \dot{r}(r,t)=\frac{\dot{𝒟}(t)}{π \:r^2 (t)}+\frac{2 \,𝒟^2 (t)}{π^2 \: r^5 (t)} .  Cela décrit une accélération “de base” augmentée par un terme dû à la diminution de section.
• Initialement  𝒟=0𝒟=0  donc :  ρ̈(r,0)=𝒟˙(0)πr2(t)=κr2\displaystyle \ddot{ρ}(r,0)=\frac{\dot{𝒟}(0)}{π \:r^2 (t)}=\frac{κ}{r^2} .


2.c. • Ceci donne :  d𝓅=μ(αρ−κ(ρ−η)2)dρ\displaystyle d𝓅=μ \:\left(\frac{α}{ρ}-\frac{κ}{(ρ-η)^2} \right) \: dρ .
• Ainsi :  𝓅(ρ)=μ∫gdρ−μ∫ρ̈dρ=μαln(ρ)+μκρ−η+Cte\displaystyle 𝓅(ρ)=μ\: ∫ g \:dρ-μ\: ∫ \ddot{ρ} \: dρ=μ \:α \; \ln(ρ)+μ \: \frac{κ}{ρ-η}+Cte .
• Au début de la tranche :  ρ=η−(R+L)ρ=η-(R+L)  et  𝓅=μαln(η−(R+L))−μκR+L+Cte=0\displaystyle 𝓅=μ \:α \; \ln\left(η-(R+L)\right)-μ \: \frac{κ}{R+L}+Cte=0 .
• À la fin de la tranche :  ρ=η−Rρ=η-R  et  𝓅=μαln(η−R)−μκR+Cte=0\displaystyle 𝓅=μ \:α \; \ln(η-R)-μ \: \frac{κ}{R}+Cte=0 .
• Par différence :  κLR.(R+L)=αln(η−Rη−(R+L))\displaystyle κ \: \frac{L}{R.(R+L)}=α \; \ln\left(\frac{η-R}{η-(R+L)}\right)   ;   Cte=μκR−μαln(η−R)\displaystyle Cte=μ \: \frac{κ}{R}-μ \:α \: \ln(η-R) .

• Ainsi :  𝓅(ρ)=μαln(ρη−R)+μαln(η−Rη−(R+L))R.(R+L)L(η−ρ)−R(η−ρ).R\displaystyle 𝓅(ρ)=μ \:α \; \ln\left(\frac{ρ}{η-R}\right)+μ \:α \; \ln\left(\frac{η-R}{η-(R+L)} \right) \: \frac{R.(R+L)}{L} \: \frac{(η-ρ)-R}{(η-ρ).R} .

ChampSpherPres_cor_Im/pression_rho.png

• Pour un champ  gg  correspondant, la surpression présente un maximum plus à droite (sur le graphique) que pour un écoulement à section constante : la masse à pousser doit être plus accélérée si on se rapproche de  ρ=η−Rρ=η-R  afin de permettre un débit uniforme dans une section plus petite.


IX. Astre avec une couche sphérique éjectée

1.a. • Pour une métrique de la forme :  ds2=A(r,t)c2dt2−C(r,t)dr2−r2dΩ2{ds}^2=A(r,t) \:c^2 \,{dt}^2-C(r,t) \:{dr}^2-r^2 \:{dΩ}^2  on obtient :

 g00=Ag_{00}=A  ;  g11=−Cg_{11}=-C  ;  g22=−r2g_{22} = -r^2  ;  g33=−r2sin2(θ)g_{33}=-r^2 \; \sin^2(θ)  ;
g00=1A\displaystyle g^{00}=\frac{1}{A}  ;  g11=−1C\displaystyle g^{11}=-\frac{1}{C}  ;  g22=−1r2\displaystyle g^{22}=-\frac{1}{r^2}  ;  g33=−1r2sin2(θ)\displaystyle g^{33}=-\frac{1}{r^2 \; \sin^2(θ)}  ;
Γ000=A˙2\displaystyle Γ_{000}=\frac{\dot{A}}{2}  ;  Γ001=−Γ100=A′2\displaystyle Γ_{001}=-Γ_{100}=\frac{A'}{2}  ;  Γ011=−Γ110=C˙2\displaystyle Γ_{011}=-Γ_{110}=\frac{\dot{C}}{2}  ;  Γ111=−C′2\displaystyle Γ_{111}=-\frac{C'}{2}  ;
Γ221=−Γ122=−rΓ_{221}=-Γ_{122}=-r  ;  Γ331=−Γ133=−rsin2(θ)Γ_{331}=-Γ_{133}=-r \; \sin^2(θ)  ;  Γ332=−Γ233=−r2sin(θ)cos(θ)Γ_{332}=-Γ_{233}=-r^2 \; \sin(θ) \: \cos(θ)  ;
Γ.000=A˙2A\displaystyle Γ_{\phantom{.}00}^0=\frac{\dot{A}}{2 \,A}  ;  Γ.010=A′2A\displaystyle Γ_{\phantom{.}01}^0=\frac{A'}{2 \:A}  ;  Γ.001=A′2C\displaystyle Γ_{\phantom{.}00}^1=\frac{A'}{2 \,C}  ;  Γ.110=C˙2A\displaystyle Γ_{\phantom{.}11}^0=\frac{\dot{C}}{2 \,A}  ;  Γ.101=C˙2C\displaystyle Γ_{\phantom{.}10}^1=\frac{\dot{C}}{2 \,C}  ;  Γ.111=C′2C\displaystyle Γ_{\phantom{.}11}^1=\frac{C'}{2 \,C}  ;
Γ.212=Γ.313=1r\displaystyle Γ_{\phantom{.}21}^2=Γ_{\phantom{.}31}^3=\frac{1}{r}  ;  Γ.221=−rC\displaystyle Γ_{\phantom{.}22}^1=-\frac{r}{C}  ;  Γ.331=−rCsin2(θ)\displaystyle Γ_{\phantom{.}33}^1=-\frac{r}{C} \: \sin^2(θ)  ;
Γ.323=cot(θ)Γ_{\phantom{.}32}^3=\cot(θ)  ;  Γ.332=−sin(θ)cos(θ)Γ_{\phantom{.}33}^2=- \sin(θ) \:\cos(θ) .
• On en déduit :  R00=A″2C−A′2C(A′2A+C′2C−2r)−C̈2C+C˙2C(A˙2A+C˙2C)\displaystyle R_{00}=\frac{A''}{2 \,C}-\frac{A'}{2 \,C} \, \left(\frac{A'}{2 \,A}+\frac{C'}{2 \,C}-\frac{2}{r}\right)-\frac{\ddot{C}}{2 \,C}+\frac{\dot{C}}{2 C} \, \left(\frac{\dot{A}}{2 \,A}+\frac{\dot{C}}{2 \,C}\right)  ;

 R01=C˙rC\displaystyle R_{01}=\frac{\dot{C}}{r \:C}  ;  R11=−A″2A+A′2A(A′2A+C′2C)+C′rC+C̈2A−C˙2A(A˙2A+C˙2C)\displaystyle R_{11}=-\frac{A''}{2 \,A}+\frac{A'}{2 \,A} \, \left(\frac{A'}{2 \,A}+\frac{C'}{2 \,C}\right)+\frac{C'}{r \:C}+\frac{\ddot{C}}{2 \,A}-\frac{\dot{C}}{2 \,A} \, \left(\frac{\dot{A}}{2 \,A}+\frac{\dot{C}}{2 \,C}\right)  ;
R22=−1C−rC(A′2A−C′2C)+1\displaystyle R_{22}=-\frac{1}{C}-\frac{r}{C} \, \left(\frac{A'}{2 \,A}-\frac{C'}{2 \,C}\right)+1   ;   R33=R22sin2(θ)R_{33}=R_{22} \; \sin^2(θ) .


1.b. • On obtient par ailleurs :  uμ=dxμds\displaystyle u^μ=\frac{dx^μ}{ds}  ;  u0=γA\displaystyle u^0=\frac{γ}{\sqrt{A}}  ;  u1=γβC\displaystyle u^1=\frac{γ \:β}{\sqrt{C}}   et   u2=u3=0u^2=u^3=0  ;

 T00=γ2𝓅+ε0A−𝓅A=γ2ε0A+(γ2−1)𝓅A\displaystyle T^{00}=γ^2 \: \frac{𝓅+ε_0}{A}-\frac{𝓅}{A}=γ^2 \: \frac{ε_0}{A}+(γ^2-1) \: \frac{𝓅}{A}  ;  T01=γ2β𝓅+ε0AC\displaystyle T^{01}=γ^2 \: β \: \frac{𝓅+ε_0}{\sqrt{A \:C}}  ;
T11=γ2β2𝓅+ε0C+𝓅C=γ2β2ε0C+γ2𝓅C\displaystyle T^{11}=γ^2 \: β^2 \: \frac{𝓅+ε_0}{C}+\frac{𝓅}{C}=γ^2 \: β^2 \: \frac{ε_0}{C}+γ^2 \: \frac{𝓅}{C}  ;  T22=𝓅r2\displaystyle T^{22}=\frac{𝓅}{r^2}   ;  T33=𝓅r2sin2(θ)\displaystyle T^{33}=\frac{𝓅}{r^2 \: \sin^2(θ)}  ;
T=gμνTμν=ε0−3𝓅T=g_{μν} \:T^{μν}=ε_0-3 \:𝓅 .
◊ remarque : pour l'interprétation dans d'éventuelles régions où le sens de variation de rr serait inversé, il faut être attentif au fait que dans ce cas  β<0β<0  pour un point qui est repoussé vers l'extérieur.
• Ceci correspond à :  T00−12g00T=A.[(γ2−12)ε0+(γ2+12)𝓅]T_{00}-\frac{1}{2} g_00 \: T=A .\left[\left(γ^2-\frac{1}{2}\right) \: ε_0+\left(γ^2+\frac{1}{2}\right) \: 𝓅\right]  ;

 T01=−ACγ2β.(𝓅+ε0)T_{01}=-\sqrt{A \:C} \; γ^2 \: β .(𝓅+ε_0 )  ;  T11−12g11T=C.[(γ2β2+12)ε0+(γ2β2−12)𝓅]T_{11}-\frac{1}{2} g_{11} \: T=C .\left[\left(γ^2 \: β^2+\frac{1}{2}\right) \: ε_0+\left(γ^2 \: β^2-\frac{1}{2}\right) \: 𝓅\right]  ;
T22−12g22T=r2ε0−𝓅2\displaystyle T_{22}-\frac{1}{2} g_{22} \: T=r^2 \; \frac{ε_0-𝓅}{2}  ;  T33−12g33T=r2sin2(θ)ε0−𝓅2\displaystyle T_{33}-\frac{1}{2} g_{33} \: T=r^2 \; \sin^2(θ) \: \frac{ε_0-𝓅}{2} .


1.c. • La loi de conservation du tenseur d'énergie-impulsion peut s'écrire :  DνTμν=0D_ν T^{μν}=0 ,  avec pour un fluide :  Tμν=(𝓅+ε0)uμuν−𝓅gμνT^{μν}=(𝓅+ε_0 ) \: u^μ \: u^ν-𝓅 \:g^{μν} .
• Ceci peut s'écrire :  ∂ν(𝓅+ε0)uμuν+(𝓅+ε0)Dν(uμuν)−∂ν𝓅gμν=0∂_ν (𝓅+ε_0 ) \; u^μ \: u^ν+(𝓅+ε_0 ) \: D_ν (u^μ \: u^ν )-∂_ν 𝓅 \:\:g^{μν}=0 .
• Pour  μ=0μ=0 ou 11  (les autres termes sont nuls) :

 ∂ν(𝓅+ε0)uμuν=γA(𝓅+ε0)⏞˙uμ+γβC(𝓅+ε0)′uμ\displaystyle ∂_ν (𝓅+ε_0 ) \; u^μ \: u^ν=\frac{γ}{\sqrt{A}} \dot{\overbrace{(𝓅+ε_0)}} \; u^μ+\frac{γ \:β}{\sqrt{C}} \: (𝓅+ε_0 )' \:u^μ .
• Par ailleurs :

 Dν(uμuν)=∂ν(uμuν)+Γ.λνμuλuν+Γ.λννuμuλD_ν (u^μ \: u^ν )=∂_ν (u^μ \: u^ν )+Γ_{\phantom{.}λν}^μ \: u^λ \: u^ν+Γ_{\phantom{.}λν}^ν \: u^μ \: u^λ  ;
∂ν(u0uν)=(γ2A)⏞˙+(γ2βAC)′\displaystyle ∂_ν (u^0 \: u^ν )=\dot{\overbrace{\left(\frac{γ^2}{A}\right)}}+\left(\frac{γ^2 \: β}{\sqrt{A \:C}}\right)'  ;  ∂ν(u1uν)=(γ2βAC)⏞˙+(γ2β2C)′\displaystyle ∂_ν (u^1 u^ν )=\dot{\overbrace{\left(\frac{γ^2 \: β}{\sqrt{A \:C}}\right)}}+\left(\frac{γ^2 \: β^2}{C}\right)'  ;
Γ.λν0uλuν=A˙2Aγ2A+A′Aγ2βAC+C˙2Aγ2β2C\displaystyle Γ_{\phantom{.}λν}^0 \: u^λ \: u^ν=\frac{\dot{A}}{2 \,A} \: \frac{γ^2}{A}+\frac{A'}{A} \: \frac{γ^2 \: β}{\sqrt{A \:C}}+\frac{\dot{C}}{2 \,A} \, \frac{γ^2 \: β^2}{C}  ;
Γ.λν1uλuν=A′2Cγ2A+C˙Cγ2βAC+C′2Cγ2β2C\displaystyle Γ_{\phantom{.}λν}^1 \: u^λ \: u^ν=\frac{A'}{2 \,C}\, \frac{γ^2}{A}+\frac{\dot{C}}{C} \, \frac{γ^2 \: β}{\sqrt{A \:C}}+\frac{C'}{2 \,C} \, \frac{γ^2 \: β^2}{C}  ;
Γ.λννuμuλ=∂λ(|g|)|g|uμuλ\displaystyle Γ_{\phantom{.}λν}^ν \: u^μ \: u^λ=\frac{∂_λ \left(\sqrt{|g|}\right)}{\sqrt{|g|}} \; u^μ \: u^λ  (pour  μ=0μ=0 ou 11 ).
• Enfin :  ∂ν𝓅g0ν=𝓅˙A\displaystyle ∂_ν 𝓅 \;g^{0ν}=\frac{\dot{𝓅}}{A}  ;  ∂ν𝓅g1ν=−𝓅′C\displaystyle ∂_ν 𝓅 \;g^{1ν}=-\frac{𝓅'}{C} .
• La combinaison de ces termes montre que la loi de la dynamique du fluide est loin d'être simple.


2.a. • Les équations du champ obtenues avec les expressions précédentes sont compliquées ; on peut se limiter à étudier le cas particulier correspondant à un état initial (hypothétique) immobile, mais ne le restant pas :  A˙=C˙=0\dot{A}=\dot{C}=0  ;  β=0β=0  ;  γ=1γ=1  ;  ε0=εε_0=ε .
• On en déduit :  R00=A″2C−A′2C(A′2A+C′2C−2r)−C̈2C\displaystyle R_{00}=\frac{A''}{2 \,C}-\frac{A'}{2 \,C} \, \left(\frac{A'}{2 \,A}+\frac{C'}{2 \,C}-\frac{2}{r}\right)-\frac{\ddot{C}}{2 \,C}  ;

 R01=0R_{01}=0  ;  R11=−A″2A+A′2A(A′2A+C′2C)+C′rC+C̈2A\displaystyle R_{11}=-\frac{A''}{2 \,A}+\frac{A'}{2 \,A} \, \left(\frac{A'}{2 \,A}+\frac{C'}{2 \,C}\right)+\frac{C'}{r \:C}+\frac{\ddot{C}}{2 \,A}  ;
R22=−1C−rC(A′2A−C′2C)+1\displaystyle R_{22}=-\frac{1}{C}-\frac{r}{C} \, \left(\frac{A'}{2 \,A}-\frac{C'}{2 \,C}\right)+1   ;   R33=R22sin2(θ)R_{33}=R_{22} \; \sin^2(θ) .

• Par ailleurs :  T00−12g00T=Aε+3𝓅2\displaystyle T_{00}-\frac{1}{2} g_{00} \: T=A \: \frac{ε+3 \,𝓅}{2}  ;  T01=0T_{01}=0  ;  T11−12g11T=Cε−𝓅2\displaystyle T_{11}-\frac{1}{2} g_{11} \: T=C \: \frac{ε-𝓅}{2}  ;

 T22−12g22T=r2ε−𝓅2\displaystyle T_{22}-\frac{1}{2} g_{22} \: T=r^2 \: \frac{ε-𝓅}{2}  ;  T33−12g33T=r2sin2(θ)ε−𝓅2\displaystyle T_{33}-\frac{1}{2} g_{33} \: T=r^2 \; \sin^2(θ) \: \frac{ε-𝓅}{2} .
• Les équations du champ peuvent donc s'écrire :

 R00=A″2AC−A′2AC(A′2A+C′2C−2r)−C̈2AC=χε+3𝓅2\displaystyle R_0^{\,\,0}=\frac{A''}{2 \,A \:C}-\frac{A'}{2 \,A \:C} \, \left(\frac{A'}{2 \,A}+\frac{C'}{2 \,C}-\frac{2}{r}\right)-\frac{\ddot{C}}{2 \,A \:C}=χ \: \frac{ε+3 \,𝓅}{2}  ;
R11=A″2AC−A′2AC(A′2A+C′2C)−C′rC2−C̈2AC=−χε−𝓅2\displaystyle R_1^{\,\,1}=\frac{A''}{2 \,A \:C}-\frac{A'}{2 \,A \:C} \, \left(\frac{A'}{2 \,A}+\frac{C'}{2 \,C}\right)-\frac{C'}{r \:C^2}-\frac{\ddot{C}}{2 \,A \:C}=-χ \: \frac{ε-𝓅}{2}  ;
R22=R33=1Cr2+1Cr(A′2A−C′2C)−1r2=−χε−𝓅2\displaystyle R_2^{\,\,2}=R_3^{\,\,3}=\frac{1}{C \:r^2}+\frac{1}{C \:r} \, \left(\frac{A'}{2 \,A}-\frac{C'}{2 \,C}\right)-\frac{1}{r^2} =-χ \:\frac{ε-𝓅}{2} .
◊ remarque : le coefficient CC est le seul intervenant par sa dérivée seconde temporelle C̈\ddot{C} .

• On obtient par combinaison :

 R00−R11=2Cr(A′2A+C′2C)=χ.(ε+𝓅)\displaystyle R_0^{\,\,0}-R_1^{\,\,1}=\frac{2}{C\:r} \, \left(\frac{A'}{2 \,A}+\frac{C'}{2 \,C}\right)=χ .(ε+𝓅)  ;
R22+R33=2Cr2+2Cr(A′2A−C′2C)−2r2=−χ.(ε−𝓅)\displaystyle R_2^{\,\,2}+R_3^{\,\,3}=\frac{2}{C \:r^2}+\frac{2}{C \:r} \, \left(\frac{A'}{2 \,A}-\frac{C'}{2 \,C}\right)-\frac{2}{r^2} =-χ .(ε-𝓅) .
• La somme et la différence donnent ainsi respectivement :

 1Cr(A′A+1r)−1r2=χ𝓅\displaystyle \frac{1}{C \:r} \, \left(\frac{A'}{A}+\frac{1}{r}\right)-\frac{1}{r^2} =χ \:𝓅  ;   1Cr(C′C−1r)+1r2=χε\displaystyle \frac{1}{C \:r} \, \left(\frac{C'}{C}-\frac{1}{r}\right)+\frac{1}{r^2} =χ \:ε .
• Ces équations semblent exactement les mêmes que pour le cas statique mais cela ne signifie pas que la métrique soit la même, car l'expression de 𝓅𝓅 est ici différente. On peut s'en convaincre en considérant la combinaison  R00−3R11R_0^{\,\,0}-3 \:R_1^{\,\,1}  qui permettait de calculer la métrique indépendamment de 𝓅𝓅 , puis d'en déduire 𝓅𝓅 par la loi de la statique ; ici cette combinaison dépend de C̈\ddot{C} , ce qui au contraire permet ensuite (quand on a déterminé la métrique initiale) d'en déduire l'évolution de CC dont dépendent ensuite celles de AA et de 𝓅𝓅 .
◊ remarque : c'est la conservation de TμνT^{μν} qui montre la différence (loi remplaçant l'équilibre statique).


2.b. • Si on simplifie de même la loi de conservation de TμνT^{μν} , l'équation fait intervenir des dérivées β˙\dot{β} et γ˙\dot{γ} qui sont en fait des dérivées secondes, donc leurs valeurs initiales ne sont pas a priori forcément nulles. On peut toutefois considérer initialement :  γ˙=γ3ββ˙=0\dot{γ}=γ^3 \: β \:\dot{β}=0  ;  seul β˙\dot{β} intervient ici pour décrire l'accélération.
• On obtient ainsi (termes non nuls) :

 Dν(u1uν)=∂ν(u1uν)+Γλν1uλuνD_ν (u^1 \: u^ν )=∂_ν (u^1 \: u^ν )+Γ_{\,\,λν}^1 \: u^λ \: u^ν  ;  ∂ν(u1uν)=(γ2βAC)⏞˙=β˙AC\displaystyle ∂_ν (u^1 \: u^ν )=\dot{\overbrace{\left(\frac{γ^2 \: β}{\sqrt{A \:C}}\right)}}=\frac{\dot{β}}{\sqrt{A \:C}}  ;  Γλν1uλuν=A′2AC\displaystyle Γ_{\,\,λν}^1 \: u^λ \: u^ν=\frac{A'}{2 \,A \:C}  ;
∂ν𝓅g1ν=−𝓅′C\displaystyle ∂_ν 𝓅 \:\:g^{1ν}=-\frac{𝓅'}{C} .
• La loi peut donc s'écrire :  (𝓅+ε)(A′2A+CAβ˙)+𝓅′=0\displaystyle (𝓅+ε) \: \left(\frac{A'}{2 \,A}+\sqrt{\frac{C}{A}} \: \dot{β} \right)+𝓅'=0 ,  où on retrouve en plus du terme A′2A\displaystyle \frac{A'}{2 \,A} (qui exprime l'effet gravitationnel), un terme décrivant l'accélération du système.


2.c. • Si on suppose le fluide incompressible, il faut écrire la conservation du volume en considérant la géométrie spatiale fixée : on raisonne à l'instant initial, fixé, pour comparer les déplacements en différents lieux.
• Pour un intervalle infinitésimal  dtdt ,  le volume infinitésimal déplacé est :  dV=πr2dρ=πr2CdrdV=π \:r^2 \: dρ=π \:r^2 \: \sqrt{C} \: dr .  L'incompressibilité peut donc s'écrire :  r2Aβ=Cster^2 \: \sqrt{A} \: β=Cste  (indépendante de rr ).
• Puisque les vitesses sont contraintes par cette relation, à la limite  t=0t=0 ,  les accélérations doivent la respecter aussi :  r2Aβ˙=κ=Cster^2 \: \sqrt{A} \: \dot{β}=κ=Cste  (indépendante de rr ).


2.d. • On est ainsi conduit au système de trois équations (où κκ se déduit des conditions aux limites) :

 1Cr(C′C−1r)+1r2=χε\displaystyle \frac{1}{C \:r} \, \left(\frac{C'}{C}-\frac{1}{r}\right)+\frac{1}{r^2} =χ \:ε  ;   1Cr(A′A+1r)−1r2=χ𝓅\displaystyle \frac{1}{C \:r} \, \left(\frac{A'}{A}+\frac{1}{r}\right)-\frac{1}{r^2} =χ \:𝓅  ;   (𝓅+ε)(A′2A+CAκr2)+𝓅′=0\displaystyle (𝓅+ε) \: \left(\frac{A'}{2 \,A}+\frac{\sqrt{C}}{A} \,\frac{κ}{r^2} \right)+𝓅'=0 .
• La résolution ne peut calculer que trois quantités ; dans le cas général il faut ajouter une relation entre εε et 𝓅𝓅 . Malgré les défauts de cette modélisation simpliste, on peut aussi étudier le cas d'une masse volumique uniforme : on en déduit alors AA , CC et 𝓅𝓅 (on s'intéresse ici au cas intérieur).
• La première équation conduit à :  rC=r−χc2∫μr2dr+Cste\displaystyle \frac{r}{C}=r-χ \:c^2 \, ∫ μ \:r^2 \: dr+Cste ,  où la constante d'intégration peut être incluse dans la borne inférieure de l'intégrale.
• On peut poser :  M(r)=∫0rμ(r′)4πr′2dr′M(r)=∫_0^r \;μ(r') \:4π \:{r'}^2 \: dr'   et  𝒶(r)=χc24πM(r)=2𝒢c2M(r)\displaystyle 𝒶(r)=\frac{χ \:c^2}{4π} \, M(r)=\frac{2 \,𝒢}{c^2} \, M(r) .  La relation précédente peut alors s'écrire sous la forme :  C(r)=rr−𝒶(r)\displaystyle C(r)=\frac{r}{r-𝒶(r)} ,  redonnant  C(0)=1C(0)=1  au centre, où le champ de gravitation est nul par symétrie.
• Pour une masse volumique uniforme :  𝒶(r)=λr3𝒶(r)=λ \:r^3   avec   λ=χε3\displaystyle λ=\frac{χ \:ε}{3} .  On obtient ainsi :  C=11−λr2\displaystyle C=\frac{1}{1-λ \:r^2}  avec  r<1λ\displaystyle r<\frac{1}{\sqrt{λ}} .  On peut alors choisir 1λ\displaystyle \frac{1}{\sqrt{λ}} comme unité pour simplifier les notations (ainsi  ρ(1)≈1,57ρ(1)≈\text{1,57} ).
• La résolution du système des deux autres équations est possible numériquement, en ajustant κκ pour obtenir  𝓅(1)=0𝓅(1)=0 .  Pour le cas d'un rayon RR tel que  ρ(R)=2,1ρ(R)=\text{2,1}  ceci correspond à  R≈0,86<1R≈\text{0,86}<1  dans la zone inversée où r(ρ)r(ρ) décroit. Le raccordement avec l'expression extérieure pour  C(R)≈3,92C(R)≈\text{3,92}  impose pour ces notations :  rs=R3≈0,64r_s=R^3≈\text{0,64} .
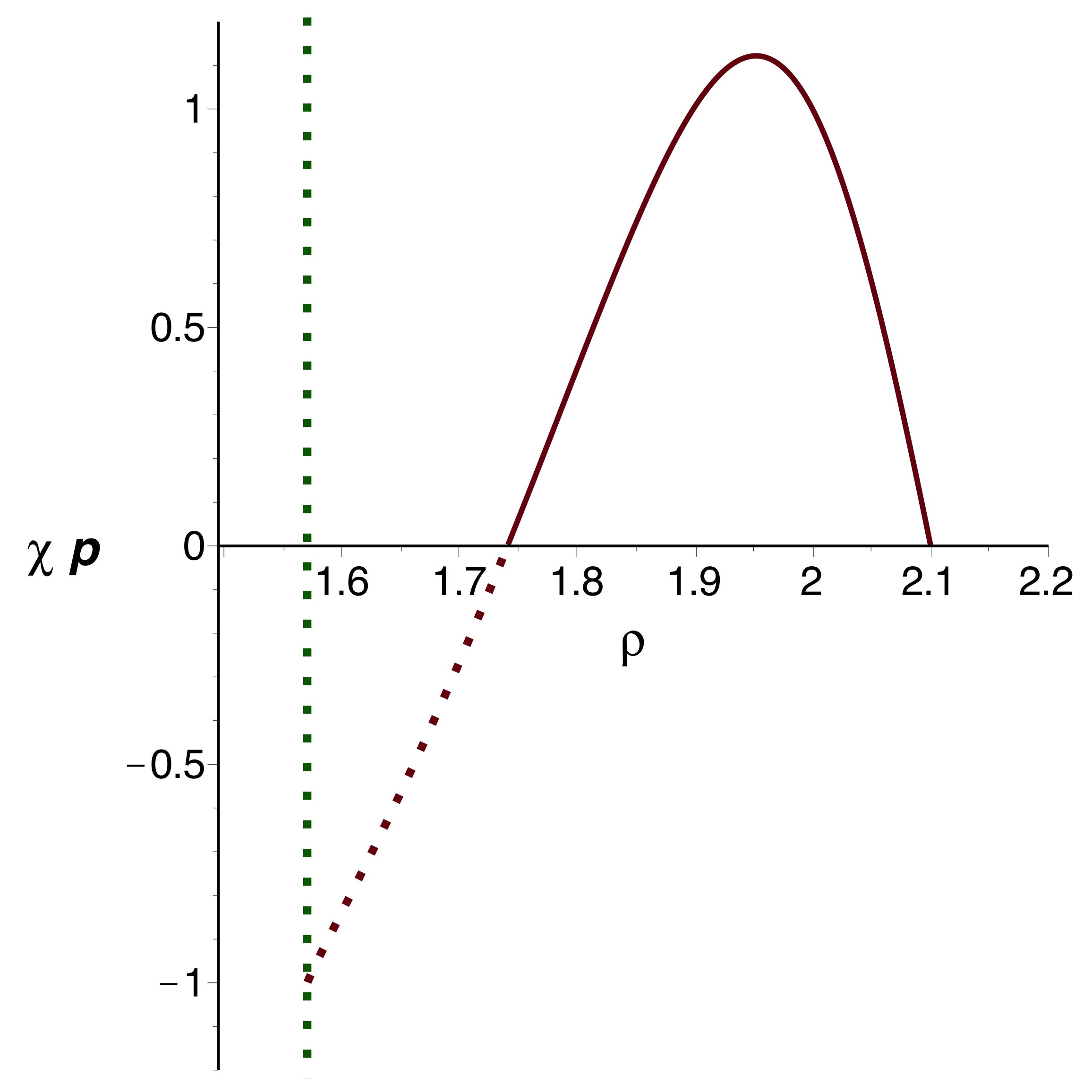
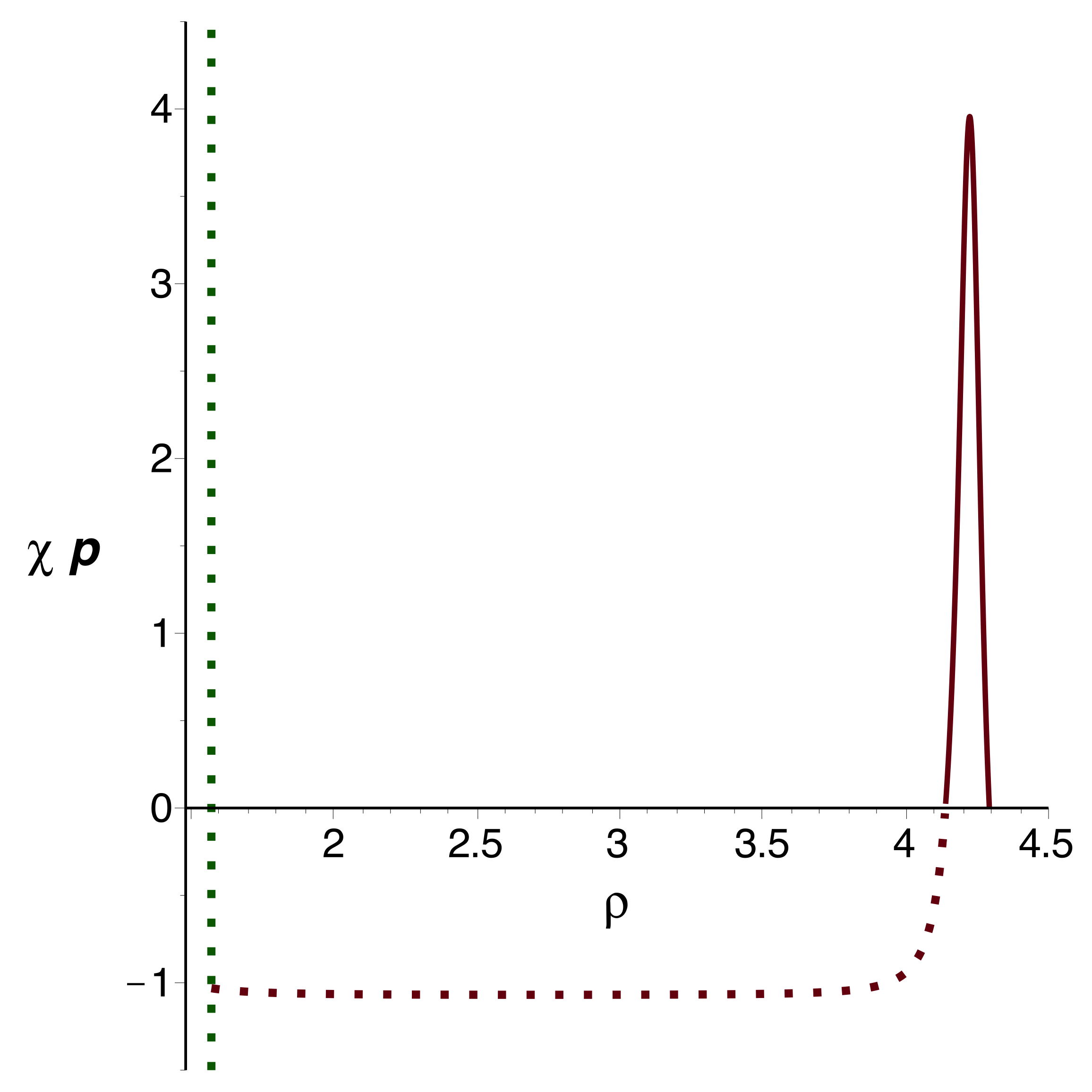
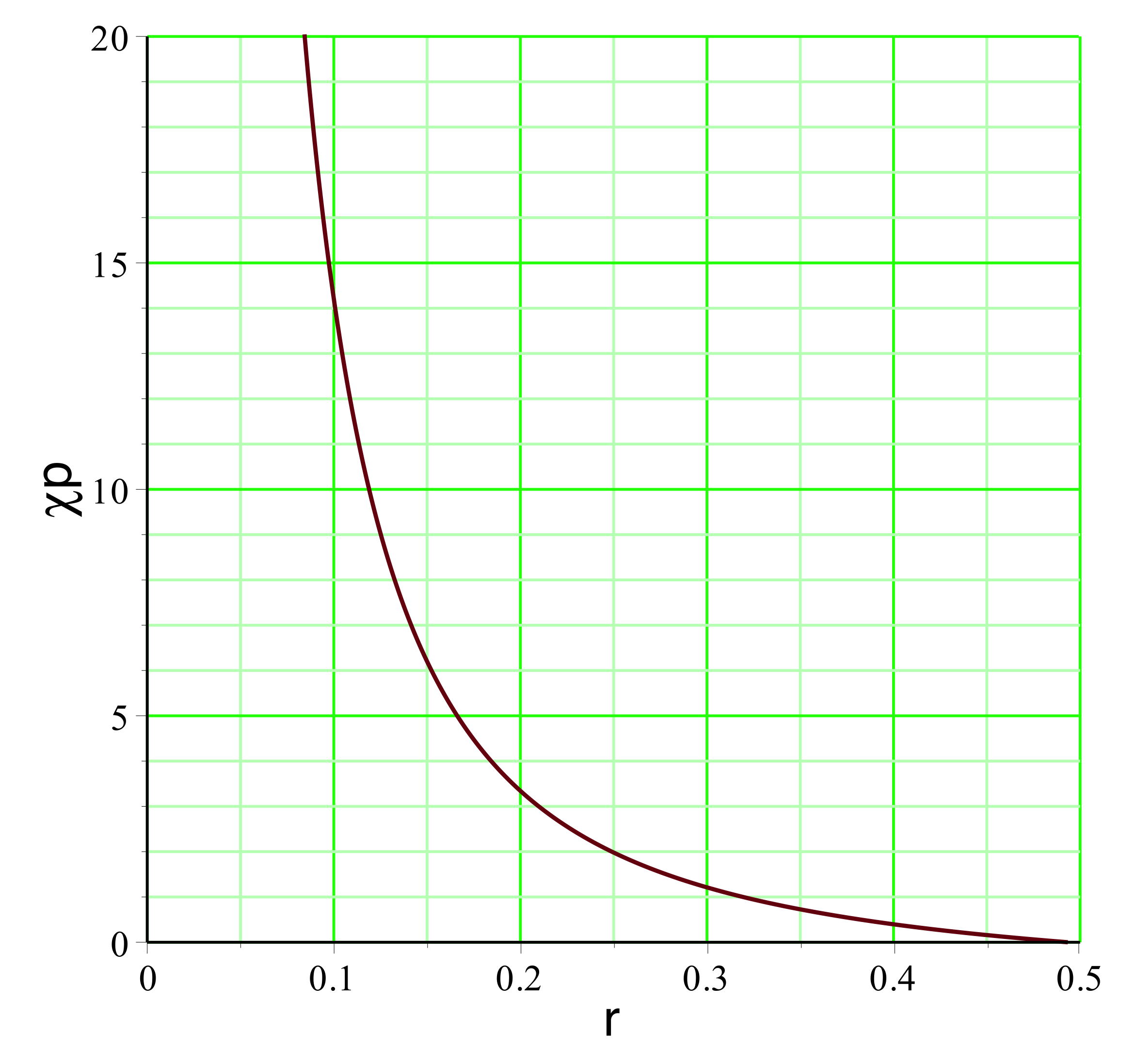
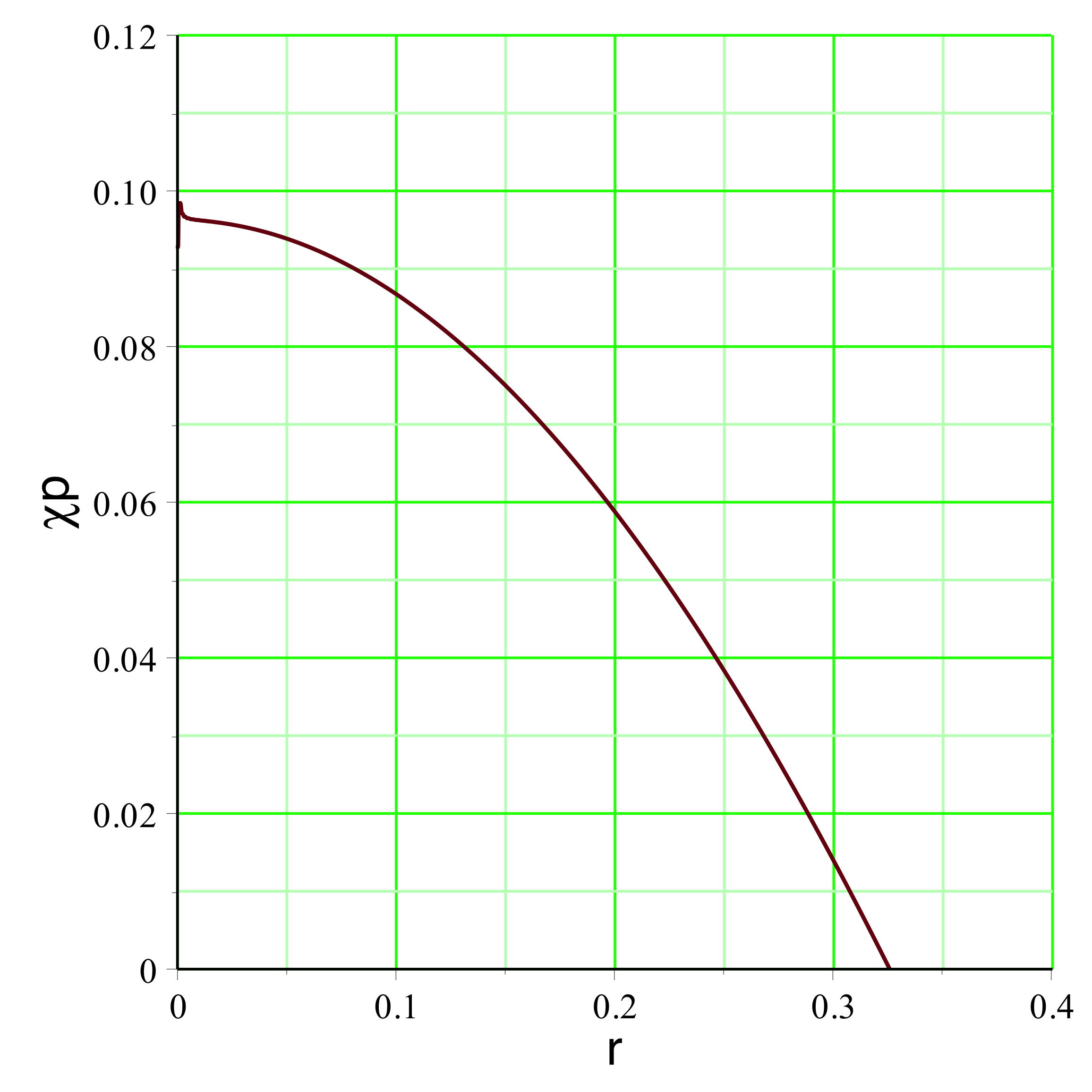
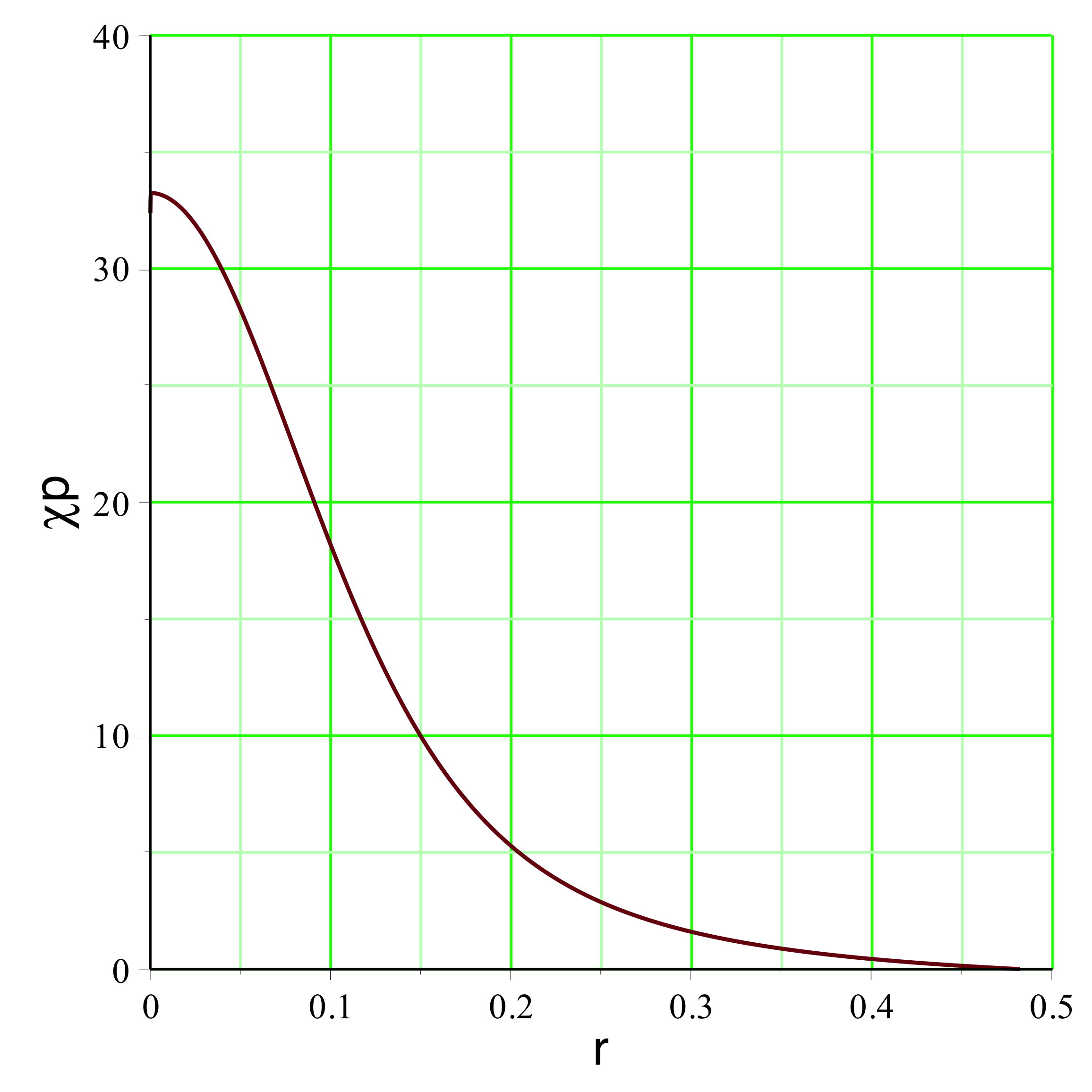
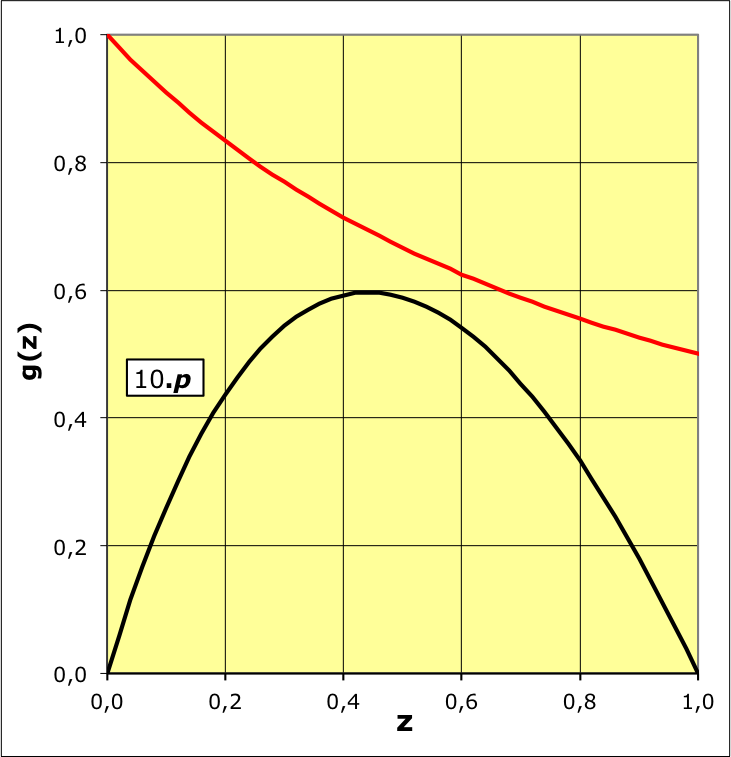
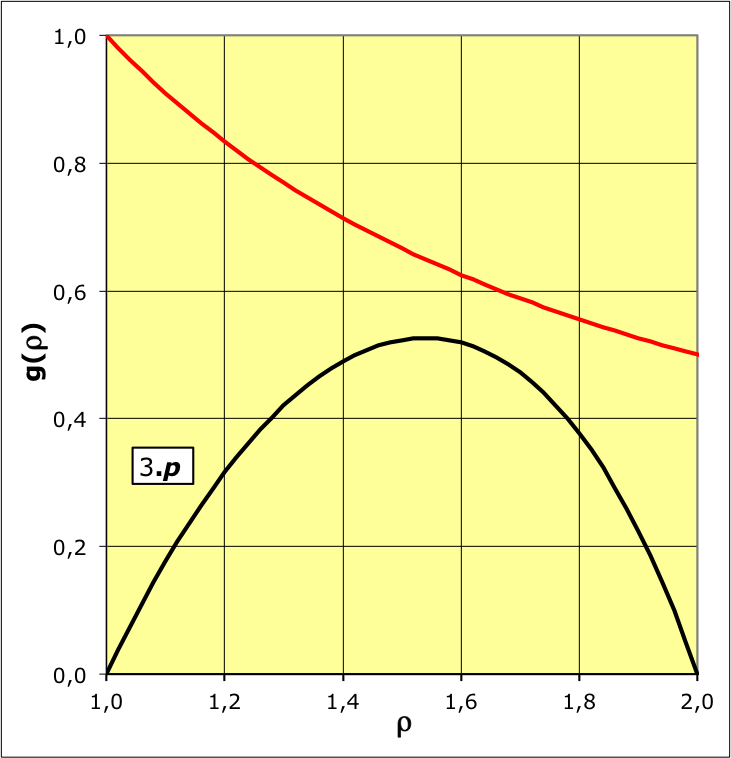
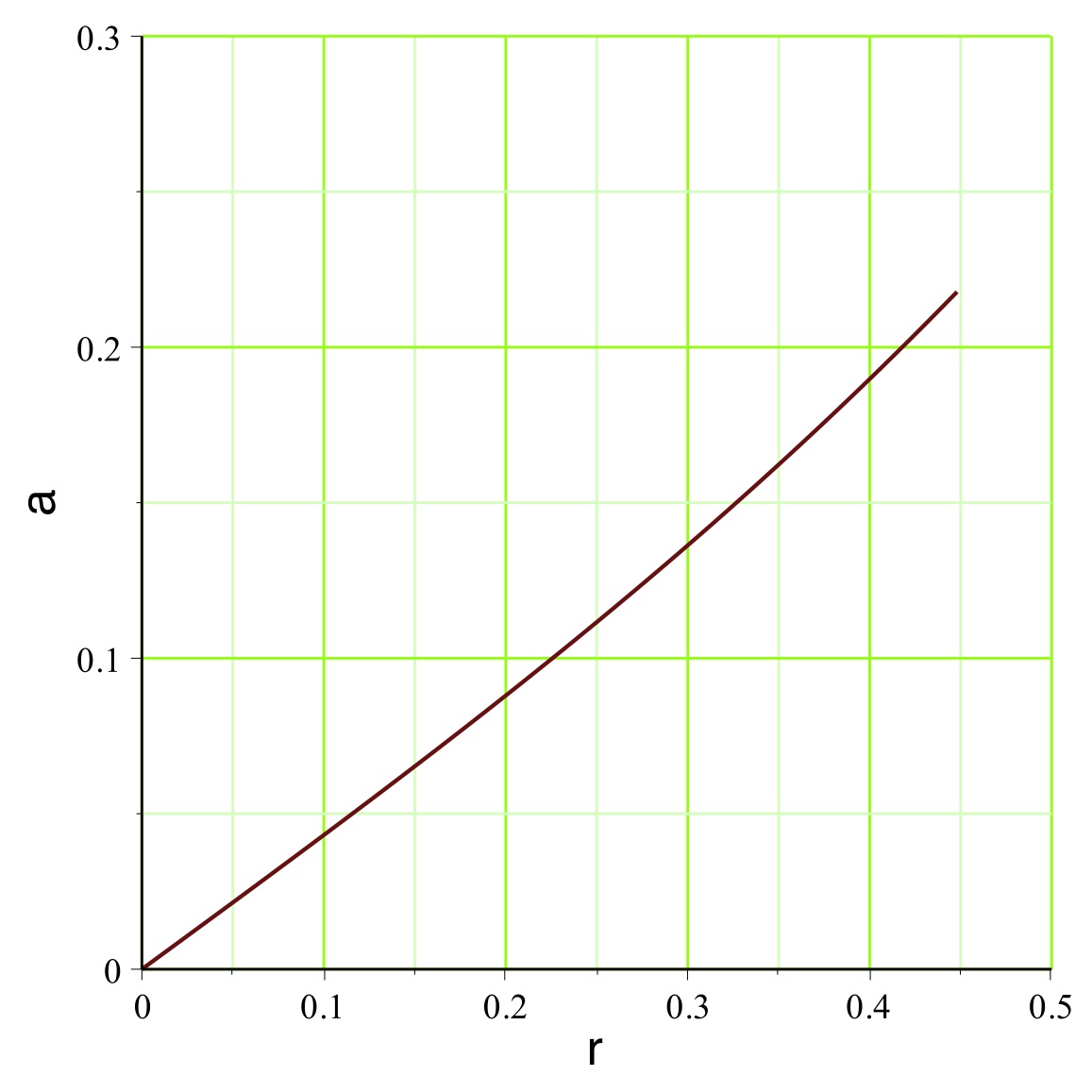
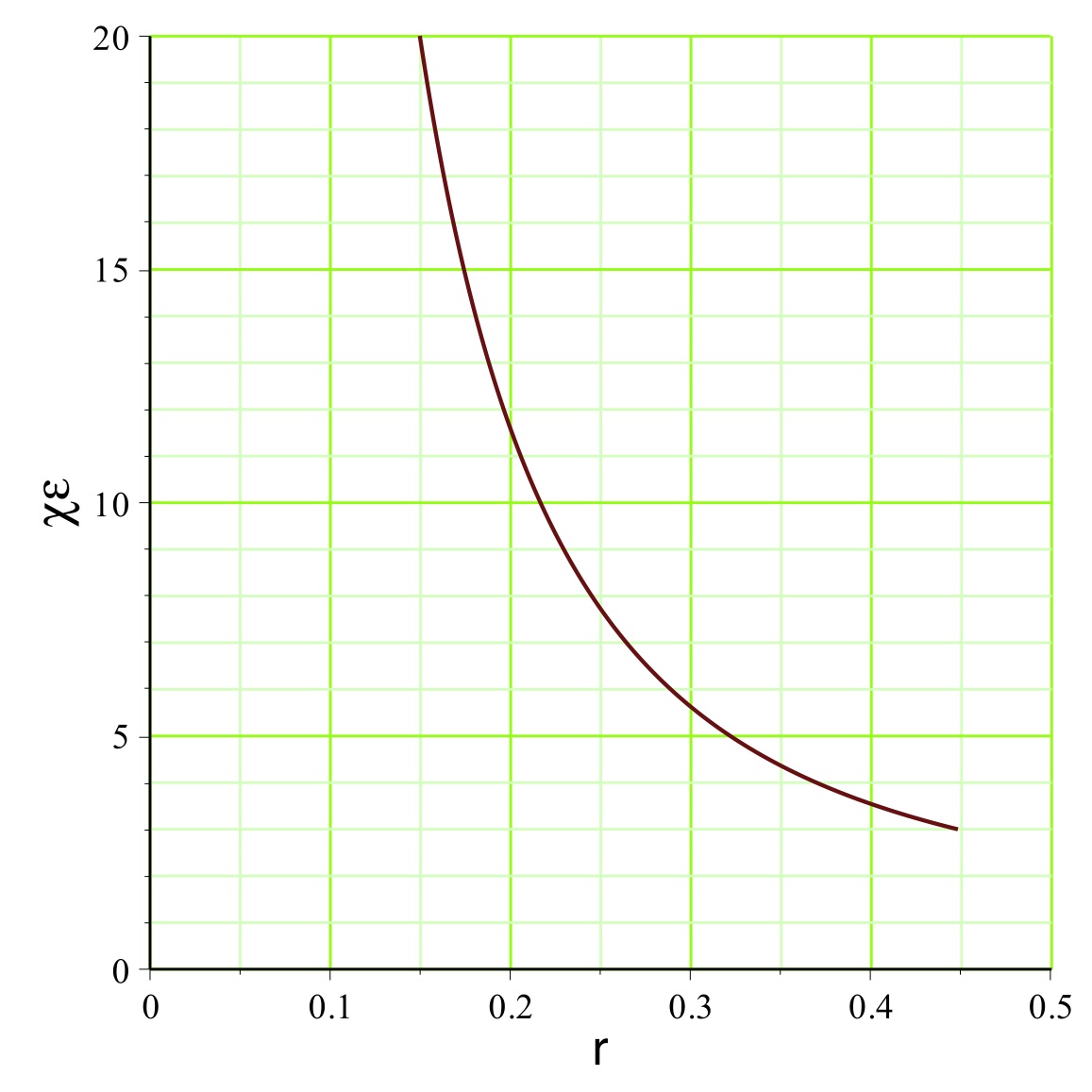
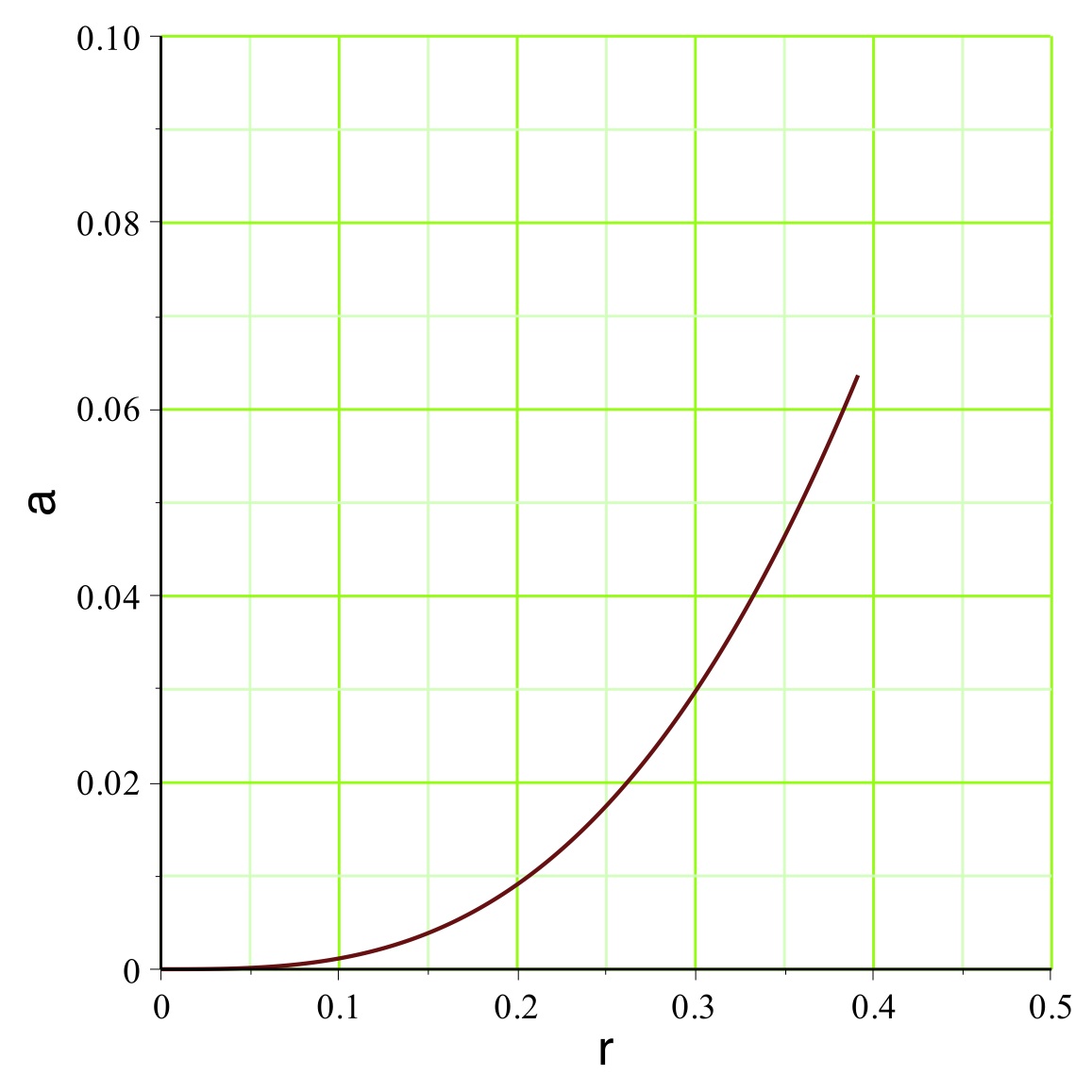
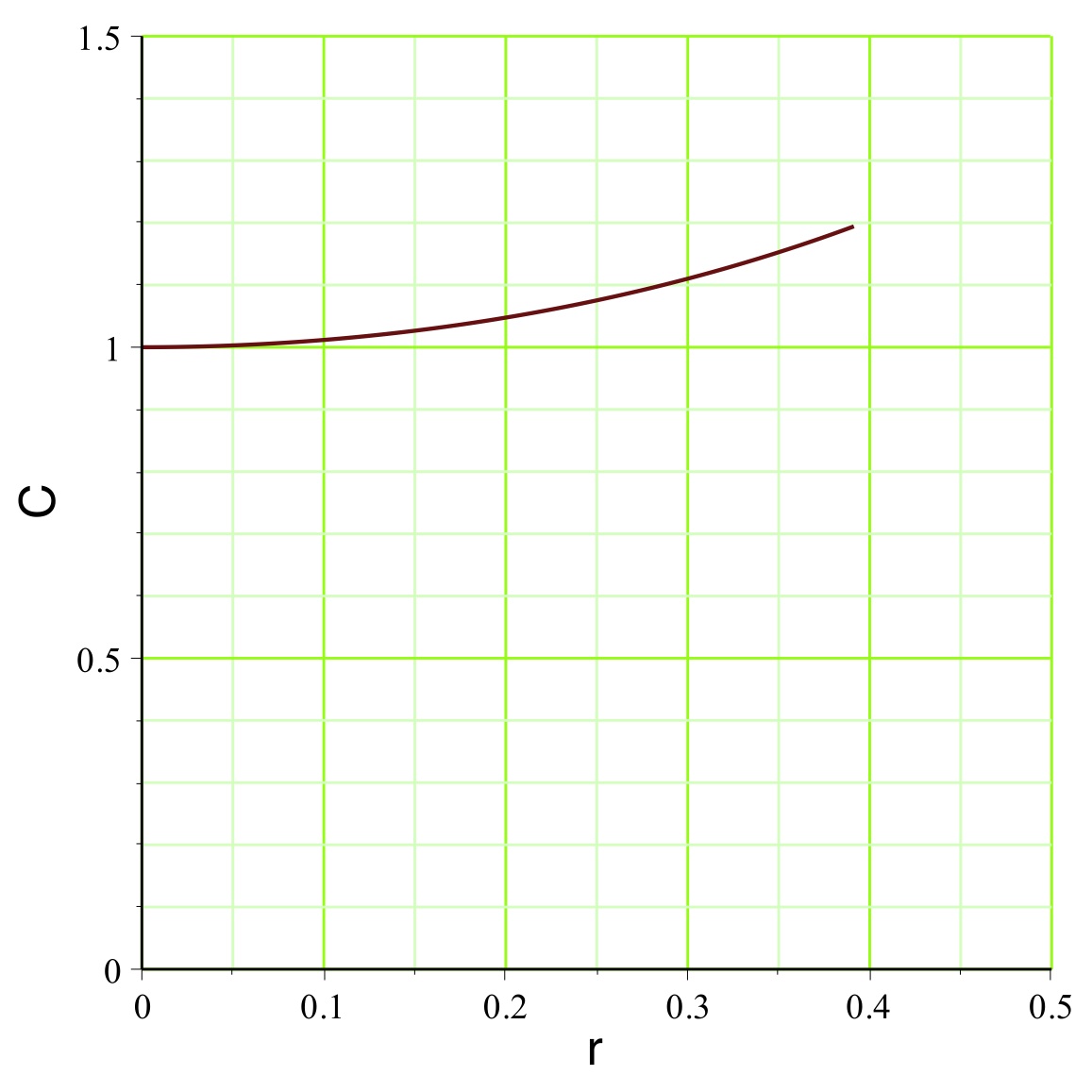
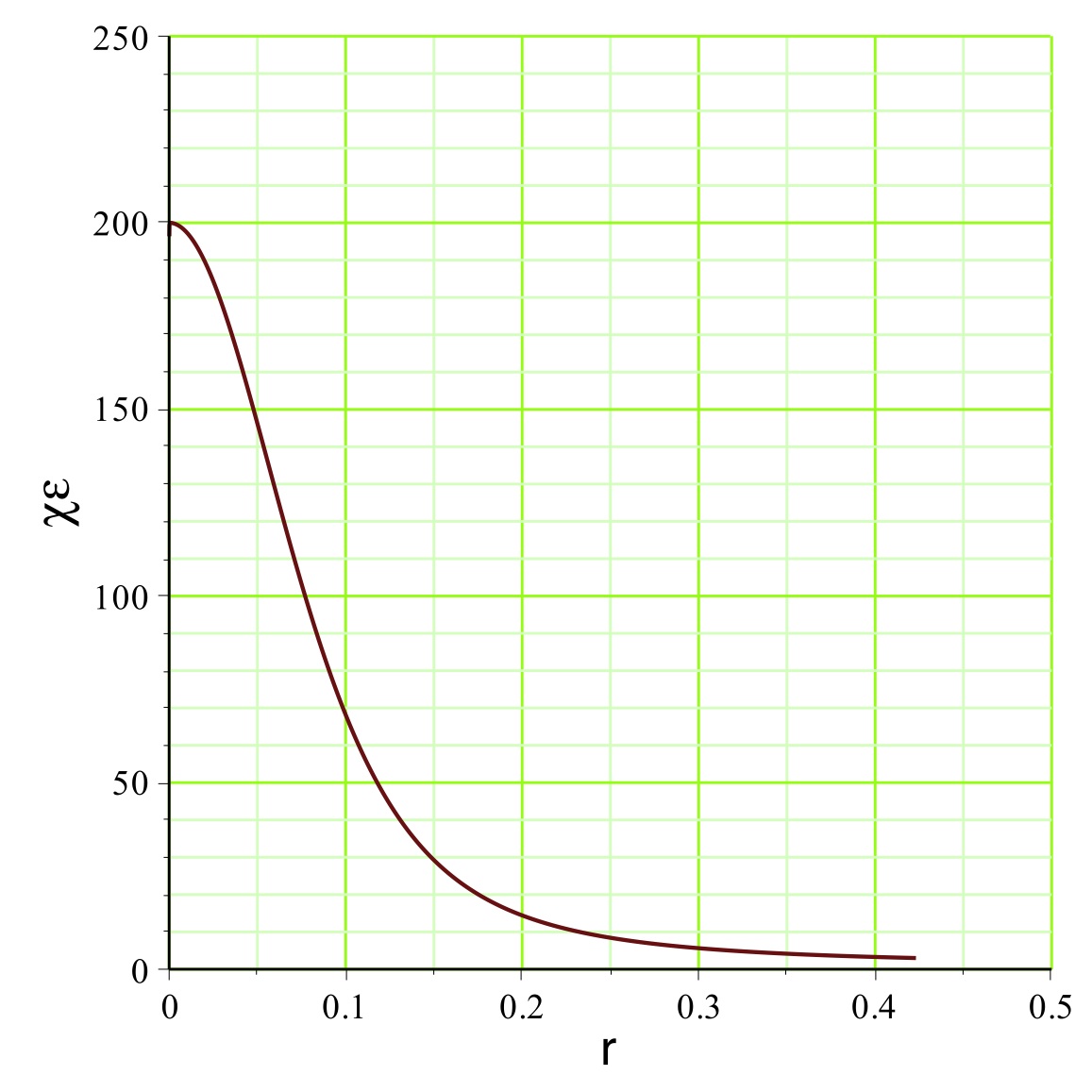
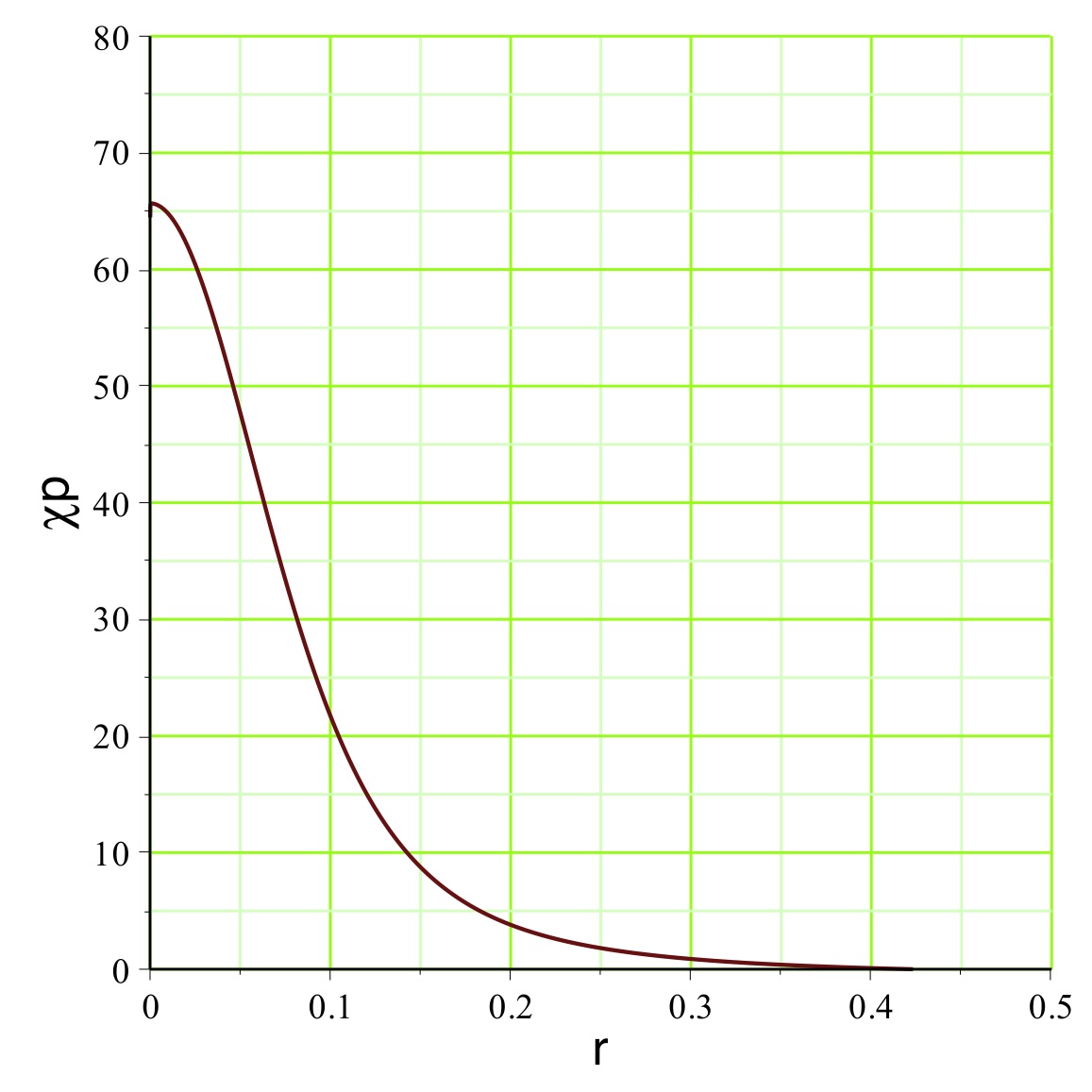
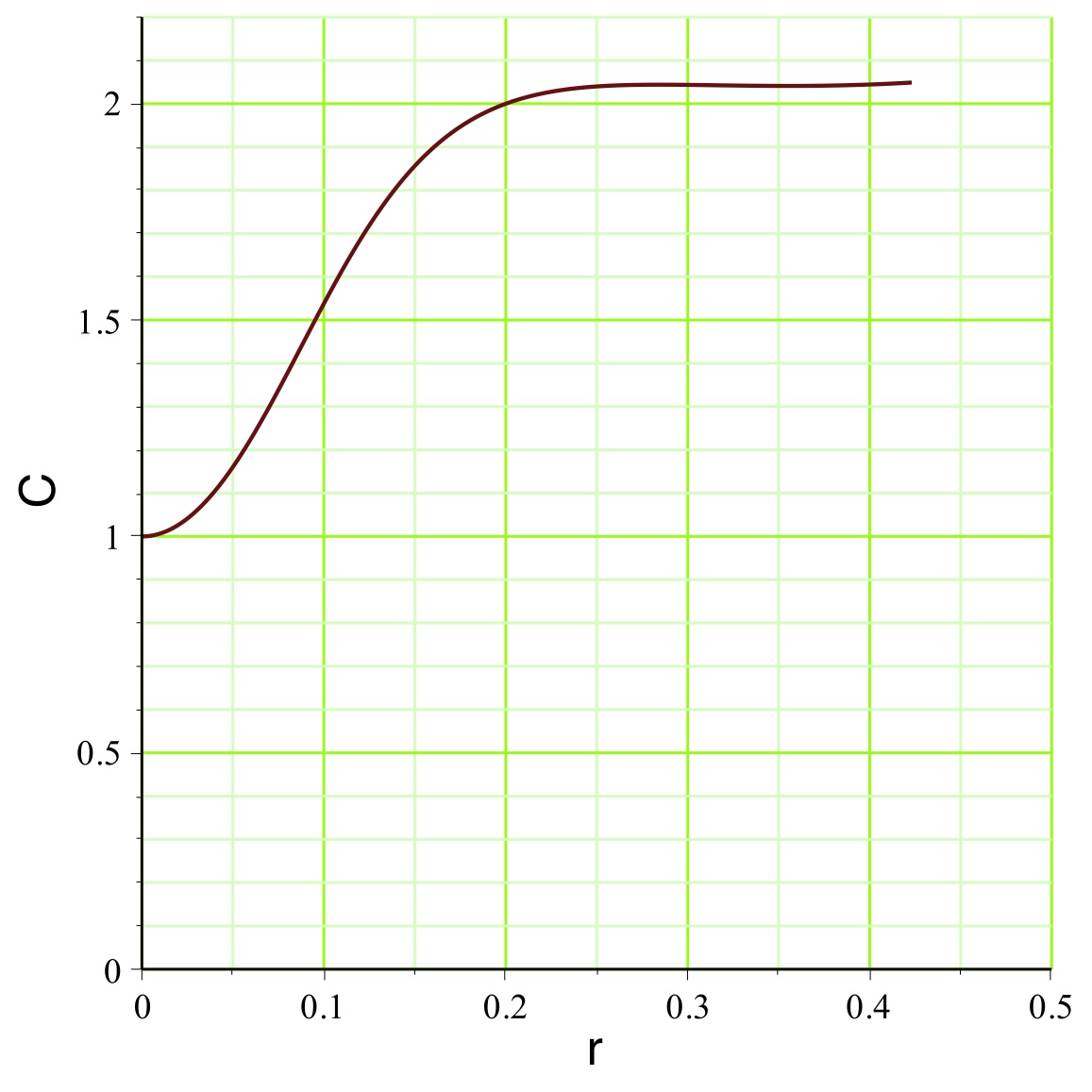
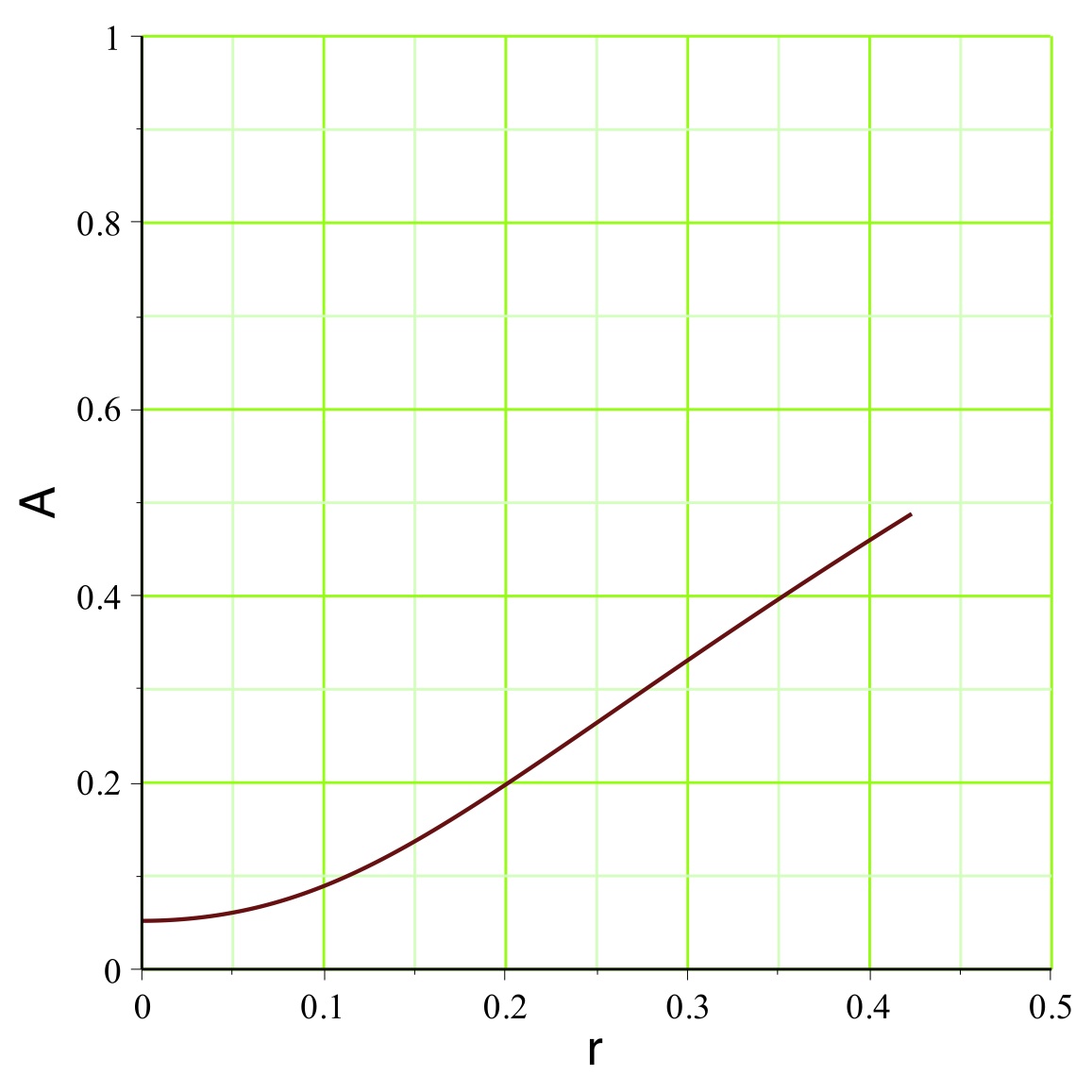
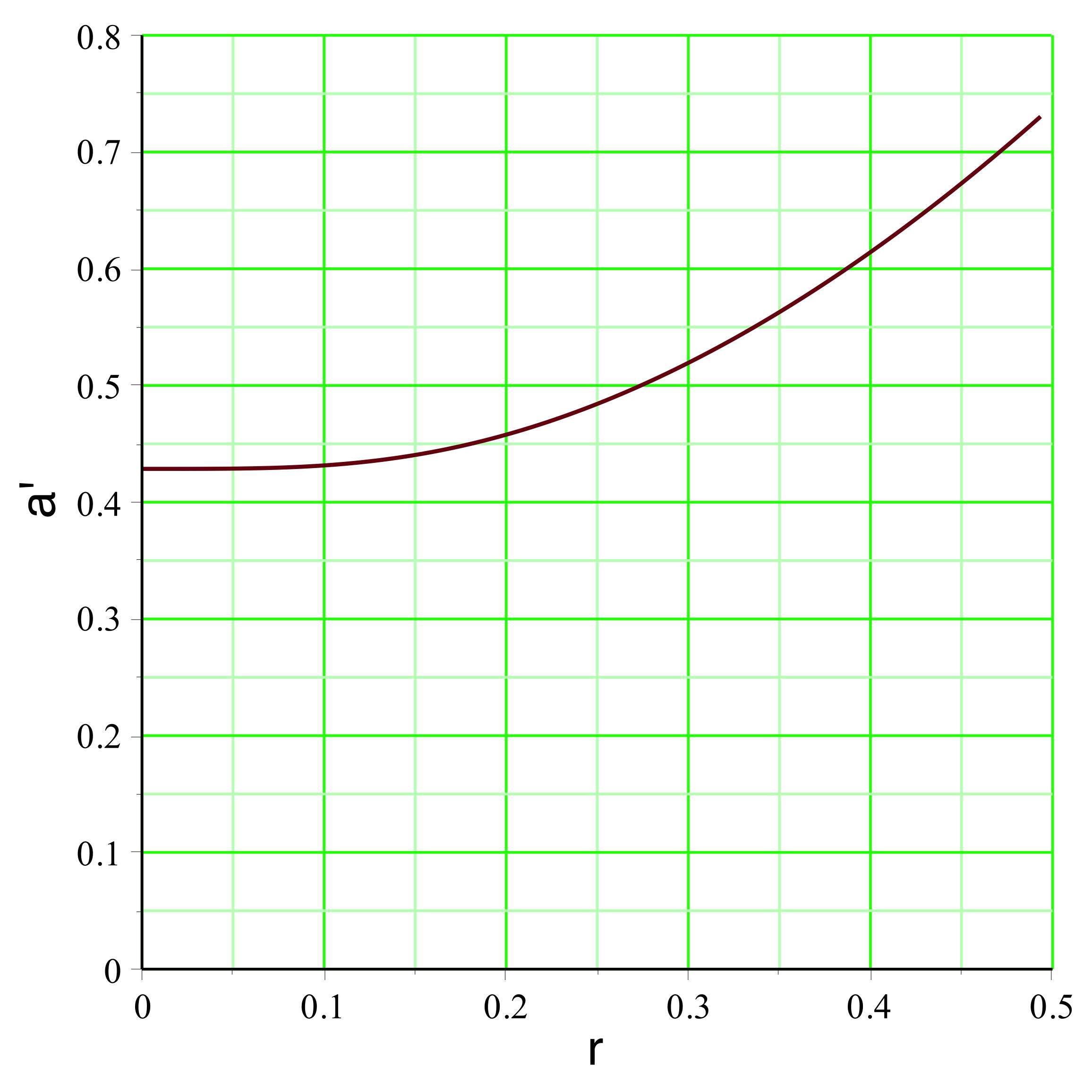
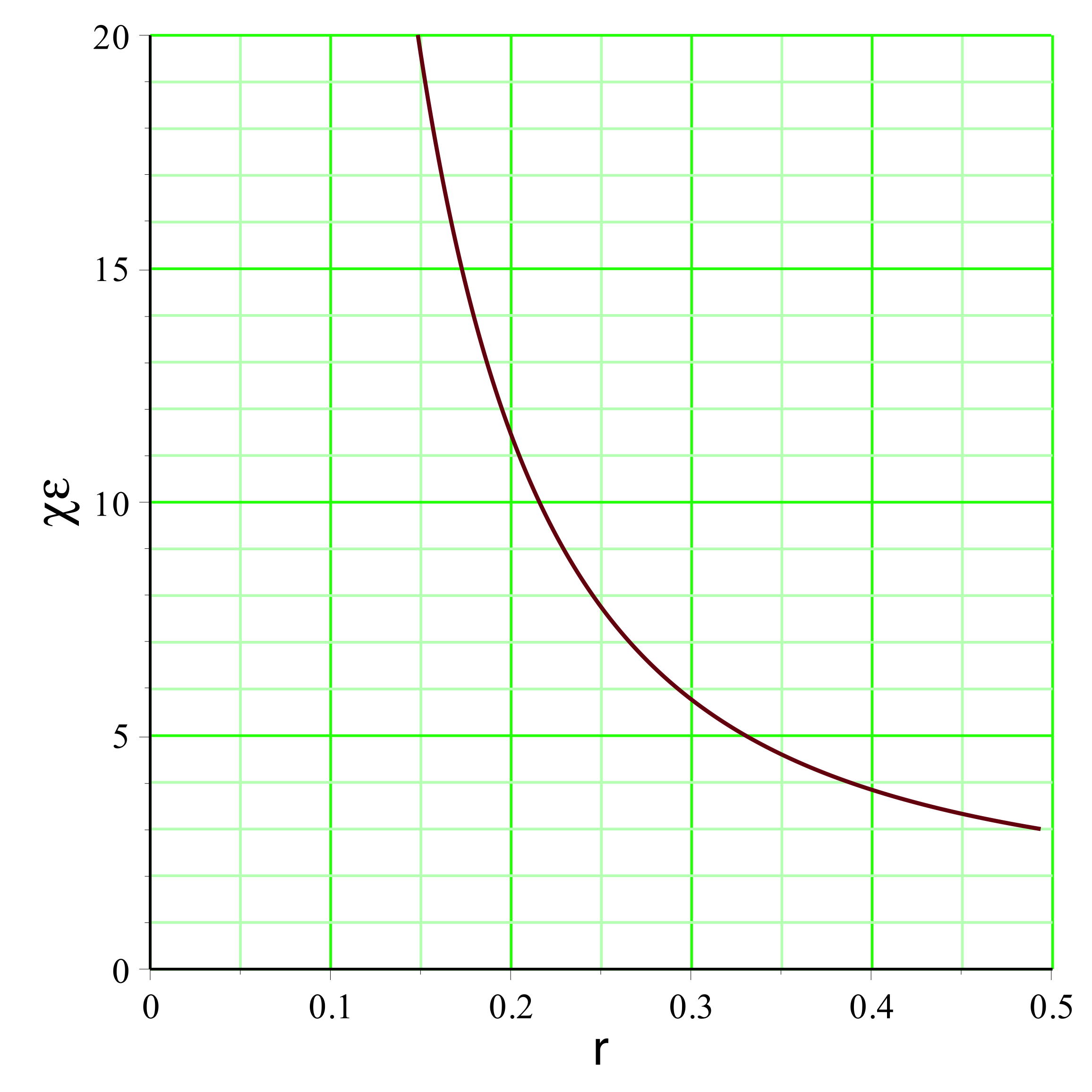
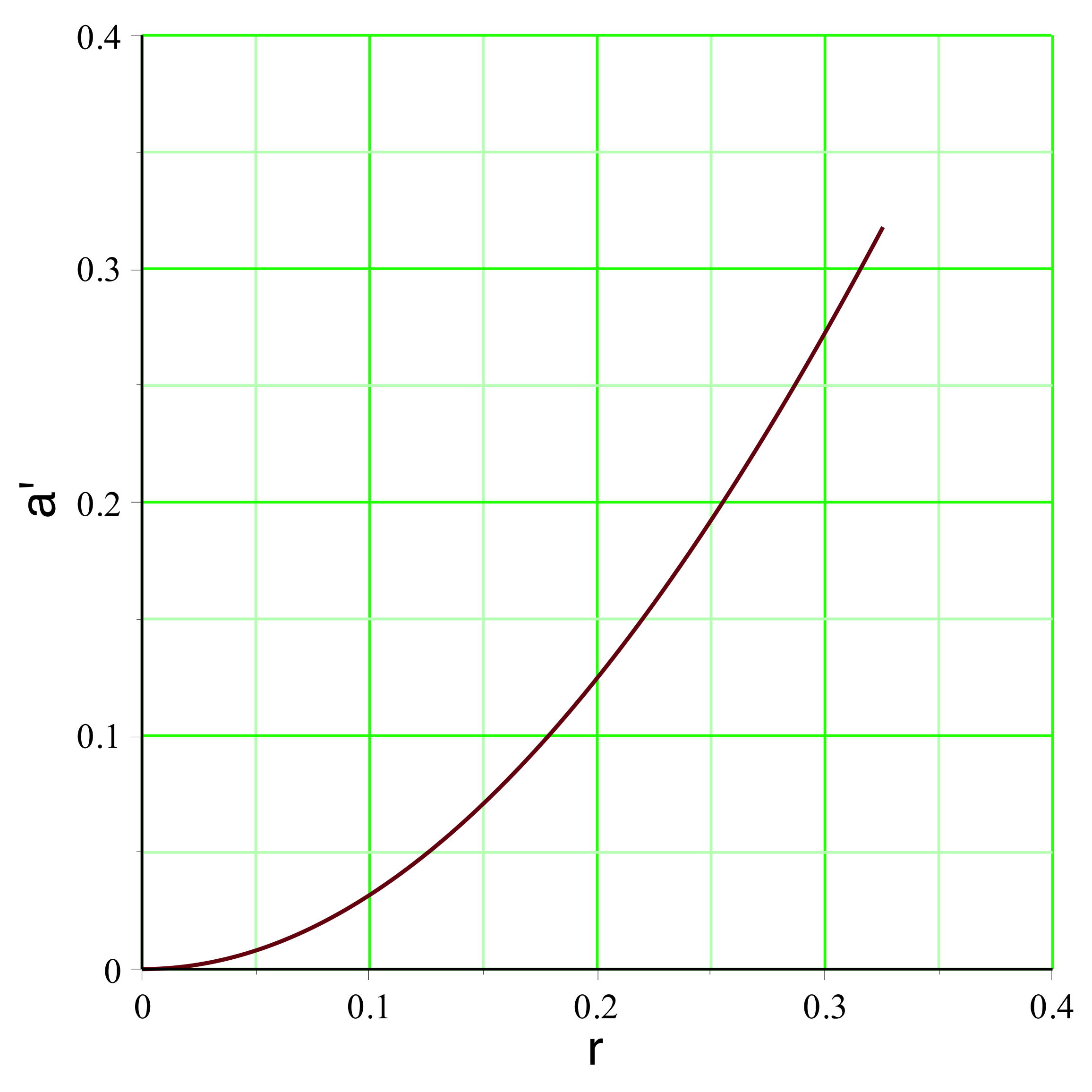
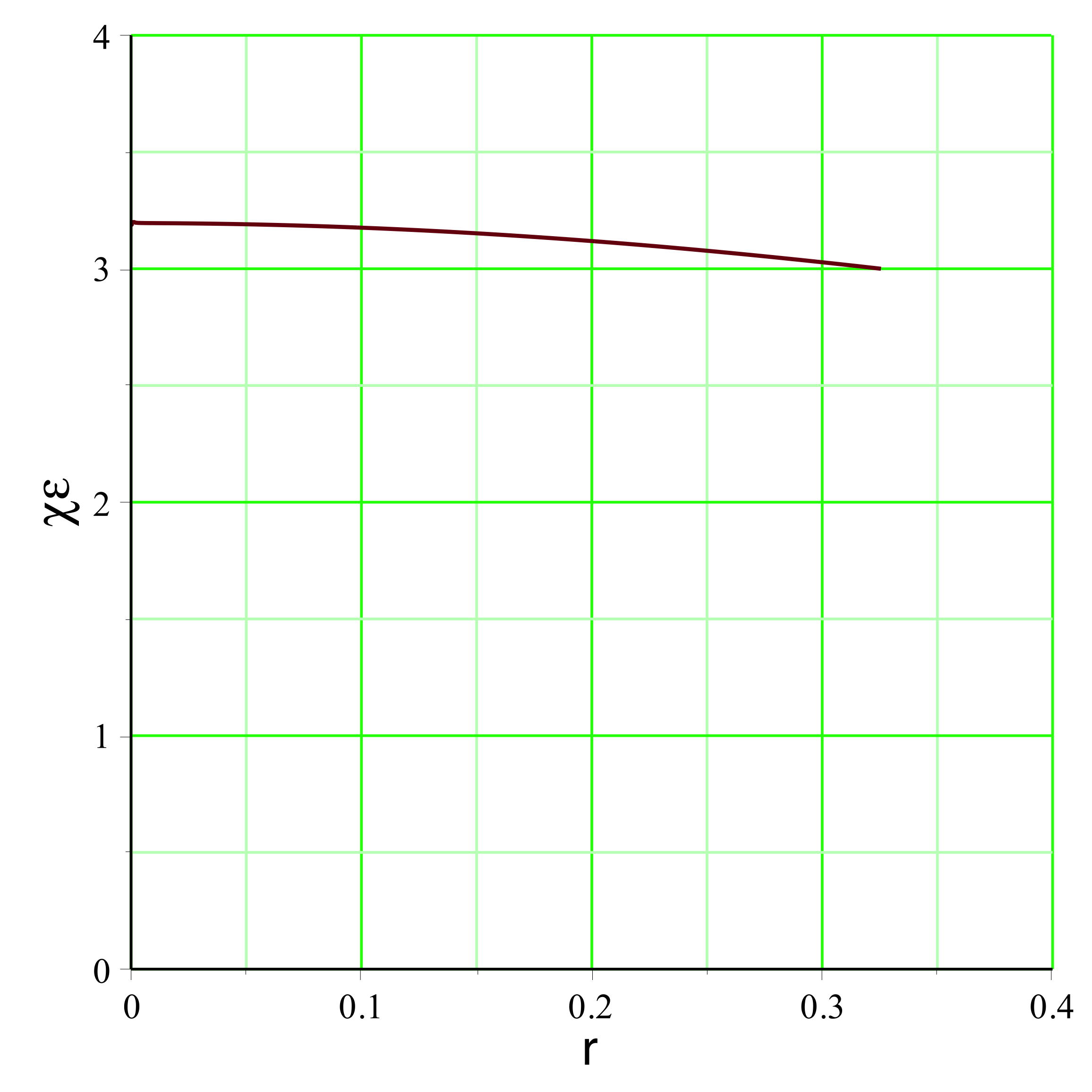
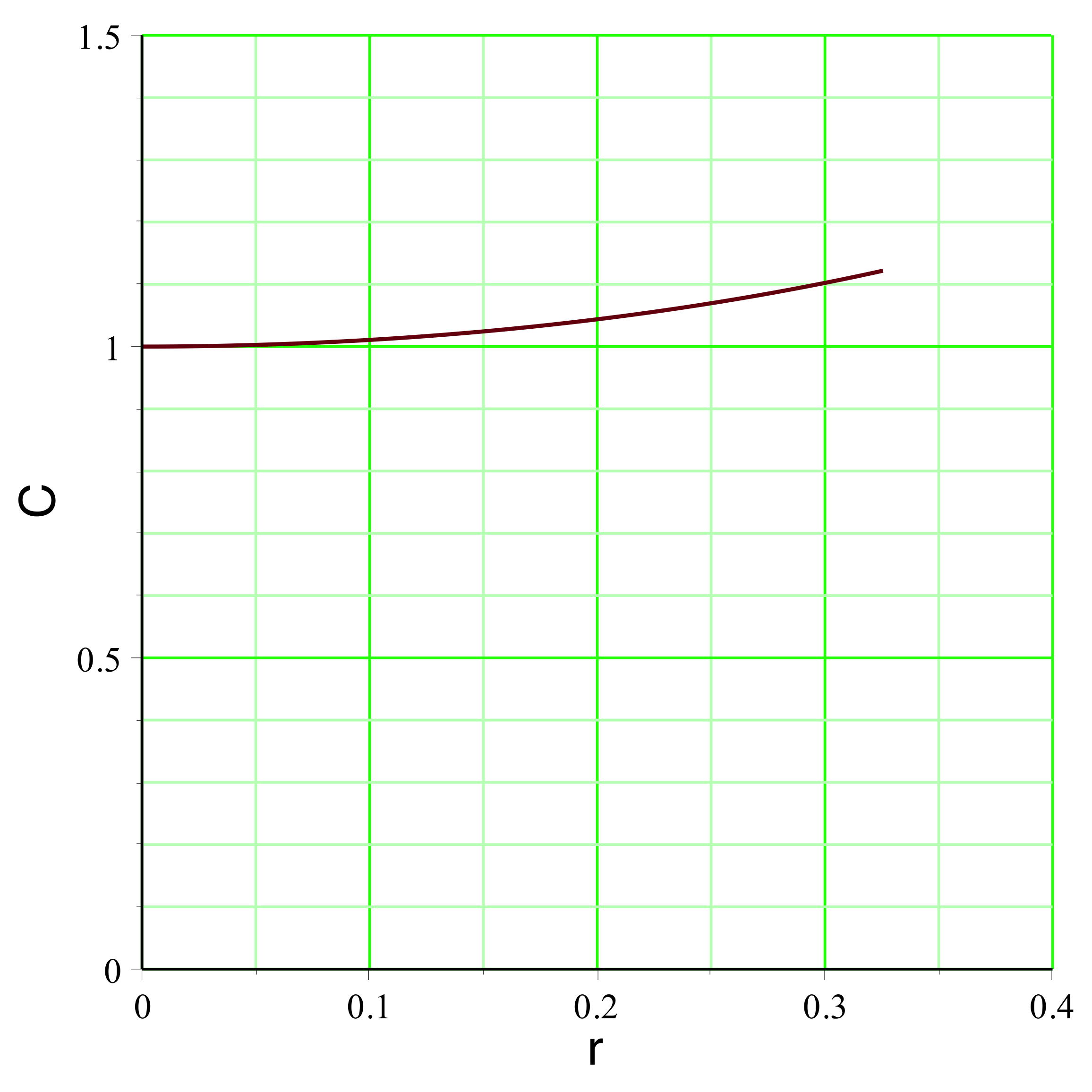
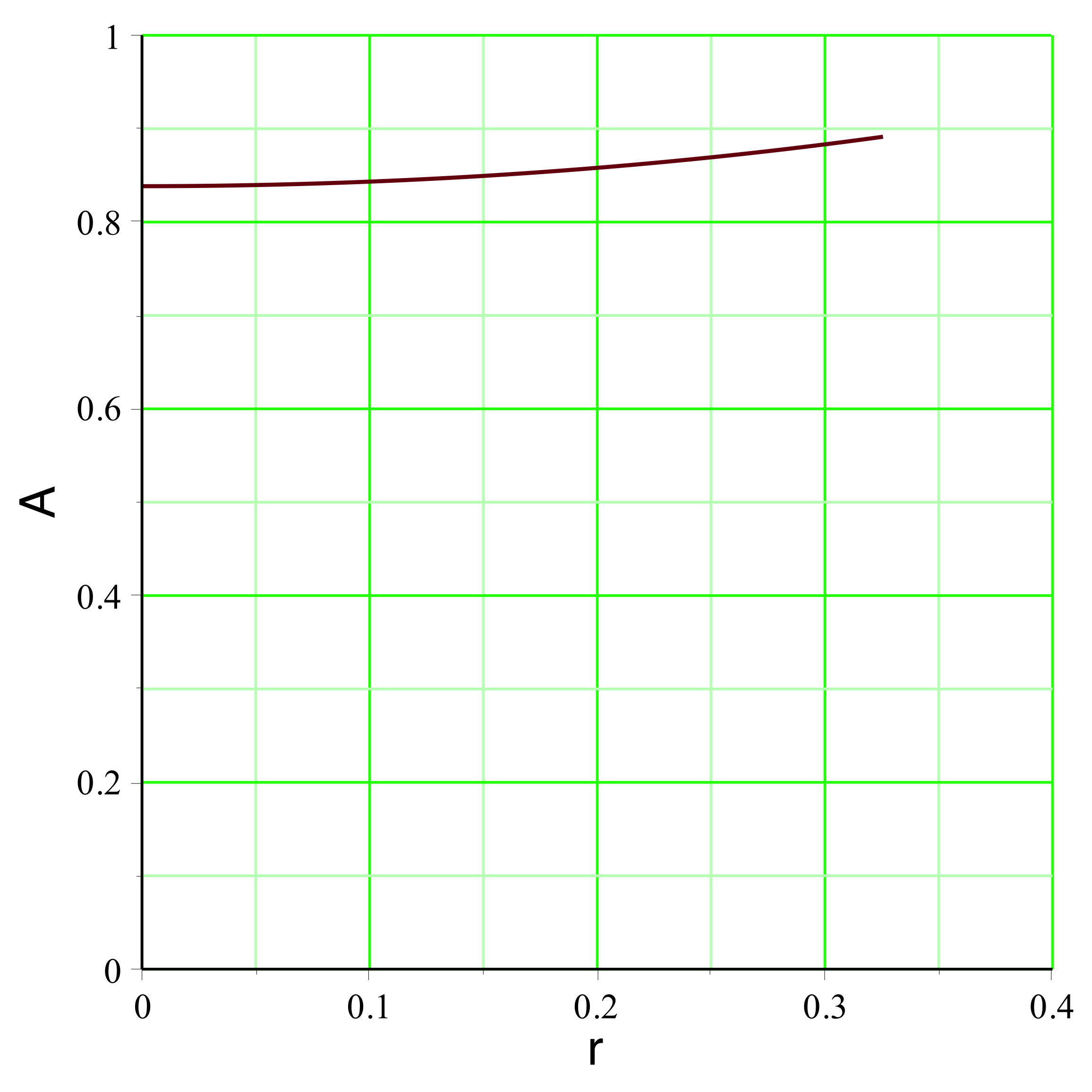
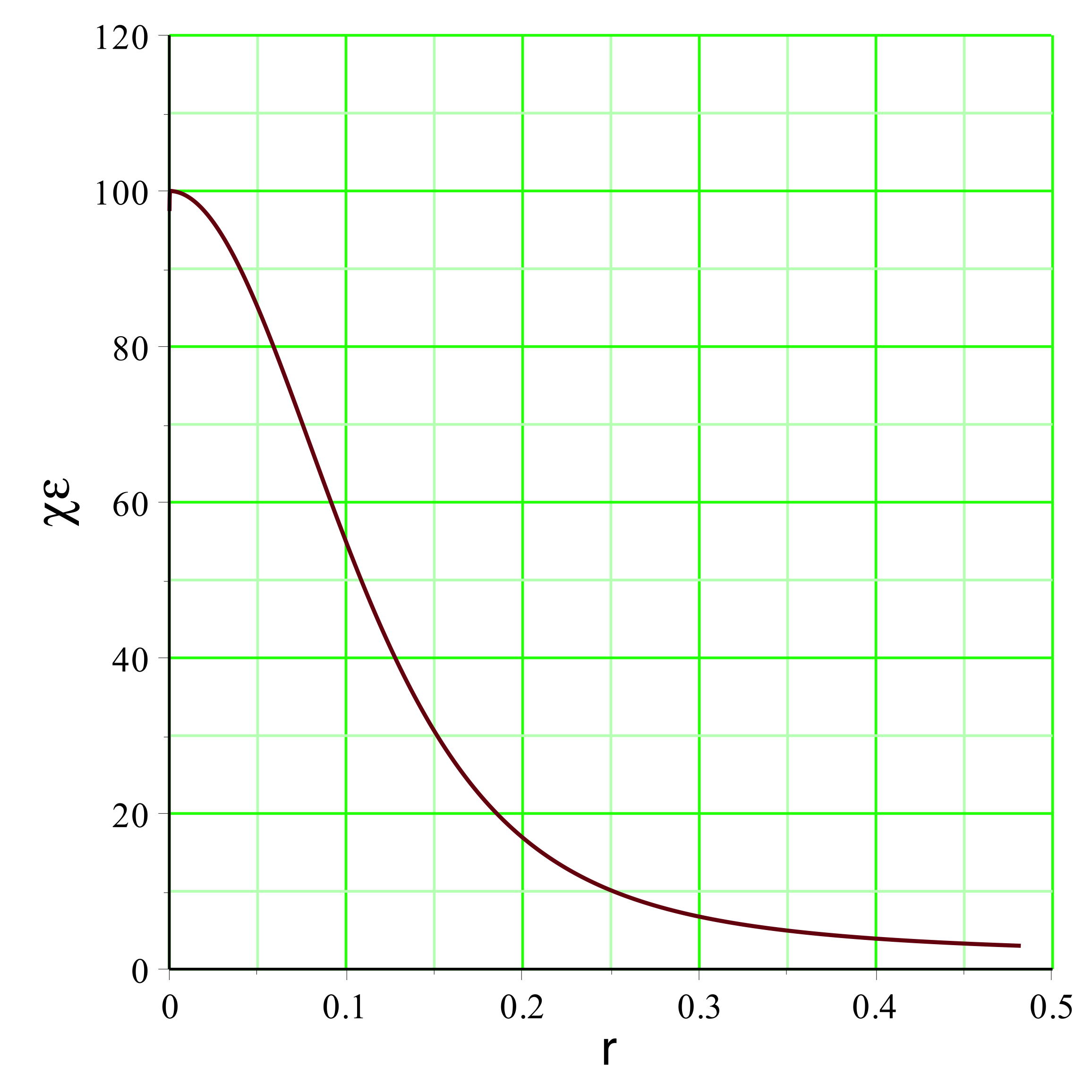
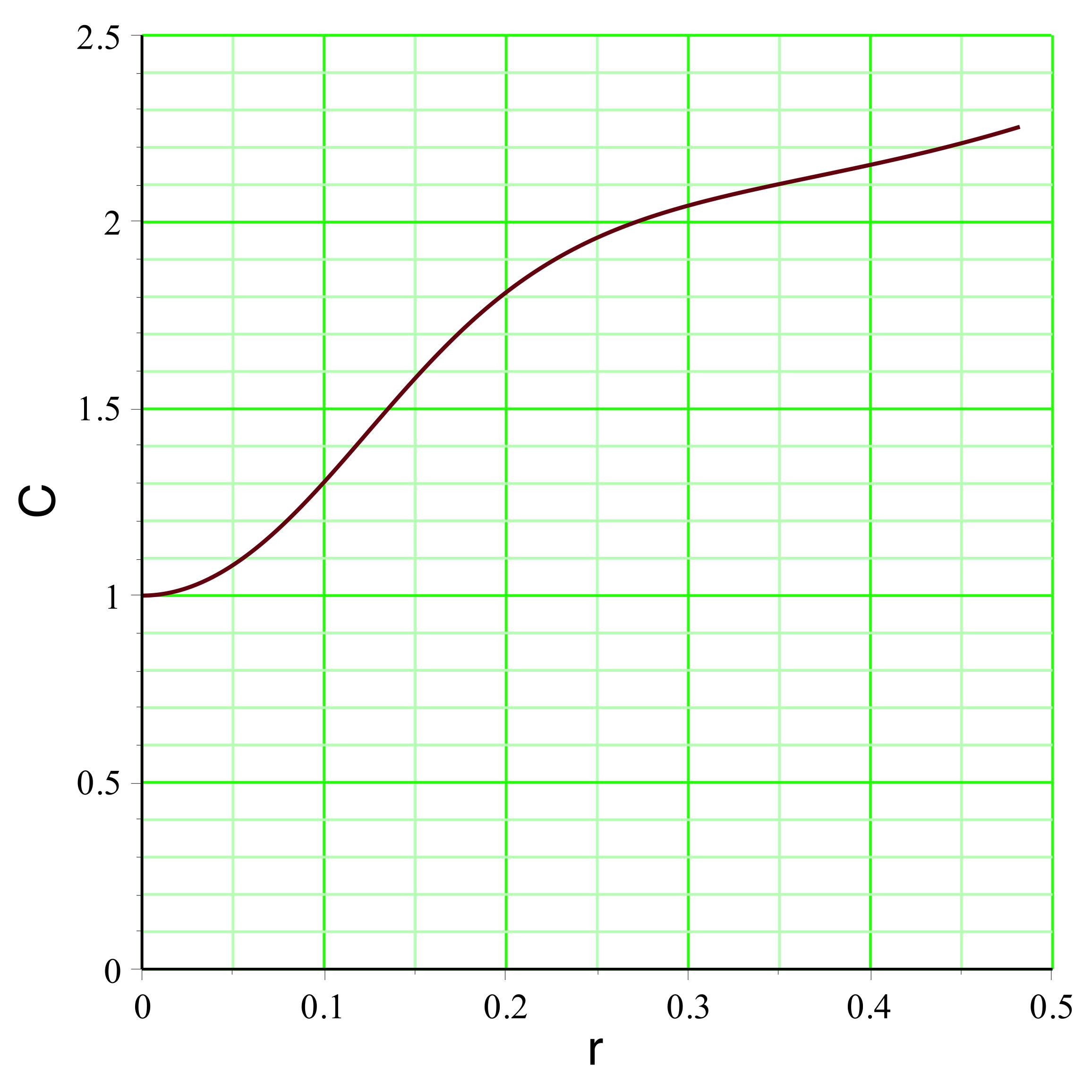
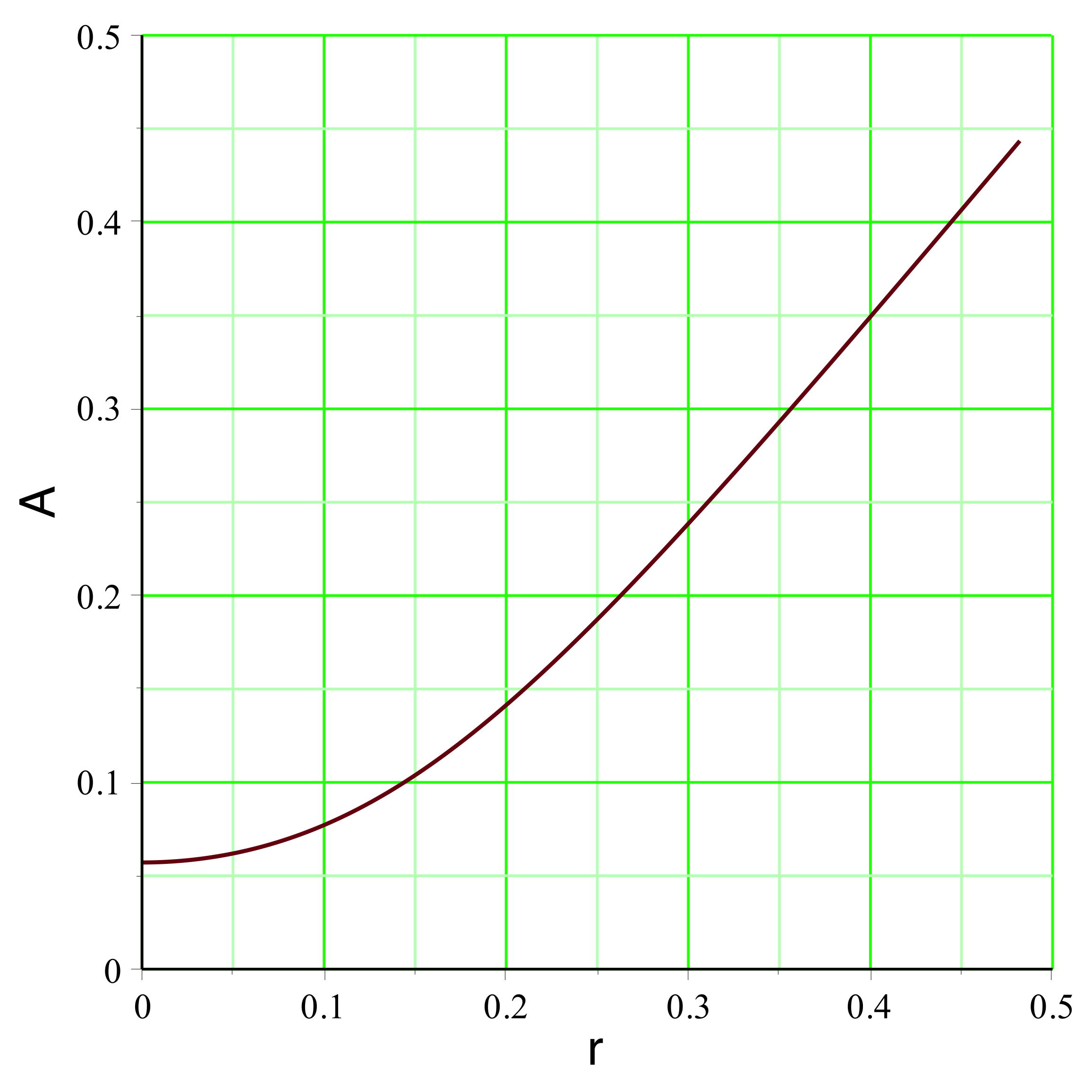
• On constate alors que l'ajustement de κκ est impossible : quel que soit κκ la pression calculée “initialement” (avant le début de l'expansion) tend vers  χ𝓅=−1χ \:𝓅=-1  pour la limite intérieure  ρ(1)≈1,57ρ(1)≈\text{1,57} .  On peut représenter l'exemple pour  κ=−1κ=-1  (β˙<0\dot{β}<0  pour un mouvement vers l'extérieur dans la zone inversée), la pression est raisonnablement non ultra-relativiste  (χ𝓅≪χεχ \:𝓅≪χ \:ε ),  ce qui justifierait la modélisation simplifiée.

ChampSpherPres_cor_Im/expansion_Xp.jpg

• De façon générale, le champ de “pesanteur” pousse plus la couche plus intérieure, causant une surpression dans l'épaisseur intermédiaire dont l'effet est de ralentir la précédente et d'augmenter l'accélération de la couche externe (limitée par l'inertie). Cet effet est renforcé dans la configuration géométrique étudiée ici : la diminution de rr correspond à un “étranglement” dont il faut forcer la traversée.
 
ChampSpherPres_cor_Im/expansion_geae.jpg

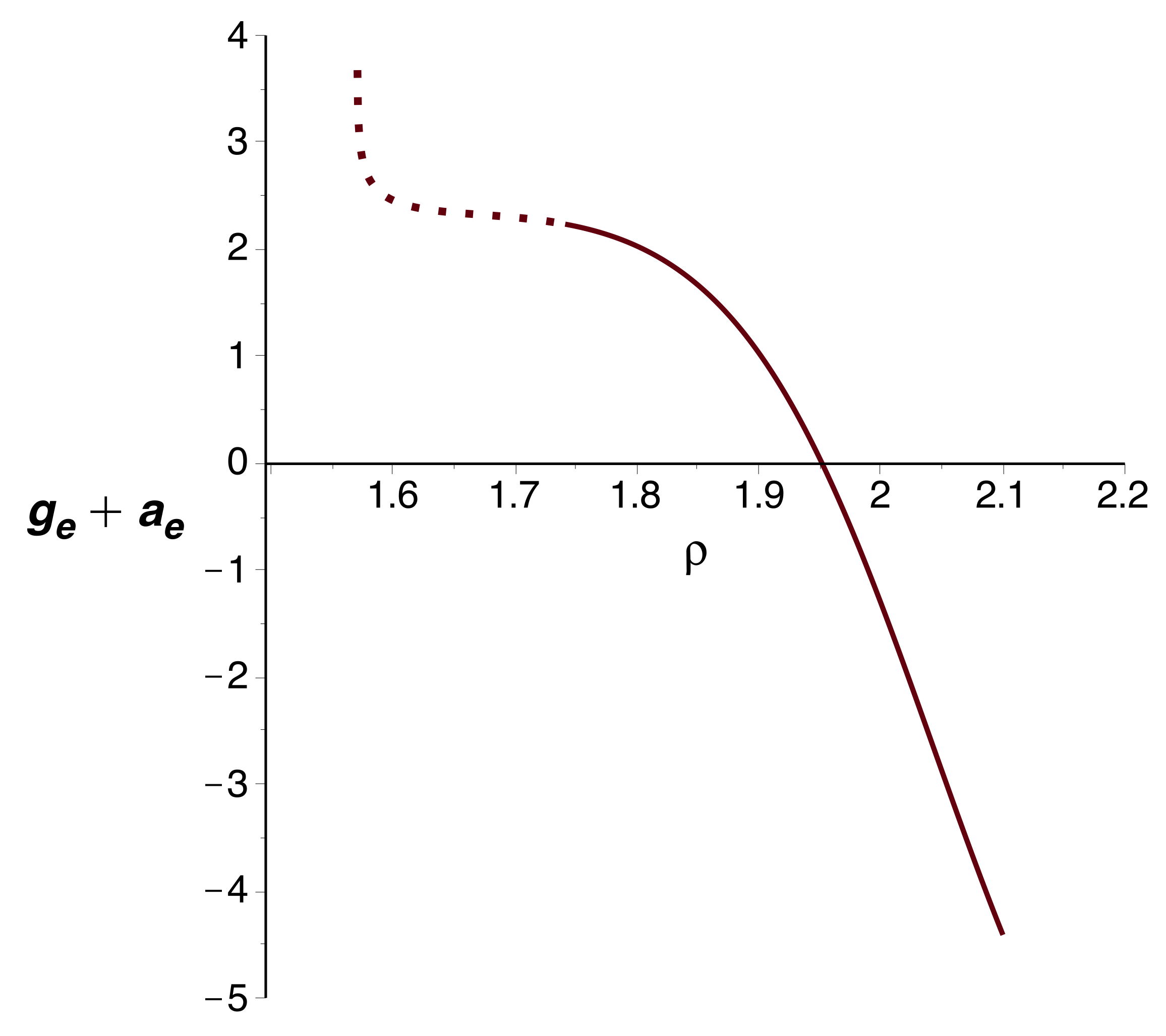
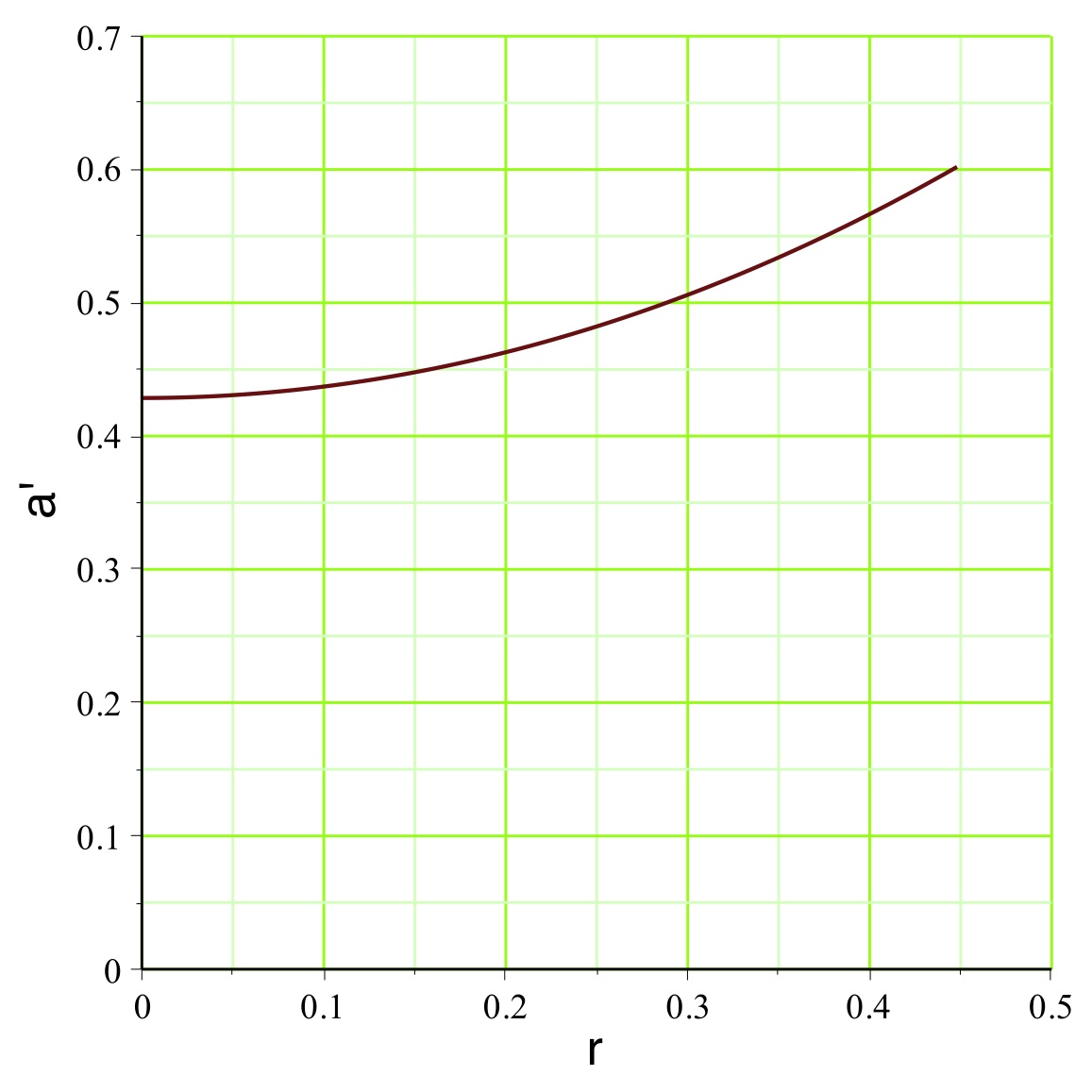
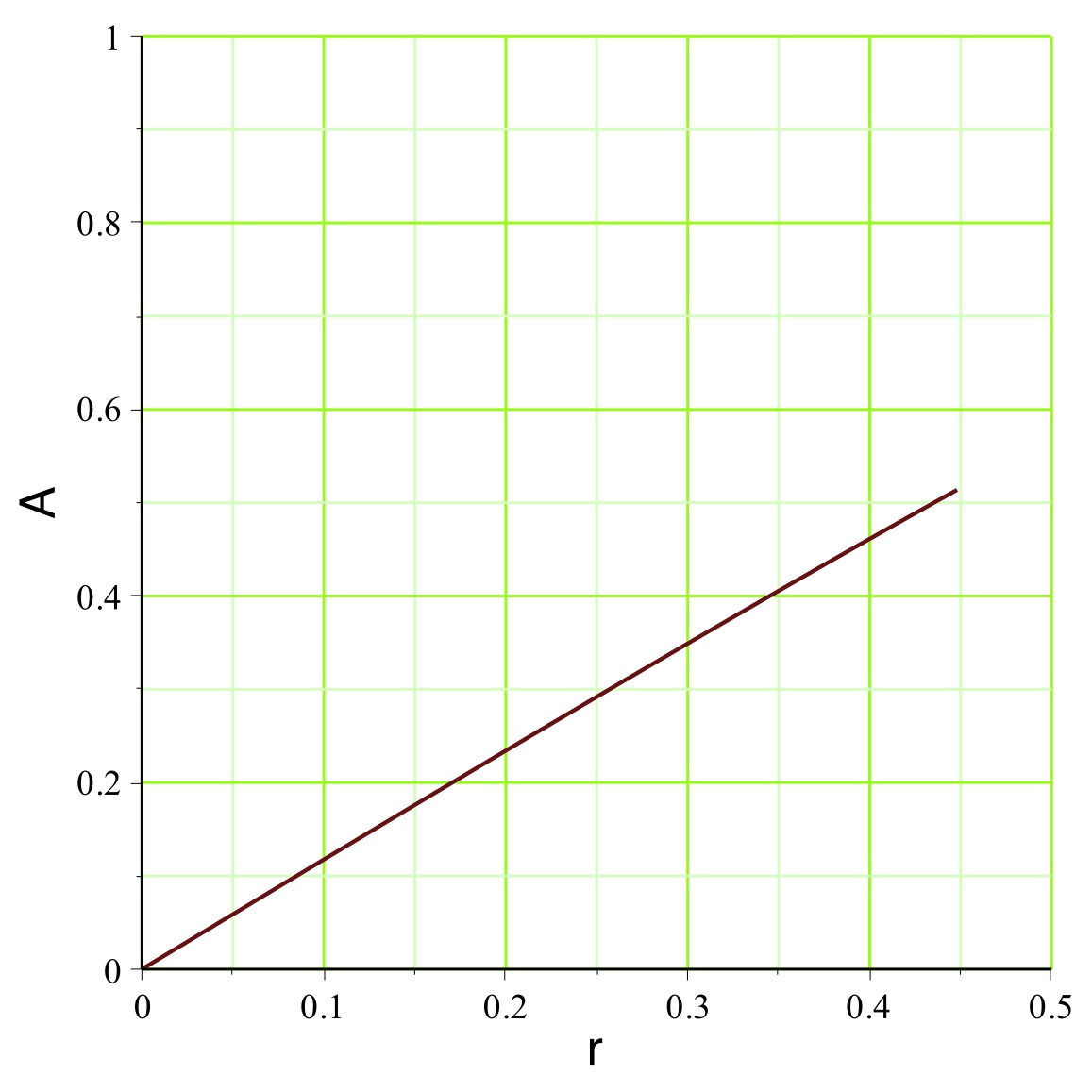
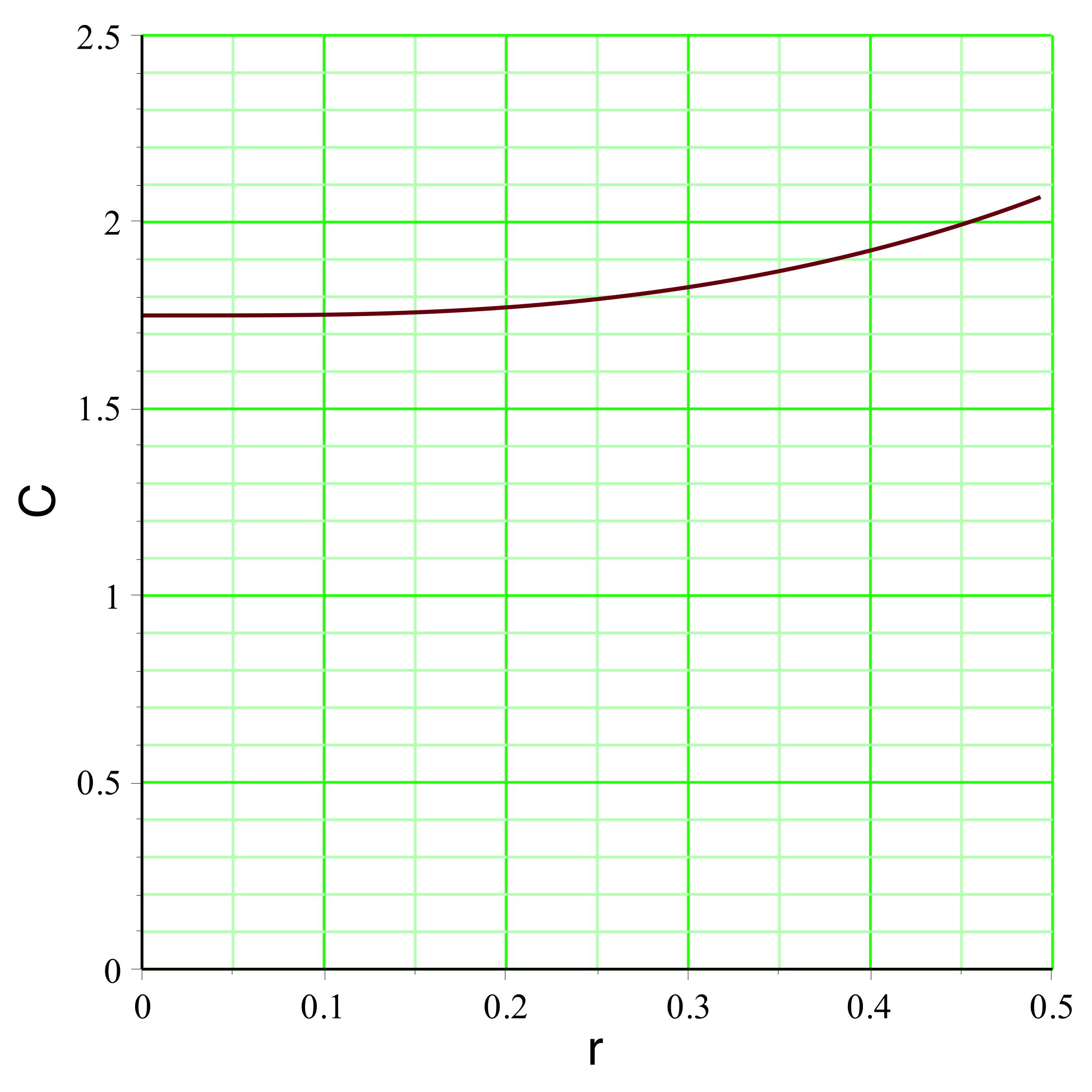
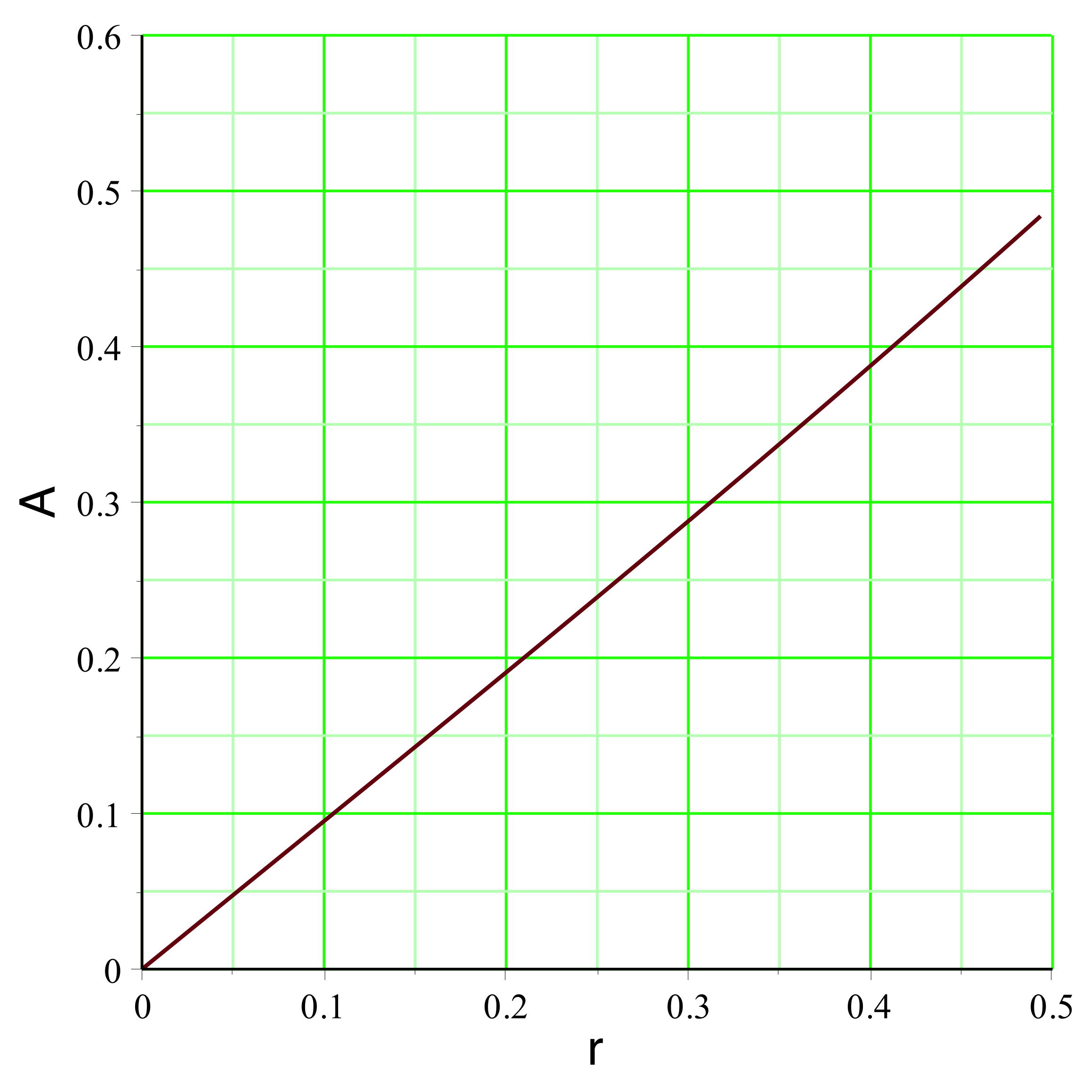
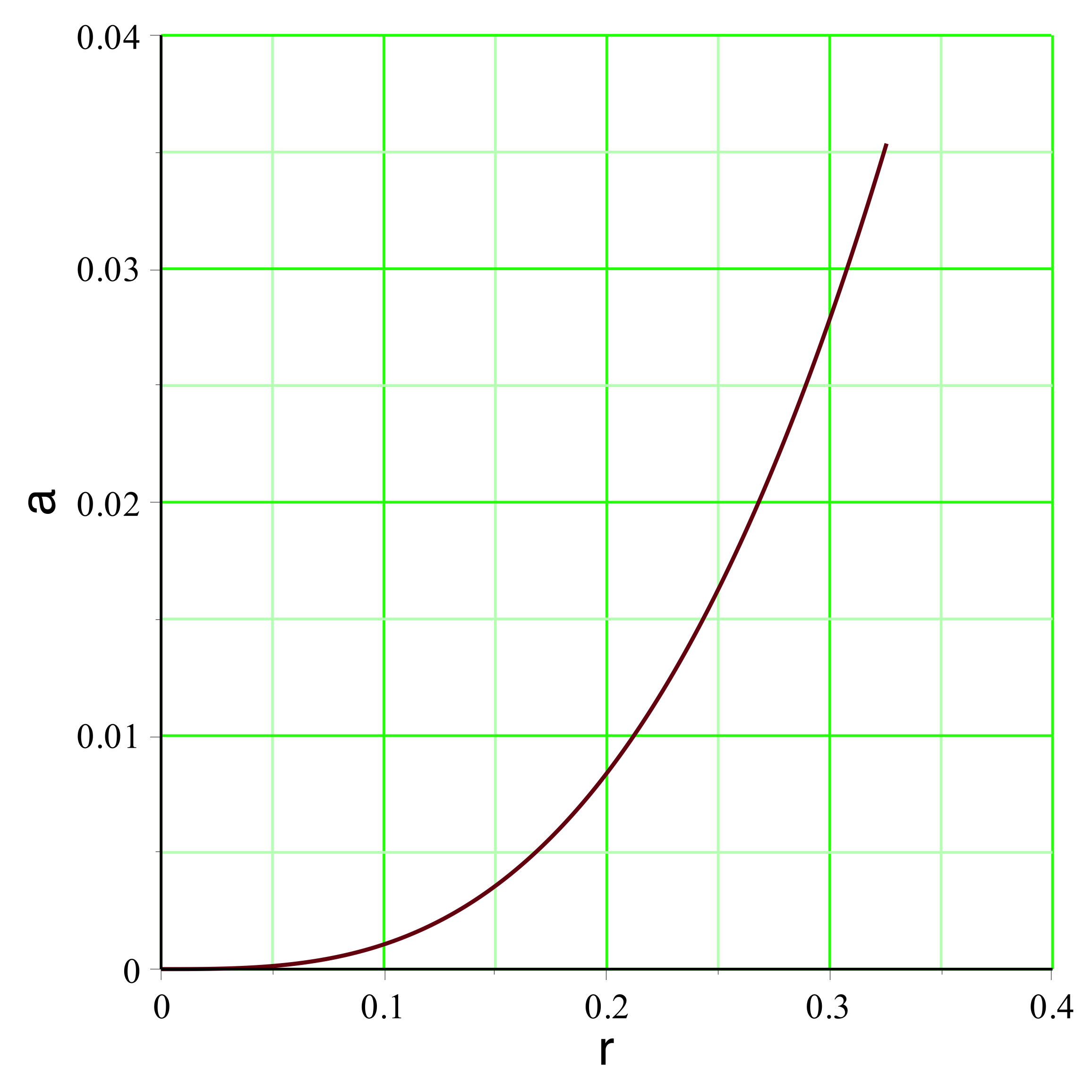
• Mais un autre effet s'ajoute en relativité générale : la surpression cause une diminution du champ, tendant à diminuer la surpression, donc à moins diminuer le champ... La convergence de cette influence réciproque, non évidente, aboutit dans l'exemple étudié aux courbes représentées ci-avant. Le champ  1CA′2A=r21+χ𝓅1−r2\displaystyle \frac{1}{\sqrt{C}} \: \frac{A'}{2 \,A}=\frac{r}{2} \:\frac{1+χ \:𝓅}{\sqrt{1-r^2}}  montre effectivement une diminution (le terme inertiel qui s'y ajoute, nettement plus faible dans cette partie, n'y change rien qualitativement), mais celle-ci est insuffisante pour retenir la couche interne, ce qui y nécessiterait une pression encore plus faible, que l'intégration numérique calcule négative (donc non physique).

• Peut-on ainsi faire l'hypothèse que la couche sous-jacente soit accélérée sans compression ? Dans ce cas la relation déduite de l'uniformité du débit (par incompressibilité) devrait être remplacée par une diminution de l'énergie volumique εε en conséquence (le modèle simplifié avec masse volumique uniforme ne peut pas s'appliquer). Outre la complexité des calculs pour raccorder les deux cas, il y a un problème essentiel : la pression s'annule au delà de la limite de la zone où cela “devrait” causer l'expansion ; le modèle est inacceptable.

• On peut alors se demander si une modélisation ultra-relativiste donnerait des résultats plus plausibles en permettant des valeurs plus grandes de κκ . Ceci est a priori très improbable, puisque l'essentiel des problèmes rencontrés vient des zones de faible pression, mais on peut vérifier qu'une étude analogue avec une équation d'état :  ε(r)=3𝓅+εRe−𝓅/εRε(r)=3 \:𝓅+ε_R \: \mathrm{e}^{-𝓅/ε_R} ,  en notant :  λ=χεR3=1\displaystyle λ=\frac{χ \:ε_R}{3}=1 ,  aboutit pour  κ=−2,5κ=-\text{2,5}  à des résultats qualitativement équivalents.

ChampSpherPres_cor_Im/expansion_ur_Xp.jpg

• Il est clair que ces modélisations “simplistes” sont trop peu efficaces ; toutefois, sans l'exclure totalement, cela suggère que l'existence de “bulles d'espace” associées à une inversion de r(ρ)r(ρ) est très improbable (selon ce modèle, la couche extérieure serait ainsi éjectée en supernova, faisant évoluer CC dans le sens d'une “ouverture de la bulle”, jusqu'à sa disparition une fois l'excès de matière complètement éjecté).