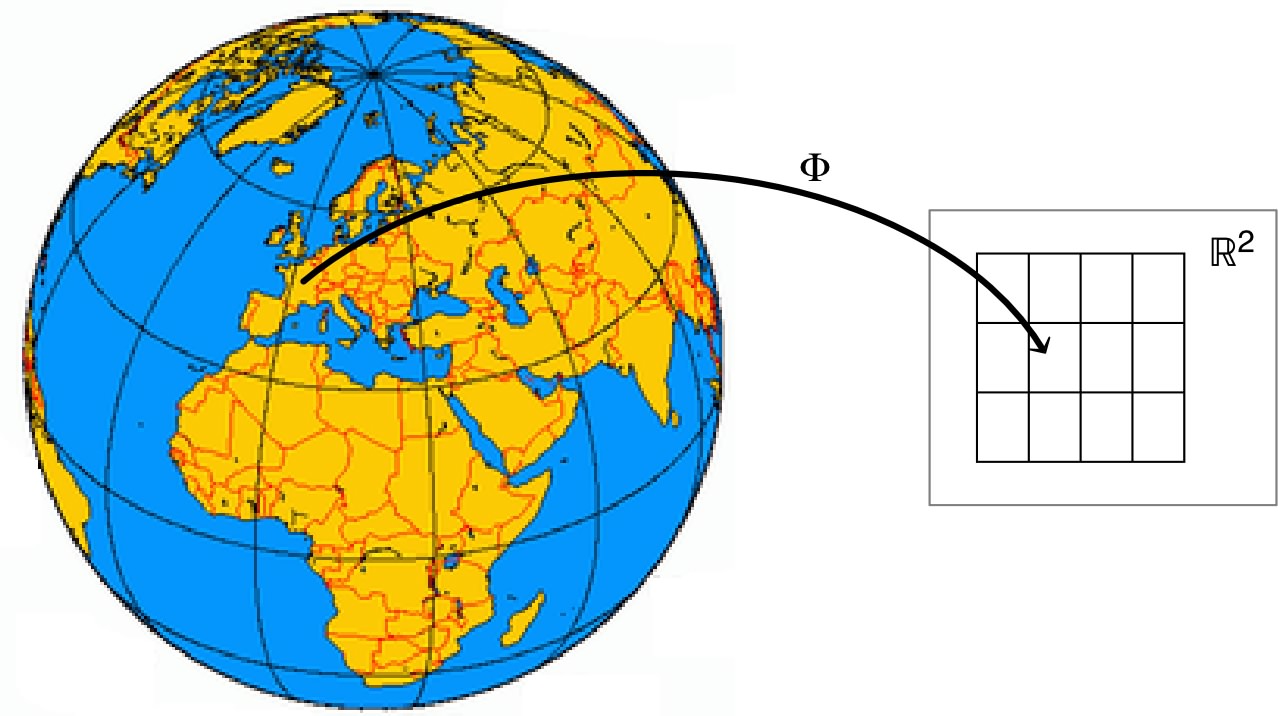
|
: |
|
|
|
|
|
|
|
. |

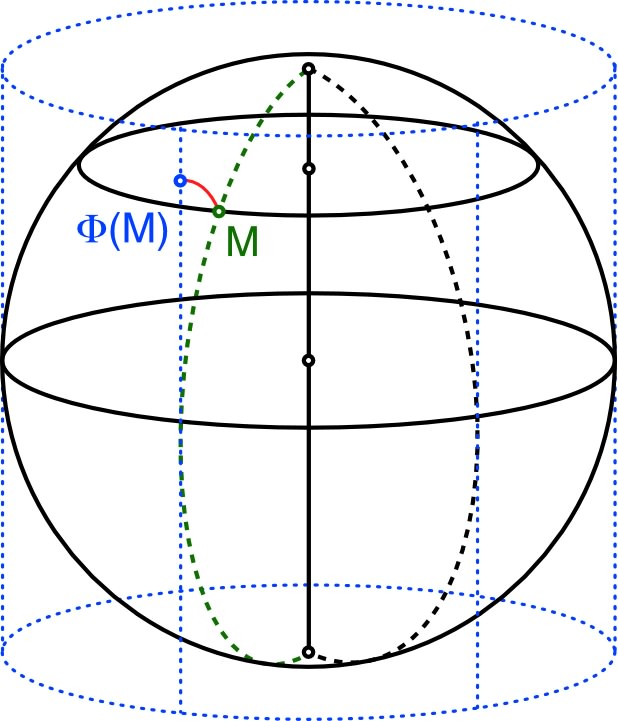 |
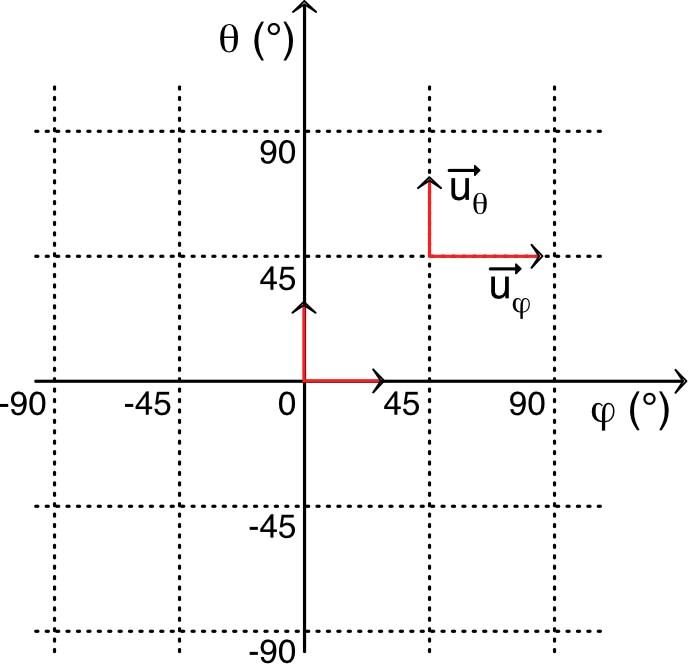 |
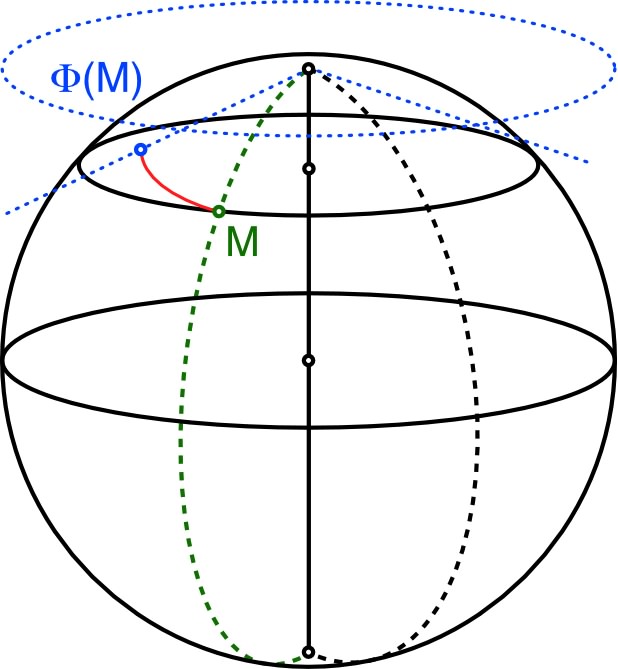 |
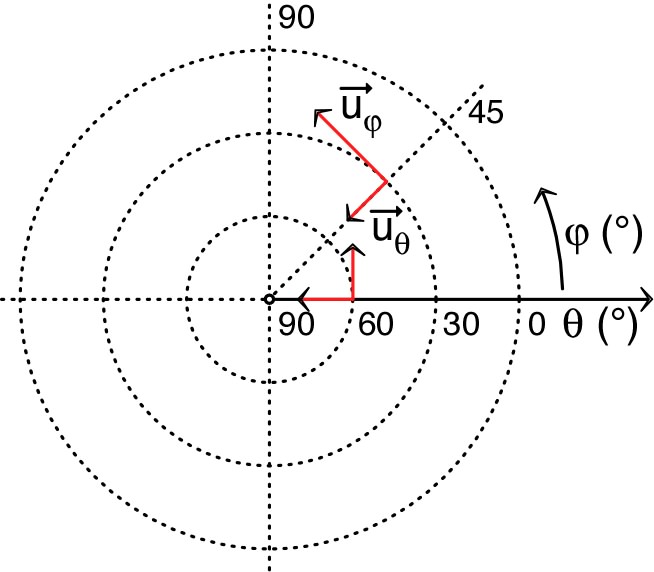 |
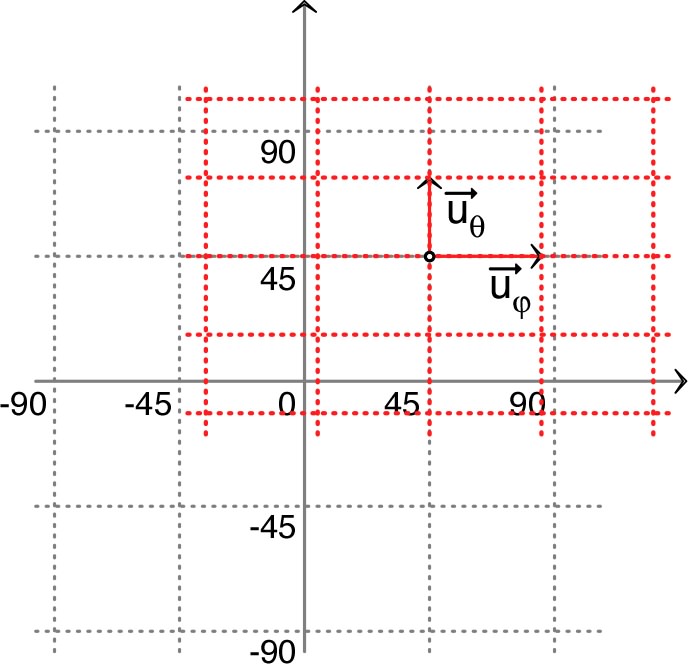 |
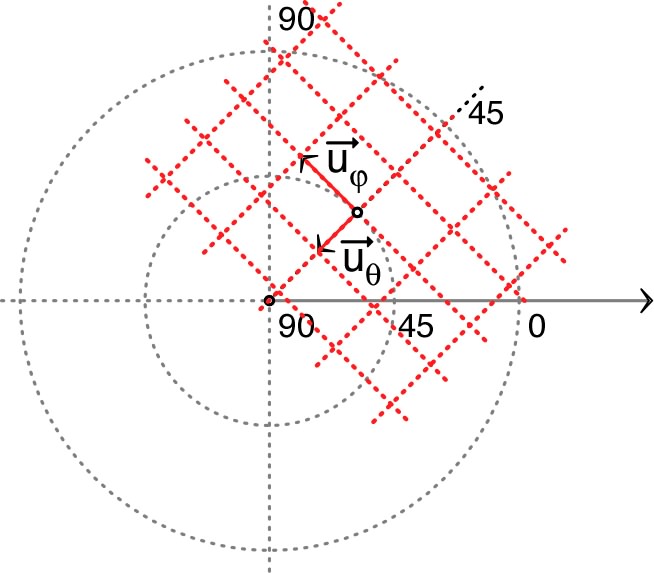 |
|
: |
|
|
|
|
|
|
|
. |
|
: |
|
|
|
|
|
|
|
. |
|
: |
|
|
|
|
|
|
|
. |
|
: |
|
|
|
|
|
|
|
|
||
|
|
|
. |
|
: |
|
|
|
|
|
|
|
|
||
|
: |
|
|
|
|
|
|
|
. |
|
: |
|
|
|
|
|
|
|
. |
|
: |
|
|
|
|
|
|
|
|
||
|
, |
, |
. |
|
: |
|
|
|
; .