RG VIII - MÉTRIQUE DE LEMAÎTRE - GÉNÉRALISATIONS


1. Généralisation pour l'espace en contraction

1.1. Formulation du problème

• Pour une particule en chute libre verticale, à partir d'une vitesse v0v_0 en  r=r0r=r_0  (notations “classiques” de Schwarzschild), la vitesse algébrique peut s'écrire :  v=−c1−A.(1−β02)A0\displaystyle v=-c \;\sqrt{1-\frac{A.(1-β_0^{\:2} )}{A_0}}   avec  A0=A(r0)A_0=A(r_0) .

Si le mobile part de l'infini avec une vitesse (limite) nulle, alors  A0=1A_0=1  et  β0=0β_0=0  donc  v=−crsr\displaystyle v=-c \;\sqrt{\frac{r_s}{r}} .  C'est à cette vitesse particulière que correspond la simplification de Lemaître.

• Pour une chute libre radiale quelconque, la transformation de Lemaître “brute” avec la vitesse correspondante  ( f=−βe≠rsr\displaystyle f=-β_e≠\sqrt{\frac{r_s}{r}} )  semble a priori ne pas simplifier la singularité. Autrement dit : une telle particule semblerait ne pas rencontrer de singularité avec la métrique de Lemaître, mais en rencontrer une dans son “référentiel propre”. Il faut préciser la généralisation.

1.2. Transformation de Lemaître généralisée

• Pour  ve=−c1−Aα\displaystyle v_e=-c \;\sqrt{1-\frac{A}{α}} ,  avec  α=A01−β02\displaystyle α=\frac{A_0}{1-β_0^{\:2}} ,  la transformation de Lemaître peut suggérer une généralisation en posant :  f=1κ=α−Aα\displaystyle f=\frac{1}{κ}=\frac{\sqrt{α-A}}{\sqrt{α}} ,  avec ici encore :

 dR_=cdt+κ(r)drA\displaystyle d\underline{R}=c \,dt+κ(r) \, \frac{dr}{A}  ;  cdT_=cdt+f(r)drA\displaystyle c \,d\underline{T}=c \,dt+f(r) \, \frac{dr}{A} .

Pour  κ(r)>0κ(r)>0 ,  ce repérage est ici encore en mouvement centripète à la vitesse d'entraînement :  ve=d𝓁dt𝓁oc=CdrAdt=−cκ\displaystyle v_e=\frac{d𝓁\:}{{dt}_{𝓁oc}} =\frac{\sqrt{C} \: dr}{\sqrt{A} \: dt}=-\frac{c}{κ} .

• Par ailleurs, la simplification de la métrique ne nécessite pas  f=rsr\displaystyle f=\sqrt{\frac{r_s}{r}}  mais plus généralement  1−f2=ΦA1-f^2=Φ \:A  où ΦΦ est une expression sans singularité. Ceci correspond à   f=±1−ΦAf=±\sqrt{1-Φ \:A}  ;  or  f=1−Aα\displaystyle f=\sqrt{1-\frac{A}{α}}  est une expression de cette forme, donc elle simplifie la métrique.

• Le seul “inconvénient” est qu'on obtient ainsi :  ds2=α.[c2dT_2−f2dR_2]{ds}^2=α.\left[c^2 \,{d\underline{T}}^2-f^2 \:{d\underline{R}}^2\right] .

On préfère donc poser dans ce cas :  ds2=c2dT2−f2dR2{ds}^2=c^2 \, {dT}^2-f^2 \: {dR}^2 ,  avec :

 dR=α[cdt+κ(r)drA]\displaystyle dR=\sqrt{α}\;\left[c \,dt+κ(r) \, \frac{dr}{A}\right]  ;  cdT=α[cdt+f(r)drA]\displaystyle c \,dT=\sqrt{α}\;\left[c \,dt+f(r) \, \frac{dr}{A}\right] .

📖 exercices n° I et II.

1.3. Expressions des coordonnées

• On obtient en simplifiant :  dR−cdT=drrsr+α−1\displaystyle dR-c \,dT=\frac{dr}{\sqrt{\frac{r_s}{r}+α-1}} .  Le cas général est compliqué ; on préfère ici deux cas simples caractéristiques.

• Pour  α=2>1α=2>1 ,  c'est le cas d'une particule partant de l'infini  (A0=1A_0=1)  avec une vitesse initiale  β0=−12<0β_0=-\frac{1}{\sqrt{2}}<0  ;  l'intégration donne (avec une constante d'intégration nulle fixant l'origine) :  R−cT=r.(r+rs)−rsarsinh(rrs)\displaystyle R-c\,T=\sqrt{r .(r+r_s )}-r_s \: \mathrm{arsinh}\left(\sqrt{\frac{r}{r_s}}\right) .

Cette fonction est strictement croissante, mais non inversible littéralement pour exprimer la partie angulaire de la métrique.

• Pour  α=0,5<1α=0,5<1 ,  c'est le cas d'une particule partant avec une vitesse initiale nulle à une distance finie  r0=2rsr_0=2 \,r_s  (A0=0,5<1A_0=0,5<1) ,  l'intégration donne (en choisissant la constante d'intégration pour ajuster l'origine) :

 R−cT=2rs√2arcsin(r2rs)−2r.(2rs−r)\displaystyle R-c\,T=2 \,r_s \: √2 \; \arcsin\left(\sqrt{\frac{r}{2 \,r_s}}\right)-\sqrt{2 \,r .(2 \,r_s-r)} .

Cette fonction est strictement croissante (restreinte à  r≤r0=2rsr≤r_0=2 \,r_s) ,  mais non inversible littéralement pour exprimer la partie angulaire de la métrique.

Ce résultat est limité à  r≤r0r≤r_0  car la méthode de Lemaître considère vev_e en fonction de rr avec une particule partant de r0r_0 (elle ne peut servir de référence que là où elle passe). Cela n'interdit pas de décrire les mouvements à d'autres vitesses, mais sans accéder à la zone  r>r0r>r_0  (à moins d'utiliser des nombres complexes ?) ; en particulier, pour le cône de lumière à l'instant “initial”, on ne peut pas tracer la trajectoire du photon sortant vers  r>r0r>r_0 .

◊ remarque : si  r>r0r>r_0  on obtient  ds2=c2dT2−f2dR2{ds}^2=c^2 \,{dT}^2-f^2 \: {dR}^2  où  f2=1−Aα<0\displaystyle f^2=1-\frac{A}{α}<0 ,  donc la variable RR n'est plus du genre espace ; c'est comme pour les coordonnées “classiques” de Schwarzschild : là où il n'y a plus de particules de référence du type choisi (statiques pour ce dernier, impossible pour  r<rsr<r_s).

◊ remarque : en revanche, contrairement à celle de Schwarzschild, cette limite ressemble plus à une sorte d'horizon, qui s'éloigne quand on s'en “approche” (ici dans l'espace des vitesses) ; pour des particules montant à plus grande vitesse, dépassant r0r_0 à vitesse non nulle pour aller jusqu'à  r1>r0r_1>r_0 ,  alors la limite “recule” en r1r_1 ; au contraire l'horizon de Schwarzschild reste au même endroit quelle que soit la vitesse subluminique à laquelle il est atteint, mais il disparait complètement si et seulement s'il est atteint à la vitesse cc, quelle que soit la façon dont cette vitesse est approchée.

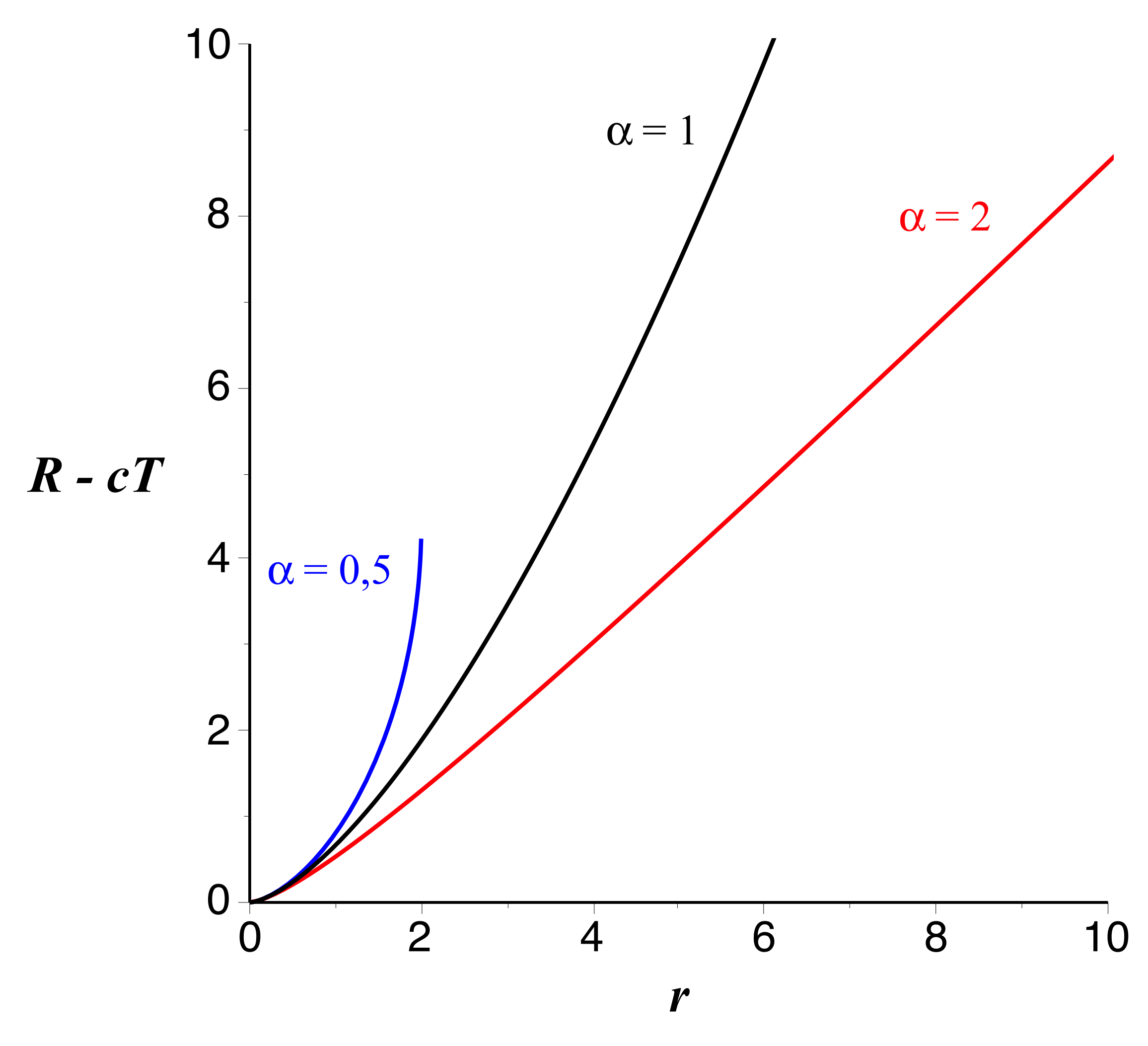
GenLemaitre_Im/R-cT_alpha.png

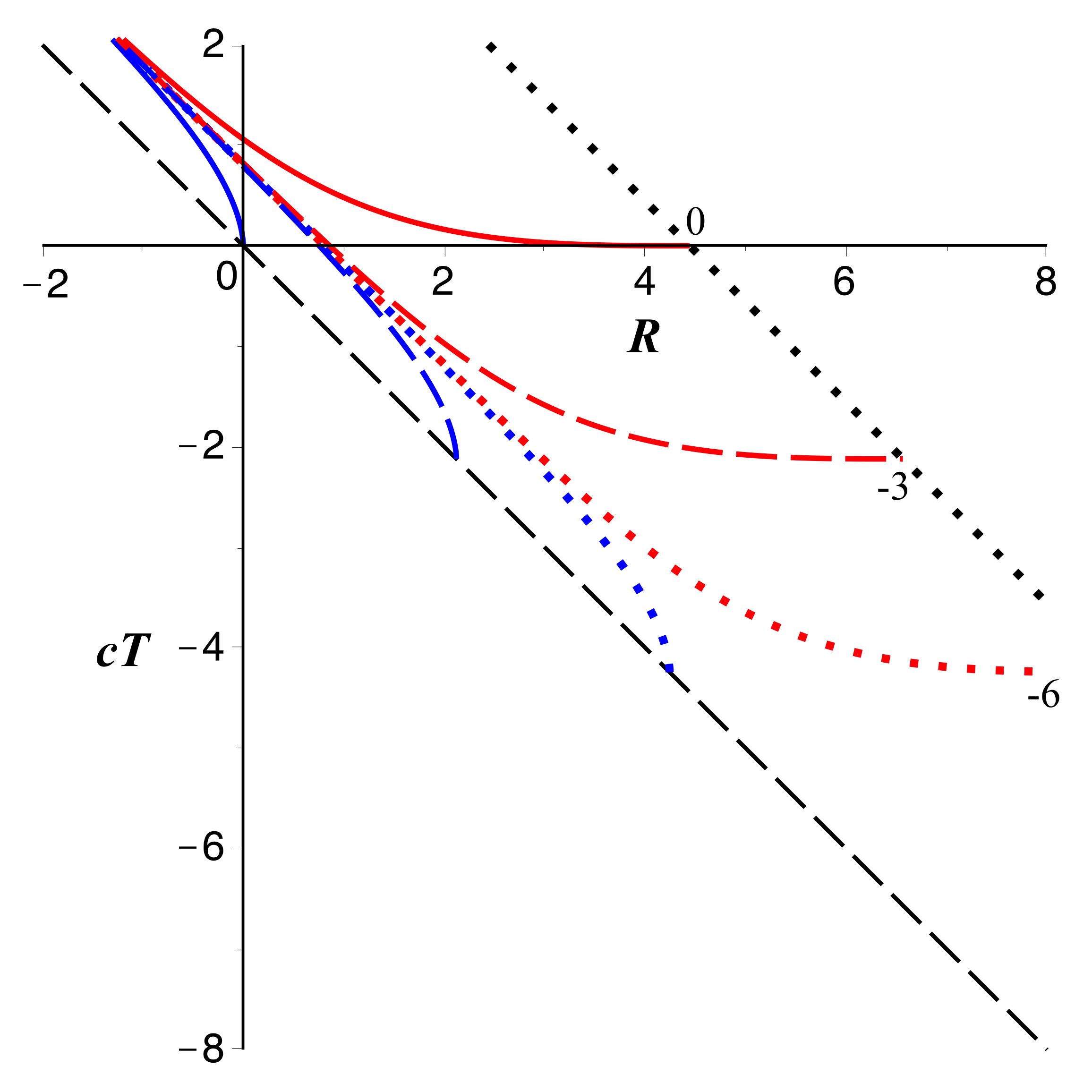
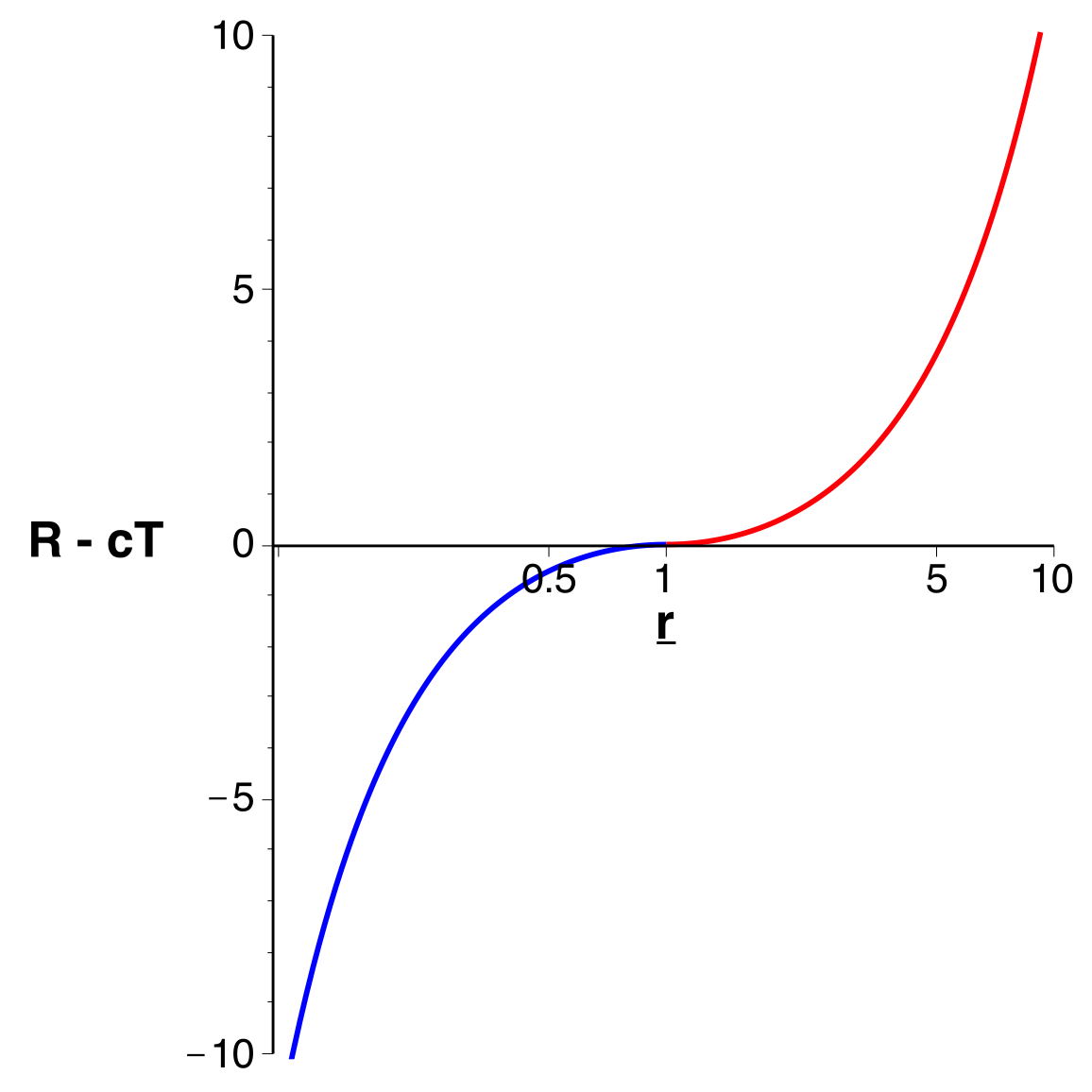
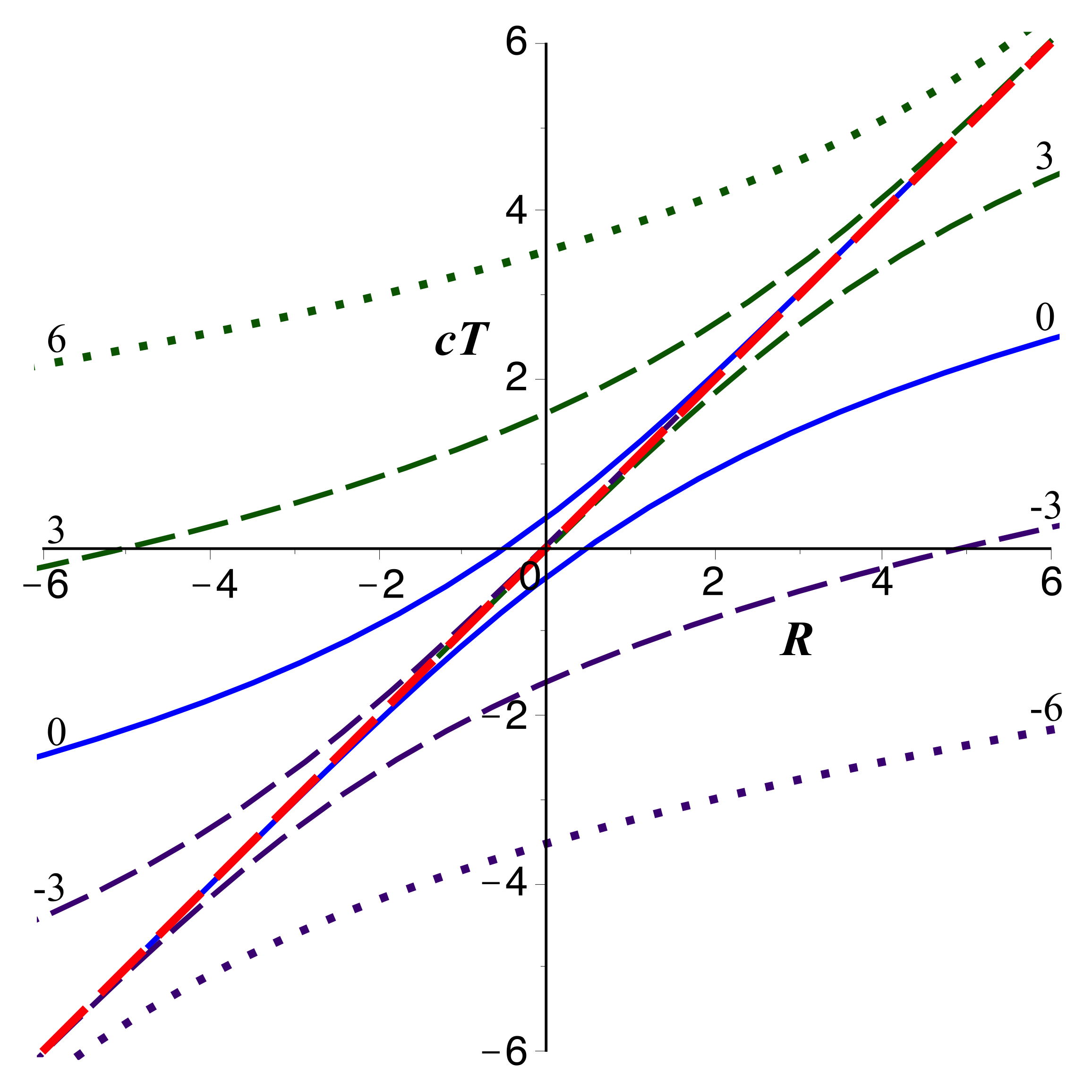
• On peut comparer l'allure des variations dans les différents cas (le graphique prend rsr_s comme unité) :

 ◊ elliptique pour  α<1α<1  (tangente verticale en  r=2rsr=2 \,r_s  pour  α=0,5α=\text{0,5})  ;
◊ parabolique pour  α=1α=1  ;
◊ hyperbolique pour  α>1α>1 .

• On obtient par ailleurs en simplifiant :

 cdT−αcdt=α−AdrA=rsr+α−11−rsrdr\displaystyle c \,dT-\sqrt{α} \: c \,dt=\sqrt{α-A} \, \frac{dr}{A}=\frac{\sqrt{\frac{r_s}{r}+α-1}}{1-\frac{r_s}{r}} \, dr .

Pour  α=2α=2  l'intégration donne :

 cT−2ct=r.(r+1)+3arsinh⁡(r)c \,T-\sqrt{2} \; c \,t=\sqrt{r.(r+1)}+3 \, \mathrm{arsinh}⁡\left(\sqrt{r}\right)

 −2arsinh⁡(r+1|r−1|)−2arsinh⁡(r−1|r+1|)\displaystyle - \sqrt{2} \;\mathrm{arsinh}⁡\left(\frac{\sqrt{r}+1}{\left|\sqrt{r}-1\right|} \right) - \sqrt{2} \;\mathrm{arsinh}⁡\left(\frac{\sqrt{r}-1}{\left|\sqrt{r}+1\right|} \right) .

Pour  α=0,5α=\text{0,5}  l'intégration donne :

 cT−12ct=r.(2−r)2−12arcosh⁡(1|r−1|)\displaystyle c \,T-\frac{1}{\sqrt{2}} \, c \,t=\frac{\sqrt{r.(2-r)}}{\sqrt{2}}-\frac{1}{\sqrt{2}} \; \mathrm{arcosh}⁡\left(\frac{1}{\left|r-1\right|} \right) .

◊ remarque : la constante imaginaire de  ctc \,t  se simplifie en général si on tient compte dans ℂℂ du comportement de  |r+1|\left|\sqrt{r}+1\right|  ou  |r−1|\left|\,r-1\right| :  les limites à l'infini des fonctions  arcosh\mathrm{arcosh}  et  arsinh\mathrm{arsinh}  se comportent comme un logarithme (dans ce cas  cTc \,T  n'a pas de composante imaginaire).

• De façon générale, ces résultats à la fois renforcent et affaiblissent la crédibilité de l'interprétation simpliste de la métrique de Lemaître selon laquelle l'espace serait en contraction.

Cela la renforce en montrant que ce qui est obtenu avec la forme classique, pour une vitesse particulière, est en fait tout aussi vrai pour n'importe quelle vitesse de chute libre radiale. En ce sens, il semble ne pas s'agir d'un artifice de calcul lié à une simplification fortuite.

Mais cela l'affaiblit en montrant qu'il est faux de croire que l'effet est lié à un mouvement d'effondrement de l'espace : ce dernier n'est associé à aucune vitesse de chute particulière.

◊ remarque : c'est différent pour la métrique de Kerr décrivant un trou noir en rotation ; dans ce cas l'étude de l'ergosphère, ou de la chute libre avec vitesse initiale nulle, montre que l'espace physique est entraîné en rotation.

 📖 exercices n° III, IV, V, VI et VII.

1.4. Représentations graphiques

• Pour  α=2α=2  avec  rsr_s  comme unité, les courbes correspondant à  r=Cster=Cste  sont ici encore des droites :  R−cT=r.(r+1)−arsinh(r)R-c\,T=\sqrt{r.(r+1)}-\mathrm{arsinh}\left(\sqrt{r}\right) .

L'allure (non représentée ici) est la même que pour  α=1α=1 ,  mais avec des droites plus rapprochées.

• Les courbes correspondant à  ct=Cstec \,t=Cste  peuvent être décrites par une représentation paramétrique (en fonction de rr) selon les expressions précédentes pour  R−cTR-c \,T  et  cTc \,T.  L'allure (non représentée ici) est la même que pour  α=1α=1 .

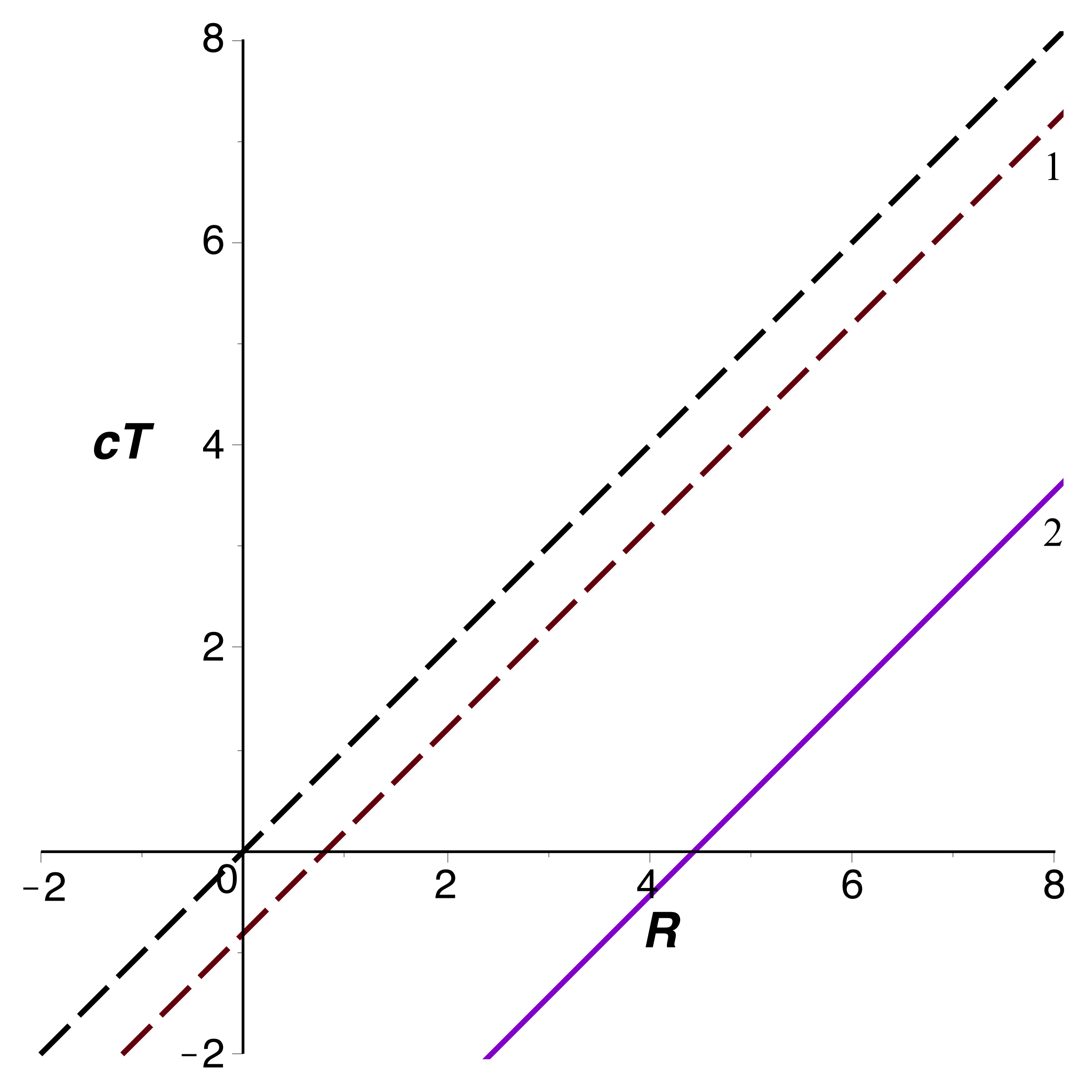
• Pour  α=12α=\frac{1}{2}  avec  rsr_s  comme unité, les courbes correspondant à  r=Cster=Cste  sont ici encore des droites :  R−cT=22arsinh(r2)−2r.(2−r)\displaystyle R-c\,T=2 \,\sqrt{2} \; \mathrm{arsinh}\left(\sqrt{\frac{r}{2}}\right)-\sqrt{2 \,r.(2-r)} .

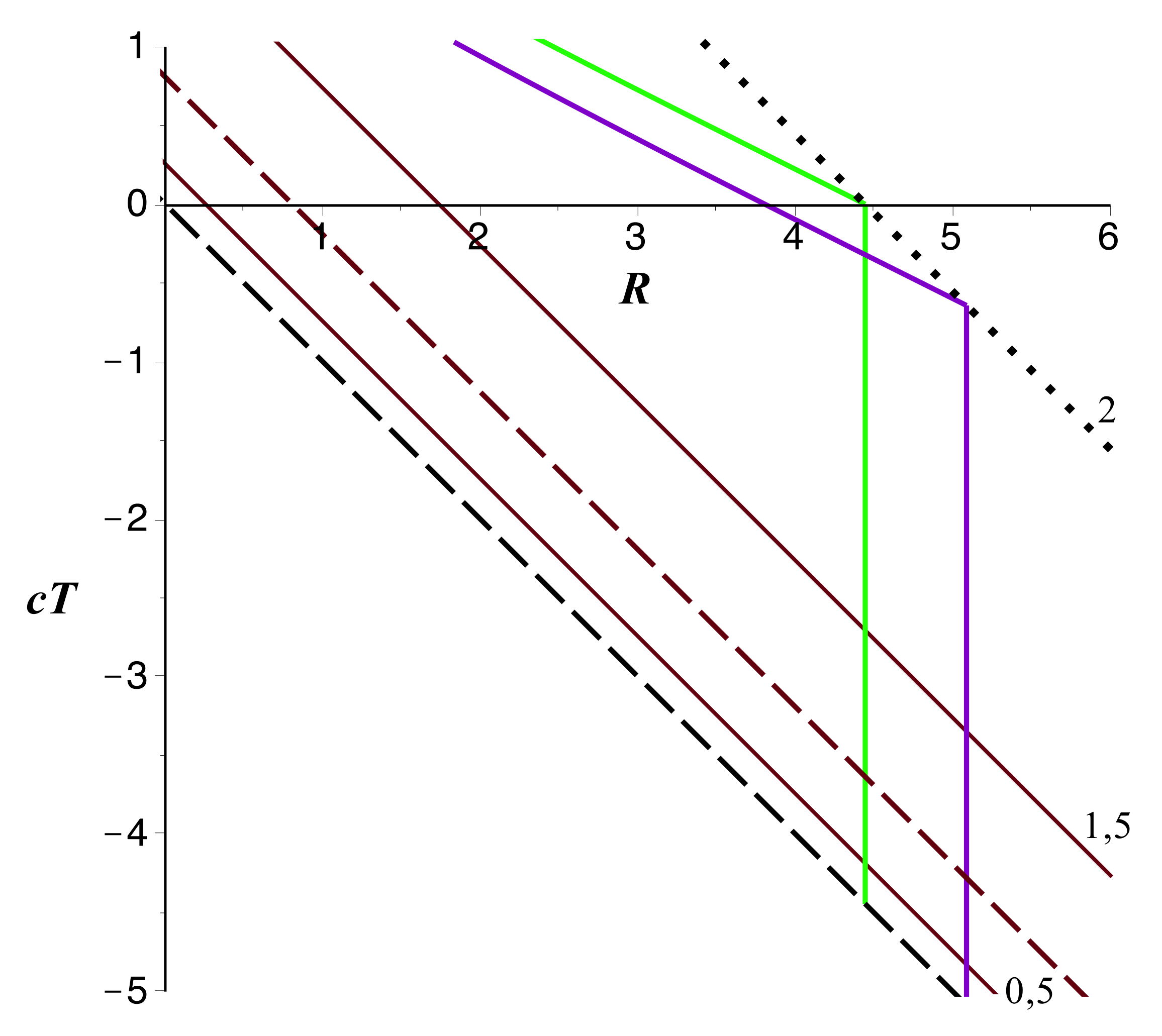
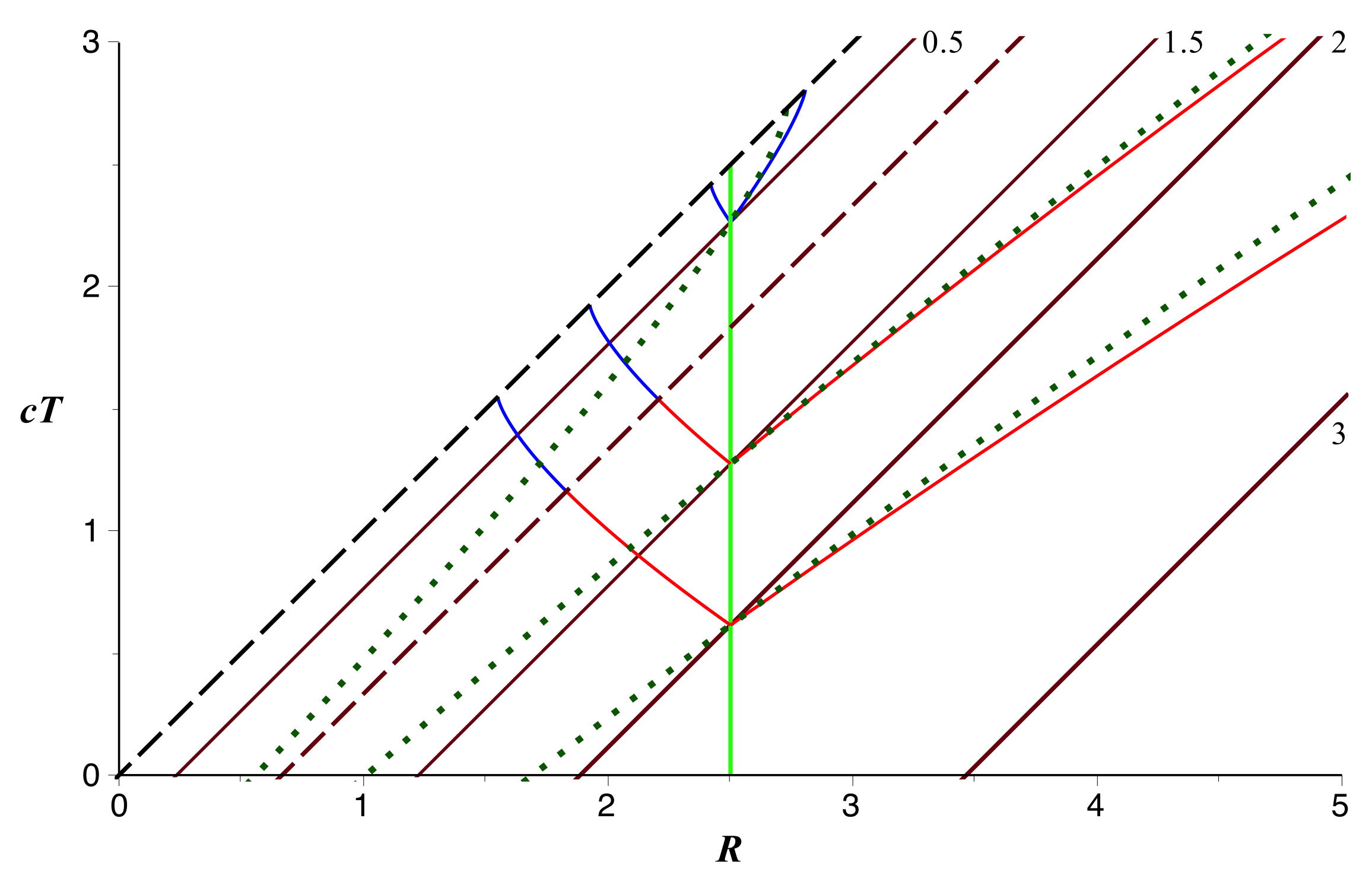
On obtient la représentation ci-après (ici pour  r=0;1;2r=0 \,;1 \,;2)  ;  la partie à gauche de la diagonale n'a pas de signification physique. L'allure est la même que pour  α=1α=1 ,  mais avec des droites plus espacées et limitées à  r≤2r≤2 .

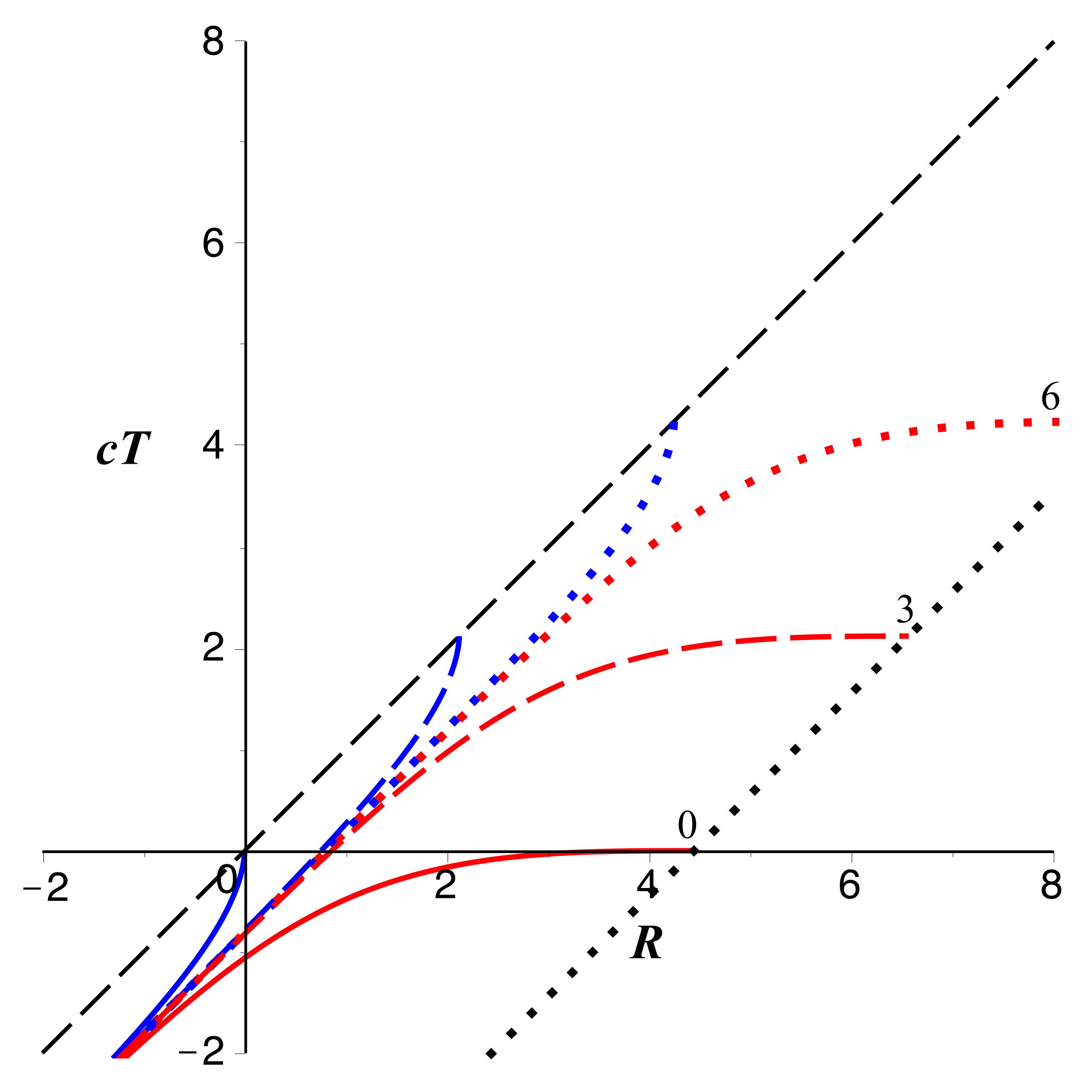
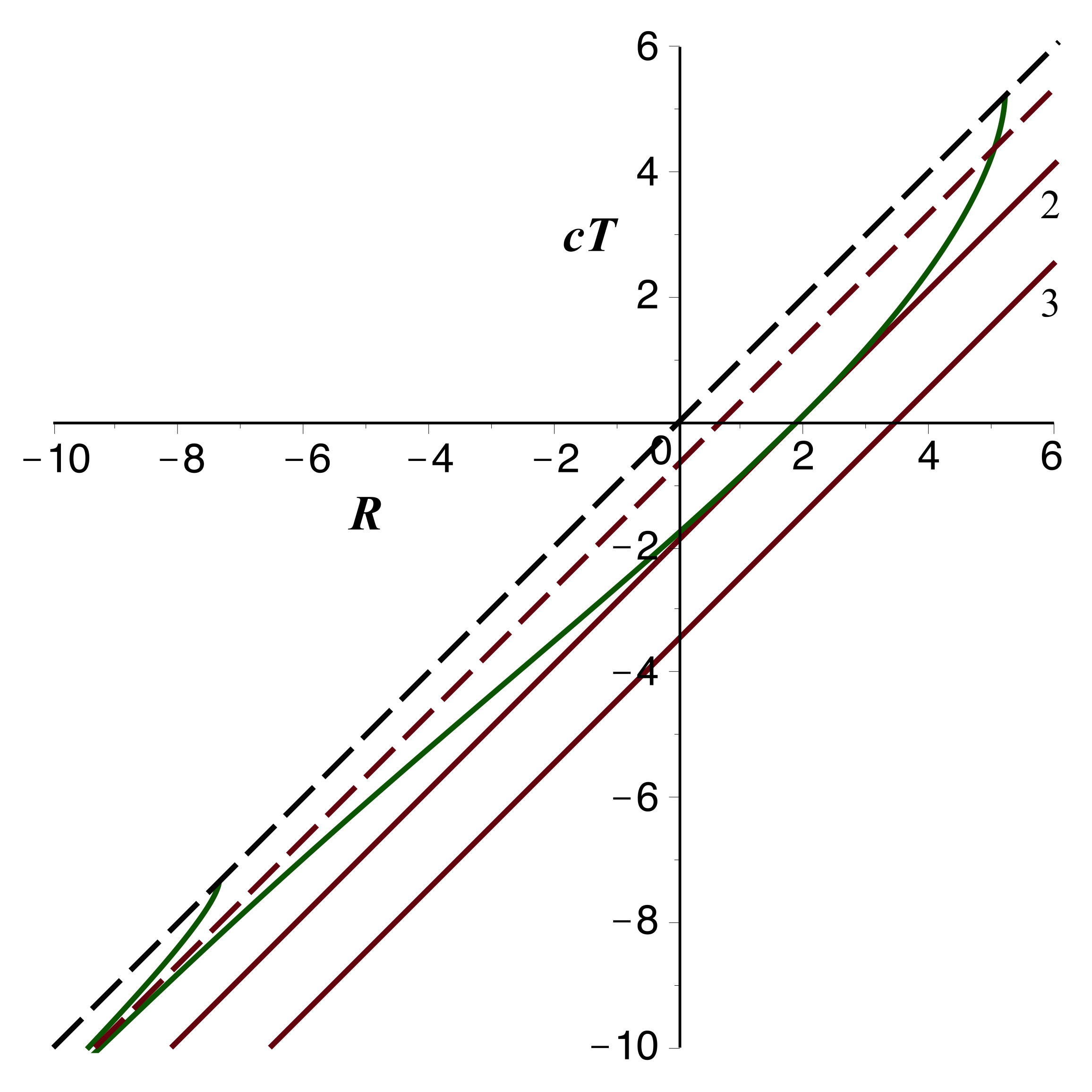
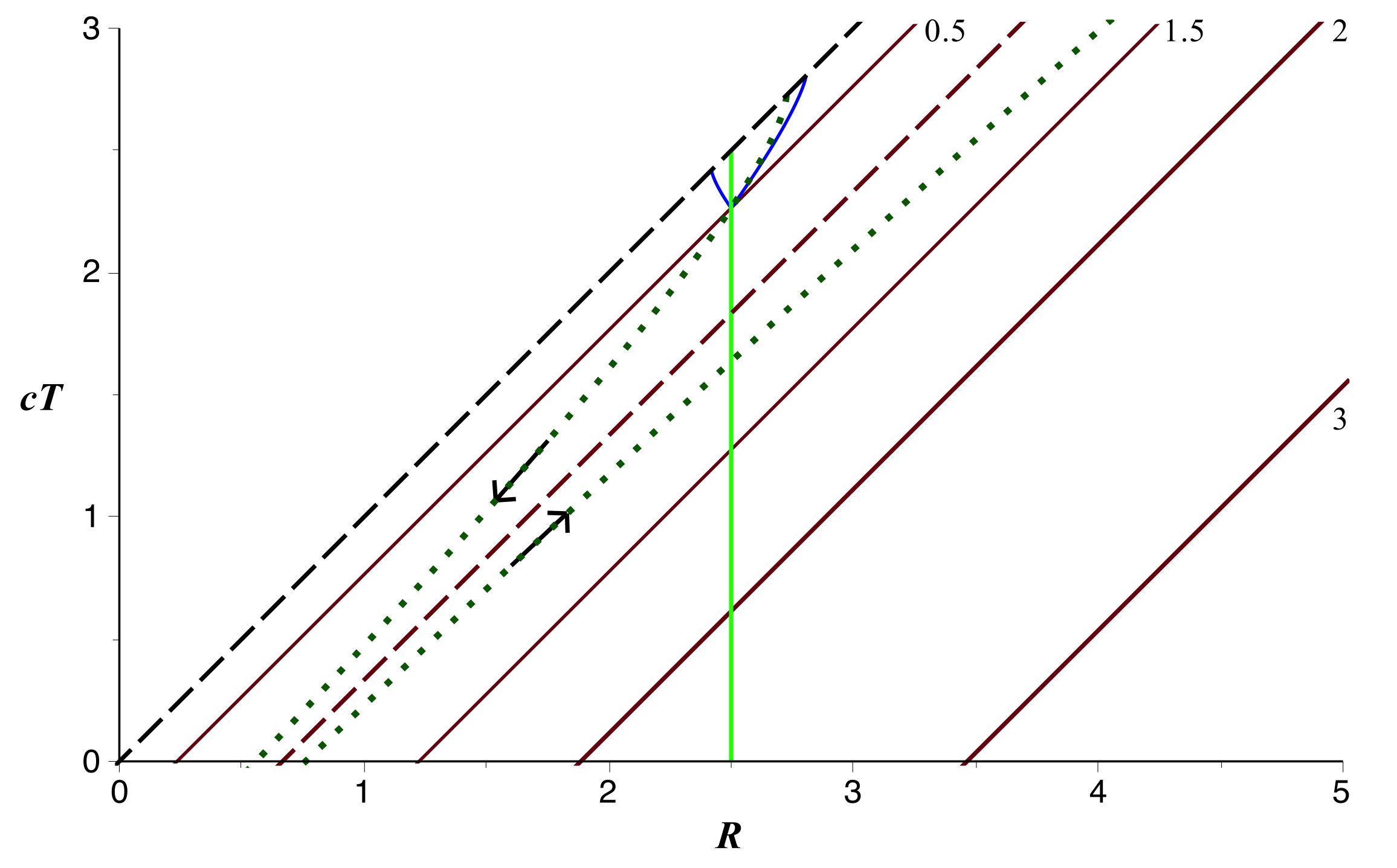
• Les courbes correspondant à  ct=Cstec \,t=Cste  peuvent être décrites par une représentation paramétrique (en fonction de rr) selon les expressions précédentes pour  R−cTR-c \,T  et  cTc \,T.  L'allure (ici pour  ct=0;3;6c t=0 \,;3 \,;6) est la même que pour  α=1α=1 ,  mais avec une limite en  r=r0r=r_0 .

GenLemaitre_Im/Lemaitre_al05_1.png

 GenLemaitre_Im/Lemaitre_al05_2.jpg

📖 exercice n° VIII.

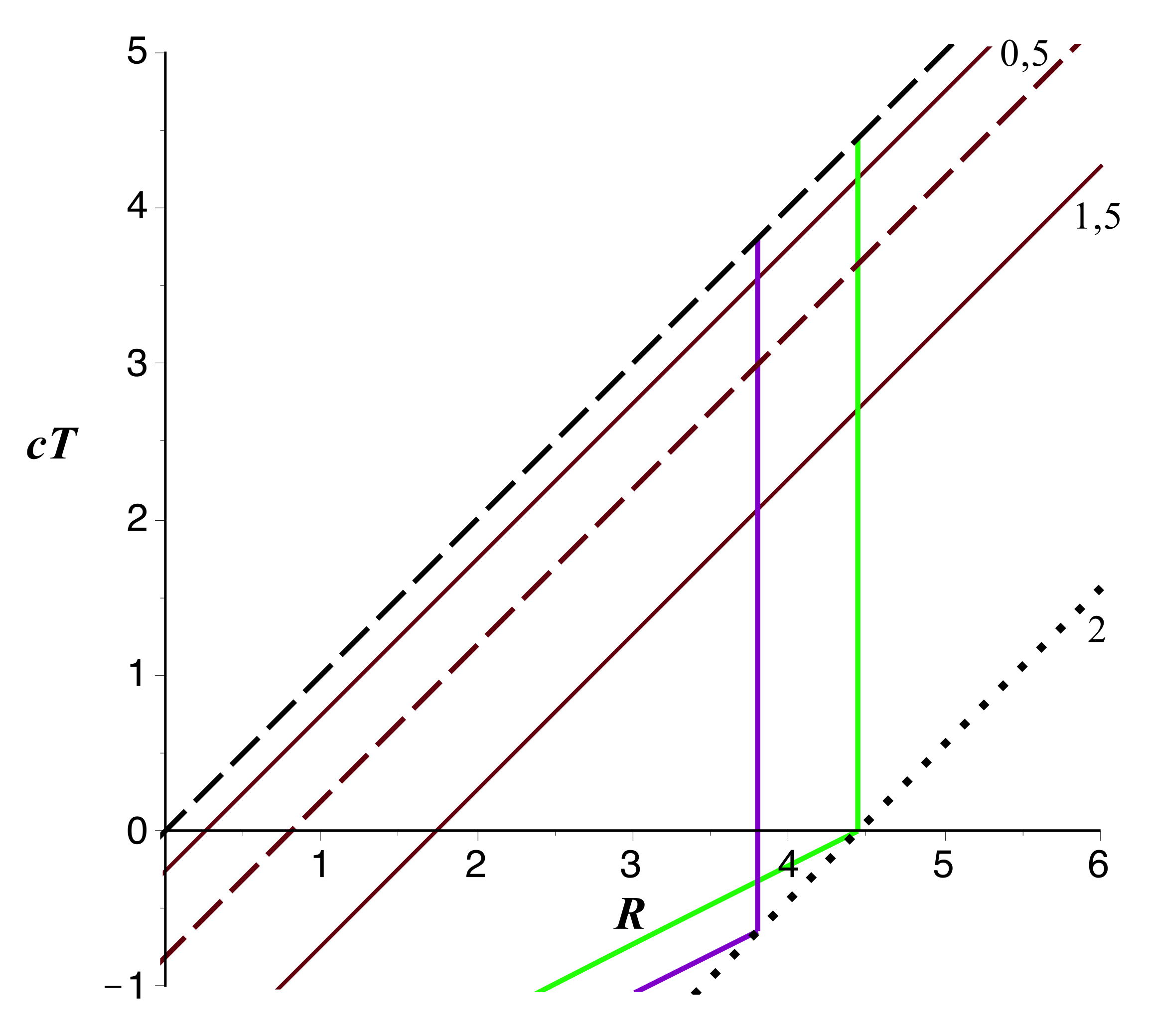
1.5. Trajectoires de particules

• On s'intéresse ici au cas  α<1α<1 ,  pour lequel existe le problème des particules qui montent jusqu'à  r=r0r=r_0  puis redescendent. On choisit comme exemple  α=0,5α=0,5 .

Toutes les trajectoires comobiles avec  R=CsteR=Cste  décrivent des mouvements identiques décalés dans le temps. En choisissant de représenter celle qui démarre en  r=r0r=r_0  à  T=0T=0  (particule de référence, ci-après en vert), on impose d'après ce qui précède :  R=2rs2arcsin(1)≈4,44rsR=2 \,r_s \:\sqrt{2} \; \arcsin(1)≈\text{4,44} \:r_s .  Les autres trajectoires analogues correspondent à des particules qui partent avant (un exemple est représenté en violet) ou après.

GenLemaitre_Im/Lemaitre_al05_3.jpg

• Mais se limiter à cela serait omettre une partie importance du tracé. La trajectoire d'une particule dont la chute est en comouvement dans la partie  R=CsteR=Cste  ne se limite pas à cette partie : l'ascension qui précède y est également représentée (avec RR non constant).

Pour une particule montante :  v=c1−Aα=d𝓁dt𝓁oc=drAdt\displaystyle v=c \;\sqrt{1-\frac{A}{α}}=\frac{d𝓁\:}{{dt}_{𝓁oc}} =\frac{dr}{A \:dt} .

Ainsi (avec  rsr_s  comme unité) :  cdt=αdrAα−A=αr2dr(r−1)r.(1−(1−α)r)\displaystyle c \,dt=\frac{\sqrt{α} \; dr}{A \;\sqrt{α-A}}=\frac{\sqrt{α} \; r^2 \: dr}{(r-1) \; \sqrt{r.\left(1-(1-α) \: r\right)}} .

Avec  α=0,5α=\text{0,5}  l'intégration donne (pour la particule de référence) :

 ct=−r.(2−r)−2arccos(r−1)−arcosh(1|r−1|)\displaystyle c \,t=-\sqrt{r.(2-r)}-2 \, \arccos(r-1)-\mathrm{arcosh}\left(\frac{1}{|r-1|} \right) .

On en déduit :

 cT=−2[arccos(r−1)+arcosh⁡(1|r−1|)]\displaystyle c \,T=-\sqrt{2} \: \left[\arccos(r-1)+ \mathrm{arcosh⁡}\left(\frac{1}{|r-1|} \right)\right]  ;
R=−2[arccos(r−1)+arcosh(1|r−1|)−2arcsin⁡(r2)+r.(2−r)]\displaystyle R=-\sqrt{2} \: \left[\arccos(r-1)+ \mathrm{arcosh}\left(\frac{1}{|r-1|} \right)-2 \, \arcsin⁡\left(\sqrt{\frac{r}{2}}\right)+\sqrt{r.(2-r)} \right] .

Ces relations donnent une représentation paramétrique de la partie montante de la trajectoire, reportée sur la figure précédente.

◊ remarque : les points anguleux des trajectoires, au niveau du raccordement à la limite  r=r0r=r_0 ,  sont liés au fait que la métrique y est singulière.

◊ remarque : on peut vérifier que la vitesse opposée redonne  dR=0dR=0  pour la partie descendante.

📖 exercices n° IX, X et XI.

2. Généralisation pour l'expansion

2.1. Expressions des coordonnées

• On s'intéresse ici au cas  α<1α<1 ,  qui contribue à décrire le référentiel d'une particule qui monte jusqu'à s'immobiliser en  r=r0r=r_0 ,  avant de retomber.

• On obtient dans ce cas :  dR+cdT=drrsr+α−1\displaystyle dR+c \,dT=\frac{dr}{\sqrt{\frac{r_s}{r}+α-1}} .

Pour  α=0,5<1α=\text{0,5}<1 ,  l'intégration donne (en choisissant la constante d'intégration nulle) :

 R+cT=2rs2arcsin(r2rs)−2r.(2rs−r)\displaystyle R+c\,T=2 \,r_s \: \sqrt{2} \; \arcsin\left(\sqrt{\frac{r}{2 \,r_s}}\right)-\sqrt{2 \,r.(2 \,r_s-r)} .

• On obtient par ailleurs en simplifiant :

 cdT−αcdt=−α−AdrA=−rsr+α−11−rsrdr\displaystyle c \,dT-\sqrt{α} \: c \,dt=-\sqrt{α-A} \: \frac{dr}{A}=-\frac{\sqrt{\frac{r_s}{r}+α-1}}{1-\frac{r_s}{r}} \: dr .

Pour  α=0,5α=\text{0,5}  l'intégration donne (avec rsr_s comme unité) :

 cT−12ct=−r.(2−r)2+12arcosh(1|r−1|)\displaystyle c \,T-\frac{1}{\sqrt{2}} \: c \,t=-\frac{\sqrt{r.(2-r)}}{\sqrt{2}}+\frac{1}{\sqrt{2}} \; \mathrm{arcosh}\left(\frac{1}{|r-1|} \right) .

2.2. Représentation graphique

Le diagramme de Lemaître représentant  r=Cster=Cste  est analogue au précédent, avec symétrie de TT en −T-T (mais les trajectoires des particules ne sont pas tout à fait symétriques).

GenLemaitre_Im/Lemaitre_al05_4.jpg

La représentation de  ct=Cstec \,t=Cste  est de même analogue.

GenLemaitre_Im/Lemaitre_al05_5.jpg

2.3. Trajectoires de particules

• Ici de même, la trajectoire d'une particule dont la montée est en comouvement avec  R=CsteR=Cste  ne se limite pas à cette partie : la chute qui suit est également représentée (avec RR non constant) sur la figure correspondante.

Pour une particule descendante :  v=−c1−Aα=drAdt\displaystyle v=-c \;\sqrt{1-\frac{A}{α}}=\frac{\: dr}{A dt} .

Ainsi (avec  rsr_s  comme unité) :  cdt=−αdrAα−A=−αr2dr(r−1)r.(1−(1−α)r)\displaystyle c \,dt=-\frac{\sqrt{α} \; dr}{A \;\sqrt{α-A}}=-\frac{\sqrt{α}\; r^2 \: dr}{(r-1) \; \sqrt{r.\left(1-(1-α) \: r\right) }} .

Avec  α=0,5α=\text{0,5}  l'intégration donne (pour la particule de référence) :

 ct=r.(2−r)+2arccos(r−1)+arcosh(1|r−1|)\displaystyle c \,t=\sqrt{r.(2-r)}+2 \, \arccos(r-1)+\mathrm{arcosh}\left(\frac{1}{|r-1|} \right) .

On en déduit (l'expression de RR est la même que dans le cas en contraction) :

 cT=2[arccos(r−1)+arcosh(1|r−1|)]\displaystyle c \:T=\sqrt{2} \: \left[\arccos(r-1)+\mathrm{arcosh}\left(\frac{1}{|r-1|} \right)\right]  ;
R=−2[arccos(r−1)+arcosh(1|r−1|)−2arcsin⁡(r2)+r.(2−r)]\displaystyle R=-\sqrt{2} \: \left[\arccos(r-1)+ \mathrm{arcosh}\left(\frac{1}{|r-1|} \right)-2 \, \arcsin⁡\left(\sqrt{\frac{r}{2}}\right)+\sqrt{r.(2-r)} \right] .

Ces relations donnent une représentation paramétrique de la partie descendante de la trajectoire.

3. Combinaison de l'expansion suivie de la contraction

• Pour construire un référentiel comobile avec une particule en mouvement radial libre, ascendant jusqu'en  r=r0r=r_0  puis redescendant, il pourrait sembler logique que le plus simple soit de raccorder les deux cas précédents.

Cela est toutefois impossible car la transformation de Lorentz locale ne donne pas des différentielles exactes ; la relation de Lemaître doit multiplier par un facteur intégrant approprié, or les variables RR et TT déduites des intégrations respectives pour la montée et la descente ont des conventions de signes incompatibles.

Si le référentiel en contraction a une vitesse d'entraînement ne dépendant que de rr, il est comobile avec toutes les particules qui descendent de la même façon, indépendamment de l'instant auquel elles passent en une valeur particulière de rr ; il ne peut donc pas en même temps être comobile avec les particules qui passent en montant en cette même valeur de rr.

◊ remarque : pour obtenir des coordonnées compatibles, il faut que l'expansion et la contraction dépendent du temps, conduisant à un repérage comme celui de Novikov (ou de Kruskal-Szekeres), étudié dans une partie ultérieure.

• La comparaison des figures précédentes montre que, si on raccorde les deux graphiques au point où la particule de référence (en vert) passe par la limite  r=r0r=r_0  (en pointillés), les parties gauche des graphiques se chevauchent.

Ceci ne signifie pas qu'il existe des points avec les mêmes valeurs de RR et TT ,  représentés deux fois, mais indique au contraire que ces coordonnées n'ont pas la même signification pendant l'ascension et pendant la descente (il est clair que, pour ces points,  rr  et  ctc \,t  ne se correspondent pas).

Cela n'empêche pas d'utiliser l'ensemble des deux représentations pour décrire la particule de référence, mais qu'en est-il des autres particules en comouvement (R=CsteR=Cste) ? Une telle particule partie plus tôt (aussi bien pour tt que pour TT) a une trajectoire plus à droite pour l'ascension (en violet), mais la suite de son mouvement donne une trajectoire plus à gauche pour la descente (en violet) ; les deux ne se raccordent pas.

• On peut tenter d'utiliser une représentation changeant le sens de l'axe de RR pour l'une des deux parties (voire de changer le signe de RR dans les relations en gardant le même sens de l'axe). Cela rendrait toutes les trajectoires en comouvement raccordables, mais serait illusoire.

L'existence des parties de trajectoires qui ne sont pas en comouvement, montre que le diagramme obtenu par raccordement serait de toute façon incomplet.

• En particulier, dans l'intervalle entre les passages en  r=r0r=r_0  des trajectoires en vert et en violet, tout photon échangé entre les deux particules rejoindrait, dans chacune des figures, une partie en comouvement et une qui ne l'est pas, cela sans passer par  r=r0r=r_0 .

Dans la réunion des deux graphiques, ces photons seraient donc représentés deux fois, d'une façon qui ne pourrait pas se raccorder au niveau de  r=r0r=r_0  pour donner une représentation unique reliant les deux graphiques, donc qui ne pourrait pas permettre de se passer des portions de trajectoires qui ne sont pas en comouvement.

• On ne peut donc pas obtenir ainsi de représentation du référentiel comobile pour l'ensemble du mouvement d'une particule montant puis redescendant. Les deux cas, contraction et expansion, donnent chacun une représentation “complète” (pour  r≤r0r≤r_0).

À part l'information théorique apportée par leur existence (montrant la généralité des transformations de type Lemaître), ces représentations apportent donc plutôt moins que les formes classiques (limitation sur les valeurs de rr et calculs plus compliqués).

La suite des raisonnements sera donc faite avec la transformation de Lemaître “classique”.

4. Trajectoire de particules montant puis descendant

• Avec les notations “classiques” de Schwarzschild, on a constaté (chapitre sur l'interprétation du champ extérieur) que dans la région  r<rsr<r_s  il peut se produire des croisements de particules montant et descendant. On peut revenir sur le cas des particules qui montent jusqu'à  r=r0r=r_0  puis redescendent.

Pour simplifier (l'expression générale est plus compliquée), on se base ici sur le cas avec  α=0,5<1α=\text{0,5}<1  (pour lequel  r0=2rs r_0=2 \,r_s ).

• Lors de la montée, on utiliser l'expression obtenue pour  ctc \,t  en notations réduites, avec l'origine de  tt  pour  r=r0r=r_0 ,  réexprimée en fonction de κκ :

 ct=−κ2.(2−κ2)−2arccos(κ2−1)−arcosh(1|κ2−1|)\displaystyle c \,t=-\sqrt{κ^2.(2-κ^2 )}-2 \; \arccos(κ^2-1)-\mathrm{arcosh}\left(\frac{1}{\left|κ^2-1\right|} \right) .

On peut utiliser les relations entre (R,cT)(R, c \,T) et (r,ct)(r, c \,t), en y modifiant la constante d'intégration pour décrire la trajectoire particulière telle que  T=0T=0  lors du passage en  r=r0r=r_0 :

 R−23κ3=cT=ct+2κ−ln(|κ+1κ−1|)−2κ0+ln(|κ0+1κ0−1|)\displaystyle R-\frac{2}{3} κ^3=c \,T=c \,t+2 \,κ-\ln\left(\left|\frac{κ+1}{κ-1}\right|\right)-2 \,κ_0+\ln\left(\left|\frac{κ_0+1}{κ_0-1}\right|\right) .

GenLemaitre_Im/part_retombant.jpg

Pour la descente, il suffit de changer le signe de  ctc \,t.  On obtient ainsi une représentation paramétrique de l'ensemble de la trajectoire

• On vérifie donc que les mêmes particules peuvent sortir de la région  r<rsr<r_s ,  puis y retomber (il s'agit de la même région). La sortie présente une divergence à  T→−∞T→-∞  mais, avec un repérage de Lemaître en expansion, ce serait au contraire le cas pour la retombée. Il existe donc également des particules pouvant sortir.

Dans la mesure où cette description est invariante par changement de l'origine du temps, on retrouve qu'il peut exister deux telles particules, P′P' sortante et PP entrante, se croisant dans la région  r<rsr<r_s .  Elles ont alors forcément un second croisement pour  r>rsr>r_s .

◊ remarque : ici encore, contrairement à ce qui est souvent affirmé, on constate que, malgré l'une des deux divergences non éliminée au niveau de l'horizon, on peut ainsi représenter entièrement les trajectoires.

• L'allure générale de ces trajectoires, très allongée selon la diagonale  r=Cster=Cste ,  amène à penser qu'une représentation en fonction de  rr,  à une échelle plus petite pour TT, donnerait une meilleure visualisation.

On outre, on peut aussi bien traiter le cas général en partant des expressions établies en coordonnées “classiques” et en utilisant les relations de changement de repérage.

La chute verticale depuis r0r_0 avec une vitesse initiale nulle donne (avec rsr_s comme unité et en omettant la composante imaginaire) :

 v=−c1−AA0=drAdt\displaystyle v=-c \;\sqrt{1-\frac{A}{A_0}}=\frac{\:dr}{A \:dt}   ;   cdt=−r0−1r2dr(r−1)r.(r0−r)\displaystyle c \:dt=-\sqrt{r_0-1} \: \frac{r^2 \: dr}{(r-1) \:\sqrt{r.(r_0-r)}}  ;
ct=r0−1r.(r0−r) c \,t=\sqrt{r_0-1} \; \sqrt{r.(r_0-r)}

 +(1+r02)r0−1arccos(2rr0−1)+arcosh(r0r−2r+r0r0.|r−1|)\displaystyle +\left(1+\frac{r_0}{2}\right) \:\sqrt{r_0-1} \; \arccos\left(\frac{2 r}{r_0} -1\right)+\mathrm{arcosh}\left(\frac{r_0 \:r-2 \,r+r_0}{r_0.|r-1|}\right) .

Avec  κ=rκ=\sqrt{r}  ;  ct=cT−2r+ln(|r+1r−1|)\displaystyle c \,t=c \,T-2 \,\sqrt{r}+\ln\left(\left|\frac{\sqrt{r}+1}{\sqrt{r}-1}\right|\right)   et   R−cT=23r3/2R-c\,T=\frac{2}{3} \: r^{3/2} ,  on obtient une représentation paramétrique des courbes en notations de Lemaître. Les droites  R=CsteR=Cste ,  qui étaient verticales, deviennent inclinées à vers la gauche (ici non représentées).

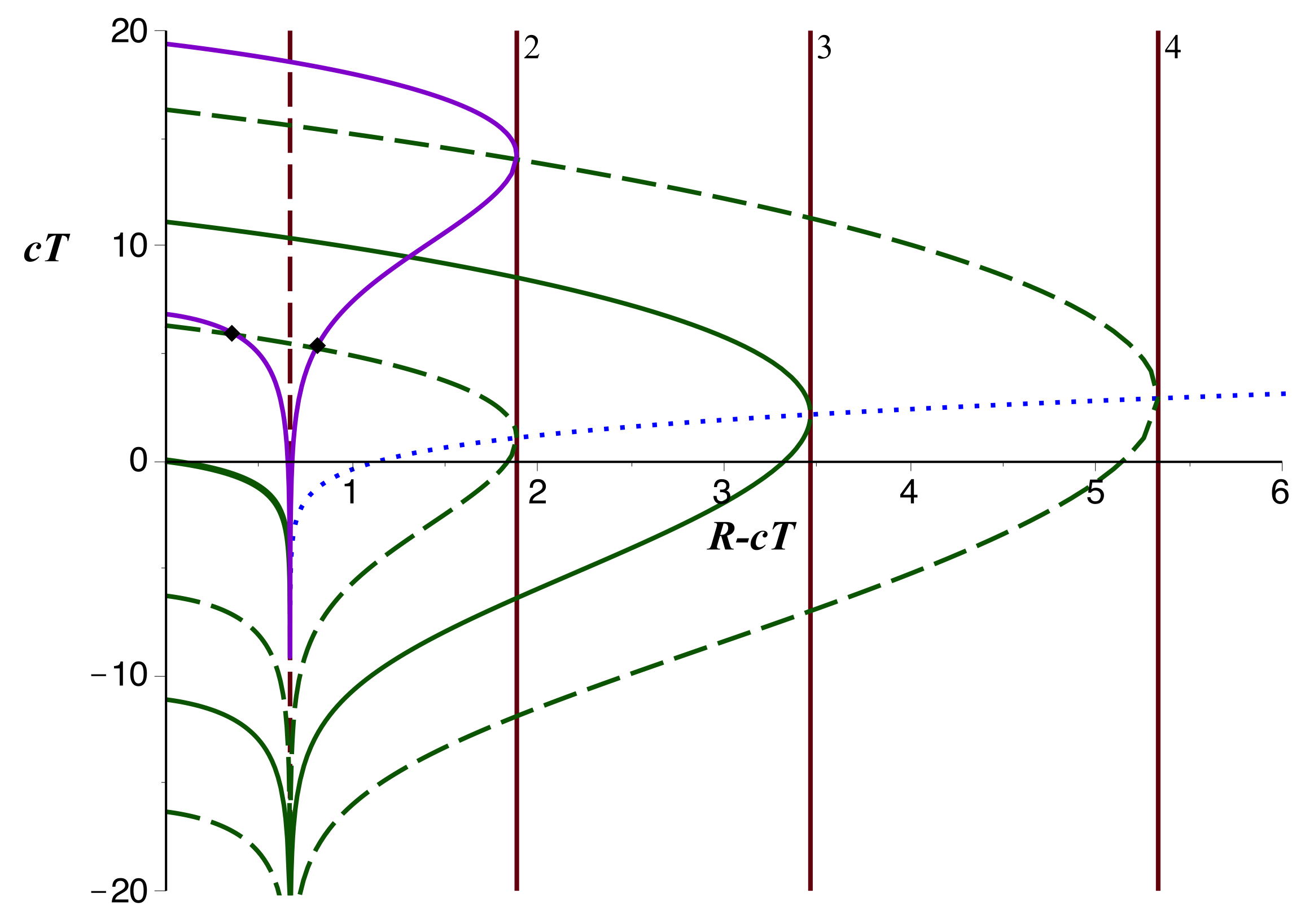
GenLemaitre_Im/part_retombant_2.jpg

• En décalant les valeurs de tt, on peut tracer (en violet) une trajectoire montant jusqu'à  r0=2rsr_0=2 \,r_s  puis redescendant, mais partant de  r=0r=0  après  t=0t=0 .  On y retrouve une double intersection avec la trajectoire analogue (en tirets verts) commençant plus tôt (et atteignant son sommet à  t=0t=0).

On retrouve aussi le même problème qu'avec les notations “classiques” pour ce qui concerne l'ordre des deux croisements vus par l'une ou l'autre des particules (le repérage de Lemaître ne résout pas le problème).

Ici encore, ces difficultés peuvent sembler liées à la forme particulière des trajectoires au niveau de la divergence ; une étude (ultérieure) plus approfondie montre qu'il n'en est rien.

5. Croisement de particules et transformations de Lorentz

5.1. Étude des transformations de Lorentz

• On considère ici un croisement d'une particule entrante PP et d'une particule sortante P′P'. Pour simplifier les calculs, on raisonne avec des particules en chute libre radiale avec une vitesse limite nulle à l'infini.

◊remarque : aucun croisement n'apparaissait sur les graphiques précédents, où seules certaines portions utiles au raisonnement étaient représentées.

• Soit ℛℛ le référentiel en comouvement avec PP, ayant une vitesse d'entraînement (vers le bas)  βe=−rsr\displaystyle β_e=-\sqrt{\frac{r_s}{r}}  par rapport à ℛ0ℛ_0 statique.

Soit de même ℛ′ℛ' le référentiel en comouvement avec P′P', ayant une vitesse d'entraînement (vers le haut)  βe′=rsr\displaystyle β'_e=\sqrt{\frac{r_s}{r}}  par rapport à ℛ0ℛ_0 statique.

• Soient  (R,cT)(R,c \,T)  les coordonnées d'un point dans ℛℛ et  (R′,cT′)(R',c \,T')  les coordonnées de ce point dans ℛ′ℛ' , la transformation permettant de passer de ℛ′ℛ' à ℛℛ (en éliminant  drdr  et  cdtc \,dt  entre les relations de Lemaître)  correspond à :

 dR=1A[(1+rsr)dR′+2cdT′]\displaystyle dR=\frac{1}{A} \:\left[\left(1+\frac{r_s}{r}\right) \: dR'+2 \,c \,dT'\right]  ;  cdT=1A[2rsrdR′+(1+rsr)cdT′]\displaystyle c \,dT=\frac{1}{A} \: \left[\frac{2 \,r_s}{r} \: dR'+\left(1+\frac{r_s}{r}\right) \: c \,dT'\right] .

Ces relations s'appliquent en particulier à P′P', pour lequel  dR′=0 dR'=0  et dont on peut noter  (R″,cT″)(R'',c \,T'')  les coordonnées dans ℛℛ :

 dR″=21AcdT′\displaystyle dR''=2 \frac{1}{A} \: c \,dT'  ;  cdT″=1A(1+rsr)cdT′\displaystyle c \,dT''=\frac{1}{A} \: \left(1+\frac{r_s}{r}\right) \: c \,dT' .

D'après la métrique, P′P' parcourt ainsi la distance  d𝓁=rsrdR″\displaystyle d𝓁=\sqrt{\frac{r_s}{r}} \:dR''  pendant une durée  dt𝓁oc=dT″{dt}_{𝓁oc}=dT'',  donc la vitesse d'entraînement de ℛ′ℛ' par  rapport à ℛℛ correspond à :  βe″=d𝓁cdt𝓁oc=2rrs+rsr\displaystyle β''_e=\frac{d𝓁}{c \,{dt}_{𝓁oc}}=\frac{2}{\sqrt{\frac{r}{r_s}}+\sqrt{\frac{r_s}{r}}} .

On vérifie que cette vitesse peut être obtenue par combinaison des transformations de Lorentz :  βe″=βe′−βe1−βe′βe\displaystyle β''_e=\frac{β'_e-β_e}{1-β'_e \: β_e} .

• Il est remarquable d'obtenir une vitesse d'entraînement qui n'est jamais supraluminique (et tend même vers zéro pour  r→0r→0),  alors qu'elle est la combinaison de deux transformations qui le sont toutes les deux pour  r<rsr<r_s .

Ainsi, si le référentiel en contraction est justifié physiquement, celui en expansion l'est forcément aussi.

5.2. Représentation graphique

• Comme pour tout point dans  ℛℛ ,  on obtient pour P′P' :

 R″−cT″=2r3rrs=2r3κ″3\displaystyle R''-c\,T''=\frac{2 \,r}{3} \sqrt{\frac{r}{r_s}}=\frac{2 \,r}{3} \,{κ''}^3 .

D'après ce qui précède :  cdT″=12(1+rsr)cdR″\displaystyle c \,dT''=\frac{1}{2} \left(1+\frac{r_s}{r}\right) \: c \,dR''.  Ainsi en combinant :

 cdT″=2rsκ″2+1κ″2−1κ″2dκ″\displaystyle c \,dT''=2 \,r_s \, \frac{{κ''}^2+1}{{κ''}^2-1}\, {κ''}^2 \: dκ''.

En intégrant, on obtient (en omettant une composante imaginaire pour  cT″c \,T'') :

 cT″=2rs3κ″3+4rsκ″+2rsln(|κ″−1κ″+1|)+Cste\displaystyle c \,T''=\frac{2 \,r_s}{3} \,{κ''}^3+4 \,r_s \: κ''+2 \,r_s \; \ln\left(\left|\frac{κ''-1}{κ''+1}\right|\right)+Cste  ;  R″=cT″+2rs3κ″3\displaystyle R''=c \,T''+\frac{2 \,r_s}{3} \,{κ''}^3.

Cela permet une représentation paramétrique de la trajectoire. On fixe la constante d'intégration en imposant le croisement avec PP :  R″=RR''=R  (constant) pour la valeur de  cT″=cTc \,T''=c \,T  qui donne la coordonnée  r=r″=r′r=r''=r'  de la position d'intersection choisie.

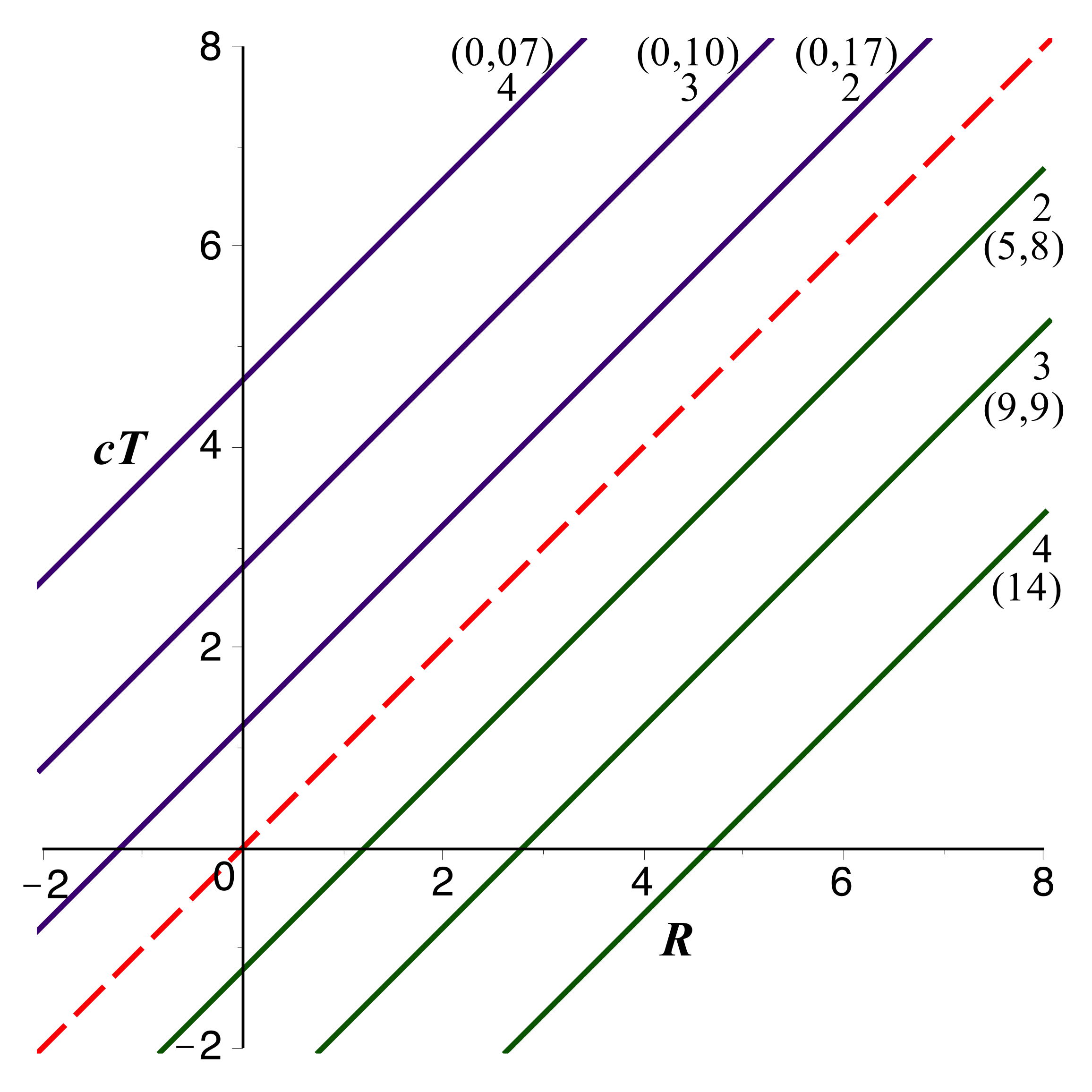
On peut ainsi ajouter sur le graphique, en pointillés, les trajectoires de trois particules P′P' sortantes croisant la particule PP en chute  (R=CsteR=Cste,  en vert) respectivement pour  r=2;1,5;0,5 r=2 \,; \text{1,5} \,; \text{0,5}  (en coordonnées réduites).

GenLemaitre_Im/part_sortantes_1.jpg

• Pour les particules sortantes P′P' croisant PP en  r>rsr>r_s ,  la particule PP entrante voit P′P' s'éloigner de l'astre, moins vite que les photons sortants, en semblant provenir de l'horizon (en principe PP ne voit pas la partie  r<rsr<r_s ).

Par contre, pour les particules sortantes P′P' croisant PP en  r<rsr<r_s ,  le diagramme semble montrer que la particule PP entrante voit P′P' “tomber” sur l'astre, plus vite que les photons dans le sens sortants (qui, selon l'interprétation usuelle, ne peuvent pas sortir), en semblant provenir de l'horizon.

La différence essentielle est que, par construction, on sait ici que P′P' sort.

◊ remarque : inversement de même, pour  r<rsr<r_s ,  il semble que la particule P′P' sortante voit la particule PP entrante incapable d'entrer.

• Une telle interprétation serait toutefois incohérente puisque  A<0A<0  implique que  dR″dR''  et  cdT″c \,dT''  sont de signes contraires à  cdT′c \,dT' : la particule P′P' se comporte comme si elle remontait le temps (quand T′T' augmente, P′P' se déplace vers le bas, donc vers l'extérieur).

◊ remarque : si P′P' est un proton qui sort, PP voit un antiproton qui entre.

GenLemaitre_Im/part_sortantes_2.jpg

Pour mieux comprendre, on peut tracer la trajectoire plus complète d'une particule P′P', sans se limiter au voisinage d'un croisement avec PP.

On constate que les deux particules se croisent deux fois : pour PP il y a un croisement extérieur puis un croisement intérieur ; pour P′P' l'ordre des croisements est inversé.

• La relativité restreinte nous habitue à penser que la simultanéité dépend du référentiel, mais qu'un changement de référentiel conduise ici à retourner l'écoulement du temps sur toute une trajectoire, cela n'a rien d'évident.

• Qui plus est, dans cette région  r<rsr<r_s ,  le photon émis dans le sens “sortant” (RR croissant, à droite de PP), qui semble ne pas pouvoir sortir, peut en réalité peut être le faire. En effet, s'il est difficile de raisonner de façon analogue pour des particules de masse nulle, puisqu'on ne peut pas se placer dans leur référentiel propre, on sait par contre que ce photon “sort” plus vite que toute particule massive... qui (d'après ce qui précède) peut sortir.

◊ remarque : comme déjà constaté avec les coordonnées “classiques” de Schwarzschild, ces propriétés étranges sont liées à l'apparente invariance par translation dans le temps ; en fait il ne peut y avoir ni trou noir ni trou blanc permanent ; comme décrit par les repérages de Kruskal-Szekeres et de Novikov, il existe forcément un instant privilégié où un trou blanc termine son expansion et commence un effondrement en trou noir ; les particules ne peuvent que sortir dans le passé et ne peuvent qu'entrer dans le futur.

📖 exercice n° XII.

6. Transformation de Lemaître et coordonnées isotropes

• La transformation de Lemaître est élaborée en présupposant que l'expression de la vitesse de chute verticale, établie pour  r>rs r>r_s  en coordonnées “classiques”, s'extrapole logiquement au delà.

Bien qu'une telle démarche ne soit pas a priori contradictoire, cela contient un biais de raisonnement : on peut tout aussi bien présupposer valide l'extrapolation prévue par le calcul en coordonnées isotropes. C'est ce qui est étudié ici.

Il est pour cela possible de raisonner simplement par l'intermédiaire de r_(r)\underline{r}(r), mais aussi de calculer directement avec r_\underline{r}.

• Avec les notations isotropes, la métrique (limitée à la partie radiale) s'écrit :

 ds2=Ac2dt2−C_dr_2=A.[c2dt2−C_Adr_2]\displaystyle {ds}^2=A \:c^2 \,{dt}^2-\underline{C} \:{d\underline{r}}^2=A .\left[c^2 \,{dt}^2-\frac{\underline{C}}{A} \,{d\underline{r}}^2 \right]  ;
A=(r_−r_sr_+r_s)2\displaystyle A=\left(\frac{\underline{r}-\underline{r}_s}{\underline{r}+\underline{r}_s}\right)^2  ;  C_=(r_+r_sr_)4\displaystyle \underline{C}=\left(\frac{\underline{r}+\underline{r}_s}{\underline{r}}\right)^4   ;  C_A=(r_+r_s)3r_2.|r_−r_s|\displaystyle \sqrt{\frac{\underline{C}}{A}}=\frac{(\underline{r}+\underline{r}_s )^3}{\underline{r}^2.\left|\underline{r}-\underline{r}_s \right|} .

• Pour une particule en chute libre verticale à partir de l'infini, avec une vitesse “initiale” (limite) nulle :  v=−c1−A=−c2r_r_sr_+r_s\displaystyle v=-c \;\sqrt{1-A}=-c \: \frac{2 \:\sqrt{\underline{r} \;\underline{r}_s}}{\underline{r}+\underline{r}_s} .

◊ remarque : on vérifie que  |v||v|  passe par un maximum pour  r_=r_s\underline{r}=\underline{r}_s .

• En construisant une transformation de Lemaître généralisée adaptée à cette vitesse, on est conduit à proposer :

 dR=cdt+κC_Adr_\displaystyle dR=c \,dt+κ \:\sqrt{\frac{\underline{C}}{A}} \; d\underline{r}  ;  cdT=cdt+fC_Adr_\displaystyle c \,dT=c \,dt+f \:\sqrt{\frac{\underline{C}}{A}} \; d\underline{r}  ;  f=1κ=2r_r_sr_+r_s\displaystyle f=\frac{1}{κ}=\frac{2\:\sqrt{\underline{r} \;\underline{r}_s}}{\underline{r}+\underline{r}_s} .

Ceci donne une métrique sans singularité :  ds2=c2dT2−f2dR2{ds}^2=c^2 \,{dT}^2-f^2 \:{dR}^2 .

• On obtient alors :  d(R−cT)=(κ−f)C_Adr_=(r_+r_s)2|r_−r_s|2r_2r_r_sdr_\displaystyle d(R-c\,T )=(κ - f)\: \sqrt{\frac{\underline{C}}{A}} \;d\underline{r}=\frac{(\underline{r}+\underline{r}_s )^2 \; \left|\underline{r}-\underline{r}_s \right|}{2 \,\underline{r}^2 \;\sqrt{\underline{r} \; \underline{r}_s}} \: d\underline{r}  ;  l'intégration donne :  R−cT=8sgn(r_−r_s)3((r_+r_s2r_r_s)3−1)\displaystyle R-c\,T=\frac{8 \:\mathrm{sgn}(\underline{r}-\underline{r}_s )}{3} \: \left(\left(\frac{\underline{r}+\underline{r}_s}{2 \;\sqrt{\underline{r} \; \underline{r}_s}}\right)^3-1\right) .

◊ remarque : compte tenu de l'interprétation isotrope, on choisit la constante d'intégration telle que  R−cT=0R-c \,T=0  pour  r_=r_s\underline{r}=\underline{r}_s .

• Avec une échelle horizontale logarithmique (mieux adaptée aux coordonnées isotropes), on obtient la représentation suivante (avec  r_s\underline{r}_s  comme unité).

GenLemaitre_Im/RmcT_iso.jpg

◊ remarque : c'est qualitativement ce que donne la coordonnée rr “classique” en raccordant les zones  r≥rsr≥r_s  en contraction puis en expansion (de l'autre côté de l'horizon), après élimination des zones  r<rsr<r_s  ;  le raccordement est sans problème car ici AA et C_\underline{C} ne changent pas de signe.

• Les lignes caractérisant  r_(R,cT)=Cste\underline{r}(R,c \,T)=Cste  sont ici encore des droites, mais leur écartement (en échelle logarithmique) tend vers l'infini quand  r_→0\underline{r}→0 .  Ceci est associé au fait que dans ces conditions la variable “classique”  rr  recroît vers l'infini.

La représentation graphique peut d'ailleurs être faite “en fonction de rr ” (ci-après pour  r=0;1;2;3;4r=0 \,;1 \,;2 \,;3 \,;4  de part et d'autre, avec rsr_s comme unité).

GenLemaitre_Im/Lemaitre_iso_r.jpg

• Lors de la chute libre radiale d'une particule, la métrique étant “synchrone”, les droites  R=CsteR=Cste  (lignes de temps) sont des géodésiques. Le mouvement se poursuit donc vers  r_<r_s\underline{r}<\underline{r}_s  correspondant à  r>rsr>r_s  ;  ceci confirme la possibilité de raccorder les zones en contraction puis en expansion dans ce diagramme de Lemaître (avec les possibilités d'oscillations qui s'en déduisent).

• On obtient par ailleurs :  d(cT−ct)=fC_Adr_=2r_r_s(r_+r_s)2r_2.|r_−r_s|dr_\displaystyle d(c \,T-c \,t)= f \;\sqrt{\frac{\underline{C}}{A}} \; d\underline{r} =\frac{2 \;\sqrt{\underline{r} \; \underline{r}_s} \;(\underline{r}+\underline{r}_s )^2}{\underline{r}^2.\left|\underline{r}-\underline{r}_s \right|} \:d\underline{r}  ;  ceci donne :  cT−ct=8sgn(r_−r_s)[r_+r_s2r_r_s+ln(|r_−r_sr_+r_s|)]\displaystyle c \,T-c \,t=8 \: \mathrm{sgn}(\underline{r}-\underline{r}_s ) \: \left[\frac{\underline{r}+\underline{r}_s}{2 \;\sqrt{\underline{r} \;\underline{r}_s}}+\ln\left(\left|\frac{\sqrt{\underline{r}}-\sqrt{\underline{r}_s}}{\sqrt{\underline{r}}+\sqrt{\underline{r}_s}}\right|\right) \right] .

On obtient la représentation suivante (pour  ct=0;±3;±6c \,t=0 \,;±3 \,;±6  avec rsr_s comme unité).

GenLemaitre_Im/Lemaitre_iso_ct.jpg

◊ remarque : ici la convention de signe pour  tt  dans la région  r_<r_s\underline{r}<\underline{r}_s  est conforme à  A>0A>0 ,  dans la mesure où  tt  reste croissant.

• L'interprétation déduite des coordonnées “isotropes” semble éviter certaines difficultés associées à l'interprétation “classique”, mais en fait apparaitre d'autres (et réciproquement).

Par contre, la méthode des repérages de Lemaître n'apporte aucun argument en ce sens. Si on calcule la vitesse de chute libre en présupposant l'une des deux interprétations, on en déduit un repérage de type Lemaître montrant que ceci est plausible, mais cela ne permet pas de discriminer.

Ces considérations physiques suggèrent ici encore que la simplification mathématique de la métrique n'est qu'un artifice de calcul fortuit. Celle-ci ne serait alors valable que pour  r>rsr>r_s ,  la limite théorique  r=rsr=r_s  étant impossible à atteindre dans les conditions physiques réelles (selon L. S. Abrams).

📖 exercice n° XIII.