MÉTRIQUE DE LEMAÎTRE - GÉNÉRALISATIONS

MÉTRIQUE DE LEMAÎTRE - GÉNÉRALISATIONS - corrigé des exercices

I. Transformation de Lemaître généralisée et transformation de Lorentz

• Pour

\displaystyle v_e=-c \;\sqrt{1-\frac{A}{α}}

avec

\displaystyle α=\frac{A_0}{1-β_0^{\:2}}

la transformation de Lorentz (locale) correspond à :

\displaystyle d\underline{R}=\frac{d𝓁-β_e \:c \,{dt}_{𝓁oc}}{\sqrt{1-β_e^{\:2}}}

;

\displaystyle c \,dT=\frac{c \,{dt}_{𝓁oc}-β_e \: d𝓁}{\sqrt{1-β_e^{\:2}}}

;

c \,{dt}_{𝓁oc}=\sqrt{A} \: c \,dt

;

d𝓁=\sqrt{C} \: dr

(algébrique).

• Ceci donne :

\displaystyle d\underline{R}=\sqrt{α-A} \; c \,dt+\sqrt{α} \: \frac{dr}{A}

;

\displaystyle c \,dT=\sqrt{α} \: c \,dt+\sqrt{α-A} \; \frac{dr}{A}

; transformation correspondant effectivement à la vitesse étudiée.
◊ remarque : pour

r<r_s

;

A

C<0

;

\left|v_e \right|>c

mais

\displaystyle \sqrt{\frac{A}{1-β_e^{\:2}}}

reste défini.
• La métrique limitée au déplacement radial serait ainsi encore plus simple que celle de Lemaître :

{ds}^2=c^2 \,{dT}^2-{d\underline{R}}^2

. En particulier les trajectoires des photons seraient des droites (

d\underline{R}=±c \,dT

).
• Le problème est ensuite de déterminer

r(\underline{R}, c \,T )

pour exprimer la partie angulaire de la métrique, mais aussi pour savoir interpréter à quoi correspond

r=r_s

. Puisqu'on part de fonctions de

r

, il faut déterminer

\underline{R}(r, c \,t)

c \,T (r, c\, t)

(ou des combinaisons) puis inverser. Or on constate que

d\underline{R}(r, c \,t)

n'est pas une différentielle totale : pour obtenir une primitive il faut la multiplier par un facteur intégrant

F(r, c \,t)

tel que

\displaystyle \frac{∂}{∂r} \left(F.\sqrt{α-A}\right)=\frac{∂}{c \,∂t} \left(\frac{F.\sqrt{α}}{A}\right)

.
• Si on cherche une solution simple indépendante du temps, la considition

\displaystyle \frac{∂}{∂r} \left(F.\sqrt{α-A}\right)=0

donne :

\displaystyle F=\frac{Cte}{\sqrt{α-A}}

. Le choix de la constante peut alors être fait de façon à simplifier l'expression de

{ds}^2

.
• Avec

\displaystyle F=\frac{\sqrt{α}}{\sqrt{α-A}}

on obtient ainsi :

\displaystyle dR=\sqrt{α} \: c \,dt+\frac{α}{\sqrt{α-A}} \, \frac{dr}{A}

.
• En posant :

\displaystyle f=\frac{1}{κ}=\frac{\sqrt{α-A}}{\sqrt{α}}

, on peut ainsi écrire :

\displaystyle \frac{dR}{\sqrt{α}}=c \,dt+κ \: \frac{dr}{A}

;

\displaystyle \frac{c \,dT}{\sqrt{α}}=c \,dt+f \: \frac{dr}{A}

.
• Finalement :

\displaystyle {ds}^2=\frac{A}{1-f^2} \left[\frac{c^2 \, {dT}^2}{α}-f^2 \: \frac{{dR}^2}{α}\right]

avec

\displaystyle 1-f^2=\frac{A}{α}

; la singularité est donc éliminée et on retrouve :

{ds}^2=c^2 \,{dT}^2-f^2 \: {dR}^2

II. Transformation de Lemaître généralisée et transformation classique

• Pour la transformation de Lemaître généralisée correspondant à :

\displaystyle β_e=\frac{\;dr}{A \:c \,dt}=- \sqrt{1-\frac{A}{α}}

, on peut écrire (avec

r_s

comme unité) :

\displaystyle c \,dt=-\sqrt{\frac{α \:r}{(α-1) \: r+1 }} \: \frac{r}{r-1} \: dr

.
• Au voisinage de

r=r_s

on constate que le radical varie de façon régulière :

\displaystyle \sqrt{\frac{α \:r}{(α-1) \: r+1}}≈\sqrt{\frac{α}{α}}=1

. Calculée au premier ordre, l'intégration donne donc toujours le même comportement qu'avec

α=1

, pour lequel

\displaystyle β_e=-\frac{1}{\sqrt{r}}

III. Expressions des coordonnées

1.a.

• D'après

\displaystyle dR=\sqrt{α} \: \left[c \,dt+κ(r) \:\frac{dr}{A}\right]

;

\displaystyle c \,dT=\sqrt{α} \: \left[c \,dt+f(r) \:\frac{dr}{A}\right]

, on peut écrire :

\displaystyle dR-c \,dT=\sqrt{α} \:(κ-f) \: \frac{dr}{A}=\sqrt{α} \: κ \:(1-f^2 ) \: \frac{dr}{A}=\frac{κ}{\sqrt{α}} \: dr=\frac{dr}{\sqrt{α-A}}=\frac{dr}{\sqrt{\frac{r_s}{r}+α-1}}

• Pour

α=2

et en prenant

r_s

comme unité, ceci donne :

\displaystyle dR-c \,dT=\sqrt{\frac{r}{r+1}} \: dr

.
• Avec la variable intermédiaire

u=\sqrt{r}

on obtient :

\displaystyle \sqrt{\frac{r}{r+1}} \: dr=\frac{2 \,u^2}{\sqrt{u^2+1}} \: du

.
• Avec la variable intermédiaire

x

telle que

u=\sinh(x)

on obtient :

\displaystyle \frac{2 \,u^2}{\sqrt{u^2+1}} \: du=2 \: \sinh^2(x) \: dx

.
• On peut alors linéariser :

2 \, \sinh^2(x) \: dx=[\cosh(2 \,x)-1] \: dx

.
• Une primitive est :

\frac{1}{2} \, \sinh(2 \,x)-x=\sinh(x) \: \cosh(x)-x=u \;\sqrt{u^2+1}-\mathrm{arsinh}(u)

.
• Finalement :

R-c \,T=\sqrt{r .(r+1)}-\mathrm{arsinh}(\sqrt{r})=\sqrt{r .(r+1)}-\ln(\sqrt{r}+\sqrt{r+1})

.
◊ remarque : on choisit la constante d'intégration nulle.

1.b.

• D'après

\displaystyle dR-c \,dT=\frac{dr}{\sqrt{\frac{r_s}{r}+α-1}}

pour

α=\frac{1}{2}

et avec

r_s

comme unité :

\displaystyle dR-c \,dT=\sqrt{\frac{2 \,r}{2-r}} \; dr

.
• Avec la variable intermédiaire

\displaystyle u=\sqrt{\frac{r}{2}}

on obtient :

\displaystyle \sqrt{\frac{2 \,r}{2-r}} \; dr=\frac{4 \,\sqrt{2} \: u^2}{\sqrt{1-u^2}} \: du

.
• Avec la variable intermédiaire

x

telle que

u=\sin(x)

on obtient :

\displaystyle \frac{4\,\sqrt{2} \: u^2}{\sqrt{1-u^2}} \: du=4 \,\sqrt{2} \: \sin^2(x) \: dx

.
• On peut alors linéariser :

4 \,\sqrt{2} \: \sin^2(x) \: dx=2 \,\sqrt{2} \: [1-\cos(2 \,x) ] \: dx

.
• Une primitive est :

\sqrt{2} \: [2 \,x-\sin(2 \,x) ]=2 \,\sqrt{2} \: [x-\sin(x) \: \cos(x) ]=2 \,\sqrt{2} \: [\arcsin(u)-u \;\sqrt{1-u^2} ]

.
• Finalement :

\displaystyle R-c \,T= 2 \,\sqrt{2} \: \arcsin\left(\sqrt{\frac{r}{2}}\right)-\sqrt{2 \,r.(2-r)}

.
◊ remarque : on choisit la constante d'intégration nulle.

1.c.

• Pour

α<1

on peut toujours considérer

α=A_0=A(r_0)

où

r_0

est le sommet de la trajectoire.
• D'après

\displaystyle dR-c \;dT=\frac{dr}{\sqrt{\frac{r_s}{r}-\frac{r_s}{r_0}}}

et avec

r_s

comme unité :

\displaystyle dR-c \,dT=\sqrt{\frac{r_0 \: r}{r_0-r}} \:\:dr

.
• Avec la variable intermédiaire

\displaystyle u=\sqrt{\frac{r}{r_0}}

on obtient comme précédemment :

\displaystyle \sqrt{\frac{r_0 \:r}{r_0-r}} \:\:dr=\frac{4\, \sqrt{2} \, u^2}{\sqrt{1-u^2}} \: du

.

• De façon plus générale on obtient donc :

a\displaystyle R-c \,T= r_0 \,\sqrt{r_0} \: \arcsin\left(\sqrt{\frac{r}{r_0}}\right)-\sqrt{r_0 \,r.(r_0-r)}

2.a.

• D'après

\displaystyle c \,dT=\sqrt{α} \: \left[c \,dt+f(r) \:\frac{dr}{A}\right]

, on peut écrire :

\displaystyle c \,dT-\sqrt{α} \: c \,dt=\sqrt{α-A} \; \frac{dr}{A}=\frac{\sqrt{\frac{r_s}{r}+α-1}}{1-\frac{r_s}{r}} \: dr

.
• Pour

α=2

et en prenant

r_s

comme unité, ceci donne :

\displaystyle c \,dT-\sqrt{α} \: c \,dt=\frac{\sqrt{r.(r+1)}}{r-1} \: dr

.
• Avec la variable intermédiaire

u=\sqrt{r}

on obtient :

\displaystyle \frac{\sqrt{r.(r+1)}}{r-1} \: dr=\frac{2 \,u^2 \: \sqrt{u^2+1}}{u^2-1} \: du=2 \,\sqrt{u^2+1} \: du+\frac{\sqrt{u^2+1}}{u-1} du-\frac{\sqrt{u^2+1}}{u+1} \: du

• Avec la variable intermédiaire

x

telle que

u=\sinh(x)

on obtient :

2 \,\sqrt{u^2+1} \: du=2 \, \cosh^2(x) \: dx=[\cosh(2 \,x)+1] \: dx

• Une primitive est :

\frac{1}{2} \: \sinh(2 \,x)+x=\sinh(x) \: \cosh(x)+x=u \:\sqrt{u^2+1}+\mathrm{arsinh}(u)=\sqrt{r .(r+1)} )+\mathrm{arsinh}(\sqrt{r})

• On peut ensuite écrire :

\displaystyle \frac{\sqrt{u^2+1}}{u-1} \: du=\frac{u^2+1}{u-1} \, \frac{du}{\sqrt{u^2+1}}=\left((u+1)+\frac{2}{u-1}\right) \,\frac{du}{\sqrt{u^2+1}}

.
• En passant par

u=\sinh(x)

on obtient une primitive de

\displaystyle (u+1) \: \frac{du}{\sqrt{u^2+1}}

\sqrt{u^2+1}+\mathrm{arsinh}(u)=\sqrt{r+1}+\mathrm{arsinh}\left(\sqrt{r}\right)

• Pour

u-1>0

, on peut par ailleurs passer par les variables

\displaystyle x=\frac{1}{u-1}

puis

y=2 \,x+1

, donnant :

\displaystyle \frac{2}{u-1} \, \frac{du}{\sqrt{u^2+1}}=-\sqrt{2} \, \frac{dx}{\sqrt{x^2+x+\frac{1}{2}}}=-\sqrt{2} \, \frac{dy}{\sqrt{y^2+1}}

• Une primitive est alors :

\displaystyle -\sqrt{2} \; \mathrm{arsinh}(y)=-\sqrt{2} \; \mathrm{arsinh}(2 \,x+1)=-\sqrt{2} \; \mathrm{arsinh}\left(\frac{u+1}{u-1}\right)=-\sqrt{2} \; \mathrm{arsinh}\left(\frac{\sqrt{r}+1}{\sqrt{r}-1}\right)

• Pour

u-1<0

, on peut de même passer par les variables

\displaystyle x=\frac{1}{1-u}

puis

y=2 \,x-1

, donnant :

\displaystyle \frac{2}{u-1} \, \frac{du}{\sqrt{u^2+1}}=-\sqrt{2} \, \frac{dx}{\sqrt{x^2-x+\frac{1}{2}}}=-\sqrt{2} \, \frac{dy}{\sqrt{y^2+1}}

;

\displaystyle -\sqrt{2} \; \mathrm{arsinh}(y)=-\sqrt{2} \; \mathrm{arsinh}(2 \,x-1)=-\sqrt{2} \; \mathrm{arsinh}\left(\frac{1+u}{1-u}\right)=-\sqrt{2} \; \mathrm{arsinh}\left(\frac{1+\sqrt{r}}{1-\sqrt{r}}\right)

• La contribution de

\displaystyle \frac{\sqrt{u^2+1}}{u-1} \: du

est donc au total :

\displaystyle \sqrt{r+1}+\mathrm{arsinh}\left(\sqrt{r}\right) -\sqrt{2} \; \mathrm{arsinh}\left(\frac{\sqrt{r}+1}{\left|\sqrt{r}-1\right|} \right)

.
• La contribution de

\displaystyle -\frac{\sqrt{u^2+1}}{u+1} \: du

est de même :

\displaystyle -\sqrt{r+1}+\mathrm{arsinh}\left(\sqrt{r}\right) -\sqrt{2} \; \mathrm{arsinh}\left(\frac{\sqrt{r}-1}{\left|\sqrt{r}+1\right|} \right)

.
• Au total :

\displaystyle c \,T-\sqrt{2} \; c \,t=\sqrt{r .(r+1)}+3 \, \mathrm{arsinh}\left(\sqrt{r}\right)-\sqrt{2} \; \mathrm{arsinh}\left(\frac{\sqrt{r}+1}{\left|\sqrt{r}-1\right|} \right) -\sqrt{2} \; \mathrm{arsinh}\left(\frac{\sqrt{r}-1}{\left|\sqrt{r}+1\right|} \right)

.
◊ remarque : la composante imaginaire

r_s \: \arg(κ - 1)

associée à

c \,t

se simplifie donc ici (c'est à dire qu'il n'y en a pas pour

c \,T

).
• L'expression est nettement moins simple mais de forme analogue à celle obtenue pour

α=1

(sauf que le comportement à l'infini est d'allure hyperbolique plutôt que parabolique).

2.b.

• Pour

α=\frac{1}{2}

et avec

r_s

comme unité :

\displaystyle c \,dT-\sqrt{α} \: c \,dt=\frac{\sqrt{\frac{r_s}{r}+α-1}}{1-\frac{r_s}{r}} \: dr=\frac{\sqrt{r.(2-r)}}{\sqrt{2} \: (r-1)} \: dr

.
• Ceci peut s'écrire :

\displaystyle \frac{\sqrt{r.(2-r)}}{\sqrt{2} \: (r-1)} \: dr=\frac{r.(2-r)}{\sqrt{2} \: (r-1) \: \sqrt{r.(2-r)}} \: dr=\frac{1-r}{\sqrt{2} \: \sqrt{r.(2-r)} } \: dr+\frac{1}{\sqrt{2} \: (r-1)\: \sqrt{r.(2-r)}} \: dr

.
• En passant par

x=r.(2-r)

on obtient :

\displaystyle \frac{1-r}{\sqrt{2} \;\sqrt{r.(2-r)}} \: dr=\frac{dx}{2 \,\sqrt{2} \: \sqrt{x}}

d'où une primitive :

\displaystyle \sqrt{\frac{x}{2}}=\frac{\sqrt{r.(2-r)}}{\sqrt{2}}

.
• Pour

r-1>0

on peut par ailleurs passer par

\displaystyle x=\frac{1}{r-1}

donnant :

\displaystyle \frac{1}{\sqrt{2} \: (r-1) \: \sqrt{r.(2-r)} } \: dr=-\frac{dx}{\sqrt{2} \: \sqrt{x^2-1}}

.
• Une primitive est alors :

\displaystyle -\frac{1}{\sqrt{2}} \: \mathrm{arcosh}(x)=-\frac{1}{\sqrt{2}} \: \mathrm{arcosh}\left(\frac{1}{r-1}\right)

.
• Pour

r-1<0

on peut de même utiliser

\displaystyle x=\frac{1}{1-r}

donnant :

\displaystyle \frac{1}{\sqrt{2} \: (r-1) \:\sqrt{r.(2-r)}} \: dr=-\frac{dx}{\sqrt{2} \: \sqrt{x^2-1}}

.
• Une primitive est alors :

\displaystyle -\frac{1}{\sqrt{2}} \: \mathrm{arcosh}(x)=-\frac{1}{\sqrt{2}} \: \mathrm{arcosh}\left(\frac{1}{1-r}\right)

.
• Au total :

\displaystyle c \,T-\frac{1}{\sqrt{2}} \: c \,t=\frac{\sqrt{r.(2-r)}}{\sqrt{2}}-\frac{1}{\sqrt{2}} \: \mathrm{arcosh}\left(\frac{1}{|r-1|} \right)

.
◊ remarque : la composante imaginaire

r_s \: \arg(κ - 1)

associée à

c \,t

se simplifie donc ici (c'est à dire qu'il n'y en a pas pour

c \,T

).
• L'expression est moins simple mais de forme analogue à celle obtenue pour

α=1

(sauf que le comportement pour les grandes valeurs de

r

est d'allure elliptique plutôt que parabolique).

2.c.

• Pour

α<1

et avec

r_s

comme unité :

\displaystyle c \,dT-\sqrt{α} \: c \,dt=\frac{\sqrt{\frac{r_s}{r}+α-1}}{1-\frac{r_s}{r}} \: dr=\frac{\sqrt{r.(r_0-r)}}{\sqrt{r_0} \: (r-1)} \:dr

.
• Ceci peut s'écrire :

\displaystyle \frac{\sqrt{r.(r_0-r)}}{\sqrt{r_0} \: (r-1)} \; dr=\frac{r.(r_0-r)}{r-1} \: \frac{dr}{\sqrt{r_0} \;\sqrt{r.(r_0-r)}}

\displaystyle =\left[-r+r_0-1+\frac{r_0-1}{r-1}\right] \: \frac{dr}{\sqrt{r_0} \; \sqrt{r.(r_0-r)}}=\left[\frac{-2 \,r+r_0}{2}+\left(\frac{r_0}{2}-1\right)+\frac{r_0-1}{r-1}\right] \: \frac{dr}{\sqrt{r_0} \; \sqrt{r.(r_0-r)}}

\displaystyle =\frac{-2 \,r+r_0}{2 \:\sqrt{r_0} \; \sqrt{r.(r_0-r)}} \; dr+\frac{\frac{r_0}{2}-1}{\sqrt{r_0}} \, \frac{dr}{\sqrt{r.(r_0-r)}}+\frac{r_0-1}{\sqrt{r_0}} \, \frac{dr}{(r-1) \; \sqrt{r.(2-r)}}

• Le premier terme se traite comme pour

α=\frac{1}{2}

en passant par

x=r.(r_0-r)

; on obtient :

\displaystyle \frac{-2 \,r+r_0}{2 \,\sqrt{r_0}\: \sqrt{r.(r_0-r)}} \: dr=\frac{dx}{2 \,\sqrt{r_0} \: \sqrt{x}}

d'où une primitive :

\displaystyle \sqrt{\frac{x}{r_0}}=\frac{\sqrt{r.(r_0-r)}}{\sqrt{r_0}}

.
• Le troisième terme se traite aussi un peu comme précédement : pour

r-1>0

on peut passer par

\displaystyle x=\frac{1}{r-1}

donnant :

\displaystyle \frac{r_0-1}{\sqrt{r_0}}\: \frac{dr}{(r-1) \:\sqrt{r.(r_0-r)}}=\frac{r_0-1}{\sqrt{r_0}} \:\frac{-1}{(r-1) \: \sqrt{r.(r_0-r)}} \,\frac{dx}{x^2}

\displaystyle =\frac{r_0-1}{\sqrt{r_0}} \,\frac{-dx}{\sqrt{(x+1)\left(x \,r_0-(x+1)\right)}}=\frac{\sqrt{r_0-1}}{\sqrt{r_0}} \,\frac{-dx}{\sqrt{(x+1)(x -\frac{1}{r_0-1})}}

Ce terme peut s'intégrer en ramenant l'argument du radical à la trigonométrie avec

y=x+λ

où

\displaystyle λ=\frac{r_0-2}{2 \,(r_0-1)}

puis

\displaystyle z=\frac{y}{μ}

où

\displaystyle μ=\frac{r_0}{2 \,(r_0-1)}

\displaystyle \frac{\sqrt{r_0-1}}{\sqrt{r_0}} \,\frac{-dx}{\sqrt{(x+1)\left(x -\frac{1}{r_0-1}\right)}}=\frac{\sqrt{r_0-1}}{\sqrt{r_0}} \, \frac{-dy}{\sqrt{(y+μ)(y -μ)}}=\frac{\sqrt{r_0-1}}{\sqrt{r_0}} \, \frac{-dz}{\sqrt{z^2-1}}=-\frac{\sqrt{r_0-1}}{\sqrt{r_0}} \, d(\mathrm{arcosh}(z) )

Pour

r-1<0

on utilise de même

\displaystyle x=\frac{1}{1-r}

donnant :

\displaystyle \frac{r_0-1}{\sqrt{r_0}} \, \frac{dr}{(r-1) \,\sqrt{r.(r_0-r)}}=-\frac{\sqrt{r_0-1}}{\sqrt{r_0}} \:d(\mathrm{arcosh}(z) )

. Au total on obtient pour primitive :

\displaystyle -\frac{\sqrt{r_0-1}}{\sqrt{r_0}} \: \mathrm{arcosh}\left(\frac{r .(r_0-2)+r_0}{r_0 .|r-1|}\right)

.
◊ remarque : ce terme, qui peut s'exprimer avec un logarithme, peut s'intégrer en notations complexes ; il fait alors apparaitre une contribution

\displaystyle \mathrm{i} π \:\arg\left(\frac{1}{r-1}\right)

provenant de

c \,t

et généralement omise (pour

r<r_s

la variable

t

comporte une partie imaginaire constante qui n'influe pas sur

dt

).
• Il s'ajoute ici le second terme (nul pour

α=\frac{1}{2}

) où on peut ramener l'argument du radical à la trigonométrie avec

\displaystyle y=\frac{r-\frac{r_0}{2}}{\frac{r_0}{2}}

\displaystyle \frac{\frac{r_0}{2}-1}{\sqrt{r_0}} \, \frac{dr}{\sqrt{r.(r_0-r)}}=\frac{\frac{r_0}{2}-1}{\sqrt{r_0}} \, \frac{dy}{\sqrt{1-y^2}}=\frac{\frac{r_0}{2}-1}{\sqrt{r_0}} \, d(\arcsin(y) )

.
• Il reste par contre pour ce terme un problème de constante d'intégration, afin qu'il soit nul à l'origine ; on trouve :

\displaystyle \frac{\frac{r_0}{2}-1}{\sqrt{r_0}} \: \left[\arcsin\left(\frac{2 r}{r_0} -1\right)+\frac{π}{2} \right]= \frac{\frac{r_0}{2}-1}{\sqrt{r_0}} \: \arccos\left(1-\frac{2 r}{r_0} \right)

.
• Au total :

c \,dT-\sqrt{α} \: c\, dt=

\displaystyle r_s .\left[\frac{\sqrt{r.(r_0-r)}}{\sqrt{r_0}}+\frac{\sqrt{r_s} \: \left(\frac{r_0}{2 \,r_s}-1\right)}{\sqrt{r_0}} \:\left[\arcsin\left(\frac{2 \,r}{r_0} -1\right)+\frac{π}{2} \right]-\frac{\sqrt{r_0-r_s}}{\sqrt{r_0}} \: \mathrm{arcosh}\left(\frac{r .\left(\frac{r_0}{r_s} -2\right)+r_0}{\frac{r_0}{r_s} .|r-r_s | }\right) \right]

• Le comportement est analogue.

IV. Variante de métrique

• Pour

\displaystyle v_e=-c\;\left(\frac{r_s}{r}\right)^{1/4}

la transformation de Lorentz (locale) correspond à :

\displaystyle d\underline{R}=\frac{d𝓁-β_e \: c \,{dt}_{𝓁oc}}{\sqrt{1-β_e^{\:2}}}

;

\displaystyle c \,d\underline{T}=\frac{c \,{dt}_{𝓁oc}-β_e \: d𝓁}{\sqrt{1-β_e^{\:2}}}

;

c \,{dt}_{𝓁oc}=\sqrt{A} \: c \,dt

;

d𝓁=\sqrt{C} \: dr

(algébrique).

◊ remarque : on considère des variations infinitésimales dans l'espace tangent, donc sans varier

β_e

.
◊ remarque : pour

r<r_s

;

A

C<0

;

\left|v_e \right|>c

mais

\displaystyle \sqrt{\frac{A}{1-β_e^{\:2}}}

reste défini.
• Ceci donne :

\displaystyle d\underline{R}=\frac{\sqrt{A}}{\sqrt{1-\sqrt{\frac{r_s}{r}}}} \: \left[\left(\frac{r_s}{r}\right)^{1/4} c \,dt+\frac{dr}{A}\right]

;

\displaystyle c \,d\underline{T}=\frac{\sqrt{A}}{\sqrt{1-\sqrt{\frac{r_s}{r}}}} \: \left[c \,dt+\left(\frac{r_s}{r}\right)^{1/4} \, \frac{dr}{A}\right]

.
• En isolant

dr

c \,dt

puis en reportant, on obtient :

{ds}^2=c^2 \,{d\underline{T}}^2-{d\underline{R}}^2

; la métrique limitée au déplacement radial serait ainsi encore plus simple que celle de Lemaître.
• Le problème est ensuite de déterminer

r(\underline{R}, c \,\underline{T} )

pour exprimer la partie angulaire de la métrique, mais aussi pour savoir interpréter à quoi correspond

r=r_s

. Puisqu'on part de fonctions de

r

, il faut déterminer

\underline{R}(r, c \,t)

c \,\underline{T} (r, c \,t)

(ou des combinaisons) puis inverser. Or on constate que ni

d\underline{R}(r, c \,t)

c \,d\underline{T} (r, c \,t)

ne sont des différentielles totales : pour obtenir une primitive il faut les multiplier par des facteurs intégrants.
• Le plus simple est ici de considérer :

\displaystyle dR=c \,dt+\left(\frac{r}{r_s} \right)^{1/4} \, \frac{dr}{A}

;

\displaystyle c \,dT=c \,dt+\left(\frac{r_s}{r}\right)^{1/4} \, \frac{dr}{A}

.
• Ceci donne en inversant une métrique dépourvue de singularité pour

r=r_s

\displaystyle \frac{dr}{\sqrt{A}}=\frac{\sqrt{A}}{\left(\frac{r}{r_s} \right)^{1/4}-\left(\frac{r_s}{r}\right)^{1/4} } \:[dR-c \,dT]

;

\displaystyle \sqrt{A} \: c \,dt=\frac{\sqrt{A}}{\left(\frac{r}{r_s} \right)^{1/4}-\left(\frac{r_s}{r}\right)^{1/4}} \: \left[\left(\frac{r_s}{r}\right)^{1/4} dR-\left(\frac{r}{r_s} \right)^{1/4} c \,dT\right]

;

\displaystyle {ds}^2=\frac{\sqrt{r}+\sqrt{r_s}}{\sqrt{r}} \:\left[c^2 \, {dT}^2-\sqrt{\frac{r_s}{r}} \: {dR}^2 \right]

◊ remarque : on utilise

\displaystyle A=1-\frac{r_s}{r}=(\sqrt{r}-\sqrt{r_s}) \: \frac{\sqrt{r}+\sqrt{r_s}}{r}

.
• Il est important de constater que ce résultat est obtenu avec une vitesse de “contraction” sans aucune signification physique : en pratique toute expression de vitesse tendant vers

c

pour

r=r_s

aboutit à une simplification de singularité. Cela confirme que la simplification n'est pas due à une contraction de l'espace.

V. Variante de métrique

• Pour

\displaystyle v_e=-c\:\frac{r_s}{r}

la transformation de Lorentz (locale) correspond à :

\displaystyle d\underline{R}=\frac{d𝓁-β_e \: c \,{dt}_{𝓁oc}}{\sqrt{1-β_e^{\:2}}}

;

\displaystyle c \,d\underline{T}=\frac{c \,{dt}_{𝓁oc}-β_e \: d𝓁}{\sqrt{1-β_e^{\:2}}}

;

c \,{dt}_{𝓁oc}=\sqrt{A} \: c \,dt

;

d𝓁=\sqrt{C} \: dr

(algébrique).

◊ remarque : on considère des variations infinitésimales dans l'espace tangent, donc sans varier

β_e

.
◊ remarque : pour

r<r_s

;

A

C<0

;

\left|v_e \right|>c

mais

\displaystyle \sqrt{\frac{A}{1-β_e^{\:2}}}

reste défini.
• Ceci donne :

\displaystyle d\underline{R}=\frac{1}{\sqrt{1+\frac{r_s}{r}}} \: \left[\frac{r_s}{r}\, c \,dt+\frac{dr}{A}\right]

;

\displaystyle c \,d\underline{T}=\frac{1}{\sqrt{1+\frac{r_s}{r}}} \: \left[c \,dt+\frac{r_s}{r} \, \frac{dr}{A}\right]

.
• En isolant

dr

c \,dt

puis en reportant, on obtient :

{ds}^2=c^2 \,{d\underline{T}}^2-{d\underline{R}}^2

; la métrique limitée au déplacement radial serait ainsi encore plus simple que celle de Lemaître.
• Le problème est ensuite de déterminer

r(\underline{R}, c \,\underline{T} )

pour exprimer la partie angulaire de la métrique, mais aussi pour savoir interpréter à quoi correspond

r=r_s

. Puisqu'on part de fonctions de

r

, il faut déterminer

\underline{R}(r, c \,t)

c \,\underline{T} (r, c \,t)

(ou des combinaisons) puis inverser. Or on constate que ni

d\underline{R}(r, c \,t)

c \,d\underline{T} (r, c \,t)

ne sont des différentielles totales : pour obtenir une primitive il faut les multiplier par des facteurs intégrants.
• Le plus simple est ici de considérer :

\displaystyle dR=c \,dt+\frac{r}{r_s} \, \frac{dr}{A}

;

\displaystyle c \,dT=c \,dt+\frac{r_s}{r} \, \frac{dr}{A}

.
• Ceci donne la métrique :

\displaystyle {ds}^2=\frac{r}{r+r_s} \:\left[c^2 \, {dT}^2-\left(\frac{r_s}{r}\right)^2 {dR}^2 \right]

dépourvue de singularité pour

r=r_s

.
• On peut écrire :

\displaystyle dR-c \,dT=\frac{r+r_s}{r} \: dr

; on en déduit :

\displaystyle R-c \,T=r.\left(1+\frac{r}{2 \,r_s}\right)

.
• Par ailleurs :

\displaystyle c \,dT=c \,dt+\frac{r_s}{r-r_s} \: dr

; on en déduit :

\displaystyle c \,T=c \,t+r_s \; \ln\left(\left|\frac{r}{r_s} -1\right|\right)

.
◊ remarque : la composante imaginaire

r_s \; \arg(κ - 1)

associée à

c \,t

se simplifie donc ici (c'est à dire qu'il n'y en a pas pour

c \,T

).
• Ces expressions ont la même allure que celles obtenues pour la métrique de Lemaître (généralisée), mais l'expression

r(R, c \,T )

est peu simple :

\displaystyle r=r_s .\left(\sqrt{1+\frac{2 \,(R-c \,T)}{r_s}}-1\right)

.
• Il est important de constater que ce résultat est obtenu avec une vitesse de “contraction” sans aucune signification physique : en pratique toute expression de vitesse tendant vers

c

pour

r=r_s

aboutit à une simplification de singularité. Cela confirme que la simplification n'est pas due à une contraction de l'espace.

VI. Coordonnées de Lemaître-Eddington-Finkelstein

1.a.	• Le mouvement radial des photons correspond à : $\displaystyle {ds}^2=A .\left[c^2 \,{dt}^2-\frac{dr^2}{A^2} \right]=0$ ; $\displaystyle c \,dt±\frac{dr}{A}=0$ . ◊ remarque : on se limite au demi-plan $(r,c \,t)$ .

1.b.	• D'après les expressions indiquées, les variations ( $dU$ et $dV$ ) des paramètres d'Eddington-Finkelstein correspondent à : $\displaystyle c \,dt∓\frac{dr}{A}$ . • La famille de courbes d'Eddington-Finkelstein décrivant les photons descendants correspond au paramètre $V$ : $\displaystyle dR=c \,dt+\frac{dr}{A}$ (ainsi pour $V$ fixé $dV=0$ sur une telle courbe $R=Cste$ ).

2.a.

• Les équations du mouvement peuvent se déduire du lagrangien quadratique

\displaystyle ℒ=\frac{1}{2} \: \left(A\: c^2 \, \dot{t}^2-\frac{1}{A} \: \dot{r}^2 \right)

(paramétré par

ς

).
• On obtient ainsi :

\displaystyle \frac{\, ∂ℒ}{c \,∂t}=0

, donc

\displaystyle \frac{d}{dς} \left(\frac{\, ∂ℒ}{c \,∂\dot{t}}\right)=A \:c \,\ddot{t}=0

. Ceci correspond à

\displaystyle A \:c \, \frac{dt}{dς}=Cste

, donc on peut choisir

dς=A \:c \,dt

.
• Le long d'une trajectoire, il semble alors logique de proposer :

c \,dT=A \:c \,dt

2.b.

• Pour un déplacement quelconque, il faut tenir compte du fait que le repérage

(R, c \,T)

n'est pas statique : les horloges sur les différentes courbes ne sont pas synchronisées.
• Ceci peut se vérifier en reportant dans la métrique les deux expressions précédentes ; le décalage de synchronisation est caractérisé par la présence du terme non diagonal :

\displaystyle c \,dt=\frac{c \,dT}{A}

;

\displaystyle \frac{dr}{A}=dR-\frac{c \:dT}{A}

;

\displaystyle {ds}^2=\frac{2}{A} \: c \,dT \:dR-{dR}^2

• Comment modifier la relation définissant

T

de façon à éviter ce problème ? Pour un changement de courbe infinitésimal, le décalage des horloges est logiquement proportionnel à

dR

(nul tant qu'on reste sur la même trajectoire) ; on cherche alors sous la forme :

\displaystyle c \,dT=A \:c \,dt+λ \:dR=(A+λ)\: c \,dt+λ \: \frac{dr}{A}

, où

λ=λ(r,t)

.
• En inversant le système de deux expression :

\displaystyle c \,dt=\frac{1}{A} \: (c \,dT-λ \:dR)

;

dr=(A+λ) \:dR-c \,dT

{ds}^2=2 \,c \,dT \:dR+(A + 2 \,λ) \:{dR}^2

• La synchronisation des horloges est impossible (on ne peut pas choisir

λ

de façon à éliminer le terme non diagonal). Ainsi, la méthode de Lemaître, même en version indirecte, ne peut pas s'appliquer aux photons.

• On peut par contre chercher à adapter

λ

de façon à simplifier le plus possible la métrique ; on peut alors proposer de choisir

\displaystyle λ=-\frac{A}{2}

correspondant à la métrique :

{ds}^2=2 \,c \,dT \:dR

.
• Il est alors intéressant de remarquer que

\displaystyle c \,dT=\frac{A}{2} \: c \,dt+\frac{1}{2} \, dr=\frac{A}{2}\: (c \,dt-\frac{dr}{A})

peut s'exprimer en fonction du paramètre

U

d'Eddington-Finkelstein :

\displaystyle c \,dT=\frac{A}{2} \: dU

;

{ds}^2=A \:dU \:dR=A \:dU \:dV

; c'est à dire qu'on retrouve la métrique d'Eddington-Finkelstein.

VII. Métrique d'Eddington-Finkelstein

1.a.

• En substituant dans la métrique de Schwarzschild, on peut écrire la métrique sous la forme (omettant la partie angulaire) :

\displaystyle {ds}^2=\left(1-\frac{r_s}{r}\right)\: c^2 \,{dt}_{+}^{\:2}-2 \, \frac{r_s}{r}\: c \,{dt}_{+} \: dr-\left(1+\frac{r_s}{r}\right) \:{dr}^2

.
• Cette expression semble éviter la “singularité divergente” du coefficient

C

de Schwarzschild, mais semble laisser subsister la “singularité temporelle” associée à l'annulation du coefficient

A

1.b.

• On obtient ainsi :

\displaystyle \frac{c \,{dt}_{+}}{dσ}=\frac{α_t \: r}{r-r_s}-\frac{α_t \: r_s}{r-r_s} \: \sqrt{1+\frac{α_r}{α_t^{\:2}} \, \frac{r-r_s}{r}}

; il est alors utile de calculer les constantes.
• Pour les photons

α_r=0

donc

\displaystyle \frac{c \,{dt}_{+}}{dσ}=α_t>0

(sinon il n'y aurait pas de propagation). Il n'y a donc dans ce cas aucun problème, seul le cas des particules massives est à préciser.
• Pour les particules partant de

r_0

(éventuellement l'infini) avec une vitesse

β_0

(éventuellement nulle) :

\displaystyle A_0^{\:2} \: \left(\frac{c \,dt}{dσ}\right)^2=α_t^{\:2}

;

\displaystyle β_0^{\:2}=\left(\frac{1}{A_0} \, \frac{dr}{c \,dt}\right)^2

;

{dσ}^2={ds}^2=A_0 \: c^2 \, {dt}^2 \: (1-β_0^{\:2} )

;

\displaystyle α_t^{\:2}=\frac{A_0}{1-β_0^{\:2}}

;

\displaystyle \left(\frac{dr}{dσ}\right)^2=α_t^{\:2}+α_r \: A_0=\left(\frac{dr}{c \,dt}\right)^2 \left(\frac{c \,dt}{dσ}\right)^2=\frac{A_0 \: β_0^{\:2}}{1-β_0^{\:2}}

;

\displaystyle α_r=\frac{β_0^{\:2}}{1-β_0^{\:2}}-\frac{1}{1-β_0^{\:2}}=-1

• On peut alors vérifier que le radical est toujours défini :

\displaystyle 1+\frac{α_r}{α_t^{\:2}} \, \frac{r-r_s}{r}=1-(1-β_0^{\:2} ) \: \frac{A}{A_0}

avec

(1-β_0^{\:2} )<1

\displaystyle \frac{A}{A_0} <1

• On peut ensuite vérifier qu'il n'y a pas divergence au niveau de la singularité :

\displaystyle \frac{c \,{dt}_{+}}{dσ}≈\frac{α_t \: r}{r-r_s}-\frac{α_t \: r_s}{r-r_s} \: \left(1+\frac{1}{2} \, \frac{α_r}{α_t^{\:2}}\, \frac{r-r_s}{r}\right)=α_t .\left(1-\frac{1}{2} \, \frac{α_r}{α_t^{\:2}} \, \frac{r_s}{r}\right)

• Il est enfin intéressant de vérifier que la variation est monotone ; puisque la dérivée est continue, on est ramené à vérifier qu'elle ne s'annule pas. En notant

\displaystyle α=\frac{A_0}{1-β_0^{\:2}}

et avec

r_s

comme unité pour simplifier :

\displaystyle (r-1)\: \frac{c \,{dt}_{+}}{dσ}=-r+\sqrt{1+\frac{1}{α}\, \frac{r-1}{r}}=0

correspond à :

\displaystyle r^2-1=-\frac{r-1}{α \,r}

.
• La solution

r=1

est à écarter car l'approximation montrant la non divergence indique qu'il faudrait

\displaystyle 1+\frac{1}{2 \,α \:r}=0

(pour

r=1

) ce qui est impossible. Cette solution apparente vient du fait qu'on a initialement multiplié par

r - 1

pour simplifier l'équation.
• Il reste donc :

\displaystyle r+1=-\frac{1}{α \:r}

c'est à dire

\displaystyle r^2+r+\frac{1}{α}=0

. Les deux solutions

\displaystyle r=\frac{-α±\sqrt{α.(α-4)}}{2 \:α}

sont soit négatives, soit complexes, donc

\displaystyle \frac{c \,{dt}_{+}}{dσ}

ne s'annule pas et la variation de

t_{+}

est monotone.

1.c.

• L'annulation de

A

dans la métrique indique que pour

r<r_s

la variable

t_{+}

devient du genre espace ; il semble donc peu raisonnable de s'en servir de paramètre temporel.
• Pour raisonner sur ce qui est subi par une particule en mouvement, il faut considérer que les horloges de ce repérage sont désynchronisées de :

\displaystyle c \:{dt}_d=\frac{1}{A}\, \frac{r_s}{r} \, dr

. Les durées “vécues” dépendent donc plutôt de

\displaystyle c \,{dt}_{+}-\frac{1}{A} \, \frac{r_s}{r} \, dr

.
• En outre, la distance radiale parcourue est :

\displaystyle {d𝓁}^2=ℊ_{11} \:{dx}^1 \:{dx}^1=\left[\frac{1}{A} \, \left(\frac{r_s}{r}\right)^2+\left(1+\frac{r_s}{r}\right)\right] \:{dr}^2

, où la métrique tridimensionnelle

\displaystyle ℊ_{ij}=\frac{g_{0i} \: g_{0j}}{g_{00}} -g_{ij}

est l'inverse de la partie spatiale

ℊ^{ij}=g^{ij}

.
• Il est alors préférable d'écrire la métrique sous la forme :

\displaystyle {ds}^2=\left(1-\frac{r_s}{r}\right) \:\left[c \,{dt}_{+}-r_s \: \frac{dr}{r-r_s} \right]^2-\left[\frac{1}{A} \, \left(\frac{r_s}{r}\right)^2+\left(1+\frac{r_s}{r}\right)\right] \:{dr}^2=A\: c^2 \,{dt}^2-C \:{dr}^2

• Cela revient à conclure qu'on n'a rien changé : le fait de décaler la synchronisation des horloges ne fait que masquer la singularité, sans modifier la représentation physique de l'espace-temps.

2.a.

• Si par contre on change aussi la coordonnée radiale de façon variable en fonction du temps, cela revient à changer de référentiel. On peut alors considérer :

\displaystyle 2 \, \frac{r_s}{r}\: c \,{dt}_{+} \: dr+\left(1+\frac{r_s}{r}\right) \:{dr}^2=\left(1+\frac{r_s}{r}\right) \: \left[dr+\frac{r_s}{r+r_s} \: c \,{dt}_{+} \right]^2-\frac{r_s^{\:2}}{r.(r+r_s )} \: c^2 \,{dt}_{+}^{\:2}

;

\displaystyle {ds}^2=\left[1-\frac{r_s}{r}+\frac{r_s^{\:2}}{r.(r+r_s )}\right] \: c^2 \,{dt}_{+}^{\:2}-\left(1+\frac{r_s}{r}\right) \: \left[dr+\frac{r_s}{r+r_s} \: c \,{dt}_{+} \right]^2

;

\displaystyle {ds}^2=\frac{r_s}{r+r_s} \: c^2 \,{dt}_{+}^{\:2}-\frac{r_s^{\:2}}{r.(r+r_s )} \: \left[\frac{r+r_s}{r_s} \: dr+c \,{dt}_{+} \right]^2

• On peut alors écrire

\displaystyle {ds}^2=\frac{r_s}{r+r_s} \: \left[c^2 \,{dt}_{+}^{\:2}-\frac{r_s^{\:2}}{r^2} \:{dr}_{+}^{\:2} \right]

(régulière pour

r=r_s

) avec une coordonnée

r_{+}

telle que :

\displaystyle {dr}_{+}=\frac{r+r_s}{r_s} \: dr+c \,{dt}_{+}

;

\displaystyle r_{+}=\frac{r^2}{2 \,r_s}+r+c \,t_{+}= \frac{r^2}{2 \,r_s}+r+c \,t+r_s \: \ln\left(\left|\frac{r}{r_s} -1\right|\right)

. Cette métrique justifie que

t_{+}

soit un “bon paramètre” du genre temps, si on raisonne dans le référentiel approprié.
◊ remarque : dans le référentiel en comouvement, il n'y a pas de décalage des horloges.

2.b.

• Une telle démarche est analogue à celle de Lemaître ; le référentiel associé à

r_{+}=Cste

correspond à :

\displaystyle dr=-\frac{r_s}{r+r_s} \: c \,{dt}_{+}=-\frac{r_s}{r+r_s} \: \left[c \:dt+\frac{r_s}{r-r_s} \: dr\right]

. Ainsi :

\displaystyle \frac{\,dr}{c \,dt}=-\frac{r_s .(r-r_s )}{r^2}

.
• La vitesse d'entraînement est :

\displaystyle β_e=\sqrt{\frac{C}{A}} \: \frac{\,dr}{c\, dt}=-\frac{r_s}{r}

; on peut vérifier que la méthode de Lemaître fonctionne avec une telle expression (même si elle n'a pas de justification physique).

• La relation

{ds}^2=0

impose :

\displaystyle \frac{c \,dt}{dr}=\frac{r+r_s}{r-r_s}

(sens sortant) ;

\displaystyle \frac{c \,dt}{dr}=-1

(sens entrant). Les tracés, obtenus par intégration, des cônes de lumière émis depuis un point intérieur à la singularité semblent indiquer qu'aucune particule ne peut en sortir ; cela doit être interprété avec toute la réserve associée aux repérages de type Lemaître.

◊ remarque : de façon analogue

\displaystyle c \,t_{-}=c \,t-r_s \: \ln\left(\left|\frac{r}{r_s} -1\right|\right)

peut décrire un référentiel en expansion ; pour d'autres calculs, Eddington et Finkelstein ont aussi utilisé :

U=c \,t_{-}-r

V=c \,t_{+}+r

VIII. Choix de l'origine du repère de Lemaître

• Le mieux est de choisir une origine commune pour la montée et la descente d'une particule choisie comme référence :

◊	fixer $c \,T=0$ au sommet de la trajectoire en $c \,t=0$ (celui pour $r>r_s$ ) et $r=r_0= 2 \,r_s$ (par exemple, pour le cas $α=\frac{1}{2}$ ) ; il se trouve que la constante d'intégration choisie nulle convient si on prend comme référence la particule telle que $R=Cste=2 \,r_s \: \sqrt{2} \; \arcsin(1)≈\text{4,44} \:r_s$ (le choix est toujours possible mais dépend de $α$ ) ;
◊	imposer que $R=0$ corresponde à $r=0$ pour $c \,T=0$ ; il se trouve que la constante d'intégration choisie nulle convient.

IX. Trajectoires de particules ascendantes puis descendantes

• Pour la montée :

\displaystyle v=c \:\sqrt{1-\frac{A}{α}}=\frac{\,dr}{A \:dt}

.
• Ainsi (avec

r_s

comme unité) :

\displaystyle c \,dt=\frac{\sqrt{α} \: dr}{A \:\sqrt{α-A}}=\frac{\sqrt{α} \: r^2 \: dr}{(r-1) \: \sqrt{r.\left(1-(1-α) \: r\right)}}

.
• Pour

α=\frac{1}{2}

on obtient :

\displaystyle c \,dt=\frac{r^2 \: dr}{(r-1) \: \sqrt{r.(2-r)}}

.
• Ceci peut s'écrire :

\displaystyle \frac{r^2 \: dr}{(r-1) \: \sqrt{r.(2-r)}}=\frac{r-1}{\sqrt{r.(2-r)}} \: dr+\frac{2}{\sqrt{1-(r-1)^2} } \:dr+\frac{1}{(r-1) \: \sqrt{1-(r-1)^2}} \: dr

• En passant par

x=r.(2-r)

on obtient :

\displaystyle \frac{r-1}{\sqrt{r.(2-r)}} \: dr=-\frac{dx}{2 \: \sqrt{x}}=-d\left(\sqrt{r.(2-r)}\right)

.
• En passant par

x=r-1

on obtient :

\displaystyle \frac{2}{\sqrt{1-(r-1)^2}} \: dr=\frac{2 \,dx}{\sqrt{1-x^2}}=2 \:d(\arcsin⁡(r-1) )

.
• Pour

r-1>0

on peut par ailleurs passer par

\displaystyle x=\frac{1}{r-1}

donnant :

\displaystyle \frac{1}{(r-1) \:\sqrt{1-(r-1)^2}} \: dr=-\frac{dx}{\sqrt{x^2-1}}=-d\left(\mathrm{arcosh}\left(\frac{1}{r-1}\right) \right)

• Pour

r-1<0

on peut de même utiliser

\displaystyle x=\frac{1}{1-r}

donnant :

\displaystyle \frac{1}{(r-1) \:\sqrt{1-(r-1)^2}} \: dr=-\frac{dx}{\sqrt{x^2-1}}=-d\left(\mathrm{arcosh}\left(\frac{1}{1-r}\right) \right)

• Au total :

\displaystyle c \,t=-\sqrt{r.(2-r)}+2 \, \arcsin⁡(r-1)-\mathrm{arcosh}\left(\frac{1}{|r-1|} \right)+Cste

.
• On veut que

c \,t=0

corresponde au passage par

r=r_0=2

0=2 \: \arcsin⁡(1)+Cste

;

Cste=-π

• En simplifiant :

\displaystyle c \,t=-\sqrt{r.(2-r)}+2 \: \arccos⁡(r-1)-\mathrm{arcosh}\left(\frac{1}{|r-1|} \right)

.
◊ remarque : étant donné que l'expression diverge pour

r=1

, il est impossible de raccorder par continuité à ce niveau, donc la constante d'intégration pour

r<1

pourrait être différente de celle imposée en

r=r_0>1

; le problème est analogue au prolongement de

\ln⁡(|z|)

comme primitive de

\displaystyle \frac{1}{z}

pour

z<0

; le passage par les complexes donne dans ce cas

\ln⁡(z)=\ln⁡(|z|)+\ln⁡(-1)=\ln⁡(|z|)+\mathrm{i} \:π

.
◊ remarque : on peut ensuite en déduire

R(r)

c \,T(r)

• Pour la descente, avec

α=\frac{1}{2}

, la vitesse opposée donne :

\displaystyle c \,dt=-\frac{r^2 \: dr}{(r-1) \: \sqrt{r.(2-r)}}

.
• Avec :

\displaystyle c \,dT=\sqrt{α} \: c \,dt+\frac{\sqrt{\frac{r_s}{r}+α-1}}{1-\frac{r_s}{r}} \: dr

on obtient dans ce cas :

\displaystyle c \,dT=-\frac{\sqrt{2 \,r}}{\sqrt{2-r}} \: dr

.
• Avec :

\displaystyle dR=c \,dT+\frac{dr}{\sqrt{\frac{r_s}{r}+α-1}}

on obtient dans ce cas :

dR=0

X. Extension pour un repérage de Lemaître généralisé avec $α<1$

1.a.	• On considère $α=A_0∈\left]0 \,;1\right[$ avec un “sommet” de trajectoire pour $\displaystyle r_0=\frac{1}{1-α}$ . • La métrique peut s'écrire : ${ds}^2=c^2 \, {dT}^2-f^2 \: {dR}^2$ avec $\displaystyle f^2=1-\frac{A}{α}$ . • Pour $r>r_0$ on obtient $f^2<0$ et la variable $R$ n'est plus du genre espace. Ceci est lié au fait que les particules de référence du repérage ne dépassent pas cette limite.

1.b.	• Afin de chercher un prolongement de la représentation de base, pour $α∈\left]0 \,;1\right[$ , on peut repartir des relations de Lemaître : $\displaystyle c \,dT-\sqrt{α} \: c \,dt=\sqrt{α-A}\; \frac{dr}{A}$ ; $\displaystyle dR-\sqrt{α} \: c \,dt=\frac{α}{\sqrt{α-A}}\, \frac{dr}{A}$ . Le sommet $r_0$ de la trajectoire des particules de référence correspond à $A=α=A_0$ ; d'après $dR=0$ , la vitesse d'entraînement correspond à : $\displaystyle -β_e=f=\frac{1}{κ}=\frac{\sqrt{α-A}}{\sqrt{α}}$ . • Puisque, pour $r<r_0$ , la vitesse d'entraînement tend vers zéro à l'approche de la limite, on pourrait envisager au delà une vitesse d'entraînement en expansion $\displaystyle -β_e=f=\frac{1}{κ}=-\frac{\sqrt{A-α}}{\sqrt{α}}$ (la continuité impose de respecter la limite $β_e=0$ pour $A=α$ ). • Cela ne permet toutefois pas de raccorder puisque ce n'est alors plus $R-c \,T$ mais $R+c \,T$ qui est une fonction simple de $r$ ; seule une situation comme celle des coordonnées isotropes, à la limite de l'horizon, permet un prolongement : il n'y a pas de problème de signe car de l'autre côté $r$ augmente à nouveau quand $R$ continue à diminuer (les deux changements de signe se compensent).

• Pour les points situés plus loin que

r_0

on obtient

A>α

et on peut envisager d'utiliser des vitesses imaginaires, dont rien n'interdit de donner une représentation graphique dans le plan réel (dans la zone non utilisée par la représentation limitée à

r_0

).
• La quantité

\sqrt{r.(r_0-r)}

est prolongeable pour

r>r_0

à l'aide de la partie imaginaire

\sqrt{r.(r-r_0)}

. La quantité

\arcsin⁡(x)

peut être prolongée pour

x>1

en considérant :

\displaystyle x=\frac{e^{\mathrm{i}y}+e^{-\mathrm{i}y}}{2 \,\mathrm{i}}

qui peut conduire à :

e^{\mathrm{i}y}=\mathrm{i} .\left(x±\sqrt{x^2-1}\right)

puis

\arcsin⁡(x)=\frac{π}{2}-\mathrm{i} \: \ln\left(x±\sqrt{x^2-1}\right)=\frac{π}{2}±\mathrm{i} \: \ln\left(x+\sqrt{x^2-1}\right)

. Pour obtenir un prolongement tel que

R-c \,T

soit partout croissant en fonction de

r

, on choisit la représentation par

\arcsin⁡(x)=\frac{π}{2}+\mathrm{i} \: \ln\left(x+\sqrt{x^2-1}\right)

.
• En pratique

R-c \,T

(complexe) est représenté par

\mathrm{Re}(R-c \,T)-\mathrm{Im}(R-c \,T)

; ici pour

r_0=2\,r_s

◊ remarque : la diminution de la pente pour

r>r_0

caractérise le fait que la partie imaginaire de la vitesse augmente.
• La quantité

\mathrm{arcosh}(x)

peut être prolongée pour

x<1

en considérant :

\displaystyle x=\frac{e^y+e^{-y}}{2}

qui peut conduire à :

e^y=x±\sqrt{x^2-1}=x±\mathrm{i}\: \sqrt{1-x^2}

avec la propriété :

\left|x±\mathrm{i} \:\sqrt{1-x^2}\right|=1

. Ainsi :

\mathrm{arcosh}(x)=\ln\left(x±\mathrm{i} \:\sqrt{1-x^2}\right)=±\mathrm{i} \; \arg\left(x±\mathrm{i} \:\sqrt{1-x^2}\right)=±\mathrm{i} \;\arccos(x)

(on choisit le signe

+

• En pratique

c \,T-\sqrt{α}\:c\,t

(complexe) est représenté par

\mathrm{Re}(c \,T-\sqrt{α}\:c\,t)+\mathrm{Im}(c \,T-\sqrt{α}\:c\,t)

; ici pour

r_0=2\,r_s

• Connaissant

r

t

, on peut déterminer

R

T

; on peut ainsi représenter

r(R,c \,T)

c \,t(R,c \,T)

dans le prolongement ; ici pour

r_0=2\,r_s

GenLemaitre_cor_Im/Lem_al05_extens_1.png

GenLemaitre_cor_Im/Lem_al05_extens_2.png

• Il est ensuite possible de représenter, comme précédemment, la trajectoire d'une particule en chute libre depuis l'infini avec une vitesse “initiale” (limite) nulle.

GenLemaitre_cor_Im/Lem_al05_extens_3.png

• On vérifie ainsi que les trajectoires sont représentées de façon acceptable : le début de la trajectoire de la particule de référence “classique” correspond à

R

décroissant (mais l'extension de la représentation est moins complètement de type Lemaître et n'a pas une interprétation intuitive aussi directe).

XI. Anomalie fondamentale de la singularité centrale

• La propriété

r=0

correspond à

dR=c \,dT

et la vitesse de la singularité (par rapport aux particules comobiles) est alors :

\displaystyle v=f \: \frac{dR}{dT}=c \: \frac{\sqrt{α-1+\frac{r_s}{r}}}{\sqrt{α}}=∞

. Pour un point atteint au bout d'une durée finie, cela rend la théorie tout a fait contradictoire.
◊ remarque : il en est de même symétriquement, pour le repérage en expansion.

XII. Croisement de particules entrantes et sortantes

1.a.

• Pour étudier la méthode de raisonnement, on peut considérer le cas associé à la transformation de Lemaître “classique”.
• Pour une particule

P

entrante en chute libre verticale, le référentiel

ℛ

de Lemaître en comouvement correspond à :

R=Cste

\displaystyle R-c \,T=\frac{2 \,r_s}{3} \: κ^3

avec

\displaystyle κ=\sqrt{\frac{r}{r_s}}

.
• Pour

P'

sortante, le référentiel

ℛ'

en comouvement correspond à :

R'=Cste

\displaystyle R'+c \,T'=\frac{2 \,r_s}{3} \:{κ'}^3

avec

\displaystyle κ'=-\sqrt{\frac{r'}{r_s}}

.
• Pour étudier

P'

dans

ℛ

on peut utiliser

\displaystyle R''-c \,T''=\frac{2 \,r_s}{3} \:{κ''}^3

avec

\displaystyle κ''=-\sqrt{\frac{r'}{r_s}}

(

r'

est une coordonnée dans

ℛ_0

statique, utilisée aussi bien dans

ℛ

ℛ'

) ; pour ce cas

R''

varie.
• La comparaison donne :

c \,T'=-R''+c \,T''-R'

(où

R'=Cste

1.b.

• D'après ce qui précède :

c \,dT'=-dR''+c \,dT''

.
• Par ailleurs pour

P'

dans

ℛ'

\displaystyle {ds}^2=c^2 \,{dT'}^2-\frac{1}{{κ'}^2} \: {dR'}^2=c^2 \,{dT'}^2

. De façon analogue pour

P'

dans

ℛ

\displaystyle {ds}^2=c^2 \,{dT''}^2-\frac{1}{{κ''}^2} \:{dR''}^2

.
• La comparaison donne :

\displaystyle c^2 \,{dT''}^2-\frac{1}{{κ''}^2} \:{dR''}^2=c^2 \,{dT'}^2=(dR''-c \,dT'')^2

. On en déduit en simplifiant :

\displaystyle dR''=\frac{2 \,{κ''}^2}{{κ''}^2+1} \: c \,dT''

.
• En utilisant

dR''-c \,dT''=2 \,r_s \:{κ''}^2 \: dκ''

(d'après

R''-c \,T''

), ceci donne :

\displaystyle dR''=2 \,r_s \: \frac{2 \,{κ''}^4}{{κ''}^2-1} \: dκ''

;

\displaystyle c \,dT''=2 \,r_s \: \frac{{κ''}^2+1}{{κ''}^2-1} \:{κ''}^2 \: dκ''

1.c.

• En intégrant :

\displaystyle c\,T''=\frac{2 \,r_s}{3} \:{κ''}^3+4 \,r_s \:κ''+2 \,r_s \: \ln\left(\left|\frac{κ''-1}{κ''+1}\right|\right)+Cste

;

\displaystyle R''=c\,T''+\frac{2 \,r_s}{3} \:{κ''}^3

(déja connu). Cela permet une représentation paramétrique de la trajectoire. On fixe la constante d'intégration en imposant le croisement avec

P

R''=R

(constant) pour la valeur de

c\,T''=c\,T

qui donne la coordonnée

r=r'

de la position d'intersection choisie.
◊ remarque : on omet ici une composante imaginaire pour

c\,T''

.
• Pour les particules sortantes

P'

croisant

P

r>r_s

, la particule

P

entrante voit

P'

s'éloigner de l'astre, moins vite que les photons sortants, en semblant provenir de l'horizon (en principe

P

ne voit pas la partie

r<r_s

• Par contre, pour les particules sortantes

P'

croisant

P

r<r_s

, de diagramme semble montrer que la particule

P

entrante voit

P'

“tomber” sur l'astre, plus vite que les photons dans le sens sortants (qui, selon l'interprétation usuelle, ne peuvent pas sortir), en semblant provenir de l'horizon.
• La différence essentielle est que, par construction, on sait ici que

P'

sort.
◊ remarque : inversement de même, pour

r<r_s

, il semble à la particule

P'

sortante que la particule

P

entrante ne peut pas entrer.
• Si on veut préserver l'interprétation usuelle, il faut admettre que le temps

T'

semble s'écouler en sens inverse du temps

T

. La relativité restreinte nous habitue à penser que la simultanéité dépend du référentiel, mais aboutir à ce qu'un changement de référentiel conduise ici à retourner l'écoulement du temps sur toute une trajectoire, cela n'a rien d'évident.
• Qui plus est, dans cette région

r<r_s

, les photons dans le sens sortant, qui semblent ne pas pouvoir sortir, peuvent en réalité peut être le faire. Il est difficile de raisonner de façon analogue pour des particules de masse nulle, puisqu'on ne peut pas se placer dans leur référentiel propre, mais ces photons “sortent” plus vite que toute particule massive... qui peut sortir.
• Une façon d'éviter ces contradictions peut consister à admettre que le prolongement pour

r<r_s

, bien que mathématiquement possible, est en réalité dépourvu de signification physique.
• Mais puisque ces raisonnements utilisent l'invariance par décalage temporel, une autre façon peut consister à éviter les croisements en imaginant un espace-temps initialement en expansion (trou blanc dans le passé), passant par une extension maximale à

t=0

, puis finalement en contraction (trou noir dans le futur) ; cela ressemble aux métriques comme celles de Novikov ou de Kruskal-Szekeres.

• Une autre démarche consiste à chercher la transformation de Lemaître généralisée passant de

ℛ'

ℛ

.
• On peut partir des relations de passage de

ℛ_0

ℛ'

(en notant

c \,t

r

les coordonnées de

P'

) :

\displaystyle -dR'=c \,dt-\sqrt{\frac{r}{r_s}}\, \frac{dr}{A}

;

\displaystyle c \,dT'=c \,dt-\sqrt{\frac{r_s}{r}} \, \frac{dr}{A}

• En inversant on obtient :

\displaystyle dr=\sqrt{\frac{r_s}{r}} \:(c \,dT'+dR')

;

\displaystyle c \,dt=\frac{1}{A} \: \left(c \,dT'+\frac{r_s}{r} \: dR'\right)

.
• On peut ensuite reporter dans les relations de passage de

ℛ_0

ℛ

(en notant

c \,t

r

les coordonnées d'un point quelconque) :

\displaystyle dR=c \,dt+\sqrt{\frac{r}{r_s}} \: \frac{dr}{A}

;

\displaystyle c \,dT=c \,dt+\sqrt{\frac{r_s}{r}} \: \frac{dr}{A}

.
• On obtient ainsi :

\displaystyle dR=\frac{1}{A} \: \left[2 \,c \,dT'+\left(1+\frac{r_s}{r}\right) \: dR'\right]

;

\displaystyle c \,dT=\frac{1}{A} \: \left[\left(1+\frac{r_s}{r}\right) \: c \,dT'+2 \,\frac{r_s}{r} \: dR'\right]

.
• Ces relation s'appliquent en particulier à

P'

, pour lequel

dR'=0

\displaystyle dR''=\frac{1}{A} \: 2 \,c \,dT'

;

\displaystyle c \,dT''=\frac{1}{A} \: \left(1+\frac{r_s}{r}\right) \: c \,dT'

• On constate, comme soupçonné précédemment, que

dR''

c \,dT''

évoluent dans le sens contraire de

c \,dT'

pour

r<r_s

(la trajectoire est parcourue dans le sens inverse de celui auquel on s'attend).
• D'après la métrique, la distance parcourue dans

ℛ

est

\displaystyle d𝓁=\sqrt{\frac{r_s}{r}} \: dR

. La vitesse d'entrainement de

ℛ

par rapport à

ℛ'

est donc (en norme) :

\displaystyle β''_e=\sqrt{\frac{r_s}{r}} \: \frac{\,dR''}{c \,dT''}=\frac{2}{\sqrt{\frac{r}{r_s}}+\sqrt{\frac{r_s}{r}}} ≤1

(seul le passage le l'horizon se fait à la vitesse de la lumière, on aboutit même à

β''_e→0

pour

r→0

).
• Puisque pour

r<r_s

le référentiel

ℛ'

évolue à une vitesse supraluminique par rapport à

ℛ_0

, qui évolue à une vitesse supraluminique par rapport à

ℛ

, on pourrait douter de la validité de la transformation combinée. On peut vérifier qu'en combinant

\displaystyle β_e=\sqrt{\frac{r_s}{r}}

\displaystyle β'_e=\sqrt{\frac{r_s}{r}}

(tendant même vers l'infini pour

r→0

) on obtient :

\displaystyle β''_e=β_e⊕β'_e=\frac{β_e+β'_e}{1+β_e \: β'_e}=\frac{2}{\sqrt{\frac{r}{r_s}} +\sqrt{\frac{r_s}{r}}}

qui n'est jamais supraluminique (si quelque chose était inapproprié pour

r<r_s

, ce serait

ℛ_0

). Ainsi, si le référentiel en contraction est justifié physiquement, celui en expansion l'est forcément aussi puisqu'on peut trouver un changement de référentiel valide qui passe de l'un à l'autre.
• Les tenants de l'existence des trous noirs suggèreront que si les deux référentiels sont possibles, il doit se produire une sorte de “brisure spontanée” de la symétrie mathématique, faisant ainsi que seul le cas en contraction a une réalité physique. D'autres physiciens concluront que c'est plutôt une incohérence du prolongement pour

r<r_s

qui est ainsi mise en évidence, rendant contradictoire l'hypothèse des trous noirs.

XIII. Coordonnées “isotropes”

• Avec les notations isotropes, la métrique (limitée à la partie radiale) s'écrit :

\displaystyle {ds}^2=A \:c^2 \,{dt}^2-\underline{C} \:{d\underline{r}}^2=A .\left[c^2 \,{dt}^2-\frac{\underline{C}}{A} \:{d\underline{r}}^2 \right]

;

\displaystyle A=\left(\frac{\underline{r}-\underline{r}_s}{\underline{r}+\underline{r}_s}\right)^2

;

\displaystyle \underline{C}=\left(\frac{\underline{r}+\underline{r}_s}{\underline{r}}\right)^4

;

\displaystyle \frac{\underline{C}}{A}=\frac{(\underline{r}+\underline{r}_s )^6}{\underline{r}^4.(\underline{r}-\underline{r}_s )^2}

;

\displaystyle \sqrt{\frac{\underline{C}}{A}}=\frac{(\underline{r}+\underline{r}_s )^3}{\underline{r}^2.|\underline{r}-\underline{r}_s |}

• Pour la chute libre verticale étudiée, la vitesse est :

\displaystyle v=-c \;\sqrt{1-A}=-c \: \frac{2\; \sqrt{\underline{r} \; \underline{r}_s}}{\underline{r}+\underline{r}_s}

.
◊ remarque : on vérifie que

\left|v\right|

passe par un maximum pour

\underline{r}=\underline{r}_s

.
• La transformation de Lorentz correspondante peut s'écrire :

\displaystyle d\underline{R}=\frac{d𝓁-β_e \: c \,{dt}_{𝓁oc}}{\sqrt{1-β_e^{\:2}}}

;

\displaystyle c \,d\underline{T}=\frac{c \,{dt}_{𝓁oc}-β_e \: d𝓁}{\sqrt{1-β_e^{\:2}}}

;

c \,{dt}_{𝓁oc}=\sqrt{A} \; c \,dt

;

d𝓁=\sqrt{\underline{C}} \; d\underline{r}

(algébrique).

• Ceci donne :

\displaystyle d\underline{R}=\frac{2 \;\sqrt{\underline{r} \; \underline{r}_s}}{\underline{r}+\underline{r}_s} \, c \,dt+\sqrt{\frac{\underline{C}}{A}} \;d\underline{r}

;

\displaystyle c \,d\underline{T}=c \,dt+\frac{2 \;\sqrt{\underline{r} \; \underline{r}_s}}{\underline{r}+\underline{r}_s} \, \sqrt{\frac{\underline{C}}{A}} \; d\underline{r}

.
• Pour construire une transformation de Lemaître généralisée adaptée à ces coordonnées, on est conduit à proposer :

\displaystyle dR=c \,dt+κ \;\sqrt{\frac{\underline{C}}{A}} \; d\underline{r}

;

\displaystyle c \,dT=c \,dt+f \;\sqrt{\frac{\underline{C}}{A}} \; d\underline{r}

;

\displaystyle f=\frac{1}{κ}=\frac{2 \;\sqrt{\underline{r} \; \underline{r}_s}}{\underline{r}+\underline{r}_s}

.
• On en déduit inversement :

\displaystyle dr=\frac{2 \:\underline{r}^2 \;\sqrt{\underline{r} \; \underline{r}_s}}{(\underline{r}+\underline{r}_s )^2.|\underline{r}-\underline{r}_s |} \: [dR-c \,dT]

;

\displaystyle c \,dt =\left(\frac{\underline{r}+\underline{r}_s}{\underline{r}-\underline{r}_s}\right)^2 c \,dT-\frac{4 \;\sqrt{\underline{r}\; \underline{r}_s}}{(\underline{r}-\underline{r}_s )^2} \: dR

• En substituant, ceci donne une métrique sans singularité :

{ds}^2=c^2 \,{dT}^2-f^2 \:{dR}^2

.

• On obtient alors :

\displaystyle d(R-c\,T)=(κ-f) \:\sqrt{\frac{\underline{C}}{A}} \; d\underline{r}=\frac{(\underline{r}+\underline{r}_s )^2.|\underline{r}-\underline{r}_s |}{2 \:\underline{r}^2 \; \sqrt{\underline{r} \; \underline{r}_s} } \;d\underline{r}

.
• Pour

\underline{r}>1

(avec

\underline{r}_s

comme unité), en passant par

u=\sqrt{\underline{r}}

l'intégration donne :

\displaystyle d(R-c \,T)=\frac{(u^2+1)^2}{2 \,u^3} \: 2 \,u \:du-\frac{(u^2+1)^2}{2 \,u^5} \: 2 \,u \:du

;

\displaystyle d(R-c \,T)=\frac{u^4+2\,u^2+1}{u^2} \: du-\frac{u^4+2\,u^2+1}{u^4} \:du

;

\displaystyle R-c \,T=\frac{1}{3} \: \left(u+\frac{1}{u}\right)^3+Cste

; minimum pour

u=1

• Pour

\underline{r}<1

(avec

\underline{r}_s

comme unité), l'intégration donne de même :

\displaystyle R-c \,T=-\frac{1}{3} \: \left(u+\frac{1}{u}\right)^3+Cste

; maximum pour

u=1

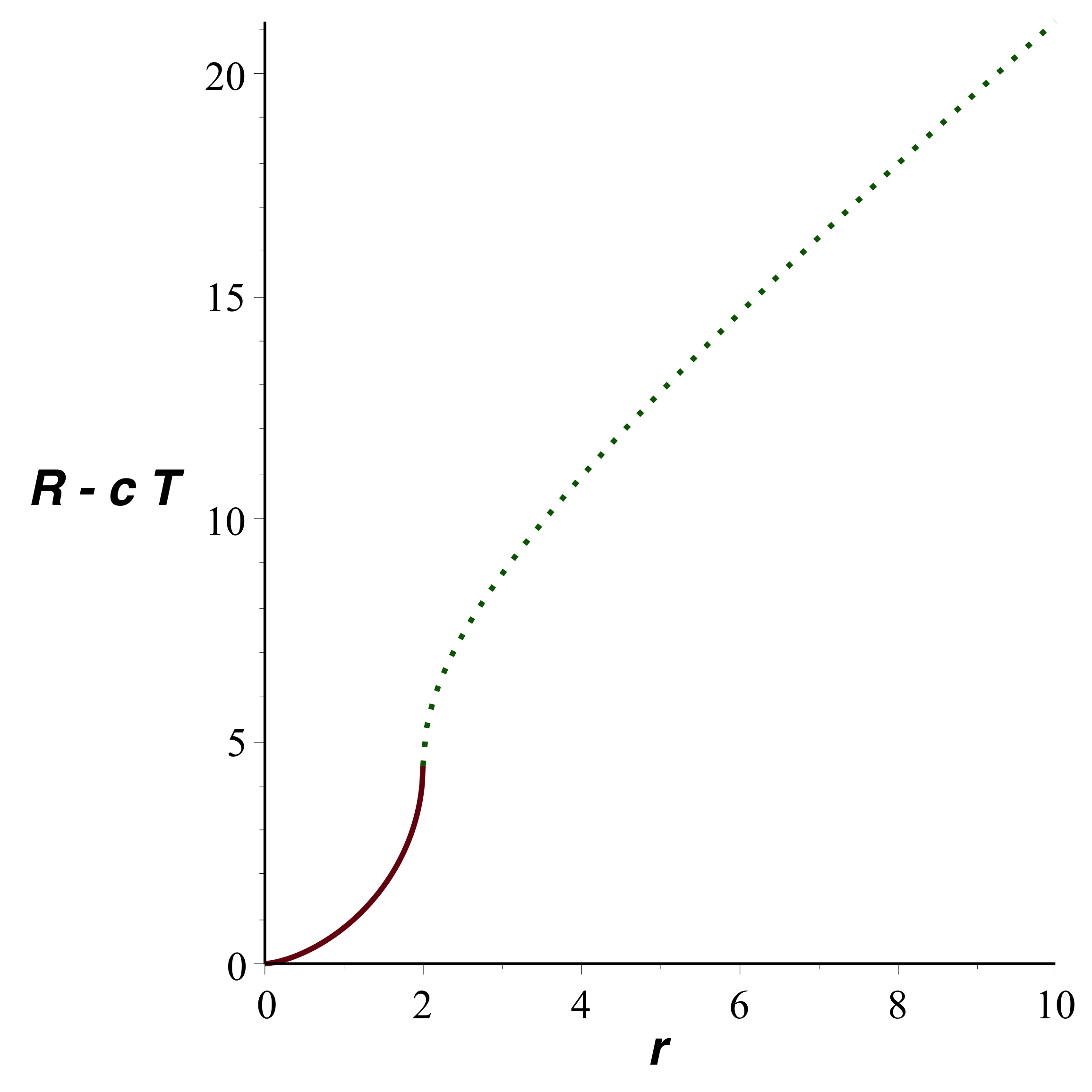
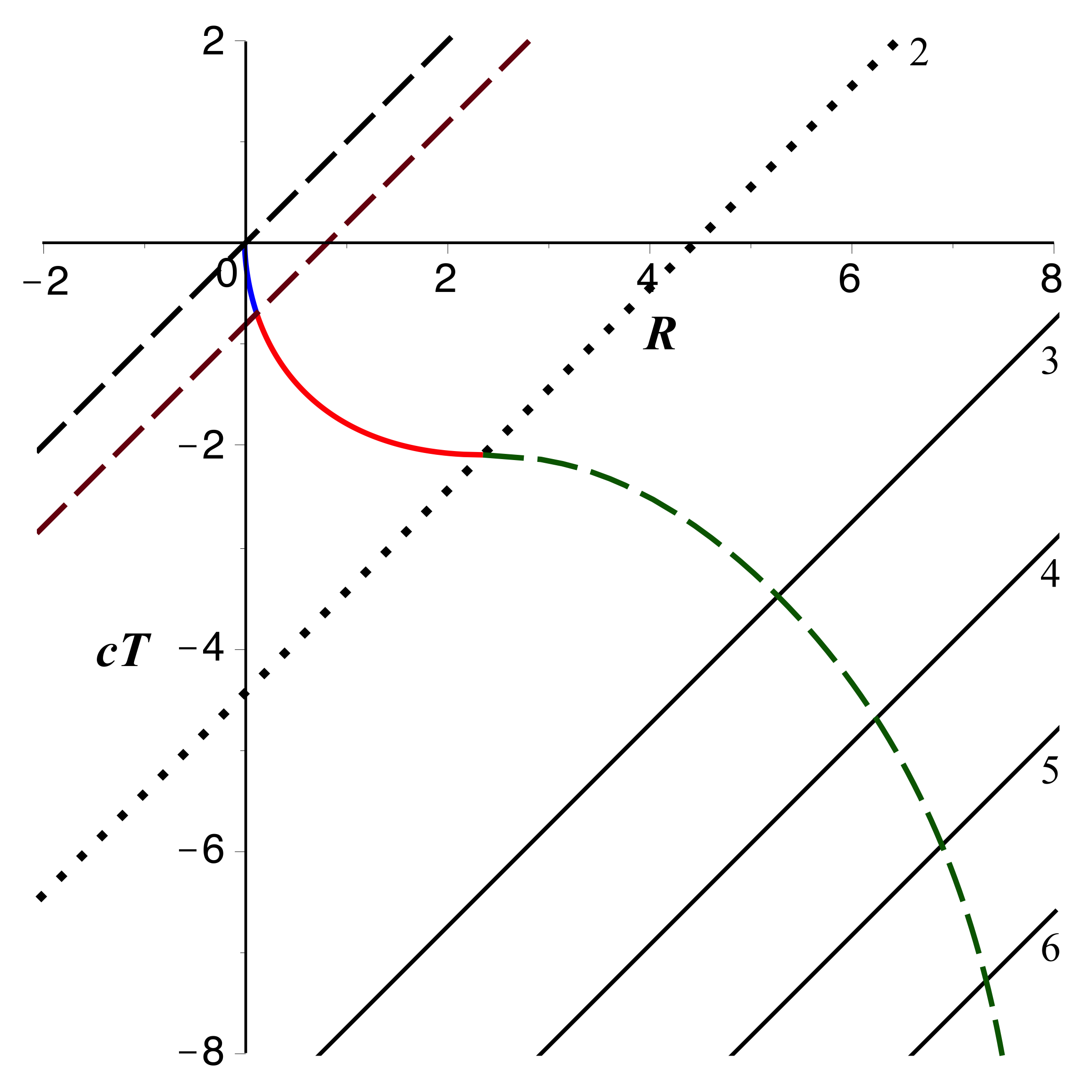
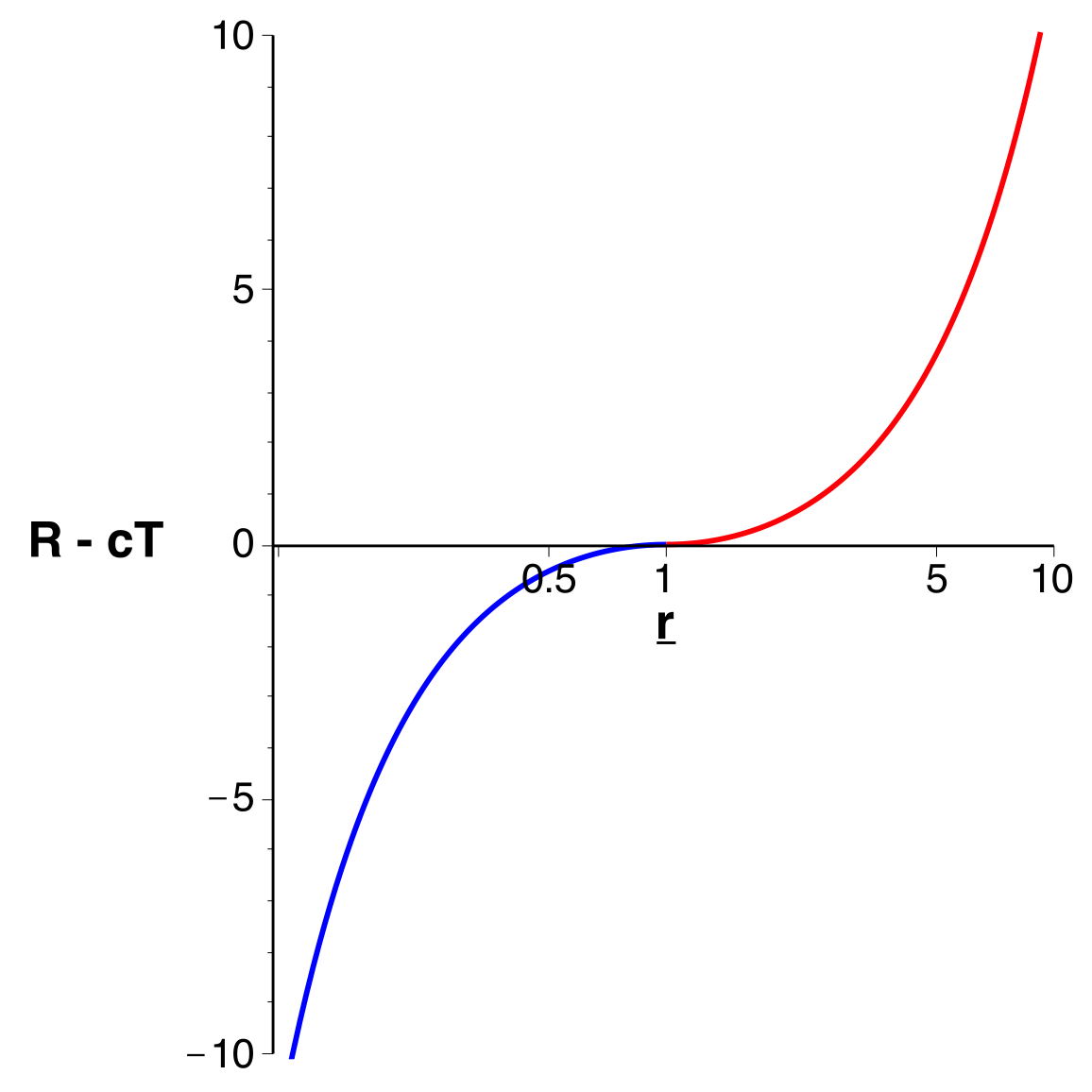
• Le raccordement pour

\underline{r}=\underline{r}_s

donne finalement :

\displaystyle R-c \,T=-\frac{8 \,\mathrm{sgn}⁡(\underline{r}-\underline{r}_s )}{3} \: \left(\left(\frac{\underline{r}+\underline{r}_s}{2 \:\sqrt{\underline{r} \; \underline{r}_s}}\right)^3-1\right)+Cste

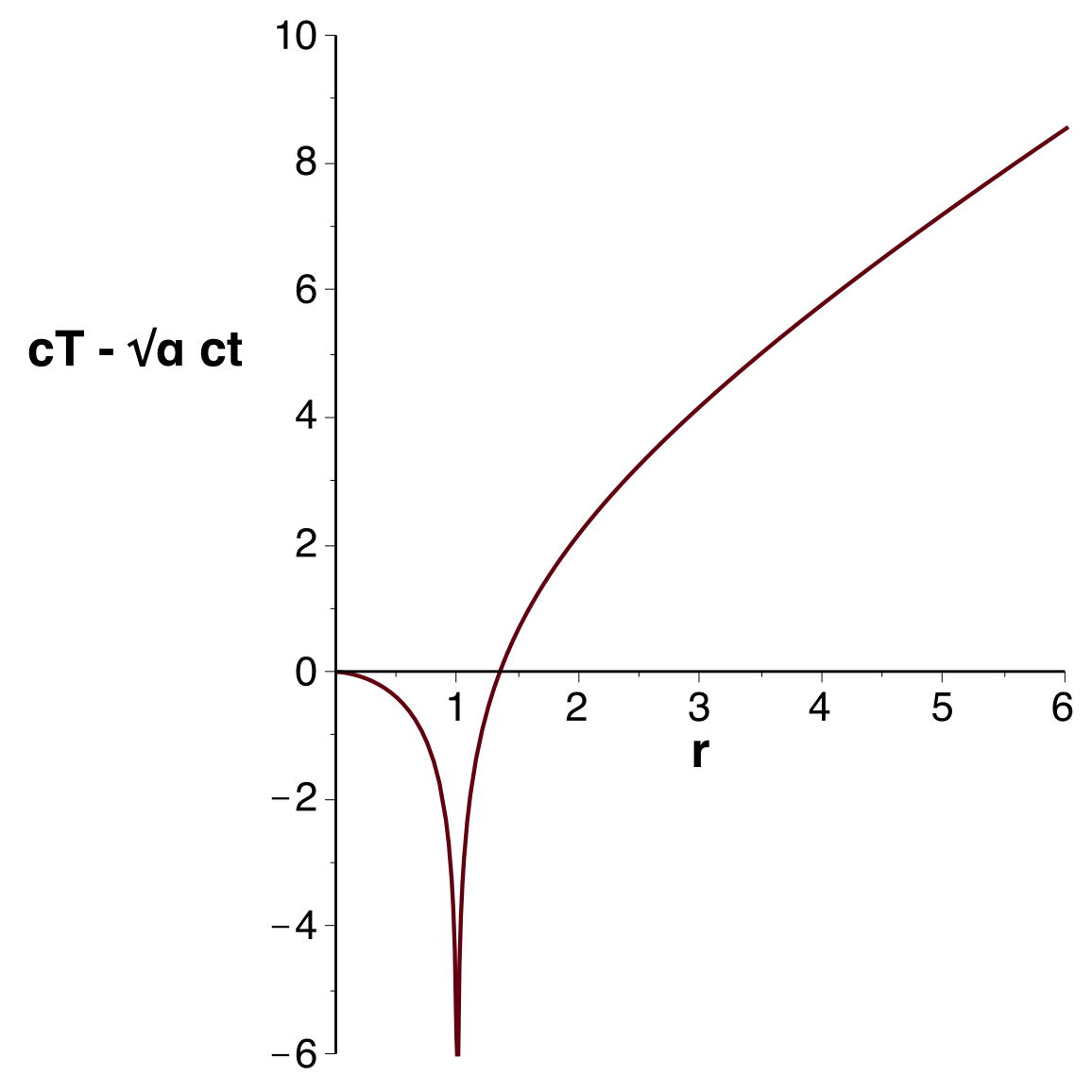
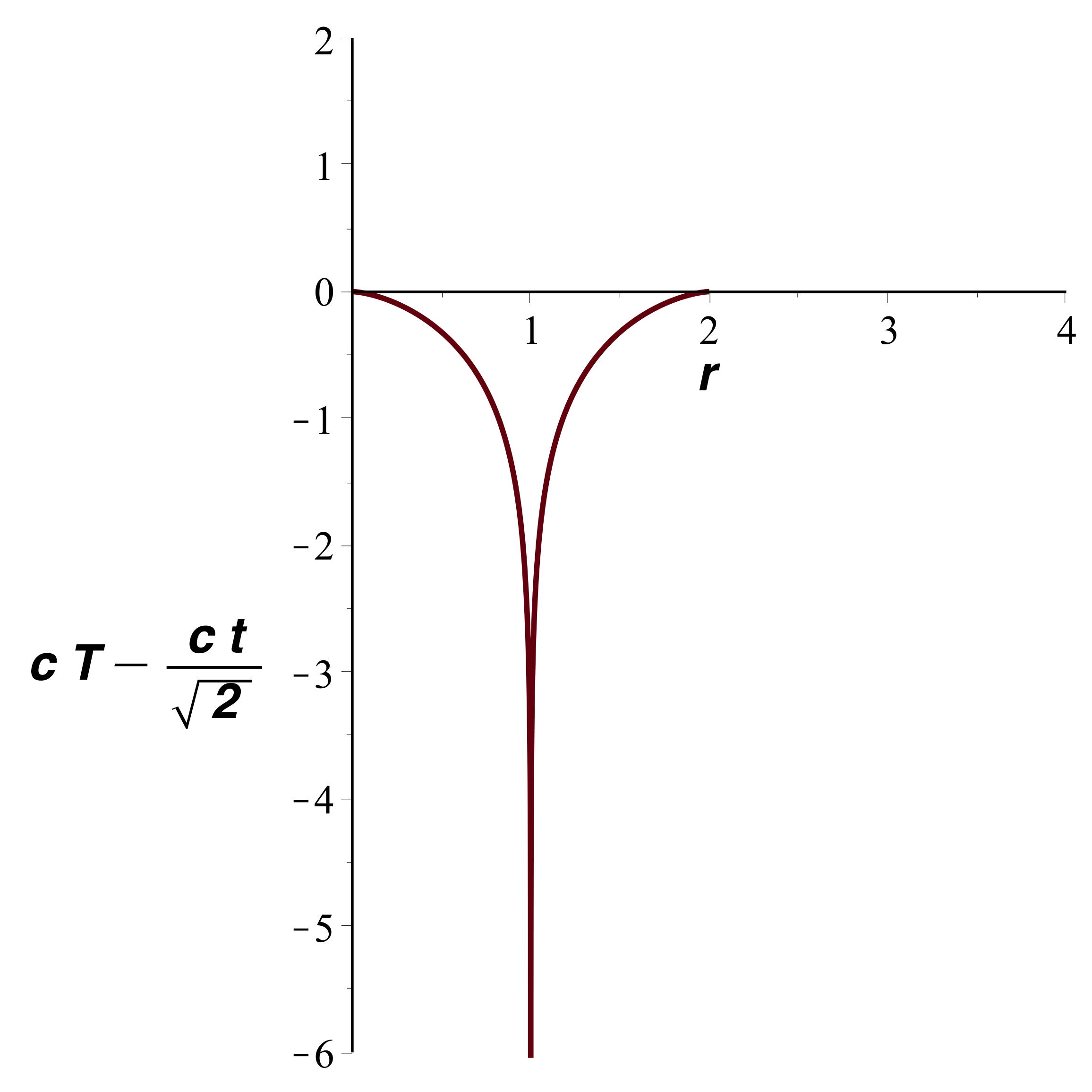
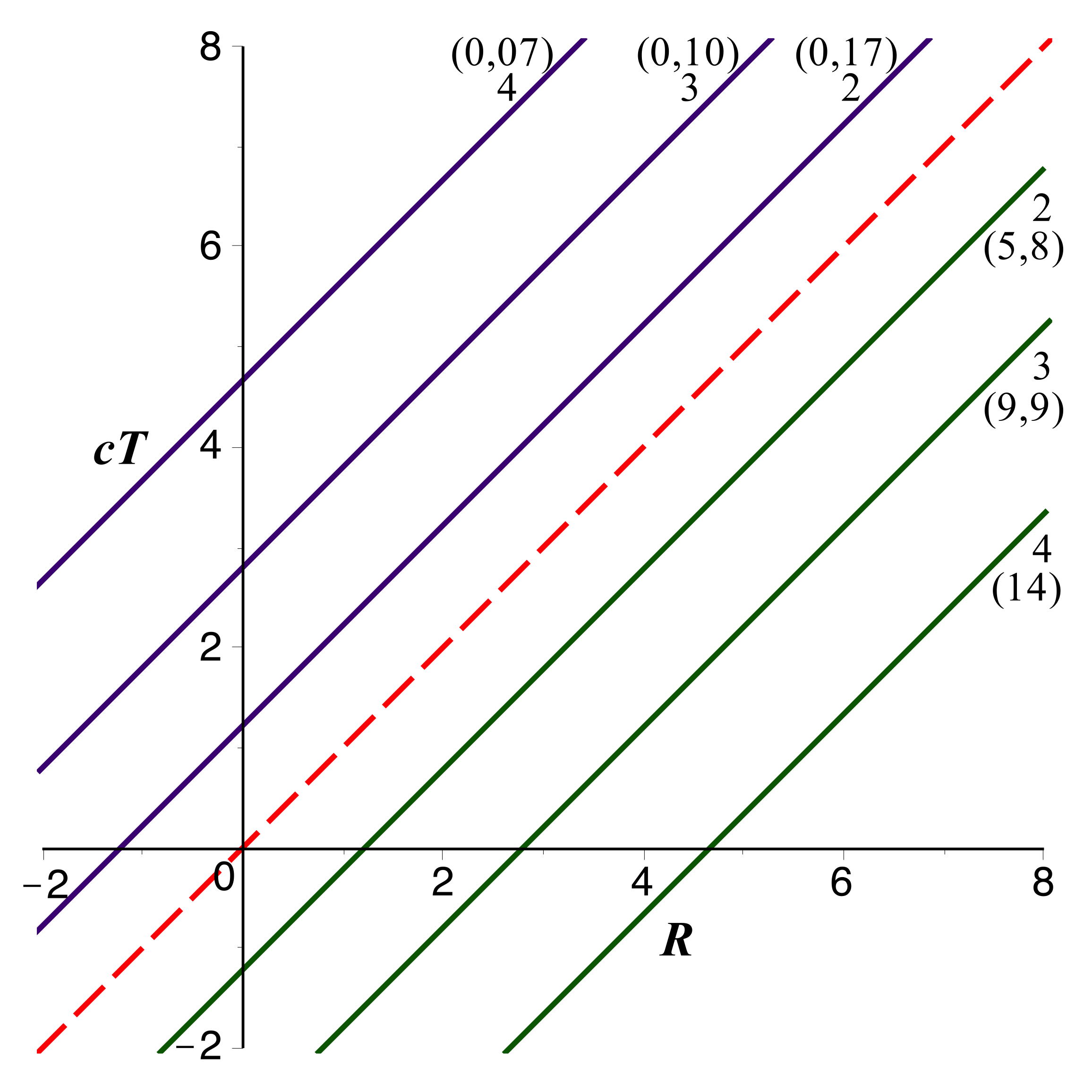
• Avec une échelle horizontale logarithmique (mieux adaptée aux coordonnées isotropes), on obtient la représentation suivante (avec

\underline{r}_s

comme unité).

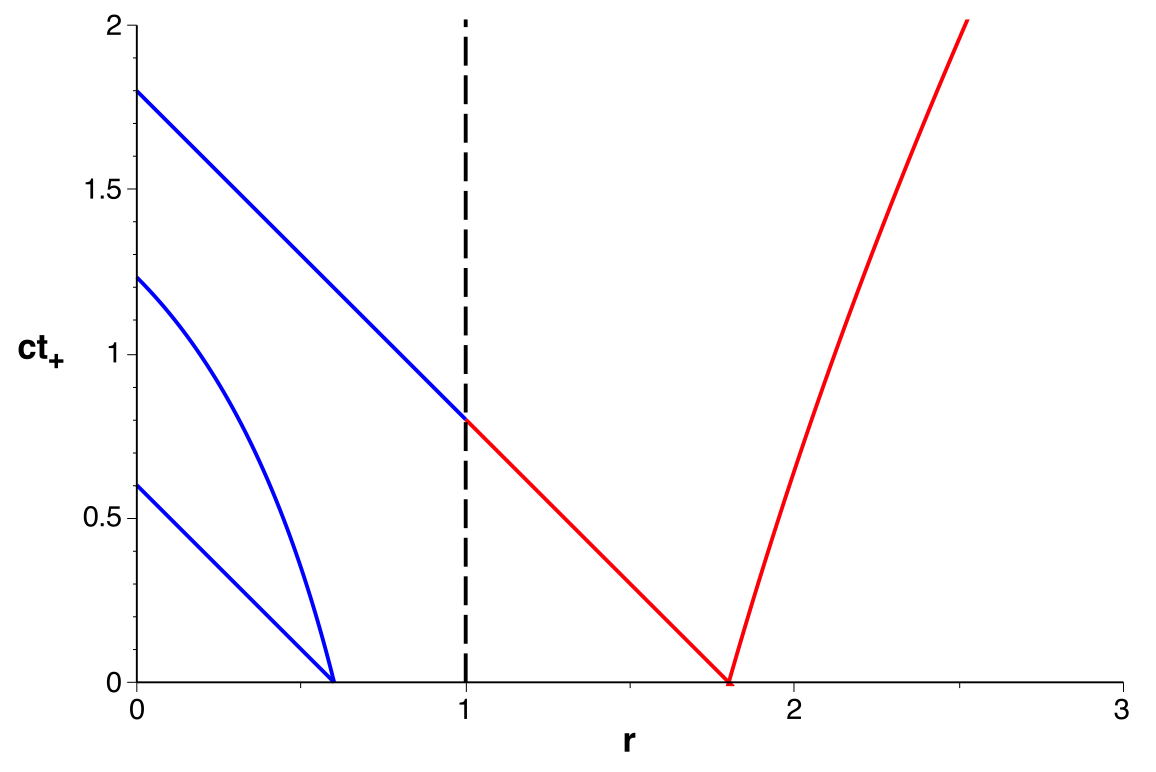
◊ remarque : c'est qualitativement ce qu'on obtient avec la coordonnée

r

“classique” en raccordant les zones

r>r_s

en contraction puis en expansion (de l'autre côté de l'horizon), après élimination des zones

r<r_s

; le raccordement est sans problème car ici

A

\underline{C}

ne changent pas de signe.

• On obtient par ailleurs :

\displaystyle d(c \,T-c \,t)=f \;\sqrt{\frac{\underline{C}}{A}} \; d\underline{r}=\frac{2 \;\sqrt{\underline{r} \; \underline{r}_s} \;(\underline{r}+\underline{r}_s )^2}{\underline{r}^2.|\underline{r}-\underline{r}_s |} \: d\underline{r}

.
• Pour

\underline{r}>1

(avec

\underline{r}_s

comme unité), en passant par

u=\sqrt{\underline{r}}

l'intégration donne :

\displaystyle d(c \,T-c \,t)=-\frac{2 \:\sqrt{\underline{r}}}{\underline{r}^2} \: d\underline{r}-\frac{3 \:\sqrt{\underline{r}}}{\underline{r}} \: d\underline{r}+\frac{8 \:\sqrt{\underline{r}}}{\underline{r}-1} \: d\underline{r} =-\frac{4}{u^2} \: du-12 \:du+\frac{16 \:u^2}{u^2-1} \: du

;

\displaystyle d(c \,T-c \,t)=-\frac{4}{u^2} \: du+4 \:du+\frac{8}{u-1} \: du-\frac{8}{u+1} \: du

;

\displaystyle c \,T-c \,t=4\: \left(u+\frac{1}{u}\right)+8 \; \ln\left(\left|\frac{u-1}{u+1}\right|\right)+Cste

• Pour

\underline{r}<1

(avec

\underline{r}_s

comme unité), l'intégration donne de même :

\displaystyle c \,T-c \,t=-4\: \left(u+\frac{1}{u}\right)-8 \; \ln\left(\left|\frac{u-1}{u+1}\right|\right)+Cste

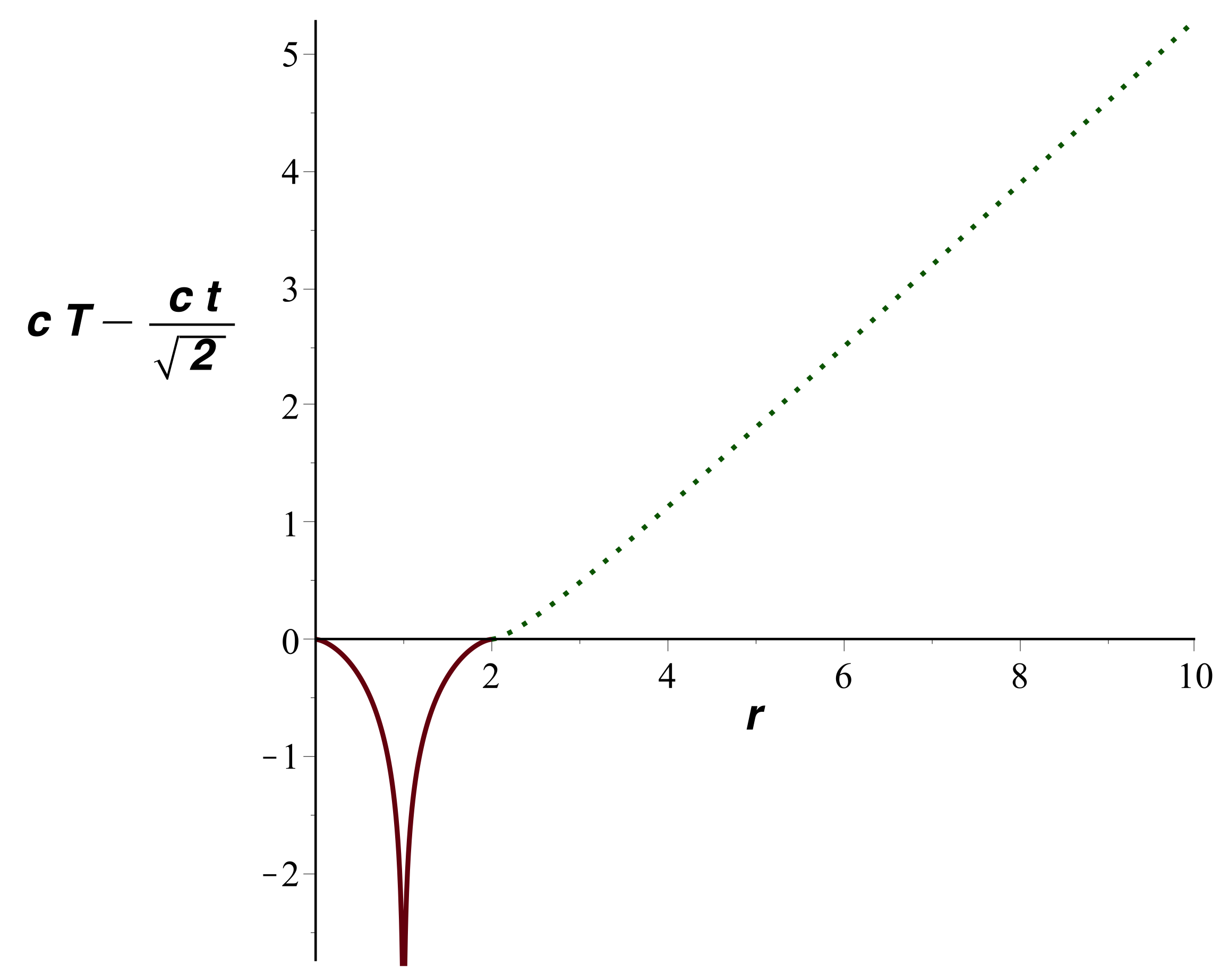
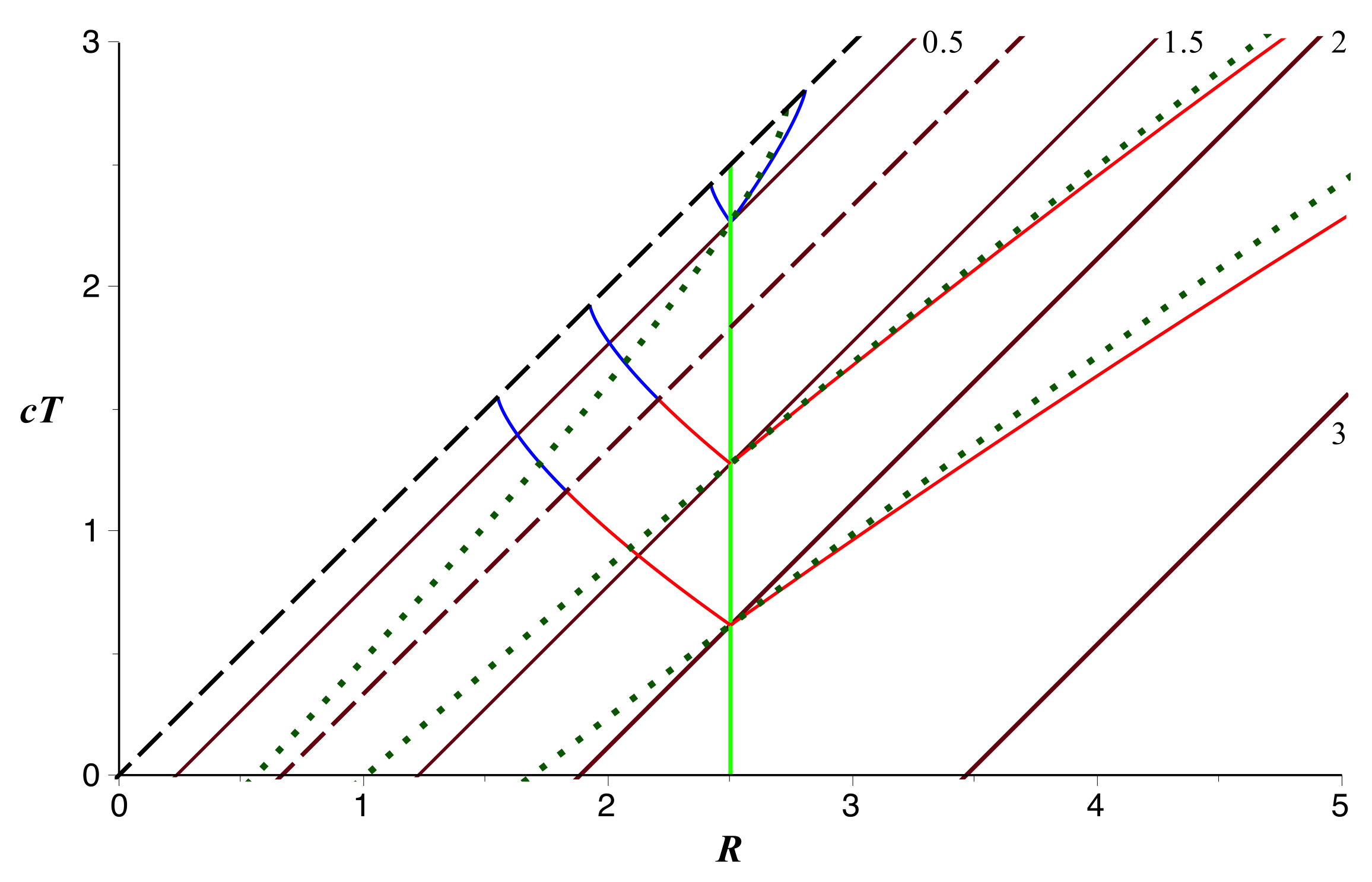
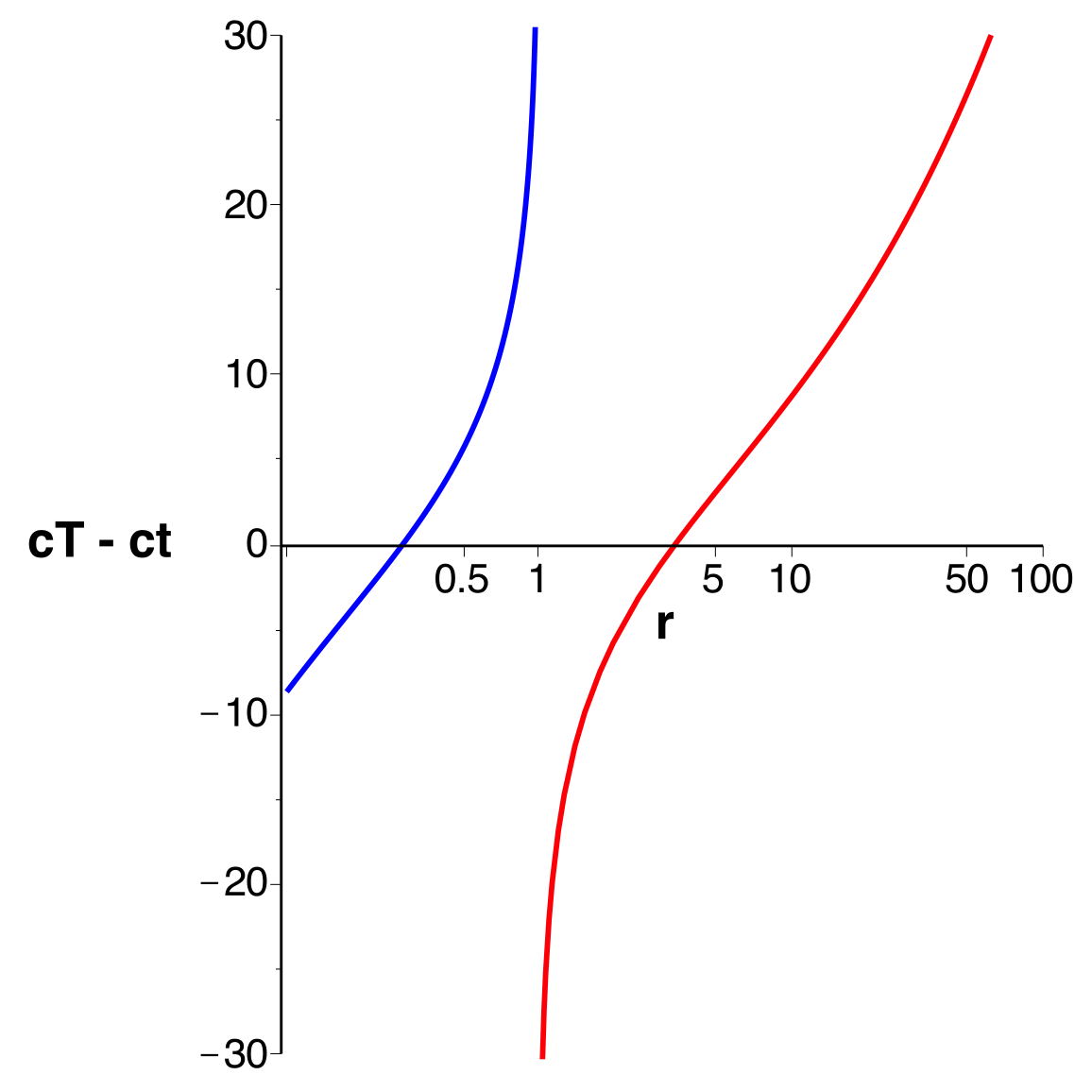
• Le raccordement pour

\underline{r}=\underline{r}_s

donne finalement :

\displaystyle c \,T-c \,t=8 \; \mathrm{sgn}(\underline{r}-\underline{r}_s ) \: \left[\frac{\underline{r}+\underline{r}_s}{2 \;\sqrt{\underline{r}\; \underline{r}_s}}+\ln\left(\left|\frac{\sqrt{\underline{r}}-\sqrt{\underline{r}_s}}{\sqrt{\underline{r}}+\sqrt{\underline{r}_s}}\right|\right) \right]

◊ remarque : ici a priori, il n'y a pas de composante imaginaire pour

\underline{r}<\underline{r}_s

car on intègre

\displaystyle \frac{1}{|\underline{r}-\underline{r}_s |}

; il n'y en a alors ni pour

c \,t

ni pour

c \,T

.
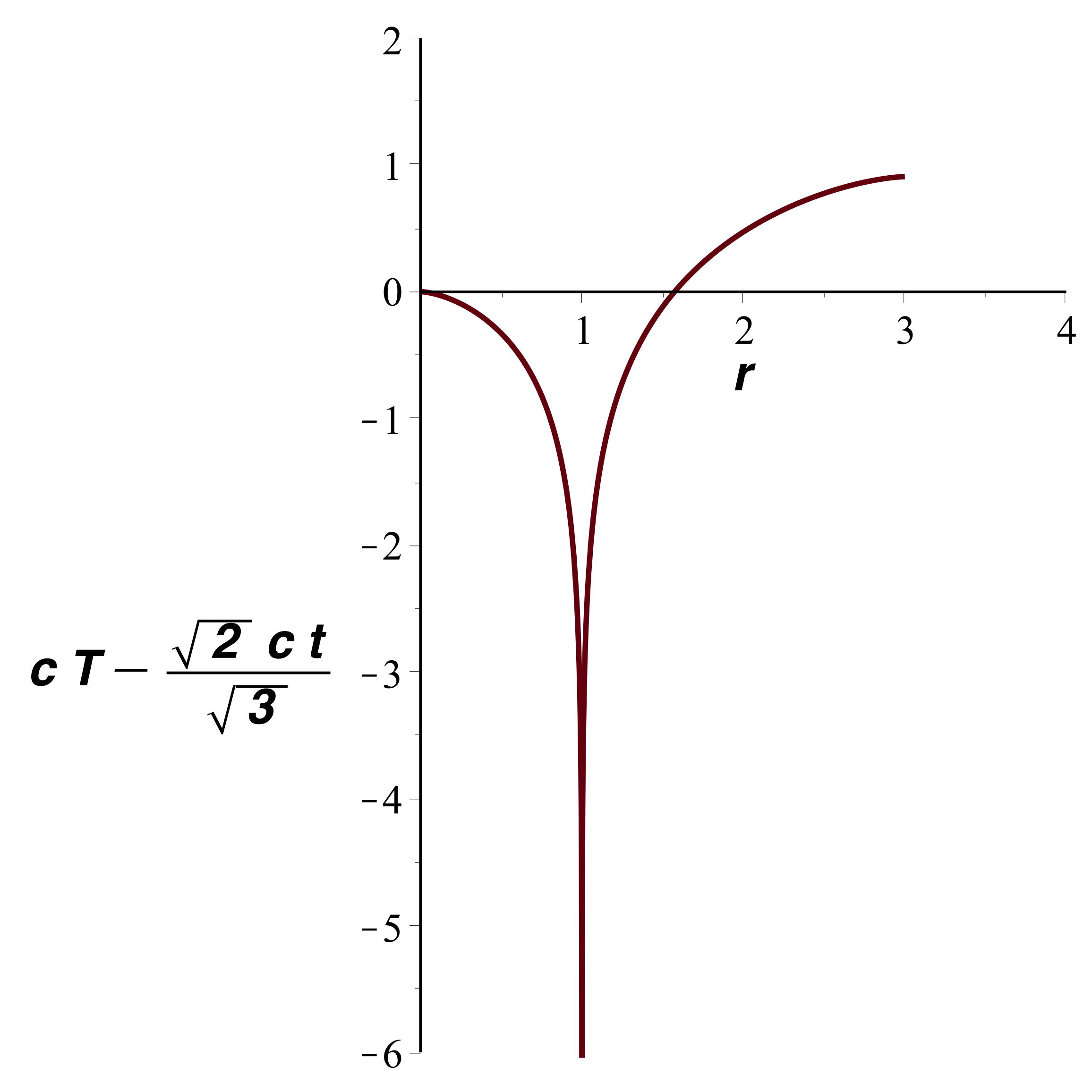
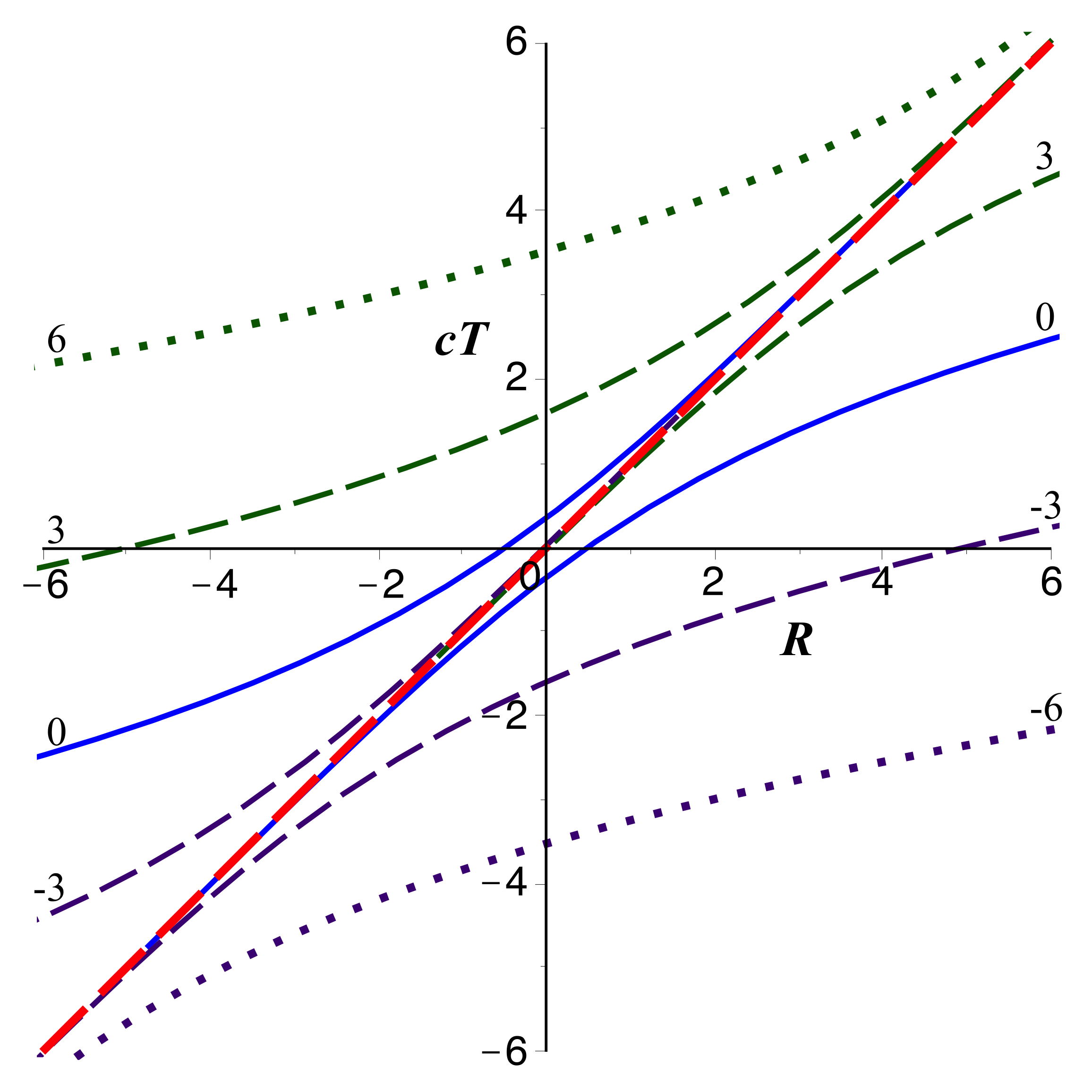
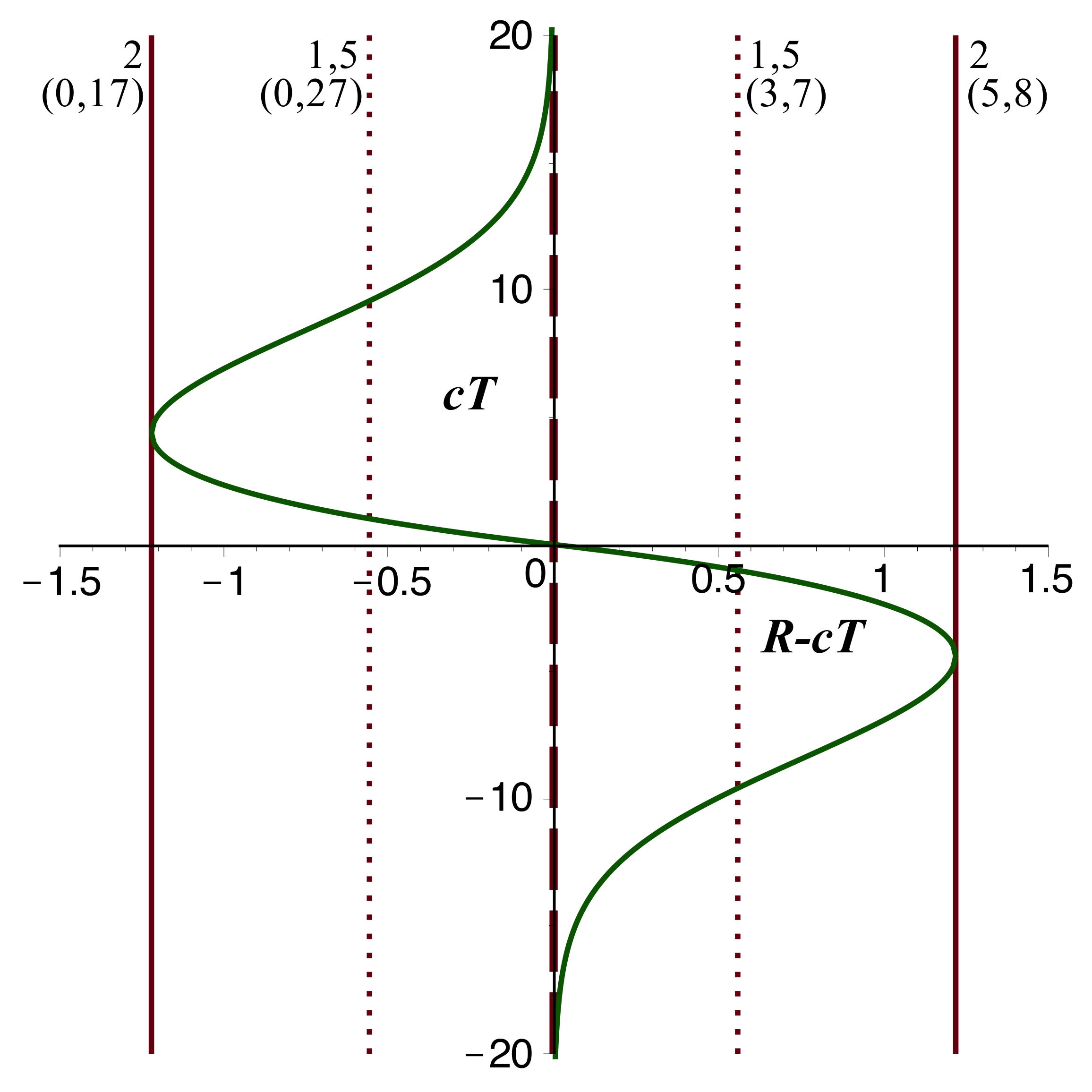
• Avec une échelle horizontale logarithmique (mieux adaptée aux coordonnées isotropes), on obtient la représentation ci-après (avec

\underline{r}_s

comme unité).
◊ remarque : ici la convention de signe pour

c \,t

dans la région

\underline{r}<\underline{r}_s

est conforme à

A>0

, dans la mesure où l'équation du mouvement

\displaystyle A \: \frac{c \,dt}{ds}=Cste

indique que

c \,t

reste croissant.

• Les lignes caractérisant

\underline{r}(R,c \,T)=Cste

sont ici encore des droites, mais leur écartement tend vers l'infini quand

\underline{r}→0

. Ceci est associé au fait que dans ces conditions la variable “classique”

r

recroît vers l'infini.
• On peut tracer un diagramme de la façon usuelle, mais il est préférable d'adapter le choix (arbitraire) de l'origine :

R=0

T=0

pour

r=r_s

(comme

\underline{r}=\underline{r}_s

) et

t=±∞

.
• Pour

\underline{r}≥\underline{r}_s

r≥r_s

;

\displaystyle d(R-c \,T)=\sqrt{\frac{r}{r_s}} \; dr

;

\displaystyle R-c \,T=\frac{2 \,r_s}{3} \: \left(\left(\frac{r}{r_s} \right)^{3/2}-1\right)

.
• Pour

\underline{r}≤\underline{r}_s

r≥r_s

;

\displaystyle d(R-c \,T)=-\sqrt{\frac{r}{r_s}} \; dr

;

\displaystyle R-c \,T=-\frac{2 \,r_s}{3} \: \left(\left(\frac{r}{r_s} \right)^{3/2}-1\right)

• Pour

\underline{r}≥\underline{r}_s

r≥r_s

;

κ=\sqrt{r}

(avec

r_s=1

) ;

\displaystyle c \,T=c \,t+2 \,κ-\ln\left(\left|\frac{κ+1}{κ-1}\right|\right)

;

\displaystyle R=c \,T+\frac{2 \,r_s}{3} \, (κ^3-1)

.
• Pour

\underline{r}≤\underline{r}_s

r≥r_s

;

κ=\sqrt{r}

;

\displaystyle c \,T=c \,t-2 \,κ+\ln\left(\left|\frac{κ+1}{κ-1}\right|\right)

;

\displaystyle R=c \,T-\frac{2 \,r_s}{3} \, (κ^3-1)

.
◊ remarque : pour

\underline{r}≤\underline{r}_s

on utilise

κ>0

bien que

r

augmente, car

\underline{r}

diminue (contraction).
◊ remarque : ici la constante d'intégration de

c \,t

est “arbitraire” (choisie nulle, comme pour le cas “classique” de Lemaître) car on ne peut pas raccorder à l'infini.

• Pour représenter les oscillations de part et d'autre de l'horizon, on peut utiliser l'expression de la vitesse de chute, reliant

c \,dt

dr

\displaystyle v=\frac{\,dr}{A \,dt}=c \;\sqrt{1-\frac{A}{A_0}}

.
• Pour une particule en chute libre radiale, avec un somment en

r_0

, l'intégration donne (avec les signes supérieurs pour la montée) :

\displaystyle c \,t=c \,t_0∓\sqrt{κ^2.(2-κ^2 )}∓2 \, \arccos⁡(κ^2-1)∓\mathrm{arcosh}\left(\frac{1}{|κ^2-1|} \right)

, où

t_0

est l'instant de passage au sommet.
• Ainsi :

\displaystyle c \,T=∓\sqrt{κ^2.(2-κ^2 )}∓2 \, \arccos⁡(κ^2-1)∓\mathrm{arcosh}\left(\frac{1}{|κ^2-1|} \right)+2 \,κ-\ln\left(\left|\frac{κ+1}{κ-1}\right|\right)+Cste

.
• On peut alors choisir l'origine du temps

T

(arbitraire) à l'instant où la chute atteint l'horizon (en fait cela fixe

t_0

). Mais ce cas particulier (

κ=1

) correspond à un point à l'infini dans le repérage

(r,c \,t)

; il faut donc simplifier pour passer à la limite :

\displaystyle \mathrm{arcosh}\left(\frac{1}{|κ^2-1|} \right)-\ln\left(\left|\frac{κ+1}{κ-1}\right|\right)=\ln\left(\frac{1+\sqrt{κ^2.(2-κ^2 )}}{|κ+1|.|κ-1|}\right)-\ln\left(\left|\frac{κ+1}{κ-1}\right|\right)=\ln\left(\frac{1+\sqrt{κ^2.(2-κ^2 )}}{(κ+1)^2} \right)

• On obtient ainsi :

Cste=\ln(2)-π-3

. Ceci donne une représentation paramétrique de la première moitié de la courbe ; l'autre moitié est symétrique par rapport à l'origine.
• Il est alors plus lisible de tracer le graphique en fonction de l'abscisse

R-c \,T

(plutôt que

R

), afin de recadrer facilement l'échelle verticale.