RG VI - INTERPRÉTATION DU CHAMP SPHÉR. EXTÉRIEUR
1. Comparaison de différentes expressions
1.1. Liberté de choix de coordonnées pour un espace physique
• On dispose d'une certaine liberté pour choisir les variables mathématiques décrivant un espace physique donné. Il est utile de les comparer pour vérifier qu'elles décrivent bien la même situation physique.
S'il peut exister plusieurs solutions mathématiques décrivant des espaces physiques différents, il semble peu plausible (sauf en cas de symétrie spontanément brisée) qu'il existe plusieurs solutions physiques dans des conditions données. Il faut alors déterminer laquelle des solutions mathématiques décrit le cas physique étudié.
Cette partie traite principalement (mais non uniquement) des aspects associés aux coordonnées statiques “classiques” et “isotropes” décrites précédemment.
1.2. Temps-date et temps-durée
• Une propriété commune aux différentes métriques “usuelles”, pour un champ central sphérique, est l'utilisation d'une variable
t
t
(temps-date) en principe définie de façon univoque dans tout l'espace.
Ceci exprime la possibilité de définir une notion de simultanéité et de synchroniser les horloges à un “instant donné” pour toutes les horloges immobiles par rapport à ce repérage.
◊ remarque : pour des unités plus cohérentes, on utilise généralement plutôt
x
0
=
c
t
x^0=c \,t
, ce qui n'interdit pas des expressions “en fonction de
t
t
”.
• Cependant, contrairement à la relativité restreinte, l'intervalle de temps-durée dépend du lieu :
d
t
𝓁
o
c
=
g
00
d
t
≠
d
t
dt_{𝓁oc}=\sqrt{g_{00}} \;dt≠dt
.
Ainsi les horloges fixes (dont les indications évoluent selon le temps-durée local) ne restent pas synchronisées.
◊ remarque : dans un espace courbe, cette situation en réalité assez banale est analogue à celle des coordonnées polaires, pour lesquelles la longueur d'arc
d
𝓁
=
r
d
θ
d𝓁=r \:dθ
n'est pas la simple variation
d
θ
dθ
de la coordonnée
θ
θ
.
• Avec la coordonnée
r
r
“classique”, cela pose problème pour
r
<
r
s
r<r_s
(horizon des événements) car
g
00
=
A
<
0
g_{00}=A<0
.
Cela peut être résolu par une transformation de type Lorentz (repérages de Lemaître, Kruskal/Szekeres ou Novikov, étudiés dans des parties ultérieures), mais c'est un comportement notablement différent de celui de la coordonnée
r
_
\underline{r}
“isotrope”, pour laquelle
A
(
r
_
s
)
=
0
A(\underline{r}_s)=0
mais
g
00
≥
0
g_{00}≥0
partout.
◊ remarque : pour
A
<
0
A<0
la variable
t
t
n'est plus “du genre temps” (mais ceci n'interdit pas de l'utiliser pour décrire l'évolution d'une particule).
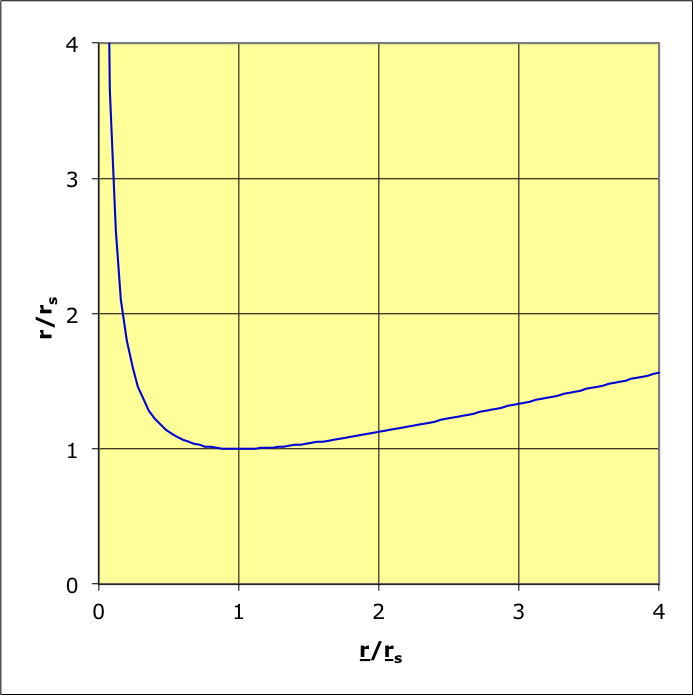
1.3. Valeurs particulières
• Ces expressions différentes de la métrique sont équivalentes à l'infini, car les coordonnées radiales
r
r
et
r
_
\underline{r}
le sont.
Elles présentent par ailleurs de même une singularité spatiale pour des valeurs qui se correspondent, mais sont différentes :
r
=
r
s
r=r_s
;
r
_
=
r
_
s
=
r
s
4
\displaystyle \underline{r}=\underline{r}_s=\frac{r_s}{4}
.
• Par contre, l'origine des coordonnées n'est pas claire. Avec la variable
r
r
“classique”
g
11
=
−
C
g_{11}=-C
diverge avec changement de signe pour
r
=
r
s
r=r_s
.
Au contraire avec la variable
r
_
\underline{r}
“isotrope”
C
_
\underline{C}
varie régulièrement pour
r
_
=
r
_
s
\underline{r}=\underline{r}_s
et
g
11
<
0
g_{11}<0
partout.
◊ remarque : pour
C
<
0
C<0
la variable
r
r
n'est plus “du genre espace” (mais ceci n'interdit pas de l'utiliser pour repérer la position d'une particule).
• D'après les comparaisons dans les parties précédentes, un point en mouvement radial vers l'origine selon
r
_
\underline{r}
décroissant, traversant la singularité pour
r
_
=
r
_
s
\underline{r}=\underline{r}_s
, repart vers l'infini par rapport à
r
=
r
_
.
(
1
+
r
_
s
r
_
)
2
\displaystyle r=\underline{r} \,.\left(1+\frac{\underline{r}_s}{\underline{r}}\right)^2
.
Si on admet l'hypothèse selon laquelle
r
_
<
r
_
s
\underline{r}<\underline{r}_s
correspond à
r
>
r
s
r>r_s
(croissant à nouveau), alors
A
(
r
)
≥
0
A(r)≥0
partout ; la divergence de
C
(
r
)
C(r)
subsiste, mais sans changement de signe. Cela rend les deux métriques plus compatibles mais indique que, selon l'interprétation, elles peuvent correspondre ou non à la même solution physique.
Cela est incompatible avec la notion de carte d'une variété topologique (ou différentielle), qui doit être bijective. Ou bien on admet qu'il existe deux solutions physiques, chacune décrite par l'une de ces deux coordonnées (dans deux contextes différents), ou bien il faut considérer que le domaine de validité physique de l'une au moins des deux coordonnées doit être limité.
• Certes, pour la plupart des astres, cette singularité est trop proche du centre pour être à l'extérieur (donc elle n'intervient pas physiquement) :
◊
pour la Terre :
r
s
≈
9
m
m
≪
R
≈
6400
k
m
r_s≈9 \:\mathrm{mm}≪R≈6400 \:\mathrm{km}
;
◊
pour le Soleil :
r
s
≈
3
k
m
≪
R
≈
700000
k
m
r_s≈3 \:\mathrm{km}≪R≈700000 \:\mathrm{km}
.
La question peut par contre se poser pour des astres d'extrêmement grande densité.
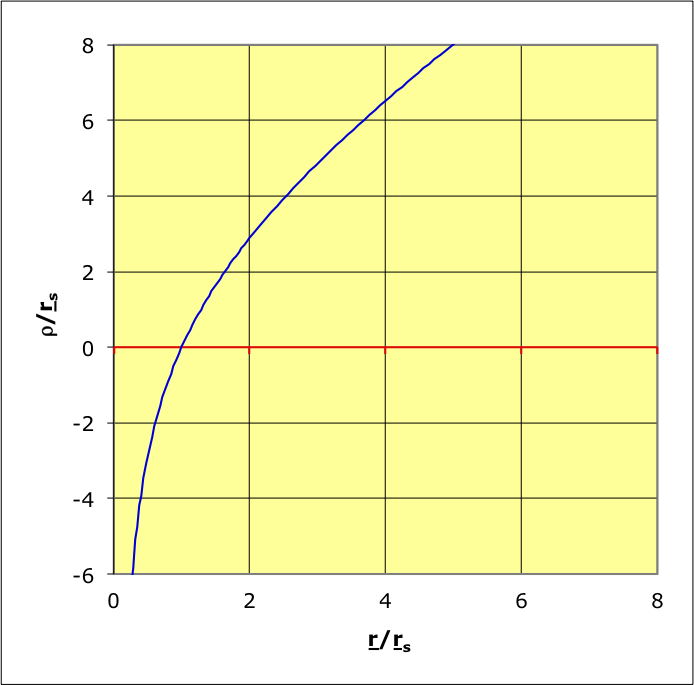
1.4. Distances radiales
• Avec une description statique, on peut considérer la coordonnée
r
_
\underline{r}
en termes de distance radiale :
d
𝓁
=
(
1
+
r
_
s
r
_
)
2
d
r
_
=
d
ρ
\displaystyled𝓁=\left(1+\frac{\underline{r}_s}{\underline{r}}\right)^2 \,d\underline{r}=dρ
(“longueur” nommée
ρ
ρ
).
On obtient un résultat régulier pour
r
_
=
r
_
s
\underline{r}=\underline{r}_s
:
ρ
=
r
_
s
ln
(
r
_
2
r
_
s
2
)
+
r
_
.
(
1
−
r
_
s
2
r
_
2
)
+
C
s
t
e
\displaystyle ρ=\underline{r}_s \:\ln\left(\frac{\underline{r}^2}{\underline{r}_s^{\:2}}\right)+\underline{r} \,.\left(1-\frac{\underline{r}_s^{\:2}}{\underline{r}^2} \right)+Cste
.
◊ remarque : la constante d'intégration rappelle ici que le choix de l'équivalence à l'infini avec le modèle newtonien ne fixe pas totalement la métrique ; on peut entre autres ajouter une constante arbitraire à la variable radiale.
• On obtient au contraire pour la coordonnée
r
r
“classique” (en admettant une variation non monotone pour pouvoir prolonger) :
d
𝓁
=
±
1
1
−
r
s
r
d
r
=
d
ρ
\displaystyle d𝓁=±\frac{1}{\sqrt{1-\frac{r_s}{r}}} \,dr=dρ
;
ρ
=
±
(
r
s
a
r
t
a
n
h
(
1
−
r
s
r
)
+
r
1
−
r
s
r
)
+
C
s
t
e
\displaystyle ρ=±\left(r_s \:\mathrm{artanh}\left(\sqrt{1-\frac{r_s}{r}}\right)+r \;\sqrt{1-\frac{r_s}{r}}\right)+Cste
.
• La solution proposée initialement par Schwarzschild n'était en fait pas celle à laquelle son nom a été “classiquement” associé. De nombreuses variantes ont été proposées, à l'époque et par la suite, mais en cherchant quelles contraintes mathématiques on pourrait imposer pour éviter les divergences, alors que c'est sur l'interprétation physique qu'il est souhaitable de chercher.
• Certains, se basant sur les approches comme celle de Lemaître (associée à une transformation de Lorentz supraluminique), réfutent le changement de sens de variation de
r
r
, jugeant préférable de considérer que l'origine des valeurs de
r
r
correspond au cas où le périmètre d'un cercle s'annule :
r
=
0
r=0
(donc avec une divergence pour
r
=
r
s
r=r_s
).
Ceci suppose que la coordonnée isotrope
r
_
\underline{r}
n'est pas physiquement acceptable au delà (hypothèse non totalement justifiée car la méthode de Lemaître peut se généraliser pour la notation isotrope).
• D'autres (par exemple L. S. Abrams) jugent préférable de supposer que l'origine correspond à une singularité comme pour le potentiel newtonien, en posant :
r
˜
=
r
−
r
s
\tilde{r}=r-r_s
(mais n'en donnent pas de justification complète).
Ceci revient à utiliser une métrique “recentrée” :
d
s
2
=
A
(
r
˜
)
c
2
d
t
2
−
C
(
r
˜
)
d
r
˜
2
−
(
r
˜
+
r
s
)
2
d
Ω
2
{ds}^2=A(\tilde{r}) \:c^2 \,{dt}^2-C(\tilde{r}) \:{d\tilde{r}}^2-(\tilde{r}+r_s)^2 \:{dΩ}^2
;
C
=
1
+
r
s
r
˜
\displaystyle C=1+\frac{r_s}{\tilde{r}}
;
A
=
1
C
\displaystyle A=\frac{1}{C}
;
ρ
=
r
s
a
r
c
o
t
h
(
1
+
r
s
r
˜
)
+
r
˜
1
+
r
s
r
˜
+
C
s
t
e
\displaystyle ρ=r_s \:\mathrm{arcoth}\left(\sqrt{1+\frac{r_s}{\tilde{r}}}\right)+\tilde{r} \;\sqrt{1+\frac{r_s}{\tilde{r}}}+Cste
.
◊ remarque : l'option d'un recentrage a l'avantage de supprimer les différences d'interprétation entre les diverses variables radiales envisagées, puisque cela ne concerne que la région au delà de l'horizon ; cela implique par contre qu'une sphère centrée de rayon nul a un périmètre non nul.
◊ remarque : on pourrait aussi chercher la métrique directement en fonction de
ρ
ρ
, mais dans ce cas la résolution des équations est “peu évidente”.
1.5. Recherche d'une interprétation physique
• On peut se demander ce qu'on obtient si on fait subir le même genre de supplice à la coordonnée radiale du plan dans un espace plat.
On peut partir d'une métrique :
d
s
2
=
c
2
d
t
2
−
d
ρ
2
−
ρ
2
d
Ω
2
{ds}^2=c^2 \:{dt}^2-{dρ}^2-ρ^2 \:{dΩ}^2
(où la coordonnée radiale est notée
ρ
ρ
par analogie avec ce qui précède, puisqu'il s'agit effectivement de la distance à l'origine).
En appliquant (par exemple) un changement de notation :
ρ
=
a
+
r
2
−
a
2
ρ=a+\sqrt{r^2-a^2}
, avec une constante
a
>
0
a>0
, on obtient inversement :
r
=
(
ρ
−
a
)
2
+
a
2
r=\sqrt{(ρ-a)^2+a^2}
et par ailleurs :
d
ρ
=
d
r
1
−
a
2
r
2
\displaystyle dρ=\frac{dr}{\sqrt{1-\frac{a^2}{r^2}}}
.
Ceci correspond à une métrique divergeant “artificiellement” pour
r
=
a
r=a
:
d
s
2
=
c
2
d
t
2
−
d
r
2
1
−
a
2
r
2
−
(
1
−
a
2
r
2
+
a
r
)
2
r
2
d
Ω
2
\displaystyle {ds}^2=c^2 \,{dt}^2-\frac{{dr}^2}{1-\frac{a^2}{r^2}}-\left(\sqrt{1-\frac{a^2}{r^2}}+\frac{a}{r}\right)^2 r^2 \:{dΩ}^2
.
En particulier, un point matériel en mouvement rectiligne uniforme vers l'origine, étudié avec coordonnée
r
r
, semblerait “rebondir” sur la limite
r
=
a
r=a
(
ρ
=
a
ρ=a
). La principale conclusion est que, même s'il y a en principe “invariance relativiste”, on ne peut tout de même pas utiliser sans précaution n'importe quelles coordonnées (l'interprétation de
r
_
\underline{r}
isotrope n'est pas évidente).
📖 exercices n° I, II, III et IV.
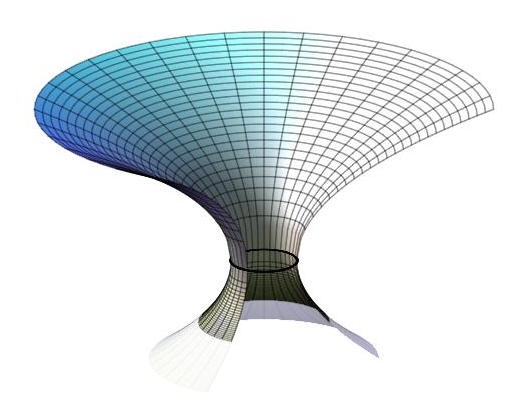
1.6. Représentation géométrique de la courbure spatiale
• Il peut être utile de représenter graphiquement la courbure spatiale (statique) associée à la métrique de Schwarzschild. L'invariance par rotation permet de se limiter à schématiser un plan correspondant à
(
r
,
φ
)
(r,φ)
pour
θ
=
π
2
θ=\frac{π}{2}
.
On peut obtenir une représentation géométrique de la courbure d'un plan de cet espace en décrivant une surface dans
ℝ
3
ℝ^3
euclidien dont la métrique induite soit celle de Schwarzschild. D'après les symétries, il suffit alors d'utiliser des coordonnées cylindriques avec une équation
z
=
z
(
r
)
z=z(r)
.
La distance radiale euclidienne est :
d
𝓁
2
=
d
r
2
+
d
z
2
=
d
r
2
.
(
1
+
(
d
z
d
r
)
2
)
\displaystyle {d𝓁}^2={dr}^2+{dz}^2={dr}^2.\left(1+\left(\frac{dz}{dr}\right)^2 \right)
; on souhaite qu'elle corresponde à :
d
𝓁
2
=
C
(
r
)
d
r
2
{d𝓁}^2=C(r) \:{dr}^2
avec
C
(
r
)
=
r
r
−
r
s
\displaystyle C(r)=\frac{r}{r-r_s}
(en coordonnées “classiques”). On obtient ainsi :
d
z
2
=
r
s
r
−
r
s
d
r
2
\displaystyle {dz}^2=\frac{r_s}{r-r_s} \:{dr}^2
.
• Pour
r
>
r
s
r>r_s
ceci donne :
z
=
z
0
±
2
r
s
r
r
s
−
1
\displaystyle z=z_0±2 \,r_s \;\sqrt{\frac{r}{r_s} -1}
où
z
0
z_0
est une constante (arbitraire) permettant au besoin de raccorder
z
(
R
)
z(R)
à la surface de l'astre. Cette équation correspond à une portion de “paraboloïde” de révolution (selon un axe parallèle à sa directrice et non son axe de symétrie).
Avec l'interprétation “classique”, la représentation cesse d'être valable pour
r
<
r
s
r<r_s
puisque la variable
r
r
n'est plus du genre espace.
Avec l'interprétation déduite des coordonnées “isotropes”, on peut procéder simplement, à partir du calcul précédent, en considérant
r
r
à nouveau croissant quand
r
_
<
r
_
s
\underline{r}<\underline{r}_s
décroît. La représentation s'obtient en raccordant deux côtés du paraboloïde, ce qui donnerait un “double espace” relié par une sorte de “trou de ver”.
La seconde partie peut être théoriquement prolongée à l'infini, mais aucun phénomène physique ne semble pouvoir causer un tel espace. Un raccordement de
z
(
R
)
z(R)
à la surface de l'astre créant le champ (nécessitant une étude de l'intérieur de ce dernier) doit alors se faire dans la partie “inversée”.
◊ remarque : un tracé en fonction de
r
_
\underline{r}
“isotrope” aurait peu d'intérêt puisque, pour permettre une réelle visualisation, les cercles sur la surface représentée doivent avoir un périmètre
2
π
r
2π \,r
, ce qui caractérise la variable
r
r
“classique”.
2. Voisinage de la singularité
2.1. Chute libre radiale
• En notations “isotropes”, la métrique limitée au mouvement radial peut s'écrire :
d
s
2
=
A
(
r
_
)
c
2
d
t
2
−
C
_
(
r
_
)
d
r
_
2
{ds}^2=A(\underline{r}) \:c^2 \,{dt}^2-\underline{C}(\underline{r}) \:{d\underline{r}}^2
. On en déduit les équations du mouvement géodésique pour une particule massive :
d
2
t
d
s
2
+
A
′
A
d
t
d
s
d
r
_
d
s
=
0
\displaystyle \frac{d^2 t}{{ds}^2} +\frac{A'}{A\,} \frac{dt}{ds} \frac{d\underline{r}}{ds}=0
;
d
2
r
_
d
s
2
+
A
′
c
2
2
C
(
d
t
d
s
)
2
+
C
_
′
2
C
_
(
d
r
_
d
s
)
2
=
0
\displaystyle \frac{d^2 \underline{r}}{{ds}^2} +\frac{A'\:c^2}{2 \,C} \left(\frac{dt}{ds}\right)^2+\frac{\underline{C}'}{2 \,\underline{C}} \left(\frac{d\underline{r}}{ds}\right)^2=0
.
• En posant
T
=
d
t
d
s
\displaystyle T=\frac{dt}{ds}
, on obtient :
T
A
=
C
s
t
e
T \:A=Cste
. Mais pour un point initialement immobile :
d
r
_
=
0
d\underline{r}=0
;
d
s
=
A
(
r
_
0
)
c
d
t
ds=\sqrt{A(\underline{r}_0)} \;c \,dt
;
T
0
=
1
c
A
0
\displaystyle T_0=\frac{1}{c \:\sqrt{A_0}}
;
T
A
=
T
0
A
0
=
A
0
c
\displaystyle T \:A=T_0 \:A_0=\frac{\sqrt{A_0}}{c}
.
Le résultat de l'autre équation est obtenu plus simplement en reportant l'expression de
T
T
dans la métrique :
c
d
t
=
A
0
A
d
s
\displaystyle c \,dt=\frac{\sqrt{A_0}}{A} ds
, donc :
d
s
2
(
A
0
A
−
1
)
=
C
_
d
r
_
2
\displaystyle {ds}^2 \:\left(\frac{A_0}{A}-1\right)=\underline{C} \:{d\underline{r}}^2
et finalement :
R
=
d
r
_
d
s
=
1
C
_
A
0
A
−
1
\displaystyle R=\frac{d\underline{r}}{ds}=\frac{1}{\sqrt{\underline{C}}} \,\sqrt{\frac{A_0}{A}-1}
.
• La durée locale est :
d
t
𝓁
o
c
=
A
d
t
{dt}_{𝓁oc}=\sqrt{A} \;dt
; la distance est :
d
𝓁
=
C
_
d
r
_
d𝓁=\sqrt{\underline{C}} \;d\underline{r}
; la vitesse est par conséquent :
v
=
d
𝓁
d
t
𝓁
o
c
=
C
_
A
d
r
_
d
t
=
C
_
A
R
T
=
c
1
−
A
A
0
\displaystyle v=\frac{d𝓁\,}{dt_{𝓁oc}}=\sqrt{\frac{\underline{C}}{A}} \:\frac{d\underline{r}}{dt}=\sqrt{\frac{\underline{C}}{A}} \:\frac{R}{T}=c \:\sqrt{1-\frac{A}{A_0}}
.
On constate que la vitesse de chute tend vers
c
c
quand
r
_
→
r
_
s
\underline{r}→\underline{r}_s
. Si on envisage alors que le point continue son mouvement au delà de cette limite, on constate que
A
=
(
r
_
−
r
_
s
r
_
+
r
_
s
)
2
\displaystyle A=\left(\frac{\underline{r}-\underline{r}_s}{\underline{r}+\underline{r}_s}\right)^2
s'annule puis redevient positif : sous l'effet de ce qui devrait être l'attraction de l'astre, la vitesse diminue !
◊ remarque : si on suppose qu'on peut utiliser un modèle limite d'astre “ponctuel”, une interprétation physique plausible serait d'admettre que le point matériel soit passé de l'autre côté de l'astre : l'origine ne correspondrait pas à
r
_
=
0
\underline{r}=0
mais à
r
_
=
r
_
s
\underline{r}=\underline{r}_s
et, lors de l'étude du voisinage de l'astre, les coordonnées devraient être “recentrées” (comme le propose L. S. Abrams).
◊ remarque : en mécanique quantique il n'existe pas de masse ponctuelle ; les particules “nues” ont une masse nulle et n'acquièrent leur masse que par interactions (avec le boson de Higgs).
• L'étude complète nécessite toutefois un raccordement avec la métrique intérieure (ne serait-ce que pour savoir si un passage à la limite justifie l'utilisation d'un modèle d'astre “ponctuel”).
On peut tout de même préciser ici que, pour l'interprétation “isotrope”, un éventuel astre avec une telle singularité extérieure serait forcément instable : la matière en surface subirait un champ vers l'extérieur et serait expulsée.
• Mais d'autre part cela peut causer, de part et d'autre de l'horizon, des oscillations verticales de particules de période finie en temps propre, mais semblant infinie à tout observateur fixe. Sauf en s'échappant dans des univers parallèles, une particule oscillant pourrait donc croiser à chaque période un même observateur extérieur fixe situé au sommet de sa trajectoire.
Or, un tel observateur verrait chaque passage durer de
t
=
−
∞
t=-∞
à
+
∞
+∞
, donc ne pourrait voir une succession de croisements qu'en voyant autant de clones de la particule oscillant. Or, les différents clones ainsi visibles pourraient interagir entre eux... Sauf à imaginer un astre très instable, durant trop peu pour permettre de telles oscillations, ce modèle semble contradictoire.
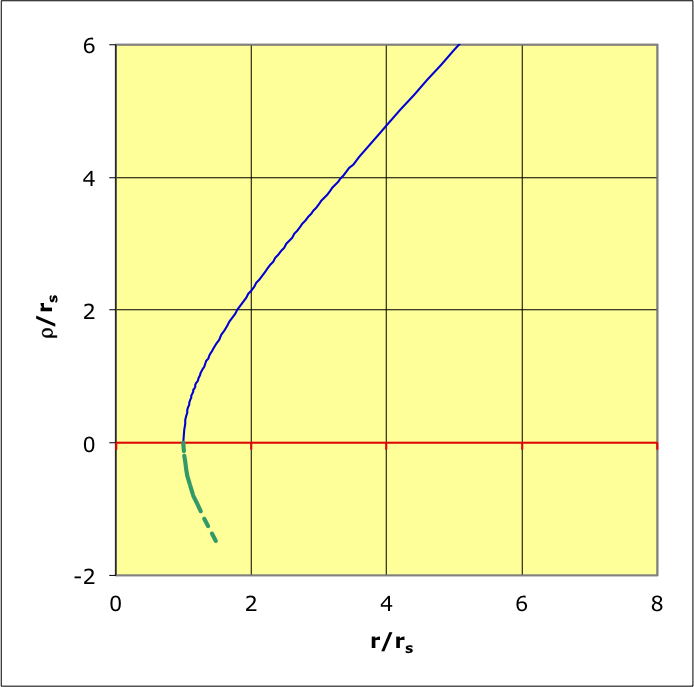
◊ remarque : avec les notations “classiques” mais l'hypothèse “isotrope”, il faut ne pas prolonger aux valeurs
r
<
r
s
r<r_s
(en pointillés), mais avec
r
>
r
s
r>r_s
dans la zone intérieure (en tirets).
📖 exercices n° V, VI, VII et VIII.
2.2. Orbites circulaires
• Avec l'interprétation “isotrope”, si les particules matérielles peuvent avoir des orbites circulaires stables pour
r
r
s
>
2
\displaystyle \frac{r}{r_s} >2
à l'extérieur de l'horizon, elles peuvent aussi en avoir de même pour
r
r
s
>
2
\displaystyle \frac{r}{r_s} >2
de l'autre côté (intérieur ?) de l'horizon.
◊ remarque : il faut toutefois considérer que le raccordement de la métrique avec celle à l'intérieur de l'astre créant le champ limite probablement grandement cette possibilité.
• Il peut en principe aussi y avoir un disque d'accrétion de chaque côté de l'horizon, avec oscillation de particules entre les deux.
📖 exercice n° IX.
3. Interprétation “classique”
3.1. Prolongement au delà de l'horizon
• D'un autre point de vue, dans la mesure où la méthode de Lemaître en donne une éventuelle justification, il est utile d'étudier aussi le prolongement de la coordonnée “classique” pour
r
<
r
s
r<r_s
.
Contrairement à ce qui est souvent affirmé, malgré une divergence au niveau de l'horizon, les notations correspondantes peuvent donner une représentation complète des trajectoires. Cela à tel point que, pour étudier des mouvements avec les représentations de Lemaître ou de Kruskal/Szekezres (abordées ultérieurement), il est souvent plus pratique de faire les calculs avec ces notations “classiques”, puis de traduire dans celles souhaitées.
• On peut ainsi étudier le mouvement d'une particule en chute libre verticale, à partir de l'infini avec une vitesse initiale (limite) nulle.
La vitesse de chute peut s'écrire :
v
=
d
𝓁
d
t
𝓁
o
c
=
1
A
d
r
d
t
=
−
c
r
s
r
\displaystyle v=\frac{d𝓁\,}{dt_{𝓁oc}}=\frac{1}{A} \frac{dr}{dt}=- c \;\sqrt{\frac{r_s}{r}}
; ce qui correspond à :
c
d
t
=
−
r
r
−
r
s
r
r
s
d
r
\displaystyle c \,dt=-\frac{r}{r-r_s} \,\sqrt{\frac{r}{r_s}} \;dr
.
En prenant
r
s
r_s
comme unité et avec la variable
κ
=
r
κ=\sqrt{r}
, ceci peut s'écrire :
c
d
t
=
−
2
κ
4
d
κ
κ
2
−
1
\displaystyle c \,dt=-\frac{2 \,κ^4 \:dκ}{κ^2-1}
; l'intégration donne :
c
t
=
−
2
κ
3
3
−
2
κ
+
ln
(
κ
+
1
|
κ
−
1
|
)
+
C
t
e
\displaystyle c\,t=- \frac{2 \,κ^3}{3}-2 \,κ+\ln\left(\frac{κ+1}{\left|κ-1\right|} \right)+Cte
.
Étant donné qu'il y a divergence pour
r
=
r
s
r=r_s
(
κ
=
1
κ=1
), les constantes de part et d'autre ne peuvent pas être raccordées par continuité ; on les choisit généralement égales.
• Ceci pose toutefois problème : l'intégration dans
ℂ
ℂ
(au lieu de
ℝ
ℝ
), donne :
c
t
=
−
2
κ
3
3
−
2
κ
+
ln
(
κ
+
1
|
κ
−
1
|
)
−
a
r
g
(
κ
−
1
)
+
C
t
e
\displaystyle c\,t=- \frac{2 \,κ^3}{3}-2 \,κ+\ln\left(\frac{κ+1}{\left|κ-1\right|} \right)-\mathrm{arg}(κ-1)+Cte
.
Ainsi, pour
r
<
r
s
r<r_s
, la constante d'intégration est décalée de
±
i
π
m
o
d
(
2
i
π
)
± \mathrm{i} π \;\mathrm{mod}(2 \,\mathrm{i} \,π)
et la variable
t
t
est complexe.
Ceci n'interdit en rien d'omettre la partie imaginaire, qui ne modifie pas
d
t
dt
, mais cela met en évidence qu'une même valeur de
t
t
n'a pas la même signification de part et d'autre de l'horizon (ce qu'on sait déjà par ailleurs, puisque pour
r
<
r
s
r<r_s
la variable
t
t
est du genre espace).
• Le calcul pour un mouvement radial quelconque est plus compliqué. Pour une chute verticale à partir d'une position
r
0
r_0
, avec une vitesse initiale nulle, on obtient (en notations réduites) en omettant la partie imaginaire :
c
t
=
r
0
−
1
r
.
(
r
0
−
r
)
+
(
1
+
r
0
2
)
r
0
−
1
a
r
c
c
o
s
(
2
r
r
0
−
1
)
⋯
\displaystyle c \,t=\sqrt{r_0-1} \:\sqrt{r .(r_0-r)}+\left(1+\frac{r_0}{2}\right) \:\sqrt{r_0-1} \; \mathrm{arccos}\left(\frac{2 \,r}{r_0} -1\right)⋯
+
a
r
c
o
s
h
(
r
0
r
−
2
r
+
r
0
r
0
.
|
r
−
1
|
)
\displaystyle + \mathrm{arcosh}\left(\frac{r_0\:r-2 \,r+r_0}{r_0.\left|r-1\right|}\right)
.
Il intervient de même une constante imaginaire si on tient compte dans
ℂ
ℂ
du comportement de
|
r
−
1
|
\left|r-1\right|
: pour une limite infinie de son argument, la fonction
a
r
c
o
s
h
\mathrm{arcosh}
se comporte comme un logarithme, incluant un terme
−
ln
(
|
r
−
1
|
)
-\ln\left(\left|r-1\right|\right)
.
◊ remarque : l'étude pour un photon donne une terme imaginaire analogue ; cela doit faire réfléchir sur la validité du prolongement au delà de l'horizon (le prolongement “isotrope” n'est pas le seul à poser problème).
• De façon générale, on constate que les trajectoires peuvent tout aussi bien sortir de la région
r
<
r
s
r<r_s
qu'elles peuvent y entrer.
📖 exercices n° X et XI.
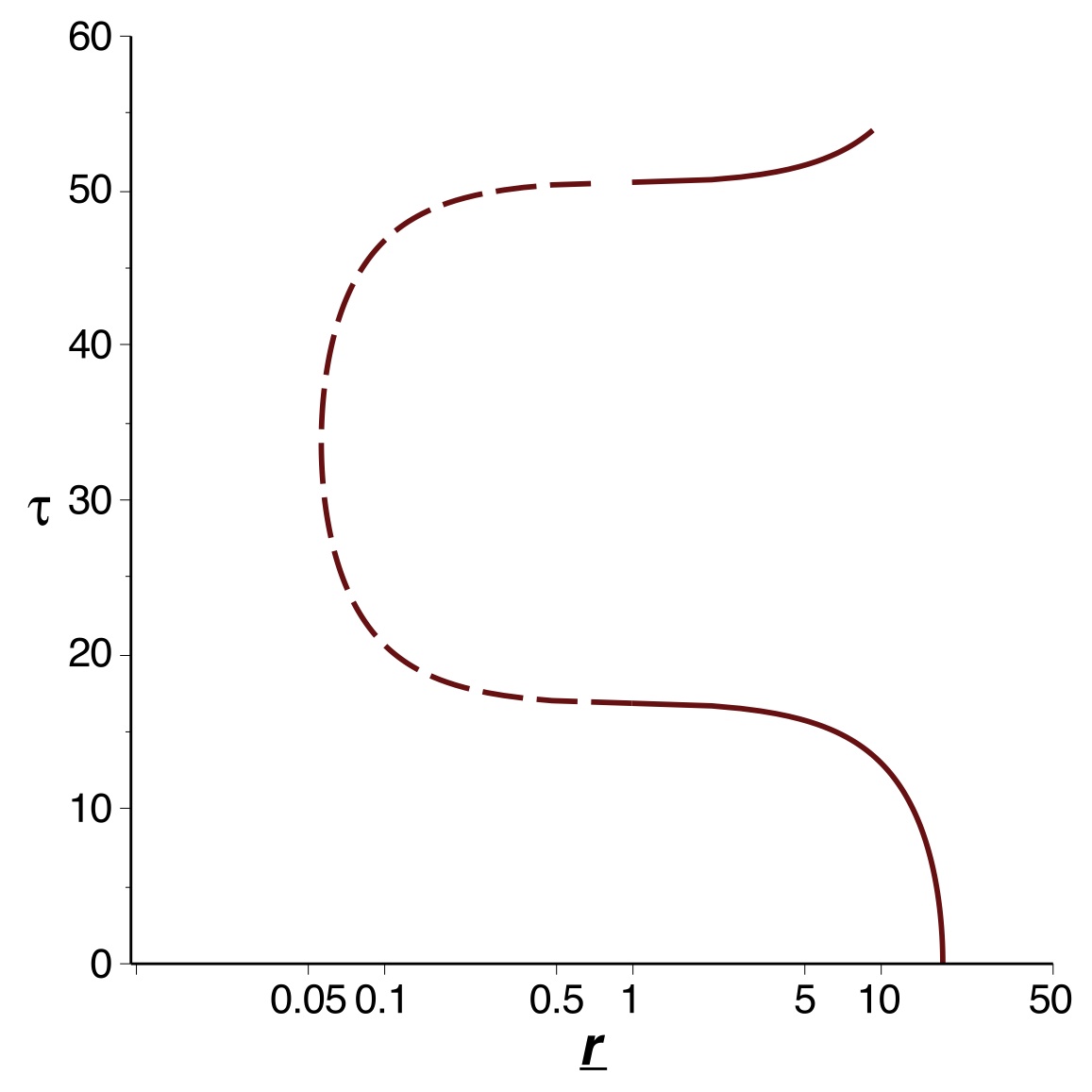
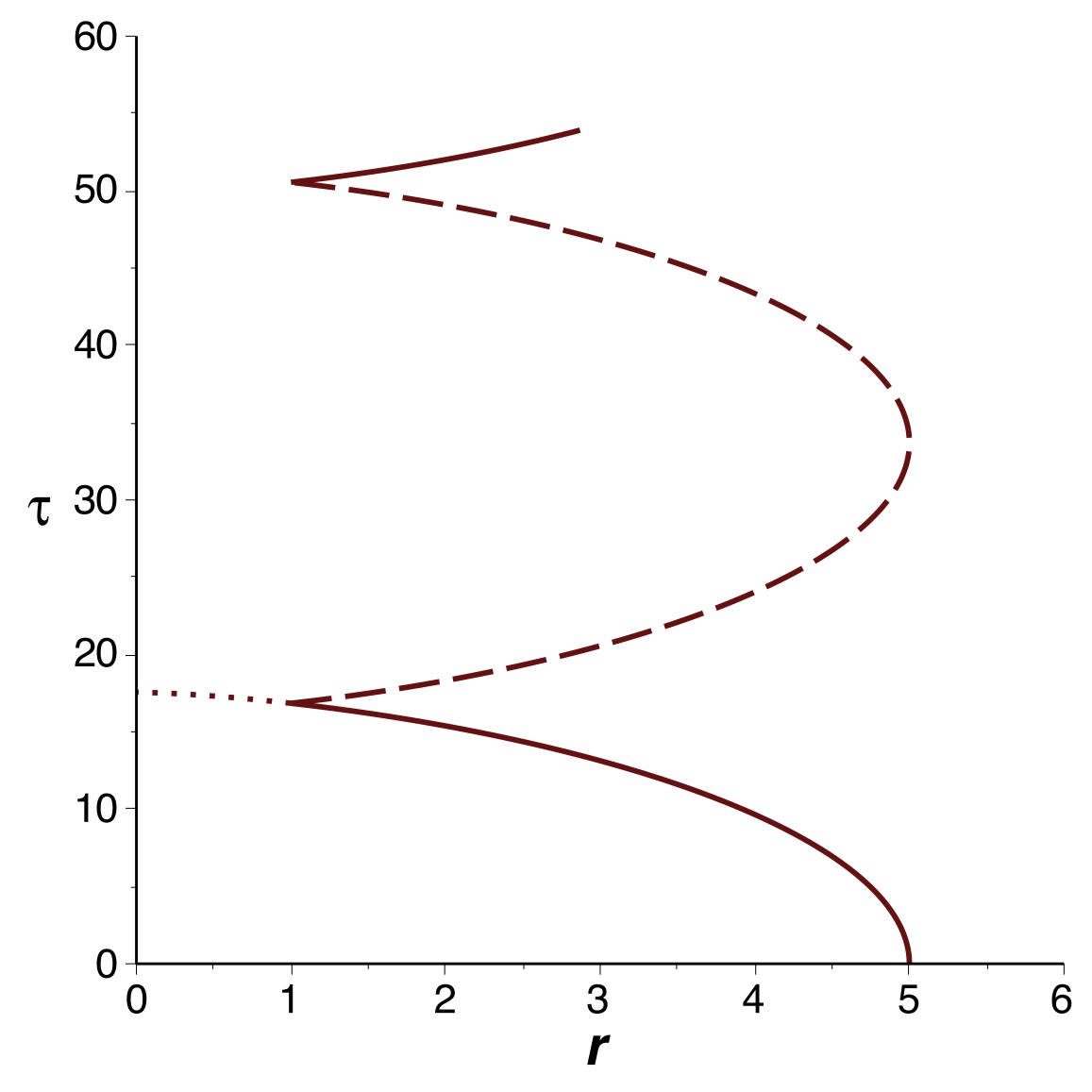
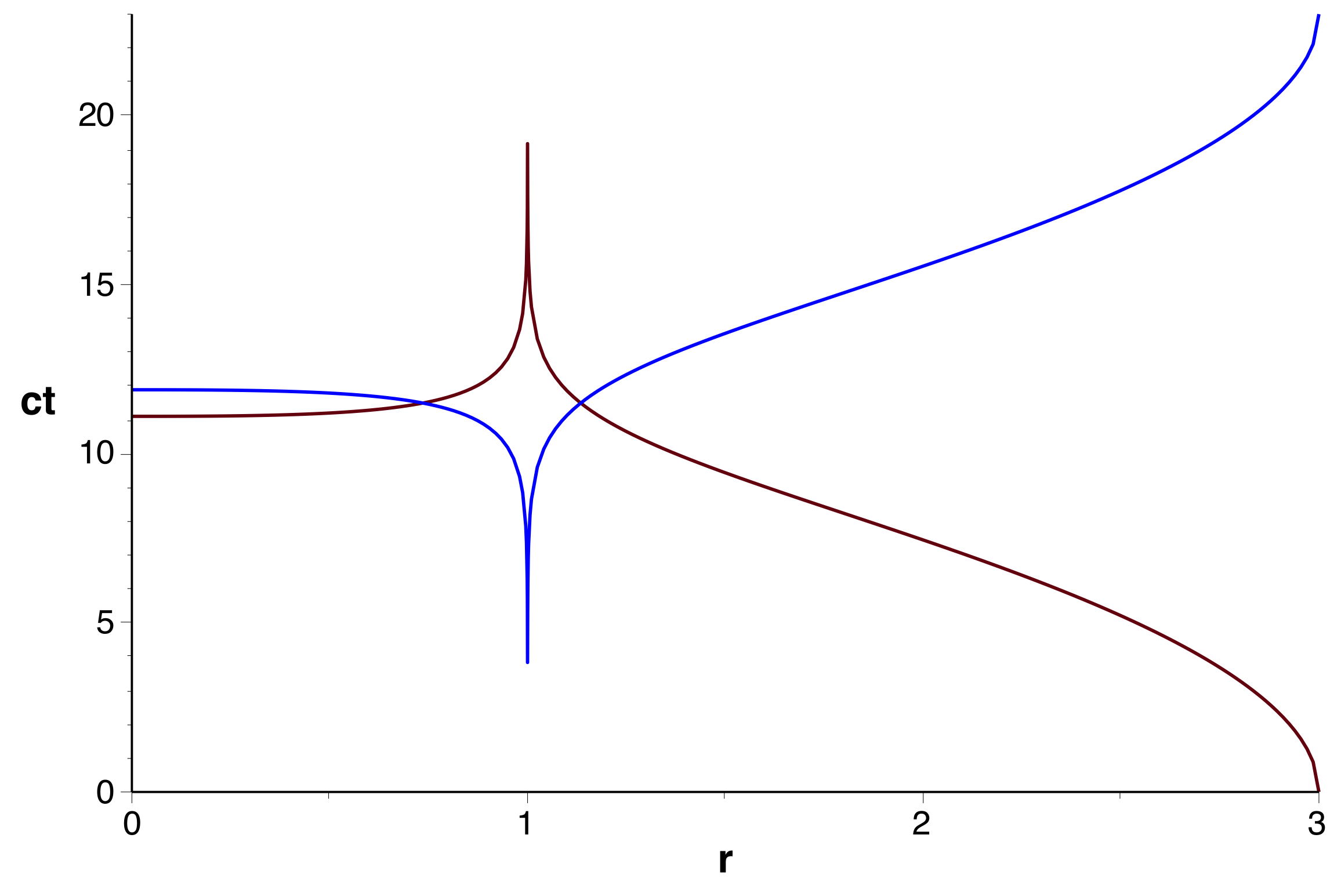
3.2. Croisements anormaux au delà de l'horizon
• Le tracé de trajectoires de particules en chute libre verticale, avec une altitude maximale en
r
0
r_0
, met en évidence que deux telles trajectoires peuvent se croiser en un point
r
<
r
s
r<r_s
(l'une en descente croisant l'autre en montée, dont la trajectoire s'obtient en changeant par symétrie le sens de
c
t
c \,t
).
Or, dans ce cas, elles se croisent une autre fois en un point
r
>
r
s
r>r_s
.
Ce qui pose problème, c'est que la particule en descente fait en premier le croisement extérieur, alors que celle en montée fait en premier le croisement intérieur.
Ce genre d'interversion temporelle apparente se produit souvent en relativité quand on considère deux événements séparés par un intervalle du genre espace. Or, le temps propre de chaque particule est un bon paramètre de temps le long de sa trajectoire : pour chacune des deux particules, l'intervalle est du genre temps.
◊ remarque : il faut considérer (par exemple) le temps propre, puisque la variable
t
t
n'est plus du genre temps pour
r
<
r
s
r<r_s
.
• Cette difficulté peut sembler liée à la forme particulière des trajectoires au niveau des divergences ; une étude (ultérieure) plus approfondie montre qu'il n'en est rien.
Le problème provient de l'apparente invariance temporelle des notations de Schwarzschild (ou de Lemaître) : la métrique au delà de l'horizon semble pouvoir correspondre à la fois à un “trou blanc” et un “trou noir”, or c'est physiquement contradictoire de supposer que c'est les deux en même temps. Cela implique qu'il ne peut exister ni trou blanc ni trou noir “permanent”.
Les notations de Kruskal-Szekeres ou de Novikov montrent qu'on est amené à privilégier un instant particulier (qu'on peut choisir comme origine du temps) où le trou blanc termine son expansion et commence une contraction en trou noir : les trajectoires peuvent sortir du trou blanc dans le passé (et uniquement) ; elles peuvent entrer dans le trou noir dans le futur (et uniquement).
3.3. Anomalie fondamentale de la singularité centrale
• Dans l'interprétation “classique”, il est considéré que l'effondrement d'un astre en trou noir aboutit à une annihilation de toute la matière en une singularité centrale, pour
r
=
0
r=0
.
Mettant à part l'absence de loi physique qui justifierait une telle “annihilation” (on ne connait que celle décrivant l'interaction matière/antimatière), on suppose alors que c'est la singularité qui est ensuite la cause du champ gravitationnel environnant. Ceci implique que ce point mathématique soit doté de propriétés physiques.
Or, cette singularité, pourtant située au delà de l'horizon, est a priori immobile par rapport au repérage de Schwarzschild ; cela semble fondamentalement contradictoire avec les conclusions de l'étude de la métrique (à cause du repérage inadapté dans cette région, tout “point matériel” doit nécessairement y avoir un mouvement supraluminique).
À ce niveau, on peut encore se dire que la contradiction n'est qu'apparente, due à l'inadaptation des coordonnées utilisées (comment y définir une “vitesse” de façon non ambigüe ?) ; la suite montre que non.
• De façon générale, il apparaît que l'interprétation “classique” pose autant de problèmes que l'interprétation “isotrope”.
