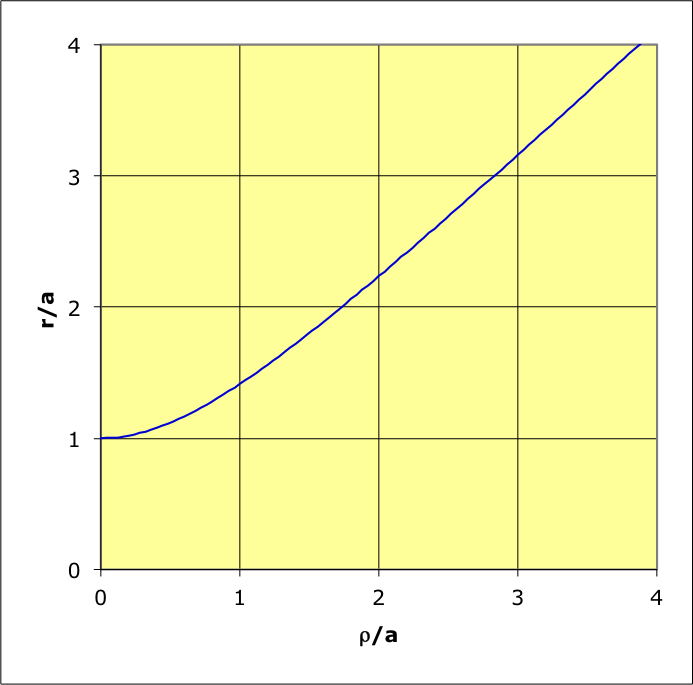
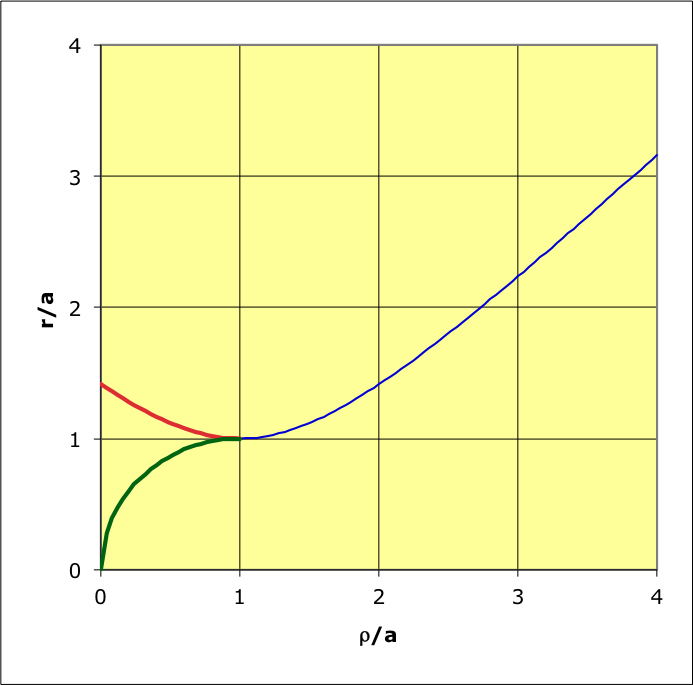
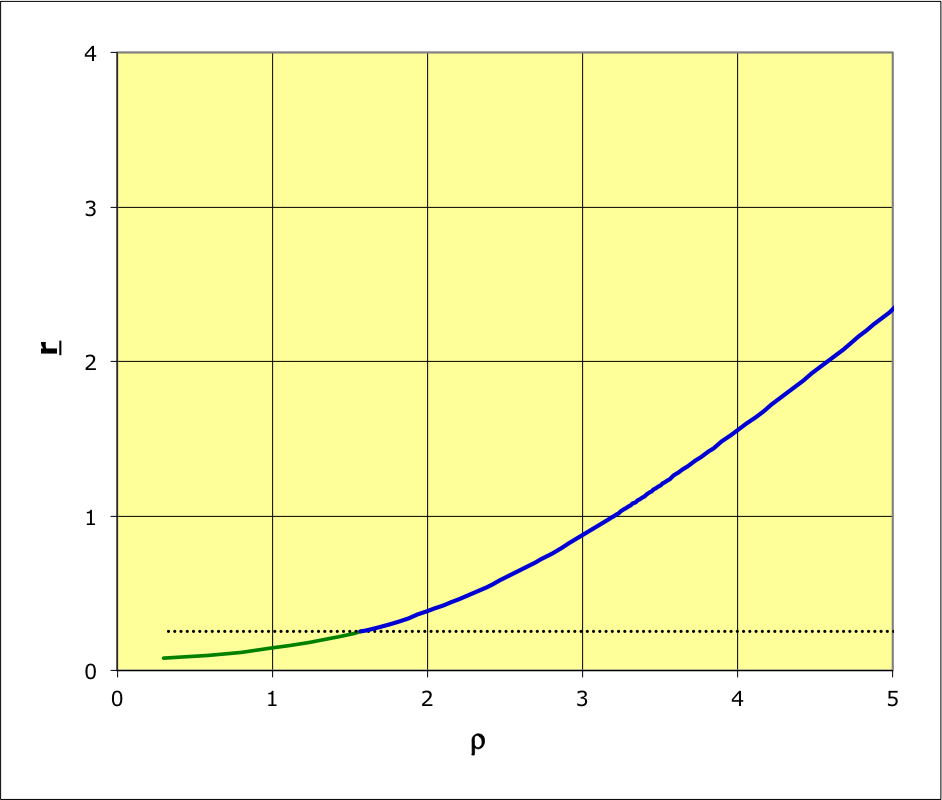
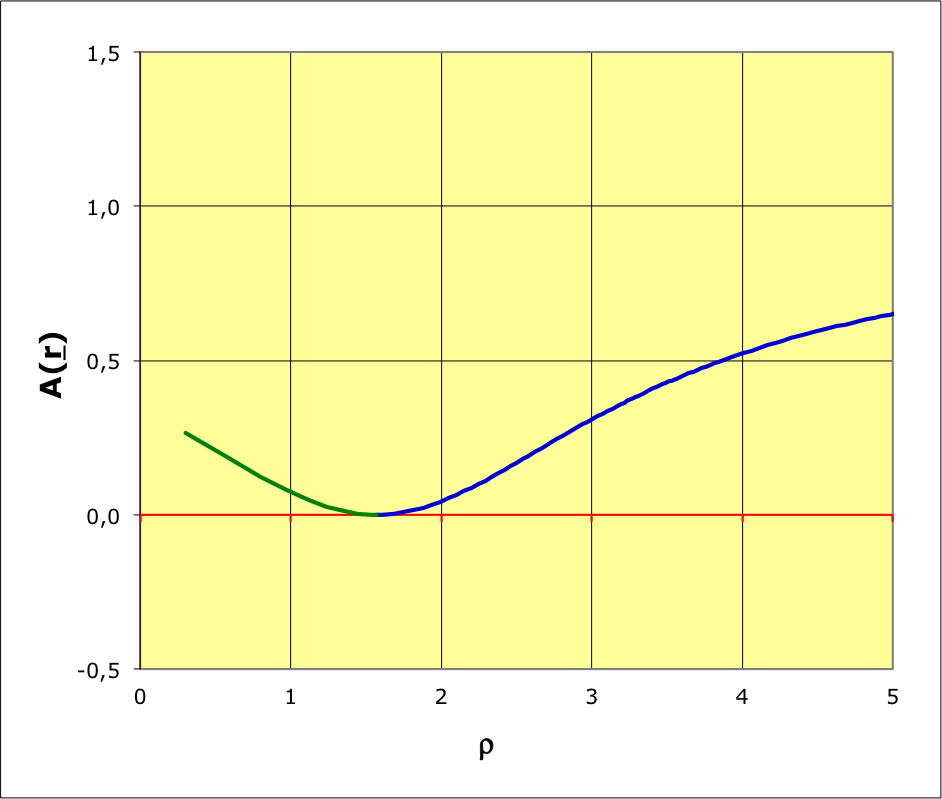
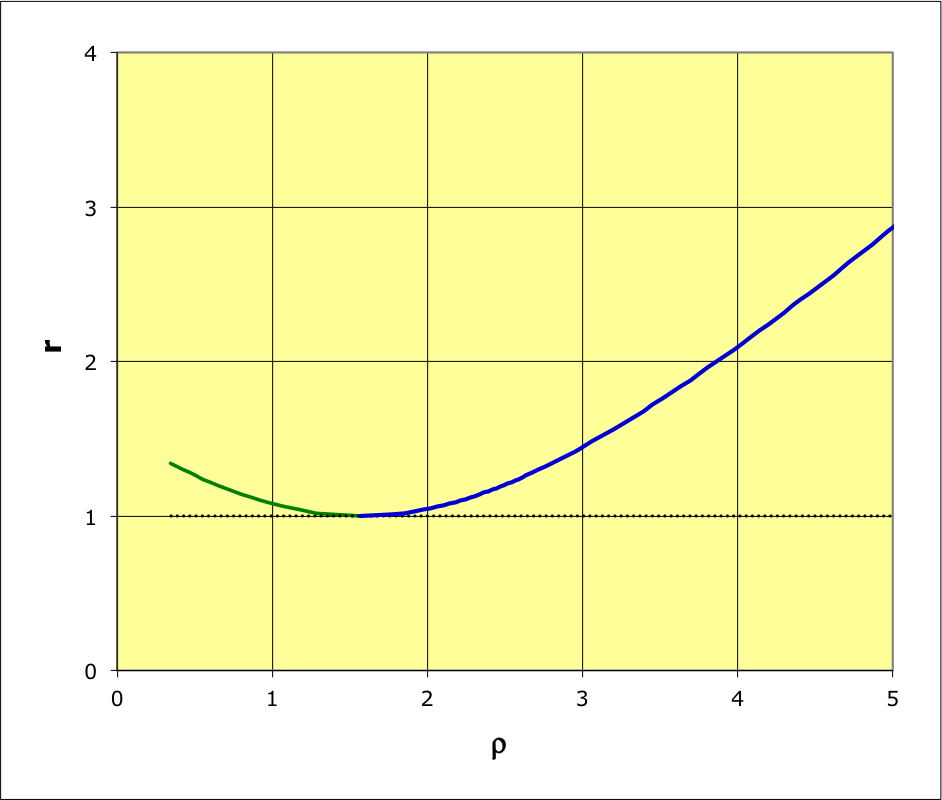
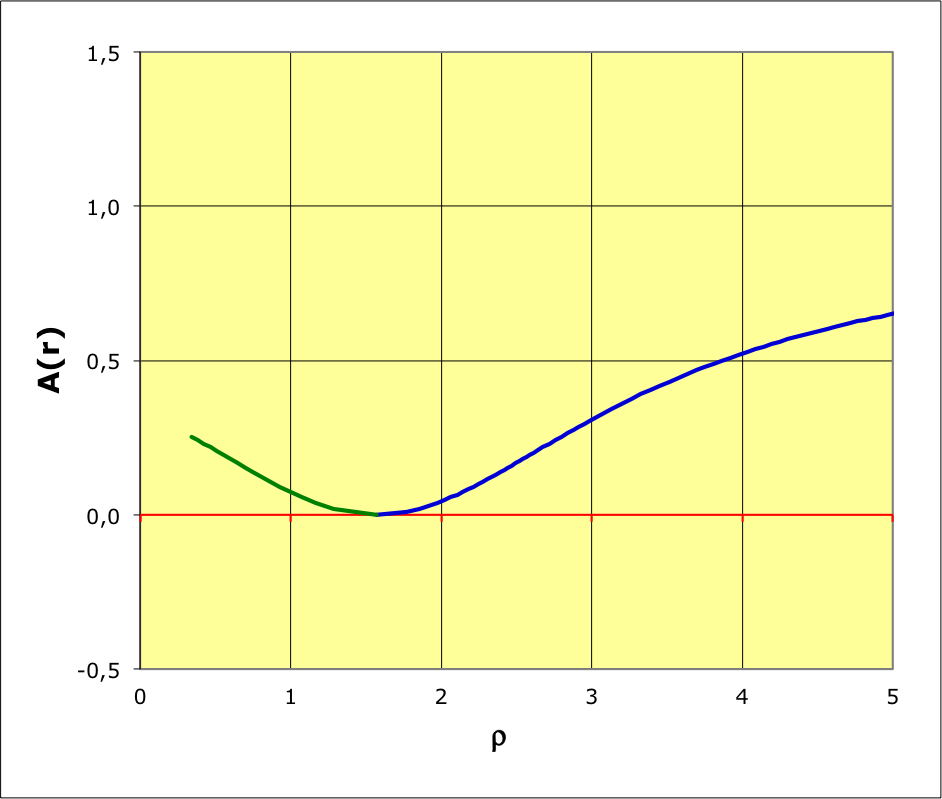
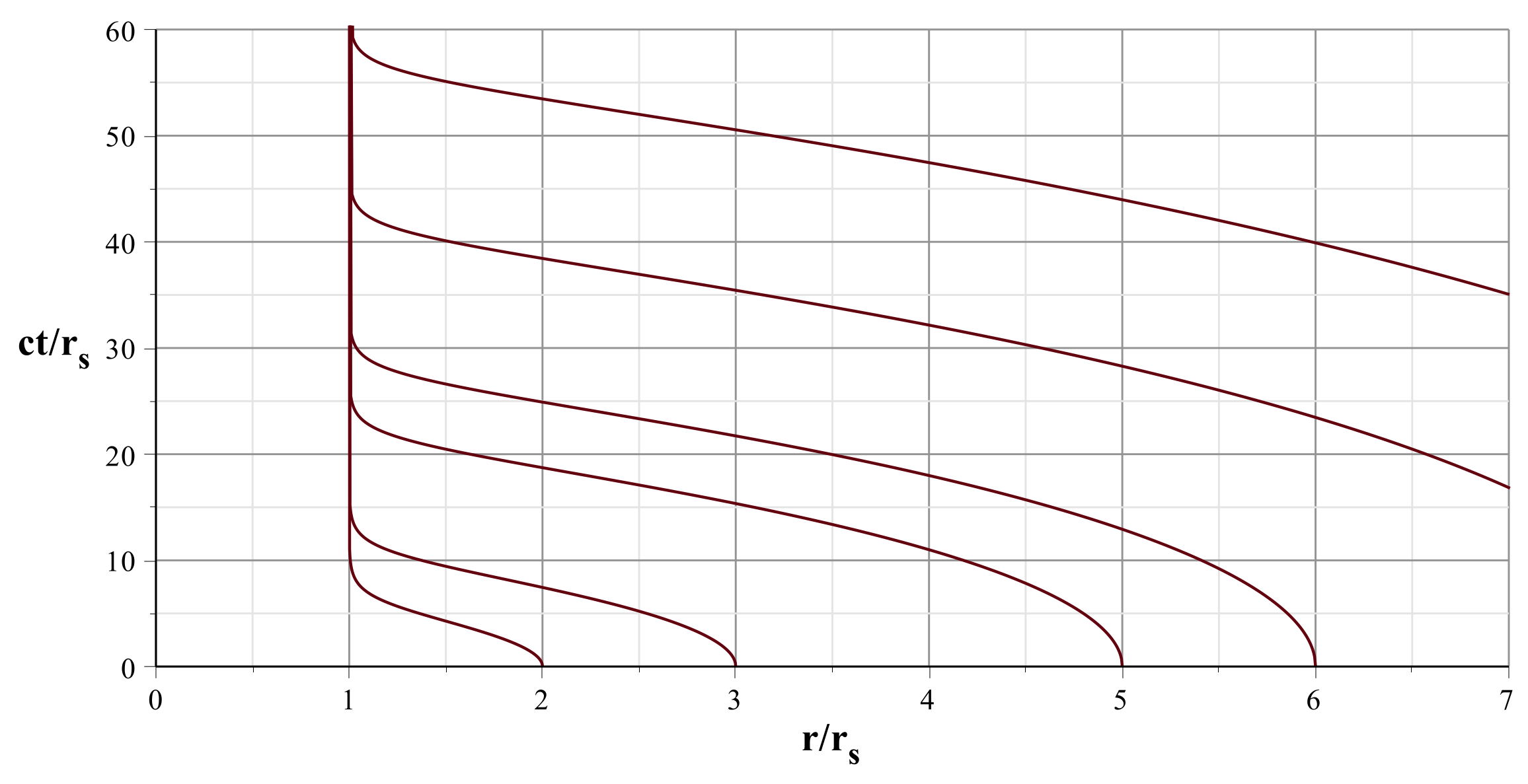
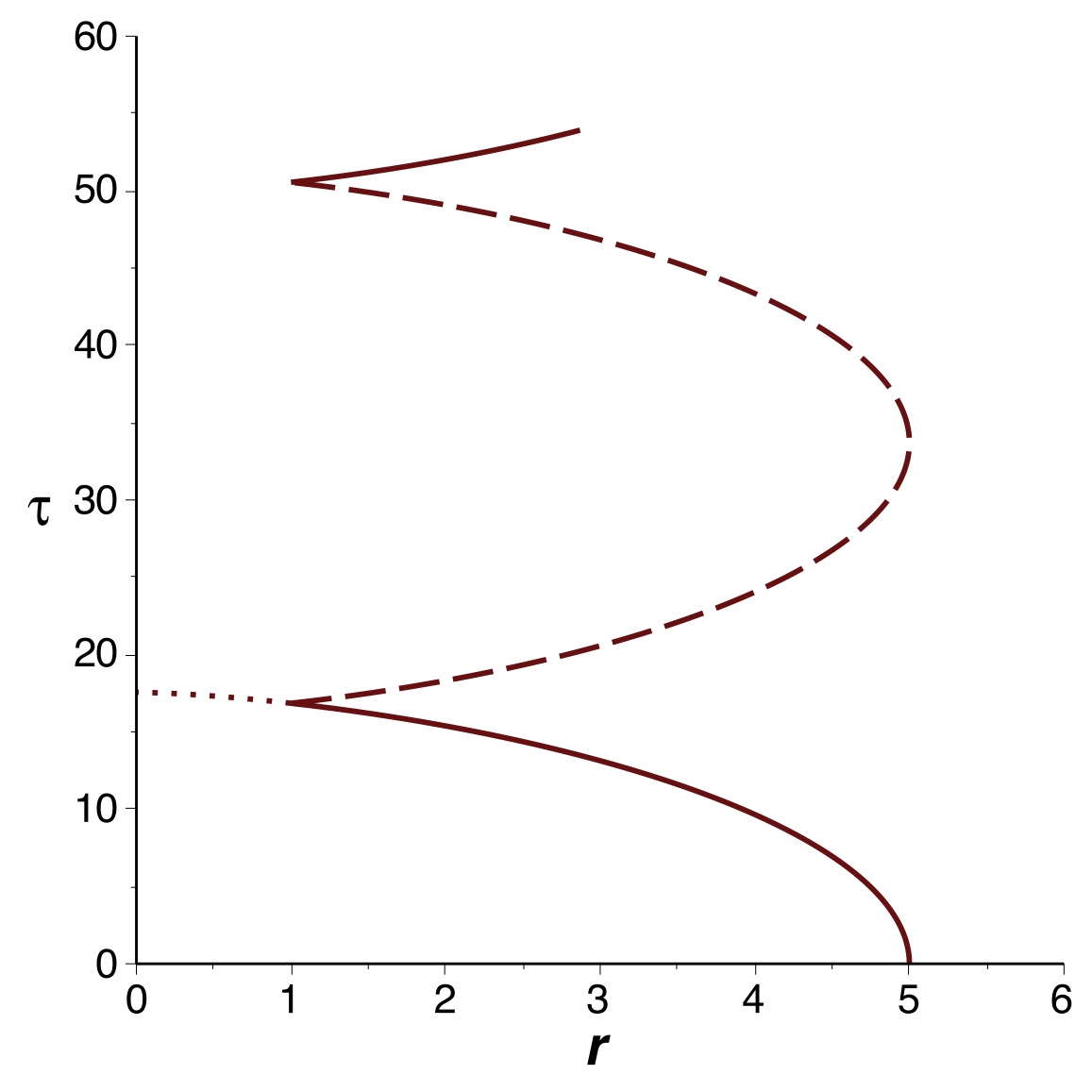
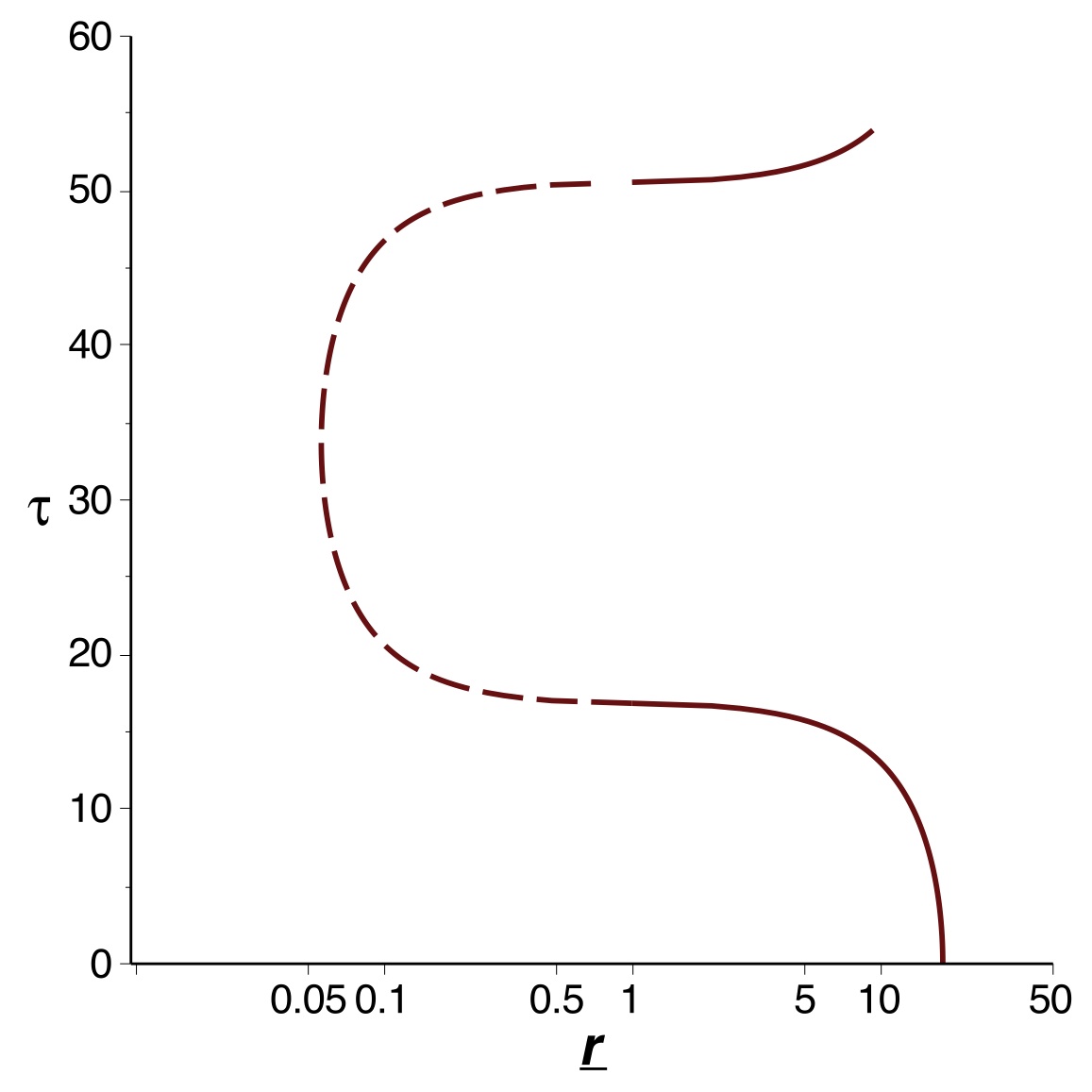
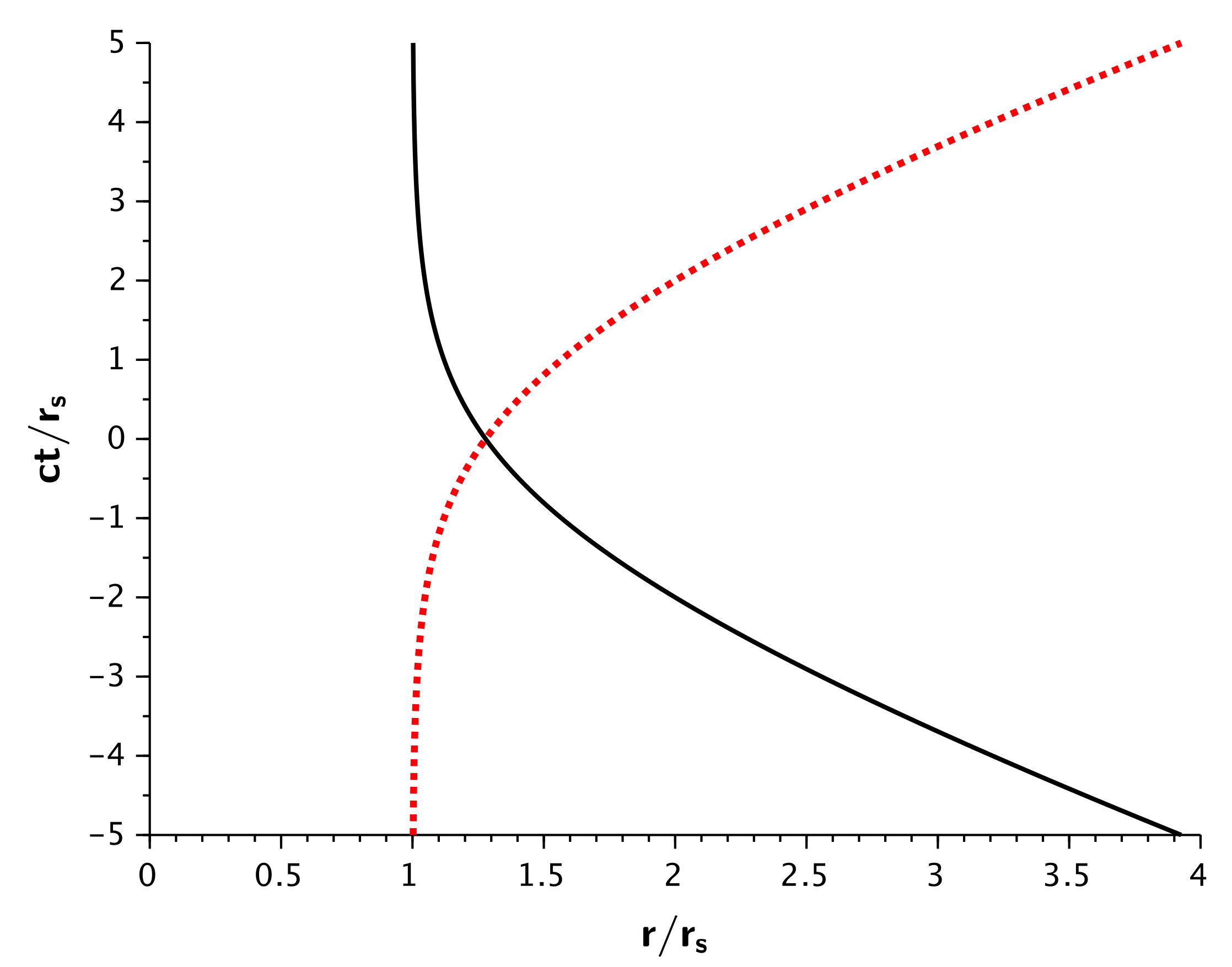
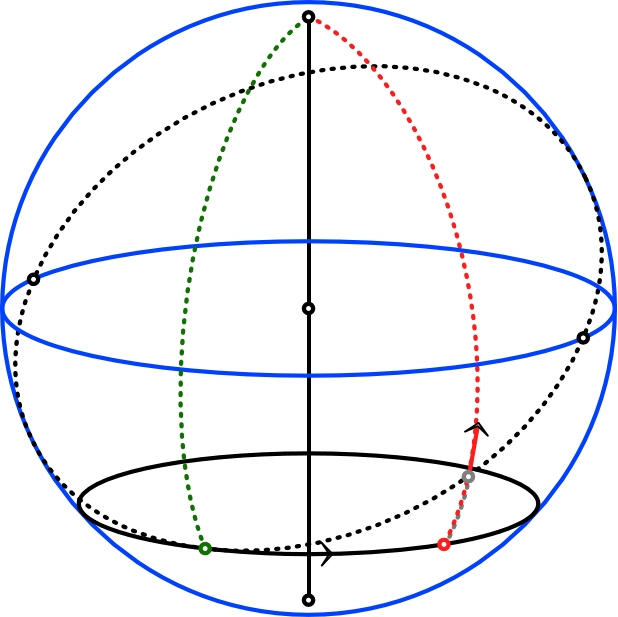
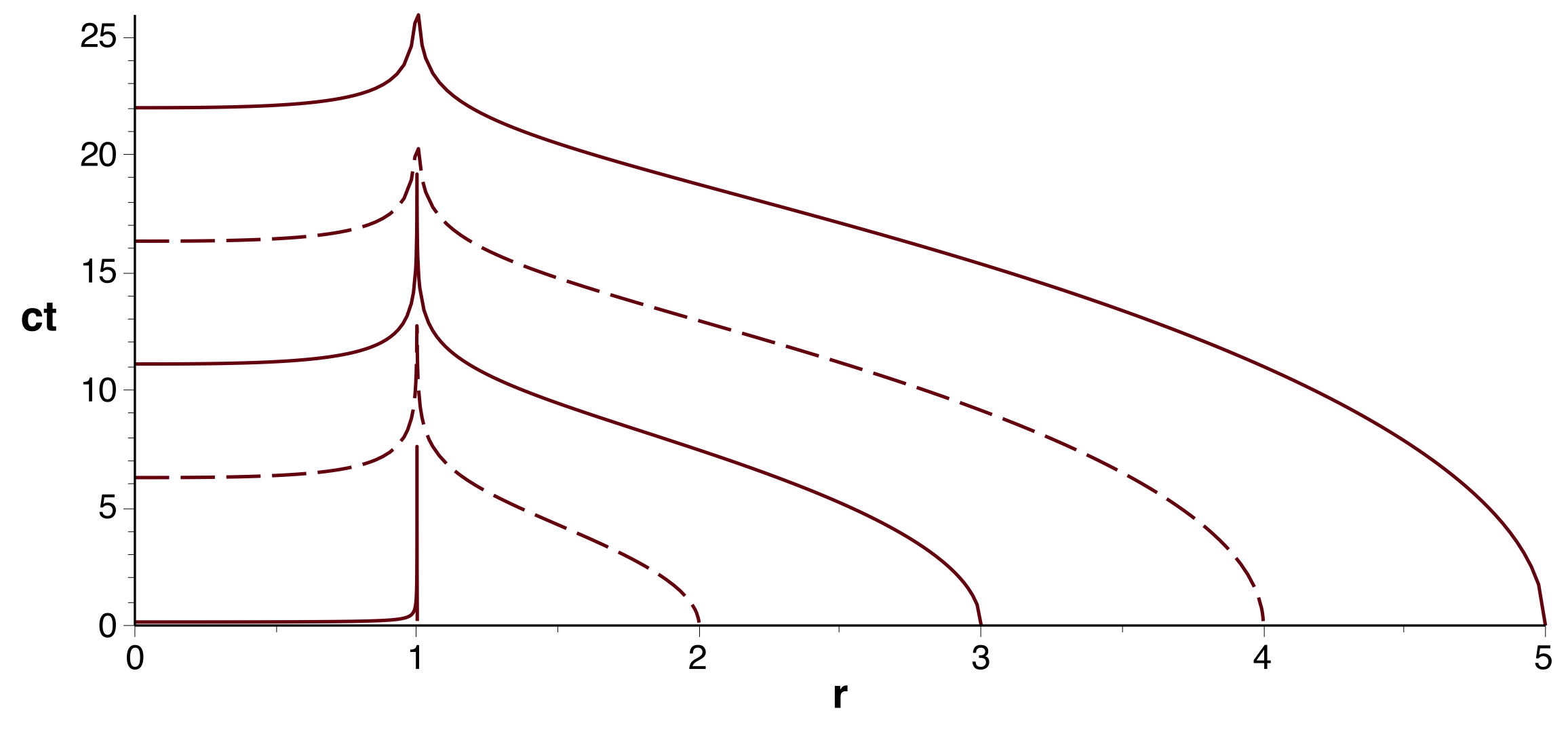
1.
|
• Pour la chute :
.
• Ainsi (avec
comme unité) :
.
• En décomposant :
on peut écrire :
.
◊ remarque : dans le premier terme, on fait apparaître la
dérivée du polynôme du radical.
• On obtient ainsi :
.
• En passant par
on obtient :
.
◊ remarque : dans ce terme on choisit la dérivée du polynôme
du radical, divisée par la racine carrée de son discriminant
(astuce “classique”, mais on peut retrouver par
tâtonnement).
• Pour
, on peut par ailleurs passer par
, donnant :
.
• En reprenant la méthode du terme précédent, on passe
par
, donnant :
.
• Cette expression suppose
, d'où en simplifiant
, ce qui est toujours vrai. Par contre, pour
, le changement de signe impliquerait
, ce qui est impossible.
• Pour
, on peut alors de même utiliser
, donnant :
.
• Avec la même méthode, on passe par
, donnant :
.
• Cette expression suppose
, d'où en simplifiant
, ce qui est toujours vrai.
• Au total :
.
• On veut que
corresponde au passage par
:
;
.
• On peut alors simplifier car
; ainsi :
.
◊ remarque : étant donné que l'expression diverge pour
, il est impossible de raccorder par continuité à ce
niveau, donc la constante d'intégration pour
peut être différente de celle imposée en
; le problème est analogue au prolongement
de
comme primitive de
pour
; le passage par les complexes donne
d'ailleurs
. |