MÉTRIQUE À LA NOVIKOV - INTERPRÉTATION - corrigé des exercices


I. Métrique à la Novikov

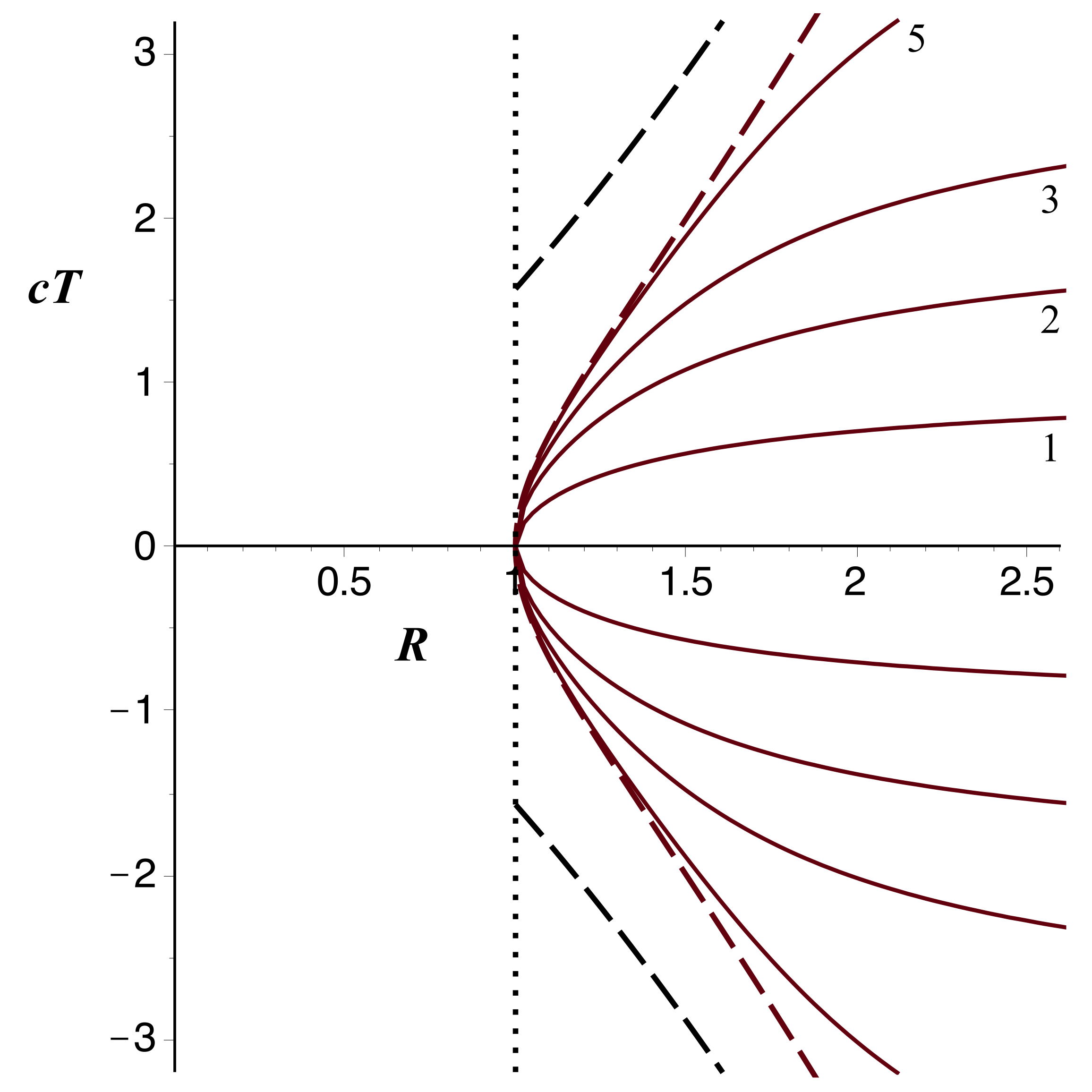
1. • Pour les régions  r>rsr>r_s  on peut utiliser le fait que l'axe  T=0T=0  correspond à  t=0 t=0  et on applique la même méthode que pour la métrique de Novikov, avec (en notations réduites) :

 r=R2[1−cos(η)]\displaystyle r=\frac{R}{2} \left[1-\cos(η)\right]  ;  cT=R3/22[π−η+sin(η)]c \,T=\frac{R^{3/2}}{2} \left[π-η+\sin(η)\right] .

IntNovikov_cor_Im/Novikov_6.jpg
 IntNovikov_cor_Im/Novikov_7.jpg


2.a. • Pour  r<rsr<r_s  cette méthode ne fonctionne pas puisqu'il est impossible de dépasser la limite  r=rsr=r_s  pour laquelle tt diverge. Elle permet par contre de montrer que  R=rsR=r_s  correspond aussi à  t=0t=0  (ici on n'a pas l'argument de symétrie par rapport à  R=0R=0 ),  permettant ensuite un raisonnement avec  T=CsteT=Cste .
• Pour une valeur constante de RR ,  la métrique donne :  Ac2dt2−1Adr2=c2dT2\displaystyle A \:c^2 \,{dt}^2-\frac{1}{A} {dr}^2=c^2 \,{dT}^2 .
• Avec  r˙2=𝒻+Fr=1r−1R\displaystyle \dot{r}^2=𝒻+\frac{F}{r}=\frac{1}{r}-\frac{1}{R}  on obtient  c2dT2=RrR−rdr2\displaystyle c^2 \,{dT}^2=\frac{R \:r}{R-r} \,{dr}^2  ;  Ac2dt2=dr2.[rr−1+RrR−r]\displaystyle A \:c^2 \,{dt}^2={dr}^2 .\left[\frac{r}{r-1}+\frac{R \:r}{R-r}\right] .  Donc pour  R=rsR=r_s  ceci donne :  dt=0dt=0 .
• Cette méthode avec  T=CsteT=Cste  ne peut toutefois pas dépasser  T=T0(R=rs)=π2T=T_0 (R=r_s)=\frac{π}{2}  (on ne peut pas partir d'un point sur l'axe avec  r<0r<0 ).  Pour prolonger les courbes au delà, on peut calculer  t(R,T) t(R,T)  le long de la courbe  r=0r=0 :  cT=π2R3/2c \,T=\frac{π}{2} \, R^{3/2} .
• Pour  r=Cster=Cste  (a priori non nulle) la métrique donne :  Ac2dt2=c2dT2−RR−1r′2(R,T)dR2\displaystyle A \:c^2 \,{dt}^2=c^2 \,{dT}^2-\frac{R}{R-1} \: {r'}^2 (R,T) \; {dR}^2 .
• Mais par ailleurs :  dr=r˙dT+r′dR=0dr=\dot{r} \: dT+r' \:dR=0 ,  donc :  Ac2dt2=c2dT2−RR−1r˙2(R,T)dT2\displaystyle A \:c^2 \,{dt}^2=c^2 \,{dT}^2-\frac{R}{R-1} \: \dot{r}^2 (R,T) \;{dT}^2 .
• Avec (en notations réduites) :  A=r−1r\displaystyle A=\frac{r-1}{r}   ;   r˙2=𝒻+Fr=1r−1R\displaystyle \dot{r}^2=𝒻+\frac{F}{r}=\frac{1}{r}-\frac{1}{R}  on obtient ensuite :

 dt2=dT2rr−1[1−RR−1(1r−1R)]=RR−1dT2\displaystyle {dt}^2={dT}^2 \, \frac{r}{r-1} \left[1-\frac{R}{R-1} \left(\frac{1}{r}-\frac{1}{R}\right)\right]=\frac{R}{R-1} \,{dT}^2 .
• À la limite  r=0r=0 ,  avec  cT=π2R3/2c \,T=\frac{π}{2} \, R^{3/2} ,  ceci donne :  cdt=3π4RR−1dR\displaystyle c \,dt=\frac{3π}{4} \, \frac{R}{\sqrt{R-1}} \, dR .
• On obtient :  ct=π2(R+2)R−1c \,t=\frac{π}{2} \, (R+2) \:\sqrt{R-1}  (compte tenu de  t=0t=0  pour  R=1R=1 ).


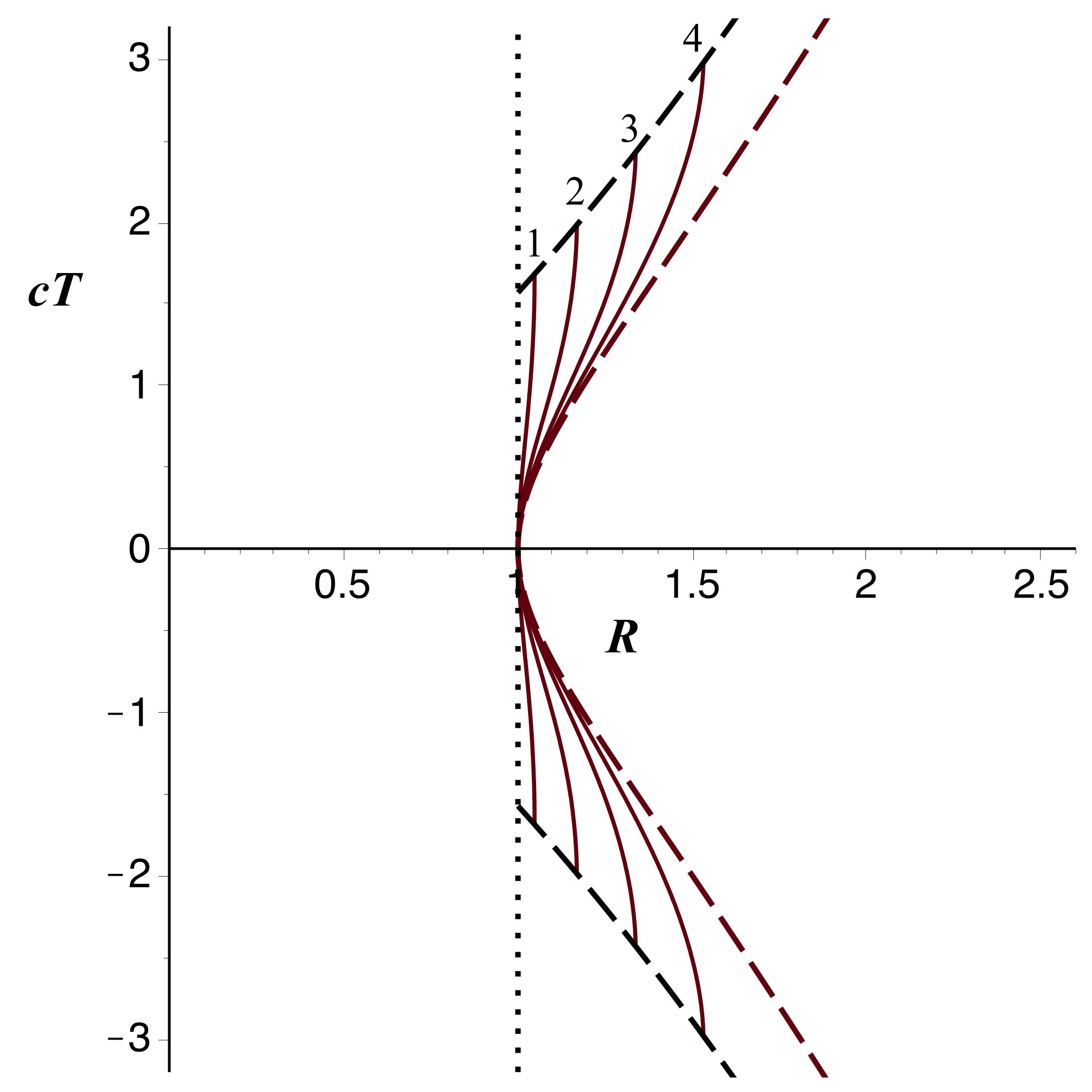
2.b. • Pour une valeur constante de TT la métrique donne :

 Ac2dt2−1Adr2=−RR−1r′2(R,T)dR2=−RR−1dr2\displaystyle A \:c^2 \,{dt}^2-\frac{1}{A} \:{dr}^2=-\frac{R}{R-1} \: {r'}^2 (R,T) \;{dR}^2=-\frac{R}{R-1} \,{dr}^2 .
• On applique la même méthode que pour la métrique de Novikov : pour  cT≤π2c \,T≤\frac{π}{2}  fixé, on augmente progressivement RR à partir de rsr_s (en augmentant ηη) jusqu'à atteindre une valeur choisie de tt .
• Pour  cT>π2c \,T>\frac{π}{2}  fixé, on procède de même en partant de  R0=(2cTπ)2/3\displaystyle R_0=\left(\frac{2 \,c \,T}{π}\right)^{2/3}  et  ct0=π2(R0+2)R0−1c \,t_0=\frac{π}{2} \, (R_0+2) \: \sqrt{R_0-1} .


II. Diagramme de Novikov en représentation de Schwarzschild


 • Pour obtenir une représentation équivalente au diagramme de Novikov (ou de Kruskal-Szekeres), on peut dessiner deux exemplaires de la famille de courbes de référence en notations de Schwarzschild.

IntNovikov_cor_Im/Novikov_9.jpg
 IntNovikov_cor_Im/Novikov-Schwarzschild.jpg

• On coupe ensuite les deux dessins selon la limite  0≤r≤rs0≤ r≤r_s  ;  t=0t=0 .  Puis on les superpose et on raccorde la moitié supérieure de la coupure du premier feuillet avec la moitié inférieure de la coupure du second et réciproquement.
◊ remarque : on peut a priori penser qu'il faut pour cela que les deux feuillets se traversent mutuellement, mais il suffit de plier les feuilles pour l'éviter.
• On obtient ainsi une représentation équivalente, dans laquelle les croisements intempestifs sont évités. Au lieu de finir sa chute du côté montant (donc dans le sens de TT ,  ou vv ,  décroissant), le photon dessiné la finit dans le feuillet “côté obscur” où toutes les particules de référence se déplacent en sens inverse (contraire par rapport à tt de Schwarzschild), donc où elles sont aussi dans le sens de la chute.
◊ remarque : symétriquement de l'autre côté, on obtient une représentation d'un photon qui sort de la région (IV)(IV) vers la région (III)(III).
• Outre les croisements intempestifs, ceci évite le sens anormal par rapport à TT ou vv (dans le sens d'évolution des particules de référence), mais au prix d'imposer un sens anormal par rapport à tt .


III. Diagramme de Novikov (ou Kruskal-Szekeres) et diagramme de Schwarzschild (ou Lemaître)

1. • Pour obtenir une représentation de Lemaître, le plus simple est de calculer en notations de Schwarzschild.
• La chute verticale depuis r0r_0 avec une vitesse initiale nulle donne :  v=−c1−AA0=drAdt\displaystyle v=-c \:\sqrt{1-\frac{A}{A_0}}=\frac{dr}{A \:dt} .
• Ainsi (avec  rsr_s  comme unité) :  cdt=−r0−1r2dr(r−1)r.(r0−r)\displaystyle c \,dt=-\sqrt{r_0-1} \: \frac{r^2 \: dr}{(r-1) \: \sqrt{r.(r_0-r) }}  ;  l'intégration donne :

 ct=r0−1r.(r0−r)+(1+r02)r0−1[arcsin(1−2rr0)+π2]+arcosh(r0r−2r+r0r0.|r−1|)\displaystyle c \,t=\sqrt{r_0-1} \; \sqrt{r.(r_0-r)}+\left(1+\frac{r_0}{2}\right) \: \sqrt{r_0-1} \; \left[\arcsin\left(1-\frac{2 \,r}{r_0} \right)+\frac{π}{2} \right]+\mathrm{arcosh}\left(\frac{r_0 \: r-2 \,r+r_0}{r_0.|r-1|}\right) .
• Avec  ct=cT−2r+ln(|r+1r−1|)\displaystyle c \,t = c \,T-2 \,\sqrt{r}+\ln\left(\left|\frac{\sqrt{r}+1}{\sqrt{r}-1}\right|\right)  et  R−cT=23r3/2R-c \,T=\frac{2}{3} \, r^{3/2} ,  on peut obtient une représentation paramétrique des courbes en notations de Lemaître.
• Les graphiques sont toutefois très étirés en biais à 45°45° et de ce fait difficiles à interpréter : pour comparer plusieurs courbes, une grande échelle est nécessaire et les détails sont peu visibles. On obtient une représentation plus efficace en inclinant les graphiques : on trace en abscisse  R−cTR-c \,T  ;  ainsi les droites  r=Cster=Cste  deviennent verticales (et les droites  R=CsteR=Cste ,  qui étaient verticales, deviennent inclinées à −45°-45°). On peut ensuite augmenter l'échelle verticale pour éviter l'étirement excessif (ce qui incline un peu plus les droites  R=CsteR=Cste ,  ici non représentées).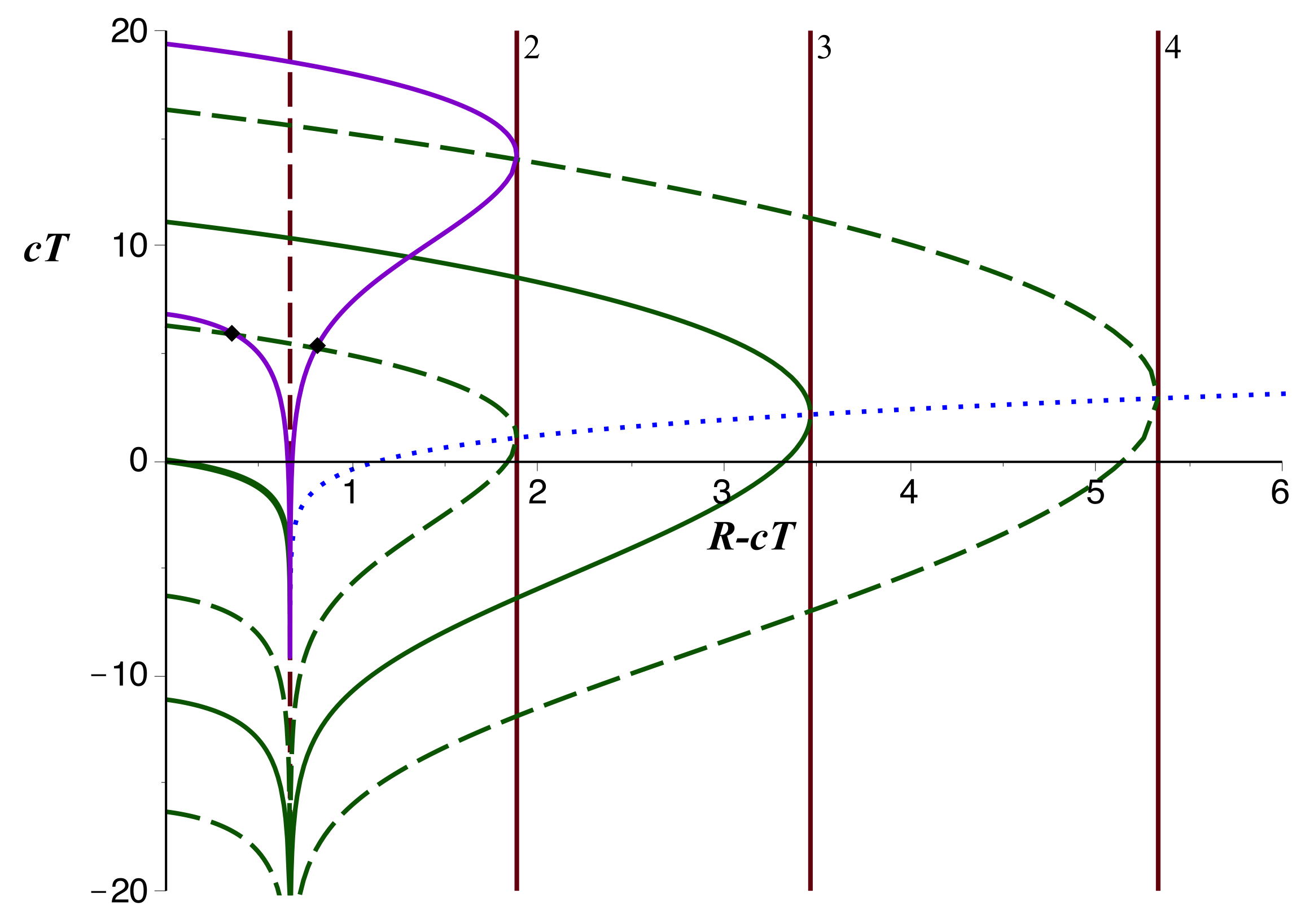

IntNovikov_cor_Im/Lemaitre-Novikov.jpg

• En décalant les valeurs de tt , on peut tracer (en violet) une trajectoire montant jusqu'à  r0=2rsr_0=2 r_s ,  puis redescendant, mais partant de  r=0r=0  après  t=0t=0 .  On y constate une double intersection avec la trajectoire analogue (en tirets verts) commençant plus tôt (et atteignant son sommet à  t=0t=0 ).

2. • Le plus simple est ici encore de calculer en notations de Schwarzschild, puis de traduire en notations de Kruskal-Szekeres (équivalentes à celles de Novikov et plus facilement manipulables).
• Ici encore se pose le problème de la représentation très étirée des trajectoires concernées ; on peut le résoudre en choisissant des exemples avec r0r_0 nettement plus proche de  r=rsr=r_s .
• On peut tracer (en vert) quelques exemples de trajectoires montant jusqu'à  r0rs=1,05;1,2;1,5\displaystyle \frac{r_0}{r_s} =\text{1,05} \,;\text{1,2} \,;\text{1,5}  (en y passant à 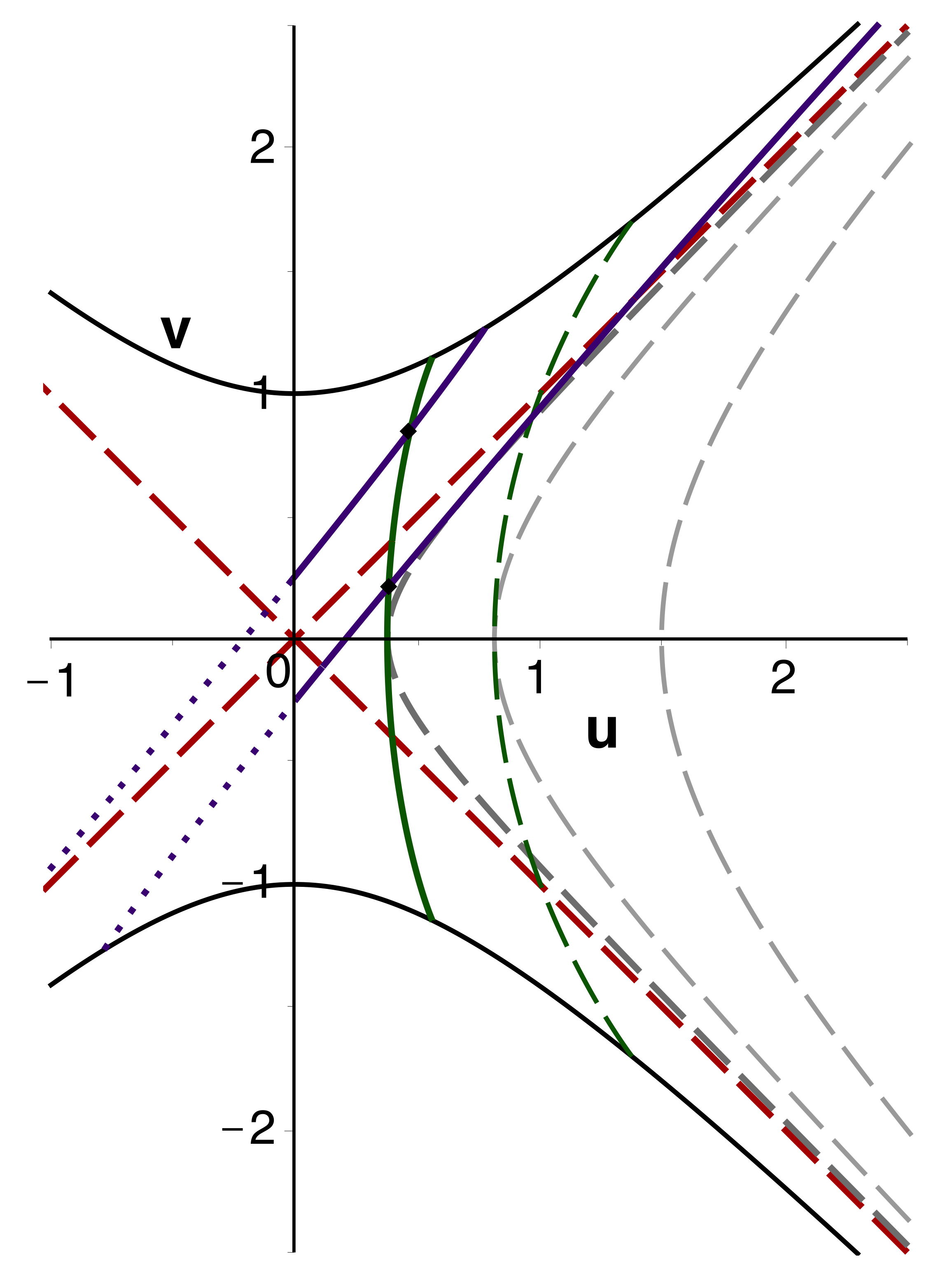 t=0 t=0 )  puis redescendant.

IntNovikov_cor_Im/K_r0_modPi.jpg

• En décalant les valeurs de tt , on peut tracer (en violet) une trajectoire montant jusqu'à  r0=1,05rsr_0=\text{1,05} \:r_s ,  puis redescendant, mais partant de  r=0r=0  après  t=0t=0  (le mouvement est l'analogue de celui représenté dans le diagramme de Lemaître précédent, mais dans cette représentation l'ordre des positions de tt pour  r<rsr<r_s  n'est pas évident).
• On y constate une simple intersection avec la trajectoire analogue (en vert) commençant plus tôt et partant de la partie gauche de la région (IV)(IV) en “remontant” le temps tt de Schwarzschild. Ceci montre bien comment Kruskal et Szekeres “évitent” les croisements intempestifs en détournant les particules du côté “obscur” du diagramme ; l'interprétation modulo ππ montre en effet le second croisement avec la portion “initiale” correspondante de la trajectoire (en pointillés violets, “remontant” le temps vv de Kruskal-Szekeres).
◊ remarque : on retrouve alors en outre que l'ordre des deux croisements n'est pas perçu de la même façon par les deux particules.