RG IX - DIAGRAMME DE KRUSKAL-SZEKERES



Singularité (horizon) de Schwarzschild

• Avec la variable radiale r r “classique”, les composantes temporelle et radiale de la métrique de Schwarzschild comportent une singularité apparente :
ds2 = A (r) c2 dt2 − C (r) dr2 − r2 dΩ2 {ds}^2=A(r) \:c^2 \,{dt}^2-C(r) \:{dr}^2-r^2 \:{dΩ}^2  ;  A= 1−rsr \displaystyle A=1-\frac{r_s}{r}  ;  C= 1A \displaystyle C=\frac{1}{A}  ;  rs= 2 𝒢M c2 \displaystyle r_s=\frac{2 \,𝒢 \:M}{c^2} .

Autre exemple de repérage statique, les coordonnées “isotropes” semblent résoudre en partie ce problème, mais impliquent d'autres difficultés.

De même les repérages comobiles de Lemaître améliorent certains aspects, mais en présentent d'autres difficilement interprétables.

On étudie ici des coordonnées d'Eddington-Finkelstein (il y en a d'autres variantes) et celles de Kruskal-Szekeres, en se limitant à la partie radiale ; ces repérages sont reliés aux trajectoires des photons.

☞ remarque : on suppose ici (interprétation “classique”) que la variable r r a une variation monotone, soit  r<rs r<r_s  au delà de la singularité.

Notations d'Eddington-Finkelstein

Notations de base

• Puisque  AC =1 A \:C=1 ,  les géodésiques radiales “nulles”  ( ds2=0 {ds}^2=0 )  décrivant le mouvement des photons correspondent à :  ±c dt= rdr r−rs \displaystyle ±c \,dt=\frac{r \:dr}{r-r_s} .

En se limitant dans un premier temps au cas  r>rs r>r_s ,  on peut écrire ceci sous la forme :  ±c dt= dr+ rs dr r−rs \displaystyle ±c \,dt=dr+\frac{r_s \: dr}{r-r_s} .

Le mouvement des photons vers l'extérieur est donc décrit par une relation de la forme :  ct= r+rs ln ( rrs−1 ) +U \displaystyle c \,t=r+r_s \: \ln\left(\frac{r}{r_s} -1\right)+U  (où U U est une constante d'intégration). De même pour les photons vers l'intérieur :  c t=−r−rs ln ( rrs−1 ) +V \displaystyle c \,t=-r-r_s \: \ln\left(\frac{r}{r_s} -1\right)+V .

• Ainsi, tout couple de géodésiques “nulles” ( U,V ) (U,V) possède un seul point d'intersection, correspondant à un point ( r, ct ) (r, \,c \,t) dans la région  r>rs r>r_s .

Kruskal_Im/Finkelstein_1.jpg

• Avec ces notations, la métrique peut s'écrire :  ds2= A(r) dU dV− r2 dΩ2 {ds}^2=A(r) \:dU \:dV-r^2 \:{dΩ}^2 .

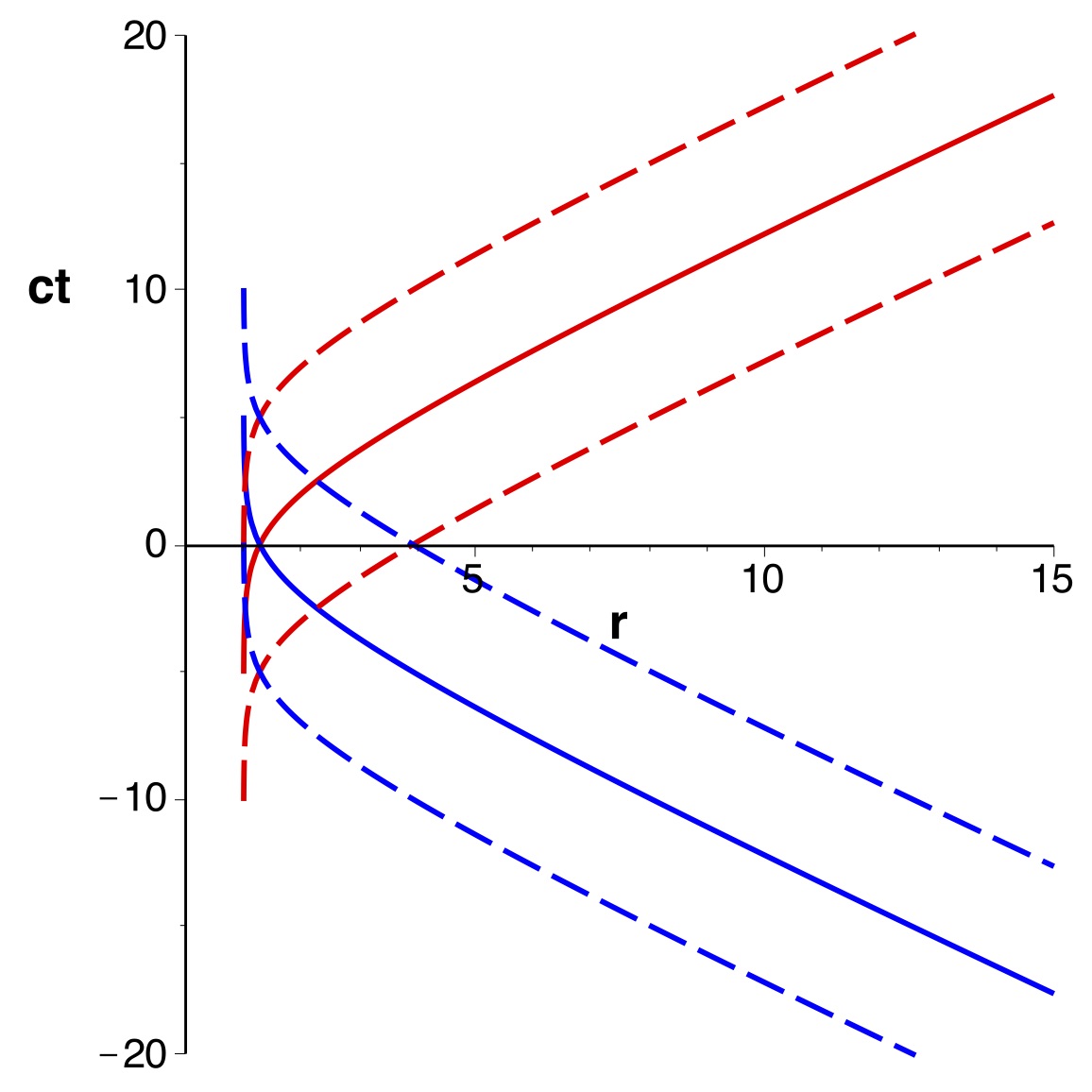
Prolongement intérieur “classique”

• Si on cherche à prolonger dans la zone  r<rs r<r_s  (en faisant l'hypothèse que cela correspond à l'intérieur de la singularité), on peut utiliser le prolongement usuel des primitives :
ct= r+rs ln ( | rrs −1 | ) +U \displaystyle c \,t=r+r_s \; \ln\left(\left|\frac{r}{r_s} -1\right|\right)+U   ;   ct= −r−rs ln ( | rrs −1 | ) +V \displaystyle c \,t=-r-r_s \; \ln\left(\left|\frac{r}{r_s} -1\right|\right)+V .

Un inconvénient est que tout point “intérieur” est associé à un point extérieur de mêmes coordonnées (U,V) (U,V) ; cela complique le repérage pour  r<rs r<r_s .

Kruskal_Im/Finkelstein_2.jpg

📖 exercices n° I, II et III.

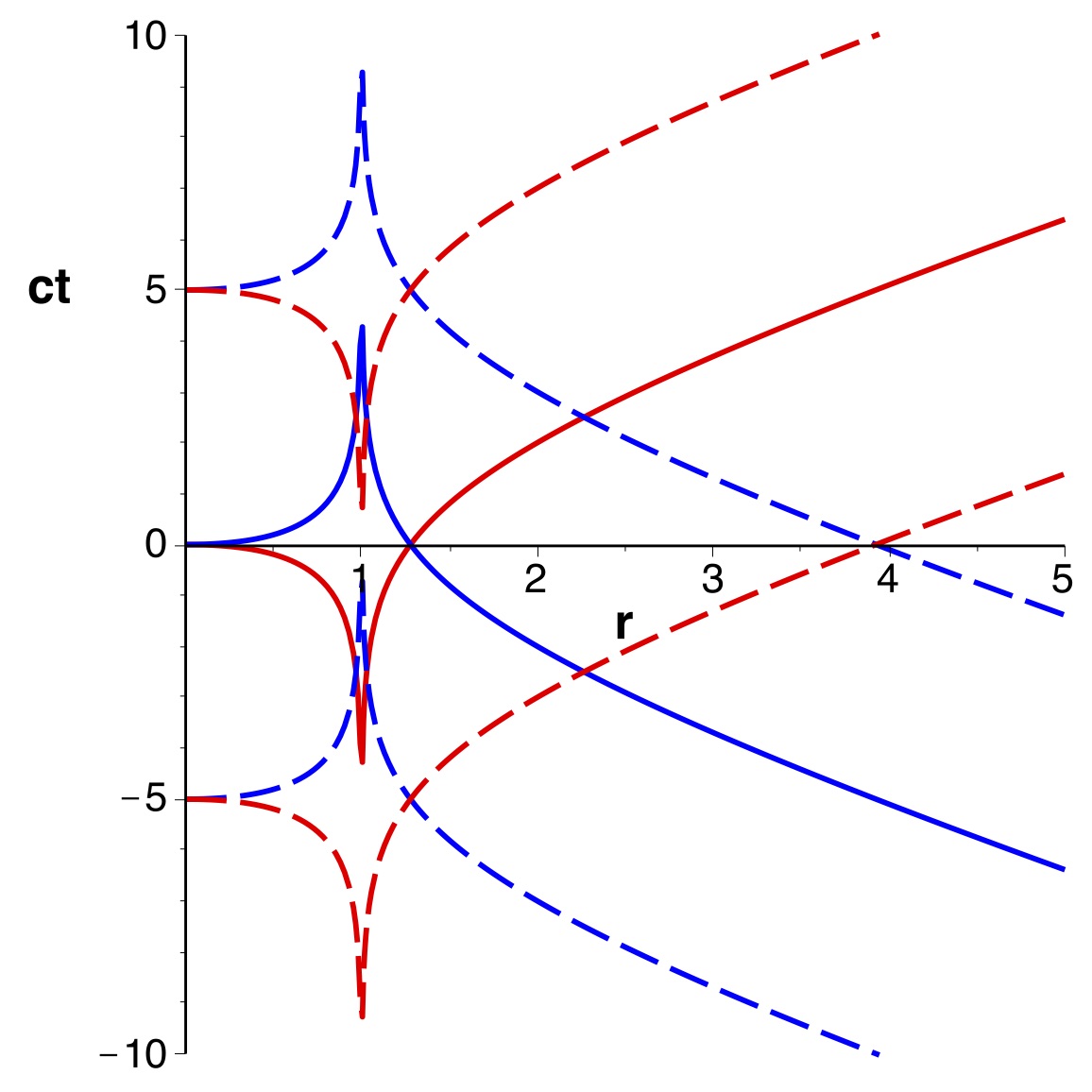
Prolongement intérieur “approfondi”

• Si on intègre dans ℝ ℝ , les constantes d'intégration s'ajoutant au logarithme de part et d'autre de la singularité ne peuvent pas être “raccordées” par continuité à cause de la divergence. On convient alors de les supposer égales.

Si on intègre dans ℂ ℂ , les constantes d'intégration peuvent être raccordées en contournant la singularité dans le plan complexe :
c t=r+rs ln ( | rrs −1 | ) ±i rs arg ( rrs−1 ) +U \displaystyle c \,t=r+r_s \; \ln\left(\left|\frac{r}{r_s} -1\right|\right)±\mathrm{i} \:r_s \; \arg\left(\frac{r}{r_s} -1\right)+U  ;
c t=−r−rs ln ( | rrs −1 | ) ±i rs arg ( rrs−1 ) +V \displaystyle c \,t=-r-r_s \; \ln\left(\left|\frac{r}{r_s} -1\right|\right)±\mathrm{i} \:r_s \; \arg\left(\frac{r}{r_s} -1\right)+V .

Le signe ± ± du terme ajouté importe peu :  arg ( rrs−1 ) =0 \displaystyle \arg\left(\frac{r}{r_s} -1\right)=0  ou  π π ,  or  −π mod [2π] =π -π \;\mod [2π]=π .

• Ceci signifie qu'en fait pour  r<rs r<r_s  la variable  ct c \,t  est complexe. La partie imaginaire, constante, est généralement ignorée (cela ne change pas  c dt c \,dt ), mais elle peut avoir des conséquences dans certains raisonnements.

Cela confirme que, de part et d'autre de la singularité, une même valeur de  ct c \,t  ne repère pas des événements “simultanés” (on le sait aussi du fait que  ct c \,t  est alors une variable du genre “espace”).

☞ remarque : sauf indication contraire, on négligera cette partie imaginaire.

Notations de Kruskal-Szekeres

Notations de base

• Pour éliminer le facteur A(r) A(r) dans la métrique d'Eddington-Finkelstein, les notations de Kruskal et Szekeres utilisent des exponentielles (ici pour  r>rs r>r_s ) :
ξ= − e −U/2rs = − rrs−1 e r/2rs e −ct/2 rs \displaystyle ξ=- \mathrm{e}^{-U/2r_s}=-\sqrt{\frac{r}{r_s} -1} \;\; \mathrm{e}^{r/2r_s} \:\: \mathrm{e}^{-ct/2r_s}  ;
η= e V/2rs = rrs−1 e r/2rs e ct/2rs \displaystyle η= \mathrm{e}^{V/2r_s}=\sqrt{\frac{r}{r_s} -1} \;\; \mathrm{e}^{r/2r_s} \:\: \mathrm{e}^{ct/2r_s} .

On obtient ainsi :  dU=−2 rs dξξ \displaystyle dU=-2 \,r_s \, \frac{dξ}{ξ}  ;  dV=2 rs dηη \displaystyle dV=2 \,r_s \, \frac{dη}{η}  ;  ceci simplifie l'expression de la métrique :  A (r) dU dV =−A (r) 4 rs 2 dξξ dηη = 4 rs 3 r e −r/rs dξ dη \displaystyle A(r) \:dU \:dV=-A(r) \:4 \,r_s^{\:2} \, \frac{dξ}{ξ} \frac{dη}{η}=\frac{4 \,r_s^{\,3}}{r} \: \mathrm{e}^{-r/r_s} \:\: dξ \:dη .

• Pour obtenir une forme diagonale de la métrique, Kruskal et Szekeres ont alors proposé d'utiliser :
u= η−ξ2 = rrs−1 e r/2rs cosh ( c t 2 rs ) \displaystyle u=\frac{η-ξ}{2}=\sqrt{\frac{r}{r_s} -1} \;\; \mathrm{e}^{r/2r_s} \:\: \cosh\left(\frac{c \,t}{2 \,r_s}\right)  ;
v= η+ξ 2 = rrs−1 e r/2rs sinh ( c t 2 rs ) \displaystyle v=\frac{η+ξ}{2}=\sqrt{\frac{r}{r_s} -1} \;\; \mathrm{e}^{r/2r_s} \:\: \sinh\left(\frac{c \,t}{2 \,r_s}\right) .

◊ remarque : ceci correspond à ce que qu'ils nomment “région (I) (I) ”.

• On obtient alors :  dη=dv+du dη=dv+du  ;  dξ=dv−du dξ=dv-du  ;  ceci permet d'écrire :
A (r) c2 dt2 −C(r) dr2 = 4 rs 3 r e −r/rs dξ dη= 4 rs 3 r e −r/rs ( dv2 −du2 ) \displaystyle A(r) \:c^2 \, {dt}^2-C(r) \:{dr}^2=\frac{4 \,r_s^{\:3}}{r} \; \mathrm{e}^{-r/r_s} \; dξ \:dη=\frac{4 \,r_s^{\:3}}{r} \; \mathrm{e}^{-r/r_s} \; ({dv}^2-{du}^2 ) .

Cette formulation a l'avantage de ne plus avoir de singularité pour  r=rs r=r_s  ;  par contre, elle présente une singularité pour  r=0 r=0 .

◊ remarque : les particules peuvent passer  r=rs r=r_s  sans singularité, mais vu de extérieur, elles doivent le faire à la vitesse de la lumière et pour  t t  “infini”.

• La variable  u u  est ainsi du genre espace, tandis que  v v  est du genre temps.

On obtient inversement (avec W0 W_0 fonction principale de Lambert) :
c t=2 rs artanh (vu) \displaystyle c \,t=2 \,r_s \: \mathrm{artanh}\left(\frac{v}{u}\right)  ;
u2−v2 = ( rrs−1 ) e r/rs \displaystyle u^2-v^2=\left(\frac{r}{r_s} -1\right) \; \mathrm{e}^{r/r_s}  ;  r=rs. [ 1+ W0 ( u2 −v2 e ) ] \displaystyle r=r_s .\left[1+W_0 \left(\frac{u^2-v^2}{\mathrm{e}}\right)\right] .

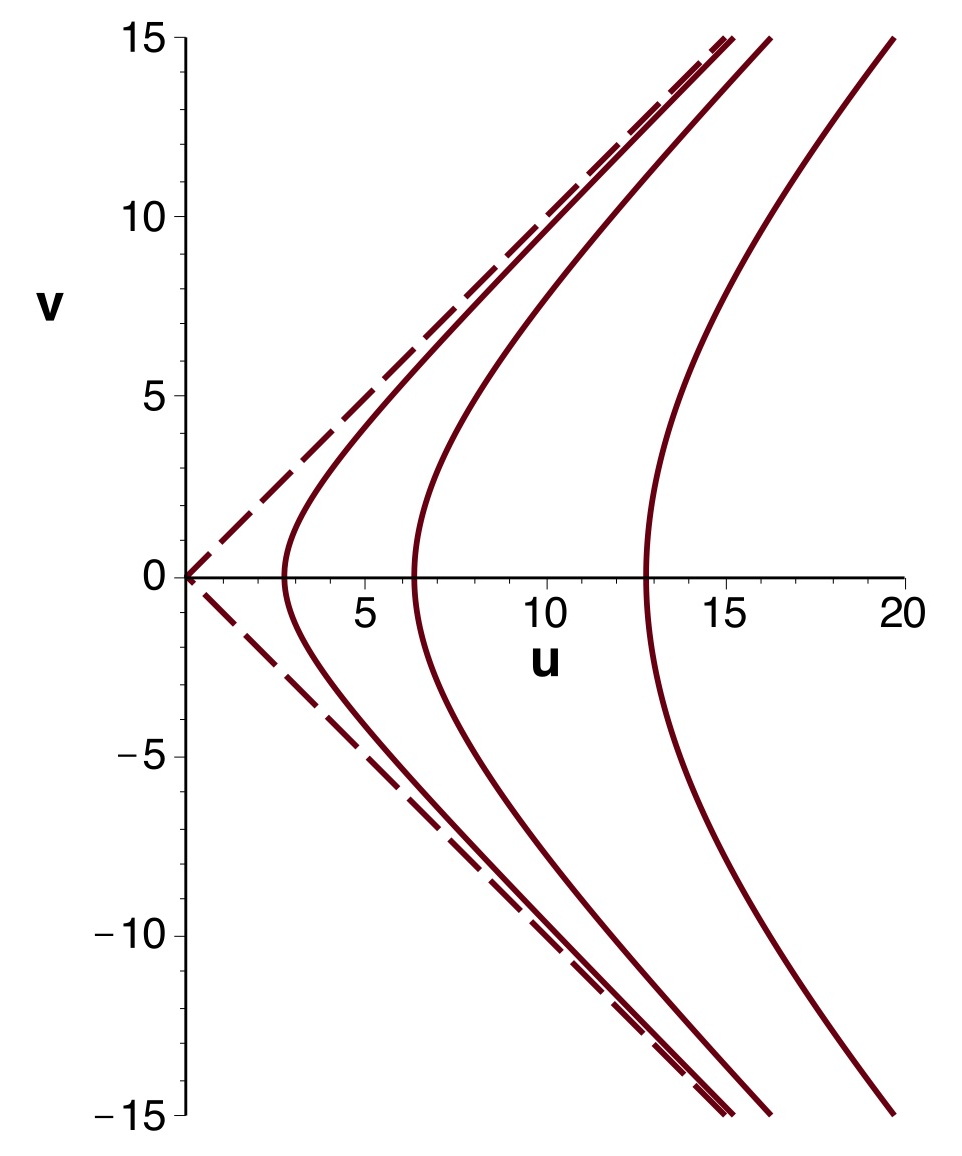
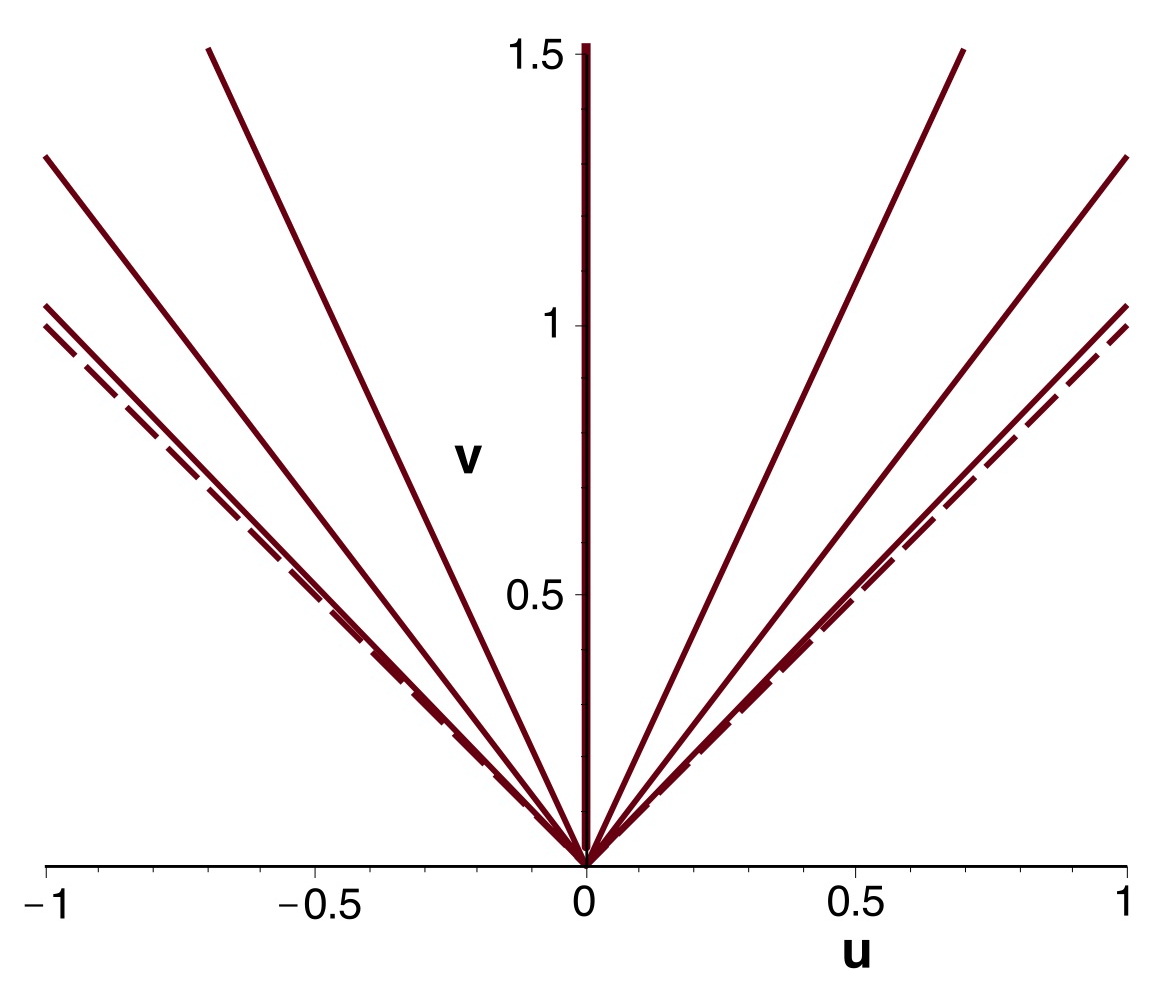
• Dans le plan ( u,v ) (u,v) les courbes correspondant à  r=Cte r=Cte  sont des branches d'hyperboles ; celles pour  ct =Cte c \,t=Cte   sont des droites passant par l'origine.

Kruskal_Im/Kruskal_I1.jpg
 Kruskal_Im/Kruskal_I2.jpg

📖 exercices n° IV et V.

Prolongement intérieur “basique”

• Si on cherche à prolonger dans la zone  r<rs r<r_s  (en faisant l'hypothèse que cela correspond à l'intérieur de la singularité), on peut proposer d'utiliser le prolongement usuel des primitives :
ξ=− e −U/2rs =− | rrs−1 | e r/2rs e −ct/2rs \displaystyle ξ=- \mathrm{e}^{-U/2r_s}=-\sqrt{\left|\frac{r}{r_s} -1\right|} \:\: \mathrm{e}^{r/2r_s} \:\: \mathrm{e}^{-ct/2r_s}  ;
η= e V/2rs = | rrs−1 | e r/2rs e ct/2rs \displaystyle η= \mathrm{e}^{V/2r_s}=\sqrt{\left|\frac{r}{r_s} -1\right|}\:\: \mathrm{e}^{r/2r_s} \:\: \mathrm{e}^{ct/2r_s}  ;
u= η−ξ2 = | rrs −1 | e r/2rs cosh ( c t 2 rs ) \displaystyle u=\frac{η-ξ}{2}=\sqrt{\left|\frac{r}{r_s} -1\right|} \:\: \mathrm{e}^{r/2r_s} \:\: \cosh⁡\left(\frac{c \,t}{2 \,r_s}\right)  ;
v= η+ξ 2 = | rrs−1 | e r/2rs sinh ( c t 2 rs ) \displaystyle v=\frac{η+ξ}{2}=\sqrt{\left|\frac{r}{r_s} -1\right|} \:\: \mathrm{e}^{r/2r_s} \:\: \sinh\left(\frac{c \,t}{2 \,r_s}\right) .

Ceci donne toutefois pour  r<rs r<r_s  (le signe de A A ne se simplifie pas) :
A(r) dU dV =− 4 rs 3 r e −r/rs dξ dη = 4 rs 3 r e −r/rs ( du 2 −dv2 ) \displaystyle A(r) \:dU \:dV=-\frac{4 \,r_s^{\:3}}{r} \; \mathrm{e}^{-r/r_s} \:\: dξ \:dη=\frac{4 \,r_s^{\:3}}{r} \; \mathrm{e}^{-r/r_s} \; ({du}^2-{dv}^2 ) .

En outre, un inconvénient de ce prolongement est que (comme évoqué pour les notations d'Eddington-Finkelstein) les valeurs de ( u,v ) (u,v) pour  r<rs r<r_s  reprennent des valeurs correspondant déjà à d'autres points pour  r>rs r>r_s .

Prolongement de Kruskal-Szekeres

• Le graphique cartésien de la région (I) (I) n'occupe qu'un quart du plan. Pour représenter les points “intérieurs” avec des valeurs ( u,v ) (u,v) différentes de l'extérieur, Kruskal et Szekeres y proposent d'autres combinaisons donnant :
u= | rrs−1 | e r/2rs sinh ( ct 2 rs ) \displaystyle u=\sqrt{\left|\frac{r}{r_s} -1\right|} \:\: \mathrm{e}^{r/2r_s} \:\: \sinh⁡\left(\frac{c \,t}{2 \,r_s}\right)  ;  v= | rrs−1 | e r/2rs cosh ( ct 2 rs ) \displaystyle v=\sqrt{\left|\frac{r}{r_s} -1\right|} \:\: \mathrm{e}^{r/2r_s} \:\: \cosh⁡\left(\frac{c \,t}{2 \,r_s}\right) .

Ceci revient à permuter u u et v v (ou changer le signe de ξ ξ ), donc correspond à une région (II) (II) globalement symétrique de la région (I) (I) par rapport à la diagonale croissante.

Ceci redonne pour  r<rs r<r_s :   A(r) c2 dt2 −C(r) dr2= 4 rs 3 r e −r/rs ( dv 2 −du2 ) \displaystyle A(r) \:c^2 \, {dt}^2-C(r) \:{dr}^2=\frac{4 \,r_s^{\:3}}{r} \; \mathrm{e}^{-r/r_s} \:\: ({dv}^2-{du}^2 ) .  En particulier la variable  v v  reste du genre temps et  u u  reste du genre espace.

◊ remarque : aucun ouvrage ne semble préciser comment Kruskal ou Szekeres en sont arrivés à choisir ces notations ; il semble que se doit pour des considérations pratiques, d'après la représentation graphique.

• On obtient ici encore :  u2− v2= ( rrs−1 ) e r/rs \displaystyle u^2-v^2=\left(\frac{r}{r_s} -1\right) \:\:\mathrm{e}^{r/r_s}  ;  r= rs. [ 1+W0 ( u2−v2 e ) ] \displaystyle r=r_s .\left[1+W_0 \left(\frac{u^2-v^2}{\mathrm{e}}\right)\right] .

Par contre dans ce cas :  ct= 2 rs artanh (uv) \displaystyle c \,t=2 \,r_s \; \mathrm{artanh}\left(\frac{u}{v}\right) .

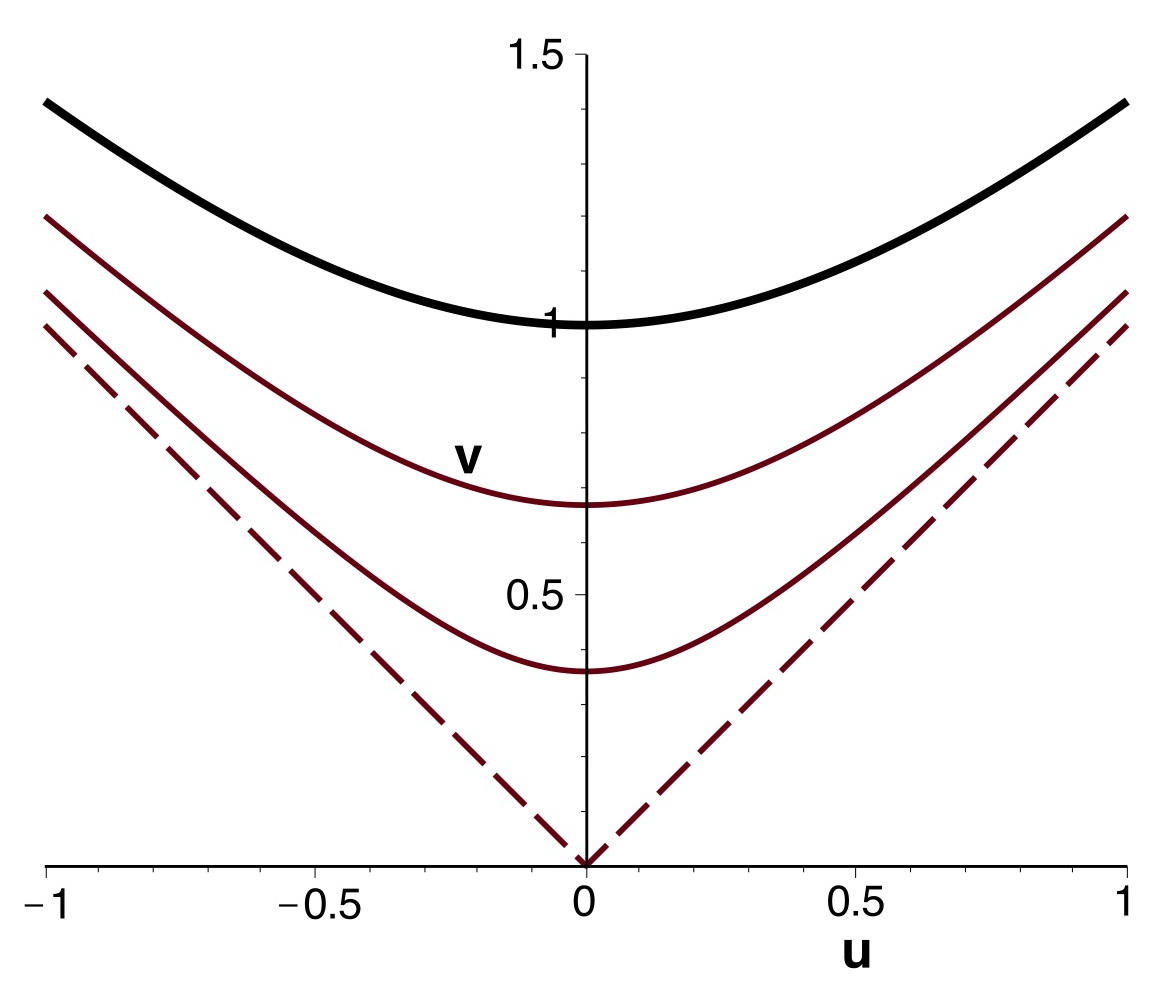
• Dans le plan (u, v) (u,v) les courbes correspondant à  r=Cte r=Cte  sont des branches d'hyperboles ; celles pour  c t=Cte c \,t=Cte  sont des droites passant par l'origine.

Kruskal_Im/Kruskal_II1.jpg
 Kruskal_Im/Kruskal_II2.jpg

◊ remarque : la branche d'hyperbole pour  r=0 r=0  (en noir) correspond à la singularité “centrale”.

◊ remarque : contrairement à la région (I) (I) , ici  t t  croît dans le sens horaire.

◊ remarque : bien qu'obtenues par des combinaisons mathématiques “heureuses”, les notations de Kruskal-Szekeres peuvent être justifiées physiquement par les repérages de Novikov (étudiés dans une partie ultérieure).

📖 exercices n° VI et VII

Prolongement intérieur “approfondi”

• Il peut être intéressant de repartir des mêmes expressions de u u et v v que dans la région (I) (I) , mais avec les notations complexes déjà considérées pour les notations d'Eddington-Finkelstein ; ceci tout en sachant qu'il faut obtenir des expressions en fonction de Re ( c t ) \mathrm{Re}(c \,t) puisque c'est la quantité généralement utilisée.

Si on repart des notations d'Eddington-Finkelstein, on retrouve le prolongement “basique” avec ses défauts :
ξ=− e −U/2rs =− | rrs−1 | e r/2rs e − Re ( ct ) / 2rs \displaystyle ξ=- \mathrm{e}^{-U/2r_s}=-\sqrt{\left|\frac{r}{r_s} -1\right|} \:\: \mathrm{e}^{r/2r_s} \:\: \mathrm{e}^{-\mathrm{Re}(ct)/2r_s}  ;
η= e V/2rs = | rrs −1 | e r/2rs e Re ( ct ) /2rs \displaystyle η= \mathrm{e}^{V/2r_s}=\sqrt{\left|\frac{r}{r_s} -1\right|} \:\: \mathrm{e}^{r/2r_s} \:\: \mathrm{e}^{\mathrm{Re}(ct)/2r_s}  .

Mais puisqu'on a vu que le choix de Kruskal-Szekeres pour la région (II) (II) revenait à changer de combinaison de ξ ξ et η η (en fait juste changer le signe pour ξ ξ ), on peut repartir des expressions pour la région (I) (I) :
u= rrs −1 e r/2rs cosh ( ct 2 rs ) =± | rrs−1 | e r/2rs sinh ( Re ( c t ) 2 rs ) \displaystyle u=\sqrt{\frac{r}{r_s} -1} \:\: \mathrm{e}^{r/2r_s} \:\: \cosh\left(\frac{c \,t}{2 \,r_s}\right)=±\sqrt{\left|\frac{r}{r_s} -1\right|} \:\: \mathrm{e}^{r/2r_s} \:\: \sinh\left(\frac{\mathrm{Re}(c \,t)}{2 \,r_s}\right)  ;
v= rrs−1 e r/2rs sinh ( ct 2 rs ) =± | rrs−1 | e r/2rs cosh ( Re ( ct ) 2 rs ) \displaystyle v=\sqrt{\frac{r}{r_s} -1} \:\: \mathrm{e}^{r/2r_s} \:\: \sinh\left(\frac{c \,t}{2 \,r_s}\right)=±\sqrt{\left|\frac{r}{r_s} -1\right|} \:\: \mathrm{e}^{r/2r_s} \:\: \cosh\left(\frac{\mathrm{Re}(c \,t)}{2 \,r_s}\right) .

Ceci conduit effectivement (mais ici de façon justifiée) à utiliser les combinaisons choisies par Kruskal et Szekeres. Il apparaît toutefois des ambiguïtés sur les signes : si l'argument de  ct rs \displaystyle \frac{c \,t}{r_s}  est défini modulo 2π 2π ,  celui de  ct 2 rs \displaystyle \frac{c \,t}{2 \,r_s}  est défini modulo π π .

◊ remarque : ceci suggère en fait que le diagramme de Kruskal-Szekeres est de même défini modulo π π , ce qui est d'ailleurs clairement considéré par Szekeres (bien qu'il ne le justifie pas précisément).

• On obtient de même :  c t=2 rs artanh (vu) \displaystyle c \,t=2 \,r_s \; \mathrm{artanh}\left(\frac{v}{u}\right)  mais  Re (c t ) =2 rs artanh (uv) \displaystyle \mathrm{Re}(c \,t)=2 \,r_s \; \mathrm{artanh}\left(\frac{u}{v}\right) .

Complétion de Kruskal-Szekeres

• Les régions (I) (I) et (II) (II) ne remplissant que la moitié du plan (u, v) (u,v) , Kruskal et Szekeres indiquent qu'on peut compléter par deux régions symétriques :

Le repérage par (ct ,r) (c \,t, r) est-il incomplet ? Kruskal reste ambigu ; Szekeres considère que le diagramme est dédoublé (défini modulo π π ).

Kruskal_Im/Kruskal_zones.jpg

📖 exercices n° VIII, IX et X

Complétion “approfondie”

• Si, d'après les notations complexes, on suppose que le diagramme est défini modulo π π , alors les régions (III) (III) et (IV) (IV) ne sont que des “duplicatas” des régions (I) (I) et (II) (II) , conformément à l'interprétation de Szekeres.

Repérage de Kruskal-Szekeres et transformation de Lorentz

• Bien que cela n'apparaisse pas dans son processus de construction, le repérage de Kruskal-Szekeres peut, comme ceux de Lemaître, être associé à une transformation de Lorentz.

• Pour  r>rs r>r_s  on considère (en prenant  rs r_s  comme unité pour simplifier) :
u= r−1 e r/2 cosh ( ct 2 ) \displaystyle u=\sqrt{r-1} \:\: \mathrm{e}^{r/2} \:\: \cosh\left(\frac{c \,t}{2}\right)  ;
du=12 rr−1 e r/2 cosh ( ct 2 ) dr+ 12 r−1 e r/2 sinh ( ct 2 ) cdt \displaystyle du=\frac{1}{2} \frac{r}{\sqrt{r-1}} \:\: \mathrm{e}^{r/2} \:\: \cosh\left(\frac{c \,t}{2}\right) \; dr+\frac{1}{2} \,\sqrt{r-1} \:\: \mathrm{e}^{r/2} \:\: \sinh\left(\frac{c \,t}{2}\right) \; c \,dt .

La variable d'espace est  u u  (et  v v  est une variable de temps), donc l'immobilité correspond à  du=0 du=0 ,  c'est-à-dire :  dr=−r−1r tanh ( ct2 ) cdt \displaystyle dr=-\frac{r-1}{r}\, \tanh\left(\frac{c \,t}{2}\right) \; c \,dt .

La vitesse d'entraînement associée est ainsi :  βe= dr A cdt =− tanh ( ct2 ) =−vu \displaystyle β_e=\frac{dr}{A \:c \,dt}=- \tanh\left(\frac{c \,t}{2}\right)=-\frac{v}{u} .

• Pour  r<rs r<r_s  on considère (en ignorant la composante imaginaire de  ct c \,t ) :
u= 1−r e r/2 sinh ( ct 2 ) \displaystyle u=\sqrt{1-r} \:\: \mathrm{e}^{r/2} \:\: \sinh\left(\frac{c \,t}{2}\right)  ;
du=−12 r1−r e r/2 sinh ( ct 2 ) dr+ 12 1−r e r/2 cosh ( ct 2 ) cdt \displaystyle du=-\frac{1}{2} \frac{r}{\sqrt{1-r}} \:\: \mathrm{e}^{r/2} \:\: \sinh\left(\frac{c \,t}{2}\right) \; dr+\frac{1}{2} \,\sqrt{1-r} \:\: \mathrm{e}^{r/2} \:\: \cosh\left(\frac{c \,t}{2}\right) \; c \,dt .

L'immobilité correspond à  du=0 du=0 ,  c'est-à-dire :  dr=− r−1r coth ( ct 2 ) cdt \displaystyle dr=-\frac{r-1}{r} \; \coth\left(\frac{c \,t}{2}\right) \; c \,dt .

La vitesse d'entraînement associée est ainsi :  βe= dr A cdt =−coth ( ct 2 ) =− vu \displaystyle β_e=\frac{dr}{A \:c \,dt}=- \coth\left(\frac{c \,t}{2}\right)=-\frac{v}{u} .  Cette expression tend vers l'infini pour  u=0 u=0  ( ct=0 c \,t=0 )  et non pour  r=0 r=0  comme pour la transformation de Lemaître.

◊ remarque : avec la composante imaginaire de  ct c \,t :  βe=− tanh ( ct 2 ) =− vu \displaystyle β_e=- \tanh\left(\frac{c \,t}{2}\right)=-\frac{v}{u} .

◊ remarque : de même qu'avec la transformation de Lemaître, pour  r<rs r<r_s  la vitesse  βe= dr A cdt \displaystyle β_e=\frac{dr}{A \:c \,dt}  n'est qu'une extrapolation puisque  r r  devient une variable de temps et  t t  une variable d'espace.

• Ainsi Kruskal et Szekeres considèrent un repérage dont le mouvement dépend du temps : expansion d'autant plus rapide que  t→−∞ t→-∞  ;  contraction d'autant plus rapide que  t→+∞ t→+∞ .

Étant donné qu'à cause de  A=0 A=0  les particules mettent un temps  t t  infini pour atteindre (ou provenir de) la singularité, cela aboutit à un résultat aussi efficace que l'approche de Lemaître : l'horizon est atteint à la célérité c c .

Une telle métrique peut toutefois sembler ne pas décrire un trou noir statique, invariant par changement de l'origine du temps, mais plutôt un “trou noir dynamique” : la matière imposant la métrique, initialement en expansion à partir d'un trou blanc, passant par une extension maximum à  t=0 t=0 ,  puis s'effondrant en un trou noir final.

📖 exercices n° XI, XII, XIII et XIV