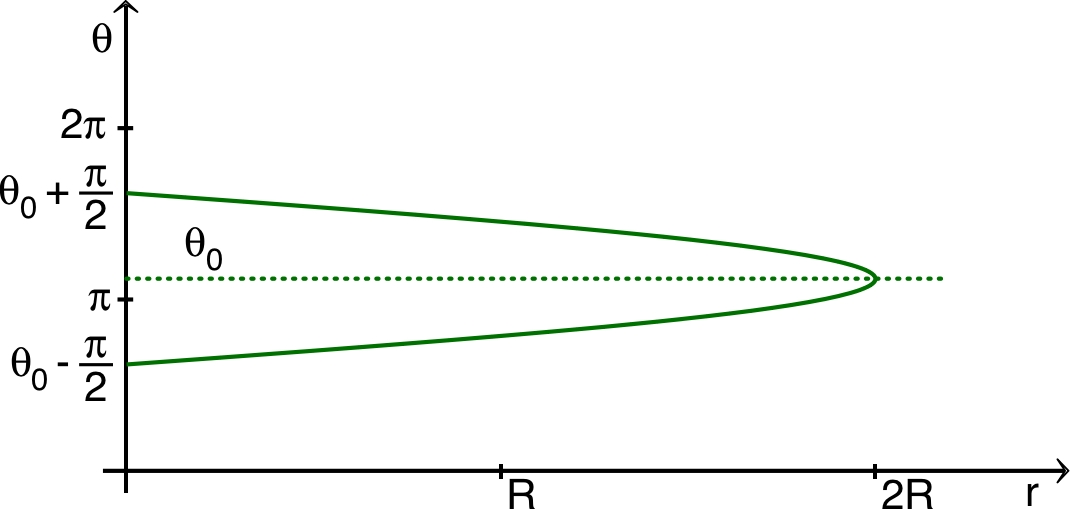
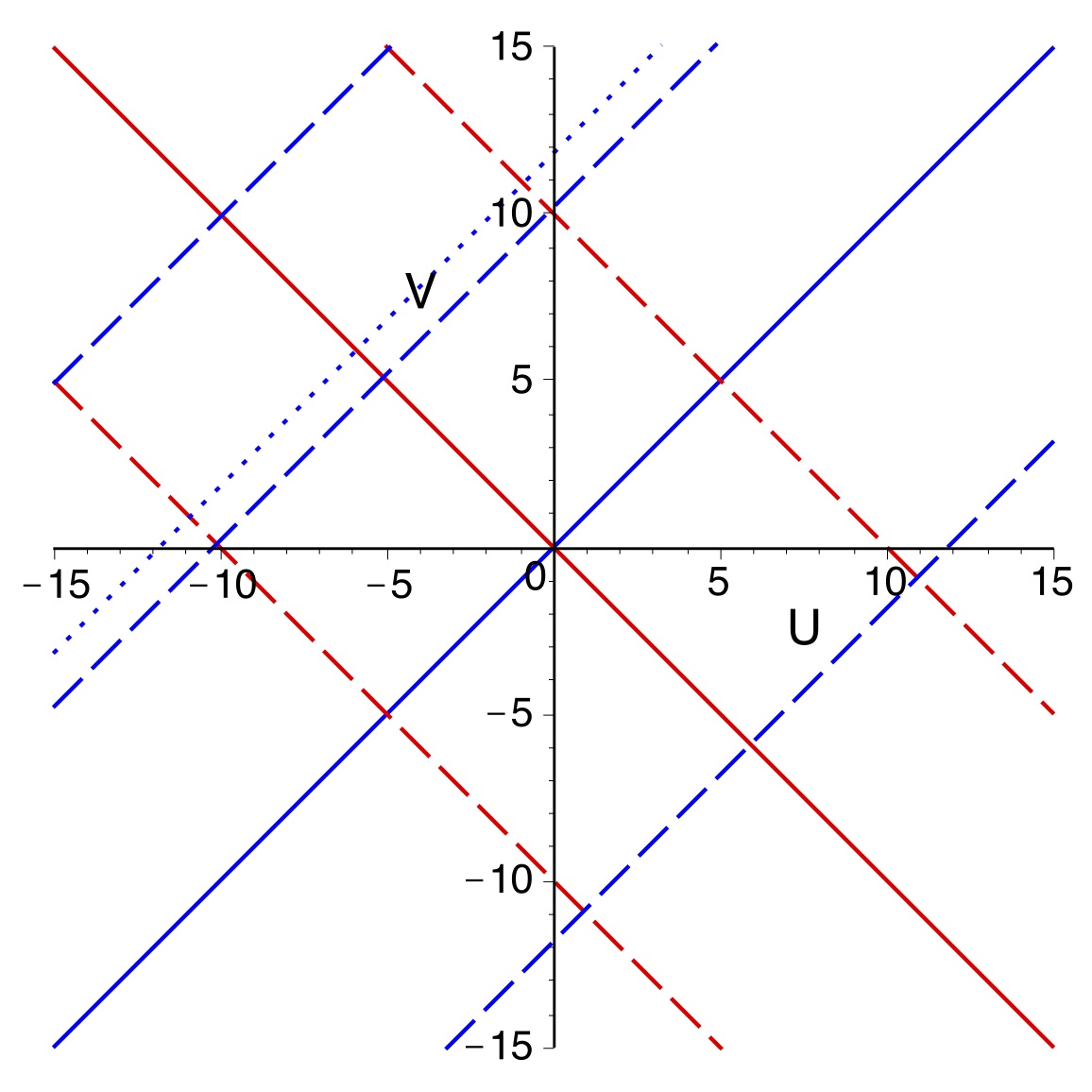
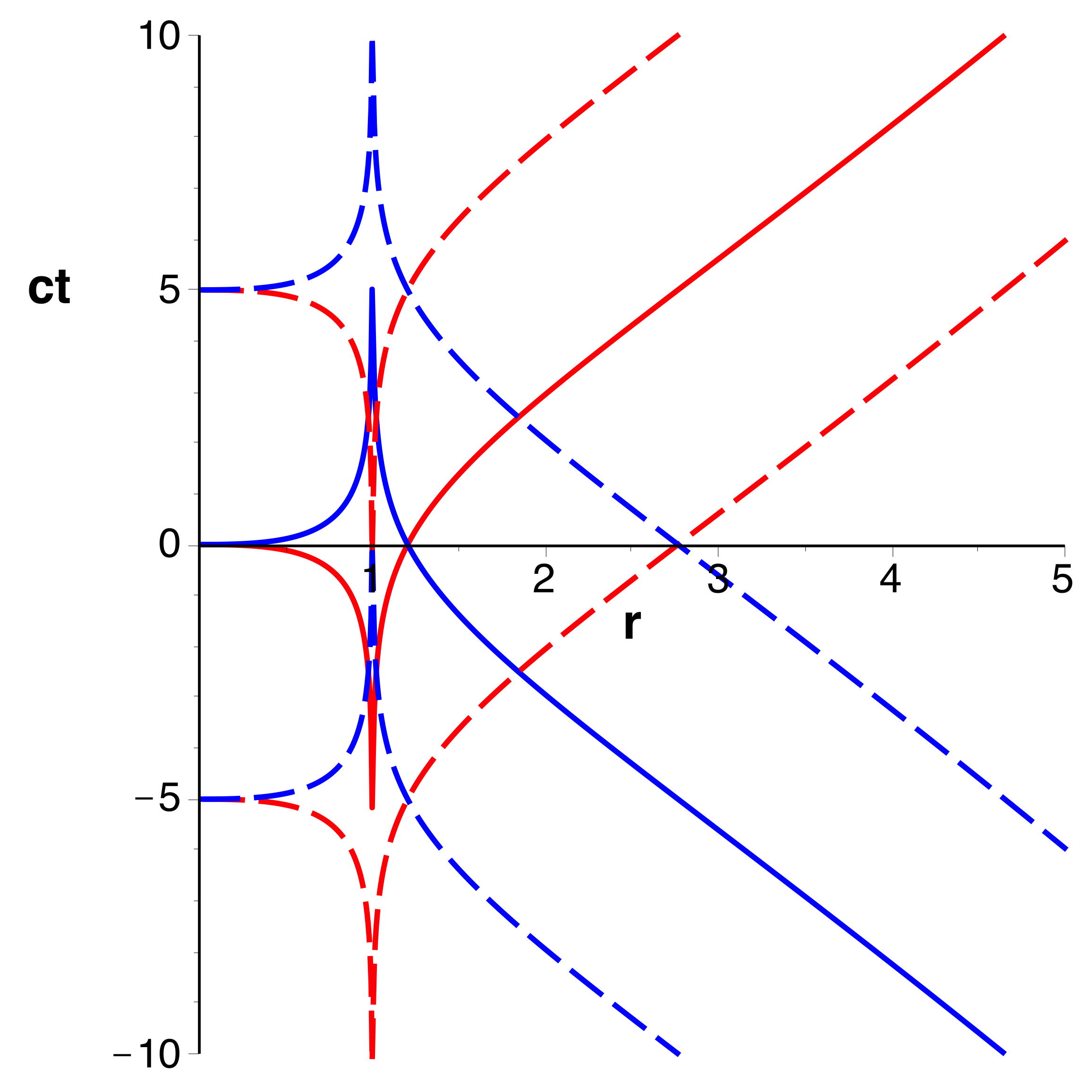
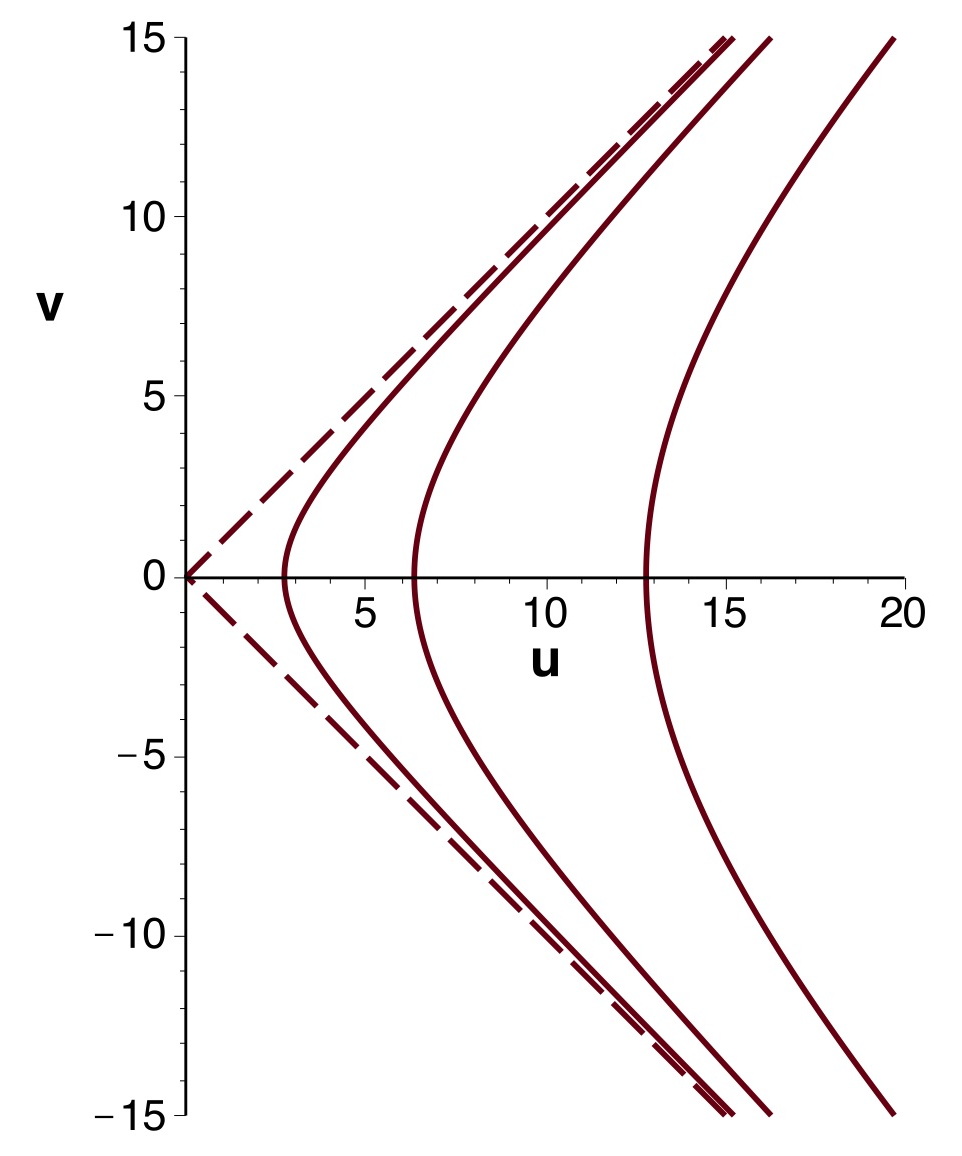
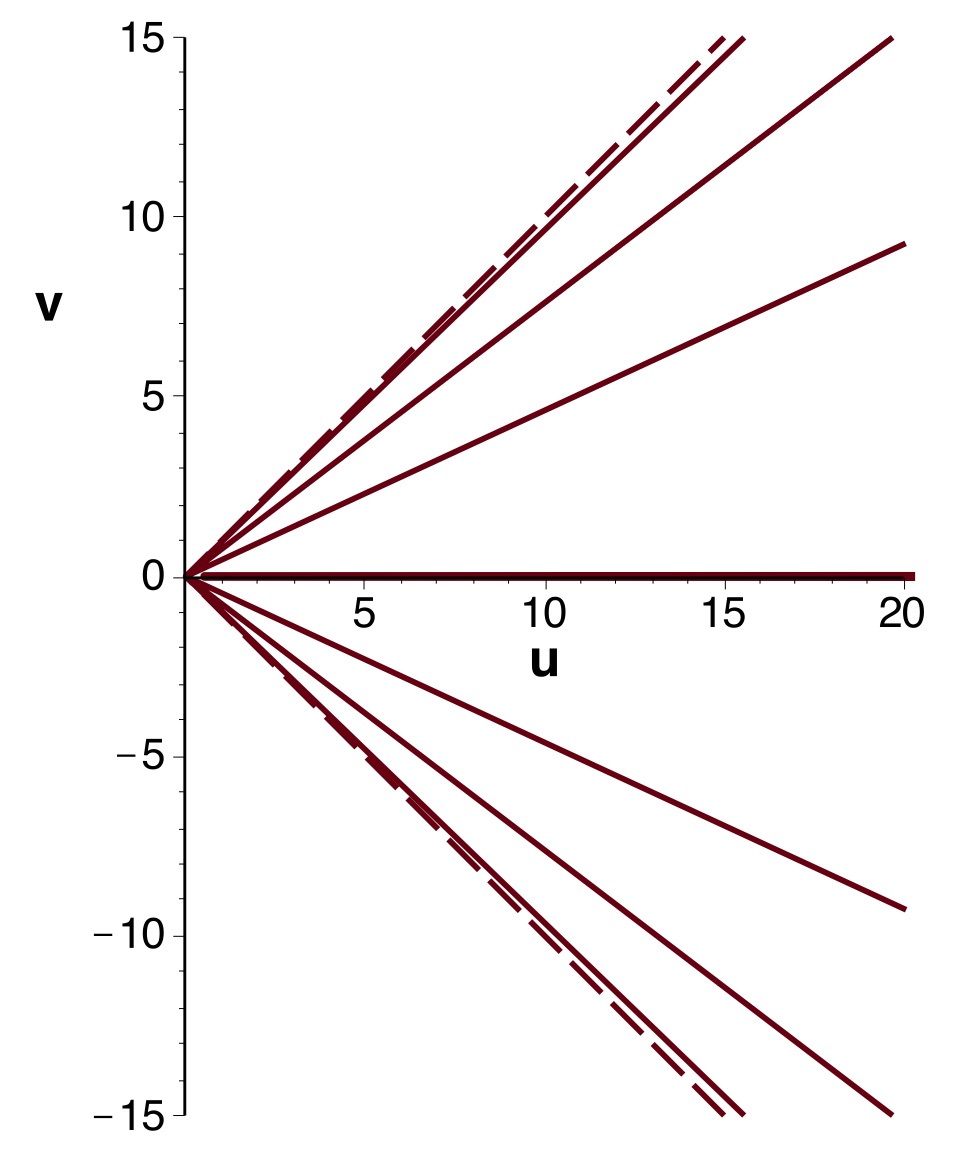
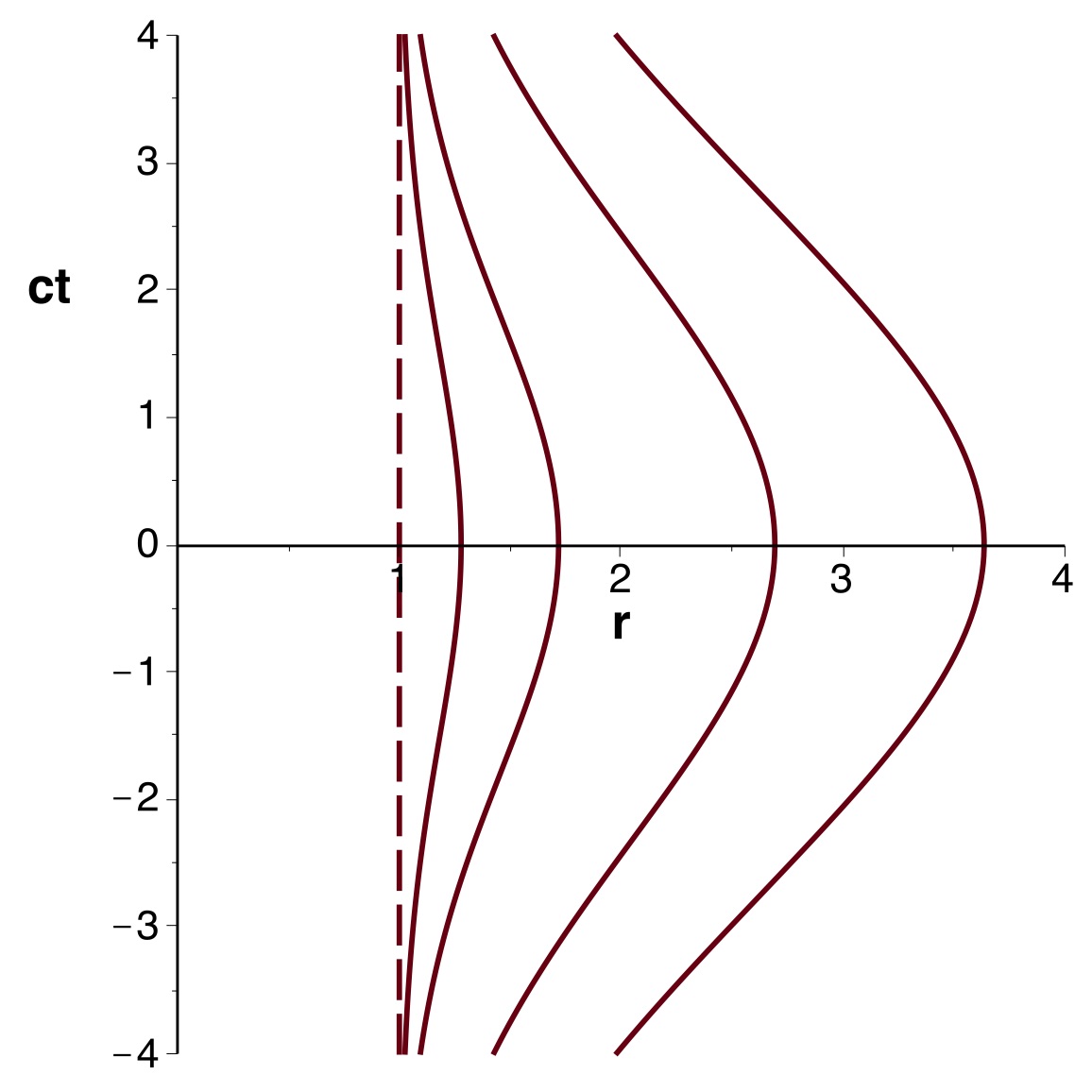
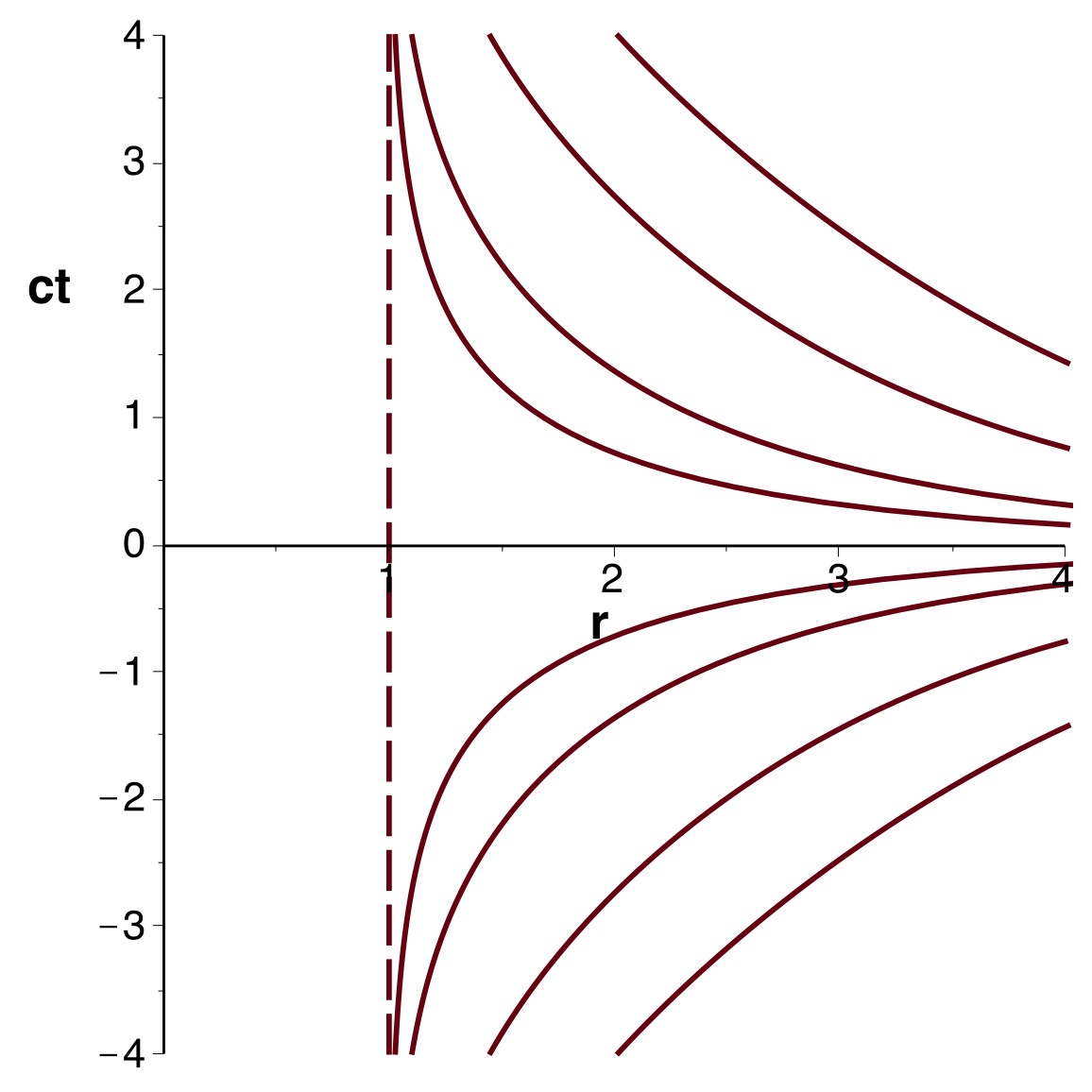
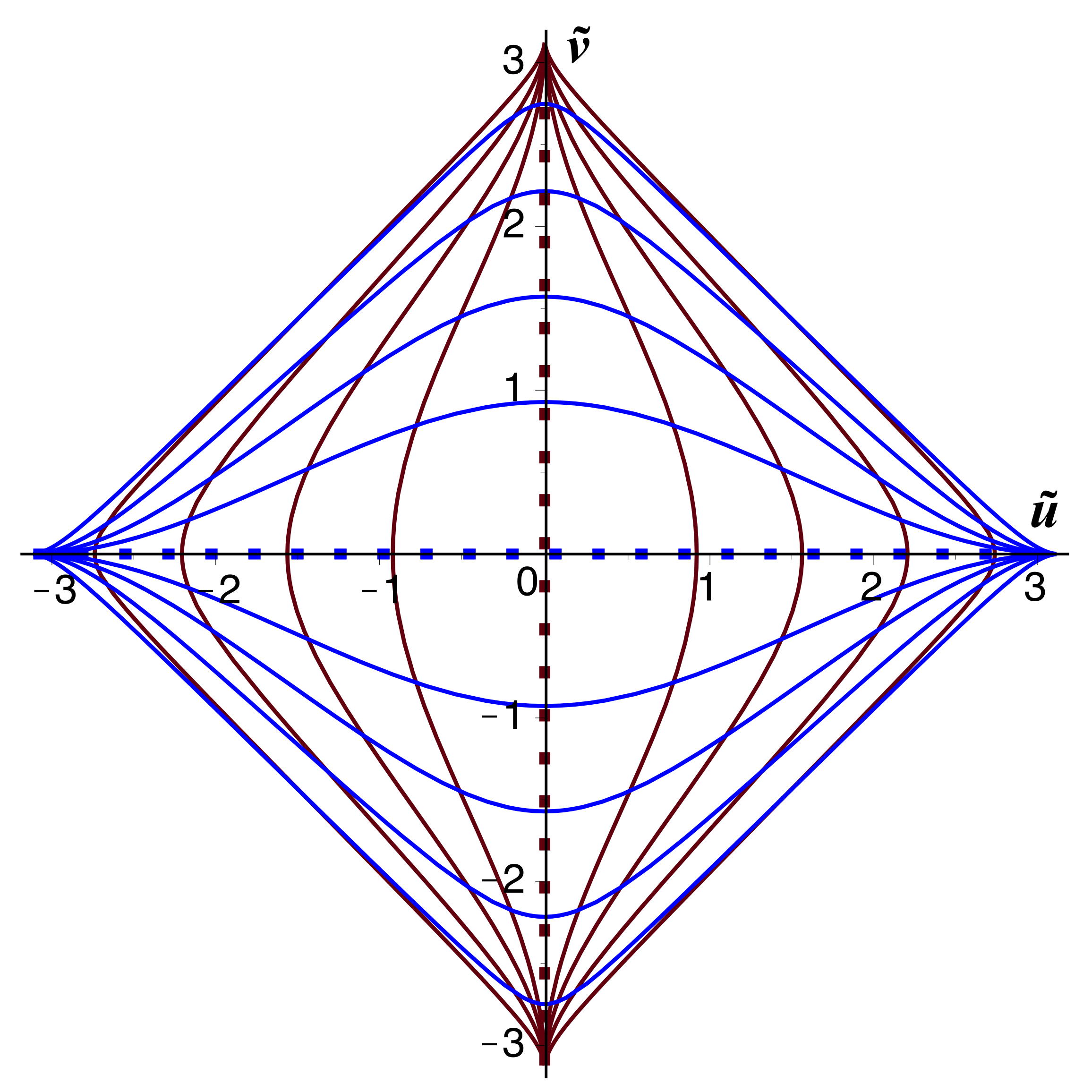
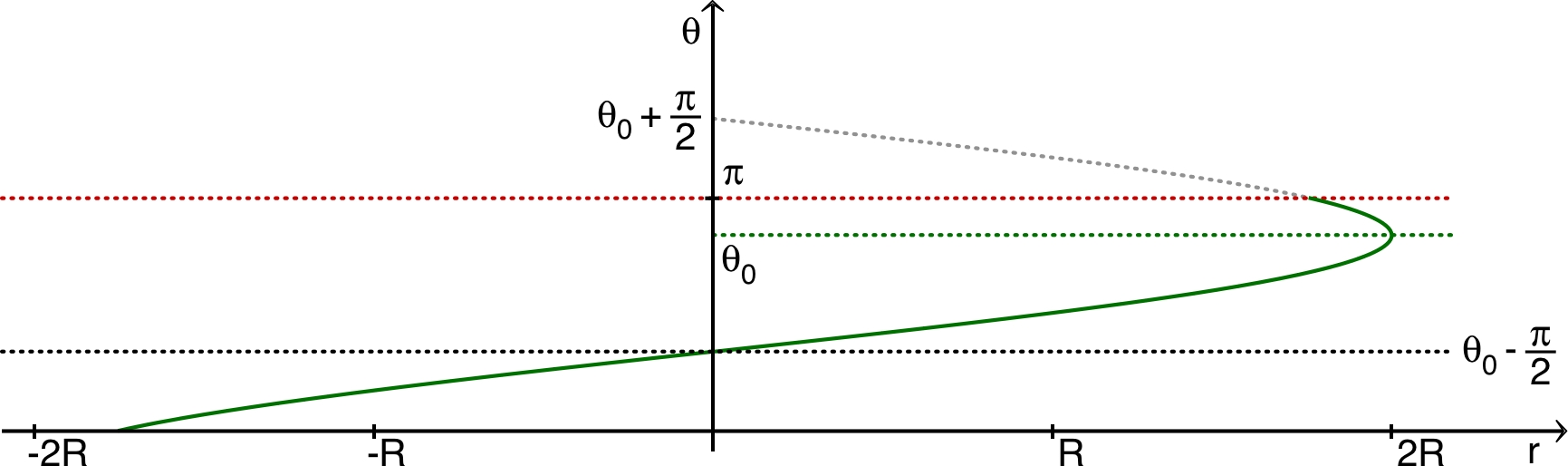
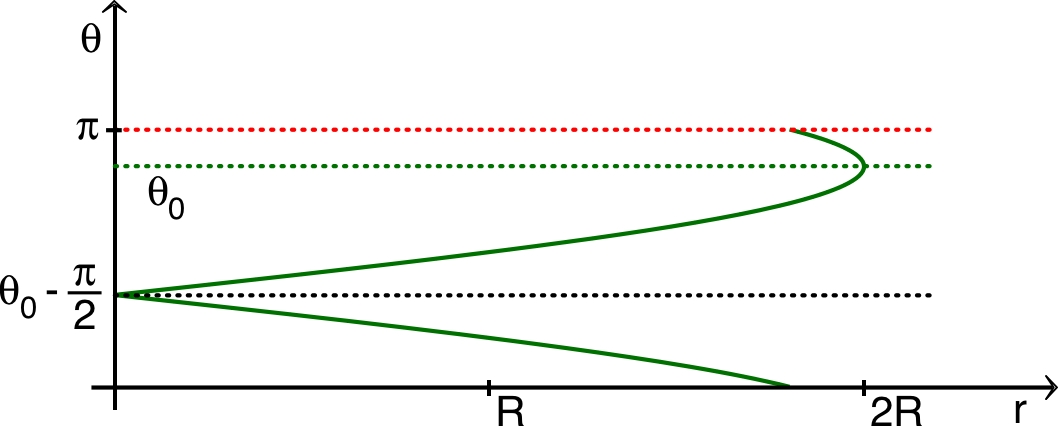
| 2.a. |
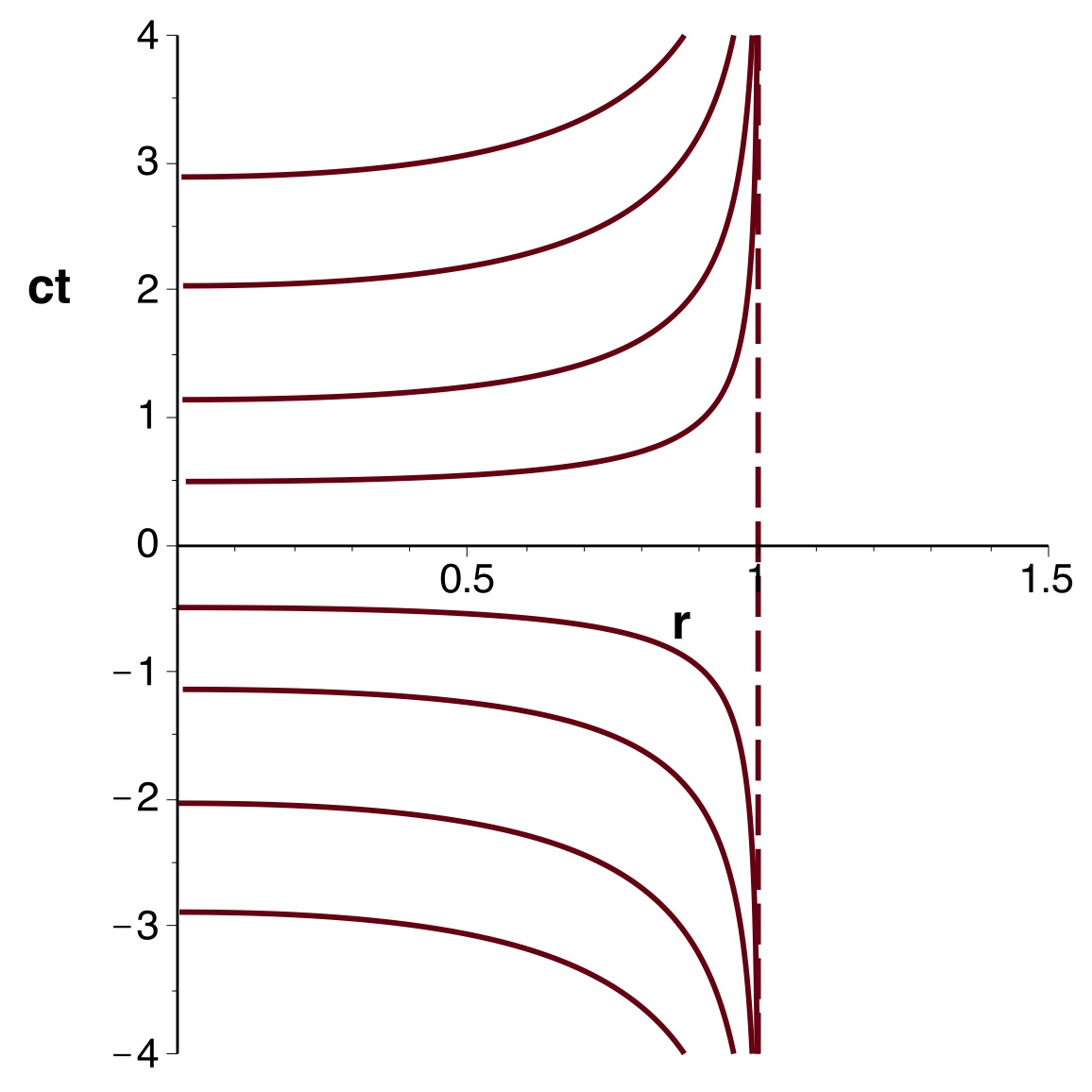
• On se limite ici au cas d'une particule
en chute, au passage de
avec
, suivie par un référentiel en contraction ; l'étude
serait analogue pour
avec un référentiel en expansion.
• Soit
le
référentiel de Kruskal-Szekeres, ayant par rapport à
statique une vitesse d'entraînement (vers le bas)
:
pour
;
pour
.
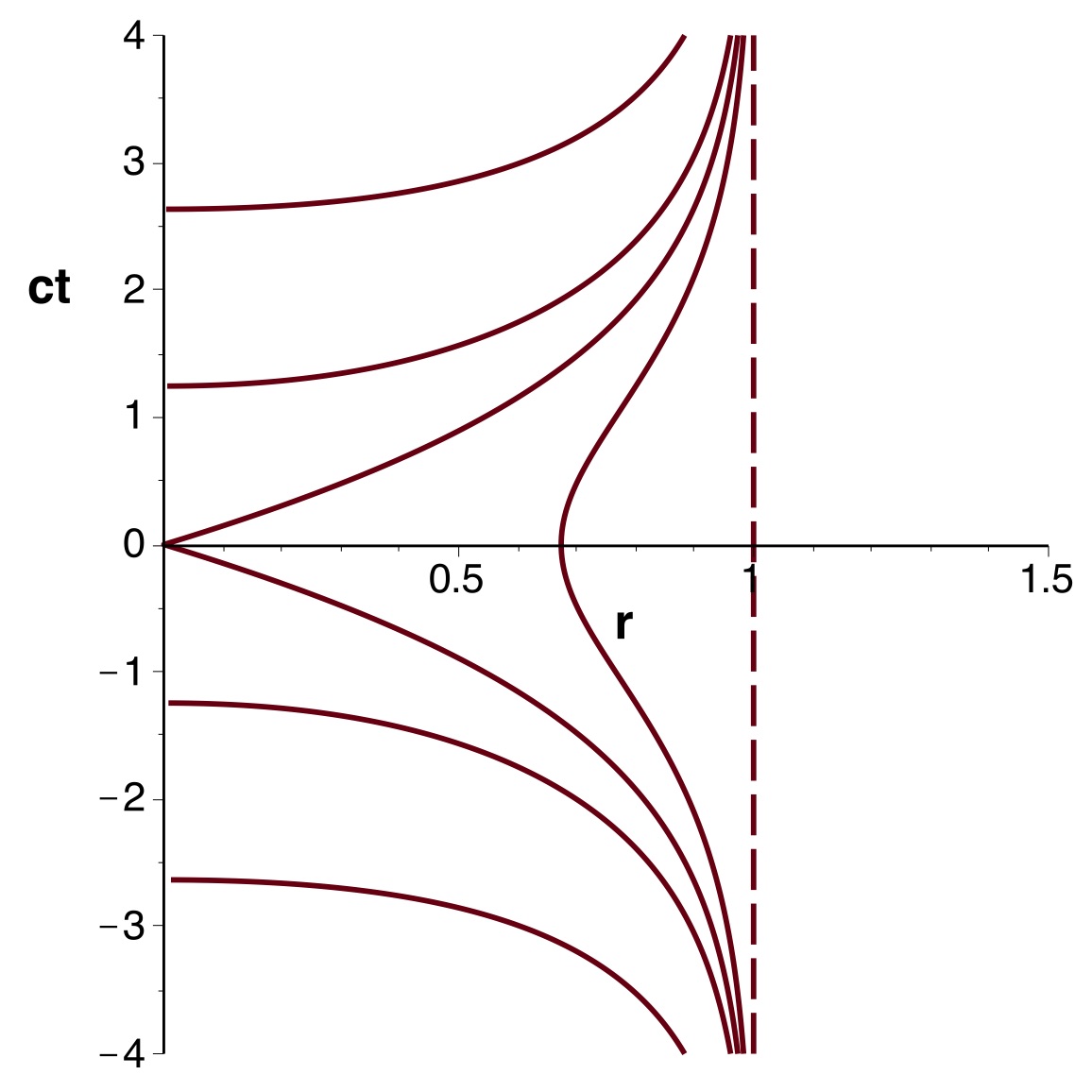
• Soit de même
le
référentiel de Lemaître en co-mouvement avec une vitesse
d'entraînement (vers le bas)
par rapport à
statique.
• Par combinaison “théorique”, la transformation
permettant de passer de
à
correspond à une vitesse d'entraînement :
.
• Ceci donne :
pour
;
pour
. |
| 2.b. |
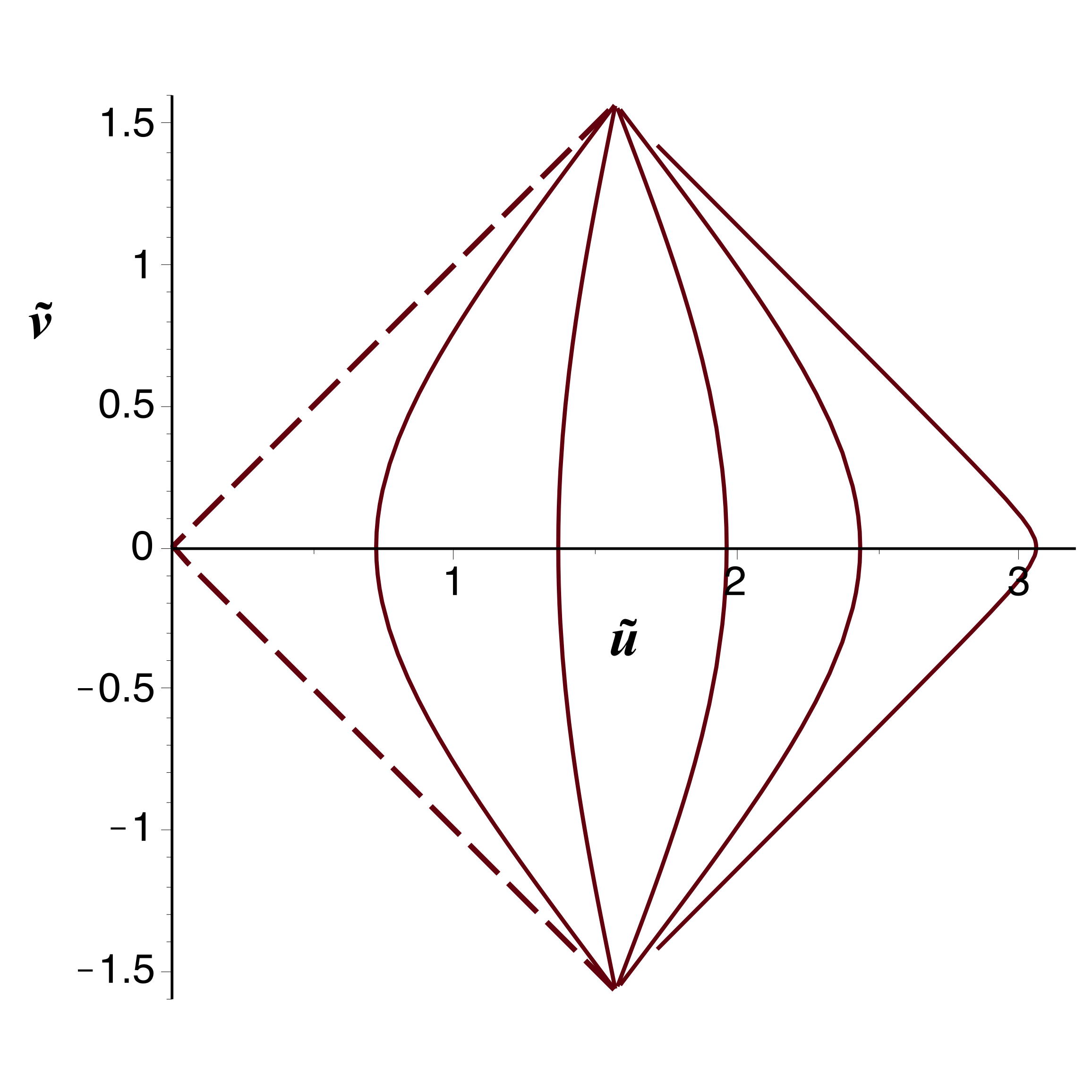
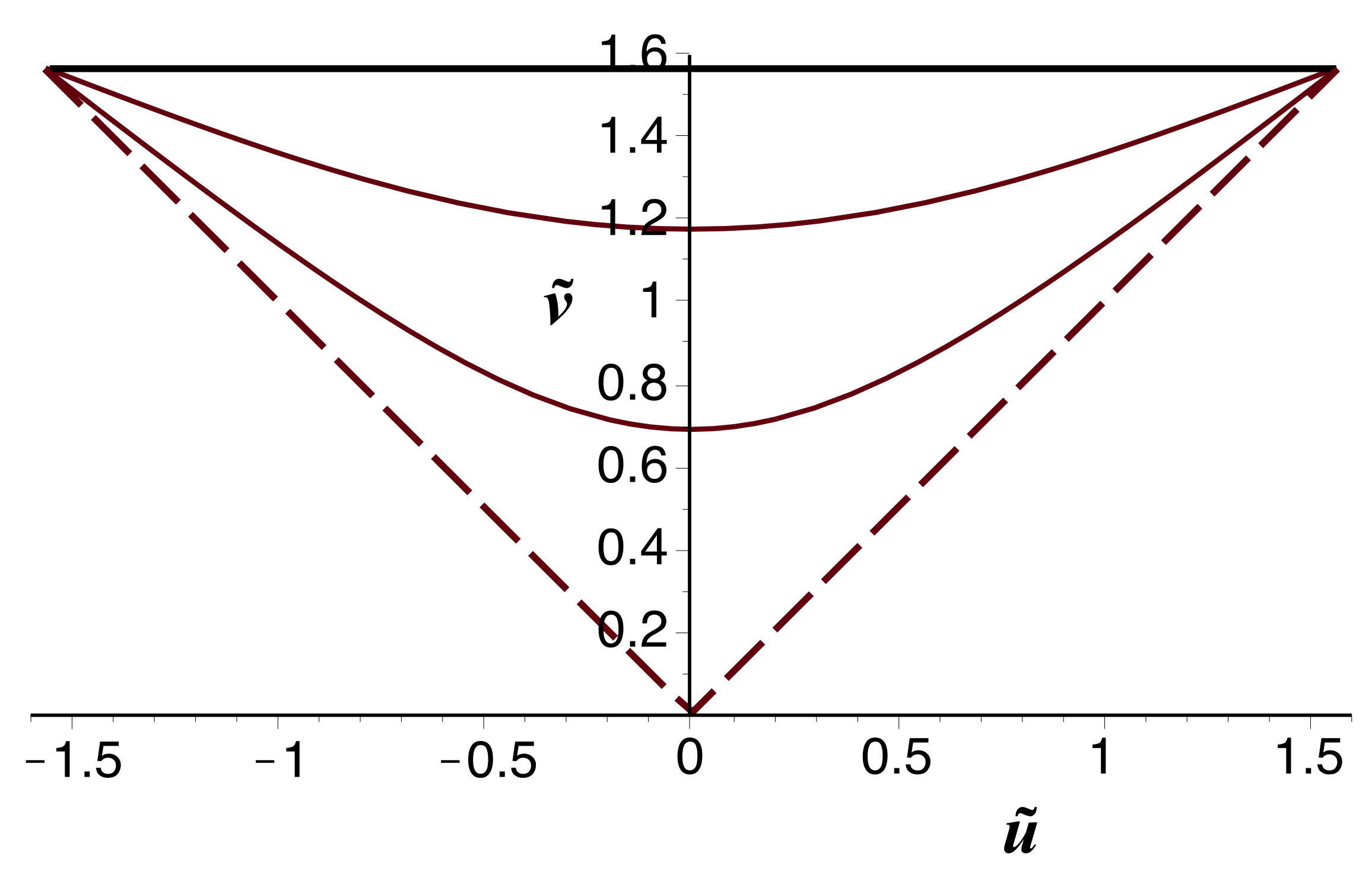
• Pour
les coordonnées de Kruskal-Szekeres s'écrivent
(avec
comme unité) :
;
.
• Ceci donne :
;
.
• Inversement :
;
.
• Par ailleurs les coordonnées de Lemaître correspondent à
:
;
.
• Pour un point fixe par rapport au repérage de
Kruskal-Szekeres, dont la variable spatiale est
,
on obtient en reportant, avec
:
;
.
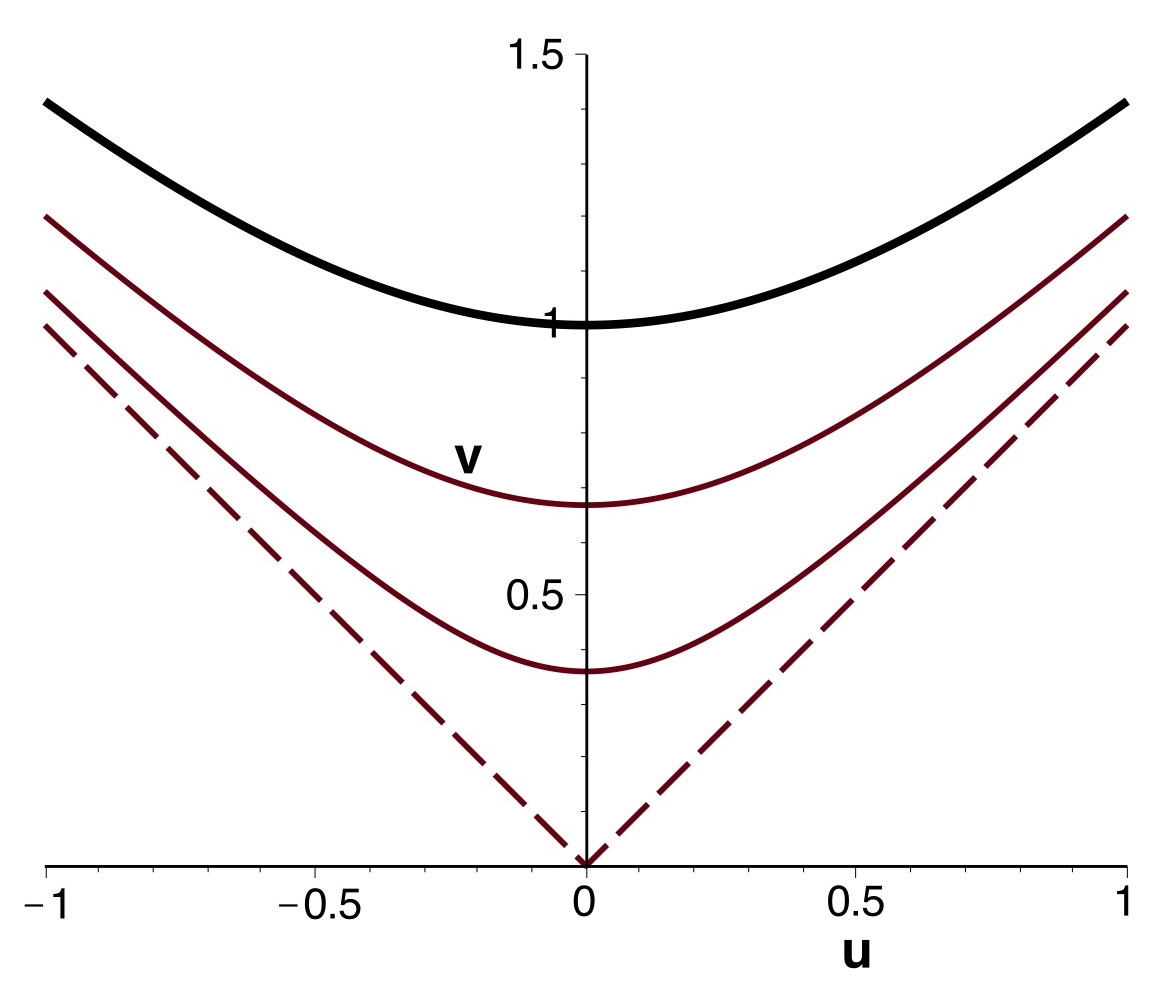
• Avec la métrique de Lemaître (réduite) :
, on retrouve le résultat “théorique” :
;
;
.
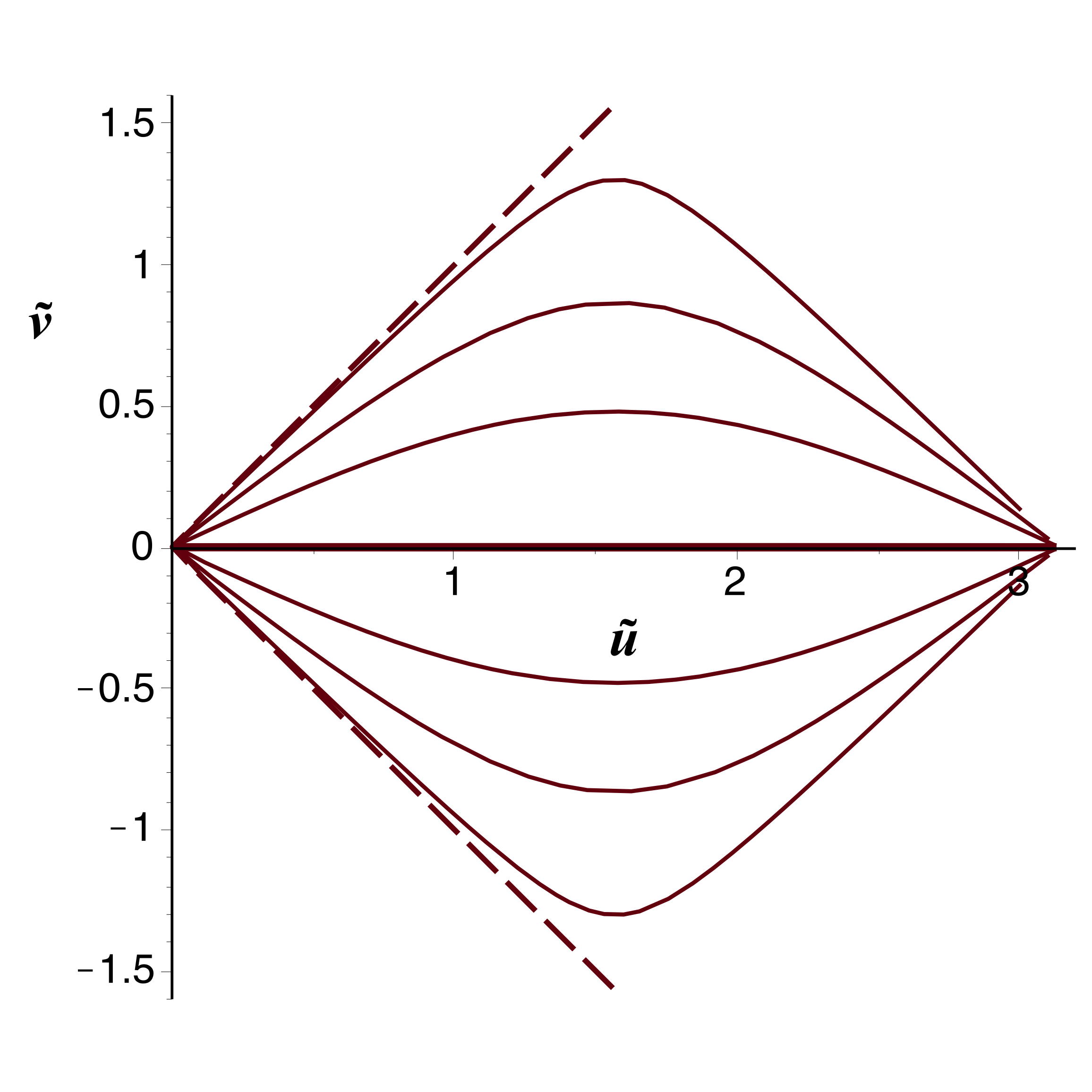
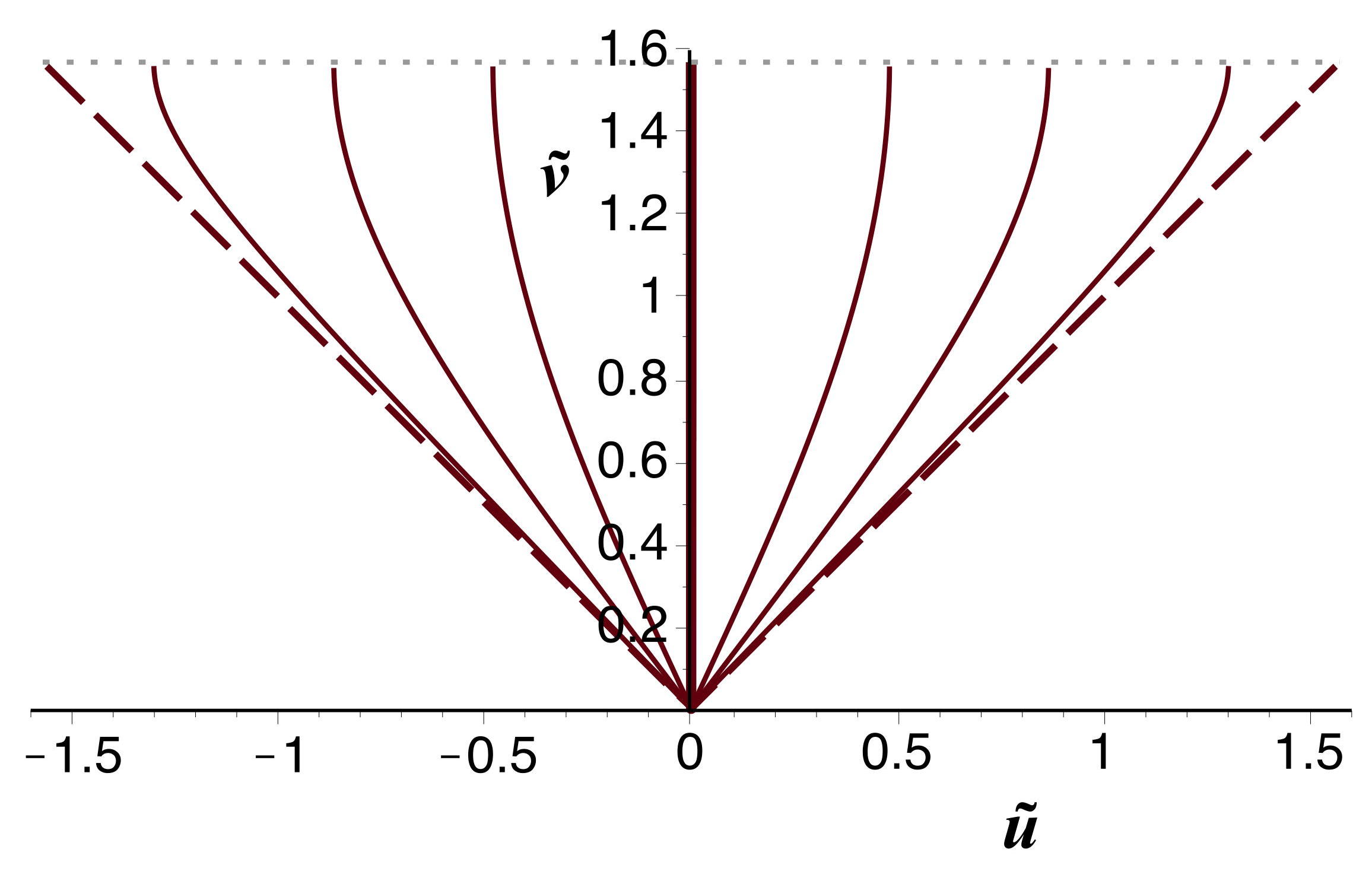
• Pour
les coordonnées de Kruskal-Szekeres s'écrivent :
;
.
• Ceci donne :
;
.
• Inversement :
;
.
• Par ailleurs les coordonnées de Lemaître correspondent à
:
;
.
• Pour un point fixe par rapport au repérage de
Kruskal-Szekeres, dont la variable spatiale est
,
on obtient en reportant, avec
:
;
.
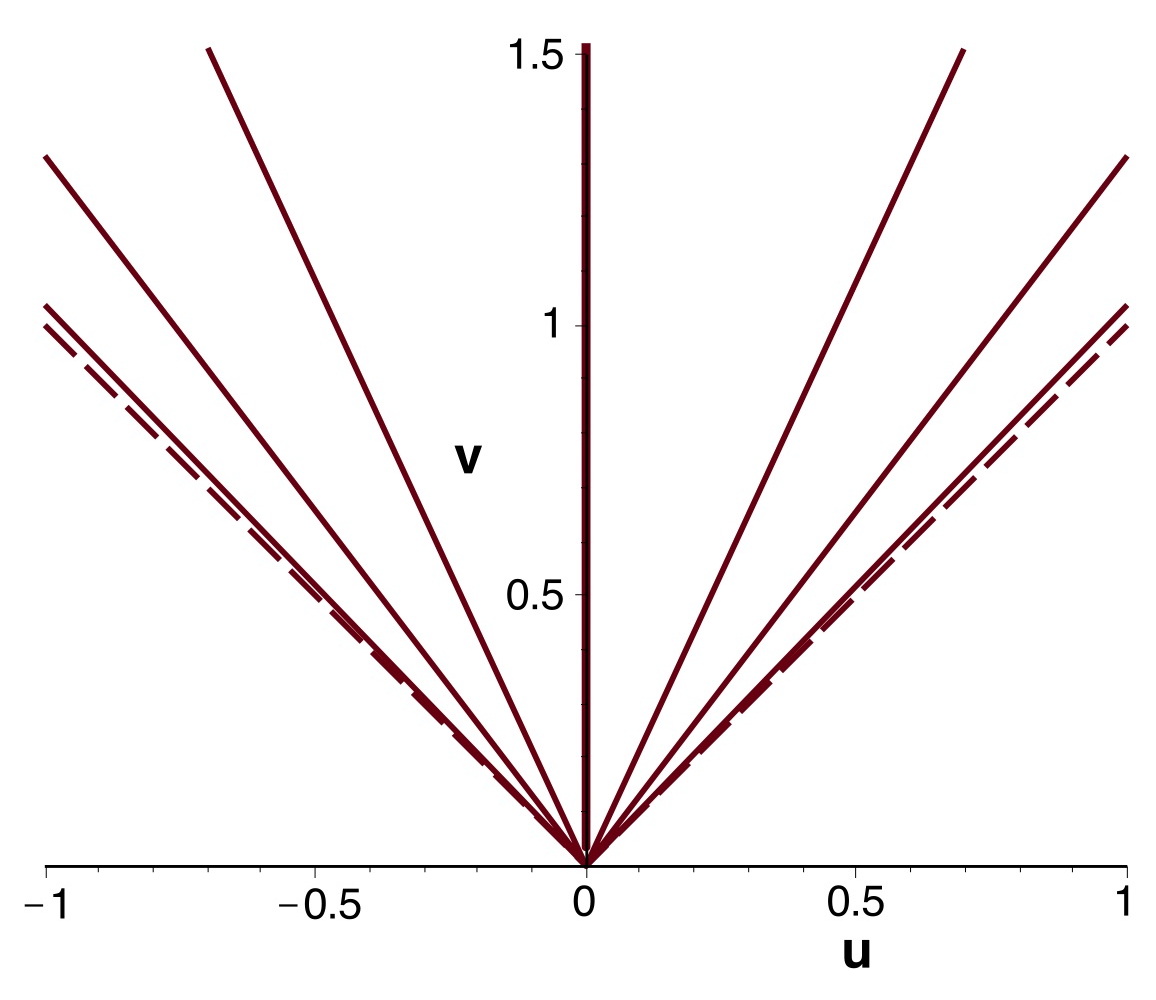
• Avec la métrique de Lemaître, on retrouve le
résultat “théorique” :
;
;
.
|