RG VII - MÉTRIQUE DE LEMAÎTRE



1. Singularité de Schwarzschild

• Avec la variable radiale rr “classique”, les composantes temporelle et radiale de la métrique de Schwarzschild comportent une singularité apparente :

 ds2=A(r)c2dt2−C(r)dr2−r2dΩ2{ds}^2=A(r) \:c^2 \,{dt}^2-C(r) \:{dr}^2-r^2 \:{dΩ}^2  ;  A=1−rsr\displaystyle A=1-\frac{r_s}{r}  ;  C=1A\displaystyle C=\frac{1}{A}  ;  rs=2𝒢Mc2\displaystyle r_s=\frac{2 \,𝒢 \:M}{c^2}  .

Les coordonnées “isotropes” proposent un point de vue différent sur ce problème, mais d'autres sont intéressantes, parmi lesquelles celles de Lemaître.

☞ remarque : contrairement à ce que suggère la métrique isotrope, on suppose ici que  rr  a une variation monotone  (r<rsr<r_s  au delà de l'horizon) ; la singularité est ici supposée due aux contractions de longueurs et dilatations de durées, à cause d'un repérage statique inadapté.

2. Transformation de Lemaître

2.1. Notations de base

• À l'approche de la singularité (“horizon”), la vitesse des particules en chute libre tend forcément vers cc ; leur immobilité devient impossible. Ceci semble pouvoir s'interpréter en supposant que l'espace est en mouvement centripète par rapport au repérage de Schwarzschild.

Pour étudier ce que subit une particule en chute libre, Lemaître envisage de considérer un repérage comobile, par rapport auquel cette particule est fixe. Une “simple” transformation de Lorentz locale n'est pas forcément facile à intégrer ; on peut chercher une transformation jouant un rôle analogue.

• En limitant à la partie radiale (pour simplifier) :  ds2=A.[c2dt2−dr2A2]\displaystyle {ds}^2=A .\left[c^2 \,{dt}^2-\frac{{dr}^2}{A^2}\right ] .

On peut alors chercher avec les combinaisons :

 dR=cdt+κ(r)drA\displaystyle dR=c \,dt+κ(r)\,\frac{dr}{A}  ;  cdT=cdt+f(r)drA\displaystyle c \,dT=c \,dt+f(r)\,\frac{dr}{A} .

Pour  κ(r)>0κ(r)>0 ,  ce repérage est en mouvement centripète par rapport au précédent, puisque  dR=0dR=0  correspond à :  dr=−Aκcdt\displaystyle dr=-\frac{A}{κ} \,c \,dt .  On peut préciser que la vitesse d'entraînement est :  ve=d𝓁dt𝓁oc=CdrAdt=−cκ\displaystyle v_e=\frac{d𝓁\:}{dt_{𝓁oc}} =\frac{\sqrt{C} \:dr}{\sqrt{A} \: dt}=-\frac{c}{κ} .

◊ remarque : on raisonne ici avec  A>0A>0  et  C>0C>0  dans l'intention de savoir s'il est possible d'extrapoler dans la zone  r<rsr<r_s .

• Ceci donne :  drA=dR−cdTκ−f\displaystyle \frac{dr}{A}=\frac{dR-c \,dT}{κ-f}  ;  cdt=fdR−κcdTf−κ\displaystyle c \,dt=\frac{f \:dR-κ \:c \,dT}{f-κ}  ;  les termes croisés dans ds2{ds}^2 s'éliminent si et seulement si :  κ=1f\displaystyle κ=\frac{1}{f} .  Ceci correspond à :  f=−βef=-β_e  ;  la transformation de Lemaître est analogue à une transformation de Lorentz.

On obtient ainsi :

 ds2=A.[κ2−1(f−κ)2c2dT2−1−f2(f−κ)2dR2]=A.[11−f2c2dT2−f21−f2dR2]\displaystyle {ds}^2=A .\left[\frac{κ^2-1}{(f-κ)^2} \;c^2 \,{dT}^2-\frac{1-f^2}{(f-κ)^2} \;{dR}^2 \right]=A .\left[\frac{1}{1-f^2} \;c^2 \, {dT}^2-\frac{f^2}{1-f^2} \;{dR}^2 \right] .

Finalement :  ds2=A1−f2[c2dT2−f2dR2]\displaystyle {ds}^2=\frac{A}{1-f^2} \:[c^2 \,{dT}^2-f^2 \: {dR}^2 ] .  La singularité est donc éliminée avec :  f(r)=±rsr\displaystyle f(r)=±\sqrt{\frac{r_s}{r}} .

◊ remarque : la métrique obtenue  ds2=c2dT2−f2dR2{ds}^2=c^2 \,{dT}^2-f^2 \: {dR}^2  a une forme telle que le temps TT est souvent nommé “temps propre” ; ce n'est toutefois le temps propre  T=τT=τ  que pour les particules immobiles  (dR=0dR=0 ,  dθ=0dθ=0 ,  dφ=0dφ=0).

• La simplification semble n'intervenir que pour une vitesse d'entraînement particulière, correspondant à une chute libre avec vitesse “initiale” (limite) nulle à l'infini. Lemaître cherchait un repérage comobile, mais dans ce référentiel particulier toutes les particules (et non seulement celles en comouvement) peuvent traverser l'horizon sans subir de singularité.

Cela signifie-il que l'espace physique est en contraction à cette vitesse particulière (comme l'éther des anciennes théories) ? Il faudrait étudier les référentiels comobiles pour les particules ayant d'autres vitesses.

📖 exercices n° I, II et III.

2.2. Expressions des coordonnées

• Avec le signe positif  (κ>0κ>0)  on obtient :  d(R−cT)=(κ−f)drA=rrsdr\displaystyle d(R-c \,T )=(κ-f) \:\frac{dr}{A}=\sqrt{\frac{r}{r_s}} \:dr  ;  l'intégration donne :  R−cT=2r3rrs\displaystyle R-c \,T=\frac{2 \,r}{3} \sqrt{\frac{r}{r_s}} .

Ceci correspond à :  r=κ2rsr=κ^2 \:r_s ,  avec  κ2=(3(R−cT)2rs)2/3\displaystyle κ^2=\left(\frac{3 \,(R-c \,T)}{2 \,r_s}\right)^{2/3}.

◊ remarque : on peut choisir deux constantes d'intégration arbitraires associées à l'origine de RR et TT ; Lemaître les choisit nulles.

• Ainsi la métrique complète peut s'écrire :

 ds2=c2dT2−1κ2dR2−rs2κ4dΩ2\displaystyle {ds}^2=c^2 \,{dT}^2-\frac{1}{κ^2} \:{dR}^2-r_s^{\:2} \: κ^4 \:{dΩ}^2 .

Elle présente une singularité spatiale pour  R−cT=0R-c \,T=0 ,  donc  r=0r=0  ;  inversement  r=rsr=r_s  donne  R−cT=2rs3\displaystyle R-c \,T=\frac{2 \,r_s}{3}  ne correspondant à aucune singularité.

• On obtient par ailleurs :  cdt=dR−κdrA=dR−rs2κ4dκκ2−1\displaystyle c \,dt=dR-κ \: \frac{dr}{A}=dR-r_s \, \frac{2 \,κ^4 \: dκ}{κ^2-1}  ;  l'intégration donne :  ct=R−2rs3κ3−2rsκ+rsln⁡(|κ+1κ−1|)\displaystyle c \,t=R-\frac{2 \,r_s}{3} \,κ^3-2 \,r_s \: κ+r_s \: \ln⁡\left(\left|\frac{κ+1}{κ-1}\right|\right) .

◊ remarque : cela donne aussi :  ct=cT−2rsκ+rsln⁡(|κ+1κ−1|)\displaystyle c \,t=c\,T-2 \,r_s \: κ+r_s \: \ln⁡\left(\left|\frac{κ+1}{κ-1}\right|\right) .

◊ remarque : l'extrapolation est possible pour  κ<1κ<1  ;  r<rsr<r_s  ;  AA  et  C<0C<0  (simplification “heureuse” ?)  ;  mais on retrouve (comme pour le calcul en coordonnées “classiques”) qu'en toute rigueur  ctc \,t  a une composante imaginaire  −rsarg⁡(κ−1)- r_s \: \arg⁡(κ-1) ,  généralement ignorée ; inversement, ceci semble indiquer que  RR  et  cTc \,T  n'en ont pas).

📖 exercices n° IV et V.

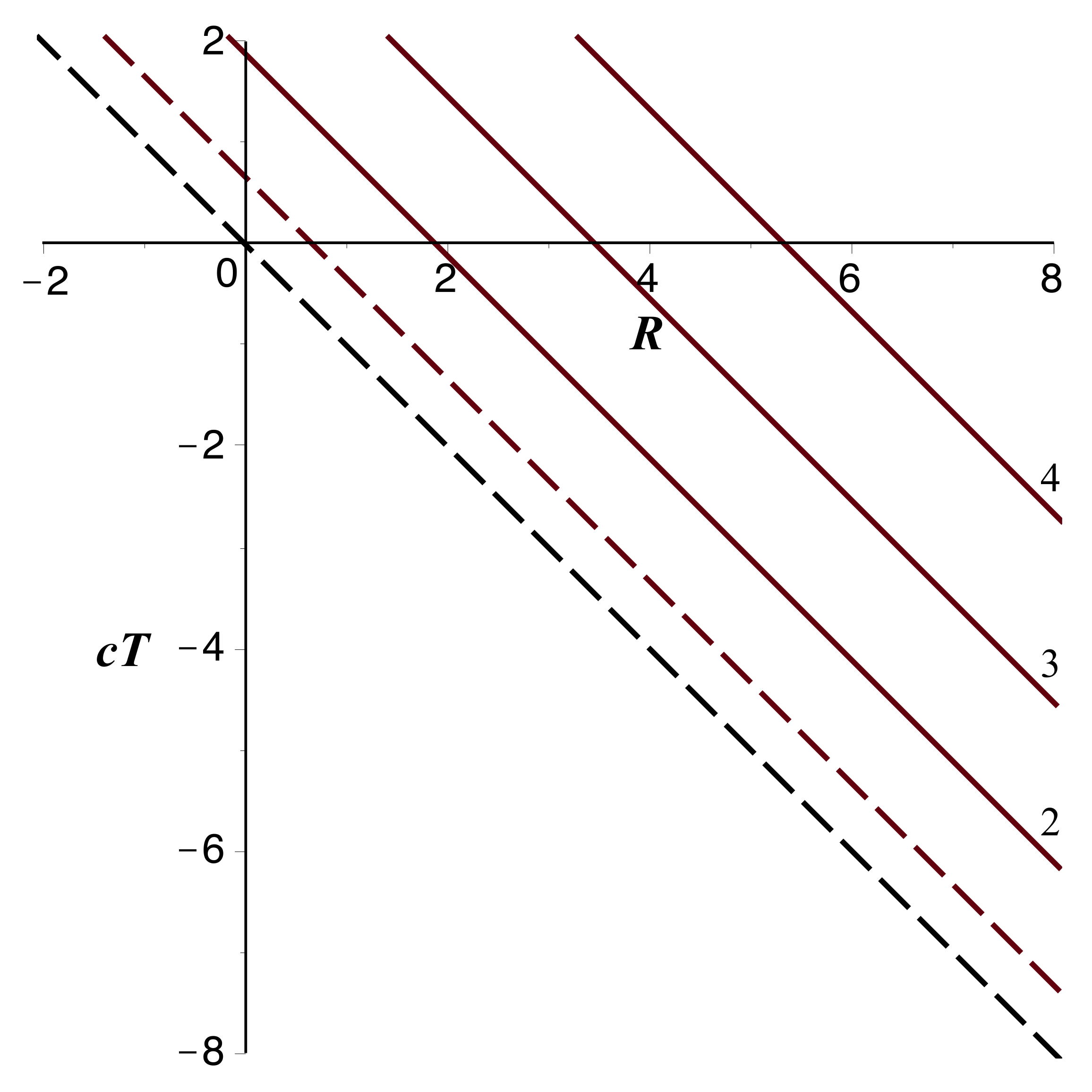
2.3. Représentations graphiques

• En prenant  rsr_s  comme unité, on peut écrire :  R−cT=23r3/2R-c \,T=\frac{2}{3} \, r^{3/2}  ;  les courbes correspondant à  r=Cste r=Cste  sont des droites.

On obtient la représentation suivante (ici pour  r=0;1;2;3;4r=0 \,; 1 \,; 2 \,; 3 \,; 4)  ;  la partie à gauche de la diagonale n'a pas de signification physique.

Lemaitre_Im/Lemaitre_1.jpg

• On peut aussi écrire :  cT=ct+2κ−ln(|κ+1κ−1|)\displaystyle c \,T=c \,t+2 \,κ-\ln\left(\left|\frac{κ+1}{κ-1}\right|\right)   et   R=cT+23κ3R=c \,T+\frac{2}{3} \, κ^3  ;  ceci définit paramétriquement (en fonction de κκ) les courbes correspondant à  ct=Cstec \,t=Cste  (ci-après pour  ct=0;3;6c \,t=0 \,; 3 \,; 6).

Ces courbes sont constituées de deux branches (vaguement hyperboliques) :

 ◊ quand  r>rsr>r_s  (en rouge) on constate que, pour RR fixé,  ctc \,t  est une fonction croissante de  cT c \,T ;
◊ quand  r<rsr<r_s  (en bleu) la particularité est que, pour RR fixé,  ctc \,t  est une fonction décroissante de  cTc \,T .

◊ remarque : la propriété que la coordonnée  ctc \,t  décroît pour la partie des trajectoires avec  r<rsr<r_s  se retrouve de même avec les notations “classiques” (ou avec celles de Kruskal-Szekeres, étudiées dans une partie ultérieure).

Lemaitre_Im/Lemaitre_2.jpg

• Il est important de noter que les parties en bleu, pour  r<rs r<r_s ,  correspondent à  κ<1κ<1  donc à une vitesse d'entraînement de norme  |ve|=cκ>c\displaystyle \left|v_e \right|=\frac{c}{κ}>c .

Une interprétation usuelle en est que la métrique statique de Schwarzschild ne serait plus valable dans cette région, car l'espace y serait en “contraction” supraluminique (d'où la présence d'une singularité “apparente” à la limite).

📖 exercice n° VI.

2.4. Chute libre radiale d'une particule

• Lors de la chute libre radiale d'une particule, la métrique de Lemaître  ds2=c2dT2−1κ2dR2\displaystyle {ds}^2=c^2 \,{dT}^2-\frac{1}{κ^2} \,{dR}^2  a l'avantage d'être “synchrone” : les droites  R=CsteR=Cste  (lignes de temps) sont des géodésiques.

On peut le vérifier avec le lagrangien  ℒ=12[c2T˙2−1κ2R˙2]\displaystyle ℒ=\frac{1}{2} \left[c^2 \,\dot{T}^2-\frac{1}{κ^2} \,\dot{R}^2 \right]  donnant les équations du mouvement :

 cT̈=1κ3R˙2∂κc∂T=−R˙22rsκ5\displaystyle c \,\ddot{T}=\frac{1}{κ^3} \,\dot{R}^2 \frac{\:∂κ}{c \,∂T}=-\frac{\dot{R}^2}{2 \,r_s \: κ^5}   ;   −1κ2R̈=1κ3R˙2∂κ∂R=R˙22rsκ5\displaystyle -\frac{1}{κ^2} \,\ddot{R}=\frac{1}{κ^3} \,\dot{R}^2 \,\frac{∂κ}{∂R}=\frac{\dot{R}^2}{2 \,r_s \: κ^5} .

Ainsi  R˙=0\dot{R}=0  initialement impose  R̈=0\ddot{R}=0  donc  R=CsteR=Cste ,  puis  cT˙=Cstec \,\dot{T}=Cste .

Par ailleurs (d'après ds2{ds}^2) :  1=c2T˙2−1κ2R˙2\displaystyle 1=c^2 \,\dot{T}^2-\frac{1}{κ^2} \,\dot{R}^2  ;  ainsi  cT˙=±1c \,\dot{T}=±1  (ou encore  dT=±dτdT=±dτ ).  Finalement, dans la mesure où  cTc \,T  est une fonction croissante de  ctc \,t  dans la région  r>rsr>r_s ,  on peut considérer  cT˙=1c \,\dot{T}=1 .

• Pour un point chutant ainsi, le graphique ci-après (représentant  R=CsteR=Cste)  montre comment rr décroit jusqu'à la limite  r=rsr=r_s  (pendant que tt tend vers l'infini) ; puis comment rr continue à décroitre jusqu'à  r=0r=0  (alors que tt décroît depuis l'infini).

• La représentation dans le plan (R,cT)(R,c \,T) peut être précisée en traçant les trajectoires de paires de photons, émises respectivement vers RR décroissant et vers RR croissant, depuis quelques positions intermédiaires de la particule en chute.

En prenant  rsr_s  comme unité, la relation  ds2=0{ds}^2=0  impose  dR=±κcdTdR=±κ \:c \,dT  avec par ailleurs  R−cT=23κ3R-c \,T=\frac{2}{3} \, κ^3  ceci correspond à :  (±κ−1)cdT=2κ2dκ(±κ-1) \:c \,dT=2 \,κ^2 \: dκ .

L'intégration donne :  cT=±κ2+2κ±2ln(|±κ−1|)+Cstec \,T=±κ^2+2 \,κ±2 \, \ln\left(\left|±κ-1\right|\right)+Cste .  Compte tenu de  R=cT+23κ3R=c \,T+\frac{2}{3} \: κ^3 ,  cela permet une représentation paramétrique des trajectoires.

◊ remarque : ceci pose problème pour les photons “sortants”, car devrait s'ajouter à  cTc \,T (puis à  RR)  une composante imaginaire  2rsarg⁡(κ−1)2 \,r_s \: \arg⁡(κ-1) .

• Ceci visualise les “cônes de lumière”, montrant que pour  r>rsr>r_s  (région I\mathrm{I}) les droites représentant  r=Cster=Cste  sont intérieures aux cônes, donc font partie des “trajectoires” a priori possibles (les trajectoires avec  R=CsteR=Cste  ne sont pas les seules ; tout dépend des conditions initiales).

Au contraire pour  r<rsr<r_s  (région II\mathrm{II}) de telles trajectoires apparaissent impossibles, la chute vers  r=0r=0  étant inévitable (et elle se fait en un temps propre fini dans la mesure où  dT≥dτdT≥dτ ).

Lemaitre_Im/Lemaitre_1p.jpg

◊ remarque : la durée propre finie de cette chute est parfois considérée comme une preuve de l'existence des trous noirs ; c'est en fait une condition nécessaire, mais non forcément suffisante.

◊ remarque : dans ce dernier cas, les trajectoires peuvent partir avec RR croissant, mais pas assez vite pour que cela corresponde à rr croissant.

📖 exercice n° VII.

2.5. Anomalie fondamentale de la singularité centrale

• Avec le repérage de Schwarzschild, on a constaté une propriété étrange de la singularité centrale ; pour  r=0r=0  ce point semble immobile au delà de l'horizon, ce qui fait qu'il ne peut pas être doté de propriétés physiques.

Or, après effondrement d'un astre en trou noir, toute la matière est annihilée et cette singularité devrait être l'unique source du champ gravitationnel. Seule une possible inadaptation des coordonnées semblait alors expliquer cette anomalie.

• Il est donc important de reprendre le raisonnement avec le repérage de Lemaître.

La propriété  r=0r=0  correspond à  dR=cdTdR=c dT  et la vitesse de la singularité (par rapport aux particules en comouvement) est alors :  v=fdRdT=crsr=∞\displaystyle v=f \: \frac{dR}{dT}=c \:\sqrt{\frac{r_s}{r}}=∞ .  Pour un point atteint au bout d'une durée propre finie, cela rend la théorie tout à fait contradictoire.

◊ remarque : il en est de même, symétriquement, pour le repérage en expansion étudié dans la suite.

3. Espace en expansion

3.1. Notations de base

• Il est à noter qu'en partant de la même métrique de Schwarzschild, mais avec une vitesse d'expansion  (ve=−cκ\displaystyle v_e=-\frac{c}{κ}   où   κ=−rrs\displaystyle κ=-\sqrt{\frac{r}{r_s}}  ;  κκ et ff négatifs), on aboutit à une métrique de la forme de Lemaître (où seul κ2κ^2 apparaît).

Afin de conserver un même sens pour les axes de rr et RR ,  avec  κ<0κ<0 ,  il faut alors toutefois utiliser des combinaisons de la forme :

 −dR=cdt+κ(r)drA\displaystyle -dR=c \,dt+κ(r)\,\frac{dr}{A}  ;  cdT=cdt+f(r)drA\displaystyle c \,dT=c \,dt+f(r)\,\frac{dr}{A} .

3.2. Expressions des coordonnées

• Pour  d(R+cT)=rrsdr\displaystyle d(R+c\,T )=\sqrt{\frac{r}{r_s}} \: dr ,  l'intégration donne :  R+cT=2r3rrs\displaystyle R+c \,T=\frac{2 \,r}{3} \sqrt{\frac{r}{r_s}} .

Ceci correspond ici encore à :  r=κ2rsr=κ^2 \: r_s ,  mais dans l'expression de la métrique  κ2=(3(R+cT)2rs)2/3\displaystyle κ^2=\left(\frac{3 \,(R+c \,T)}{2 \,r_s}\right)^{2/3},  bien que cela corresponde à la même valeur de rr .

• On obtient par ailleurs :  cdt=−dR−κdrA=−dR−rs2κ4dκκ2−1\displaystyle c \,dt=-dR-κ \, \frac{dr}{A}=-dR-r_s \frac{2 \,κ^4 \: dκ}{κ^2-1}  ;  l'intégration donne :  ct=−R−2rs3κ3−2rsκ+rsln(|κ+1κ−1|)\displaystyle c \,t=-R-\frac{2 \,r_s}{3} \,κ^3-2 \,r_s \: κ+r_s \: \ln\left(\left|\frac{κ+1}{κ-1}\right|\right) .

◊ remarque : cela donne aussi :  ct=cT−2rsκ+rsln(|κ+1κ−1|)\displaystyle c \,t=c \,T-2 \,r_s \: κ+r_s \: \ln\left(\left|\frac{κ+1}{κ-1}\right|\right) ,  ici encore avec une composante imaginaire  −rsarg(κ−1)- r_s \:\arg(κ-1) ,  généralement ignorée.

3.3. Représentations graphiques

• En prenant  rsr_s  comme unité, on peut écrire :  R+cT=23r3/2R+c \,T=\frac{2}{3} \: r^{3/2}  ;  les courbes correspondant à  r=Cste r=Cste  sont des droites.

On obtient la représentation suivante (ici pour  r=0;1;2;3;4r=0 \,; 1 \,; 2 \,; 3 \,; 4)  ;  la partie à gauche de la diagonale n'a pas de signification physique.

Lemaitre_Im/Lemaitre_exp_1.jpg

• On peut aussi écrire :  cT=ct+2κ−ln(|κ+1κ−1|)\displaystyle c \,T=c \,t+2 \:κ-\ln\left(\left|\frac{κ+1}{κ-1}\right|\right)   et   R=−cT−23κ3R=-c \,T-\frac{2}{3} \: κ^3  ;  ceci définit paramétriquement (en fonction de κκ) les courbes correspondant à  ct=Cstec \,t=Cste  (ci-après pour  ct=0;3;6c \,t=0 \,; 3 \,; 6).

Ces courbes sont constituées de deux branches (vaguement hyperboliques) :

 ◊ quand  r>rsr>r_s  (en rouge) on constate que, pour RR fixé,  ctc \,t  est une fonction croissante de  cTc \,T ;
◊ quand  r<rsr<r_s  (en bleu) la particularité est que, pour RR fixé,  ctc \,t  est une fonction décroissante de  cTc \,T .

• Il est important de noter que les parties en bleu, pour  r<rsr<r_s ,  correspondent à  |κ|<1\left|κ\right|<1  donc à une vitesse d'entraînement de norme  ve=c|κ|>c\displaystyle v_e=\frac{c}{|κ|} >c .  L'interprétation peut en être que la métrique statique de Schwarzschild ne serait plus valable dans cette région, car l'espace y serait en “expansion” supraluminique (d'où la présence d'une singularité “apparente” à la limite).

Lemaitre_Im/Lemaitre_exp_2.jpg

📖 exercice n° VIII.

3.4. “Ascension libre” radiale d'une particule

• Lors de “l'ascension libre” radiale d'une particule, la métrique de Lemaître étant “synchrone”, les droites  R=CsteR=Cste  (lignes de temps) sont des géodésiques. Ces trajectoires sont parcourues dans le sens de rr croissant.

• La représentation dans le plan (R,cT)(R,c \,T) peut être précisée en traçant les trajectoires de paires de photons, émises respectivement vers RR décroissant et vers RR croissant, depuis quelques positions intermédiaires de la particule en ascension.

En prenant  rsr_s  comme unité, la relation  dR=±κcdTdR=±κ \:c \,dT  avec  R+cT=−23κ3R+c \,T=-\frac{2}{3} \, κ^3  donne ici :  (±κ+1)cdT=−2κ2dκ(±κ+1) \:c \,dT=-2 \,κ^2 \: dκ .

L'intégration donne :  cT=∓κ2+2κ∓2ln(|±κ+1|)+Cstec \,T=∓κ^2+2 \,κ∓2 \: \ln\left(\left|±κ+1\right|\right)+Cste .

Avec  R=−cT−23κ3R=-c \,T-\frac{2}{3} \, κ^3 ,  cela permet une représentation paramétrique des trajectoires.

Lemaitre_Im/Lemaitre_exp_1p.jpg

◊ remarque : ici de même, pour les photons “entrants”, devrait s'ajouter à  cTc \,T  (puis à  RR)  une composante imaginaire  2rsarg⁡(κ+1)2 \,r_s \: \arg⁡(κ+1) .

• Les trajectoires avec  R=CsteR=Cste  peuvent “sortir” de la zone  r<rsr<r_s ,  celles avec RR croissant peuvent sortir plus vite.  

Pour  r>rsr>r_s  (région III\mathrm{III}) les droites représentant  r=Cster=Cste  sont intérieures aux cônes, donc font partie des “trajectoires” a priori possibles. Selon les conditions initiales, des particules peuvent se déplacer vers les rr décroissants, mais semblent tendre asymptotiquement vers  r=rsr=r_s  et il n'est pas évident de savoir si elles peuvent ou non “rentrer".

Au contraire pour  r<rsr<r_s  (région IV\mathrm{IV}) de telles trajectoires apparaissent impossibles ; l'expulsion vers  r=rs r=r_s  semblant inévitable, mais de façon analogue celle limite ne peut être “atteinte” qu'asymptotiquement.

◊ remarque : dans ce dernier cas, les trajectoires peuvent partir avec RR décroissant, mais pas assez vite pour que cela corresponde à r r décroissant.

3.5. Comparaison contraction-expansion

• Ces comportements différents, obtenus pour la même forme de métrique, ne sont pas incompatibles entre eux puisqu'ils correspondent à des interprétations différentes du plan (R,cT)(R,c \,T) ; les variables de mêmes noms ne désignent pas les mêmes quantités.

• À ce point du raisonnement, il semble que la métrique de Lemaître ne correspond pas à une, mais à deux vitesses possibles (opposées).

Le fait que ces vitesses particulières soient déduites de la méthode pourrait ici encore suggérer que cela corresponde à un mouvement de l'espace physique, dans un sens ou dans l'autre. Il est alors intéressant de revenir sur le calcul de la partie 2.1, pour savoir si les référentiels comobiles avec les particules ayant d'autres vitesses radiales présentent ou non une singularité.