MÉTRIQUE DE LEMAÎTRE - corrigé des exercices


I. Transformation de Lemaître et transformation de Lorentz


 • Pour  ve=−crsr\displaystyle v_e=-c \;\sqrt{\frac{r_s}{r}} ,  la transformation de Lorentz (locale) correspond à :

 dR_=d𝓁−βecdt𝓁oc1−βe2\displaystyle d\underline{R}=\frac{d𝓁-β_e \:c \,{dt}_{𝓁oc}}{\sqrt{1-β_e^{\:2}}}  ;  cdT=cdt𝓁oc−βed𝓁1−βe2\displaystyle c \,dT=\frac{c \,{dt}_{𝓁oc}-β_e \:d𝓁}{\sqrt{1-β_e^{\:2}}}  ;  cdt𝓁oc=Acdtc \,{dt}_{𝓁oc}=\sqrt{A} \: c \,dt  ;  d𝓁=Cdrd𝓁=\sqrt{C} \: dr  (algébrique).
◊ remarque : on considère des variations infinitésimales dans l'espace tangent, donc sans varier βeβ_e .
◊ remarque : on raisonne pour  r>rsr>r_s  (AA  et  C>0C>0),  puis on vérifie que le prolongement est possible.
• Ceci donne :  dR_=rsrcdt+drA\displaystyle d\underline{R}=\sqrt{\frac{r_s}{r}} \; c \,dt+\frac{dr}{A}  ;  cdT=cdt+rsrdrA\displaystyle c \,dT=c \,dt+\sqrt{\frac{r_s}{r}}\: \frac{dr}{A} .  On constate que  dR_=rsrdR\displaystyle d\underline{R}=\sqrt{\frac{r_s}{r}} \;dR .
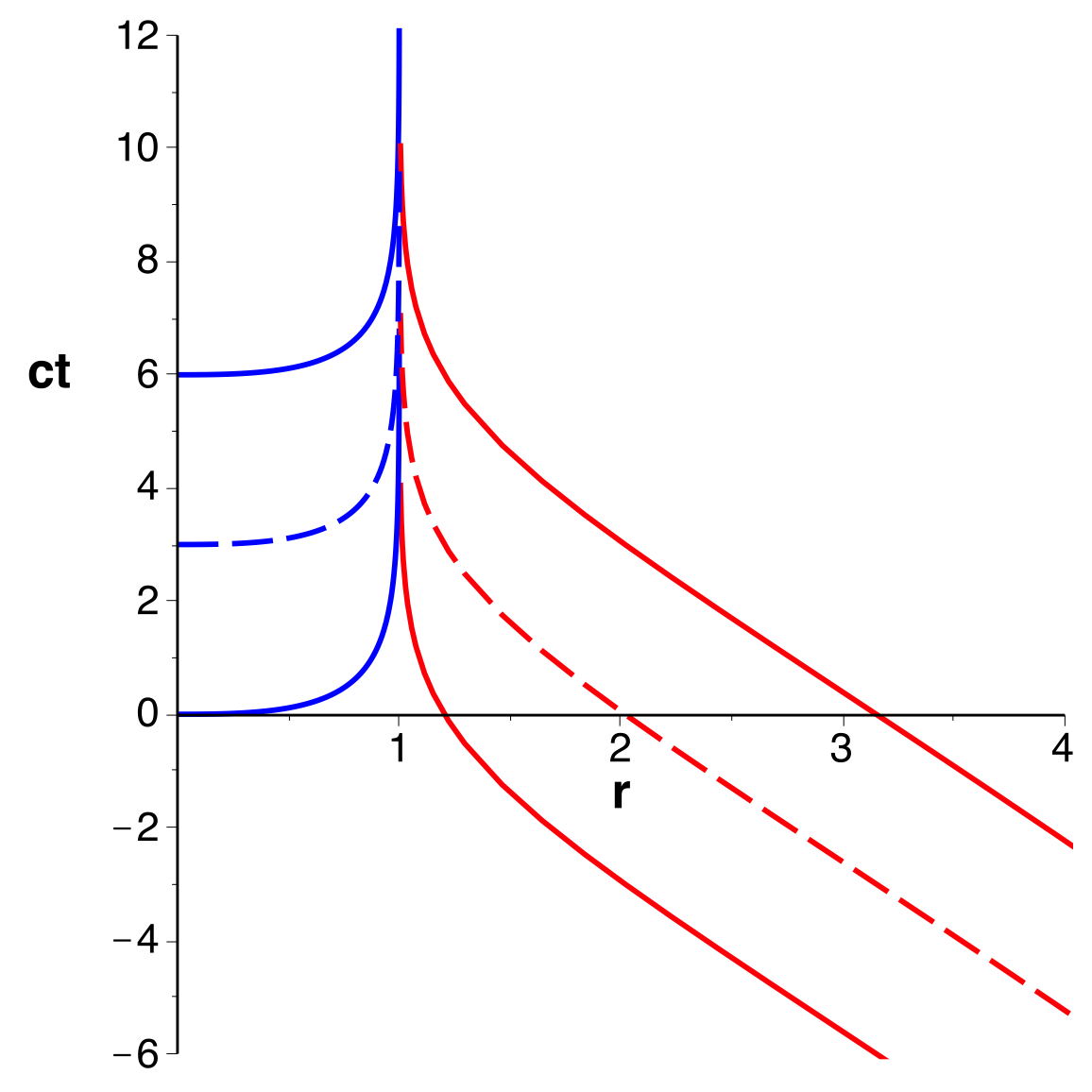
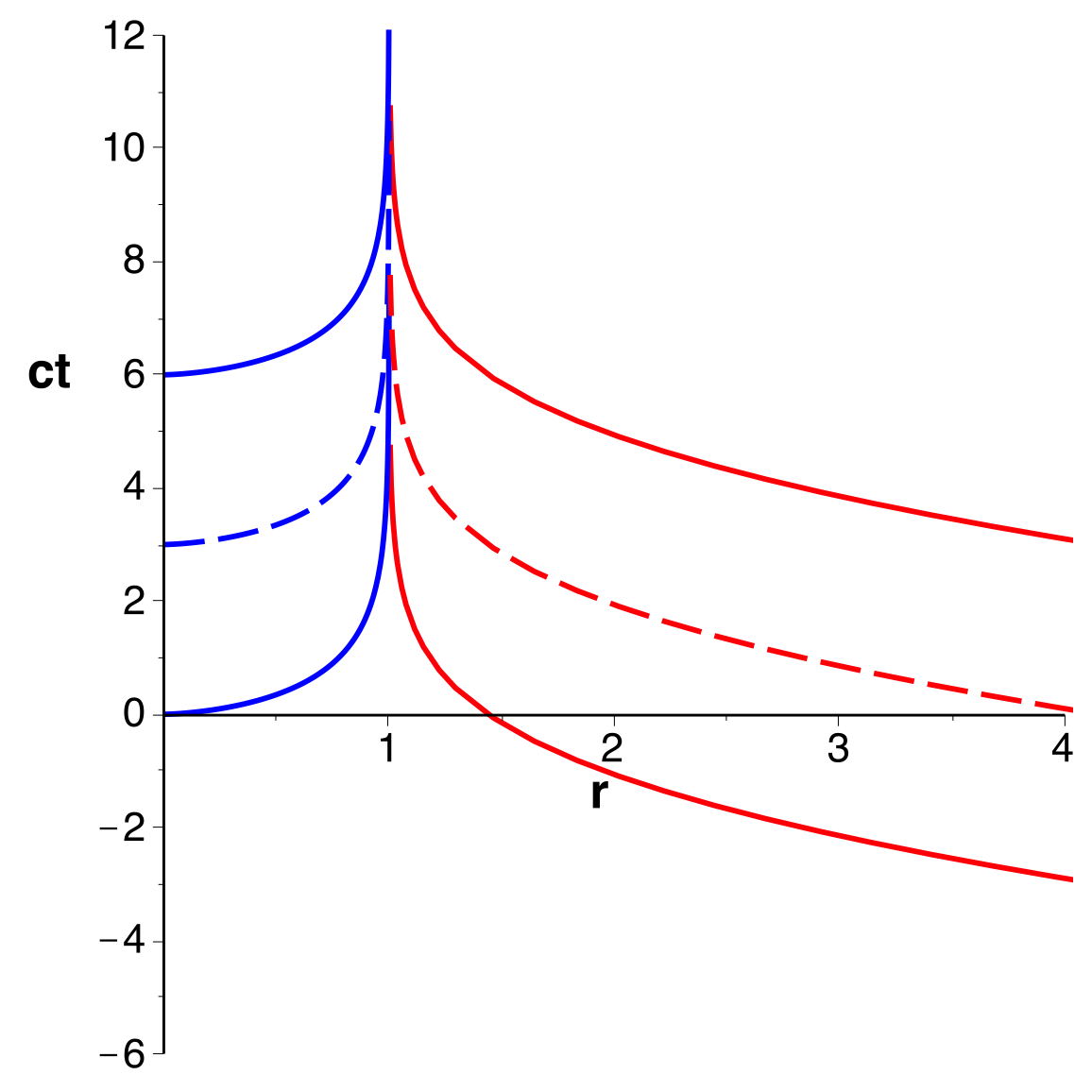
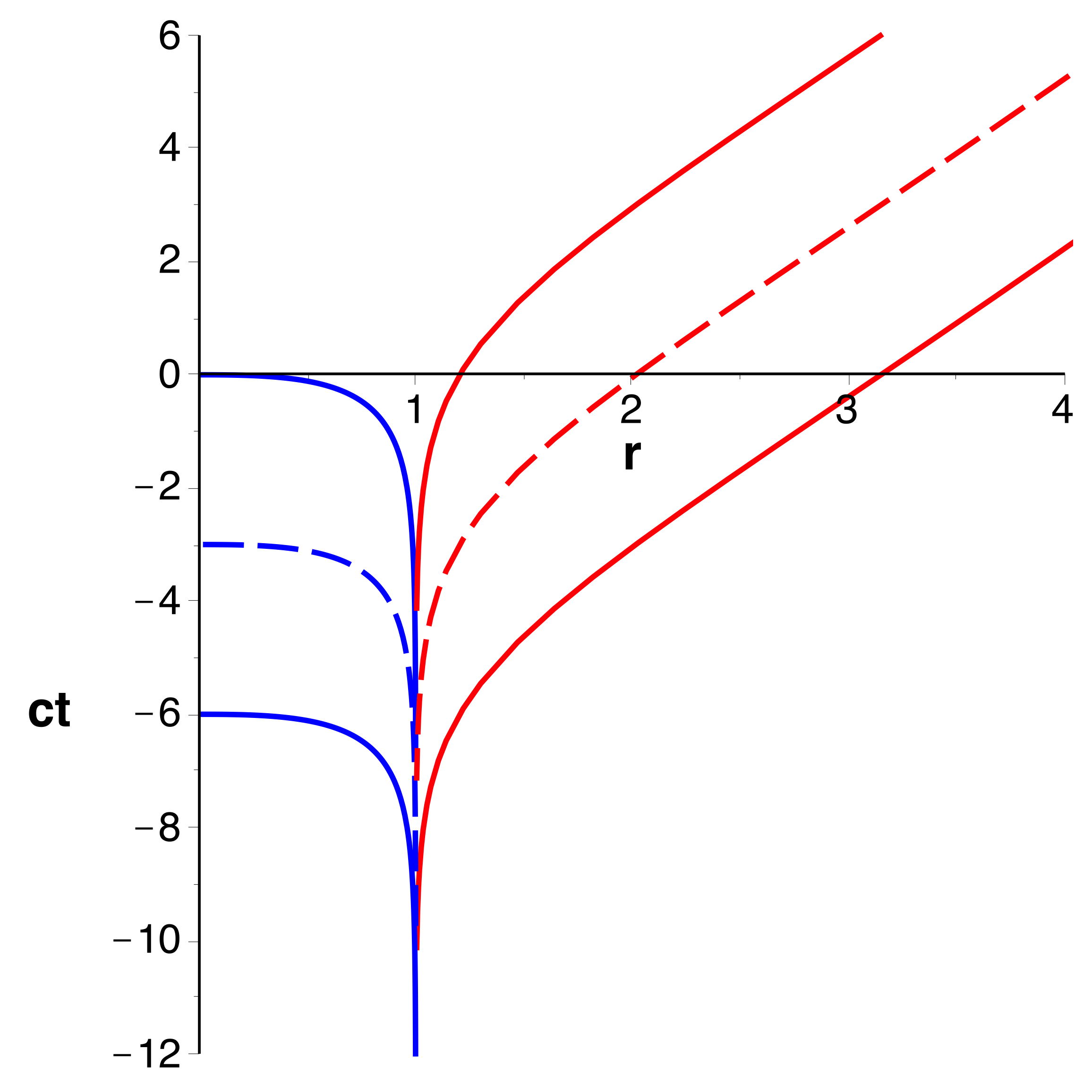
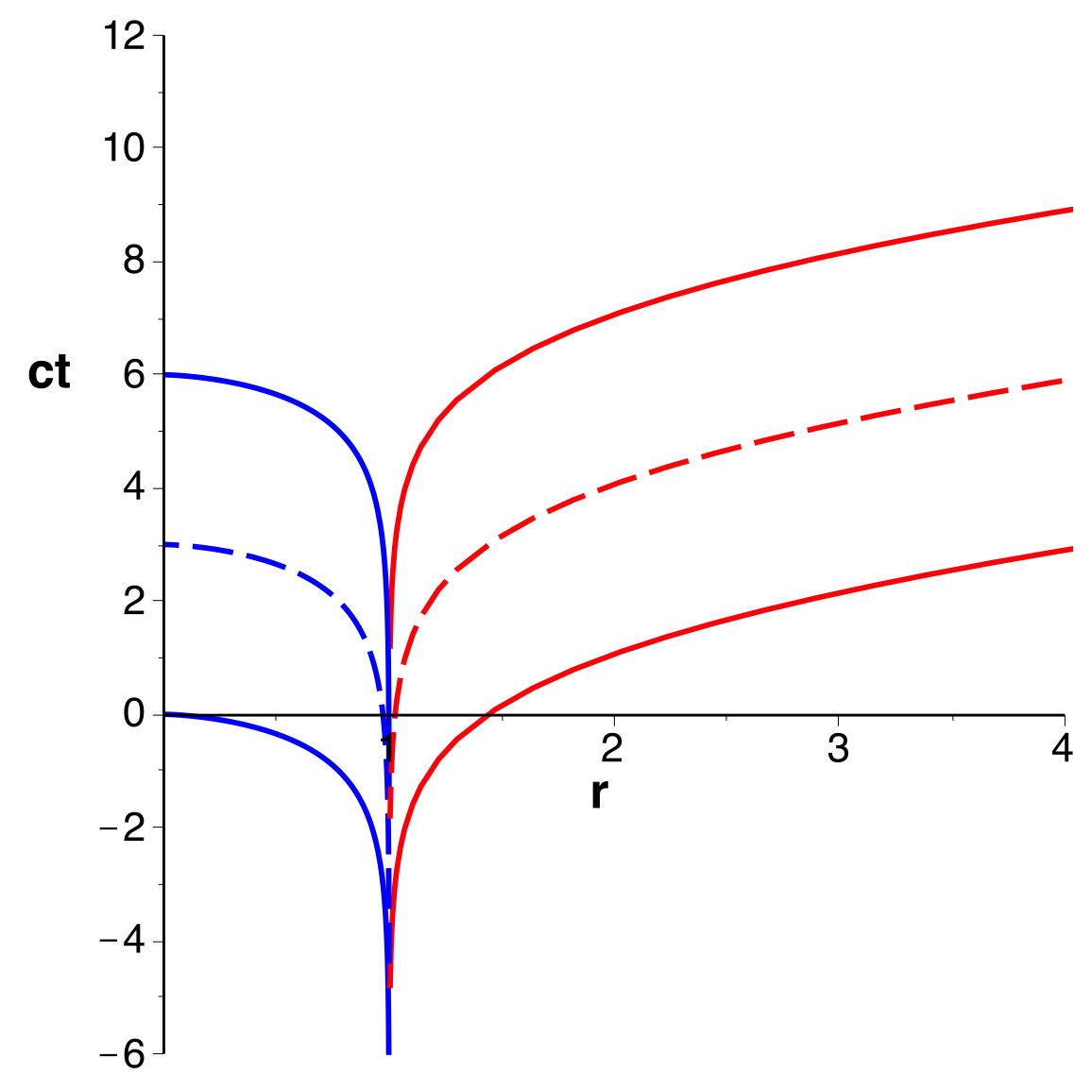
• La métrique limitée au déplacement radial serait ainsi encore plus simple que celle de Lemaître :  ds2=c2dT2−dR_2{ds}^2=c^2 \,{dT}^2-{d\underline{R}}^2 .  En particulier les trajectoires des photons seraient des droites  (dR_=±cdTd\underline{R}=± c \,dT).
• Le problème est ensuite de déterminer  r(R_,cT)r(\underline{R},c \,T)  pour exprimer la partie angulaire de la métrique, mais aussi pour savoir interpréter à quoi correspond  r=rsr=r_s .  Puisqu'on part de fonctions de rr, il faut déterminer  R_(r,ct)\underline{R}(r, c \,t)  et  cT(r,ct)c \,T (r, c \,t)  (ou des combinaisons) puis inverser. Or on constate que  dR_(r,ct)d\underline{R}(r, c \,t)  n'est pas une différentielle totale : il n'existe pas de telle fonction R_(r,ct)\underline{R}(r, c \,t) définie de façon univoque dans tout l'espace-temps. Pour obtenir une primitive il faut multiplier dR_d\underline{R} par un facteur intégrant  F(r,ct)F(r, c \,t)  tel que  ∂∂r(Frsr)=∂∂t(FA)\displaystyle \frac{∂}{∂r} \left(F \:\sqrt{\frac{r_s}{r}}\right)=\frac{∂}{∂t} \left(\frac{F}{A}\right) .  Rétrospectivement, on comprend donc que Lemaître a utilisé le facteur  F=rrs\displaystyle F=\sqrt{\frac{r}{r_s}}  et qu'il a ainsi obtenu la variable RR.


II. Transformation de Lemaître et transformation de Lorentz


 • Pour  ve=−crsr\displaystyle v_e=-c \;\sqrt{\frac{r_s}{r}} ,  la transformation de Lorentz (locale) correspond à :

 dR_=d𝓁−βecdt𝓁oc1−βe2\displaystyle d\underline{R}=\frac{d𝓁-β_e \: c \,{dt}_{𝓁oc}}{\sqrt{1-β_e^{\:2}}}  ;  cdT=cdt𝓁oc−βed𝓁1−βe2\displaystyle c \,dT=\frac{c \,{dt}_{𝓁oc}-β_e \: d𝓁}{\sqrt{1-β_e^{\:2}}}  ;  cdt𝓁oc=Acdtc \,{dt}_{𝓁oc}=\sqrt{A} \; c \,dt  ;  d𝓁=Cdrd𝓁=\sqrt{C} \; dr  (algébrique).
• Généralement on raisonne pour  r>rsr>r_s  (AA  et  C>0C>0),  puis on vérifie que le prolongement est possible. Ainsi avec  ve=d𝓁dt𝓁oc=drAdt\displaystyle v_e=\frac{d𝓁\;}{{dt}_{𝓁oc}} =\frac{dr}{A \;dt}  le résultat reste possible, même si  d𝓁d𝓁  et  dt𝓁oc{dt}_{𝓁oc}  posent problème.
• Ceci donne :  dR_=rsrcdt+drA\displaystyle d\underline{R}=\sqrt{\frac{r_s}{r}} \; c \,dt+\frac{dr}{A}  ;  cdT=cdt+rsrdrA\displaystyle c \,dT=c \,dt+\sqrt{\frac{r_s}{r}} \; \frac{dr}{A} .
• On multiplie ensuite par un facteur intégrant pour obtenir une différentielle totale :

 dR=rsrdR_=cdt+rrsdrA\displaystyle dR=\sqrt{\frac{r_s}{r}} \; d\underline{R}=c \,dt+\sqrt{\frac{r}{r_s}} \: \frac{dr}{A} .
• Pour  r<rsr<r_s  (AA  et  C<0C<0),  la variable rr devient du genre temps et la variable tt devient du genre espace. Comment peut-on continuer à considérer que la vitesse d'entraînement est  ve=d𝓁dt𝓁oc\displaystyle v_e=\frac{d𝓁\;}{{dt}_{𝓁oc}}  (avec les notations précédentes) dans ces conditions ?
• On peut alors proposer de réinterpréter :  d𝓁=−Acdtd𝓁=\sqrt{-A} \; c \,dt  ;  cdt𝓁oc=−−Cdrc \,{dt}_{𝓁oc}=-\sqrt{-C} \; dr  (pour conserver un sens croissant de l'évolution temporelle). Ainsi :  ve=d𝓁dt𝓁oc=Ac2dtdr=−crrs\displaystyle v_e=\frac{d𝓁\;}{{dt}_{𝓁oc}} =A \:c^2 \, \frac{dt}{dr}=-c \;\sqrt{\frac{r}{r_s}} .  Il est inattendu d'aboutir à la conclusion que le mouvement n'est pas supraluminique ; d'autant plus que cette vitesse tend vers zéro pour  r→0r→0 ,  ce qui correspondrait à un champ gravitationnel répulsif.
• Il est tout autant inattendu de constater que si on applique la transformation de Lorentz avec cette expression, on obtient ainsi le même résultat qu'avec les notations “classiques” :

 dR_=−Acdt−rrs−Cdr1−rrs=rsr−Acdt−−Cdr−A=rsrcdt+drA\displaystyle d\underline{R}=\frac{\sqrt{-A} \; c \,dt-\sqrt{\frac{r}{r_s}} \: \sqrt{-C} \; dr}{\sqrt{1-\frac{r}{r_s}}}=\frac{\sqrt{\frac{r_s}{r}} \: \sqrt{-A} \; c \,dt- \sqrt{-C} \; dr}{\sqrt{-A}}=\sqrt{\frac{r_s}{r}} \; c \,dt+\frac{dr}{A} .
• On obtient de même :  cdT=cdt+rsrdrA\displaystyle c \,dT=c \,dt+\sqrt{\frac{r_s}{r}} \: \frac{dr}{A} .  Les coordonnées de Lemaître paraissent donc “justifiées”, mais avec une toute autre interprétation.


III. Repérage de Lemaître

1.a. • Pour une métrique de la forme :  ds2=c2dT2−C(R−cT)dR2−D(R−cT)dΩ2{ds}^2=c^2 \,{dT}^2-C(R-c \,T) \:{dR}^2-D(R-c \,T) \:{dΩ}^2 ,  on obtient :

 g00=1g_{00}=1  (avec  x0=cTx_0=c\,T)  ;  g11=−Cg_{11}=-C  ;  g22=−Dg_{22}=-D  ;  g33=−Dsin2⁡(θ)g_{33}=-D \: \sin^2⁡(θ)  ;
g00=1g^{00}=1   ;  g11=−1C\displaystyle g^{11}=-\frac{1}{C}  ;  g22=−1D\displaystyle g^{22}=-\frac{1}{D}  ;  g33=−1Dsin2⁡(θ)\displaystyle g^{33}=-\frac{1}{D \:\sin^2⁡(θ)}  ;
Γ110=−Γ011=C′2\displaystyle Γ_{110}=-Γ_{011}=\frac{C'}{2}  ;  Γ220=−Γ022=D′2\displaystyle Γ_{220}=-Γ_{022}=\frac{D'}{2}  ;  Γ330=−Γ033=sin2(θ)D′2\displaystyle Γ_{330}=-Γ_{033}= \sin^2(θ) \:\frac{D'}{2}  ;
Γ111=−C′2\displaystyle Γ_{111}=-\frac{C'}{2}  ;  Γ221=−Γ122=−D′2\displaystyle Γ_{221}=-Γ_{122}=-\frac{D'}{2}  ;  Γ331=−Γ133=−D′2sin2(θ)\displaystyle Γ_{331}=-Γ_{133}=-\frac{D'}{2} \:\sin^2(θ)  ;
Γ332=−Γ233=−Dsin(θ)cos(θ)Γ_{332}=-Γ_{233}=-D \: \sin(θ) \: \cos(θ)  ;
Γ.110=−C′2\displaystyle Γ_{\phantom{.}11}^0=-\frac{C'}{2}  ;  Γ.101=C′2C\displaystyle Γ_{\phantom{.}10}^1=\frac{C'}{2 \,C}  ;  Γ.220=−D′2\displaystyle Γ_{\phantom{.}22}^0=-\frac{D'}{2}  ;  Γ.330=−D′2sin2(θ)\displaystyle Γ_{\phantom{.}33}^0=-\frac{D'}{2} \: \sin^2(θ)  ;  Γ.202=Γ.303=−D′2D\displaystyle Γ_{\phantom{.}20}^2=Γ_{\phantom{.}30}^3=-\frac{D'}{2 \,D}  ;
Γ.111=C′2C\displaystyle Γ_{\phantom{.}11}^1=\frac{C'}{2 \,C}  ;  Γ.221=−D′2C\displaystyle Γ_{\phantom{.}22}^1=-\frac{D'}{2 \,C}  ;  Γ.331=−D′2Csin2(θ)\displaystyle Γ_{\phantom{.}33}^1=-\frac{D'}{2 \,C} \: \sin^2(θ)  ;  Γ.212=Γ.313=D′2D\displaystyle Γ_{\phantom{.}21}^2=Γ_{\phantom{.}31}^3=\frac{D'}{2 \,D}  ;
Γ.332=−sin(θ)cos(θ)Γ_{\phantom{.}33}^2=-\sin(θ) \: \cos(θ)   ;  Γ.323=cotan(θ)Γ_{\phantom{.}32}^3=\mathrm{cotan}(θ) .


1.b. • Si on cherche la métrique dans le vide entourant l'astre, les équations du champ correspondent à :  Rμν=0R_{μν}=0  ;  en simplifiant (ces quatre équations à deux inconnues ne sont pas indépendantes) :

 (2CC″−C′2)D2+2C2(2DD″−D′2)=0\left(2 \,C \:C''-{C'}^2 \right) \: D^2+2 \,C^2 \: \left(2 \,D \:D''-{D'}^2 \right)=0   (R00R_{00}) ;
C(2DD″−D′2)−DC′D′=0C \;\left(2 \,D \:D''-{D'}^2 \right)-D \:C' \:D'=0   (R01R_{01}) ;
(2CC″−C′2)D2−2C(2DD″−D′2)+2DC′D′(C+1)=0\left(2 \,C \:C''-{C'}^2 \right) \: D^2-2 \,C \;\left(2 \,D \:D''-{D'}^2 \right)+2 \,D \:C' \:D' \;(C+1)=0   (R11R_{11}) ;
2CD″(C−1)+C′D′(C+1)+4C2=02 \,C \:D'' \:(C-1)+C' \:D' \:(C+1)+4 \:C^2=0   (R22R_{22} et R33R_{33}).


2.a. • La seconde équation peut s'écrire :  2D″D′−C′C−D′D=0\displaystyle 2 \,\frac{D''}{D'}-\frac{C'}{C}-\frac{D'}{D}=0  ;  on en déduit :  D′2CD=Cste\displaystyle \frac{{D'}^2}{C \:D}=Cste .
• Les combinaisons  (R00+CR11)(R_{00}+C \:R_{11})  et/ou  (R00−2CR01) (R_{00}-2 \,C \:R_{01})  donnent :  2C″C′−C′C+2D′D=0\displaystyle 2 \,\frac{C''}{C'}-\frac{C'}{C}+2 \,\frac{D'}{D}=0  ;  on en déduit :  D′2D2C=Cste\displaystyle \frac{{D'}^2 \: D^2}{C}=Cste .


2.b. • En comparant ces deux équations :  D−3/2dDdC=Cste\displaystyle D^{-3/2} \; \frac{dD}{dC}=Cste  ;  on en déduit :  D−1/2=Cste.C+Cte′D^{-1/2}=Cste.C+Cte' .
• Connaissant la solution obtenue par Lemaître, on peut se limiter au cas :  DC2=CsteD \:C^2=Cste .


2.c. • En reportant, on obtient (avec  X=R−cTX=R-c \,T) :  C−5/2dCdX=Cste\displaystyle C^{-5/2} \; \frac{dC}{dX}=Cste  ;  on en déduit :  C=CsteX2/3\displaystyle C=\frac{Cste}{X^{2/3}}  .
• Ces résultats sont tout à fait conformes à la solution de Lemaître :  DC2=rs2D \:C^2=r_s^{\:2}  ;  C=(2rs3X)2/3\displaystyle C=\left(\frac{2 \,r_s}{3 \,X}\right)^{2/3} ;  on en confirme ainsi la validité, puisqu'il n'apparaît aucune singularité pour  r=rsr=r_s .


3. • La quatrième équation (non utilisée) n'est pas indépendante ; compte tenu de sa plus grande complexité, on peut se limiter à vérifier sa compatibilité. En notant :  C=λX−2/3C=λ \;X^{-2/3}   et  D=μX4/3D=μ \;X^{4/3}  le report dans cette équation donne simplement :  μλ=94\displaystyle \frac{μ}{λ}=\frac{9}{4} .  La solution de Lemaître correspond à  λ=(2rs3)2/3\displaystyle λ=\left(\frac{2 \,r_s}{3}\right)^{2/3}  et vérifie  μλ=rs2λ3=94\displaystyle \frac{μ}{λ}=\frac{r_s^{\:2}}{λ^3} =\frac{9}{4} .


IV. Expressions des coordonnées


 • On peut écrire :  cdt=dR−κdrA\displaystyle c \,dt=dR-κ \, \frac{dr}{A}   avec :  r=κ2rsr=κ^2 \: r_s ,  donc  dr=2rsκdκdr=2 \,r_s \: κ \:dκ  ;   A=r−rsr=κ2−1κ2\displaystyle A=\frac{r-r_s}{r}=\frac{κ^2-1}{κ^2}  .
• Ainsi :  cdt=dR−rs2κ4dκκ2−1=dR−rsκ3dκκ−1−rsκ3dκκ+1\displaystyle c \,dt=dR-r_s \, \frac{2 \,κ^4 \: dκ}{κ^2-1}=dR-r_s \, \frac{κ^3 \: dκ}{κ-1}-r_s \, \frac{κ^3 \: dκ}{κ+1} .
• Avec la variable intermédiaire  u=κ−1u=κ-1  on obtient :  κ3dκκ−1=(u3+3u2+3u+1)duu\displaystyle \frac{κ^3 \: dκ}{κ-1}=\frac{(u^3+3 \,u^2+3 \,u+1) \: du}{u} .  Une primitive est :  u33+3u22+3u+ln⁡(|u|)=(κ−1)33+3(κ−1)22+3(κ−1)+ln⁡(|κ−1|)=κ33+κ22+κ−116+ln⁡(|κ−1|)\displaystyle \frac{u^3}{3}+3 \, \frac{u^2}{2}+3 \,u+\ln⁡(|u|)=\frac{(κ-1)^3}{3}+3 \, \frac{(κ-1)^2}{2}+3 \,(κ-1)+\ln⁡(|κ-1|)=\frac{κ^3}{3}+\frac{κ^2}{2}+κ-\frac{11}{6}+\ln⁡(|κ-1|) .
• Avec la variable intermédiaire  u=κ+1u=κ+1  on obtient :  κ3dκκ+1=(u3−3u2+3u−1)duu\displaystyle \frac{κ^3 \: dκ}{κ+1}=\frac{(u^3-3 \,u^2+3 \,u-1) \: du}{u} .  Une primitive est :  u33−3u22+3u−ln(|u|)=(κ+1)33−3(κ+1)22+3(κ+1)−ln(|κ+1|)=κ33−κ22+κ+116−ln(|κ+1|)\displaystyle \frac{u^3}{3}-3 \, \frac{u^2}{2}+3 \,u-\ln(|u|)=\frac{(κ+1)^3}{3}-3 \, \frac{(κ+1)^2}{2}+3 \,(κ+1)-\ln(|κ+1|)=\frac{κ^3}{3}-\frac{κ^2}{2}+κ+\frac{11}{6}-\ln(|κ+1|) .
• Au total on obtient (Lemaître choisit la constante nulle) :  ct=R−2rs3κ3−2rsκ+rsln(|κ+1κ−1|)\displaystyle c \,t=R-\frac{2 \,r_s}{3} \, κ^3-2 \,r_s \: κ+r_s \: \ln\left(\left|\frac{κ+1}{κ-1}\right|\right) .
◊ remarque : cela correspond aussi à :  ct=cT−2rsκ+rsln(|κ+1κ−1|)\displaystyle c \,t=c\,T-2 \,r_s \: κ+r_s \: \ln\left(\left|\frac{κ+1}{κ-1}\right|\right) .
◊ remarque : il reste le problème de la composante imaginaire  rsarg⁡(κ±1)r_s \: \arg⁡(κ±1) .


V. Accélération relative du repérage de Schwarzschild

1.a. • Un point “fixe”  (r=r0=Cster=r_0=Cste)  dans le repérage de Schwarzschild correspond à :

 R−cT=2r03r0rs=Cste\displaystyle R-c \:T=\frac{2 \,r_0}{3} \sqrt{\frac{r_0}{r_s}}=Cste .
• Cela correspond à :  dRdT=c\displaystyle \frac{dR}{dT}=c   et   d2RdT2=0\displaystyle \frac{d^2 R}{{dT}^2} =0  ;  pourtant, le point fixe considéré accélère par rapport au repérage de Lemaître puisque la réciproque est forcément vraie, par construction.


1.b. • On obtient par ailleurs :  c2dτ2=c2dT2−1κ2dR2=c2dT2(1−1κ2)\displaystyle c^2 \, {dτ}^2=c^2 \, {dT}^2-\frac{1}{κ^2} \,{dR}^2=c^2 \,{dT}^2 \: \left(1-\frac{1}{κ^2} \right) ,  où  κ2=(3(R−cT)2rs)2/3=r0rs\displaystyle κ^2=\left(\frac{3 \,(R-c \,T)}{2 \,r_s}\right)^{2/3}=\frac{r_0}{r_s} .  Ainsi :  dTdτ=κ2κ2−1=r0r0−rs\displaystyle \frac{dT}{dτ}=\sqrt{\frac{κ^2}{κ^2-1}}=\sqrt{\frac{r_0}{r_0-r_s}} .
• On en déduit :  dRdτ=cr0r0−rs\displaystyle \frac{dR}{dτ}=c \;\sqrt{\frac{r_0}{r_0-r_s}}  puis  d2Rdτ2=0\displaystyle \frac{d^2 R}{{dτ}^2} =0 ... étrange, non ?...
• Le référentiel de Lemaître est un référentiel d'inertie pour toutes les particules en comouvement, qui y évoluent avec  R=CsteR=Cste .  Le champ de gravitation y disparaît pour ces particules ; de ce fait elles y ont un mouvement rectiligne uniforme.
• Ce n'est pas un référentiel d'inertie pour les autres particules : celles qui sont lancées verticalement vers le haut par rapport au repérage de Schwarzschild, puis retombent, n'ont pas un mouvement rectiligne uniforme dans le référentiel de Lemaître (leur mouvement sous l'effet de la gravitation se déduit des équations du mouvement pour ce repérage).
• Pour rester immobile par rapport au repérage de Schwarzschild, un point matériel n'est pas en mouvement libre, il doit être soumis à des forces qui compensent le champ gravitationnel qu'il subit. Il se trouve qu'un tel point a, par construction, un mouvement rectiligne uniforme avec le repérage de Lemaître.
• Ceci vient du fait qu'on a effectué une transformation de Lorentz avec une vitesse d'entraînement ne dépendant que de rr (et non pas fonction de tt et indépendante de rr) ; pour une valeur fixe de rr la vitesse locale par rapport au repérage de Lemaître est forcément toujours la même, d'où un accélération locale nulle.


2. • La contradiction apparente vient du fait que, en même temps qu'il est localement en contraction par rapport au repérage de Schwarzschild, celui de Lemaître est globalement en expansion. Deux particules de référence (en chute libre pour Schwarzschild) sont immobiles à RR constant pour Lemaître, mais leur distance augmente avec TT. La distance séparant deux valeurs fixes de RR correspond à l'intégrale de  d𝓁=1κdR\displaystyle d𝓁=\frac{1}{κ} \, dR  ;  quand TT augmente pour RR fixé, κκ diminue et d𝓁d𝓁 augmente.
• Pour connaître l'accélération par rapport à un observateur fixe de Lemaître, il faut ajouter la vitesse d'expansion à la vitesse de déplacement local (ici constante). L'accélération observée avec le repérage de Schwarzschild correspond donc ici à l'accélération d'expansion, associée à la dérivée de  1κ=−vec\displaystyle \frac{1}{κ}=-\frac{v_e}{c} ,  donc effectivement liée à la vitesse d'entraînement.
• Pour calculer la vitesse relative, l'effet d'expansion n'intervient qu'au second ordre puisqu'on prend la limite d'un déplacement infinitésimal ; on obtient localement des vitesses opposées. Au contraire pour calculer l'accélération relative (calcul du second ordre), on compare des vitesses en des points différents, donc l'effet d'expansion intervient ; si on n'en tient pas compte on ne trouve pas des accélérations opposées.


VI. Représentations graphiques

1. • En prenant  rsr_s  comme unité, on peut écrire :  r=κ2r=κ^2   et   ct=R−23κ3−2κ+ln(|κ+1κ−1|)\displaystyle c \,t=R-\frac{2}{3} \, κ^3-2 \,κ+\ln\left(\left|\frac{κ+1}{κ-1}\right|\right)  ;  ceci définit paramétriquement (en fonction de κκ) les courbes correspondant à  R=CsteR=Cste  (ci-après pour  R=0;3;6R=0 \,; 3 \,; 6).
◊ remarque : il reste le problème de la composante imaginaire  rsarg⁡(κ±1)r_s \: \arg⁡(κ±1) .

Lemaitre_cor_Im/Lemaitre_cor_1.jpg

• Ces courbes sont constituées de deux branches (vaguement hyperboliques) :

 ◊ quand  r>rsr>r_s  (en rouge) on constate que, pour  ctc \,t  fixé,  RR  est une fonction croissante de rr ;
◊ quand  r<rsr<r_s  (en bleu) la particularité est que, pour  ctc \,t  fixé,  RR  décroît en fonction de rr .


2. • On peut aussi écrire :  r=κ2 r=κ^2   et   ct=cT−2κ+ln(|κ+1κ−1|)\displaystyle c \,t=c \,T-2 \,κ+\ln\left(\left|\frac{κ+1}{κ-1}\right|\right)  ;  ceci définit paramétriquement (en fonction de κκ) les courbes correspondant à  cT=Cstec \,T=Cste  (ci-après pour  cT=0;3;6c \,T=0 \,; 3 \,; 6).

• Ces courbes sont constituées de deux branches (vaguement hyperboliques) ; on y constate que, pour rr fixé,  cTc \,T  est partout une fonction croissante de ctc \,t .

◊ remarque : en comparant ces courbes aux précédentes, on vérifie graphiquement que  R≈cTR≈c \,T  pour  κ≈0κ≈0  (début des courbes en bleu) ; en outre l'écart  R−cTR-c \,T  dépend seulement de rr (et non de  ctc \,t ).

Lemaitre_cor_Im/Lemaitre_cor_2.jpg


VII. Trajectoires des photons


 • Dans le plan (R,cT)(R, c \,T) les trajectoires des photons correspondent à la relation  ds2=0{ds}^2=0 .  En prenant  rsr_s  comme unité pour simplifier, ceci impose la relation  dR=±κcdTdR=±κ \:c \,dT  avec par ailleurs  R−cT=23κ3R-c \,T=\frac{2}{3} \, κ^3  correspond à :  (±κ−1)cdT=2κ2dκ(±κ-1) \:c \,dT=2 \,κ^2 \: dκ .  Ainsi :  cdT=2κ2dκ±κ−1\displaystyle c \,dT=\frac{2 \,κ^2 \: dκ}{±κ-1} .
• Avec la variable intermédiaire  u=±κ−1u=±κ-1  on obtient :  κ2dκ±κ−1=±(u2+2u+1)duu\displaystyle \frac{κ^2 \: dκ}{±κ-1}=±\frac{(u^2+2 \,u+1) \: du}{u} .
• Une primitive est :

 ±[u22+2u+ln(|u|)]=±[(±κ−1)22+2(±κ−1)+ln(|±κ−1|)]=±κ22+κ∓32+ln(|±κ−1|)\displaystyle ±\left[\frac{u^2}{2}+2 \,u+\ln(|u|) \right]=±\left[\frac{(±κ-1)^2}{2}+2 \,(±κ-1)+\ln(|±κ-1|) \right]=±\frac{κ^2}{2}+κ∓\frac{3}{2}+\ln(|±κ-1|) .
• L'intégration donne finalement :  cT=±κ2+2κ±2ln(|±κ−1|)+Cstec \,T=±κ^2+2 \,κ±2 \: \ln(|±κ-1|)+Cste .
◊ remarque : pour les photons sortants, il apparaît une composante imaginaire  2rsarg⁡(κ−1)2 \,r_s \: \arg⁡(κ-1)  généralement omise.
• Avec  R=cT+23κ3R=c \,T+\frac{2}{3} \, κ^3 ,  cela permet une représentation paramétrique des trajectoires.


VIII. Représentations graphiques

1. • La zone “expansion” est essentiellement caractérisée par  κ<0κ<0 .
• Avec  rsr_s  comme unité, on obtient :  r=κ2r=κ^2   et   ct=−R−23κ3−2κ+ln(|κ+1κ−1|)\displaystyle c \,t=-R-\frac{2}{3} \,κ^3-2 \,κ+\ln\left(\left|\frac{κ+1}{κ-1}\right|\right)  ;  ceci définit paramétriquement (en fonction de κκ) les courbes correspondant à  R=CsteR=Cste  (ci-après pour  R=0;3;6R=0 \,; 3 \,; 6).
◊ remarque : il reste le problème de la composante imaginaire  rsarg⁡(κ±1)r_s \; \arg⁡(κ±1) .

Lemaitre_cor_Im/Lemaitre_cor_3.jpg

• Ces courbes sont constituées de deux branches (vaguement hyperboliques) :

 ◊ quand  r>rsr>r_s  (en rouge) on constate que, pour  ctc \,t  fixé,  RR  est une fonction croissante de rr ;
◊ quand  r<rsr<r_s  (en bleu) la particularité est que, pour  ctc \,t  fixé,  RR  décroît en fonction de rr .

2. • On peut aussi écrire :  r=κ2r=κ^2   et   ct=cT−2κ+ln(|κ+1κ−1|)\displaystyle c \,t=c \,T-2 \,κ+\ln\left(\left|\frac{κ+1}{κ-1}\right|\right)  ;  ceci définit paramétriquement (en fonction de κκ) les courbes correspondant à  cT=Cstec \,T=Cste  (ci-après pour  cT=0;3;6c \,T=0 \,; 3 \,; 6).

Lemaitre_cor_Im/Lemaitre_cor_4.jpg

• Ces courbes sont constituées de deux branches (vaguement hyperboliques) ; on y constate que, pour rr fixé,  cTc \,T  est partout une fonction croissante de  ctc \,t .
◊ remarque : en comparant ces courbes aux précédentes, on vérifie graphiquement que  R≈−cTR≈- c \,T  pour  κ≈0κ≈0  (début des courbes en bleu) ; en outre la somme  R+cTR+c \,T  dépend seulement de rr (et non de  ctc \,t ).