RG XVII - MATIÈRE NOIRE ; LAGRANGIEN EN f(R)...

RG XVII - MATIÈRE NOIRE ; LAGRANGIEN EN $f\left(R\right)$ ...

1. Au delà de la théorie d'Einstein

• Bien qu'elle conduise à des calculs souvent compliqués, la théorie relativiste d'Einstein possède une simplicité théorique d'une certaine “esthétique”.

D'autres théories gravitationnelles sont possibles, par exemple la théorie de Rosen avec un champ tensoriel d'ordre 2 dans un espace plat. Un avantage important est sa linéarité, conduisant souvent à des calculs plus simples.

Les test expérimentaux permettent de départager : ils confirment de façon très générale la théorie d'Einstein. Des difficultés apparaissent toutefois pour décrire quelques observations expérimentales particulières, suggérant la nécessité de rechercher plus avant. Quelques uns de ces effets et quelques modifications théoriques possibles sont considérées dans ce qui suit.

2. Stabilité des étoiles et effondrement

• L'énergie des étoiles est fournie par la nucléosynthèse ; d'abord la fusion des atomes d'hydrogène en hélium. Quand l'hydrogène est épuisé, l'étoile s'effondre en éjectant une partie de sa matière (nova) ; ce qui subsiste change de régime avec la fusion de l'hélium en carbone et oxygène (principalement).

Un autre changement de régime se produit quand l'hélium est à son tour épuisé, avec la fusion de l'oxygène en magnésium et silicium. Puis de même avec la fusion du silicium en fer (le plus stable des éléments), dans des étoiles très compactes : les naines blanches. Dans la plupart des cas, une fois le silicium épuisé, ces dernières finissent par se refroidir pour donner des étoiles éteintes : les naines noires.

• Mais si ces dernières sont “trop” massives (plus de

1,5

masse solaire environ), elles s'effondrent à leur tour avec fusion des électrons et des protons donnant des étoiles à neutrons.

De façon analogue, les modèles semblent indiquer qu'au delà d'une certaine limite les étoiles à neutrons ne pourraient que s'effondrer en trous noirs.

• Certains aspects de la métrique extérieure à un astre sphérique pouvant sembler étranges, on peut suspecter l'hypothèse d'effondrement en trou noir : les étoiles les plus denses se rapprochant de la limite sans l'atteindre. Les expulsions de matière successives, aux changements de régime, sont-elles toujours suffisantes pour éviter un effondrement final ?

Vu la grande diversité des circonstances, y compris celles avec augmentation de masse par regroupement d'étoiles doubles, on peut en douter ; mais des modifications de l'équation d'équilibre intérieur pourraient éviter l'effondrement.

3. Masse manquante dans les galaxies

3.1. Problème expérimental

• En première approximation, les galaxies sont composées d'un noyau sphérique et de bras périphériques contenant en comparaison une quantité de masse de faible effet.

La mécanique newtonienne (les effets relativistes sont faibles) prédit que la vitesse de rotation des étoiles à la distance

r

du centre devrait :

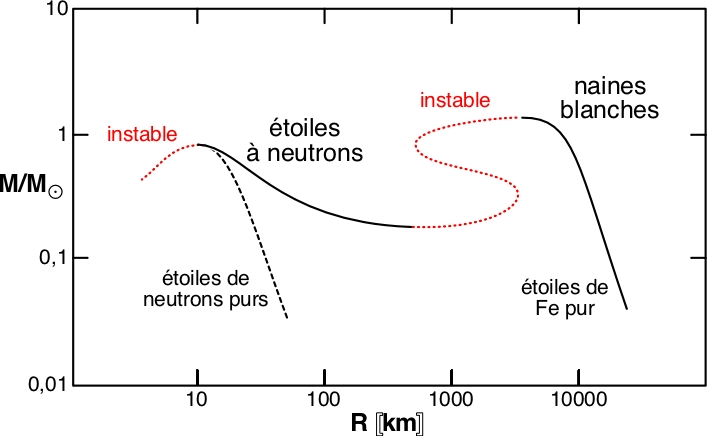
	◊ croître environ comme $r$ dans le noyau ;
	◊ décroître environ comme $\frac{1}{\sqrt{r}}$ dans les bras.

◊ remarque : un calcul théorique plus précis peut être fait en considérant la répartition de masse visible dans la galaxie ; cela ne modifie pas la conclusion qualitative.

• L'expérience montre que la vitesse ne décroît pratiquement pas à la périphérie des galaxies. Le même effet est observé pour la vitesse de rotation de ces dernières dans les amas de galaxies.

Cela semble indiquer :

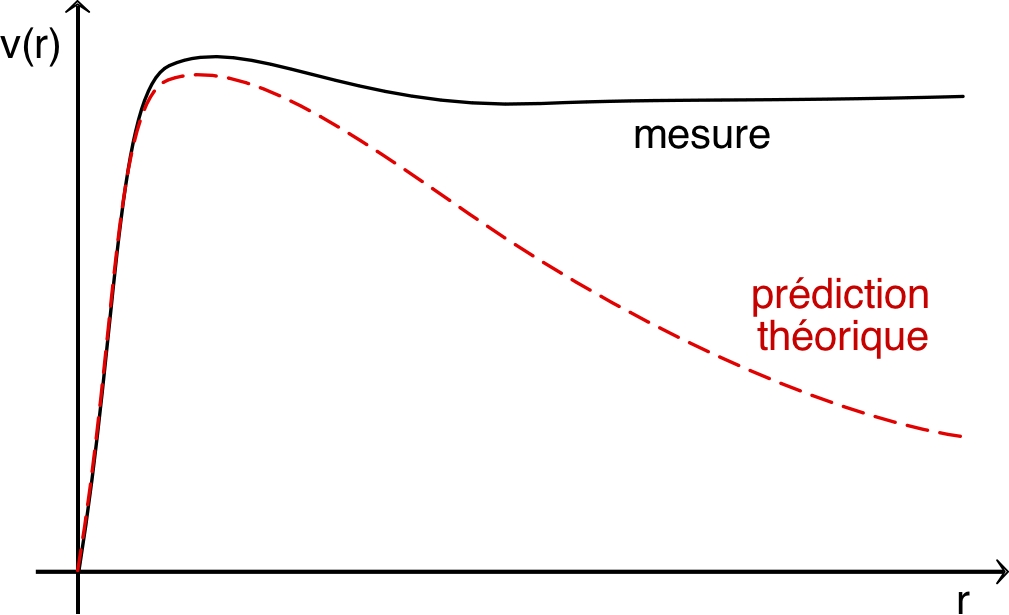
◊	soit qu'il existe un important halo de “matière noire” (non visible) couvrant l'ensemble de chaque galaxie (nettement plus loin que les étoiles visibles les plus éloignées, qui seraient en comparaison “près de centre”) ;
◊	soit que pour les champs gravitationnels forts la théorie d'Einstein ne serait qu'approximative et qu'il faudrait y ajouter des termes correctifs.

◊ remarque : il faut prendre garde au fait que la rotation du centre galactique (décrite avec la métrique de Kerr) contribue à diminuer la décroissance radiale des vitesses déduites de l'effet Doppler.

◊ remarque : les variations observées pour

v\left(r\right)

correspondraient à une densité de masse

μ∝\frac{1}{r^2}

prédite pour un fluide ultra-relativiste en équilibre.

📖 exercice n° I.

3.2. Matière noire

• La principale difficulté vient du fait que la masse visible ne constitue qu'environ

10 \:%

de la masse attractive au centre des galaxies (ou amas).

On peut alors chercher la masse manquante sous forme de nuages de gaz ou de poussières. Les estimations aboutissent à la conclusion que cela ne peut constituer qu'environ

10 \:%

de la masse attractive.

On peut aussi chercher cette masse manquante sous forme d'objets massifs compacts :

◊	naines brunes (“étoiles” trop petites pour briller ; Jupiter serait d'ailleurs “presque” assez gros pour être un tel astre) ;
◊	naines blanches ou étoiles à neutrons (résidus d'étoiles en fin de vie) ;
◊	trous noirs.

Cela soulève alors des problèmes :

◊	pour les étoiles en fin de vie, cela devrait se voir en observant les galaxies très éloignées car l'image obtenue provient d'un lointain passé : il faudrait qu'il y ait eu dans le passé un nombre d'étoiles très supérieur ;
◊	pour les trous noirs, leur champ gravitationnel important provoquerait des perturbations visibles des disques galactiques ;
◊	pour les naines brunes, c'est en principe possible mais en pratique inobservable.

Ici de même, les estimations aboutissent à la conclusion que cela ne peut constituer qu'environ

10 \:%

30 \:%

de la masse attractive.

• D'un autre point de vue, si les galaxies ont un halo très important :

◊	pourquoi n'y a-t-il d'étoiles visibles que dans le plan galactique ?
◊	comment expliquer qu'il n'y a pas d'étoiles plus périphériques ?

Des études sont en cours pour rechercher d'éventuelles particules “exotiques” pouvant constituer la masse manquante tout en permettant la répartition observée des étoiles. Des modifications théoriques seraient aussi possibles.

4. Évolution de l'univers

• L'étude expérimentale de l'évolution de l'univers met aussi en évidence des difficultés d'interprétation : des modèles décrivent effectivement une expansion, mais à une vitesse évoluant de façon apparemment incompatible avec les observations. Les modifications théoriques sur les conditions d'équilibre et d'évolution au niveau cosmologique sont aussi associées à ce problème.

Par rapport aux modélisations les plus plausibles, on observe en outre un net excès de phénomènes très énergiques, décelés par les rayonnements cosmiques. Des effets quantiques pourraient en être l'explication.

5. Autres théories variationnelles

5.1. Théorie avec champ scalaire

• Les considérations précédentes ont suggéré de chercher une théorie compatible avec celle d'Einstein pour les champs gravitationnels modérés (puisqu'elle est dans ce cas confirmée par de nombreux tests expérimentaux), mais conduisant à d'autres conclusions pour les champs forts.

Une approche consiste à utiliser une méthode variationnelle avec un lagrangien différent de la courbure

R

.

• On peut envisager de décrire la gravitation avec un champ scalaire

φ

en plus du champ tensoriel associé au graviton de spin 2.

Le lagrangien du champ scalaire correspond à un terme cinétique et un terme potentiel. Le lagrangien matériel est dans ce cas couplé au champ non plus par l'intermédiaire du tenseur

g_{μν}

mais par

g_{μν}^{*}={A^*}^2 \left(φ\right) \:g_{μν}

où

A^* \left(φ\right)

est une expression décrite par les propriétés de

φ

.

Cela correspond à une action de la forme (A. Barrau, J. Grain) :

S=\frac{1}{2c} \frac{1}{χ} \:∫ \left(R-\frac{1}{2} ∂_μ φ \:∂^μ φ-V\left(φ\right)\right) \:\sqrt{\left|g\right|} \;d^4 x \;+ \frac{1}{2c} \:∫ T\left(g_{μν}^* \right) \:\sqrt{\left|g\right|} \;d^4 x

.

Les théories de ce type sont extrêmement limitées par les contraintes imposées d'après les observations expérimentales ; elles ne semblent pas pouvoir résoudre les problèmes rencontrés.

• On peut montrer que l'ajout de termes en dérivées de

R

équivaut en fait à ajouter des champs scalaires supplémentaires ; cela n'apporte rien de vraiment nouveau.

Si on cherche à ajouter au lagrangien d'autres scalaires obtenus par contraction de

R_{μνρσ}

, le seul qui ne rend pas la théorie instable est proportionnel à l'invariant de Gauss-Bonnet :

W=R_{μνρσ} \:R^{μνρσ}-4 \:R_{μν} \:R^{μν}+R^2

; rien de vraiment efficace ne semble en avoir été déduit.

5.2. Théories variationnelles en $f\left(R\right)$

• Une autre possibilité est de n'utiliser dans le lagrangien que le scalaire

R

, mais par l'intermédiaire d'une expression

f\left(R\right)

qui tend vers

R

dans la limite d'un espace plat (pour lequel

R=0

).

Une difficulté est qu'il y a une assez grande liberté de choix de

f\left(R\right)

; une part importante de l'étude consiste alors à trouver des justifications physiques de ces choix, ainsi que des tests expérimentaux permettant de les discriminer.

• Il a toutefois été montré qu'une expression de la forme

f\left(R\right)=R^{1+ϵ}

(où

ϵ

est une constante infinitésimale) permet de rendre compte des observations dans les galaxies sans avoir besoin de faire intervenir de la matière noire (référence vue sur arXiv, à retrouver).

6. Corrections quantiques

6.1. Principe

• Il ne s'agit pas ici de décrire une théorie quantique de la gravitation, mais d'étudier l'effet de corrections à la théorie d'Einstein issues de la description quantique de la matière.

Une telle approche doit être abordée avec prudence car les corrections quantiques ne respectent pas forcément les invariances relativistes.

Plusieurs phénomènes de ce type ont été étudiés ; les plus connus sont l'effet Hawking et l'effet Unruh.

6.2. Effet Hawking

• La notion de “vide” en mécanique quantique n'est pas la même qu'en mécanique “classique” (non quantique).

Dans le vide quantique, des particules peuvent apparaître, puis disparaître après une durée d'autant plus courte que leur énergie est grande. Le “vide” n'est alors que l'état quantique de plus basse énergie.

Bien sûr la “création” des particules doit respecter les lois de conservation. Par exemple des électrons (fermions, leptons) ne peuvent le faire qu'en association avec des positons (leurs antiparticules).

• Au voisinage immédiat de l'horizon d'un trou noir, la création de telles paires est favorisée car le champ gravitationnel très intense : l'une des deux particules tombe dans le trou noir, permettant à l'autre de s'en échapper. Ceci constitue l'effet Hawking, supposé pouvoir expliquer l'évaporation des trous noirs.

• En effet, parmi les astres candidats trous noirs, l'étude de ceux qui sont associés à un astre compagnon a montré que leur masse diminue au cours du temps (“évaporation”). Ceci semble anormal dans la mesure où rien ne devrait pouvoir s'échapper d'un trou noir ; l'effet Hawking pourrait l'expliquer.

• Or, s'il est vrai que l'effet est a priori faible, la présence des particules qui s'échappent fait que l'espace n'y est pas vide. Plus le champ gravitationnel est intense, plus il y a de particules... qui participent à la création du champ.

Ce dernier ne peut donc pas tendre vers l'infini au niveau de l'horizon, comme le prédit le calcul supposant l'espace vide, car cela ferait apparaître une infinité de particules, qui empêcheraient le champ de tendre vers l'infini. Un calcul complet nécessite donc d'inclure la correction quantique correspondante.

◊ remarque : un autre phénomène semble pouvoir intervenir si de nombreuses particules chargées se forment au voisinage de ce qui devrait être l'horizon des événements, se comportant alors comme un plasma qui empêche la propagation lumineuse ; l'astre serait alors “trou noir” mais non pas par effet gravitationnel direct.

6.3. Effet Unruh

• L'effet Unruh concerne de façon analogue la “création” de photons (bosons, pouvant apparaître relativement sans contrainte).

• L'origine de l'effet provient du fait que le “vide” quantique n'est pas le même pour deux observateurs accélérés l'un par rapport à l'autre.

Là où un observateur inertiel voit un espace vide, un observateur accéléré y voit des photons, en équilibre thermique à une température

T=\frac{ℏ}{ck_B} \frac{a}{2π}

(où

a

est l'accélération).

La loi de Stéphan donne alors la densité d'énergie :

ε=\frac{π^2 \:{k_B}^4}{15 \:ℏ^3 c^3} T^4

. La pression est, dans ce cas, ultra-relativiste :

p=\frac{ε}{3}

.

• Par ailleurs, la relativité générale considère qu'il n'y a pas de champ de gravitation dans un référentiel d'inertie. Or, le référentiel statique de Schwarzschild est accéléré par rapport au précédent (en chute libre) ; donc le champ de gravitation devrait y être calculé en tenant compte d'une densité d'énergie-impulsion associée aux photons correspondants.

📖 exercice n° II.

6.4. Calcul du champ incluant l'effet Unruh

6.4.1. Équations du champ

• L'étude générale est évidemment très complexe. On s'intéresse ici à déterminer la métrique dans le “vide”, pour le cas statique à symétrie sphérique.

Pour un point fixe du repérage de Schwarzschild, l'accélération par rapport à un observateur (inertiel) en chute libre radiale n'est pas simple à calculer, mais on peut la déduire simplement comme l'opposé de l'accélération réciproque. On obtient ainsi :

a=\frac{c^2}{2} \frac{A'}{A\:\sqrt{C}}

.

• Dans les équations d'Einstein, cela correspond à ajouter une contribution :

χ \:ε=η.\left(\frac{A'}{A\:\sqrt{C}}\right)^4

avec :

η=χ \frac{ℏc}{15.4^4.π^2}=1,734.{10}^{-73} \:\mathrm{m^2}

.

Ce terme correctif semble petit quand on considère

η

, mais il tendrait vers l'infini à l'approche de l'horizon d'un trou noir si la métrique n'était pas modifiée par sa contribution ; celle-ci est donc fondamentale.

◊ remarque : la quantité

\sqrt{η}≈4.{10}^{-37} \:\mathrm{m}

(ordre de grandeur de la longueur de Planck) peut être comparée au rayon de Schwarzschild

r_s=\frac{2𝒢M}{c^2}

; pour un trou noir stellaire (

M≈10 \:M_s

) :

\frac{\sqrt{η}}{r_s} ≈{10}^{-42}

; pour un trou noir galactique (

M≈{10}^9 \:M_s

) :

\frac{\sqrt{η}}{r_s} ≈{10}^{-50}

; l'effet intervient donc dans une couche extrêmement mince.

• Les équations correspondantes peuvent s'écrire :

\frac{A'}{A}-\frac{C-1}{r}=\frac{r}{C} \frac{η}{3} \left(\frac{A'}{A}\right)^4

;

\frac{C'}{C}+\frac{C-1}{r}=\frac{r}{C} \:η. \left(\frac{A'}{A}\right)^4

.

Ces équations sont fortement non-linéaires et la résolution littérale est difficilement envisageable.

6.4.2. Intégration par une méthode numérique

• L'intégration numérique peut être obtenue par une méthode d'Euler, en prenant comme condition limite le résultat “classique” de Schwarzschild à une distance assez grande pour que le terme correctif soit négligeable, mais pas trop pour limiter les propagations d'incertitudes des calculs numériques.

Les calculs ne peuvent pas être effectués avec

η

aussi petit, à cause des approximations numériques. On peut tester une série de valeurs décroissantes et vérifier que le comportement qualitatif semble toujours le même.

Les valeurs accessibles sont toutefois limitées : on peut augmenter la précision des calculs dans le logiciel mais, même si cela n'augmente pas trop le temps de calcul, on est limité par la précision de la méthode d'Euler (qui doit déjà être au minimum du second ordre).

Pour

\frac{\sqrt{η}}{r_s} ≈{10}^{-5}

on obtient les allures suivantes (avec

r_s

comme unité) :

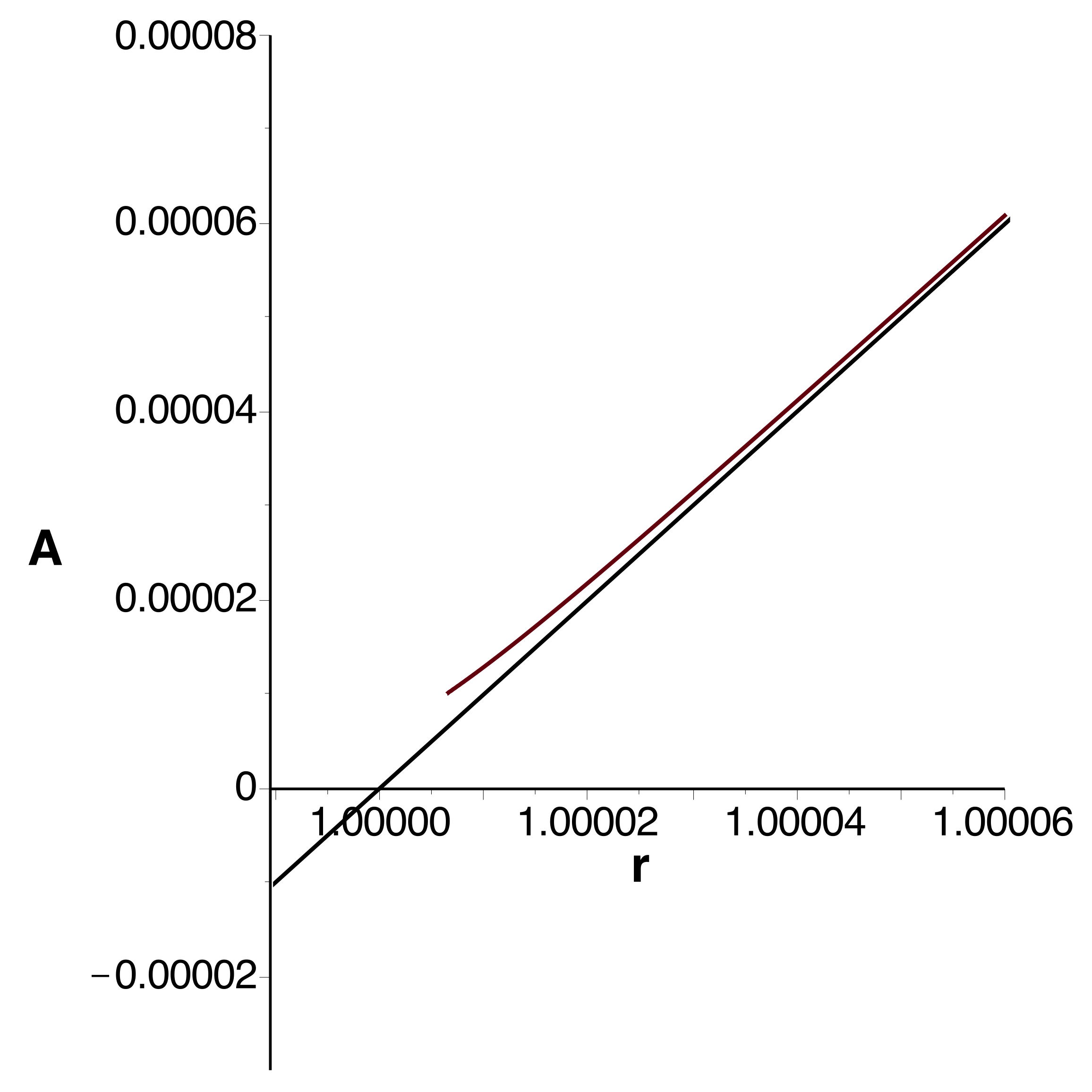MatiereNoire_Im/Unruh-2Euler_10-10_A.jpg

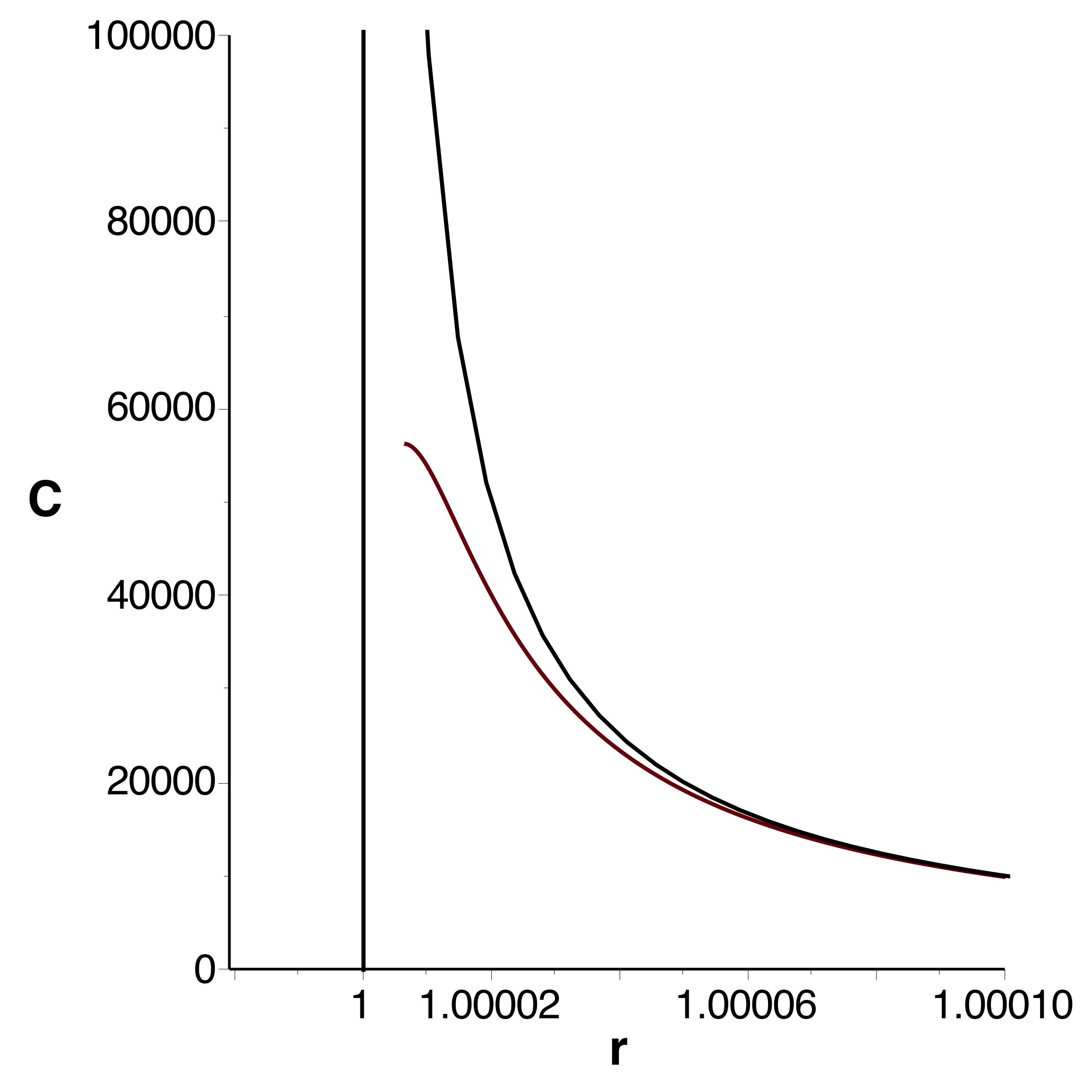MatiereNoire_Im/Unruh-2Euler_10-10_C.jpg

• Pour toutes les valeurs de

η

accessibles, on constate qu'il existe une valeur minimum de

r

en dessous de laquelle l'intégration numérique ne permet plus de résoudre le système d'équations :

r_{min}≈1+\sqrt{η}

(avec

r_s

comme unité). Celle limite correspond à un maximum de

C

.

Ceci met en évidence l'incompatibilité de l'effet Unruh avec l'existence d'un horizon : si on se limite à l'étude d'astres stables, les valeurs plus petites de

r

seraient à raccorder avec ce qui se déduit de l'étude à l'intérieur de l'astre.

Compte tenu de la très faible épaisseur de la couche limite, on peut tout de même remarquer qu'un tel astre serait un “quasi trou noir” : impossible de voir la différence pour un observateur éloigné.

📖 exercices n° III, IV et V.

6.4.3. Intégration par développement en série “à l'infini”

• En utilisant la notation de Binet

u=\frac{1}{r}

, on peut essayer d'intégrer par développement en série au voisinage de

u≈0

.

On peut poser (avec

r_s

comme unité) :

	$A=A_0+A_η$ et $C=C_0+C_η$ ;
	$A_0=1-u$ et $C_0=\frac{1}{1-u}=1+u+u^2+⋯$ (solution “classique”).

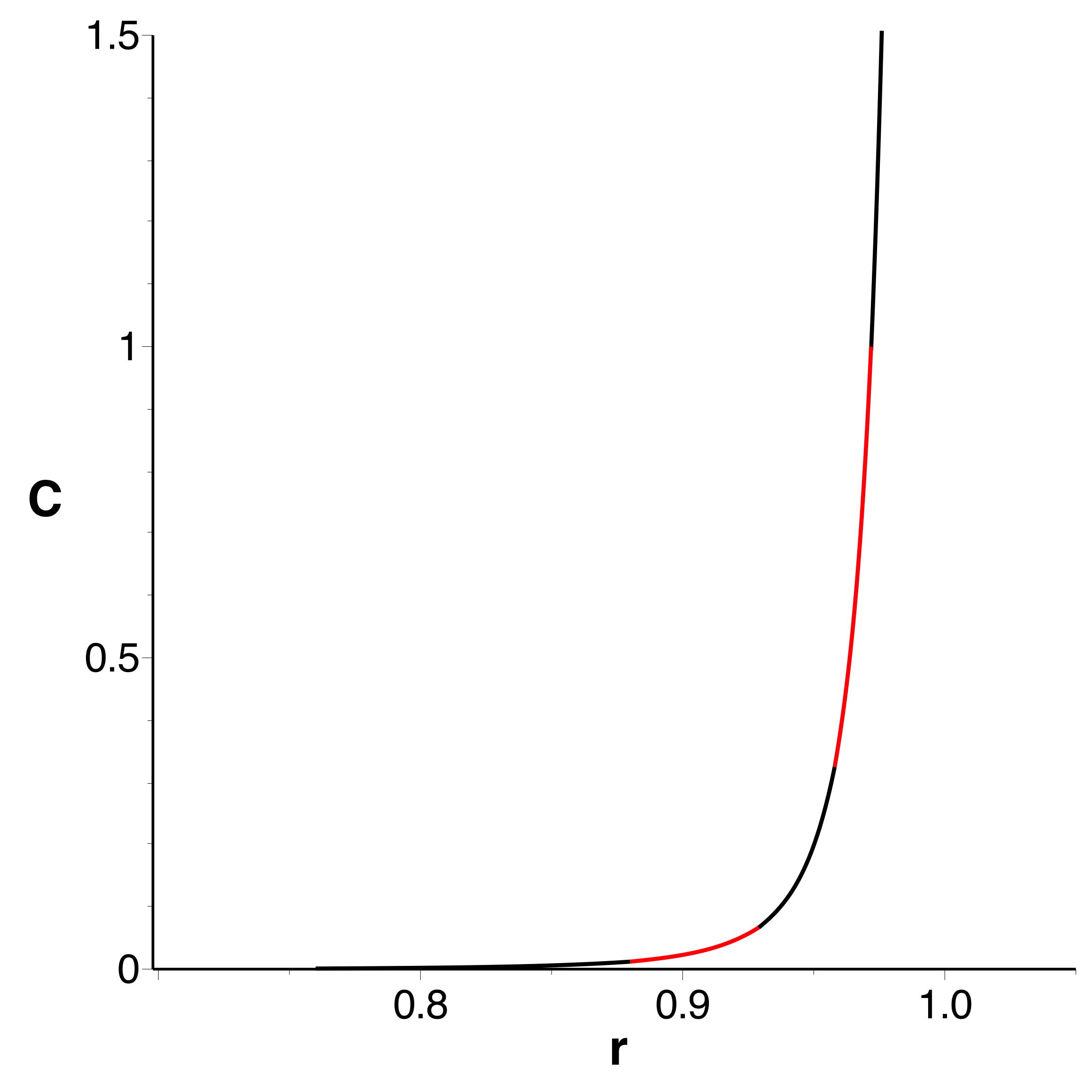Le report dans les équations donne par récurrence les coefficients

A_{ηn}

A_η

C_{ηn}

C_η

.

• Vu que l'effet Unruh est d'ordre 4 (soit 3 de plus que le terme de l'équation “classique”), les coefficients correspondants n'interviennent qu'à partir de l'ordre 6 (

η

est le carré d'une longueur).

Ainsi (il est préférable d'utiliser un logiciel de calcul formel) :

	$A_η=-\frac{1}{45} η \:u^6-\frac{1}{63} η \:u^7+\frac{1}{54} η \:u^9+\frac{1}{27} η \:u^10+\left[\frac{3}{55} η-\frac{28}{2475} η^2 \right] \:u^{11}+𝒪\left(u^{12} \right)$ ;
	$C_η=-\frac{1}{5} η \:u^6-\frac{11}{15} η \:u^7-\frac{178}{105} η \:u^8-\frac{221}{70} η \:u^9-\frac{326}{63} η \:u^{10}-\left[\frac{4909}{630} η+\frac{4}{75} η^2 \right] \:u^{11}+𝒪\left(u^{12} \right)$ .

L'avantage d'un développement littéral est qu'il peut ensuite être utilisé pour comparer plusieurs valeurs de

η

; l'inconvénient est qu'il nécessite des calculs assez longs : augmentant, en fonction de l'ordre

N

, comme

N^8

(difficile de dépasser

N=140

).

On peut ainsi vérifier que le comportement est semblable pour les différentes valeurs

η

, mais on est limité à

\frac{\sqrt{η}}{r_s} ≈{10}^{-1}

.

• Pour

\frac{\sqrt{η}}{r_s} ≈{10}^{-1}

on obtient les allures ci-après, montrant pour

A

une “convergence”, puis une divergence (pour

N≳60

) de la partie

r≲1,05 \:r_s

De même pour

C

avec divergence (pour

N≳60

) de la partie

r≲1,10 \:r_s

Les valeurs de

A

semblent pouvoir être extrapolées jusqu'à

r≈1,05 \:r_s

, mais elles sont liées à celles de

C

qui ne peuvent être estimées que jusqu'à

r≈1,10 \:r_s

, où on retrouve un maximum.

Ces résultats sont tout à fait compatibles avec ceux de l'intégration numérique.

📖 exercices n° VI et VII.

6.4.4. Intégration par raccordement de développements en série

• À part pour certains points singuliers (l'origine

r=0

, le maximum de

C

) il est possible d'intégrer par développement en série au voisinage d'une valeur

r_0

, ce qui est intéressant pour prolonger vers les faibles valeurs de

r

les résultats des calculs précédents.

Ce type de développement n'est valable que dans un intervalle de convergence limité, mais on peut reconstituer les courbes par raccordement de plusieurs déterminations dans des intervalles successifs. Bien que la précision des calculs devienne insuffisante pour les trop faibles valeurs de

r

, il semble que les quantités

A

C

tendent vers zéro à l'origine (ce sont les trop faibles valeurs de

C

qui limitent la précision).

• Pour

\frac{\sqrt{η}}{r_s} ≈{10}^{-2}

on obtient les allures ci-après, montrant un bon raccordement avec les courbes déduites des autres méthodes (seules les portions où le terme correctif est visible sont représentées). Il est clair que

A

ne s'annule pas pour

r=r_s

et que

C

n'y diverge pas.

• Il semble improbable que ce prolongement “intérieur” de la métrique puisse correspondre à un astre constitué uniquement de photons (“auto-polarisation” de l'espace-temps causée par une violente perturbation extérieure ?).

De tels objets (quasi-trous noirs) pourraient être candidats pour constituer la matière noire recherchée. Mais la partie “intérieure”, pour laquelle

C\left(r\right)

croît, ne décrit pas un astre en équilibre car elle ne respecte pas la loi de variation de la pression pour un fluide ultra-relativiste :

A∝r

;

C=Cste

p∝\frac{1}{r^2}

; avec une pression trop faible au centre, un tel astre devrait normalement “imploser”.

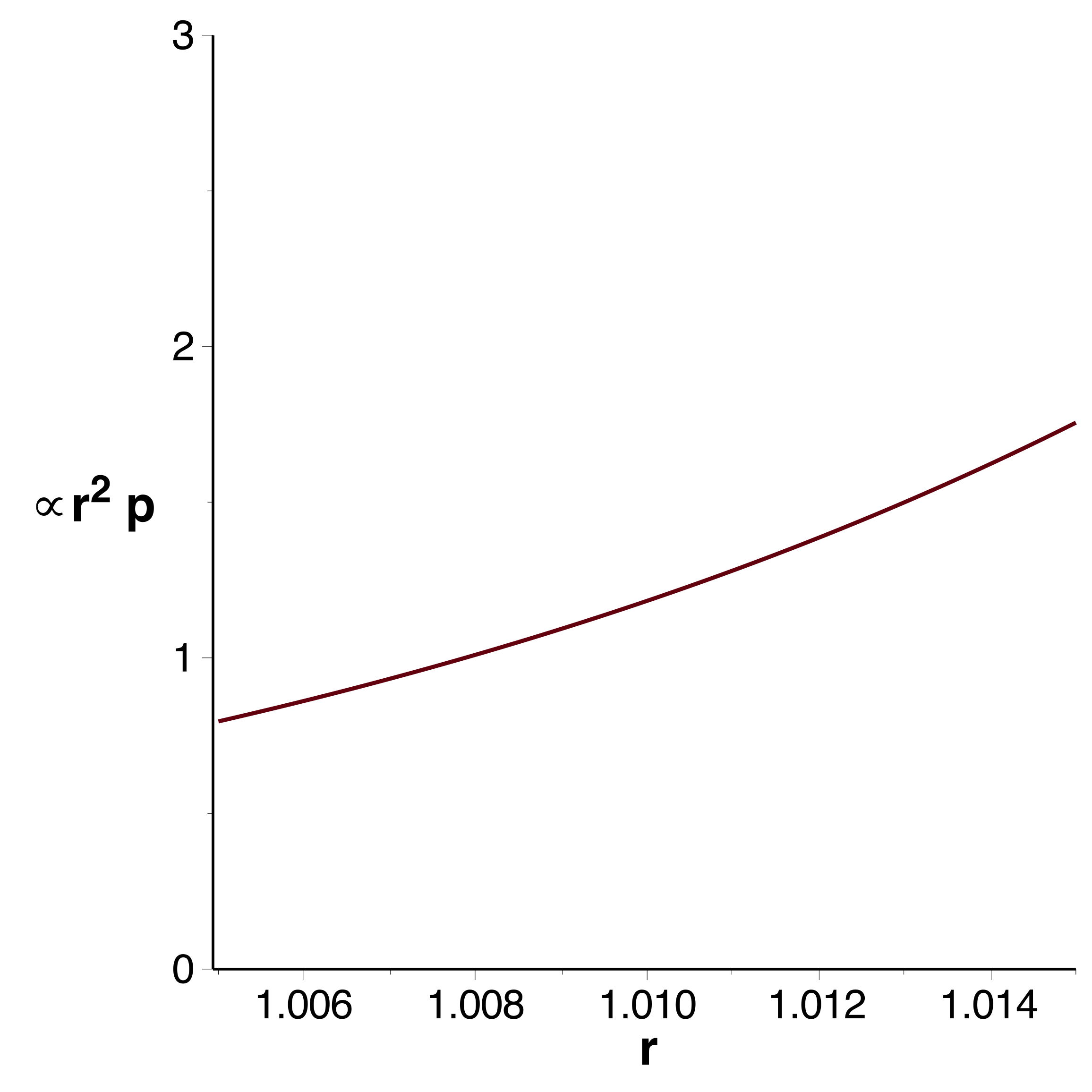
MatiereNoire_Im/Unruh-devnum_10-4_rp1_r2p.jpg

Par contre, compte tenu des très faibles valeurs de

A

près de sa “surface”, un tel objet pourrait sembler durer très longtemps pour un observateur à l'infini.

◊ remarque : l'effet Hawking doit pouvoir donner lieu à des résultats analogues, mais je n'ai pas trouvé de documentation suffisante pour tester cela (et tout réinventer me semble un travail plutôt colossal).

📖 exercice n° VIII.

7. Modification de la loi d'équilibre

• Certains calculs, incluant des effets quantiques pour un champ scalaire dans un espace temps de (de)_Sitter, font apparaitre un changement de la loi de conservation du tenseur d'énergie-impulsion :

D_μ T^{μν}=\frac{1}{48 \,π} \:D^ν R

.

La théorie de P. Rastall est basée sur l'idée que la conservation du tenseur d'énergie-impulsion (

D_μ T^{μν}=0

) serait vérifiée uniquement dans l'espace-temps de Minkowski. Il considère qu'il pourrait y en avoir une violation dans un espace-temps courbe, de la forme :

D_μ T^{μν}∝D^ν R

(avec une constante de proportionnalité à déterminer).

Cela a été proposé dans le cadre de la cosmologie, pour tenter de décrire l'évolution de l'univers, mais pourrait être adapté pour tenir compte du fait que le “vide” (où rien n'a été introduit) n'est pas “vide” (il peut contenir des particules), ce qui pourrait aussi influencer l'équilibre des étoiles.

• Comme le décrit M. Visser, cela revient à modifier la définition du tenseur énergie-impulsion, ce qui ne modifie pas vraiment la relativité générale.

En supposant qu'il existe

𝒯_{μν}

tel que

D_μ 𝒯^{μν}=\frac{λ}{4} g^{μν} \:D_μ R

, on est conduit à des équations de la forme :

\left(R_{μν}-\frac{1}{2} g_{μν} \:R\right)+\frac{λ}{4} g_{μν} \:R=χ \;𝒯_{μν}

ce qui implique :

\left(λ-1\right)\:R=χ \:𝒯

.

• Pour le cas général

λ≠1

, en présence de “matière” décrite par

𝒯_{μν}≠0

on peut écrire :

R=\frac{χ}{λ-1} \:𝒯

, donc on retrouve

\left(R_{μν}-\frac{1}{2} g_{μν} \:R\right)=χ \;T_{μν}

en posant :

T_{μν}=𝒯_{μν}+\frac{λ}{4\,\left(1-λ\right)} \,𝒯 \:g_{μν}

. Cela semblerait donc pouvoir éventuellement décrire un “vide” qui n'est pas “vide” (

T_{μν}=0

avec

𝒯_{μν}≠0

).

Mais cela impose

T=\frac{λ}{4 \,\left(1-λ\right)} \:𝒯

donc inversement :

𝒯_{μν}=T_{μν}-\frac{λ}{4} \:T \:g_{μν}

par suite

T_{μν}=0

implique

𝒯_{μν}=0

; on n'obtient pas l'effet souhaité de ce point de vue.

En fait le “vide” décrit par

𝒯_{μν}=0

correspond à

R=0

et redonne les équations usuelles

R_{μν}=0

.

◊ remarque : le cas particulier

λ=1

correspond en fait à ajouter une constante cosmologique ; il n'est pas adapté à la description des étoiles.

• Cela n'interdit pas totalement que des notations de ce type conduisent à modifier l'équilibre intérieur et les conditions de stabilité des étoiles, mais jusqu'à présent aucun progrès concluant ne semble avoir été obtenu ainsi.

8. Modification de la “relation de dispersion”

• Pour expliquer certaines observations à haute énergie, contredisant les modèles “classiques” selon lesquels l'énergie devrait être bornée par la limite de Planck

E_{pl}=\sqrt{\frac{c^5ℏ}{𝒢}}=1,96.{10}^9 \:\mathrm{J}

, G. Amelino-Camelia et T. Piran ont proposé d'ajouter des termes correctifs dans la relation entre

E

p

sous la forme :

E^2=c^2 p^2+m^2 c^4+ λ \:E^3+⋯

(où l'ordre de grandeur de la constante

λ

se déduit de la longueur de Planck

𝓁_{pl}=\sqrt{\frac{ℏ \:𝒢}{c^3}}=1,62.{10}^{-35} \:\mathrm{m}

).

◊ remarque : cela intervient de façon un peu analogue à la “relation de dispersion” en optique, associée à la dispersion du spectre lumineux, ce pourquoi les théories de ce type sont appelées “théories arc-en-ciel”.

• De façon analogue, J. Magueijo et L. Smolin ont proposé une modification de la forme :

f_0^{\:2} \left(ϵ\right) \:E^2=f_1^{\:2} \left(ϵ\right) \;c^2 p^2+m^2 c^4

avec

ϵ=\frac{E}{E_{pl}}

et où les fonctions

f_0

f_1

tendent vers

1

à basse énergie.

Cela est associé à une “gravitation arc en ciel” avec (pour le cas statique à symétrie sphérique) une métrique de la forme :

{ds}^2=\frac{A(r)}{f_0^{\:2} \left(ϵ\right)} \:c^2{dt}^2-\frac{C\left(r\right)}{f_1^{\:2} \left(ϵ\right)}\:dr^2-\frac{r^2}{f_1^{\:2} \left(ϵ\right)} \:dΩ^2

◊ remarque : un certain nombre de physiciens supposent

f_0\left(ϵ\right)=1

f_1\left(ϵ\right)=\sqrt{1+ϵ^2}

mais il semble ne pas y avoir de véritable justification théorique autre qu'une approximation à la limite des basses énergies.

• Les recherches de ce type se poursuivent sans montrer de cohérence nette, les tentatives diverses ressemblant surtout à un tâtonnement dans l'espoir de dénicher (presque par hasard) un solution intéressante.

9. Réinterprétation “à la Dirac”

• Pour résoudre certaines difficultés de la mécanique quantique relativiste, associées au caractère quadratique des équations comme celle de Klein-Gordon, P. Dirac a proposé d'écrire la relation de dispersion sous une forme linéarisée qu'on peut noter :

(c \,γ^μ \:\widehat{p_μ} - m \,c^2 ) \: ψ(x^α )=0

avec

\widehat{p_μ}=i\,ℏ\:∂_μ

.

Les matrices

γ^μ

de Dirac correspondent à des “nombres” intervenant dans un espace spinoriel, de dimension 4 pour les électrons, telles que

[γ^μ,γ^ν ]=0

γ^μ \,γ^ν+γ^ν \,γ^μ=2 \,g^{μν} \: I_{(4)}

où

I_{(4)}

est l'identité dans l'espace spinoriel.

• Sachant que la mécanique “classique” (non quantique) n'est qu'une approximation de la forme quantique dans la limite

ℏ→0

, on peut être tenté d'imaginer rétro-incorporer cette démarche dans le cas “classique”.

La relativité considère dans le lagrangien un terme d'interaction électromagnétique en

j^μ \:A_μ

, produit d'un courant par un potentiel.

La relativité générale considère une action de la forme

𝒮=-m \,c \:∫ \,ds

où on réintroduit une expression quadratique :

\displaystyle ds=\frac{ds}{ds} \,ds=\sqrt{g_{μν} \, \frac{dx^μ}{ds} \frac{dx^ν}{ds}} \; ds

; or elle utilise

\displaystyle p^μ=m \,c \: \frac{dx^μ}{ds}

, ce qui correspond à faire intervenir

\sqrt{g_{μν} \: p^μ \: p^ν}

.

• Une approche qui semble ne pas avoir été testée (ou qui est passée inaperçue, noyée dans la bibliographie à profusion) serait de tenter une linéarisation gravitationnelle analogue à celle de P. Dirac (contrairement à celle de N. Rosen, qui utilise des tenseurs réels d'ordre 2).

Ceci se baserait sur une action prenant comme potentiels gravitationnels non pas la métrique

g_{μν}

mais des matrices

γ_μ

(dans un espace à préciser) jouant ainsi un rôle analogue (mais non commutatif ?) à celui des potentiels

A_μ

de l'électromagnétisme :

\displaystyle 𝒮=- ∫ \,γ_μ \: p^μ \: ds=-m \,c\: ∫ \,γ_μ \frac{dx^μ}{ds} \, ds=-m \,c \:∫\,γ_μ \: dx^μ

.

Dans ce cas, la métrique se déduirait ensuite à partir des produits des

γ_μ

.

◊ remarque : un tel terme d'action correspondrait au produit d'un “potentiel” par un “courant d'énergie-impulsion” ; il est très possible que cela s'avère fondamentalement impossible dès la première tentative d’approfondissement...