MATIÈRE NOIRE ; LAGRANGIEN EN $f\left(R\right)$... - corrigé des exercices

I. Modélisation d'une galaxie

1.

• On raisonne dans l'approximation newtonienne car les corrections relativistes sont qualitativement négligeables dans le cas étudié. • La vitesse d'une étoile en rotation circulaire de rayon $r$, autour d'un astre de masse $M$, peut s'écrire :  $v=\sqrt{\frac{𝒢M}{r}}$ .  Cela peut s'appliquer aux étoiles des bras de la galaxie si on suppose que leur action gravitationnelle est négligeable en comparaison de celle du noyau galactique. • D'après le théorème de Gauss, l'action du noyau sphérique de rayon $R$ sur chacune de ses étoiles est limitée à celle de la masse  $M\left(r\right)=M \frac{r^3}{R^3}$   contenue dans la sphère concentrique de rayon $r$. La vitesse correspondante est ainsi :  $v=\sqrt{\frac{𝒢M\left(r\right)}{r}}=\sqrt{\frac{𝒢M}{R^3}} \;r$ . • La variation de $v\left(r\right)$ a l'allure suivante (approximation très basique mais qualitativement efficace) :

II. Accélération d'un point en chute libre radiale

III. Intégration numérique de l'effet Unruh

1.a.	• Pour une méthode d'Euler il faut pouvoir isoler une expression de la dérivée. La première équation ne dépend que de $A'$ (et non de $C'$) :  $\frac{A'}{A}-\frac{C-1}{r}=\frac{r}{C} \frac{η}{3} \left(\frac{A'}{A}\right)^4$. • En prenant comme condition limite le résultat “classique” de Schwarzschild à une distance assez grande pour que le terme correctif soit négligeable, mais pas trop pour limiter les propagations d'incertitudes des calculs numériques, la résolution numérique donne deux solutions réelles pour $A'$ ; la comparaison avec le cas limite montre que c'est la plus petite qui convient. ◊ remarque : le fait de devoir choisir “à la main” l'une des deux valeurs de la dérivée bloque les logiciels de calcul formel. • La dérivée $C'$ est alors obtenue en reportant dans l'autre équation :  $\frac{C'}{C}+\frac{C-1}{r}=\frac{r}{C} \:η .\left(\frac{A'}{A}\right)^4$. • Les dérivées $A'$ et $C'$ permettent de calculer $A$ et $C$ au point suivant, puis ainsi de suite.
1.b.	• pour s'assurer que la méthode est acceptable, on peut tester si solution “classique” est correctement retrouvée pour le cas  $η=0$.  On constate ainsi que la précision est insuffisante à l'échelle où on souhaite étudier le terme correctif.

2.a.	• Avec la méthode au premier ordre, on calcule la dérivée en un point pour estimer la variation jusqu'au point suivant, mais cette variation dépend de la pente moyenne sur l'intervalle. • Pour obtenir un calcul du second ordre, en tenant compte de la variation de la dérivée, on fait une première approximation du point suivant, d'où on déduit une estimation de la dérivée en ce point. Pour ré-estimer plus précisément le point suivant, on utilise ensuite comme dérivée la moyenne des valeurs obtenues aux deux extrémités de l'intervalle. On constate que la précision est ainsi raisonnablement correcte (l'écart est inférieur à l'épaisseur du tracé).
2.b.	• On obtient des comportements très semblables pour $η$ allant de ${10}^{-2}$ à ${10}^{-10}$ ; on note toutefois (principalement pour $A$) que cette dernière valeur montre la limite de la méthode d'Euler au second ordre. ◊ remarque : pour $η$ plus petit, il ne suffit pas d'augmenter le nombre de chiffres significatifs dans le logiciel, il faut aussi utiliser une méthode d'Euler à un ordre encore plus grand. • Pour toutes les valeurs de $η$ accessibles, on constate qu'il existe une valeur minimum de $r$ en dessous de laquelle l'intégration numérique ne permet plus de résoudre le système d'équations :  $r_{min}≈1+\sqrt{η}$  (avec $r_s$ comme unité). Celle limite correspond à un maximum de $C$.

IV. Effet de type Unruh à l'ordre 3

2.

• Par exemple pour  $η={10}^{-1}$  (une valeur plus petite n'apporte qualitativement rien de plus et rend les graphiques moins lisibles), on obtient les courbes suivantes. • Il est remarquable de constater que ces courbes peuvent se prolonger jusqu'à  $r≈0$  ;  la précision de la méthode d'Euler limite toutefois l'intégration d'autant plus qu'on diminue $η$. ◊ remarque : on peut aussi étudier des effets analogues pour diverses valeurs de l'ordre entre $2,5$ et $3,6$ ; plus on se rapproche de l'ordre $4$, plus la partie “intérieure” devient difficile à calculer, puis incalculable à partir de $3,5$. • Cette partie “intérieure”, pour laquelle $C(r)$ croît, ne décrit toutefois pas “une espèce d'astre” en équilibre car elle ne respecte pas la loi de variation de la pression pour un fluide ultra-relativiste :  $A∝r$  ;  $C=Cste$  et  $p∝\frac{1}{r^2}$ .  Si on se limite à des solutions stables, l'utilisation correcte de ces courbes consisterait à les raccorder avec celles obtenues pour la description de l'intérieur de l'astre.

V. Effet de type Unruh à l'ordre 2

2.

• Par exemple pour  $η={10}^{-1}$  (une valeur plus petite n'apporte qualitativement rien de plus et rend les graphiques moins lisibles), on obtient les courbes ci-après. • Il est remarquable de constater que ces courbes peuvent se prolonger jusqu'à  $r≈0$  ;  la précision de la méthode d'Euler limite toutefois l'intégration d'autant plus qu'on diminue $η$. • Cette partie “intérieure”, pour laquelle $C(r)$ est quasi constant, ne décrit toutefois pas “une espèce d'astre” en équilibre car elle ne respecte pas la loi de variation de la pression pour un fluide ultra-relativiste :  $A∝r$  ;  $C=Cste$  et  $p∝\frac{1}{r^2}$ .  Si on se limite à des solutions stables, l'utilisation correcte de ces courbes consisterait à les raccorder avec celles obtenues pour la description de l'intérieur de l'astre.

VI. Calcul de l'effet Unruh par développement en série

1.	• On peut choisir par exemple  $η={10}^{-3}$  et effectuer les calculs pour quelques valeurs de $N$ sur quelques machines et logiciels ; on constate une variation environ comme $N^3$.

2.a.	• Pour obtenir un résultat satisfaisant, il faut effectuer les développements jusqu'à  $N≈1500$. ◊ remarque : compte tenu du nombre important de reports d'un calcul numérique dans le suivant, cela nécessite en outre de calculer avec suffisamment de chiffres significatifs (au moins $30$). • Compte tenu du fait que  $N≈150$  est nécessaire pour  $η={10}^{-2}$,  la comparaison montre qu'il faudrait un ordre  $N≈1500000$  pour décrire  $η={10}^{-10}$  (limite de la méthode d'Euler) ; on retombe alors dans un problème de temps de calcul (et éventuellement de taille mémoire). Ceci montre que, même si cette méthode numérique peut décrire des valeurs de $η$ plus petites que pour un développement en série littéral, elle semble rester plus limitée que la méthode d'Euler.
2.b.	• On obtient les allures suivantes, montrant pour $A$ une “convergence”, puis une divergence (pour  $N≳500$)  de la partie  $r≲1,003 \:r_s$ : • De même pour $C$ avec divergence (pour  $N≳800$)  de la partie  $r≲1,003 \:r_s$ : • Les valeurs de $A$ semblent pouvoir être extrapolées jusqu'à  $r≈1,003 \:r_s$,  mais elles sont liées à celles de $C$ qui ne peuvent être estimées que jusqu'à  $r≈1,004 \:r_s$,  tout de même en deçà du maximum. • Ces résultats sont tout à fait compatibles avec ceux obtenus par intégration numérique : les courbes obtenues par les deux méthodes se superposent à mieux que $1 \:$ près (incertitudes numériques).

VII. Calcul de l'effet Unruh par développement en série

VIII. Calcul de l'effet Unruh par développements en série

3.

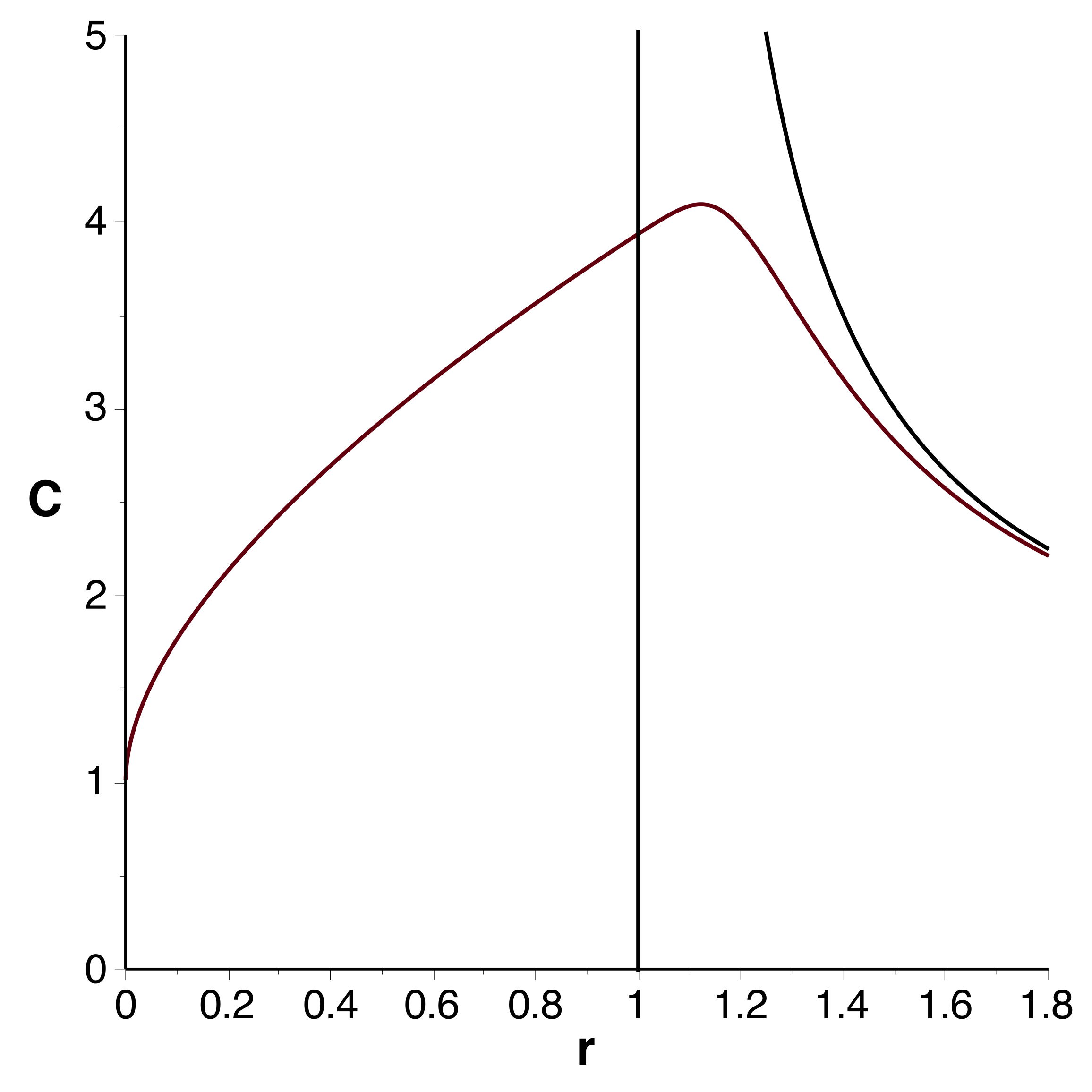
• Pour  $\frac{\sqrt{η}}{r_s} ={10}^{-2}$  les autres méthodes donnent un maximum de $C$ pour  $r_{extr}=1,0079±0,0001$  (en fait  $\frac{r_{extr}}{r_s}$ )  à la limite de validité des calculs ; on peut commencer par vérifier cet extremum à l'aide d'un développement en série pour  $r_0=1,010$.  Le raccordement impose  $a_0=0,0118$  et  $c_0=57,15$  ;  on obtient ainsi  $a_1=58,78$  et  $c_1=-917,3$  ...  puis ainsi de suite. 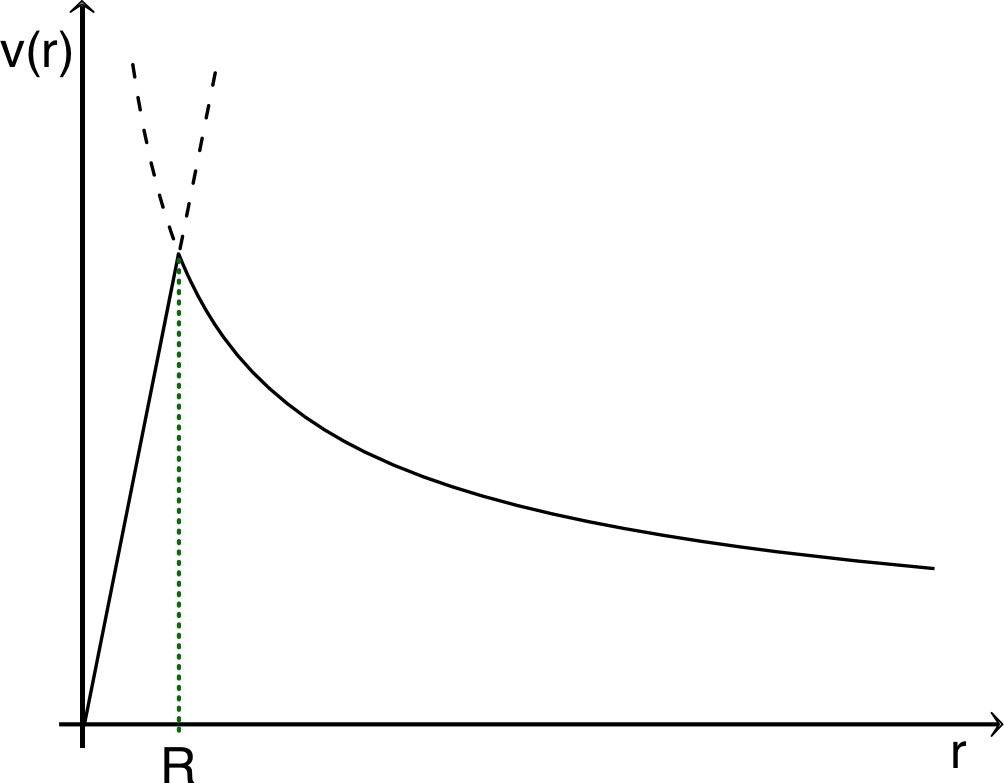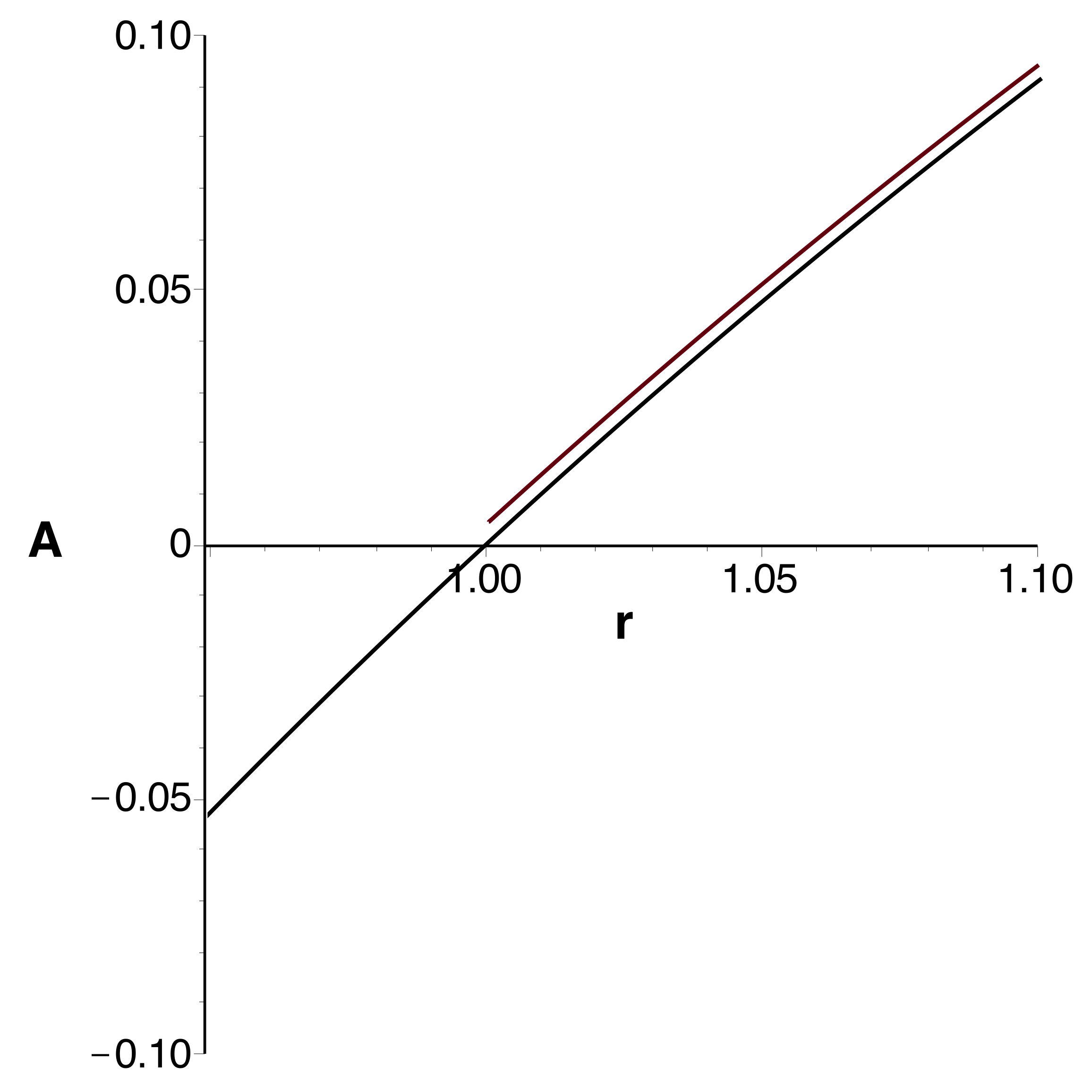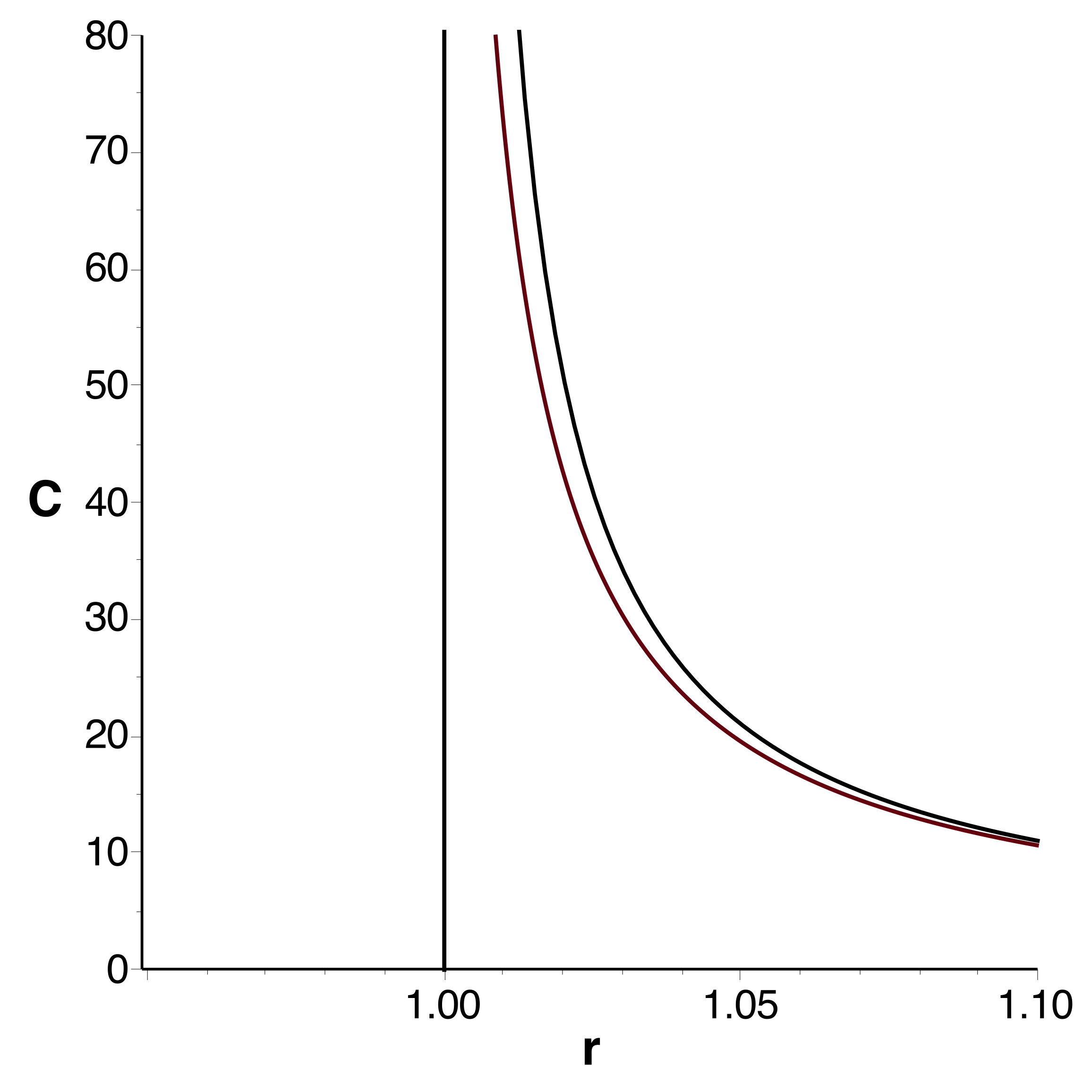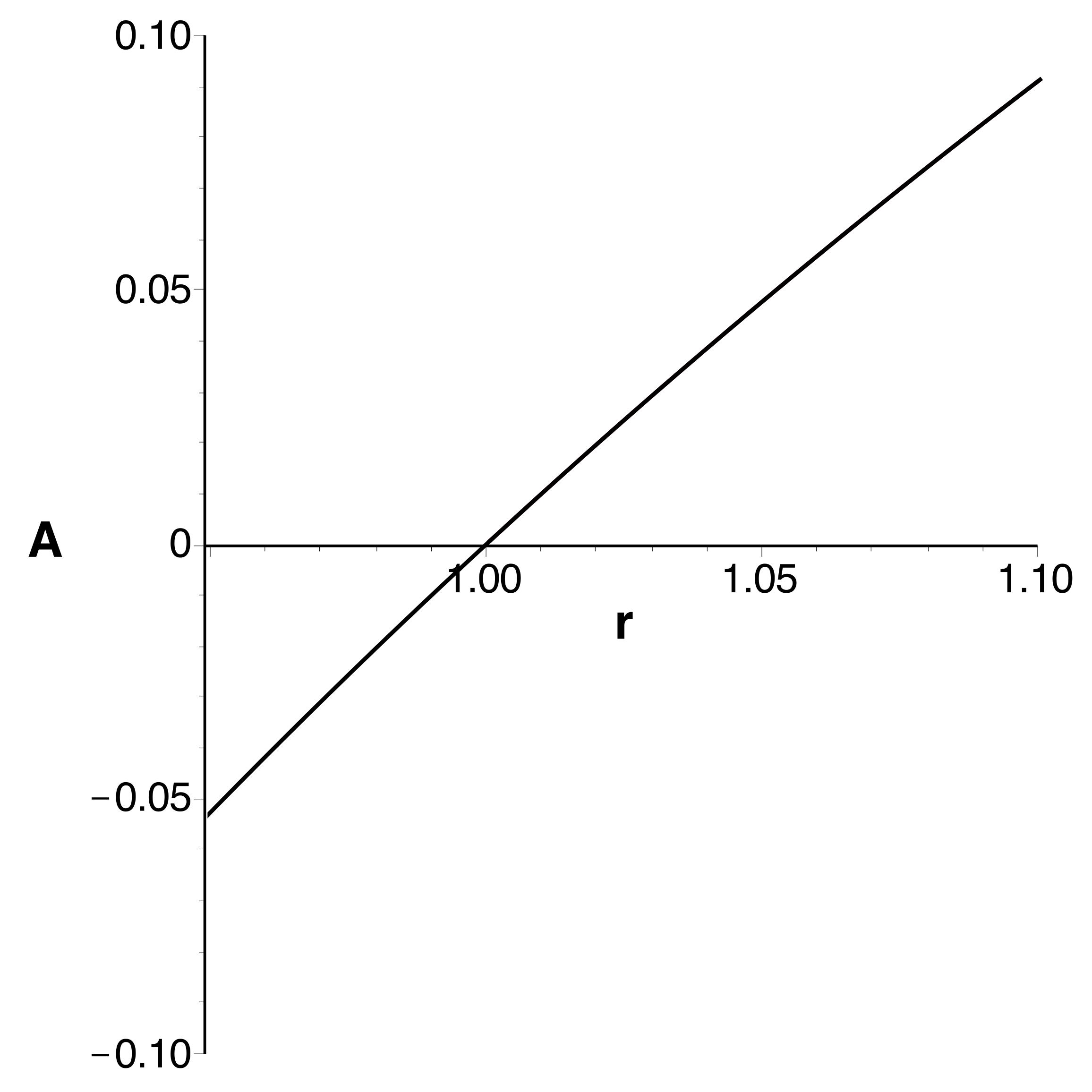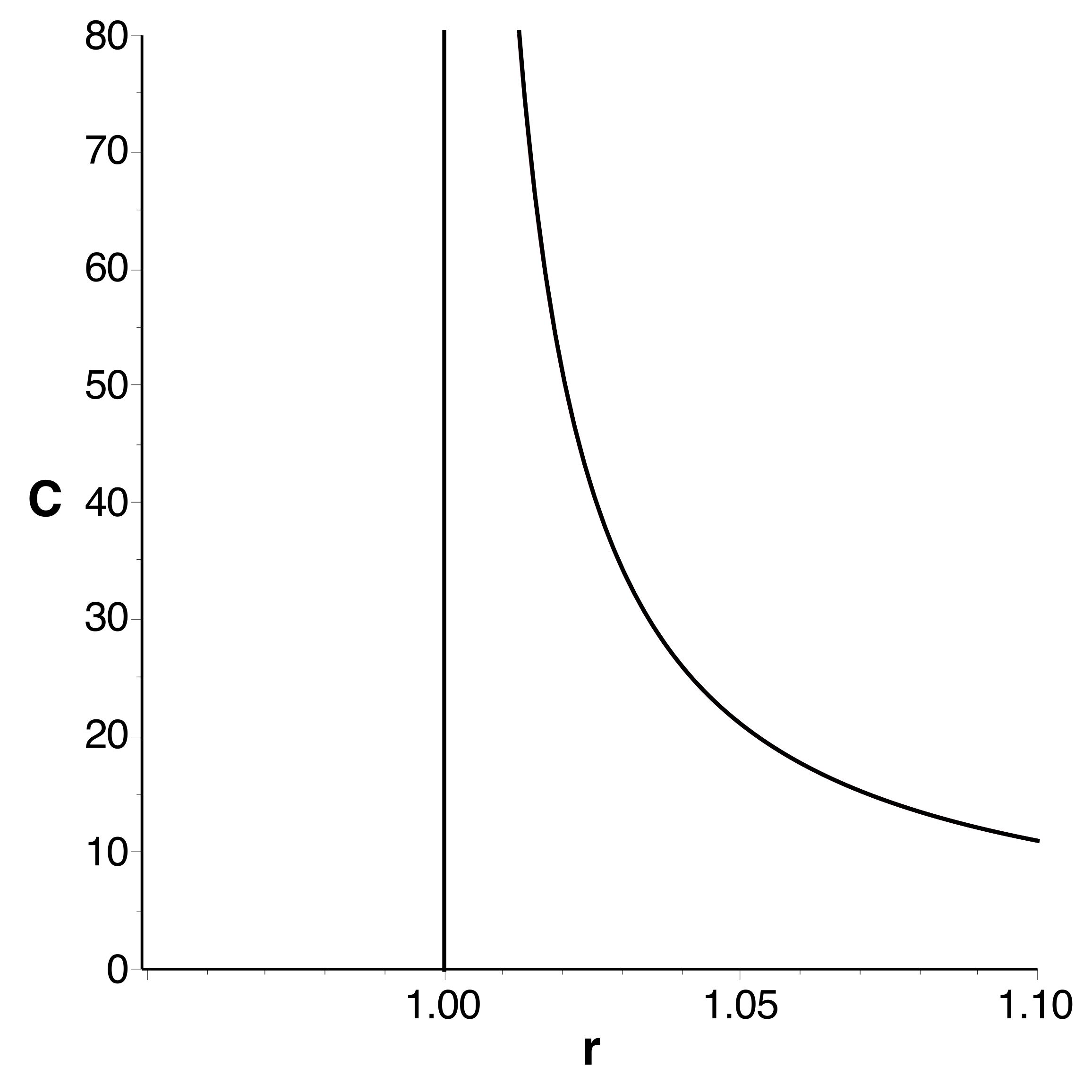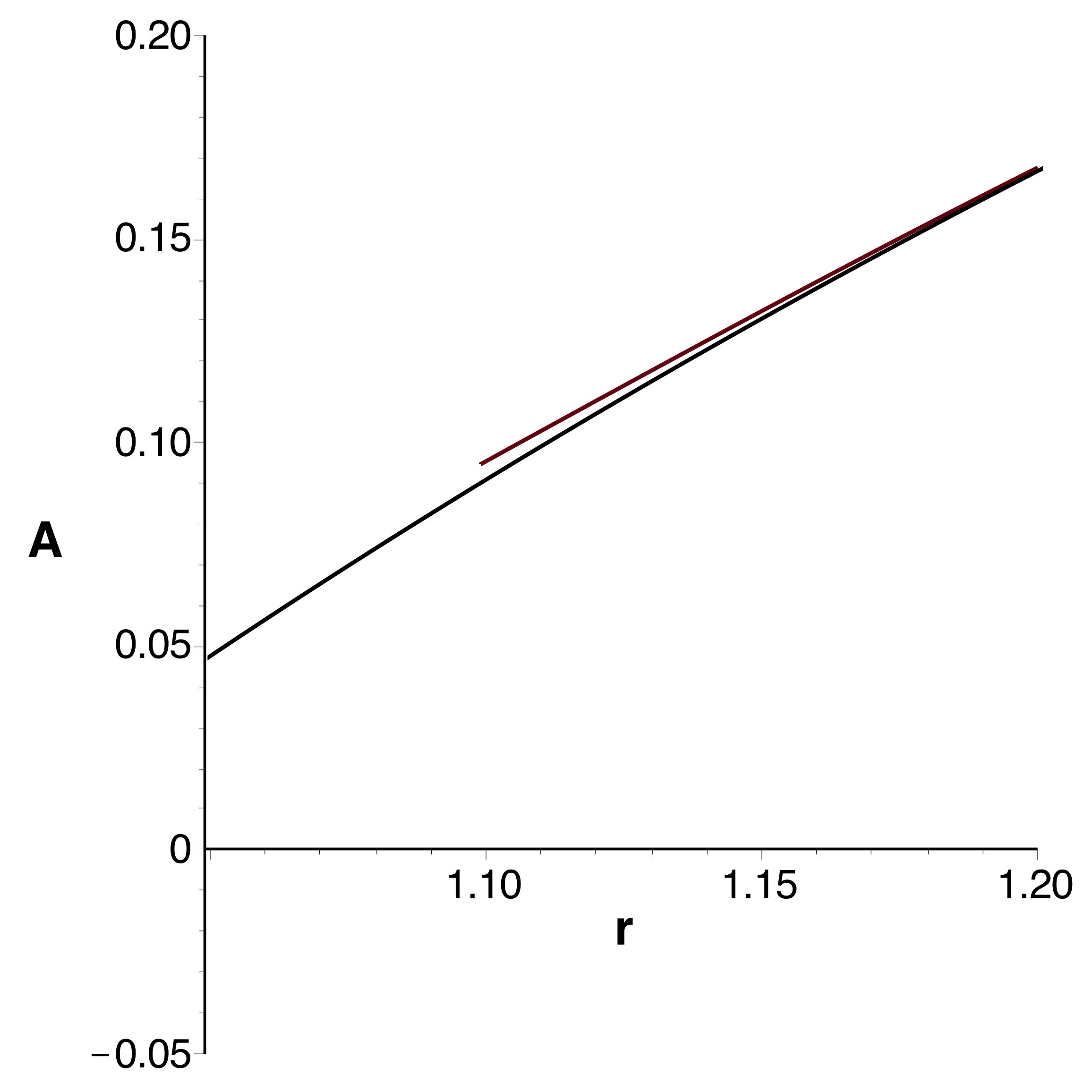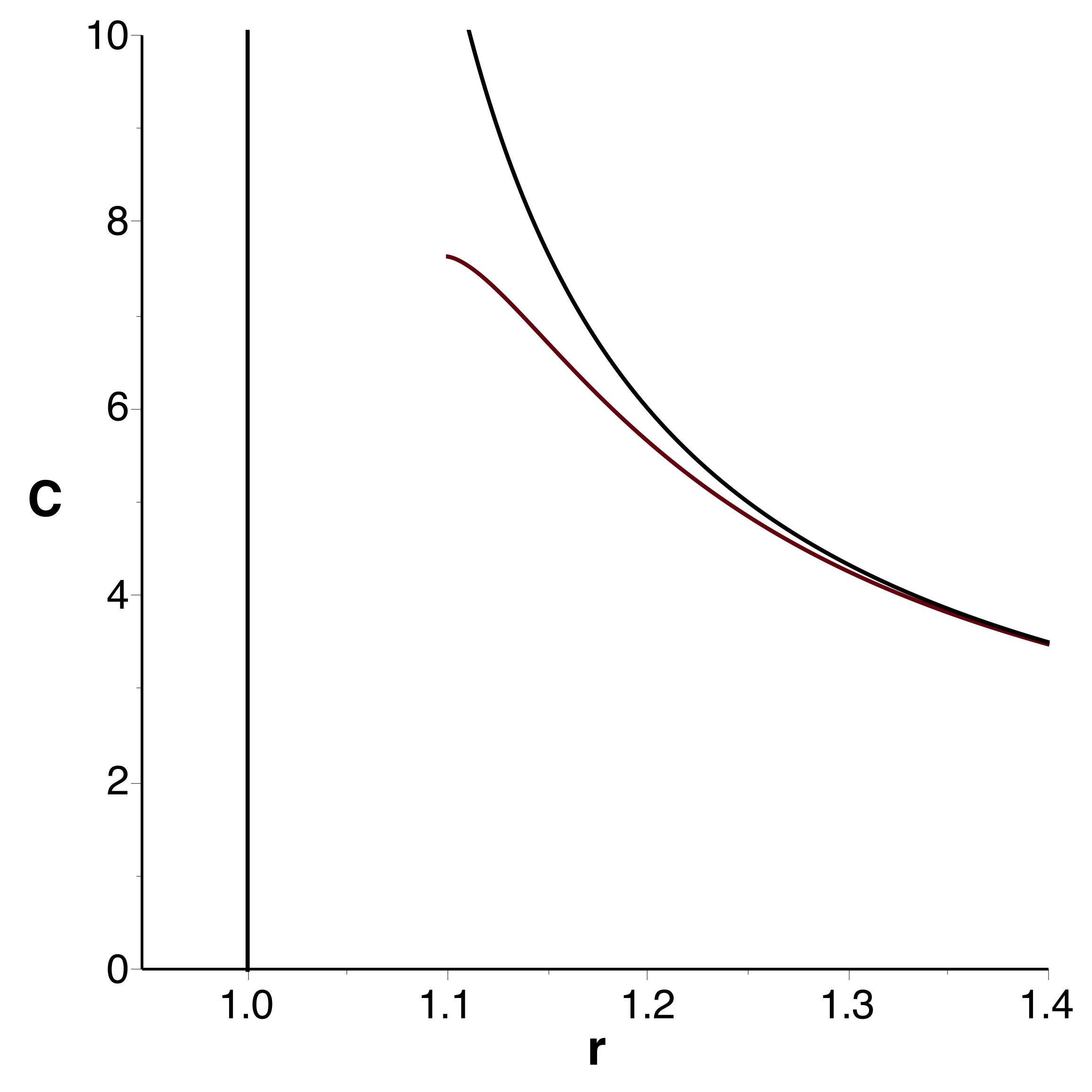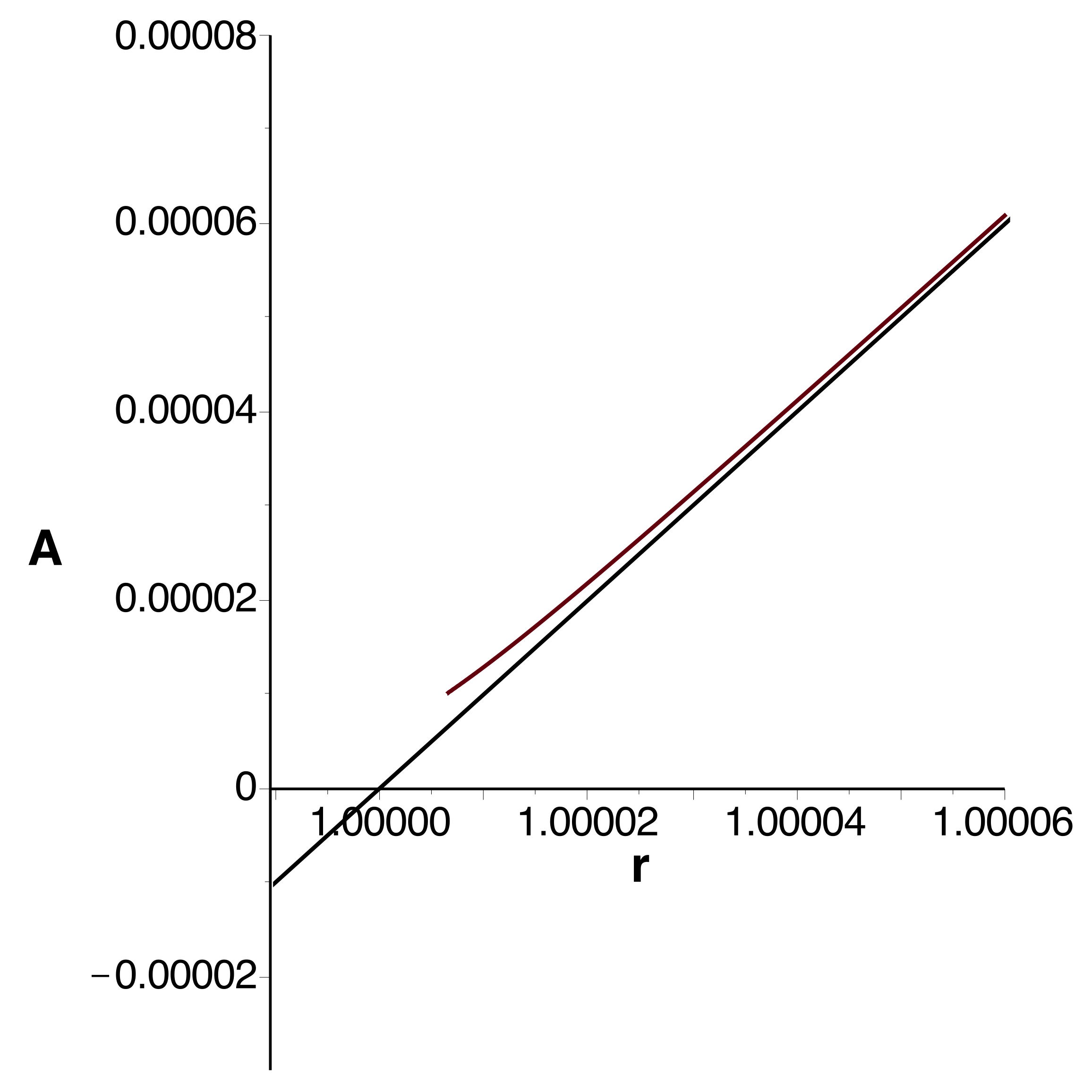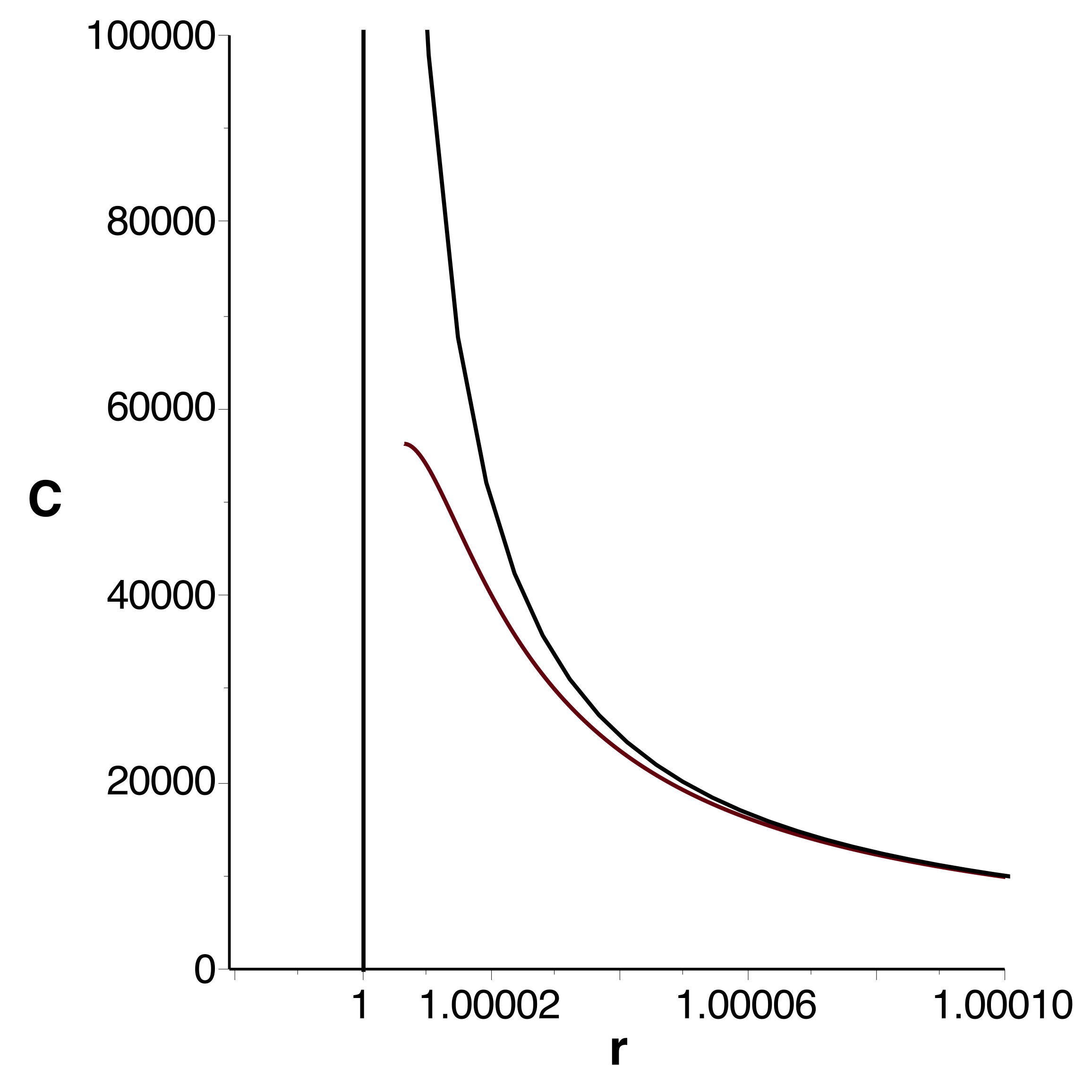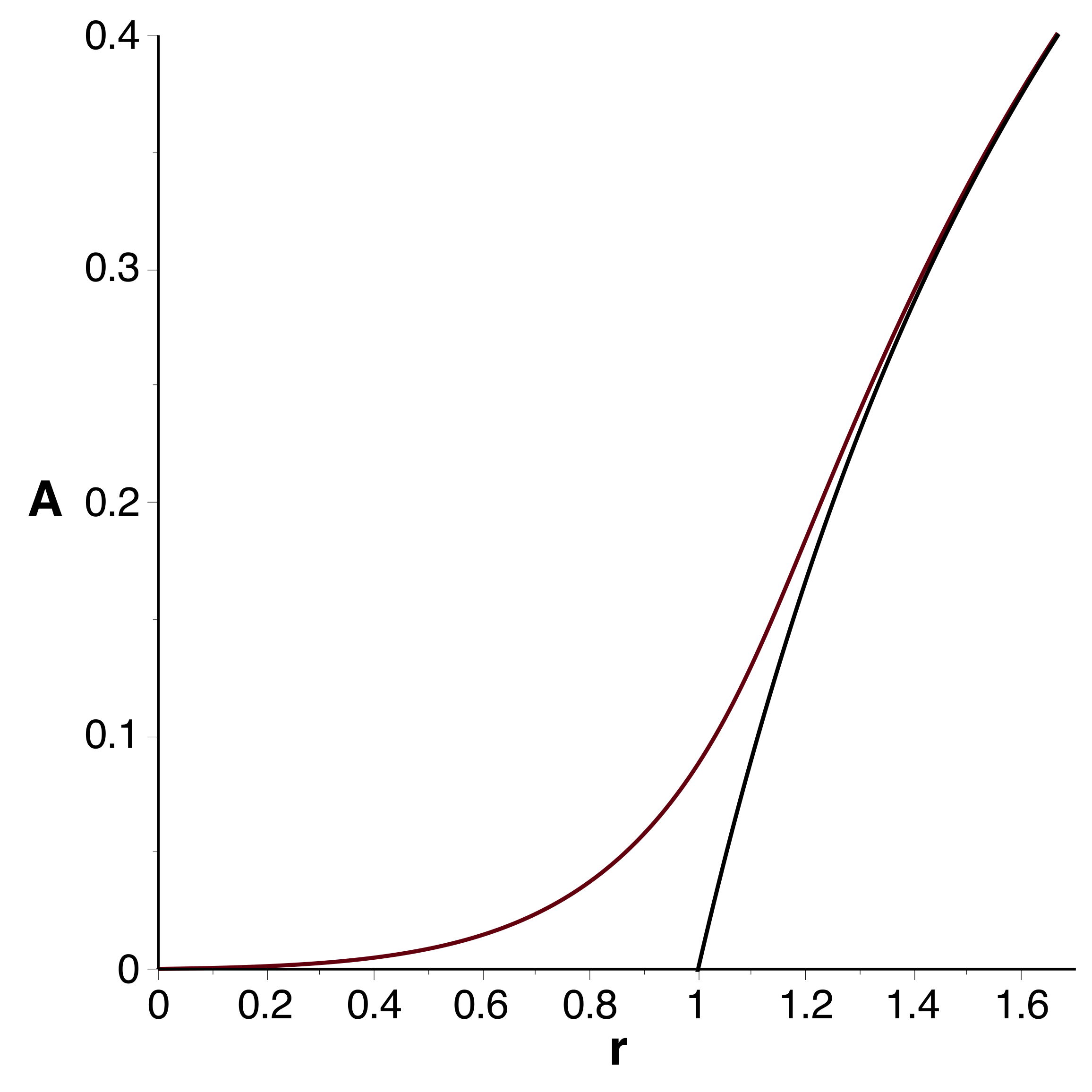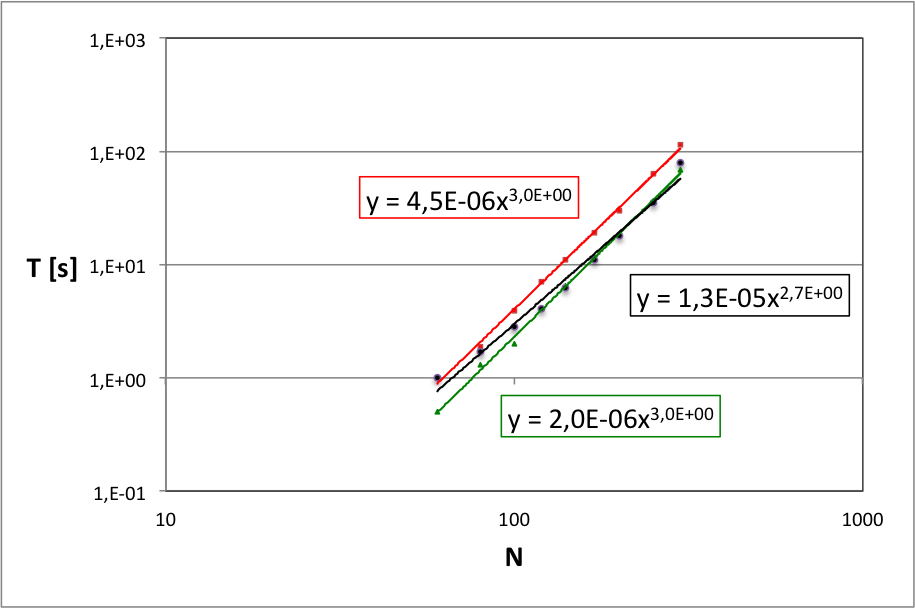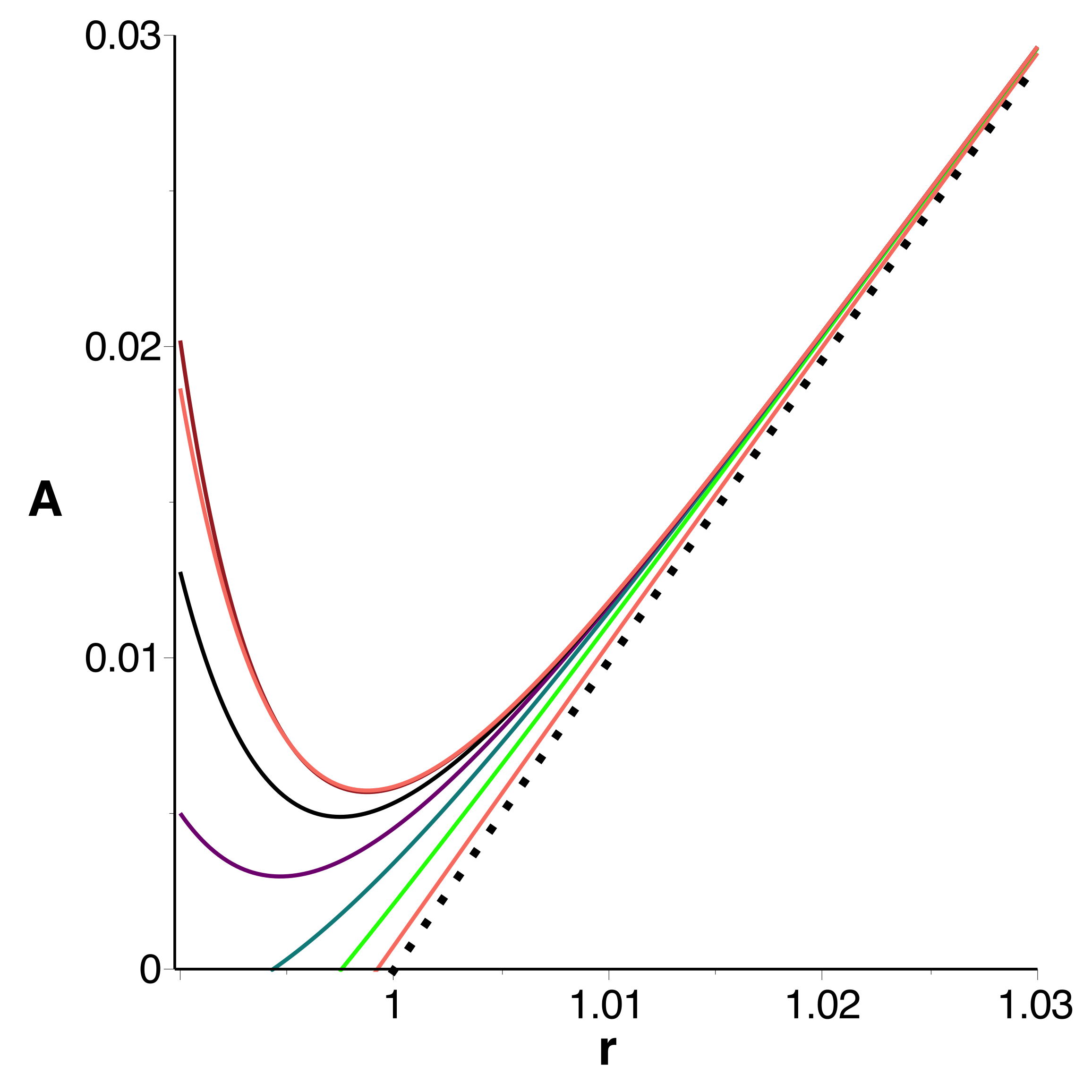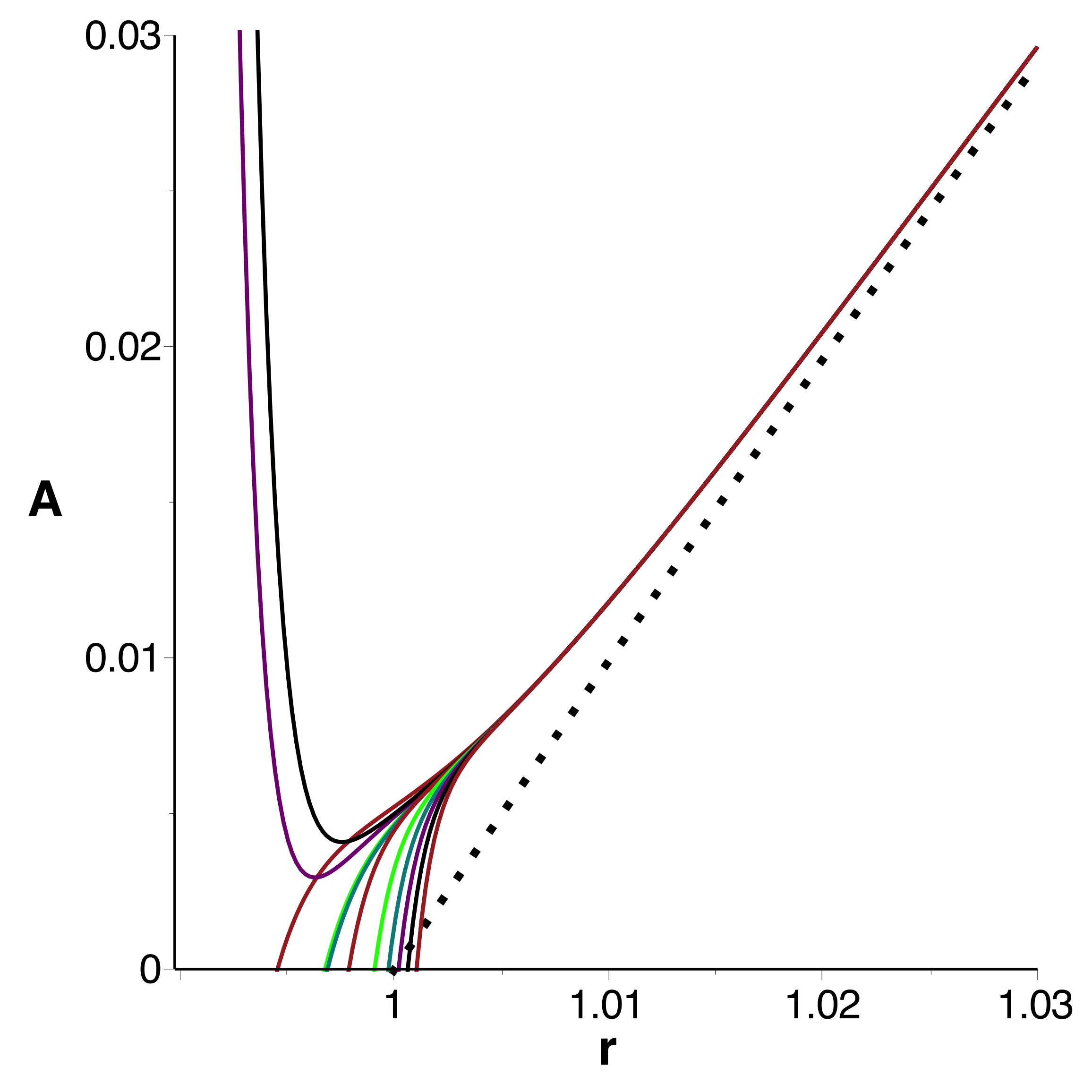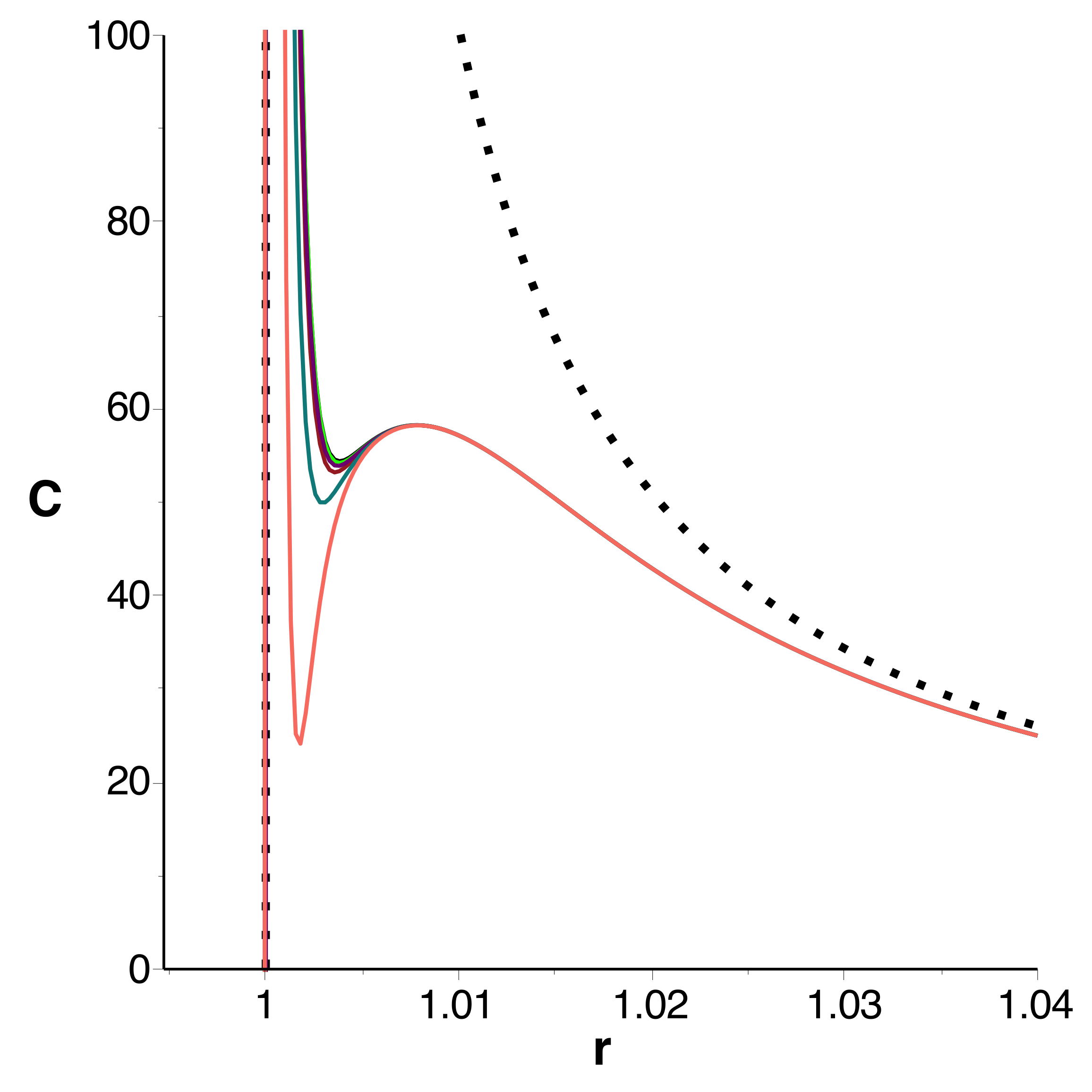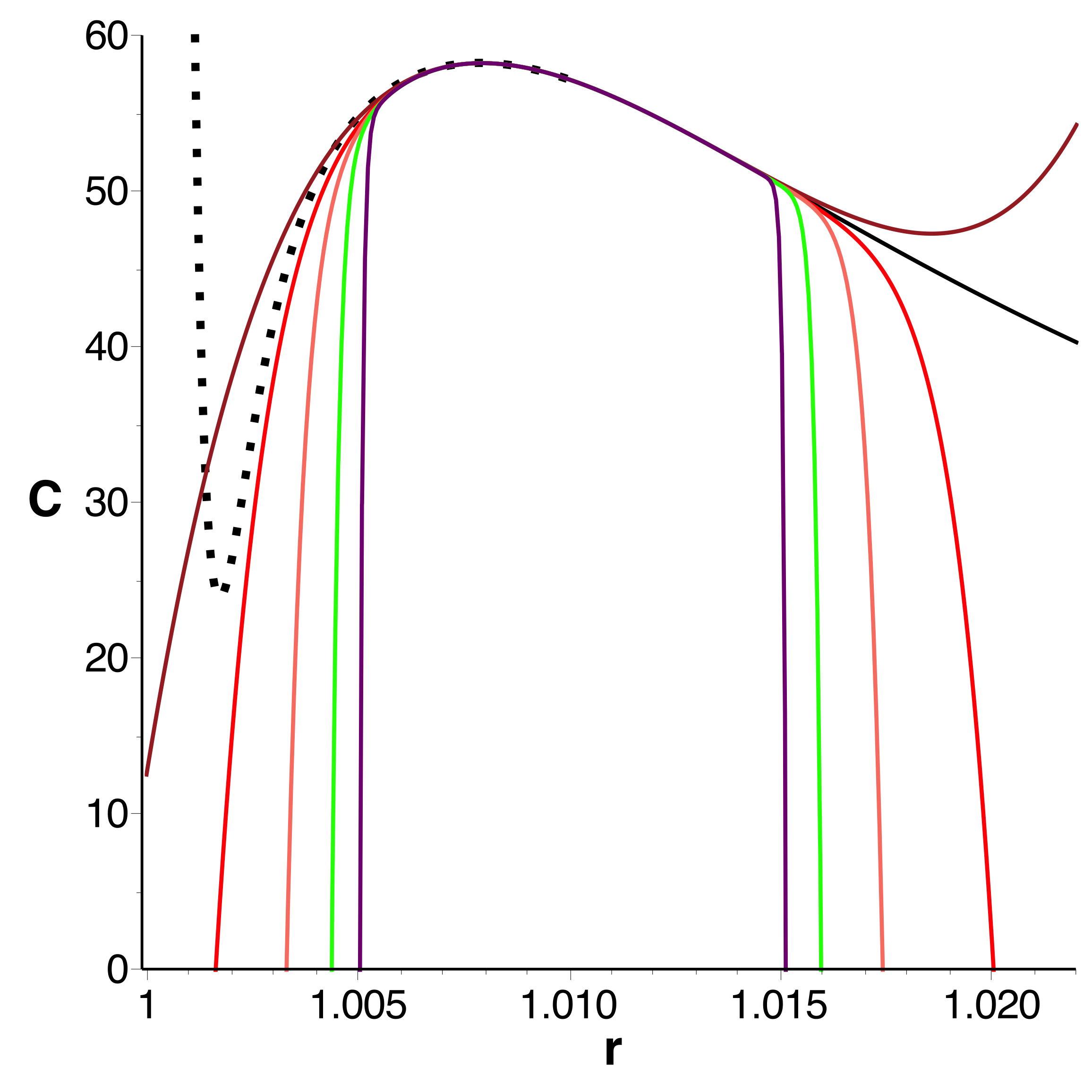• Les courbes obtenues se raccordent bien et confirment l'extremum (en le précisant très peu) ; celles tracées à l'ordre $80$ montrent bien la limitation de l'intervalle de validité. • Pour  $r_0=1,007$  le raccordement d'un second développement impose  $a_0=0,00946$  et  $c_0=57,99$ .  On obtient ainsi  $a_1=77,79$  et  $c_1=405,8$  ...  puis ainsi de suite. 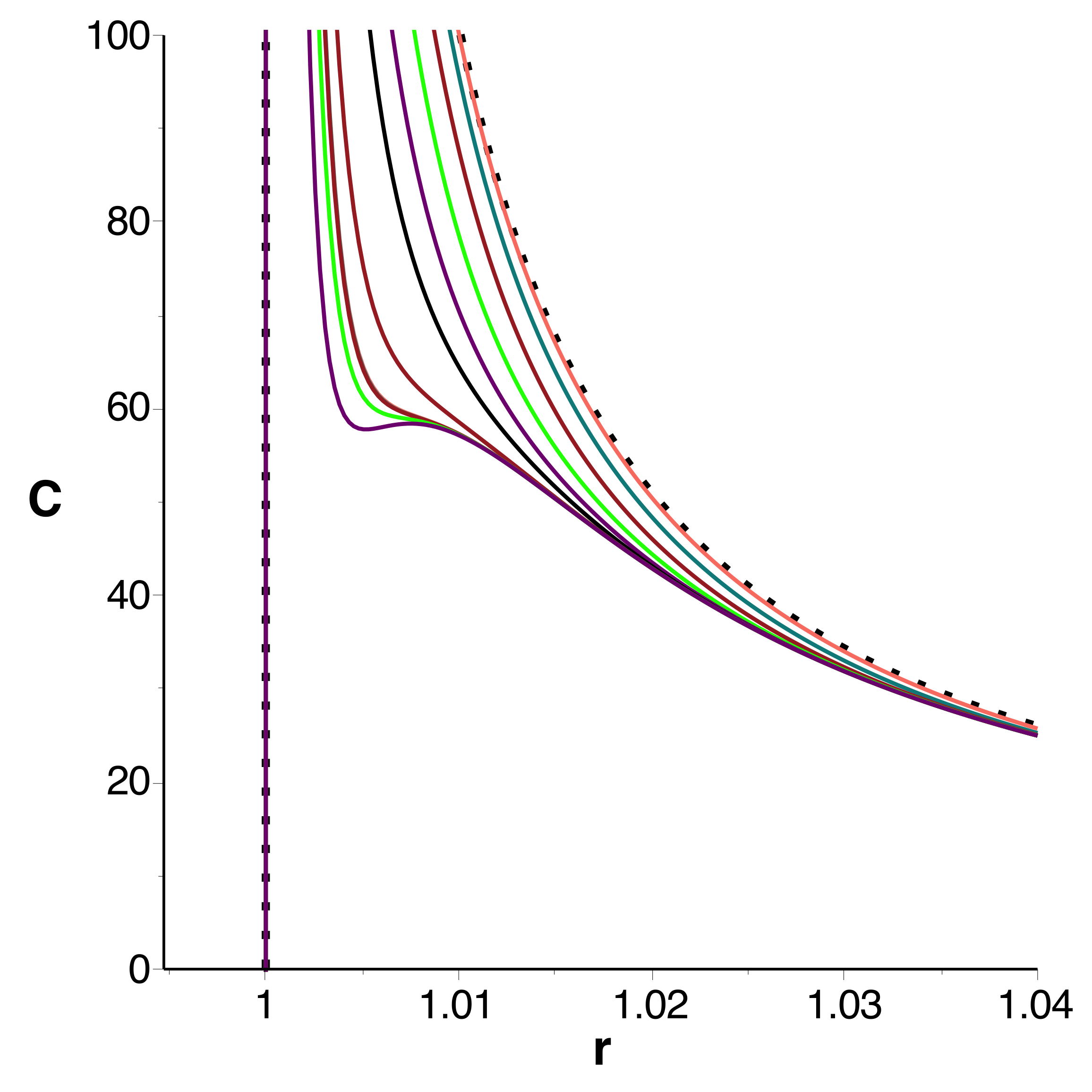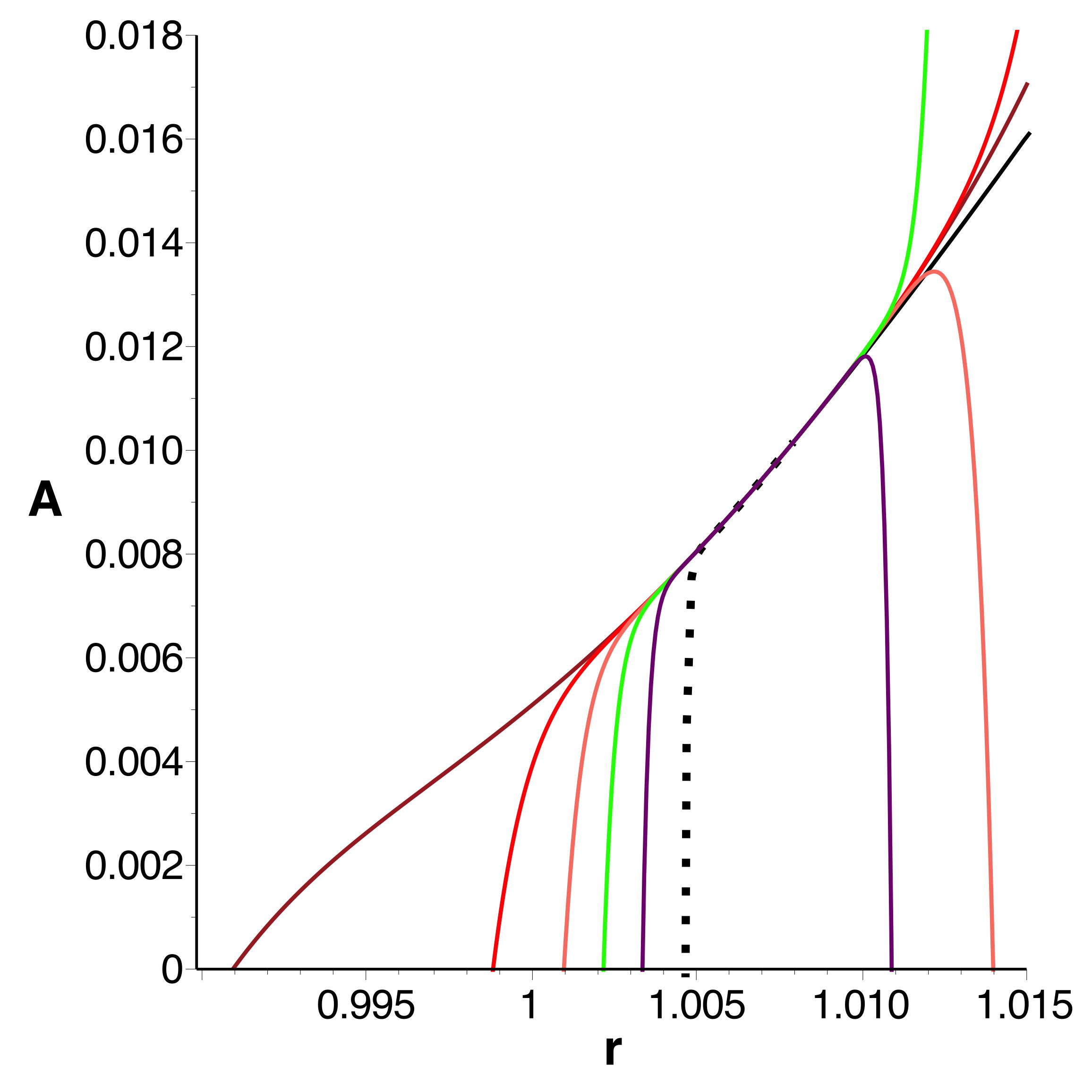◊ remarque : l'équation sur $A'$ a plusieurs solutions et il faut choisir celle qui permet le raccordement des courbes ; le choix n'est pas le même pour les parties croissante et décroissante de $C$ (le maximum est un point singulier), donc il faut effectuer un raccordement à l'extremum. 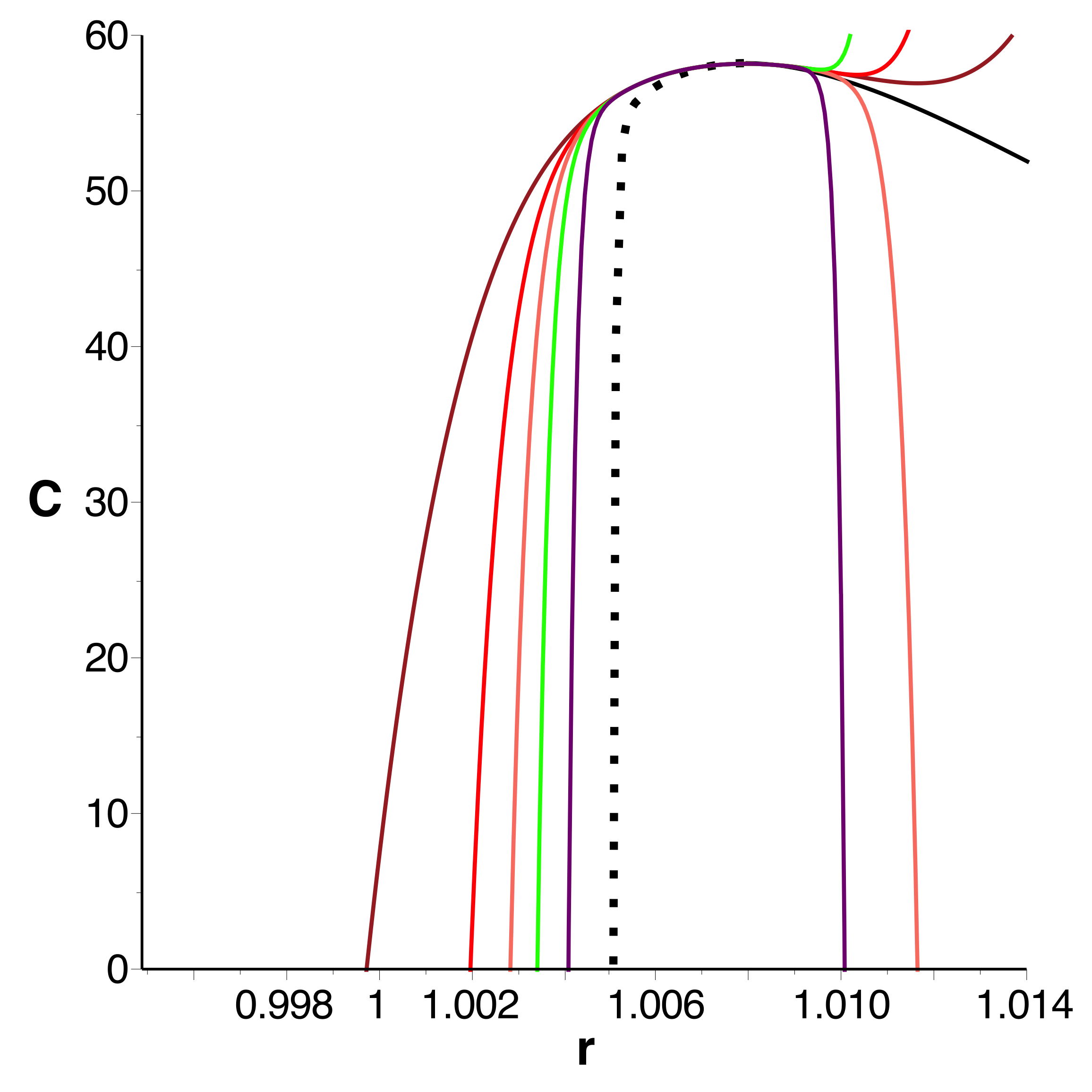• Ceci permet en principe d'obtenir de proche en proche l'ensemble des courbes, avec une succession de développements raccordés de façon analogue, mais seulement à condition que la méthode ne soit pas limitée par la précision numérique.

4.a.	• Le report dans les équations montre que l'hypothèse  $C=1$  impose  $A=Cste$  ;  rien a priori n'exclut les solutions de cette forme.
4.b.	• La quantité $A$ se comporte un peu qualitativement comme un potentiel de gravitation, donc doit être continue à dérivées continues. Le report dans les équations montre qu'il en est donc de même pour $C$ (de façon générale, les $g_{μν}$ sont des “potentiels”).
4.c.	• Puisque le passage par  $C=1$  doit se faire avec dérivées continues, on ne peut raccorder à ce niveau une solution avec celle correspondant à  $C=1$  que si le raccordement se fait avec dérivée nulle (et de même pour  $A=Cste$)  ;  les calculs montrent que ce n'est pas le cas. ◊ remarque : ce point de croisement semble être lui aussi un point singulier ; il faut y raccorder deux développements de part et d'autre.