RG X - PROPRIÉTÉS du DIAGRAMME de KRUSKAL-SZEKERES



Trajectoires radiales de photons

• Les trajectoires radiales des photons correspondent à  dv2− du2=0 {dv}^2-{du}^2=0  (pour  ds2=0 {ds}^2=0 ).  Dans le diagramme de Kruskal-Szekeres, ce sont des droites parallèles aux diagonales.

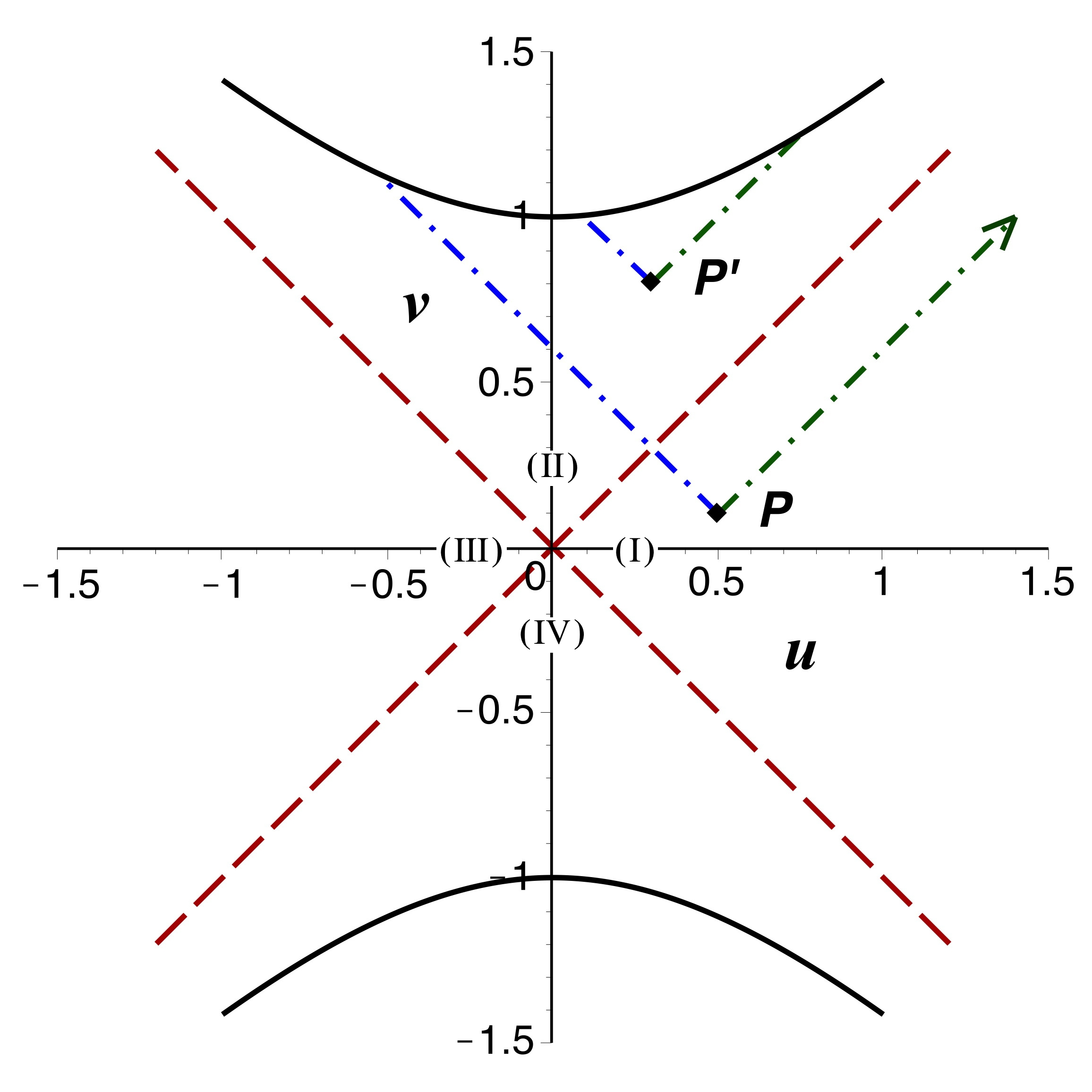
Selon l'interprétation “classique” (ci-dessous à gauche), partant d'un point P P “extérieur” dans la région (I) (I) ,  un photon sortant rejoint l'infini dans le sens des t t croissants, ce qui est selon les v v croissants. Un photon entrant rejoint l'horizon dans le sens des t t croissants, ce qui est selon les v v croissants, puis semble pouvoir rejoindre  r=0 r=0  sans discontinuité.

PropKruskal_Im/Kruskal_T1_zones.jpg
 PropKruskal_Im/Kruskal_T2_zones.jpg

Partant d'un point P’ P “intérieur” avec  u>0 u>0  dans la région (II) (II) , un photon entrant semble de même pouvoir rejoindre  r=0 r=0  dans le sens des v v croissants, ce qui correspond à t t décroissant comme le prévoit le calcul avec les notations “classiques” de Schwarzschild.

Par contre un photon “sortant” évolue en principe selon t t croissant, donc u u croissant, ce qui correspond aussi à v v croissant ; il rejoint ainsi de même  r=0 r=0  donc ne peut pas sortir.

Ainsi cette région est inobservable depuis l'extérieur ; en particulier, il est impossible de synchroniser les horloges “intérieures” avec celles de l'extérieur.

• Cette description “classique” fait toutefois apparaître un problème d'interprétation si on suppose que la moitié gauche du diagrame n'est qu'un duplicata du côté droit (ci-avant à droite).

Si certains des photons entrants précédents atteignent la singularité centrale avec  u<0 u<0 , ils doivent alors être considérés comme terminant leur trajet dans la partie  u>0 u>0  de la région (IV) (IV) avec un sens inversé du temps v v , rejoignant ainsi la singularité dans le passé (les repérages de Lemaître ont montré que l'interprétation est parfois délicate).

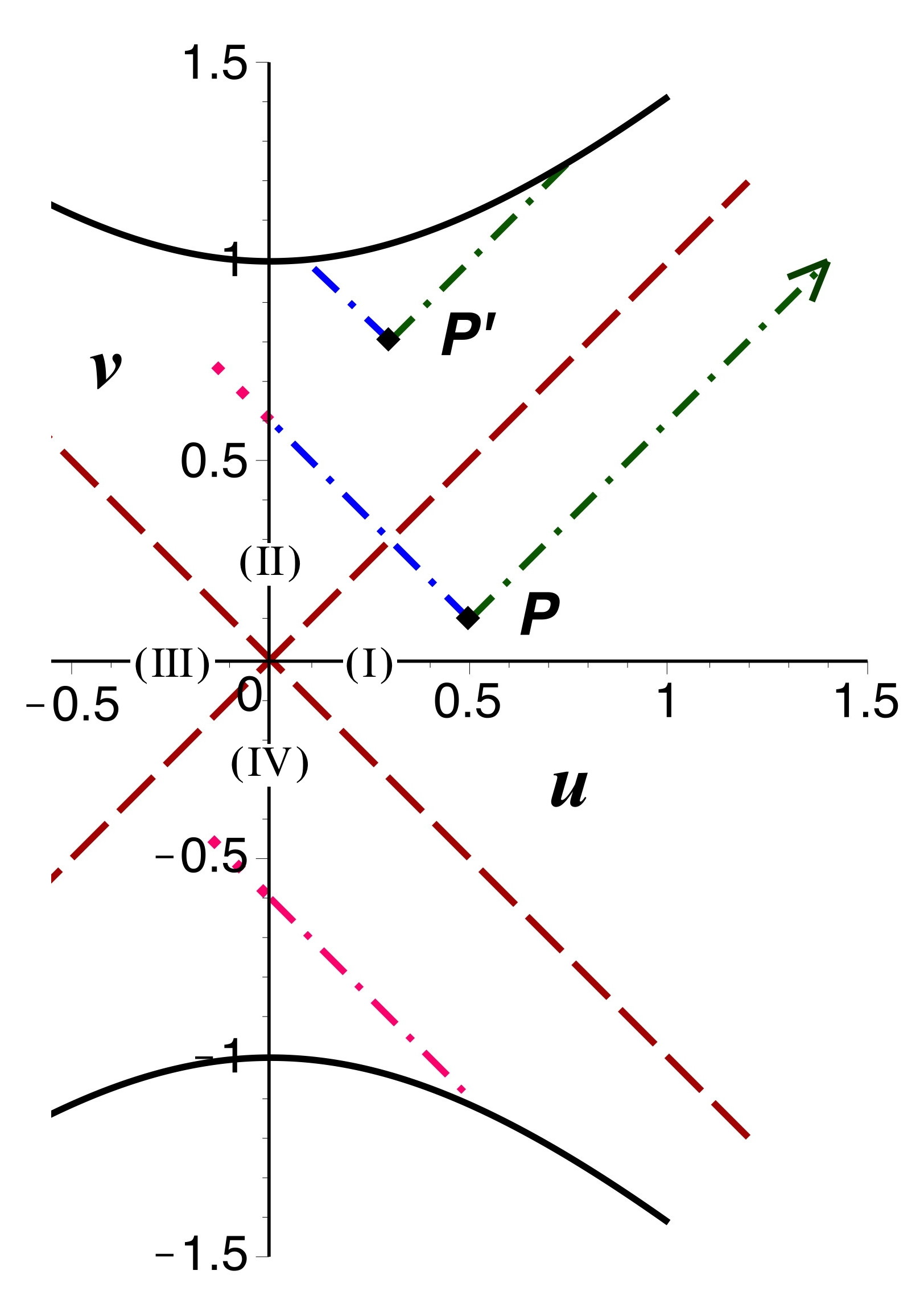
• Selon l'interprétation “classique”, partant d'un point P P “extérieur” dans la région ( III ) (III) ou d'un point P’ P\text{’} “intérieur” avec  u<0 u<0  dans la région ( IV ) (IV) , des photons peuvent être émis dans le sens des v v croissants dans un “monde parallèle”, presque sans interaction avec le notre. Les photons sortant depuis P’ P\text{’} semblent toutefois pouvoir aboutir dans la région (I) (I) .

PropKruskal_Im/Kruskal_T3_zones.jpg

Au contraire, si on adopte l'hypothèse selon laquelle la moitié gauche du diagramme n'est qu'un duplicata, cela décrit en réalité la même situation déjà représentée précédemment à gauche. Les seuls de ces photons rejoignant le côté droit sont ceux aboutissant sur la singularité passée à droite de la région (IV) (IV) selon le sens décroissant de v v .

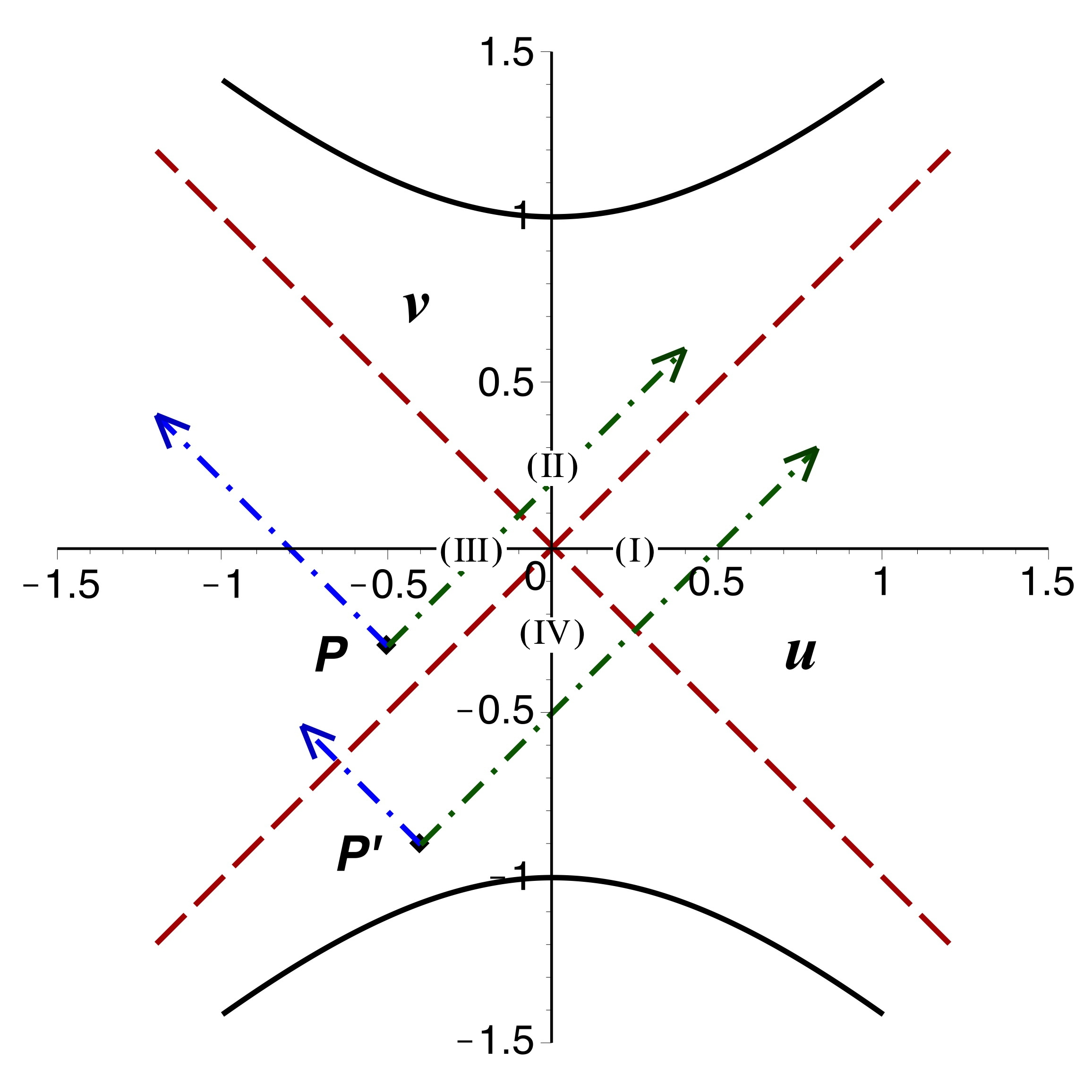
• On peut enfin considérer des photons émis d'un point P P “intérieur” avec  u>0 u>0  dans la région (IV) (IV) . L'interprétation “classique” comporte, ici sans ambigüité, des photons sortant dans la région (I) (I) .

PropKruskal_Im/Kruskal_T4_zones.jpg
 PropKruskal_Im/Kruskal_T5_zones.jpg

Mais en interprétant le côté gauche comme un duplicata, les photons entrants correspondants rejoignent aussi la région (I) (I) , en ressortant par la région (II) (II) avec un sens inversé du temps v v .

En outre, on constate la présence de doubles intersections comme avec les représentations de Schwarzschild et de Lemaître.

📖 exercice n° I.


Trajectoires radiales de particules massives

• On considère l'exemple d'une particule initialement immobile en un point extérieur, puis tombant en mouvement radial jusqu'à l'intérieur.

Dans un diagramme de Kruskal-Szekeres, un point immobile suit une branche d'hyperbole d'équation  r=Cste r=Cste .  La trajectoire d'une particule massive initialement immobile commence donc tangentiellement à une telle hyperbole.

Toutes ces particules franchissent  r=rs r=r_s   avec la vitesse de la lumière par rapport au référentiel statique. Par contre ici, leur trajectoire n'y est pas parallèle à la diagonale décroissante (comme les photons entrants) : leur vitesse est inférieure à c c par rapport au repère de Kruskal-Szekeres.

PropKruskal_Im/Kruskal_Tm1.jpg

◊ remarque : pour tracer les trajectoires des particules massives, l'intégration numérique avec ( u,v ) (u,v) est possible mais le plus simple est d'appliquer le changement de repérage aux expressions obtenues en intégrant avec les notations “classiques” de Schwarzschild.

• Lors d'une telle chute, on peut imaginer d'éventuels photons émis par la particule vers un expérimentateur observant depuis son point de départ immobile (qui décrit l'hyperbole correspondant à r0 r_0 ). Les photons émis avant l'horizon atteignent l'observateur à des dates tendant de plus en plus vers l'infini ; les photons éventuellement émis après l'horizon sont inobservables (d'où le nom qui est donné à cette limite).

Par contre, bien que la durée de chute de toute particule massive semble infinie pour tout observateur extérieur, la durée propre de chute est finie.

◊ remarque : non seulement les photons émis par la particule en chute sont reçus par l'observateur à des dates  t→∞ t→∞ ,  mais de plus ces photons sont déjà préalablement émis par la particule à des dates  t→∞ t→∞ .

◊ remarque : pour décrire une étoile qui s'effondre vers une singularité centrale  ( r=0 r = 0 )  lors de la formation éventuelle d'un trou noir, ces hypothèses doivent être adaptées car le champ intérieur à l'astre est différent du champ extérieur.

📖 exercices n° II et III.


Croisements anormaux au-delà de l'horizon

Absence d'anomalie pour l'interprétation "classique"

• Par construction, les trajectoires dans le diagramme de Kruskal-Szekeres étant forcément dans les cônes de lumière, elles sont parcourues selon v v croissant.

D'après ce qui précède, pour les particules en chute libre verticale, les trajectoires qui sortent d'au-delà de l'horizon proviennent de la région (IV) (IV) , celles qui y tombent vont dans la région (II) (II) . Puisque ces deux zones sont disjointes, aucun croisement n'est possible au-delà de l'horizon.

Cela peut sembler résoudre le problème constaté en notations “classiques” de Schwarzschild ; on peut en outre penser que cela est lié à la forme des trajectoires, effet de la disparition des divergences au niveau de l'horizon. L'étude un peu plus précise qui suit montre que ce n'est pas le cas.

Existence d'anomalies pour l'interprétation avec “duplicata”

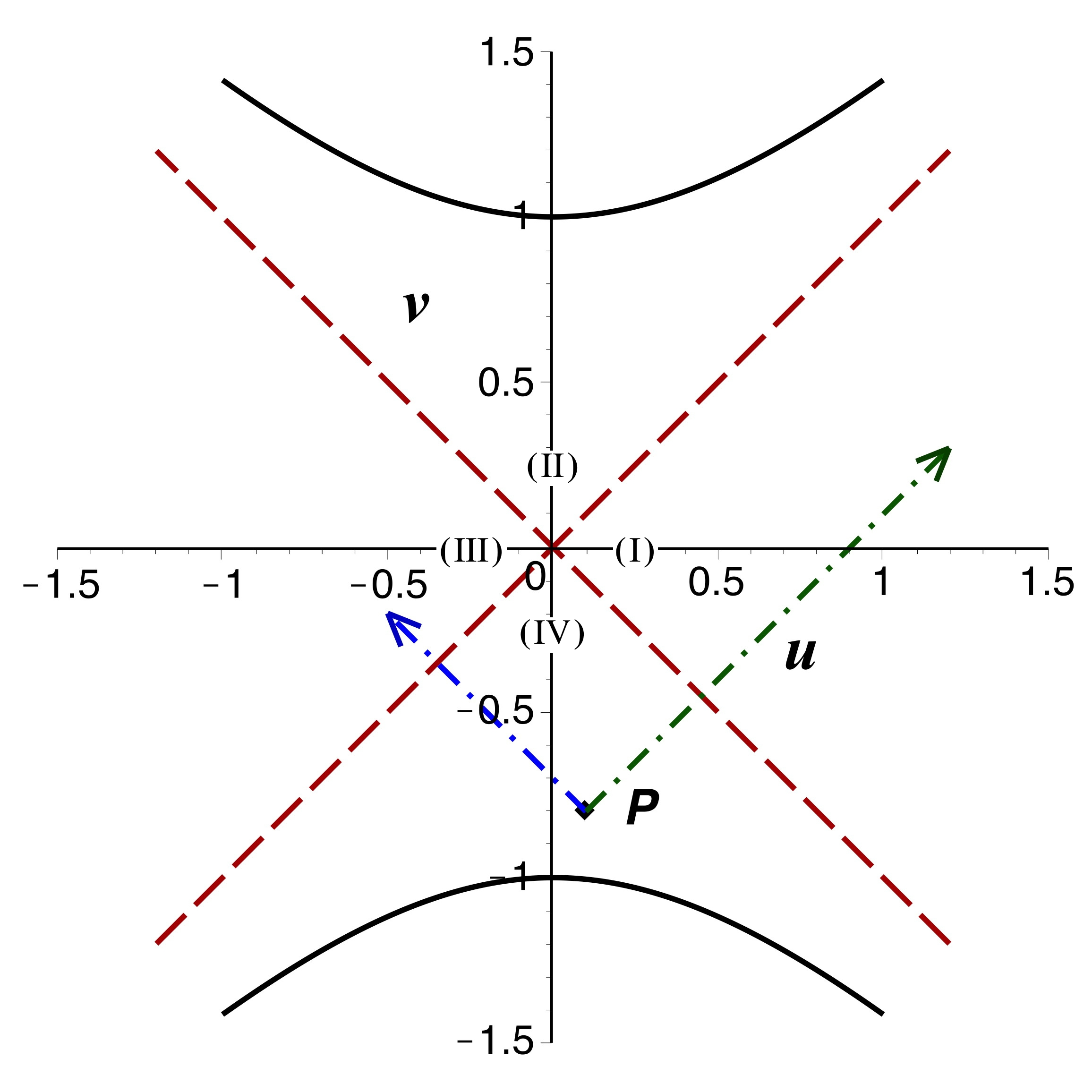
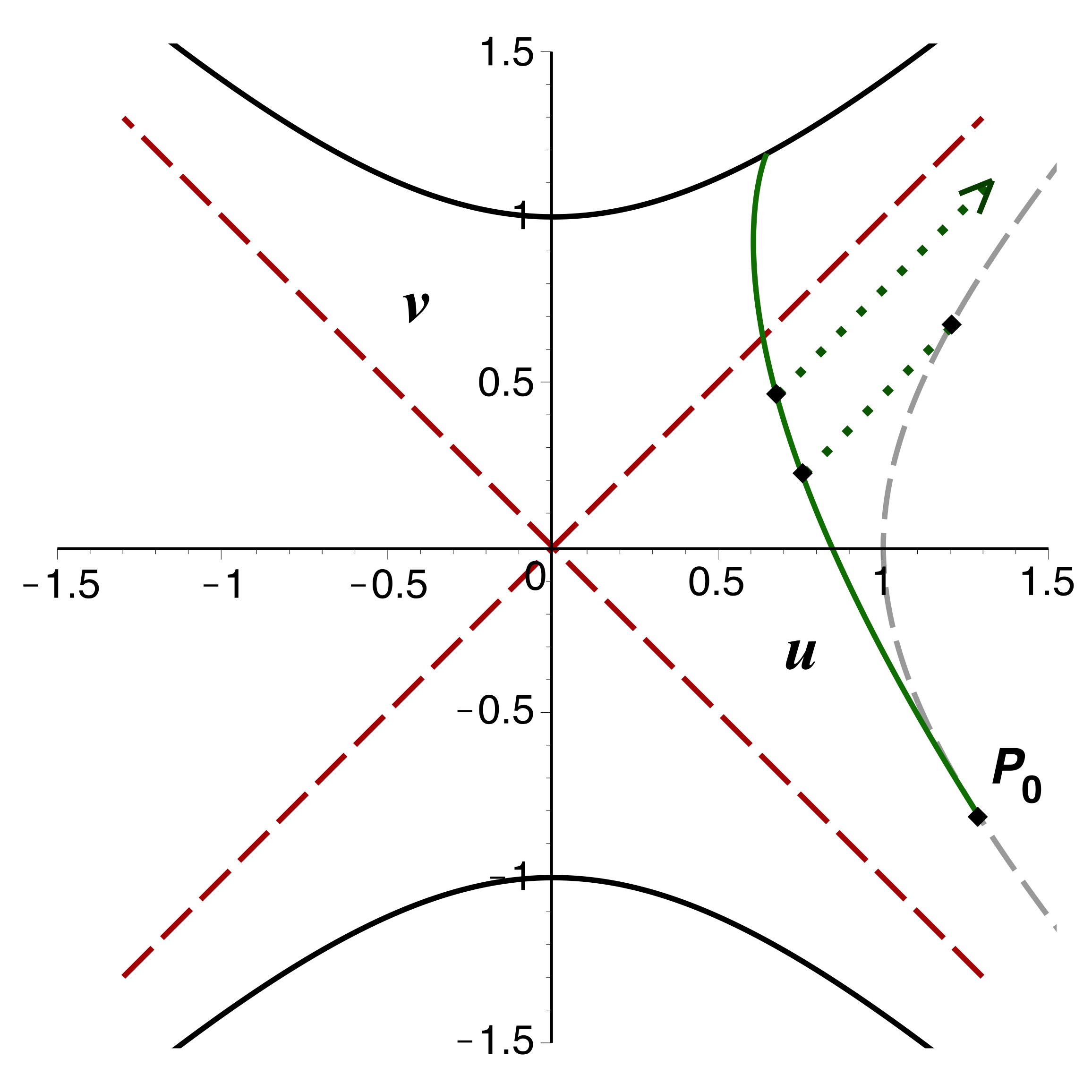
• Le cas le plus simple, déjà évoqué précédemment, est celui des photons. On peut considérer (ci-après à gauche) un photon entrant dans la région (II) (II) et finissant son trajet à “contretemps” sur la singularité dans la région (IV) (IV) , qui croise deux fois un photon sortant de la région (IV) (IV) mais provenant à contretemps de la singularité dans la région (II) (II) . Un intérêt particulier de cet exemple est que l'ordre de ces deux croisements n'est pas le même pour les deux photons.

PropKruskal_Im/Kruskal_T6_zones.jpg
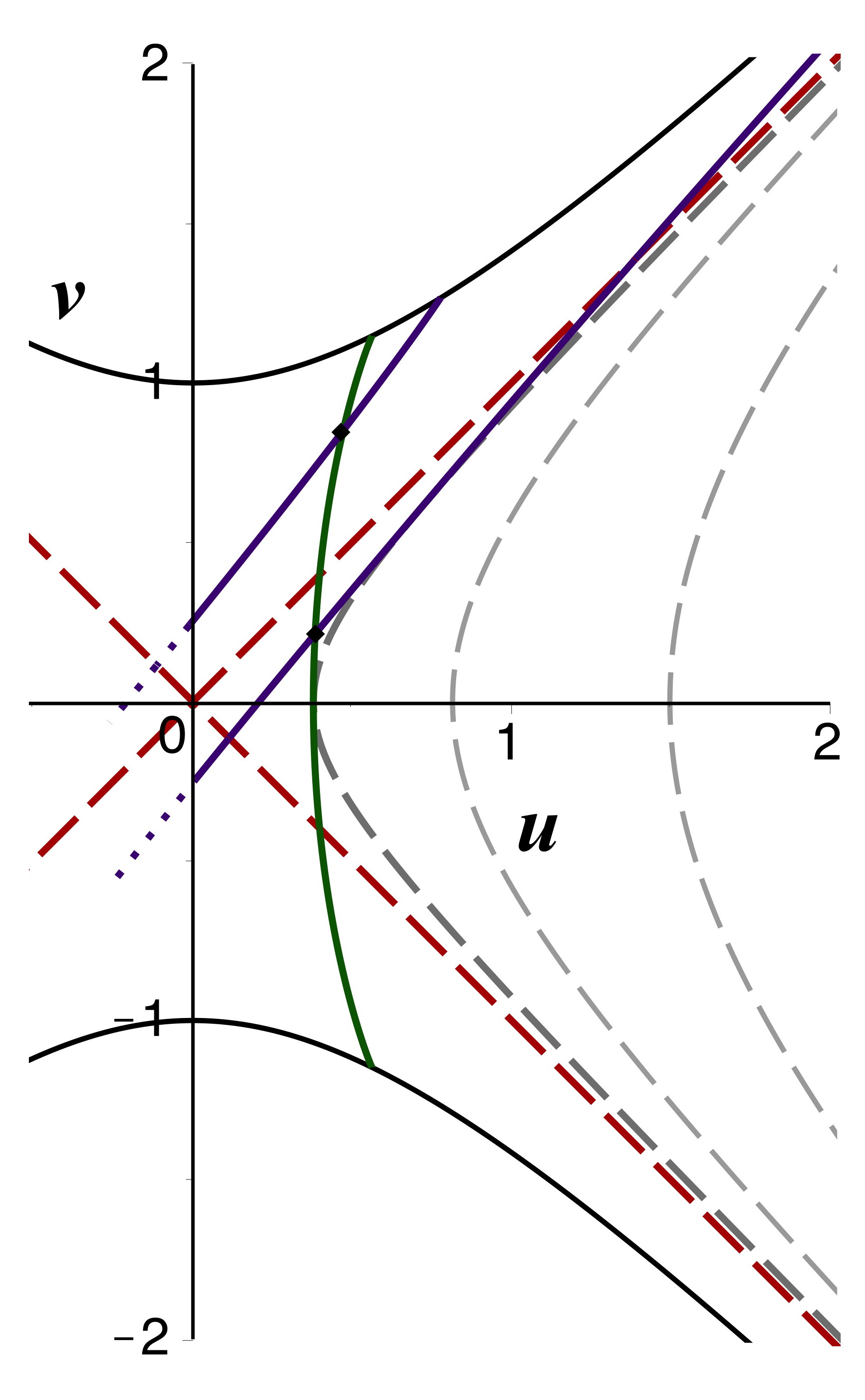
 PropKruskal_Im/K_r0_mod.jpg

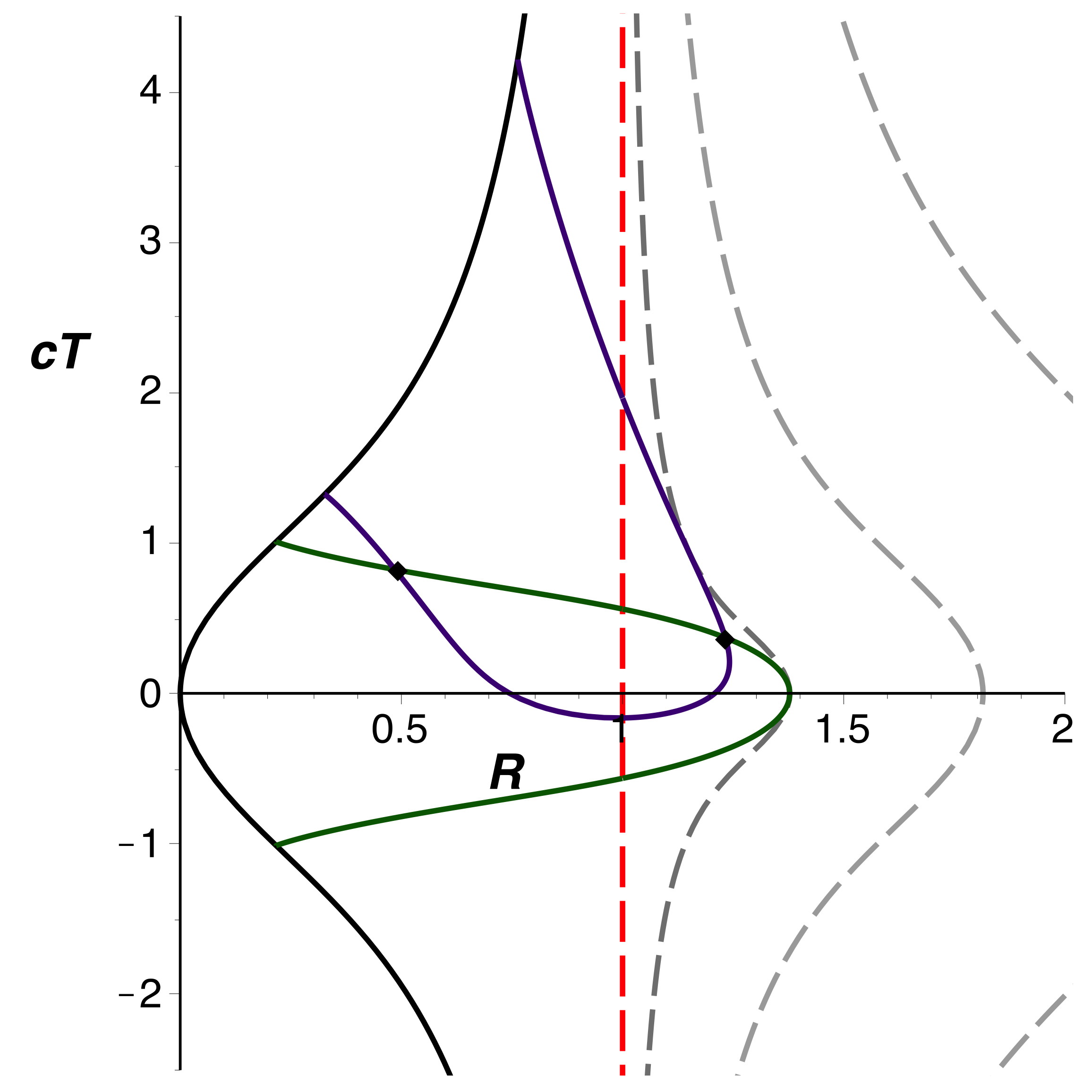
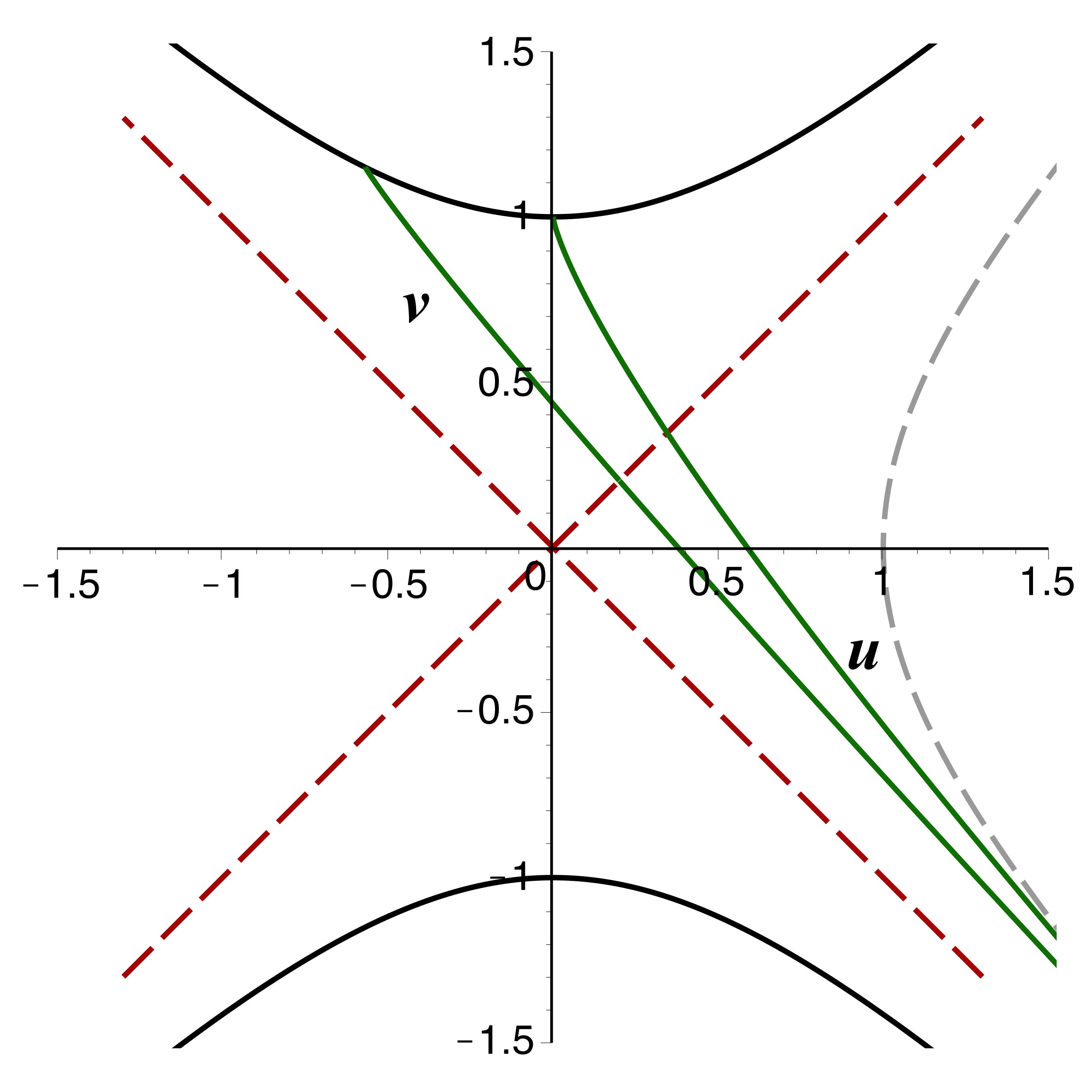
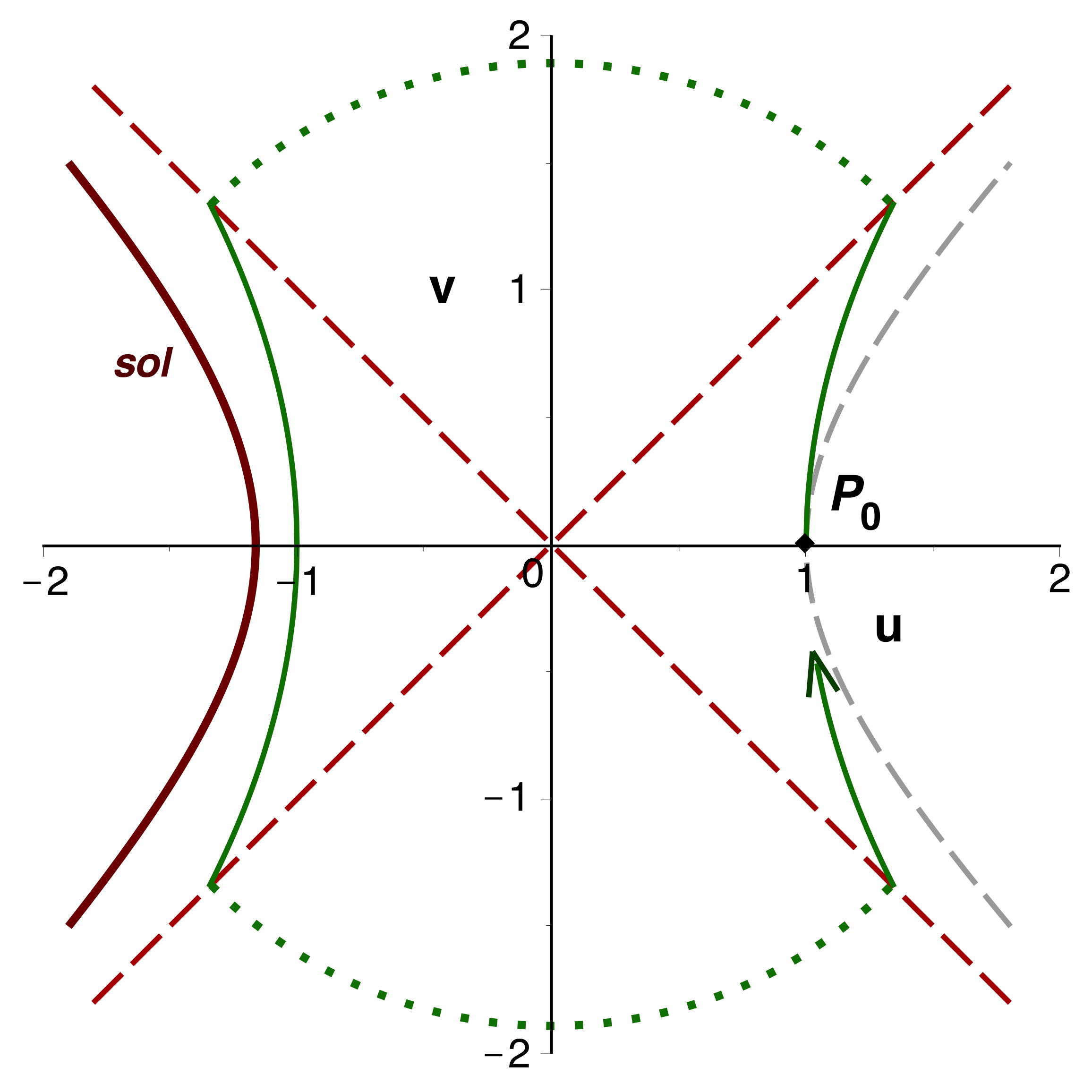
• Le tracé est possible aussi pour les particules massives (ci-dessus à droite) : les coordonnées  ( u,v ) (u,v)  se déduisent de  ( ct ( r ) ,r ) (c\,t(r), r) .

Quelques courbes  r=Cste r=Cste  sont représentées (tirets gris), ainsi qu'une trajectoire (en vert) avec maximum en  r0= 1,05 rs r_0=1\text{,}05 \:r_s  pour  t=0 t=0 .

Est également représentée (en violet) une trajectoire analogue avec maximum en r0 r_0 mais retardée afin que son départ, au lieu d'être du côté  u>0 u>0  de la région (IV) (IV) , soit à “contretemps” dans la région (II) (II) .  Le retard est en outre choisi suffisamment grand pour que ce début fasse un second croisement anormal avec la fin de la trajectoire non retardée.

Diagramme de Kruskal-Szekeres anamorphosé

• Pour les particules en chute libre verticale, l'observation des trajectoires passant par un sommet r0 r_0 montre que quand  r0 → rs r_0→r_s  le tracé en notations de Schwarzschild tend vers un aller-retour selon le segment  r∈ [ 0 ;rs ] r∈[0 \,; r_s]  avec  t=0 t=0 .

Au contraire, dans le diagramme de Kruskal-Szekeres, le tracé tend vers la succession de deux segments  v∈ [ −rs ;0 ] v∈[-r_s \,; 0]  et  v∈ [ 0; rs ] v∈[0 \,; r_s]  avec  u=0 u=0  (et  t=0 t=0 ).

• Pour mieux visualiser les effets, on peut procéder à une anamorphose dans le diagramme de Kruskal-Szekeres, en multipliant l'angle par deux par rapport au point  ( u=0 ; v=0 ) (u=0\,;v=0) .  Ceci revient à “refermer” selon l'aller-retour évoqué en notations de Schwarzschild.

◊ remarque : on passe par  ρ= u2+ v2 ρ=\sqrt{u^2+v^2}   et   ψ=arctan (vu) \displaystyle ψ=\arctan\left(\frac{v}{u}\right)  puis on utilise les coordonnées  R=ρ cos ( 2ψ ) R=ρ\;\cos(2\,ψ)   et   cT =ρ sin ( 2ψ ) c\,T=ρ\;\sin(2\,ψ) .

◊ remarque : en découpant selon  u=0 u=0  et en recollant bord à bord les deux moitiés de cet axe, on obtient un cône ; l'anamorphose proposée donne ce qu'on observe depuis un point sur l'axe du cône au dessus du sommet.

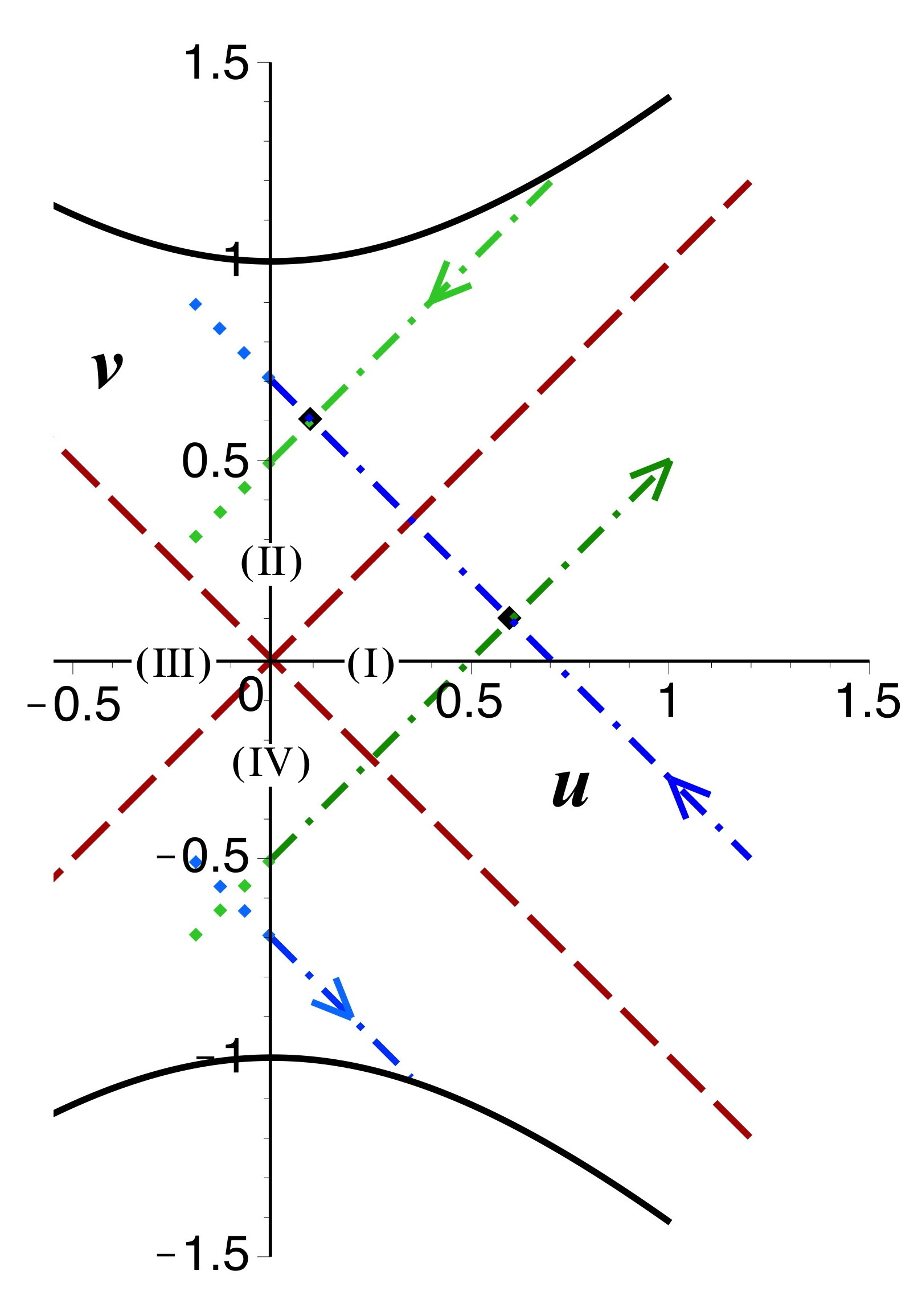
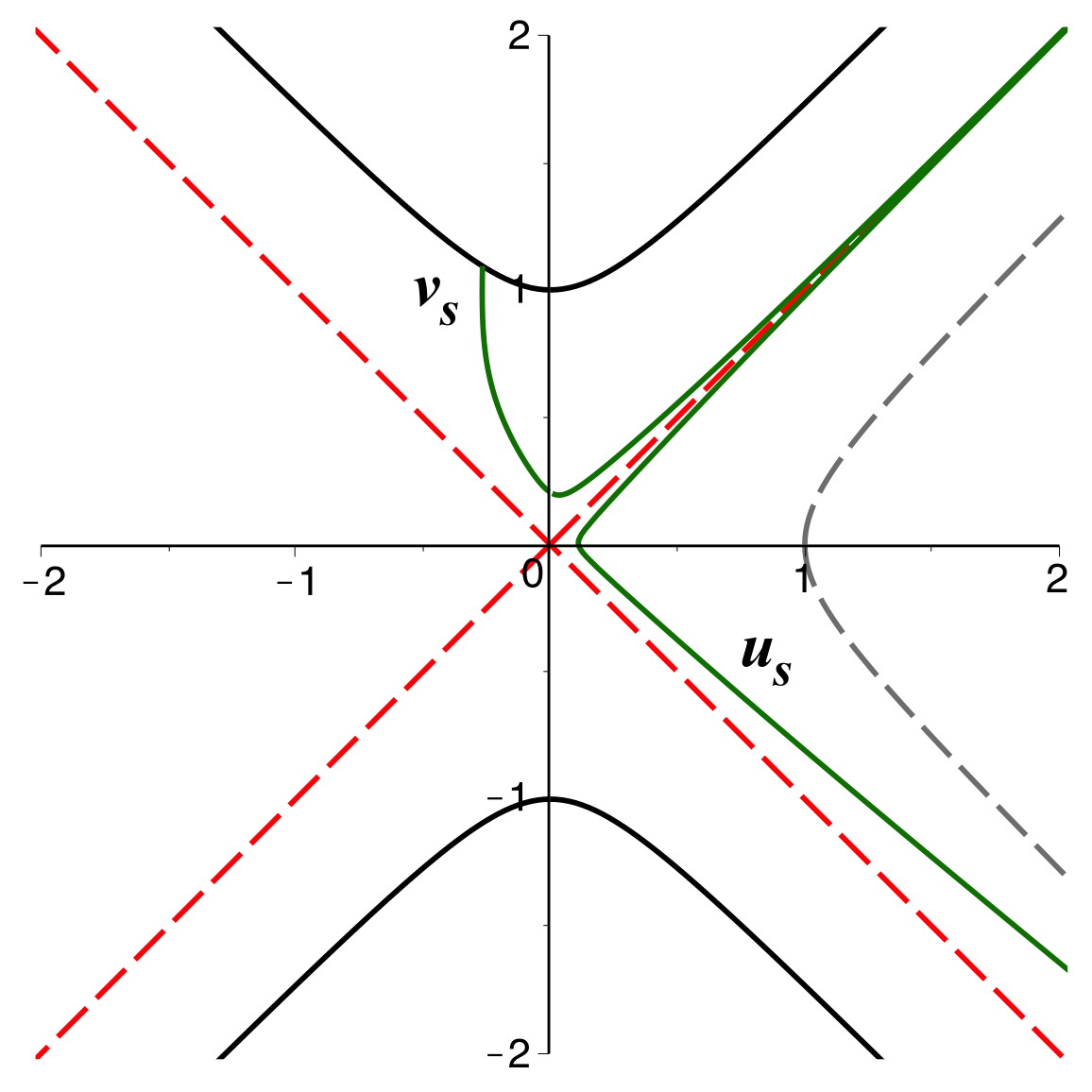
• Le cas le plus simple est celui des photons, dont les trajectoires rectilignes sont transformées en courbes d'allure parabolique (ci-après à gauche).

On vérifie que malgré l'absence de divergence au niveau de l'horizon, certaines trajectoires de photons entrants et sortants se coupent deux fois (la variable T T change de sens de variation) dans un ordre contradictoire.

On retrouve ainsi une description à la fois anormale, mais tout à fait en accord avec les effets constatés en notations de Schwarzschild ou de Lemaître.

PropKruskal_Im/K_anam.jpg
 PropKruskal_Im/K_anam_r0.jpg

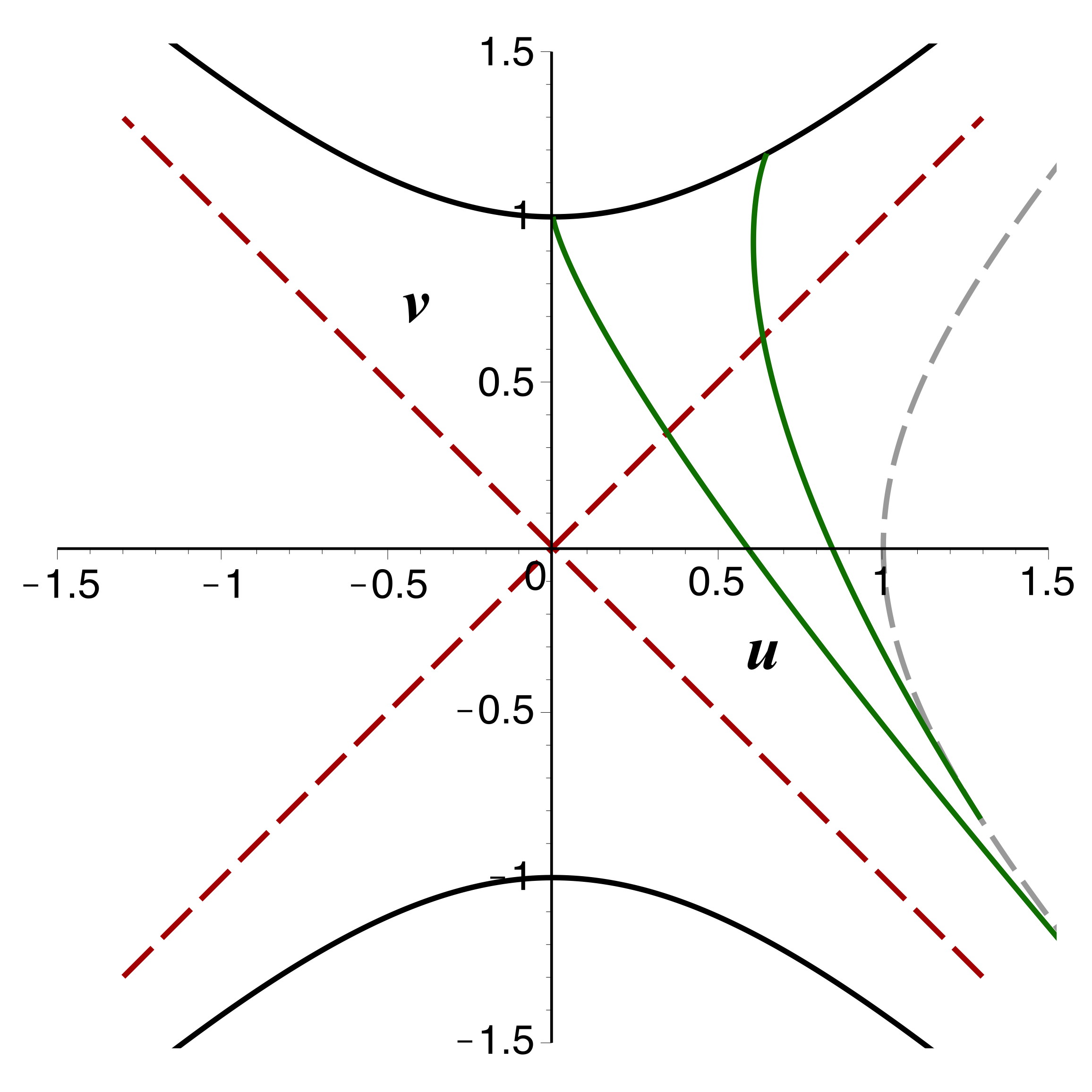
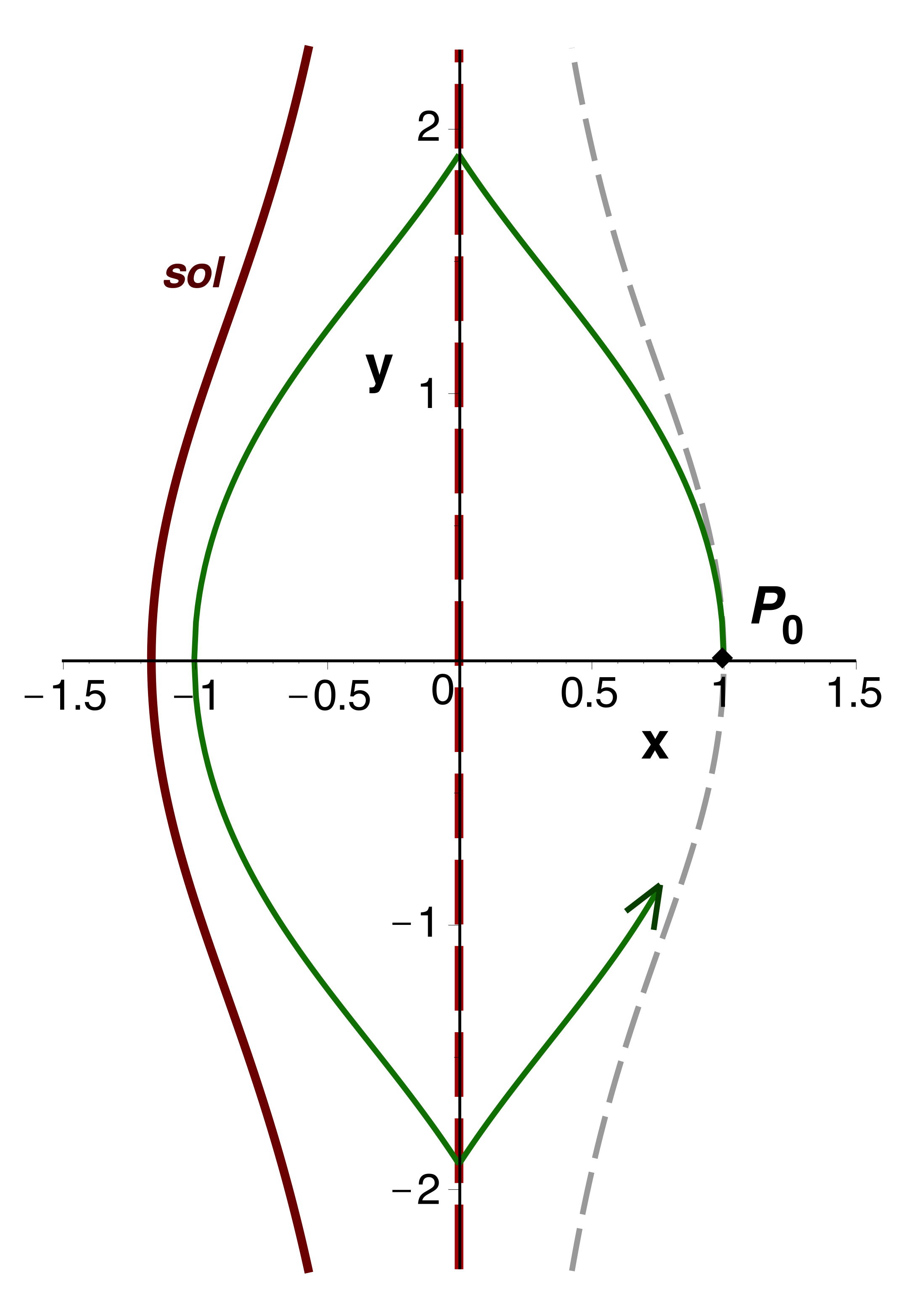
• Le comportement est analogue pour le cas des particules massives (ci-avant à droite), pour lesquelles on applique la transformation aux coordonnées  ( u,v ) (u,v)  déduites de  ( ct (r) ,r ) (c\,t(r), r) .

Au-delà de l'horizon, la variable temporelle T T change de sens de variation pour la partie des trajectoires qui causent les intersections contradictoires.

• Aussi bien pour les photons ou les particules massives, il apparaît que cela nécessite la traversée de l'intervalle avec  c T=0 c\,T=0  et  R∈ [ 0 ;1 ] R∈[0 \,;1] ,  qui correspond à la limite droite/gauche du diagramme de Kruskal-Szekeres. L'interprétation avec côté gauche “duplicata” redonne une description analogue à celles de Schwarzschild et de Lemaître, avec les mêmes problèmes.

📖 exercice n° IV.

Diagramme de Schwarzschild anamorphosé

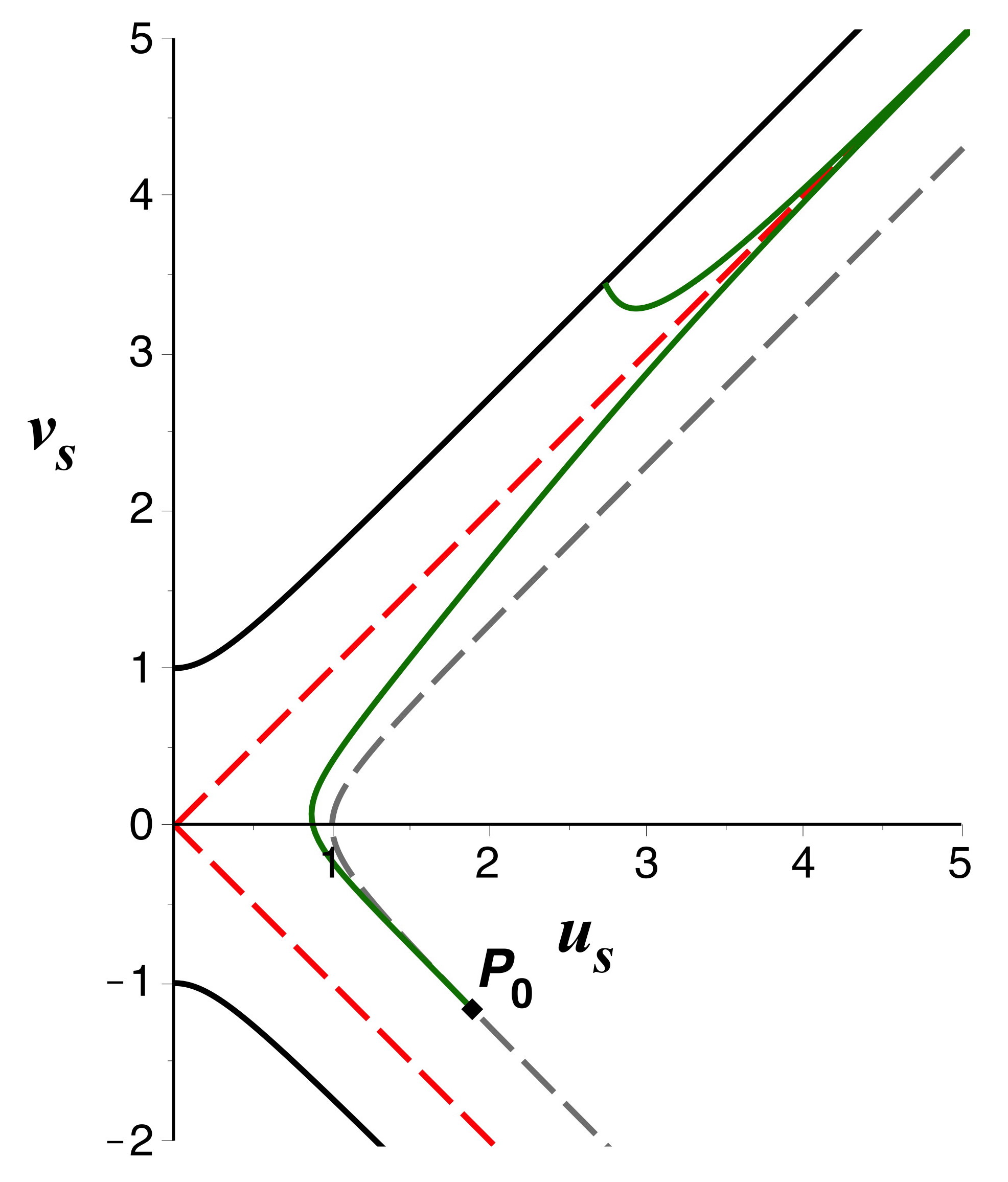
• On peut réciproquement appliquer pour les notations de Schwarzschild une transformation analogue mais de sens contraire : on “coupe” selon le segment de l'aller-retour, puis on “ouvre” en divisant par deux l'angle par rapport au point  ( r=rs ; t=0 ) (r=r_s \,; t=0) .

On obtient ainsi quatre régions possibles, analogues à celles de Kruskal-Szekeres, où on peut tracer les trajectoires en fonction des variables us u_s et vs v_s associées (ici pour l'exemple de particules massive).

PropKruskal_Im/S_anam_r0a.jpg
 PropKruskal_Im/S_anam_r0b.jpg


• En procédant ainsi, on n'a absolument pas éliminé les divergences au niveau de l'horizon.

Pourtant, ceci élimine les croisements anormaux : les trajectoires qui tombent au-delà de l'horizon vont dans la région (II) (II) , celles qui en sortent (symétriques verticales des exemples précédents) proviennent de la région (IV) (IV) . C'est le dédoublement de l'espace-temps qui a cet effet.

Si on souhaite que la représentation de Kruskal-Szekeres apporte une meilleure description que celles de Schwarzschild et de Lemaître, il faut accepter le dédoublement, mais ceci implique de l'interpréter physiquement.

📖 exercice n° V.


Étrangetés de la singularité centrale avec dédoublement

Particules rejoignant la singularité centrale

• D'après le repérage de Kruskal-Szekeres, des photons et des particules massives peuvent finir leur mouvement sur la singularité centrale en  r=0 r=0 ,  avec  v>0 v>0 ,  mais avec  u≤0 u≤0  ou  u≥0 u≥0  selon les conditions initiales.

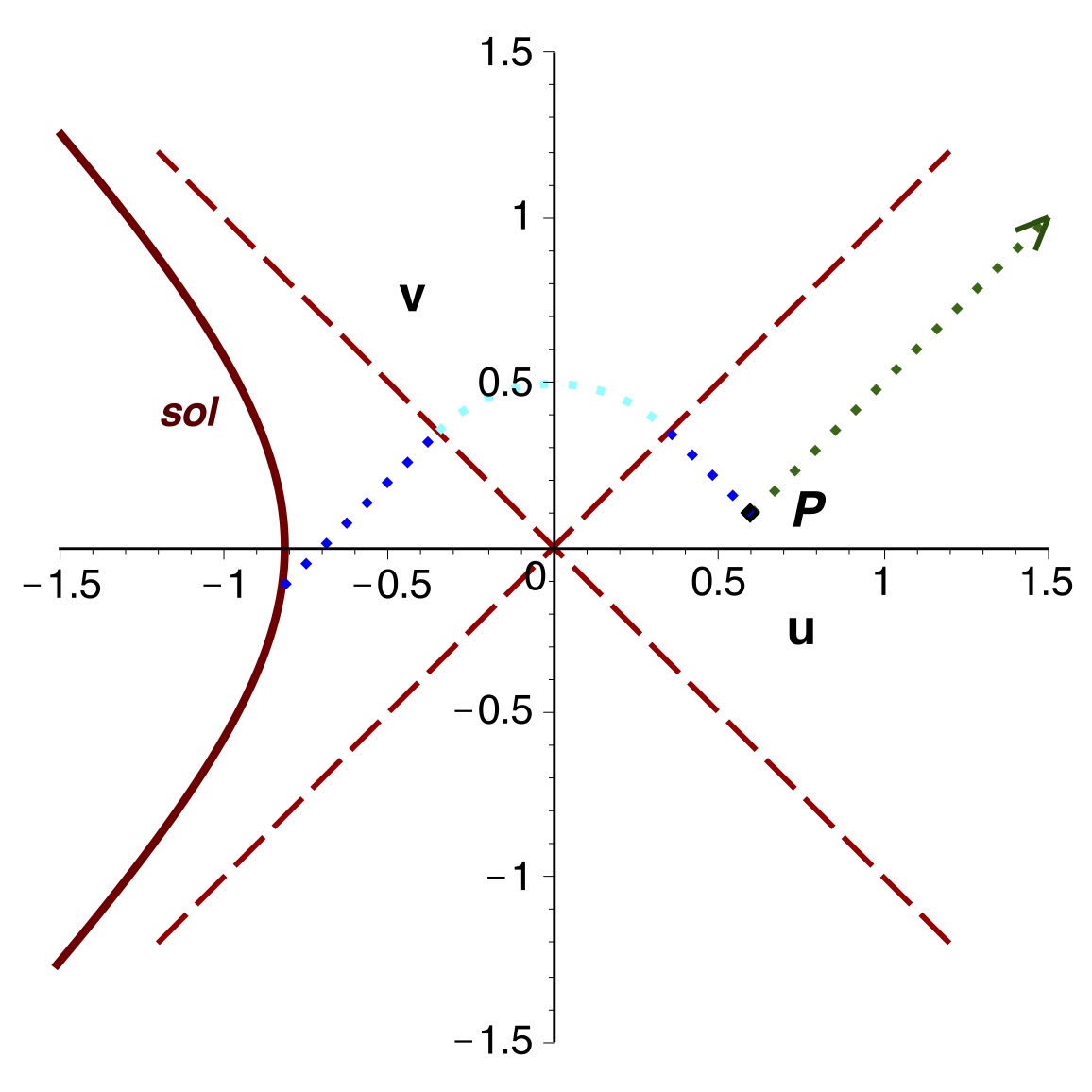
• L'interprétation de certains cas peut sembler ambigüe. Ainsi pour deux particules en mouvement radial, partant à vitesse nulle d'une même position r0 r_0 , puis rejoignant la singularité en  r=0 r=0 .

PropKruskal_Im/Kruskal_Tm2a.jpg
 PropKruskal_Im/Kruskal_Tm2b.jpg

Si les deux arrivent avec  u≥0 u≥0  (ci-avant à gauche) alors celle partie en premier arrive en premier (pour le temps v v ). Il en est de même en représentation de Lemaître.

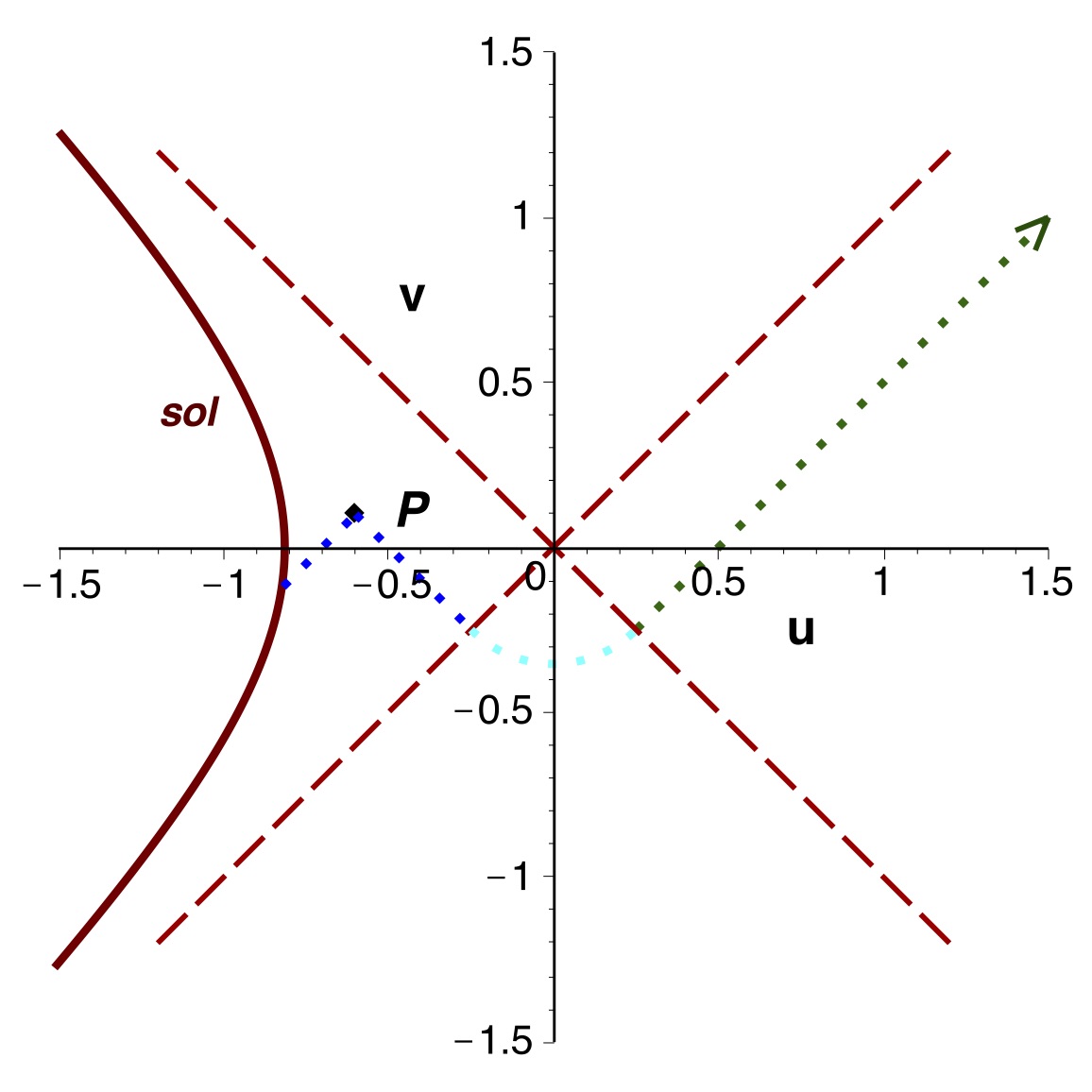
Au contraire, si les deux arrivent avec  u≤0 u≤0  (ci-avant à droite) alors celle partie en premier arrive en second (pour le temps v v ) sans que les trajectoires semblent se croiser. Ce n'est pas ce que donne la représentation de Lemaître. Comment interpréter cette interversion ?

Devenir des particules ayant rejoint la singularité centrale

• La matière ayant franchi l'horizon ne peut pas rester accumulée sous forme d'un astre intérieur immobile de rayon strictement positif, car toute particule massive doit dans cette zone se déplacer à une vitesse supraluminique par rapport au repérage de Schwarzschild.

Cette matière ne peut également pas s'accumuler en  r=0 r=0  sous forme d'une masse ponctuelle (de masse volumique infinie ? ), pour la même raison.

Les particules matérielles sont-elles mystérieusement “annihilées” en atteignant cette limite, au mépris de la conservation du nombre baryonique ? Selon quelle loi physique ? Quelle serait par la suite la source du champ de gravitation ?

◊ remarque : le problème réciproque est symétrique pour l'indispensable formation de particules lors de la disparition d'un trou-blanc.

• Dans l'ensemble, on aboutit ainsi à des aspects des coordonnées dont la signification semble très douteuse.

Évolution de la singularité centrale

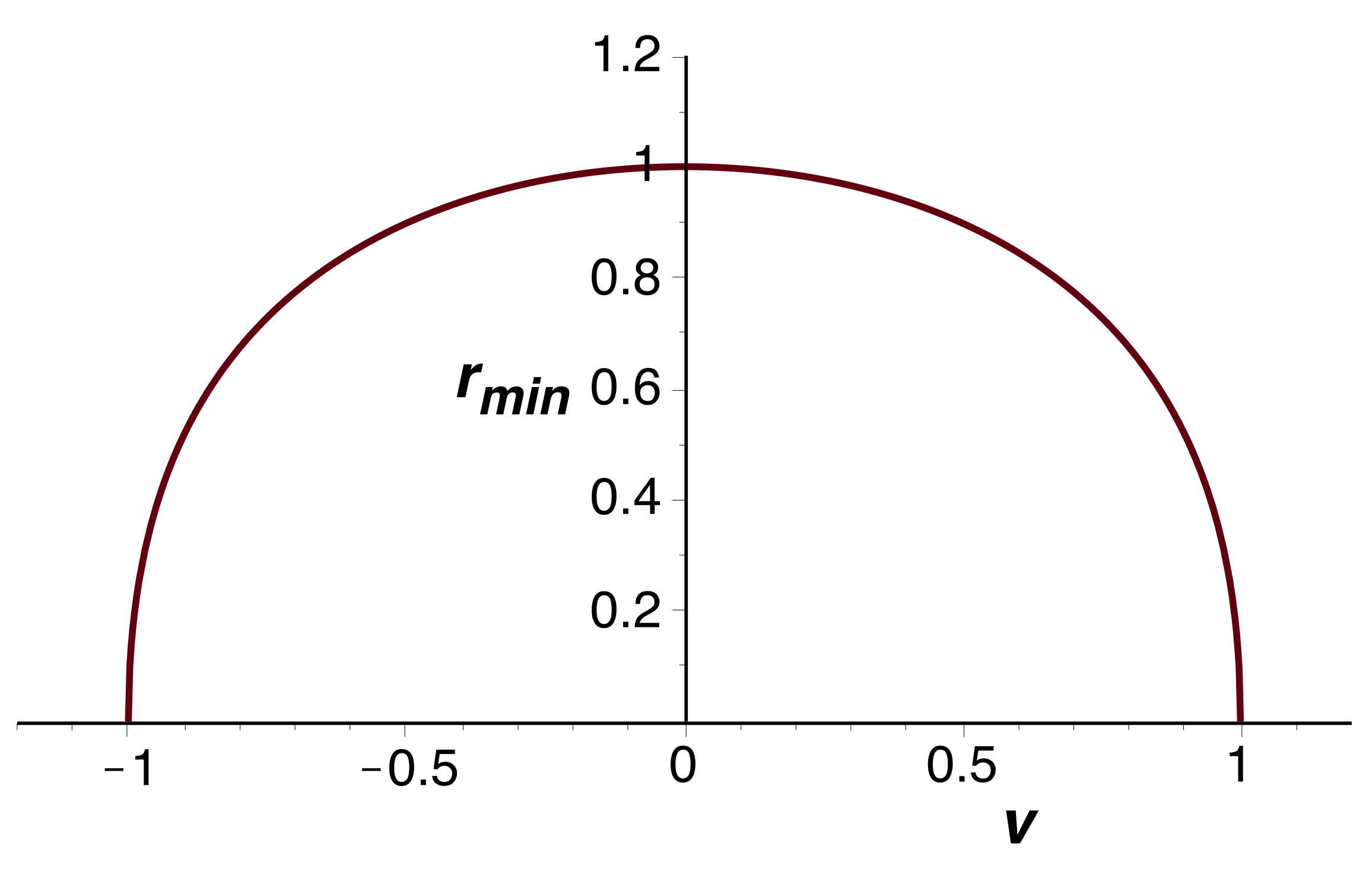
• Le diagramme indique que la singularité centrale n'existe pas dans l'intervalle de “temps”  -1<v<1 -1<v<1  (en unités réduites) ; cela semble décrire un espace initialement en expansion à partir d'un “trou-blanc”, passant par un extremum à  t=0 t=0 ,  puis finalement en contraction formant ainsi un trou noir.

PropKruskal_Im/rmin.jpg

Dans l'intervalle correspondant du temps v v , la valeur de r r présente un minimum rmin =rs. [ 1+W0 ( −v2 e ) ] r_{min}=r_s .\left[1+W_0 \left(\frac{-v^2}{\mathrm{e}}\right)\right] .  Cela suggère nettement que la partie centrale est alors occupée par un astre (qui s'expand puis s'effondre) à l'intérieur duquel la métrique, différente, doit être raccordée avec celle de Kruskal-Szekeres.

• Mais par ailleurs avec le dédoublement du diagramme, pour  u=0 u=0 ,  la singularité qui apparait pour  v=1 v=1  (en unités réduites) se scinde en deux points spatialement distincts (séparées par  ∫ d𝓁=∞ ∫\,d𝓁=∞ )  selon le signe de u u ; cela semble incohérent.

• On doit alors se rappeler que, dans le diagramme de Kruskal-Szekeres, la succession de deux segments  v∈ [ rs ;0 ] v∈[r_s \,; 0]  et  v∈ [ 0 ;rs ] v∈[0 \,; r_s]  décrit, en notations de Schwarzschild, un aller-retour selon le segment  r∈ [ 0 ;rs ] r∈[0 \,; r_s]  avec  t=0 t=0 .

Pour que la singularité associée au trou-noir apparaisse, il faut que de la matière s'y effondre ; cette matière doit suivre la trajectoire “retour” correspondante. De même, pour que la singularité associée au trou-blanc disparaisse, il a fallu que de la matière soit éjectée selon la trajectoire “aller” correspondante.

Cela implique donc que cette limite droite/gauche du diagramme soit “infranchissable” : le côté gauche correct doit décrire l'intérieur de l'astre (avec des équations différentes) et le côté gauche “classique” n'est qu'un “double” inutile.

• En fait, bien que la métrique soit la même, trou-blanc et trou-noir sont deux comportements incompatibles.

Aucun des deux ne peut avoir une invariance temporelle : un trou-noir a forcément un instant de formation et un trou-blanc a forcément un instant de disparition. Éventuellement, la matière éjectée par un trou-blanc peut ensuite retomber et former un trou-noir, mais seulement après la disparition du trou-blanc.

📖 exercices n° VI et VII.

Anomalie fondamentale de la singularité centrale

• Avec le repérage de Schwarzschild, on a constaté une caractéristique étrange de la singularité centrale ; pour  r=0 r=0  ce point semble immobile au-delà de l'horizon, ce qui fait qu'il ne peut pas être doté de propriétés physiques (tout “point matériel” devant y avoir une vitesse supraluminique).

Or, après effondrement d'un astre en trou noir, toute la matière est supposée s'y être annihilée et c'est cette singularité qui serait seule source du champ gravitationnel environnant.

Cette anomalie fondamentale est en outre confirmée avec le repérage de Lemaître et ses généralisations.

• Il est alors utile de reprendre le raisonnement avec le repérage de Kruskal-Szekeres.

Conformément à la métrique, avec la distance locale  d𝓁=du 4 rs 3 r e −r/ rs \displaystyle d𝓁=du \;\sqrt{\frac{4 \,r_s^{\:3}}{r} \: \mathrm{e}^{-r/r_s}}  et la durée locale   d t 𝓁oc =1c dv 4 rs 3 r e −r/ rs \displaystyle dt_{𝓁oc}=\frac{1}{c} \:dv \;\sqrt{\frac{4 \,r_s^{\:3}}{r} \: \mathrm{e}^{-r/r_s}} ,  la vitesse d'un point matériel par rapport au repérage peut s'écrire :  vr= d𝓁 d t 𝓁oc =c dudv \displaystyle v_r=\frac{d𝓁\:}{dt_{𝓁oc}}=c \: \frac{du}{dv} .

La propriété  r=0 r=0  correspond à  v2= 1+u2 v^2=1+u^2  donc  vr= c vu>c \displaystyle v_r=c \: \frac{v}{u}>c  (avec u u et v>0 v>0 ).  On obtient ici encore une anomalie.

• On peut éventuellement douter du raisonnement à cause du passage à la limite pour  d𝓁 d𝓁   et  d t𝓁oc dt_{𝓁oc}  dans le cas  r=0 r=0  ;  mais la suite confirme (avec le repérage comobile de Novikov) qu'il n'en est rien.

Diagramme “isotrope” à la Kruskal-Szekeres

Comportement des coordonnées “isotropes”

• L'étude de la chute libre radiale d'une particule en coordonnées isotropes aboutit à une traversée de l'horizon en  r_= r_s \underline{r}=\underline{r}_s  (à la vitesse de la lumière) après une durée apparemment infinie (date  t→∞ t→∞ )  mais une durée propre finie. La particule ralentit “ensuite”, ce qui semble caractériser un effet gravitationnel répulsif ; ce prolongement de trajectoire semble toutefois provenir de  t=−∞ t=-∞ .

L'interprétation paraît ne pas poser les mêmes problèmes, car la variable r_ \underline{r} reste partout du genre espace et la variable t t reste partout du genre temps.

• Certains physiciens adoptant les notations de Kruskal-Szekeres considèrent alors que pour  r_< r_s \underline{r}<\underline{r}_s  la trajectoire passe directement dans la région ( III ) (III) , qu'ils interprètent dans ce cas comme la région “intérieure” à l'horizon.

On peut alors utiliser des représentations “sautant” les régions (II) (II) et ( IV ) (IV) , ou avec raccordement de  u=±v u=± v  selon une anamorphose de part et d'autre.

◊ remarque : dans un tel graphique, on peut représenter symboliquement une limite  r=Cte r=Cte   indiquant ce que serait “le sol” d'un astre intérieur... si cela pouvait exister.

Trajectoires radiales des photons

• Un avantage du diagramme de Kruskal-Szekeres est que les trajectoires des photons sont des droites parallèles aux diagonales. Le plus pratique est alors d'éclipser simplement les régions (II) (II) et (IV) (IV) en “raccordant” symboliquement par des arcs de cercle (le “raccord” ne fait pas partie de la trajectoire).

Les photons entrants émis de l'extérieur atteignent la surface de l'astre (qui ne peut d'ailleurs pas être en équilibre). Mais réciproquement, les photons émis de l'intérieur peuvent en principe tout aussi bien sortir.

PropKruskal_Im/Kruskal_T7.jpg
 PropKruskal_Im/Kruskal_T8.jpg

◊ remarque : contrairement à R. Penrose, S. Hawking a suggéré (pour des raisons quantiques) que trous-noirs et trous-blancs seraient plus ou moins les mêmes objets ; le comportement décrit ici est incidemment un peu de ce type (alors que la représentation “classique” correspond à trou-blanc dans le passé et trou-noir dans le futur).

• Cela suggère de chercher s'il existe une possibilité de synchronisation des horloges, de part et d'autre de la singularité, par la méthode “classique” :

Ce procédé est toutefois inefficace car, selon la façon dont on fait tendre les deux points (de part et d'autre) vers la limite, le signal de retour peut sembler arriver aussi bien avant qu'après le départ du signal initial.

Même si on utilise une même variable t t des deux côtés de la singularité, les valeurs de part et d'autre ne peuvent donc pas être comparées.

📖 exercices n° VIII et IX.

Trajectoires radiales de particules massives

• On considère l'exemple d'une particule initialement immobile en un point extérieur, puis tombant en mouvement radial jusqu'à l'intérieur.

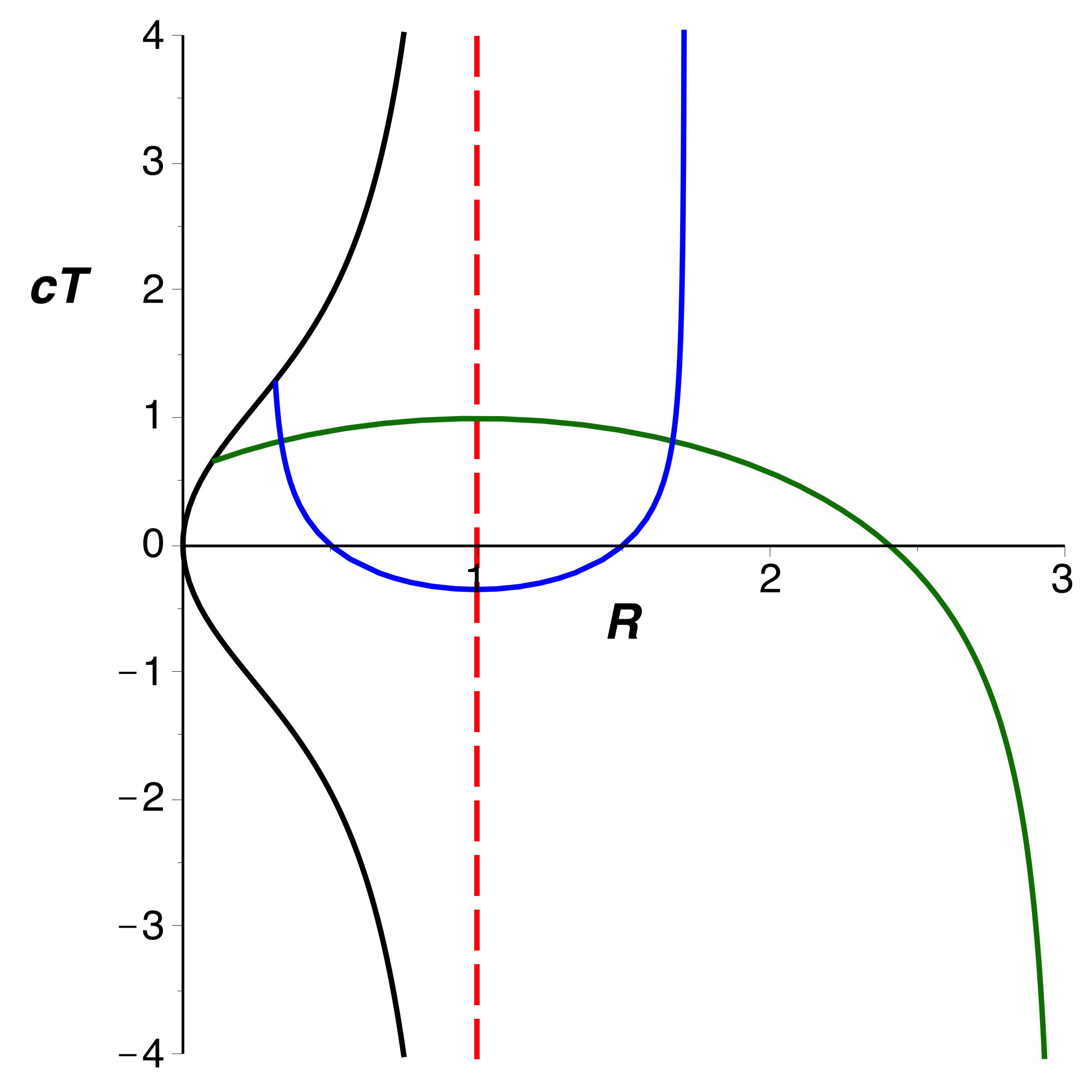
Dans un diagramme de Kruskal-Szekeres modifié (ci-après à gauche), le passage de la région (I) (I) à la région ( III ) (III) correspond à un changement de signe de u u au point où  u=v u=v .  Les particules atteignent  r_= r_s \underline{r}=\underline{r}_s  avec la vitesse de la lumière mais leur trajectoire n'y est pas parallèle à la diagonale décroissante (comme les photons entrants) ; de ce fait, le raccordement par un arc de cercle y semble moins “naturel”.

PropKruskal_Im/Kruskal_T9.jpg
 PropKruskal_Im/Kruskal_T10.jpg

On retrouve les oscillations déjà décrites avec d'autres repérages : la particule ralentit après avoir franchi l'horizon, puis s'immobilise et repart vers l'extérieur (si elle ne rencontre pas le “sol”) ; enfin, après avoir retraversé la singularité, elle rejoint sa position initiale où sa vitesse s'annule.

Outre les contradictions liées à ces oscillations (précédemment décrites), la particule parait ici rejoindre sa position initiale à l'instant initial... ce qui semble contradictoire (les coordonnées utilisées ne sont pas adaptées pour cela).

De plus, si les sens d'évolution de  t t  et  r r  sont corrects dans la seconde partie, la variation est inversée pour la variable temporelle  v v  (contrairement à ce qui est obtenu pour la représentation correspondante de Lemaître).

• On peut redessiner le diagramme (ci-avant à droite) avec une anamorphose analogue à celle utilisée pour le tracé “classique”, mais centrée sur l'horizon.

Les inévitables ruptures de pente subsistant au niveau de l'horizon sont dues à la singularité de la métrique, de façon analogue déjà constatée au raccordement en r0 r_0 entre montée et descente dans une représentation de Lemaître généralisée.

Pertinence de la région ( III ) (III)

• L'étude précédente montre que le calcul classique de Kruskal-Szekeres est loin d'être exempt d'aspects étranges, même si certains peuvent être justifiés, mais sa réinterprétation déduite des coordonnées isotropes soulève des difficultés conceptuelles.

Dans le modèle de L. S. Abrams, la limite de compacité d'un astre correspondrait à une masse ponctuelle avec  r=rs r=r_s  à l'origine. Si le champ extérieur change de sens quand on dépasse cette valeur, ce serait pour la simple raison que la région ( III ) (III) correspond à l'autre côté (de même que quand on dépasse  r=0 r=0  en coordonnées polaires planes).

Ainsi la singularité en  r=rs r=r_s  serait une limite impossible à atteindre. par exemple si tout astre dont la singularité est intérieure mais trop proche de la surface, devenant instable, ne s'effondrait pas en trou noir mais explosait en supernova.

Dans cette interprétation les régions (II) (II) et ( IV ) (IV) n'ont pas raison d'être et la région ( III ) (III) n'est qu'un duplicata inutile de la région (I) (I) . Reste à accepter qu'un point puisse avoir un périmètre  2π rs 2π \:r_s .

Une étude de la métrique intérieure à l'astre est indispensable pour préciser.