| 3.a. |
• Les équations du mouvement peuvent s'écrire
:
.
• Ainsi :
;
. |
| 3.b. |
• On peut considérer les combinaisons :
;
.
• Il apparaît que cela peut s'écrire plus simplement
avec
et
:
;
.
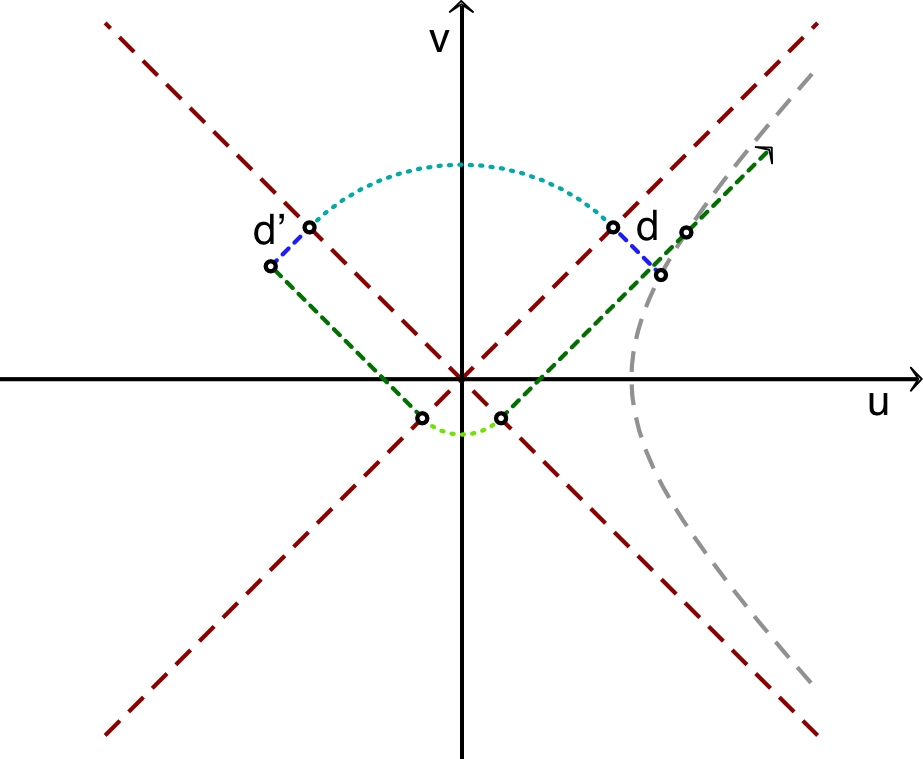
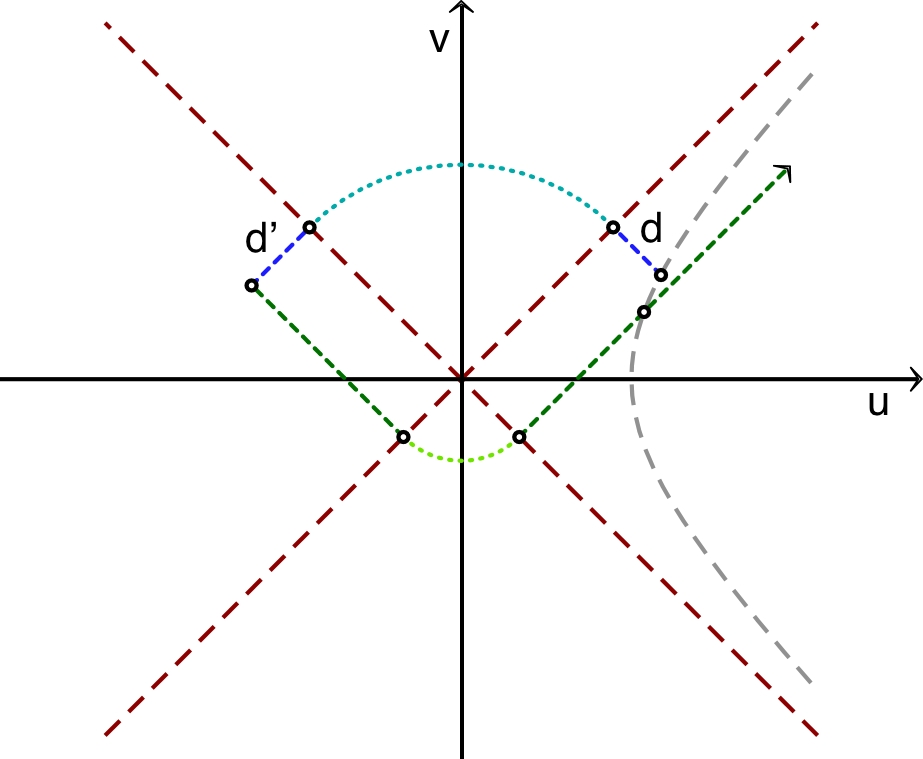
• Pour
, on obtient
donc
puis
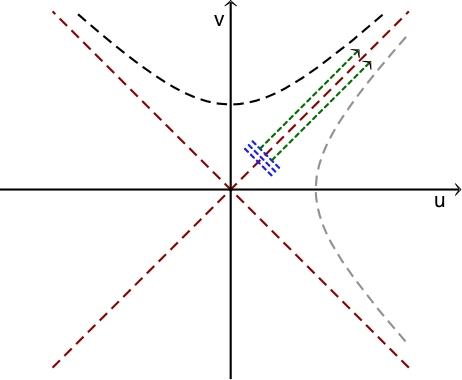
; ceci décrit les trajectoires des photons
entrants. Il en est de même pour
; cela décrit les photons sortants.
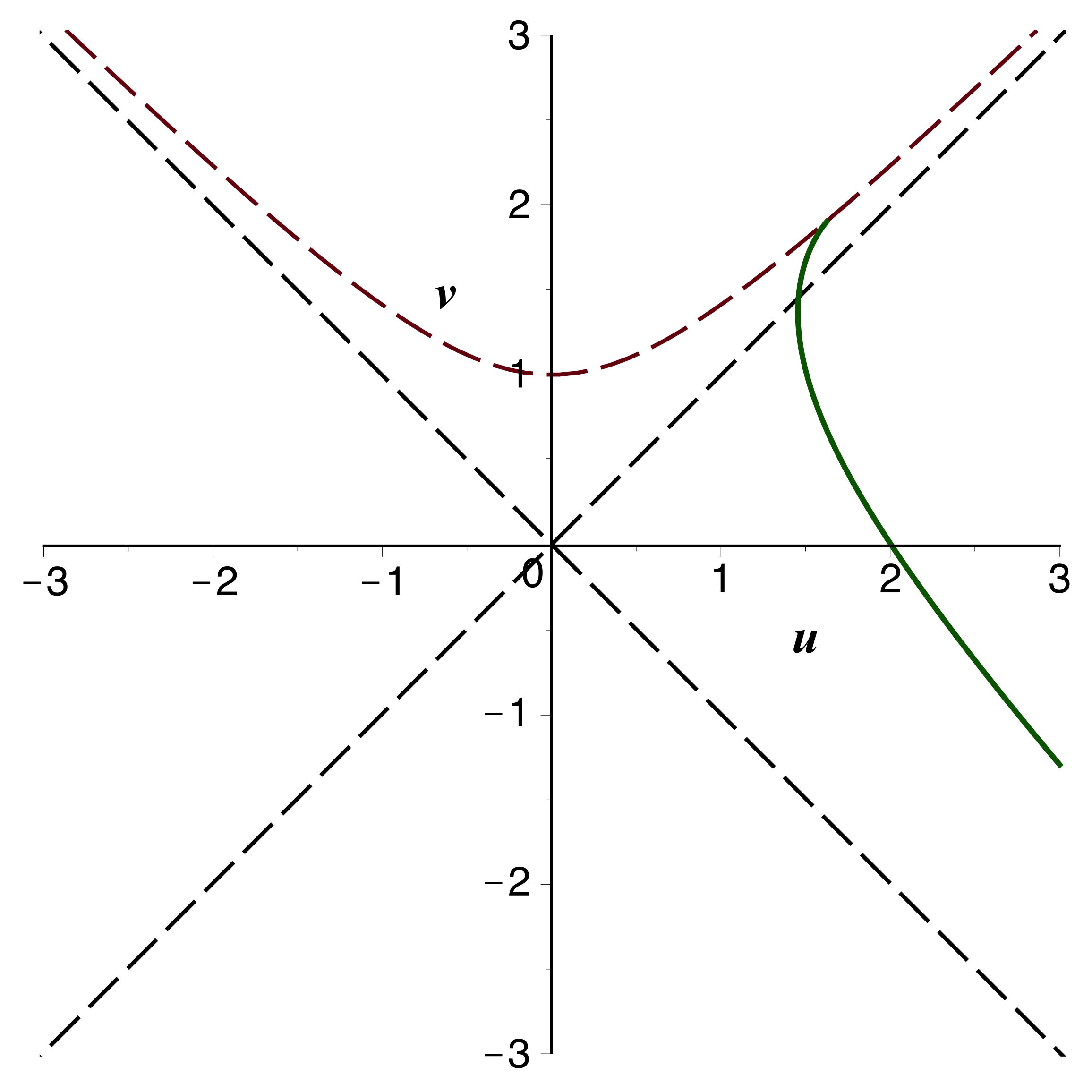
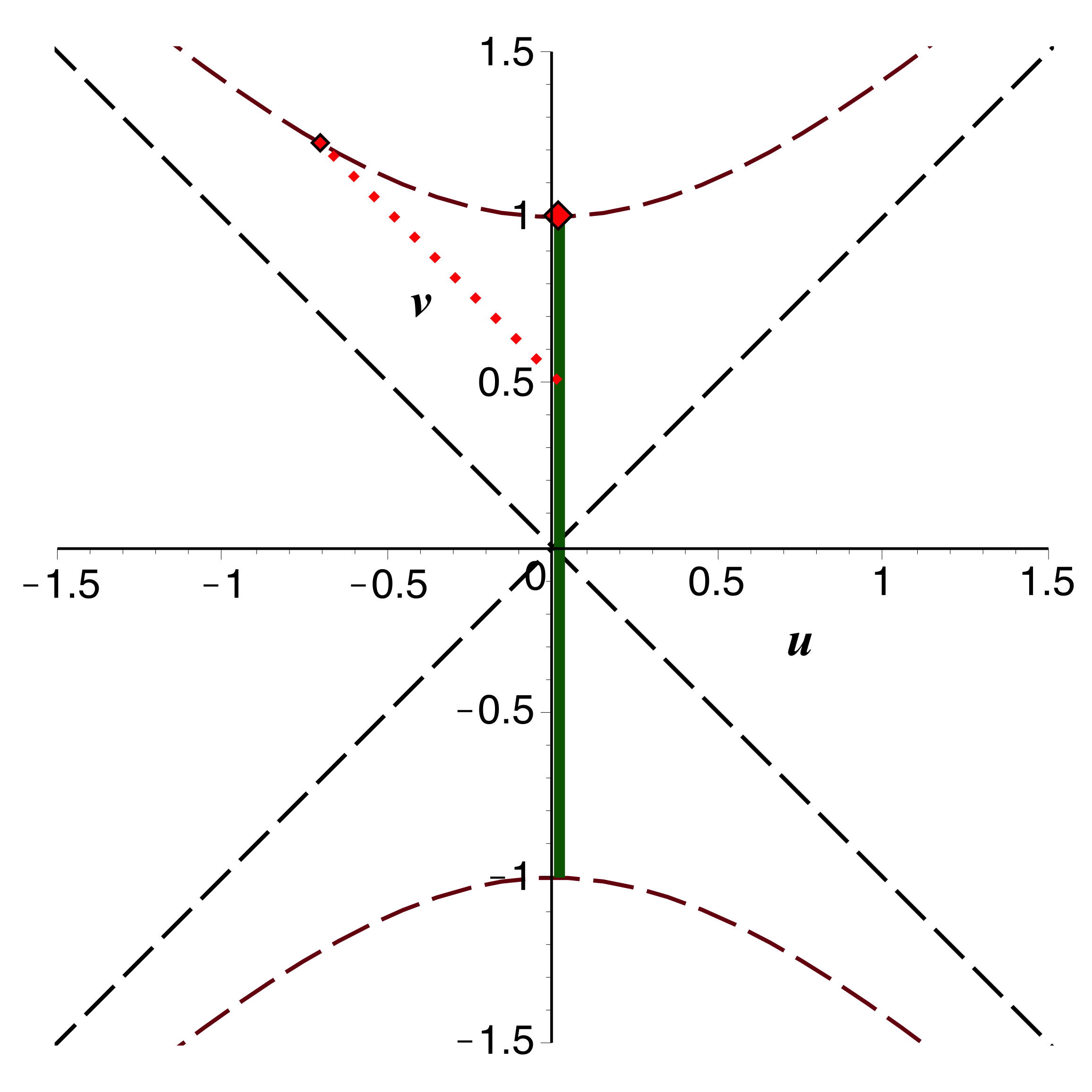
• Pour les particules matérielles
et
ne s'annulent pas, mais
ou
s'annule au passage de l'horizon. On constate que dans ce
cas
ou
s'annule, donc (puisque
y est régulier) la traversée se fait sans irrégularité : on
peut donc envisager une résolution numérique par la méthode
d'Euler.
◊ remarque : si on cherche à appliquer une méthode d'Euler
en fonction de
mais en partant des expressions
et
déduites de celle de
et
, on est confronté à un passage à la limite délicat au
niveau de l'horizon ; cette difficulté est évitée ici.
• Mais par ailleurs, la métrique :
impose pour les particules
matérielles
; les deux dérivées premières n'étant pas
indépendantes, il faut en tenir compte pour imposer leurs
conditions initiales. Plus efficacement, on peut à profit
remplacer l'une des deux équations différentielles
précédentes, du second ordre, par cette dernière, du premier
ordre.
◊ remarque : pour les photons
redonne directement
ou
.
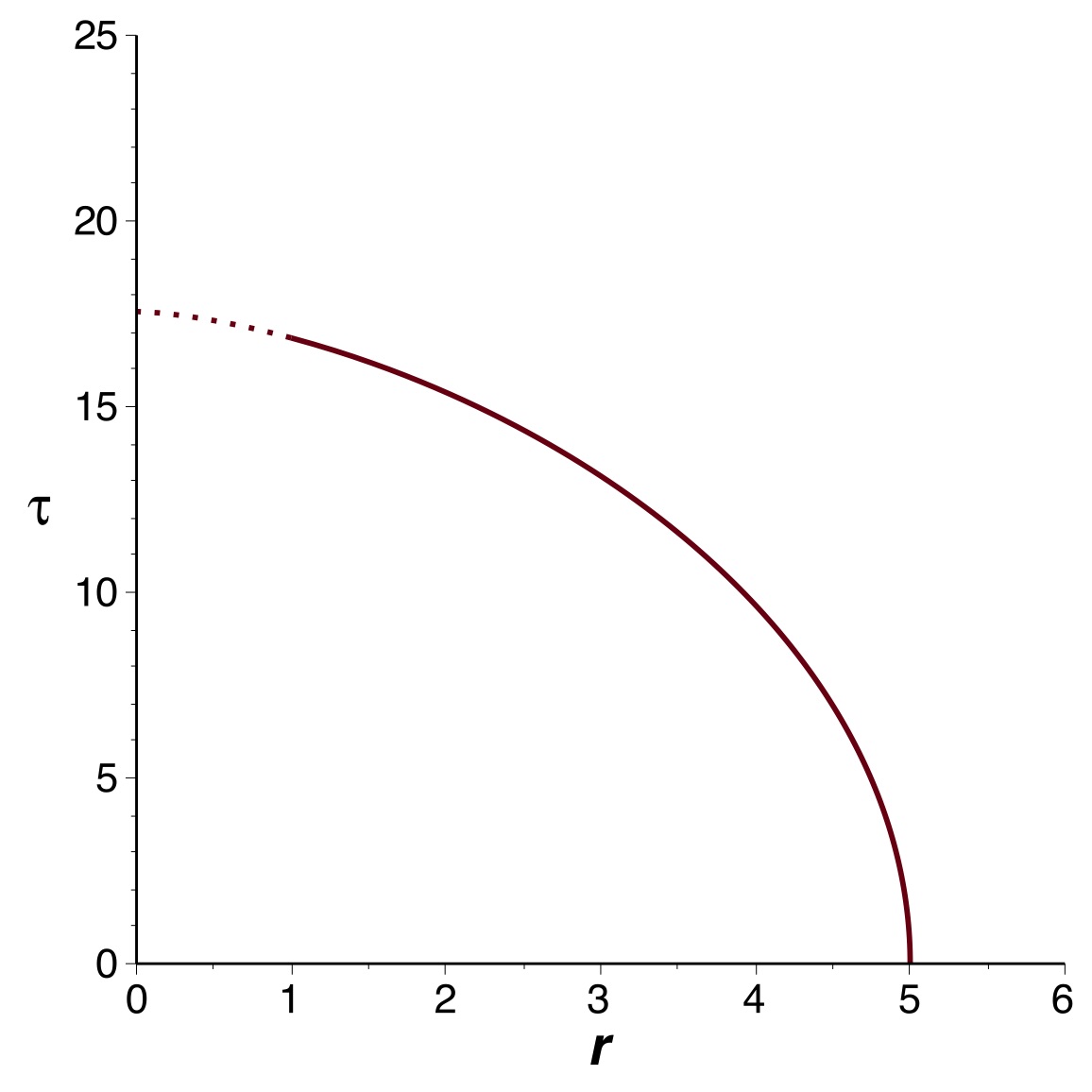
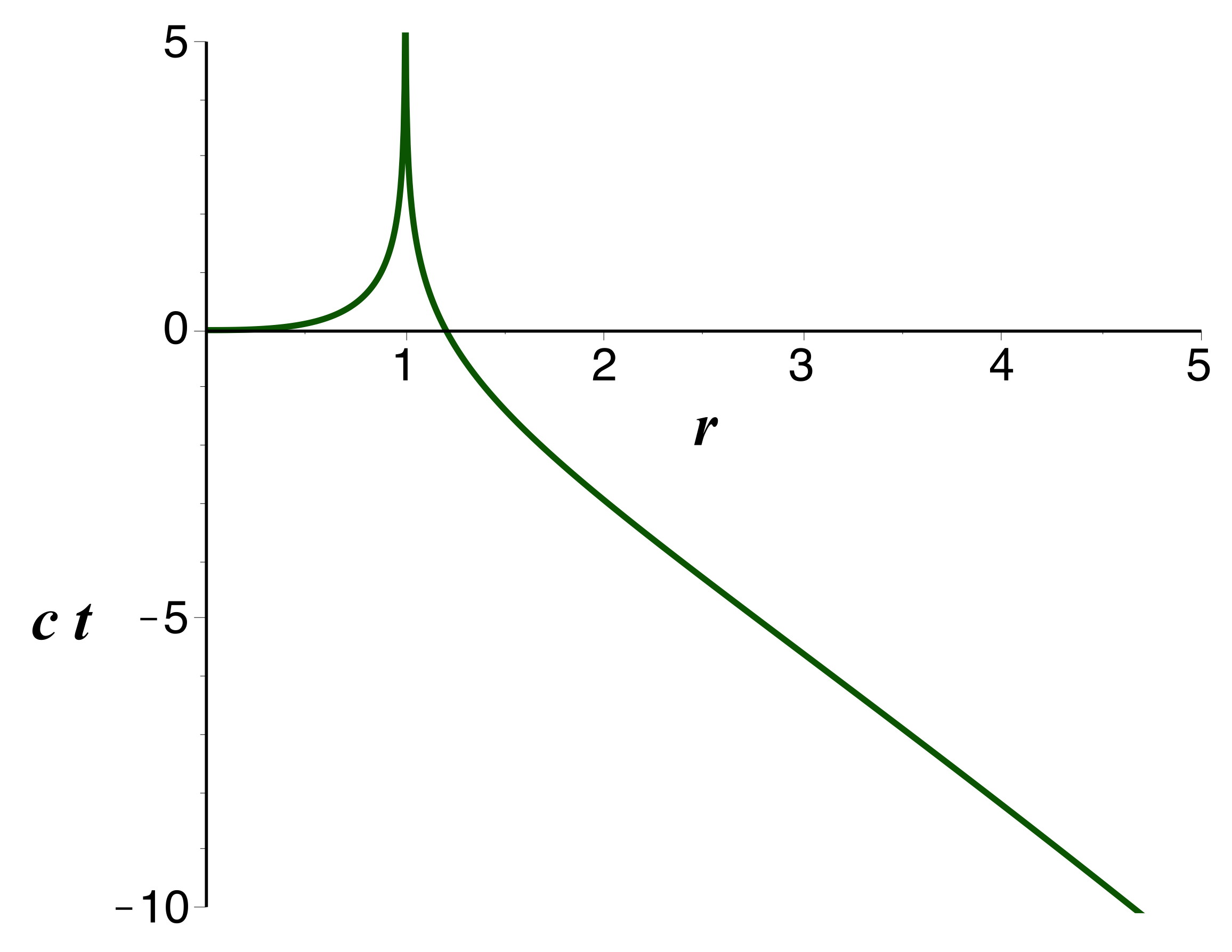
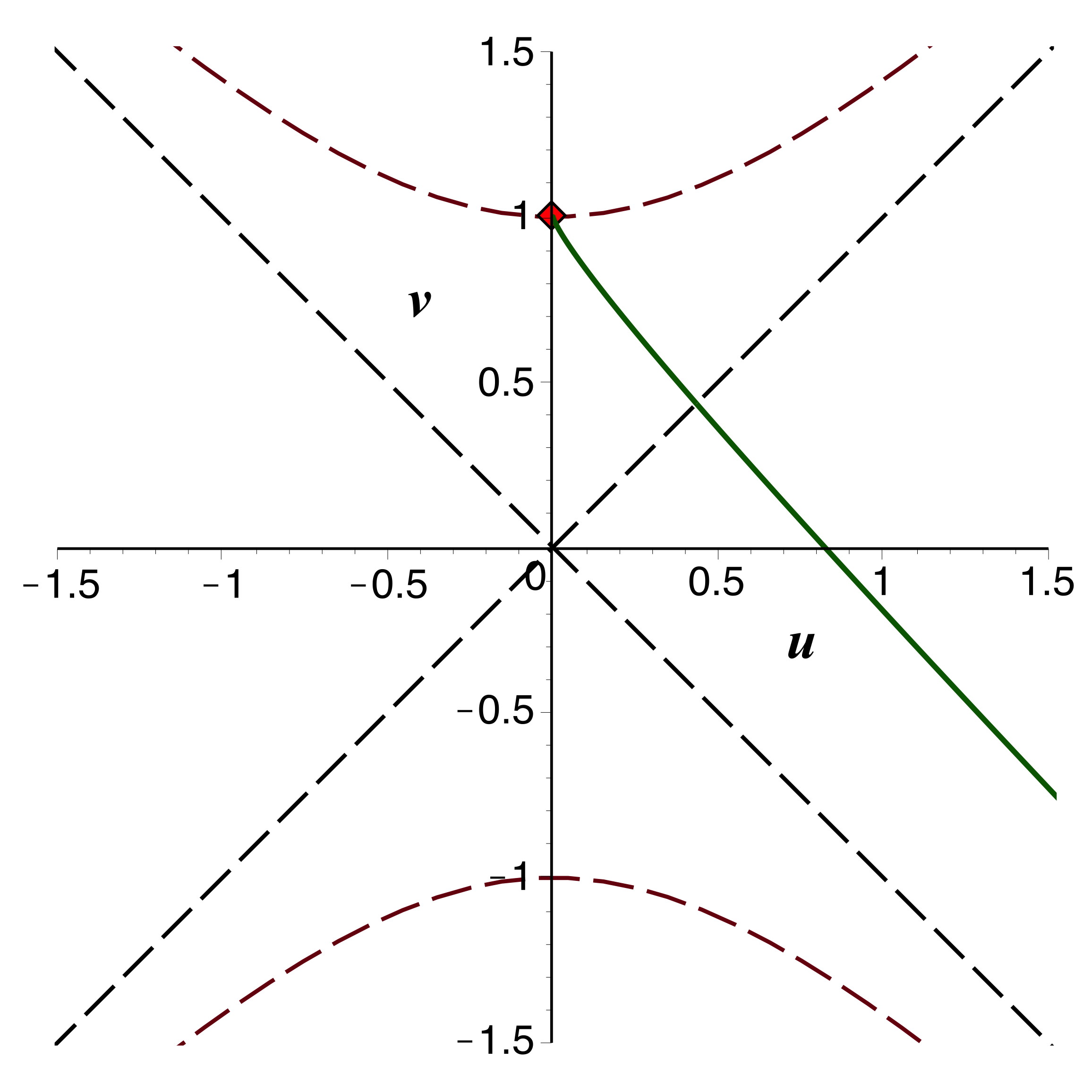
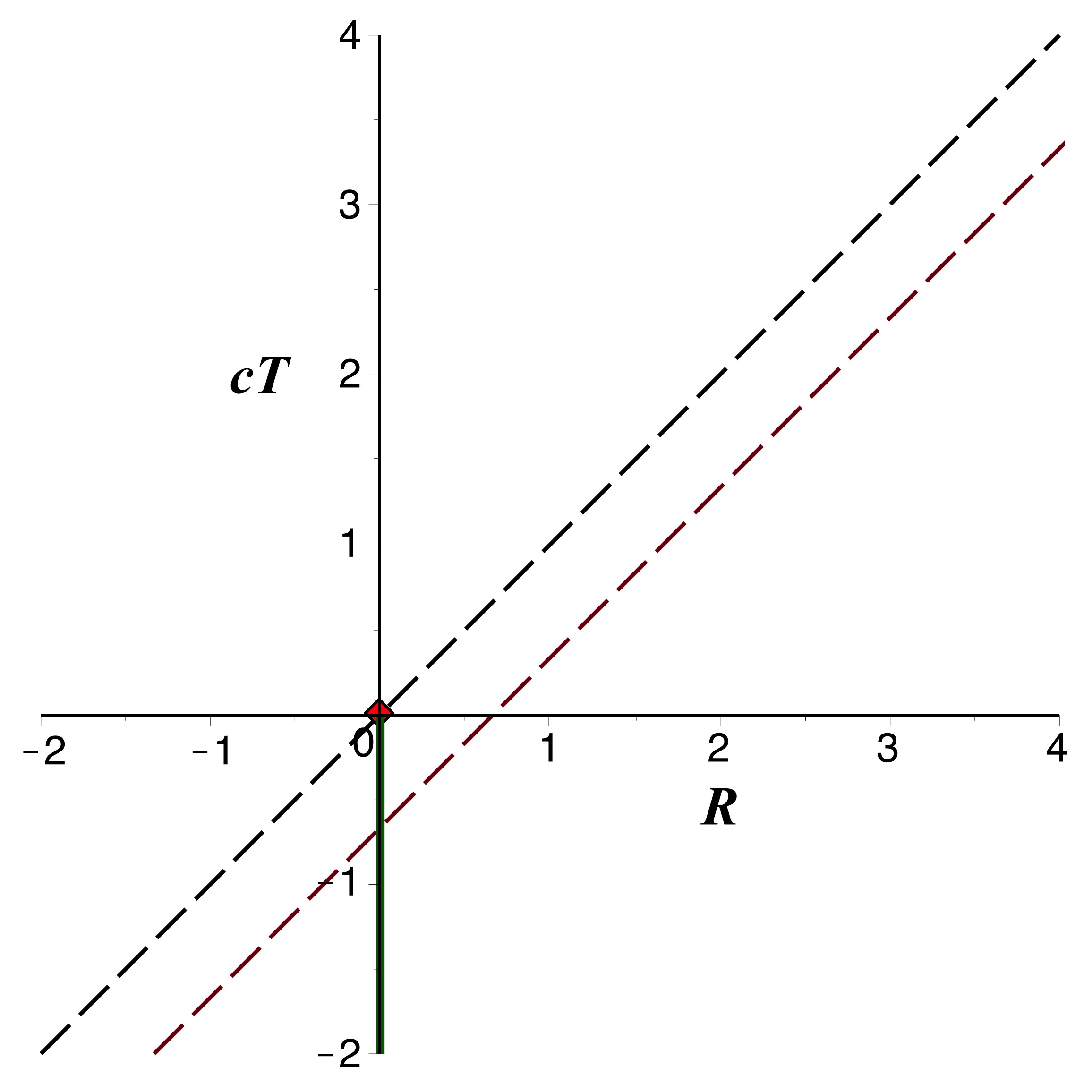
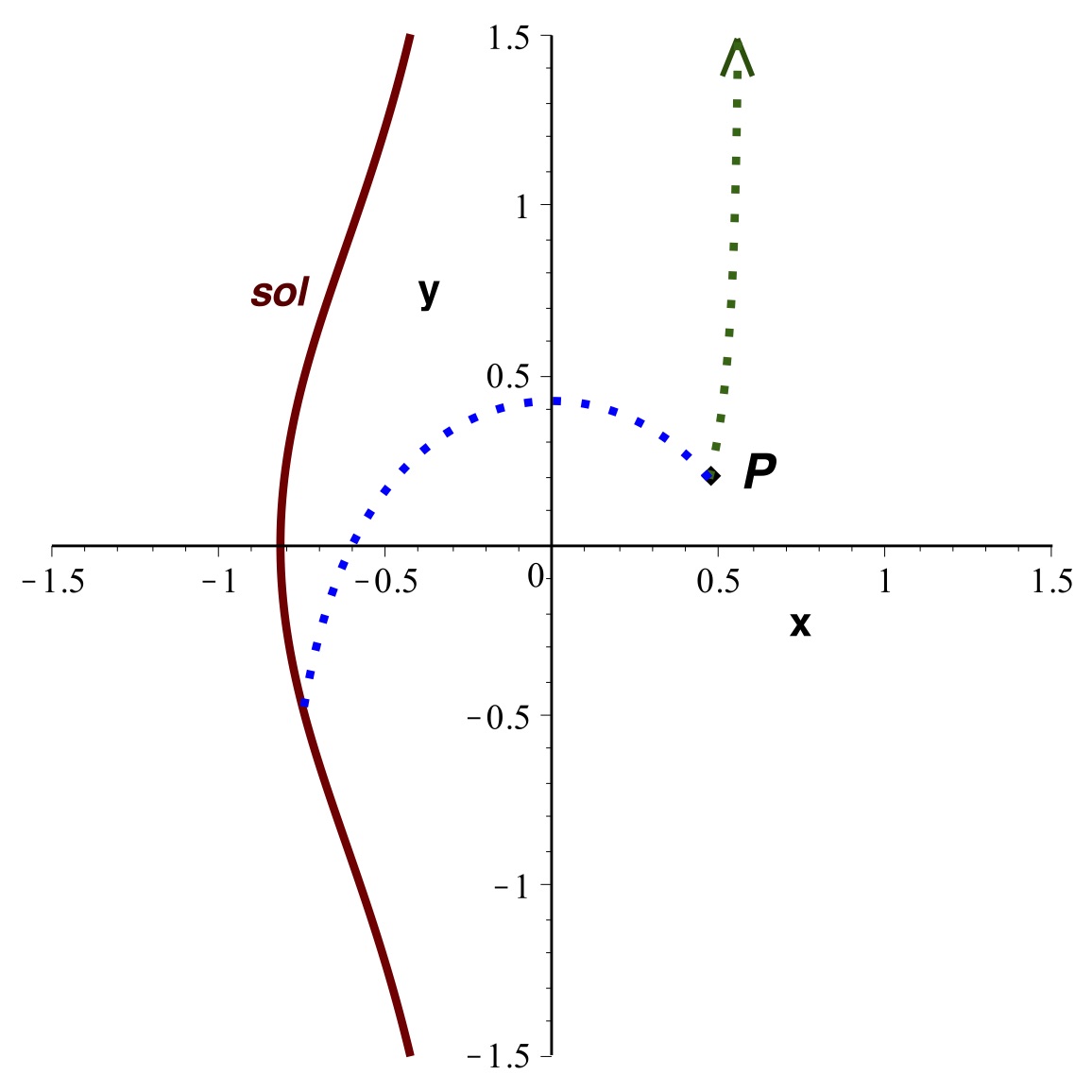
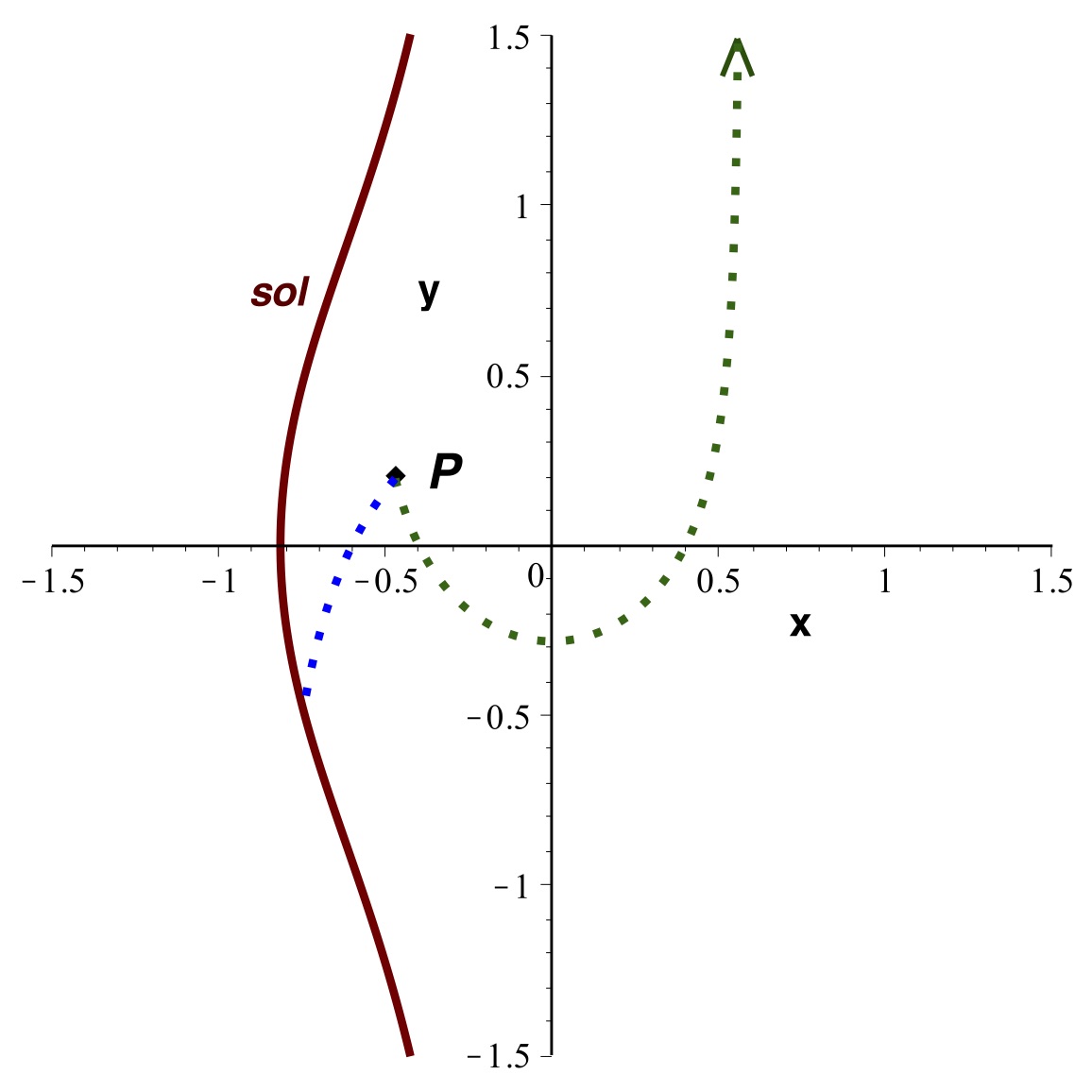
• Ceci permet de tracer les trajectoires par intégration
numérique.
|