PROPRIÉTÉS du DIAGRAMME de KRUSKAL-SZEKERES - exercices




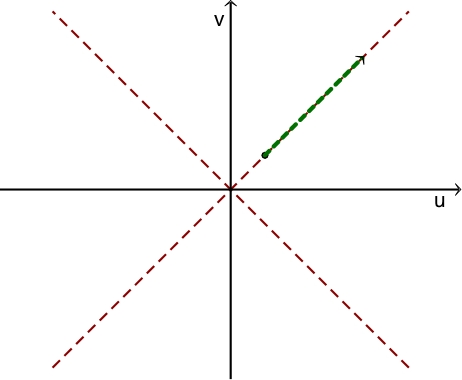
Trajectoire de photons

        • La structure du diagramme de Kruskal-Szekeres a pour conséquence la possibilité d'une propagation de photons “le long” de la singularité (évolution du “temps” selon v v ). Ce sont des photons dans le “sens sortant”, mais qui sont à la limite de ne plus pouvoir sortir.
        • En particulier, un tel photon peut être émis par une particule en chute libre franchissant l'horizon, puis capté “ensuite” par une autre particule traversant de même. Étant donné que les photons correspondants évoluent “sur place” en ce sens qu'ils restent en  r=rs r=r_s  (avec  t=∞ t=∞ ?),  cela n'est-il pas contradictoire ?		 PropKruskal_ex_Im/ph_stat_1.jpg


Durée de chute d'une particule massive et diagramme de Kruskal-Szekeres

1.     • La durée de chute de toute particule massive traversant l'horizon de Schwarzschild semble infinie pour tout observateur extérieur. En se limitant pour simplifier à une chute libre radiale, montrer que la durée propre de chute est finie (hormis pour les particules provenant de l'infini, dont la durée propre de chute est forcément infinie pour cette autre raison).
        ◊ remarque : la partie finale de l'intégration ne peut être faite que numériquement.

2.     • Toujours en se limitant au mouvement radial, il est parfois dit (par exemple H. Andrillat) qu'on peut “lire” cette propriété sur le diagramme de Kruskal-Szekeres, car la longueur de l'arc de trajectoire (fini) mesure ∫ds ∫ds .  Commenter.


Trajectoires de particules massives

        • On considère un astre créant dans le vide environnant un champ statique à symétrie sphérique. On utilise la métrique de Kruskal-Szekeres :
ds2= K(r) ( dv2 −du2 ) −r2 dΩ 2 {ds}^2=K(r) \:\left({dv}^2-{du}^2\right)-r^2 \:{dΩ}^2  ;
K(r) = 4 rs 3 r e −r/rs \displaystyle K(r)=\frac{4 \,r_s^{\:3}}{r} \: \mathrm{e}^{-r/r_s}  ;  r ( u,v ) =rs. [ 1+W ( u2− v2 e ) ] \displaystyle r(u,v)=r_s .\left[1+W\left(\frac{u^2-v^2}{\mathrm{e}}\right)\right]  ;  c t ( u,v ) =2 rs artanh (vu) \displaystyle c \,t(u,v)=2 \,r_s \; \mathrm{artanh}\left(\frac{v}{u}\right) .
        ◊ remarque : on note ici W(x) W(x) la fonction principale de Lambert  W0 W_0 ,  définie par  W0 e W0 =x W_0 \; \mathrm{e}^{W_0}=x .
        ◊ remarque : pour simplifier les notations, on peut prendre rs r_s comme unité et noter  X= u2− v2 e \displaystyle X=\frac{u^2-v^2}{\mathrm{e}} .

1.     • Pour étudier les propriétés de cette métrique, il est utile d'effectuer quelques calculs préliminaires.
        a) Exprimer K′ K' en fonction de r r .
        b) Exprimer W′ W' en fonction de W W ; en fonction de K K .

2.     • Exprimer la connexion :  Γ αβγ Γ_{αβγ}  et  Γ .βγ α Γ_{\phantom{.}βγ}^α .

3.     a) Écrire les équations du mouvement pour les variables v v et u u .
        b) Proposer une résolution.


Diagramme de Kruskal-Szekeres revisité

        • Pour les particules en chute libre verticale, l'observation des trajectoires passant par un sommet r0 r_0 montre que quand  r0 →rs r_0→r_s  le tracé en notations de Schwarzschild tend vers un aller-retour selon le segment  r∈ [0 ; rs ] r∈[0 \,;r_s]  avec  t=0 t=0 .
        • Au contraire, dans le diagramme de Kruskal-Szekeres, le tracé tend vers la succession de deux segments  v∈ [ −rs ;0 ] v∈[-r_s \,;0]  et  v∈ [ 0 ;rs ] v∈[0 \,;r_s]  avec  u=0 u=0  (et  t=0 t=0 ).
        • On peut alors appliquer une transformation inverse pour les notations de Kruskal-Szekeres : on “referme” le diagramme selon le segment de l'aller-retour des notations de Schwarzschild en multipliant par deux l'angle par rapport au point  ( u=0 ;v=0 ) (u=0 \,; v=0) .

1.     • Exprimer, en fonction de  u u  et  v v ,  les variables  R R  et  cT c \,T  associées au diagramme ainsi obtenu.

2.     • Montrer que cela donne une représentation paramétrique pour tracer l'horizon  ( r=1 r=1  avec rs r_s pris comme unité).

3.     • Montrer que cela donne une représentation paramétrique pour tracer le courbe  r=0 r=0  (et en fait plus généralement les courbes  r=Cste r=Cste ).

4.     • Montrer que cela donne une représentation paramétrique pour tracer les trajectoires des photons.


Diagramme de Schwarzschild revisité

        • Pour les particules en chute libre verticale, l'observation des trajectoires passant par un sommet r0 r_0 montre que quand  r0 →rs r_0→r_s  le tracé en notations de Schwarzschild tend vers un aller-retour selon le segment  r∈ [ 0; rs ] r∈[0 \,;r_s]  avec  t=0 t=0 .
        • Au contraire, dans le diagramme de Kruskal-Szekeres, le tracé tend vers la succession de deux segments  v∈ [ −rs ;0 ] v∈[-r_s \,;0]  et  v∈ [ 0; rs ] v∈[0 \,;r_s]  avec  u=0 u=0  (et  t=0 t=0 ).
        • On peut alors appliquer le même genre de transformation pour les notations de Schwarzschild : on “coupe” le diagramme selon le segment de l'aller-retour, puis on “ouvre” en divisant par deux l'angle par rapport au point  ( r=rs ; t=0 ) (r=r_s \,; t=0) .

1.     • Exprimer, en fonction de  r r  et  c t c \,t ,  les variables us u_s et vs v_s associées au diagramme ainsi obtenu.

2.     • Montrer que cela donne une représentation paramétrique pour tracer les courbes  r=Cste r=Cste .

3.     • Montrer que cela donne une représentation paramétrique pour tracer les trajectoires des particules.


Particularités de la singularité centrale

        • Selon le diagramme de Kruskal-Szekeres, la singularité centrale ( r=0 r=0 ) apparaissant pour  v=1 v=1  (unités réduites) semble “ensuite” (quand v v augmente) se séparer en deux parties avec  u>0 u>0  ou  u<0 u<0 .  Or cette limite n'est pas invariante par changement de l'origine du temps (a priori arbitraire).

1.     • Commenter l'effet d'un changement de l'origine du temps dans la région (I) (I) .

2.     • Commenter l'effet d'un changement de l'origine du temps dans la région (II) (II) .

3.     • On considère une quantité de matière partant de la singularité centrale et sortant du trou blanc pour  v<0 v<0  puis retombant dans le trou noir jusqu'à la singularité pour  v>0 v>0 ,  en suivant une trajectoire selon  u≈0 u≈0  (mais  u>0 u>0 ). Cette matière peut-elle émettre vers l'intérieur un photon rejoignant la singularité ? Commenter.


Limite de la zone extérieure

1.     • Le diagramme de Kruskal-Szekeres ne se limite pas à la description de la disparition d'un trou-blanc suivie de la formation d'un trou-noir.
        • En représentation de Schwarzschild, puis celle de Kruskal-Szekeres, tracer l'allure de la trajectoire d'une sphère de matière finissant en trou-noir en partant de l'infini à vitesse (limite) nulle. Commenter.

2.     • Tracer la trajectoire en représentation de Lemaître. Commenter.


Diagramme de Kruskal-Szekeres “isotrope” revisité

        • On suppose valide l'interprétation des coordonnées de Kruskal-Szekeres déduite des coordonnées isotropes, avec seulement les régions (I) (I) et ( III ) (III) dans le diagramme.
        • Pour visualiser autrement la traversée de la singularité, on propose ici de redessiner le diagramme. Il ne s'agit pas de changer les coordonnées ( u,v ) (u,v) mais de les dessiner autrement. On souhaite que l'intervalle angulaire entre les diagonales soit étendu à un demi-plan, visualisant ainsi ce qu'on obtiendrait en reproduisant le diagramme sur la surface d'un cône d'angle au sommet 45° 45° , puis en projetant sur un plan perpendiculaire à l'axe.
        • Sur un tel diagramme, représenter les courbes  u=Cste u=Cste  ;  v=Cste v=Cste .  Représenter de même les trajectoires des photons entrants et sortants.


Synchronisation des horloges

        • On suppose valide l'interprétation des coordonnées de Kruskal-Szekeres déduite des coordonnées isotropes, avec seulement les régions (I) (I) et ( III ) (III) dans le diagramme.
        • Étudier la possibilité de synchronisation des horloges, de part et d'autre de la singularité, par la méthode “classique” :