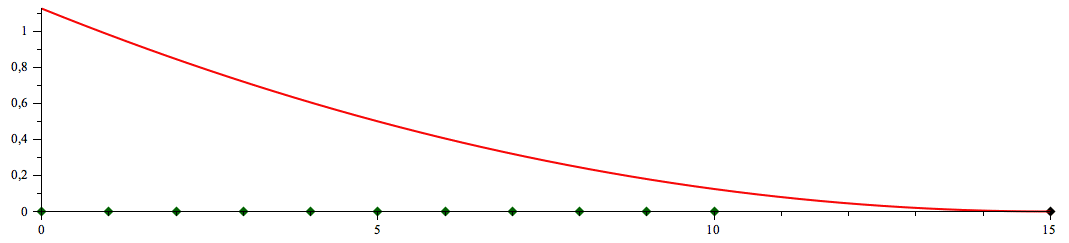
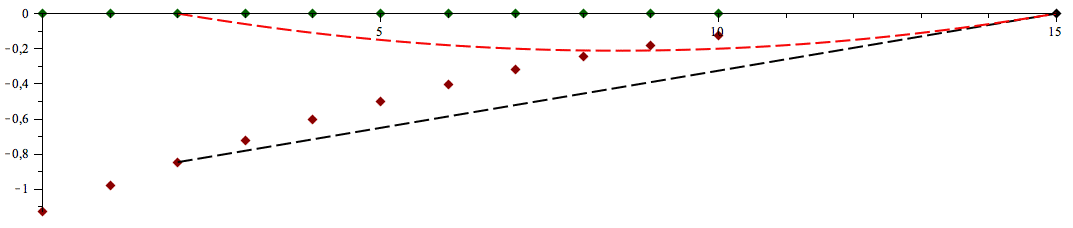
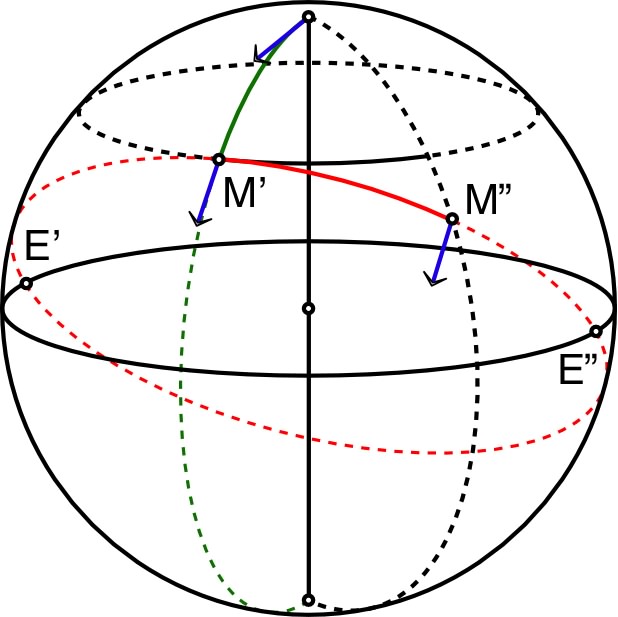
Pour la sphère, ces géodésiques sont des “grands cercles” centrés au centre de la sphère. Les méridiens sont géodésiques, mais non les parallèles (par exemple le géodésique partant de tangentiellement au parallèle local, recoupe l'équateur en et ).
; .
| Le transport le plus “parallèle” possible
est selon l'orientation des géodésiques (lignes les plus
courtes joignant deux points donnés). Pour la sphère, ces géodésiques sont des “grands cercles” centrés au centre de la sphère. Les méridiens sont géodésiques, mais non les parallèles (par exemple le géodésique partant de tangentiellement au parallèle local, recoupe l'équateur en et ). |
 |
;
;
.
; ; ;
; symboles de Christoffel.
;
.
.
.
;
.
;
.