• Les équations des géodésiques de la surface correspondent ainsi à :
; .
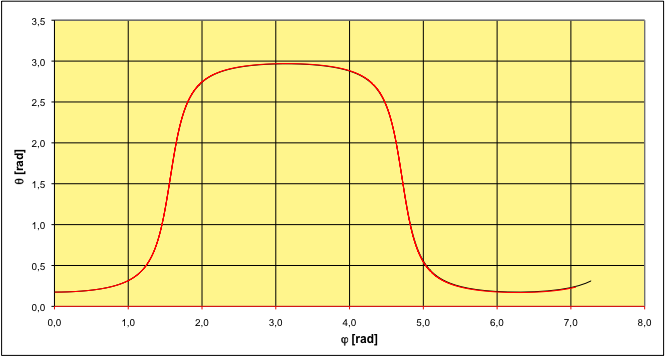
• La méthode d'Euler donne une courbe indiscernable de celle obtenue à la question (3).
| 1. | • Dans un changement de coordonnées ()
la transformation correspond à un tenseur :; ; ; . |
| 2.a. | • La variation
se déduit de celles des vecteurs : . |
| 2.b. | • La variation étant linéaire, elle se
généralise à tout tenseur
:. |
| 3. | • On obtient ainsi :
. • On en déduit les “dérivées covariantes” : . ◊ remarque : le principe se généralise à tout tenseur, quel que soit le nombre d'indices covariants et/ou contravariants. |
| 1. | • Dans on
peut considérer
avec
. • Ceci correspond à : ; ; . • Cette métrique est celle correspondant à des coordonnées cartésiennes dans un plan, mais la surface est par ailleurs “cyclique” sur la variable (provenant de ). ◊ remarque : en pratique, dans , un cylindre découpé selon une droite parallèle à son axe peut être déroulé et superposé à une bande d'un plan. |
| 2.a. | • En déplaçant
parallèlement à lui même au sens de
,
on obtient
. • En déplaçant parallèlement à lui même au sens de , on obtient . |
| 2.b. | • Le vecteur
n'existe pas en tant que vecteur de la surface (il
n'est pas dans le plan tangent). • Perpendiculaire en chaque point à l'axe , le cercle est l'équivalent d'un axe cartésien (il s'agit d'une géodésique). • Le “transport parallèle” au sens de la surface est donc en fait parallèle à cet axe : on obtient , ce qui est cohérent pour un espace localement plat. |
| 1. | • Dans un espace courbe, le transport parallèle de en dépend du chemin suivi, donc de façon générale ceci n'est éventuellement possible que pour la limite de points quasi-confondus (séparés par une distance infinitésimale). |
| 2. | • En supposant qu'on puisse définir une méthode de transport parallèle telle que ne soit pas ambigu, alors on pourrait définir en une somme . Mais par ailleurs, on pourrait alors aussi, par la même méthode, définir , puis ; le problème est qu'un transport inverse donnerait en général : . Ainsi, pour des grandeurs définies en des points distincts, on ne peut considérer que des sommes de scalaires. |
• À partir de
, on obtient :;• En appliquant la transformation inverse : ;• La comparaison avec donne , ou par changement des indices : . |
| 1.a. | • Chaque point de la demi-sphère a une projection et une seule (on se limite à ) ; ce repérage donne une représentation sans ambiguïté. |
| 1.b. | • Ces coordonnées ne sont pas cartésiennes en tant que coordonnées sur la demi-sphère, car elles ne correspondent pas à des “axes” rectilignes. |
| 2.a. | • Dans on
peut utiliser
avec
; le sous-espace considéré impose :
, donc :
. • On en déduit par substitution : .
|
||
| 2.b. | • Le déterminant est
; la matrice inverse
correspond à :; ; ; . |
| 3.a. | • On obtient ainsi :; ; |
| 3.b. | • On obtient enfin :; ; |
| 1.a. | • On peut considérer
avec
. • Ceci correspond à : ; ; . |
| 1.b. | • Le déterminant est
; la matrice inverse
correspond à :; ; . |
| 2.a. | • On obtient ainsi : . |
| 2.b. | • On obtient enfin : ; . |
| 3.a. | • Les coordonnées cartésiennes peuvent
s'écrire (avec un indice
pour les valeurs en
) :; ; .• L'équation du plan considéré peut s'écrire sous la fome : . |
| 3.b. | • De façon analogue :
;
;
. • L'équation d'un grand cercle peut donc s'écrire : .• Ceci peut se simplifier sous la forme : . |
| 4.a. | • L'équation temporelle des géodésiques
s'écrit
. Ceci implique la proportionnalité
; il en découle donc aussi
(correspondant à un déplacement à vitesse constante). • Les équations des géodésiques de la surface correspondent ainsi à : ; . |
| 4.b. | • Si on pose
, la seconde équation peut s'écrire :
; les solutions sont de la forme :
(on peut trouver une intégrale première équivalente avec la
première équation), mais la seconde intégration est très
ardue ; on se limite donc ici à une intégration numérique. • La méthode d'Euler donne une courbe indiscernable de celle obtenue à la question (3).  |
| 1.a. | • Dans on
peut considérer
avec :.• Ceci correspond à : ; ; . |
| 1.b. | • Le déterminant est
; la matrice inverse
correspond à :; ; . |
| 2.a. | • On obtient ainsi : . |
| 2.b. | • On obtient enfin : ; . |
| 3.a. | • Dans on
peut utiliser
avec
. • On peut alors considérer et regrouper : . • Pour retrouver une métrique équivalente (avec notations adaptées) : , il faut et il suffit donc que : , c'est à dire : . • Ceci correspond à : ; . On en déduit par intégration (en choisissant pour ) : ; . • La surface ainsi définie est “localement équivalente” puisqu'elle a la même métrique. Elle n'est pas globalement équivalente car elle est par ailleurs “cyclique” sur la variable (provenant de ) ; la situation est analogue au cas d'un cylindre, “localement plat” mais non plan. |
| 3.b. | • La première formulation peut suggérer une
torsion (avec un sens de vissage arbitraire parmi deux
possibles). La seconde formulation montre par contre qu'il
n'y a pas de torsion intrinsèque. • L'ambiguïté vient du fait qu'il y a une sorte de “torsion” dans , mais que ce n'est pas une propriété intrinsèque de la surface : c'est une propriété de la façon dont elle est modélisée dans . On peut obtenir une autre modélisation dans , localement équivalente (à par le fait qu'elle est cyclique sur ), mais sans aspect de “torsion”. • La “torsion intrinsèque” d'une surface est associée à la non commutation des dérivées covariantes. |
| 4.a. | • L'équation temporelle des géodésiques
s'écrit
. Ceci implique la proportionnalité
; il en découle donc aussi
(correspondant à un déplacement à vitesse constante). • Les équations des géodésiques de la surface correspondent ainsi à : ; . |
| 4.b. | • Si on pose
, la seconde équation peut s'écrire :
; les solutions sont de la forme :
(on peut trouver une intégrale première équivalente avec la
première équation), mais la seconde intégration est très
ardue ; on se limite donc ici à une intégration numérique. • La méthode d'Euler donne des courbes très vraisemblables pourvu que le pas de calcul soit assez petit. Il y a deux types de géodésiques, selon qu'ils coupent ou non l'axe . 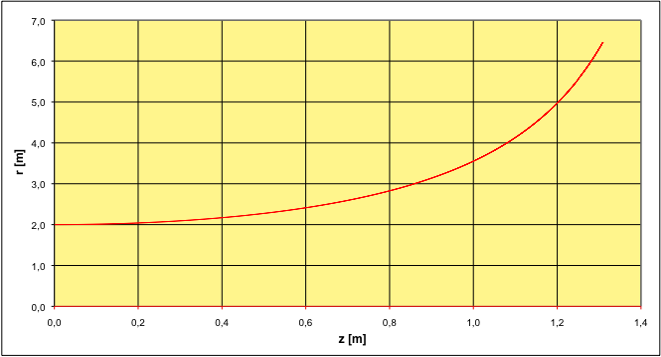 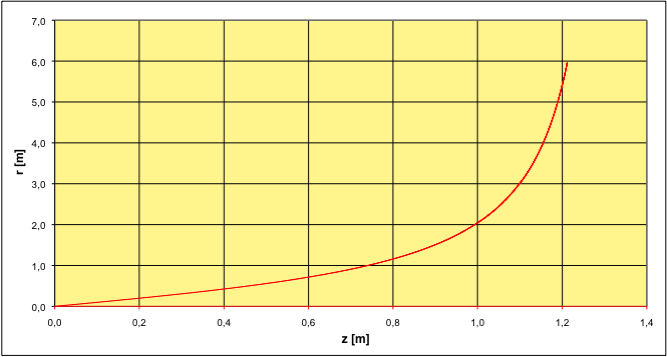 |