GÉOMÉTRIE RIEMANNIENNE EN ESPACE PLAT - exercices


Coordonnées sphériques

1.     • Le tenseur métrique  gijg_{ij}  définit l’élément de longueur selon  ds2=gijdxidxj{ds}^2=g_{ij} \: {dx}^i \: {dx}^j .  Quelle est l’expression du tenseur métrique en coordonnées sphériques ?

2.     • Le tenseur  gijg_{ij}  variant suivant le lieu, on utilise le repère local  e→i\overset{→}{e}_i  tel que :  dM→=∂iM→dxi=e→idxid\overset{→}{M}=∂_i \overset{→}{M} \: {dx}^i=\overset{→}{e}_i \: {dx}^i .  Les e→i\overset{→}{e}_i ne sont généralement pas unitaires ; ainsi :  gij=∂iM→∙∂jM→=e→i∙e→jg_{ij}=∂_i \overset{→}{M}∙∂_j \overset{→}{M}=\overset{→}{e}_i∙\overset{→}{e}_j .
        • Quelle sont les expressions des e→i\overset{→}{e}_i en coordonnées sphériques, par comparaison aux (u→r,u→θ,u→φ)\left(\overset{→}{u}_r \,,\overset{→}{u}_θ \,,\overset{→}{u}_φ\right) utilisés habituellement ?

3.     • En un point voisin  M→′=M→+dM→\overset{→}{M}'=\overset{→}{M}+d\overset{→}{M} ,  le repère local devient  e→i′=e→i+de→i\overset{→}{e}_i'=\overset{→}{e}_i+d\overset{→}{e}_i  ;  on exprime alors les  de→id\overset{→}{e}_i  dans la base des e→i\overset{→}{e}_i :  de→i=Γ.ijkdxje→kd\overset{→}{e}_i=Γ_{\phantom{.}ij}^k \: {dx}^j \:\, \overset{→}{e}_k .
        • Quelle sont les expressions des  Γ.ijkΓ_{\phantom{.}ij}^k  en coordonnées sphériques ?

4.     • On peut par ailleurs considérer que :  Γ.ijke→k=∂je→iΓ_{\phantom{.}ij}^k \; \overset{→}{e}_k=∂_j \overset{→}{e}_i   d’où on déduit :  Γ.ijke→k∙e→𝓁=Γ.ijkgk𝓁=Γ𝓁ijΓ_{\phantom{.}ij}^k \; \overset{→}{e}_k∙\overset{→}{e}_𝓁=Γ_{\phantom{.}ij}^k \: g_{k𝓁}=Γ_{𝓁ij} .
        • Quelle sont les expressions des  Γ𝓁ijΓ_{𝓁ij}  en coordonnées sphériques ?


Dérivations en coordonnées sphériques

1.     • Calculer le tenseur gijg^{ij} en coordonnées sphériques.

2.     • Établir l'expression du gradient en coordonnées sphériques, en fonction de la base orthonormée “usuelle” (u→r,u→θ,u→φ)\left(\overset{→}{u}_r \,,\overset{→}{u}_θ \,,\overset{→}{u}_φ\right) .

3.     • Établir de façon analogue les expressions :
        a) de la divergence ;
        b) du laplacien.


Dérivations en coordonnées sphériques

1.     • Calculer le tenseur gijg^{ij} en coordonnées sphériques.

2.     • À partir de cette métrique et de son déterminant, établir les expressions :
        a) de la divergence ;
        b) du laplacien.


Coordonnées bipolaires

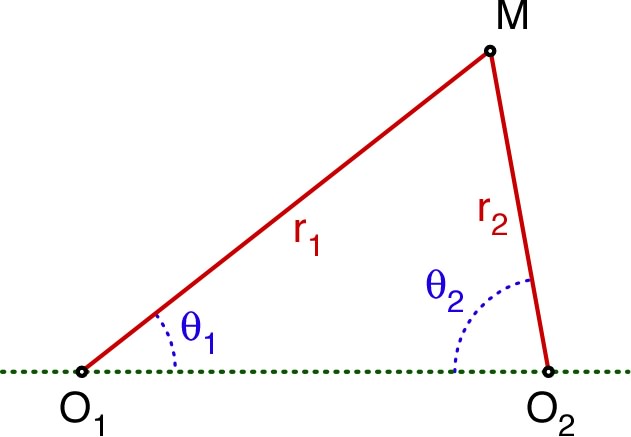
        • On choisit de repérer un point MM du plan à l'aide de ses distances r1r_1 et r2r_2 par rapport à deux origines O1O_1 et O2O_2 (cela ne pose pas d'ambiguïté tant que le point MM ne change pas de côté par rapport à la droite O1O2O_1 O_2 ).
        ◊ remarque : ce type de coordonnées est utile par exemple pour calculer la position d'un objet détecté par deux radars ; une autre démarche consisterait à utiliser les deux angles, mais ce n'est pas le sujet ici.
RiemannPlat_ex_Im/RiemannPlat_ex_Im1.jpg

1.     a) Justifier que le repère local est tel que e→1\overset{→}{e}_1 est orienté comme le vecteur unitaire polaire u→θ2\overset{→}{u}_{θ_2} (et inversement).
        b) En notant  L→=O1O2⟶=O1M⟶−O2M⟶\overset{→}{L}=\overset{⟶}{O_1O_2}=\overset{⟶}{O_1 M}-\overset{⟶}{O_2 M} ,  justifier que :  cos(θ1+θ2)=L2−r12−r222r1r2\displaystyle \cos(θ_1+θ_2 )=\frac{L^2-r_1^{\:2}-r_2^{\:2}}{2 \,r_1 \:r_2} .
        c) Justifier que :  ‖e→1‖=‖e→2‖=1sin(θ1+θ2)=11−(r12+r22−L22r1r2)2\displaystyle \left\|\,\overset{→}{e}_1\right\|=\left‖\,\overset{→}{e}_2 \right‖=\frac{1}{\sin(θ_1+θ_2 )} =\frac{1}{\sqrt{1 - \left(\frac{r_1^{\:2}+r_2^{\:2}-L^2}{2 \,r_1 \:r_2}\right)^2}} .
        d) En considérant en outre  e→1∙e→2\overset{→}{e}_1∙\overset{→}{e}_2 ,  justifier que l’élément de longueur est :
ds2=gijdxidxj=dr12+dr22−2(r12+r22−L22r1r2)dr1dr21−(r12+r22−L22r1r2)2\displaystyle {ds}^2=g_{ij} \: {dx}^i \: {dx}^j=\frac{{dr}_1^{\:2} +{dr}_2^{\:2} - 2 \:\left(\frac{r_1^{\:2}+r_2^{\:2}-L^2}{2 \,r_1 \:r_2}\right) \; dr_1 \:dr_2}{1 - \left(\frac{r_1^{\:2}+r_2^{\:2}-L^2}{2 \,r_1 \:r_2}\right)^2} .

2.     • Par une méthode géométrique, calculer les expressions des  Γ.ijkΓ_{\phantom{.}ij}^k  en coordonnées bipolaires.
        ◊ remarque : il peut être judicieux de passer par l'intermédiaire de  cos(θ1+θ2)\cos(θ_1+θ_2 )  et  sin(θ1+θ2)\sin(θ_1+θ_2 ) .

3.     a) Calculer les expressions des  Γ𝓁ijΓ_{𝓁ij}  en coordonnées bipolaires à partir de la métrique gijg_{ij} .
        b) En déduire une vérification du résultat de la question précédente (vérification non inutile...).


Dérivations en coordonnées sphériques

1.     • Calculer le tenseur gijg^{ij} en coordonnées sphériques.

2.     • Établir l'expression du rotationnel en coordonnées sphériques, en fonction de la base orthonormée “usuelle” (u→r,u→θ,u→φ)\left(\overset{→}{u}_r \,,\overset{→}{u}_θ \,,\overset{→}{u}_φ\right) .

3.     • Établir la notation vectorielle du rotationnel.