MOUVEMENTS DE PARTICULES - corrigé des exercices

Transformation de Lorentz

1.a.	• Rien n'interdit d'utiliser ces notations : bien qu'il est probable qu'elles soient moins pratiques que les coordonnées prévues par la transformation de Lorentz, elles ont au moins l'avantage de correspondre à $x''=0$ pour $x=v\:t$ . Un inconvénient est par contre qu'a priori on ne sait pas comment mesurer ces coordonnées dans $ℛ'$ .

1.b.	• La métrique correspond à : $ds^2=c^2 \,dt^2-dx^2-dy^2-dz^2=\left(c^2-v^2 \right) \:{dt''}^2-2\,v \;dt'' \,dx''-{dx''}^2-{dy'}^2-{dz'}^2$ . Cette métrique étant en principe invariante, les notations proposées paraissent plutôt peu pratiques.

2.a.	• A priori, la synchronisation systématique n'est pas forcément possible car il existe des termes croisés en $dt'' \:dx''$ ; tout dépend du comportement de ce terme le long d'un contour fermé. • Plus précisément, deux événements simultanés, en deux points voisins, sont ainsi séparés par un décalage : $\displaystyle dt''=-\frac{g_{01}}{g_{00}} \:dx''=\frac{v}{c^2-v^2} \:dx''$ . Il se trouve que cette quantité donne toujours un décalage nul pour un déplacement le long d'un contour fermé ; les horloges sont donc synchronisables dans ce cas particulier. ◊ remarque : le coefficient 2 dans la métrique vient de l'égalité des termes en $dx'' \:dt''$ et en $dt'' \:dx''$ intervenant dans la sommation.

2.b.	• La notion locale de distance est décrite par $d𝓁^2=ℊ_{ij} \:dx^i \:dx^j$ avec un tenseur métrique tridimensionnel $\displaystyle ℊ_{ij}=\frac{g_{0i} \:g_{0j}}{g_{00}} -g_{ij}$ . Ainsi : $\displaystyle d𝓁^2=\frac{c^2}{c^2-v^2} \:d{x''}^2+d{y'}^2+d{z'}^2$ .

3.a.	• Pour simplifier la synchronisation des horloges, on peut proposer de “compenser” le décalage en utilisant la notation : $\displaystyle t'''=t''-\frac{v}{c^2-v^2} \:x''=t-v \:\frac{x-v \,t}{c^2-v^2} =\frac{c^2 \,t-v \,x}{c^2-v^2}$ . • Ceci correspond en fait à éliminer les termes croisés dans la métrique : $ds^2=\left(c^2-v^2 \right) \:d{t''}^2-2\,v \:dt''\, dx''-d{x''}^2-d{y'}^2-d{z'}^2$ ; $\displaystyle ds^2=\left(c^2-v^2 \right) \:\left(dt''-\frac{v}{c^2-v^2} \:dx''\right)^2-\frac{c^2}{c^2-v^2} \:d{x''}^2-d{y'}^2-d{z'}^2$ ; $\displaystyle ds^2=\left(c^2-v^2 \right) \:d{t'''}^2-\frac{c^2}{c^2-v^2} \:d{x''}^2-d{y'}^2-d{z'}^2$ . • Afin de retrouver une forme de métrique “plus usuelle” pour un référentiel $ℛ'$ galiléen (en translation rectiligne uniforme par rapport à $ℛ$ galiléen), on peut finalement choisir : $\displaystyle t'=\sqrt{1-\frac{v^2}{c^2}} \;\:t'''=\frac{t-\frac{v}{c^2} \:x}{\sqrt{1-\frac{v^2}{c^2}}}$ (comme la transformation de Lorentz) donnant : $\displaystyle ds^2=c^2 \,d{t'}^2-\frac{c^2}{c^2-v^2} \:d{x''}^2-d{y'}^2-d{z'}^2$ .

3.b.	• La métrique spatiale est maintenant simplement : $\displaystyle d𝓁^2=\frac{c^2}{c^2-v^2} \:d{x''}^2+d{y'}^2+d{z'}^2$ (inchangée).

3.c.	• On peut proposer d'utiliser $\displaystyle x'=\frac{x''}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{x-v\:t}{\sqrt{1-\frac{v^2}{c^2}}}$ ; l'avantage est qu'on retrouve une métrique cartésienne usuelle, ce qui est cohérent avec le fait que $ℛ'$ est galiléen ; en outre, ceci est conforme à la transformation de Lorentz et donne (métrique invariante) : $ds^2=c^2 \,{dt'}^2- d{x'}^2-d{y'}^2-d{z'}^2$ .

Métrique associée à un indice optique

1.a.	• Dans un tel milieu, la description envisagée impose que la partie temporelle de la métrique soit inchangée : $ds^2=c^2 \,dt^2$ pour retrouver les durées “usuelles” indépendamment du milieu. • Afin de décrire la propagation lumineuse à la vitesse $\displaystyle c'=\frac{c}{n}$ il faut par ailleurs obtenir $ds=0$ pour $d𝓁=c' \,dt$ (où $d𝓁$ correspond à la métrique spatiale “usuelle”) ; ceci impose de raisonner à l'aide d'une métrique : $ds^2=c^2 \,dt^2-n^2 \:d𝓁^2$ dont la partie spatiale décrit la quantité nommée “chemin optique” en optique géométrique ou ondulatoire.

1.b.	• Si on veut décrire ainsi d'autres phénomènes, cela pose problème car l'intérieur des objets solides plongés dans le fluide ne sera pas influencé par les propriétés de ce dernier : ce n'est pas l'espace au sens propre qui est modifié par l'indice, mais seulement la propagation de la lumière dans le fluide. Il existera alors inévitablement des dispositifs expérimentaux dont le fonctionnement ne sera pas correctement décrit par la métrique envisagée (en particulier les règles graduées).

2.a.	• Dans ces conditions, la description envisagée impose que la partie temporelle de la métrique soit changée : $ds^2={c'}^2 \,dt^2$ pour retrouver les durées “mesurées” selon le milieu. • Plus précisément, dans une cavité résonante où la lumière se propage moins vite, l'étalon de durée est allongé donc les valeurs des durées “mesurées” sont plus petites (les durées semblent plus courtes). • Afin de décrire la propagation lumineuse à la vitesse $\displaystyle c'=\frac{c}{n}$ il faut par ailleurs obtenir $ds=0$ pour $d𝓁=c' \,dt$ (où $d𝓁$ correspond à la métrique spatiale “usuelle”) ; ceci impose de raisonner à l'aide d'une métrique : $\displaystyle ds^2=\frac{c^2}{n^2} \:dt^2-d𝓁^2$ . ◊ remarque : ceci pourrait être associé à une quantité $\displaystyle \frac{dt}{n}$ nommée “durée optique”.

2.b.	• Si on veut décrire ainsi d'autres phénomènes, cela pose a fortiori problème car l'intérieur des objets solides plongés dans le fluide ne sera pas influencé par les propriétés de ce dernier : il existera inévitablement des dispositifs expérimentaux dont le fonctionnement ne sera pas correctement décrit par la métrique envisagée (en particulier des horloges).

Référentiel d'une particule accélérée par une force constante

1.a.	• Sous l'effet d'une force constante, on peut considérer algébriquement dans $ℛ$ : $\displaystyle f=\frac{dp}{dt}$ ; on en déduit : $\displaystyle p=\frac{m \:v}{\sqrt{1-\frac{v^2}{c^2}}}=f \:t$ , puis : $\displaystyle v=c \:\frac{\frac{f \:t}{m\,c}}{\sqrt{1+\frac{f^2 \,t^2}{m^2 \,c^2}}}$ . • L'intégration donne finalement pour la particule : $\displaystyle x=\frac{m\,c^2}{f} \left(\sqrt{1+\frac{f^2 \,t^2}{m^2 \,c^2}}\: -1\right)$ , ce qui correspond à l'origine du repère associé à $ℛ'$ . • Rien n'interdit d'utiliser ces notations : il n'est pas évident qu'elles soient les plus pratiques, mais elles ont au moins l'avantage de correspondre à $x'=0$ pour $\displaystyle x=\frac{m\,c^2}{f} \left(\sqrt{1+\frac{f^2 \,t^2}{m^2 \,c^2}}\: -1\right)$ . Un inconvénient est par contre qu'a priori on ne sait pas comment mesurer ces coordonnées dans $ℛ'$ . ◊ remarque : on retrouve à l'occasion que l'accélération par une force constante fait tendre la vitesse vers $c$ , sans dépasser cette limite.

1.b.	• La métrique (simplifiée) correspond à : $\displaystyle ds^2=c^2 \,dt^2-dx^2 =\frac{m^2 \,c^4}{m^2 \,c^2+f^2 \,{t'}^2} \:d{t'}^2-2\,c \:\frac{f \:t'}{\sqrt{m^2 \,c^2+f^2 \,{t'}^2}} \:dt' \,dx'-d{x'}^2$ . • Cette métrique étant en principe invariante, les notations proposées paraissent plutôt peu pratiques.

2.a.	• A priori, la synchronisation systématique n'est pas forcément possible car il existe des termes croisés en $dt' \:dx'$ ; tout dépend du comportement de ce terme le long d'un contour fermé. • Plus précisément, deux événements simultanés, en deux points voisins, sont ainsi séparés par un décalage des horloges : $\displaystyle \underset{\quad d}{dt'}=-\frac{g_{01}}{g_{00}} \:dx' =\frac{f \:t'}{m\,c^2} \:\sqrt{1+\frac{f^2 \:{t'}^2}{m^2 \,c^2}} \;\:dx'$ . Cette quantité ne donne pas toujours un décalage nul pour un déplacement le long d'un contour fermé ; les horloges ne sont donc généralement pas synchronisables dans ce cas. ◊ remarque : le coefficient 2 dans la métrique vient de l'égalité des termes en $dx' \:dt'$ et en $dt' \:dx'$ intervenant dans la sommation.

2.b.	• La notion locale de distance est décrite par $d𝓁^2=ℊ_{ij} \:dx^i \:dx^j$ avec un tenseur métrique tridimensionnel $\displaystyle ℊ_{ij}=\frac{g_{0i} \:g_{0j}}{g_{00}} -g_{ij}$ . Ainsi : $\displaystyle d𝓁^2=\frac{m^2 \,c^2+f^2 \:{t'}^2}{m^2 \,c^2} \:d{x'}^2$ .

Référentiel en rotation uniforme

1.a.	• Rien n'interdit d'utiliser ces notations : il n'est pas évident qu'elles soient les plus pratiques, mais elles ont au moins l'avantage de correspondre à $θ'=0$ pour $θ=ω \:t$ . Un inconvénient est par contre qu'a priori on ne sait pas comment mesurer ces coordonnées dans $ℛ'$ .

1.b.	• La métrique correspond à : $ds^2=c^2 \,dt^2-dr^2-r^2 \:dθ^2-dz^2$ ; $ds^2=\left(c^2-{r'}^2 \,ω^2 \right) \;d{t'}^2-2\,{r'}^2 \,ω \;dt' \,dθ'-d{r'}^2-{r'}^2\, d{θ'}^2-d{z'}^2$ . • Cette métrique étant en principe invariante, les notations proposées paraissent plutôt peu pratiques.

2.a.	• A priori, la synchronisation systématique n'est pas forcément possible car il existe des termes croisés en $dt' \:dθ'$ ; tout dépend du comportement de ce terme le long d'un contour fermé. • Plus précisément, deux événements simultanés, en deux points voisins, sont ainsi séparés par un décalage des horloges : $\displaystyle \underset{\quad d}{dt'}=-\frac{g_{02}}{g_{00}} \:dθ' =\frac{{r'}^2 \,ω}{c^2-{r'}^2 ω^2} \:dθ'$ . Il se trouve que cette quantité dépendant de $r'$ ne donne pas toujours un décalage nul pour un déplacement le long d'un contour fermé (indépendamment d'éventuels problèmes dus au fait que $θ$ est “périodique”) ; les horloges ne sont donc pas globalement synchronisables dans ce cas particulier.

2.b.	• La notion locale de distance est décrite par $d𝓁^2=ℊ_{ij} \:dx^i \,dx^j$ avec un tenseur métrique tridimensionnel $\displaystyle ℊ_{ij}=\frac{g_{0i} \:g_{0j}}{g_{00}} -g_{ij}$ . Ainsi : $d𝓁^2=d{r'}^2+\frac{c^2}{c^2-{r'}^2 \,ω^2} \;{r'}^2 \,d{θ'}^2+d{z'}^2$ .

• L'espace-temps existe pour

r≥r_h

puisqu'il y existe des points matériels correspondants utilisés comme référence du référentiel

ℛ

. Aucune particule matérielle fixe par rapport à

ℛ'

ne peut par contre y exister : les particules y ont forcément un mouvement (compensant au moins en partie la rotation de

ℛ'

par rapport à

ℛ

) tel qu'elles aient par rapport à

ℛ

une vitesse inférieure à

c

.
◊ remarque : d'une certaine façon, on peut dire qu'il s'agit dans cette zone d'un repère mais non d'un référentiel : prolongement mathématique symbolique de la partie “physique” de

ℛ'

4.a.	◊ remarque : l'oubli du décalage de synchronisation est envisageable pour un individu qui, au même endroit, assiste à l'émission puis à la réception (mais le fait que ce soit au même endroit ne suffit pas à ce que l'horloge à la réception soit synchronisée “avec elle même” en tant qu'horloge à l'émission). • La propagation de la lumière correspond à $ds^2=c^2 \,dτ^2-d𝓁^2=0$ avec (compte tenu de la synchronisation) : $\displaystyle dτ=\sqrt{1-\frac{R^2 \,ω^2}{c^2}} \;\:\left(dt'-\frac{R^2 ω}{c^2-R^2 \,ω^2} \:dθ'\right)$ et $\displaystyle d𝓁=\frac{1}{\sqrt{1-\frac{R^2 \,ω^2}{c^2}}} \:R \:dθ'$ . Un observateur tenant compte du décalage de synchronisation entre émission et réception calcule $\displaystyle c=\frac{d𝓁}{dτ}$ . • Un observateur fixe omettant le décalage calculerait $\displaystyle dτ_{app}=\sqrt{1-\frac{R^2 \,ω^2}{c^2}} \:\:dt'$ ; or, pour le photon : $c \:dτ=±d𝓁$ (selon le sens du mouvement). On en déduit dans ce cas particulier (le calcul dépend du trajet) : $R \:dθ'=\left(±c-R\:ω\right) \:dt'$ , puis $\displaystyle dτ=\sqrt{\frac{1∓\frac{R\:ω}{c}}{1±\frac{R\:ω}{c}}} \:\:dt'$ . L'observateur calculerait donc une célérité apparente : $\displaystyle c'=\frac{d𝓁}{dτ_{app}}= c \:\frac{dτ}{dτ_{app}}=\frac{c}{1±\frac{R\:ω}{c}}$ .

4.b.	◊ remarque : le cas précédent montre que la différence entre $dτ$ et $dt'$ est du second ordre alors que l'effet étudié est du premier ordre ; ceci justifie l'approximation utilisée pour la généralisation. • En se limitant au premier ordre par rapport à $\displaystyle \frac{r \,ω}{c}$ , la métrique peut s'écrire : $\displaystyle ds^2=c^2 \:\left(dt'-\frac{{r'}^2 \,ω}{c^2} \:dθ'\right)^2-d{r'}^2-{r'}^2 \,d{θ'}^2-d{z'}^2 =c^2 \:\left(dt'-\frac{{r'}^2 \,ω}{c^2} \:dθ'\right)^2-d𝓁^2$ . • Pour un expérimentateur placé au point de départ (et d'arrivée) du photon, la durée locale est $T_{app}=∫dt'$ (la correction du temps local par rapport à $t'$ est du second ordre). Mais pour calculer correctement il doit tenir compte du temps écoulé par rapport aux lieux successivement parcourus par le photon ; il doit donc ajouter (selon le sens de parcours) : $\displaystyle T=T_{app}∓\frac{ω}{c^2} \; ∫{r'}^2 \:dθ'=T_{app}∓\frac{2\,ω\,S}{c^2}$ où $S$ est l'aire délimitée par la projection de la trajectoire sur le plan perpendiculaire à l'axe de rotation. • Pour un trajet de longueur $L=∫d𝓁$ un groupe de physiciens répartis sur le trajet (et synchronisant de proche en proche leurs horloges) calcule ainsi une célérité $\displaystyle c=\frac{L}{T}$ . Au contraire, la célérité apparente en omettant le décalage serait : $\displaystyle c'=\frac{L}{T_{app}} =\frac{c}{1±\frac{2\,ω\,S}{c \:L}}$ . ◊ remarque : on retrouve bien une limite égale à $c$ quand $S→0$ , ce qui est indispensable au principe utilisé pour la synchronisation ; la notion de “durée” n'est pas ambiguë (si on précise bien de laquelle il s'agit) mais il peut y avoir ambiguïté dans la notion de “date” car la durée infinitésimale n'est pas une différentielle totale.

Énergie-impulsion

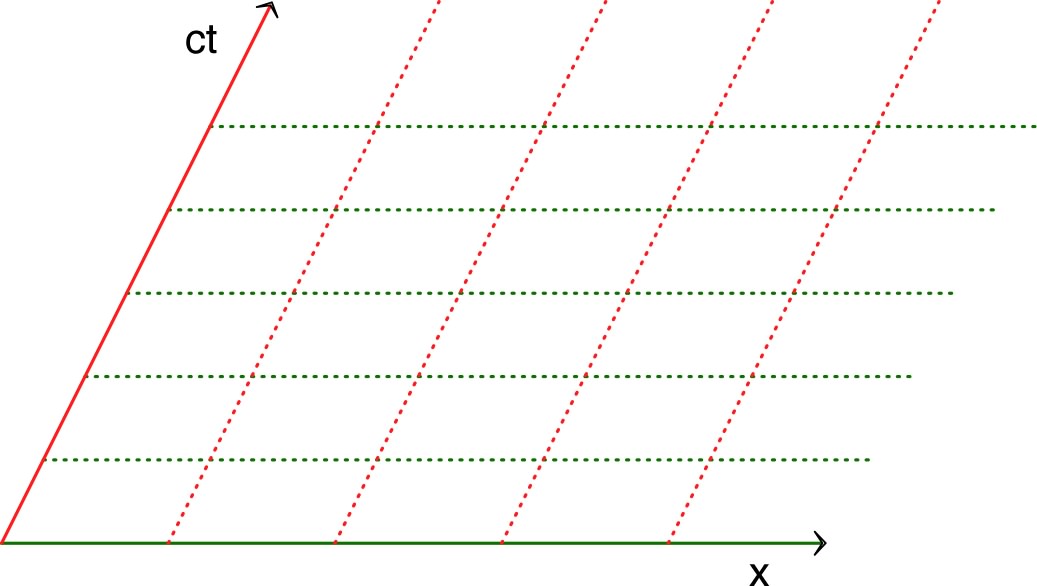
1.a.	• On peut proposer la représentation suivante, où les droites correspondant à $t=Cste$ sont parallèles à l'axe $Ox$ , donc non orthogonales à l'axe du temps.

1.b.	• Puisque $g_{0i}=\overset{↔}{e}_0∙\overset{↔}{e}_i$ , on peut utiliser $\displaystyle \overset{↔}{\underline{e}}_0=\overset{↔}{e}_0-∑_{\,i} \left(\frac{g_{0i}}{g_{ii}} \:\overset{↔}{e}_i\right)$ . Localement (dans un voisinage du point considéré), il peut suffire pour cela de resynchroniser les horloges en ajoutant au temps $t$ une fonction affine des coordonnées spatiales, avec des coefficients choisis de façon à annuler les $g_{0i}$ au point considéré (savoir si cela peut être généralisé à l'ensemble de l'espace-temps est un autre problème). • On obtient ainsi : $\displaystyle \underline{g}_{0i}=\overset{↔}{\underline{e}}_0∙\overset{↔}{e}_i =\overset{↔}{e}_0∙\overset{↔}{e}_i-∑_{\,k} \left(\frac{g_{0k}}{g_{kk}} \:\overset{↔}{e}_k∙\overset{↔}{e}_i \right) =0$ .

2.a.	• Puisque $\displaystyle \overset{↔}{e}_0=\overset{↔}{\underline{e}}_0+∑_{\,i} \left(\frac{g_{0i}}{g_{ii}} \:\overset{↔}{e}_i \right)$ , on obtient : $\overset{↔}{p}=p^0 \:\overset{↔}{\underline{e}}_0+\underset{i}{∑}\left(\underline{p}^i \:\overset{↔}{e_i} \right)$ ; $\underline{p}^0=p^0$ ; $\displaystyle \underline{p}^i=p^i+\frac{g_{0i}}{g_{ii}} \, p^0$ .

2.b.	• Les $g_{ij}$ sont inchangés, par contre : $\displaystyle \underline{g}_{00}=\overset{↔}{\underline{e}}_0∙\overset{↔}{\underline{e}_0} =g_{00}-∑_{\,i}\frac{\left(g_{0i} \right)^2}{g_{ii}}$ donc $\displaystyle \frac{E}{c}=\sqrt{\underline{g}_{00} } \:\:p^0$ .

2.c.	• On obtient en substituant et simplifiant : $\displaystyle \frac{E^2}{c^2} -\overset{↔}{\underline{p}}^2 = g_{00} .\left(p^0 \right)^2 +∑_{\,i} \left(g_{ii} .\left(p^i \right)^2 \right) +2\:∑_{\,i} \left(g_{0i} \:p^0 \,p^i \right) =g_{αβ} \:p^α \,p^β$ .

Énergie-impulsion

1.a.	• Puisque dans ce cas $ds^2=g_{00} .\left(dx^0 \right)^2$ on obtient $\displaystyle \frac{dx^0}{ds}=\frac{1}{\sqrt{g_{00}}}$ donc le 4-vecteur vitesse d'un observateur immobile peut s'écrire : $\displaystyle \overset{↔}{u}_{obs}=\left(\frac{1}{\sqrt{g_{00}}}\,; 0\,; 0\,; 0\right)$ .

1.b.	• On obtient : $\overset{↔}{u}_{obs}∙\overset{↔}{P}=g_{00} \:u_{obs}^0 \:P^0 =\sqrt{g_{00}} \:\,P^0=E$ .

• L'expression précédente a une formulation “covariante”, donc elle reste valable pour désigner l'énergie mesurée par un observateur dans son référentiel propre (où il est immobile), même s'il est en mouvement par rapport au référentiel dans lequel on raisonne.
• On peut toutefois le redémontrer par différentes méthodes ; par exemple en considérant la transformation de Lorentz où on choisit des repères d'espace orthonormés (

g_{11}=g_{22}=g_{33}=-1

), avec un axe

\left(Ox\right)

dans la direction du mouvement de l'observateur.
• Dans ce cas

\displaystyle \overset{↔}{u}_{obs}=γ_{obs} .\left(\frac{1}{\sqrt{g_{00}}}\,; \frac{v_{obs}}{c}\,; 0\,; 0\right)

avec

\displaystyle γ_{obs}=\frac{1}{\sqrt{1-\frac{v_{obs}^2}{c^2}}}

.
• Le raisonnement étant local, la transformation de Lorentz s'applique de façon analogue à la relativité restreinte ; ceci donne :

\displaystyle E'=γ_{obs} .\left(E-c\:p_x \frac{v_{obs}}{c}\right)=g_{00} \:u_{obs}^0 \:P^0+g_{11} \:u_{obs}^1 \:P^1=\overset{↔}{u}_{obs}∙\overset{↔}{P}

.
◊ remarque : il n'y a par contre pas d'expression simple donnant directement (de façon analogue) l'impulsion mesurée par un observateur en mouvement.

Étude lagrangienne et hamiltonienne des géodésiques

1.a.	• La relation $δ\left(\,∫ ds\right)=0$ peut s'écrire $δ\left(\,{\displaystyle{∫}} \sqrt{g_{μν} \:\dot{x}^μ \:\dot{x}^ν\,} \:ds \right) =δ\left(\,∫ ℒ\left(x^α, \dot{x}^β \,\right) \:ds \right)=0$ , avec le lagrangien $\displaystyle ℒ\left(x^α, \dot{x}^β \,\right)=\sqrt{g_{μν} \:\dot{x}^μ \:\dot{x}^ν\,} =\frac{ds\left(x^α, \dot{x}^β \,\right)}{ds}=1$ . ◊ remarque : en toute rigueur $\displaystyle ℒ=m\,c \:\frac{ds\left(x^α, \dot{x}^β \,\right)}{ds}$ car l'action est plutôt $𝒮=m\,c \;∫ ds$ (ici simplifiée).

1.b.	• Cette paramétrisation peut introduire des difficultés d'interprétation dans la mesure où on ajoute une variable $s$ non indépendante des variables $x^μ$ (ces quantités sont contraintes par la métrique). • Un premier effet visible est qu'en utilisant $ℒ=1$ on doit dériver $ℒ$ sans tenir compte de cette propriété (quitte à l'imposer pour simplifier les résultats seulement en fin de calcul) ; cela peut causer des ambiguïtés.

1.c.	• La variation s'écrit : $\displaystyle ∫ \left(\frac{∂ℒ}{∂x^γ} \:δx^γ+\frac{∂ℒ}{∂\dot{x}^γ} \:δ\dot{x}^γ \right) \:ds=0$ . En remarquant que $\displaystyle δ\dot{x}^γ=\frac{d\left(δx^γ \right)}{ds}$ , l'intégration par parties entre deux extrémités fixes donne : $\displaystyle ∫ \left(\frac{∂ℒ}{∂x^γ}-\frac{d}{ds} \left(\frac{∂ℒ}{∂\dot{x}^γ}\right)\right) \:δx^γ \:ds=0$ . • Puisque ceci doit être valable pour toute variation $δx^γ$ , les équations des géodésiques peuvent alors s'écrire : $\displaystyle \frac{∂ℒ}{∂x^γ}=\frac{d}{ds} \left(\frac{∂ℒ}{∂\dot{x}^γ}\right)$ . • On obtient ainsi : $\displaystyle \frac{∂ℒ}{∂\dot{x}^α}=\frac{1}{ℒ} \,g_{αμ} \:\dot{x}^μ$ ; $\displaystyle \frac{∂ℒ}{∂x^α}=\frac{1}{2 \,ℒ} \:∂_α g_{μν} \:\dot{x}^μ \,\dot{x}^ν$ ; $\displaystyle \frac{d}{ds} \left(\frac{∂ℒ}{∂\dot{x}^α}\right)=-\frac{1}{ℒ^2} \frac{dℒ}{ds} \:g_{αμ} \:\dot{x}^μ+\frac{1}{ℒ} \:∂_ν g_{αμ} \:\dot{x}^ν \,\dot{x}^μ+\frac{1}{ℒ} \:g_{αμ} \:\ddot{x}^μ$ ; $\displaystyle \frac{1}{ℒ} \,∂_ν g_{αμ} \:\dot{x}^ν \,\dot{x}^μ=\frac{1}{2 \,ℒ} \:\left(∂_ν g_{αμ}+∂_μ g_{αν} \right) \:\dot{x}^μ \,\dot{x}^ν$ ; $\displaystyle g_{αμ} \ddot{x}^μ+\frac{1}{2} \left(∂_ν g_{αμ}+∂_μ g_{αν}-∂_α g_{μν} \right) \:\dot{x}^μ \,\dot{x}^ν=\frac{1}{ℒ} \frac{dℒ}{ds} \:g_{αμ} \:\dot{x}^μ=0$ . ◊ remarque : lors des variations “quelconques” de l'intégrale, on ne suppose pas $ℒ=1$ ; par contre une fois établies les équations des trajectoires, on sait qu'elles vérifient cette relation, donc : $\displaystyle \frac{dℒ}{ds}=0$ . • Ceci donne finalement : $\ddot{x}^α+Γ_{\phantom{.}μν}^α \:\dot{x}^μ \,\dot{x}^ν=0$ .

1.d.	• Avec la quadri-vitesse $u^α=\frac{dx^α}{ds}$ , cela donne finalement la généralisation d'une accélération nulle : $\displaystyle \frac{du^α}{ds}+Γ_{\phantom{.}μν}^α \:u^μ \,u^ν=\frac{Du^α}{ds}=0$ . • Les équations paramétriques des géodésiques qui ne sont pas du genre lumière correspondent à imposer que le vecteur $u^α$ soit conservé par déplacement géodésique. • Dire qu'un vecteur est conservé par déplacement le long d'une géodésique, c'est dire qu'il ne varie que dans les directions orthogonales : $\displaystyle \frac{DA^α}{ds}=D_μ A^α \:u^μ=0$ (“gradient” perpendiculaire à $u^μ$ ). Le déplacement géodésique s'effectue en conservant la vitesse $u^μ$ .

1.e.	• En utilisant une paramétrisation par $σ$ “quelconque”, la relation $δ\left(\,∫ ds\right)=0$ peut s'écrire : $δ\left(\,{\displaystyle{∫}} \sqrt{g_{μν} \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν\,}\; dσ\right)=δ\left(\,∫ \tilde{ℒ}\left(x^α, \dot{\tilde{x}}^β \,\right) \:ds\right)=0$ . • Avec ce lagrangien $\displaystyle \tilde{ℒ}\left(x^α, \dot{\tilde{x}}^β\, \right)=\frac{ds\left(x^α, \dot{\tilde{x}}^β \,\right)}{dσ}$ , la variation s'écrit : $\displaystyle ∫ \left(\frac{∂\tilde{ℒ}}{∂x^γ} \:δx^γ+\frac{∂\tilde{ℒ}}{∂\dot{\tilde{x}}^γ} \:δ\dot{\tilde{x}}^γ \right) \:dσ=0$ . L'intégration par parties entre deux extrémités fixes donne : $\displaystyle ∫ \left(\frac{∂\tilde{ℒ}}{∂x^γ}-\frac{d}{dσ} \left(\frac{∂\tilde{ℒ}}{∂\dot{\tilde{x}}^γ}\right)\right) \:δx^γ \:dσ=0$ . • Puisque ceci doit être valable pour toute variation $δx^γ$ , les équations des géodésiques peuvent alors s'écrire : $\displaystyle \frac{∂ℒ}{∂x^γ}=\frac{d}{dσ} \left(\frac{∂\tilde{ℒ}}{∂\dot{\tilde{x}}^γ}\right)$ , mais on obtient ainsi : $\displaystyle \frac{∂\tilde{ℒ}}{∂\dot{\tilde{x}}^α}=\frac{1}{\tilde{ℒ}} \:g_{αμ} \:\dot{\tilde{x}}^μ$ ; $\displaystyle \frac{∂\tilde{ℒ}}{∂x^α}=\frac{1}{2 \,\tilde{ℒ}} \:∂_α g_{μν} \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν$ ; $\displaystyle \frac{d}{dσ} \left(\frac{∂\tilde{ℒ}}{∂\dot{\tilde{x}}^α} \right)=-\frac{1}{\tilde{ℒ}^2} \,\frac{d\tilde{ℒ}}{dσ} \:g_{αμ} \:\dot{\tilde{x}}^μ+\frac{1}{\tilde{ℒ}} \: ∂_ν g_{αμ} \:\dot{\tilde{x}}^ν \,\dot{\tilde{x}}^μ+\frac{1}{\tilde{ℒ}} \:g_{αμ} \:\ddot{\tilde{x}}^μ$ ; $\displaystyle \frac{1}{\tilde{ℒ}} \,∂_ν g_{αμ} \:\dot{\tilde{x}}^ν \,\dot{\tilde{x}}^μ=\frac{1}{2 \,\tilde{ℒ}} \:\left(∂_ν g_{αμ}+∂_μ g_{αν} \right) \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν$ ; $\displaystyle g_{αμ} \:\ddot{\tilde{x}}^μ+\frac{1}{2} \left(∂_ν g_{αμ}+∂_μ g_{αν}-∂_α g_{μν} \right) \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν=\frac{1}{\tilde{ℒ}} \frac{d\tilde{ℒ}}{dσ} \:g_{αμ} \:\dot{\tilde{x}}^μ$ . • Ceci donne finalement : $\displaystyle \ddot{\tilde{x}}^α+Γ_{\phantom{.}μν}^α \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν=\frac{1}{\tilde{ℒ}} \frac{d\tilde{ℒ}}{dσ} \:\dot{\tilde{x}}^α≠0$ ; l'équation se simplifie si et seulement si on utilise un paramètre $σ$ affine en fonction de $s$ (ça peut être $τ$ ) : $\ddot{x}^α+Γ_{\:\:\:μν}^α \:\dot{x}^μ \,\dot{x}^ν=0$ . • La quantité $\displaystyle \frac{1}{\tilde{ℒ}} \frac{d\tilde{ℒ}}{dσ}$ est en général non nulle car, s'il est vrai que $\displaystyle \frac{Du^α}{ds}=0$ implique $\displaystyle \frac{Du^α}{dσ}=0$ , on obtient au contraire $\displaystyle \frac{Dυ^α}{dσ}≠0$ pour $\displaystyle υ^α=\frac{dx^α}{dσ}≠\frac{dx^α}{ds}=u^α$ . Plus précisément, le second membre n'est nul que si $\displaystyle \frac{d^2 s}{dσ^2}=0$ et $\displaystyle \frac{ds}{dσ}≠0$ , c'est à dire si $s\left(σ\right)$ est affine (et réciproquement).

• Si on paramètre par

s

, alors

\displaystyle ℒ=\frac{ds}{ds}=1

peut être remplacé par

\underline{ℒ}=ℒ^2=1

dans la mesure où

ℒ^2 \:ds=ℒ \:ds=ds

(le calcul variationnel est différent mais le résultat est le même) ; l'avantage est que cela fait intervenir l'expression de

ds^2

qui ne comporte pas de racine carrée.
• Si on paramètre par

σ

, alors

\displaystyle \tilde{ℒ}=\frac{ds}{dσ}≠1

ne peut pas être remplacé par

\underline{\tilde{ℒ}}=\tilde{ℒ}^2

dans la mesure où

\tilde{ℒ}^2 \:dσ=\tilde{ℒ} \:ds≠ds

3.a.	• Avec le lagrangien $ℒ$ , paramétré par $s$ , les impulsions sont $\displaystyle p_α=\frac{∂L}{∂\dot{x}^α}=\frac{1}{ℒ} \:g_{αμ} \:\dot{x}^μ$ et le hamiltonien est : $\displaystyle ℋ=p_α \:\dot{x}^α-ℒ=\frac{ℒ^2}{ℒ}-ℒ=0$ , ce qui peut sembler étrange. ◊ remarque : cela tient au fait que la méthode “classique” pour trouver l'expression du hamiltonien à partir du lagrangien suppose que ce dernier est quadratique. ◊ remarque : ceci correspond à $p_α=u_α$ parce que l'intégrale d'action a été simplifiée par $m\,c$ ; en toute rigueur $p^α=m\,c \:u^α$ . • Toutefois, outre qu'il faut y exprimer les $\dot{x}^α$ en fonction des $p_α$ , on peut (de façon opportuniste) en profiter pour diviser par 2 (pour retrouver l'utilisation classique) et simplifier $ℒ=1$ à certains endroits : $ℋ=\frac{1}{2} \left(g_{αβ} \,p^α \,p^β-1\right)=0$ (on dérive alors formellement sans tenir compte que $ℋ=0$ , de même qu'on ne tenait pas compte de $ℒ=1$ ). ◊ remarque : en toute rigueur $\displaystyle ℋ=\frac{1}{2\,m\,c} \left(g_{αβ} \,p^α \,p^β-m^2 \,c^2 \right)$ . • Avec ces notations, les équations d'Euler-Lagrange deviennent : $\displaystyle \frac{dp_α}{ds}=-\frac{∂ℋ}{∂x^α}$ (redonnant le même résultat) ; en outre, les relations $\displaystyle \frac{dx_α}{ds}=\frac{∂ℋ}{∂p^α}$ permettent de retrouver $u^α=p^α$ (plus précisément $\frac{p^α}{m\,c}$ ) à partir des notations de Hamilton. • Puisque ce hamiltonien ne dépend pas explicitement de $s$ , on peut croire pouvoir en déduire qu'il décrit une constante du mouvement : $\displaystyle \frac{dℋ}{ds}=\frac{∂ℋ}{∂s}=0$ (par analogie à la dépendance en $t$ dans la paramétrisation non relativiste). Toutefois, cela serait considérer $s$ comme une variable indépendante des $x^α$ , ce qui n'est pas le cas ici (quand on dérive par rapport aux $x^α$ et $p^α$ , cela inclut des effet sur $s$ ). Par contre, on sait que c'est une constante du mouvement puisqu'on obtient $ℋ=0$ (valable sur la trajectoire une fois celle-ci déterminée).

3.b.	• Le lagrangien $\underline{ℒ}$ paramétré par $s$ ne donne pas l'expression “classique” des impulsions (le carré donne un facteur 2 ). On peut par contre utiliser $\underline{ℒ}=\frac{1}{2} ℒ^2$ ; ainsi $\displaystyle p_α=\frac{∂\underline{ℒ}}{∂\dot{x}^α}=g_{αμ} \:\dot{x}^μ$ et le hamiltonien est : $ℋ=p_α \:\dot{x}^α-\underline{ℒ}=\underline{ℒ}$ . Il faut toutefois l'exprimer en éliminant les $\dot{x}^α$ ; on considère donc : $ℋ=\frac{1}{2} g_{αβ} \,p^α \,p^β$ (on dérive formellement sans tenir compte que $ℋ=\underline{ℒ}=\frac{1}{2}$ ). ◊ remarque : en toute rigueur $p^α=m\,c \:u^α$ et $\displaystyle ℋ=\frac{1}{2\,m\,c} \,g_{αβ} \:p^α \,p^β$ sont ici simplifiés. • Avec ces notations, les équations d'Euler-Lagrange deviennent : $\displaystyle \frac{dp_α}{ds}=-\frac{∂ℋ}{∂x^α}$ (redonnant le même résultat) ; en outre, les relations $\displaystyle \frac{dx_α}{ds}=\frac{∂ℋ}{∂p^α}$ permettent de retrouver $u^α=p^α$ (plus précisément $\displaystyle \frac{p^α}{m\,c}$ ) à partir des notations de Hamilton. • Puisque ce hamiltonien ne dépend pas explicitement de $s$ , on peut croire pouvoir en déduire qu'il décrit une constante du mouvement : $\displaystyle \frac{dℋ}{ds}=\frac{∂H}{∂s}=0$ (par analogie à la dépendance en $t$ dans la paramétrisation non relativiste). Toutefois, cela serait considérer $s$ comme une variable indépendante des $x^α$ , ce qui n'est pas le cas ici (quand on dérive par rapport aux $x^α$ et $p^α$ , cela inclut des effet sur $s$ ). Par contre, on sait que c'est une constante du mouvement puisqu'on obtient $ℋ=\frac{1}{2}$ (valable sur la trajectoire une fois celle-ci déterminée).

Étude lagrangienne des géodésiques

• La relation

δ\left(\,∫ ds\right)=0

peut s'écrire

δ\left(\,{\displaystyle{∫}} \sqrt{g_{μν} \:\dot{x}^μ \,\dot{x}^ν\,} \:dt\right)=δ\left(\,∫ ℒ\left(x^α, \dot{x}^β\,\right) \:dt\right)=0

, avec le lagrangien

\displaystyle ℒ\left(x^α, \dot{x}^β \,\right)=\sqrt{g_{μν} \:\dot{x}^μ \,\dot{x}^ν\,} =\frac{ds\left(x^α, \dot{x}^β\,\right)}{dt}

; toutefois

x^0=c\,t

n'est pas une fonction inconnue à faire varier et

\dot{x}^0=c

est une constante.
◊ remarque : en toute rigueur

\displaystyle ℒ=m\,c \:\frac{ds}{dt}

car l'action est plutôt

𝒮=m\,c\:∫ ds

(ici simplifiée) ; en relativité restreinte, on utilise même

𝒮=-m\,c\:∫ ds

pour obtenir les variables conjuguées

\displaystyle p_i=\frac{∂ℒ}{∂\dot{x}^i}

telles que

p^i=η^{ij} \:p_j

avec

η^{ii}=-1

redonne l'impulsion “classique” pour la limite non relativiste.

• La variation s'écrit :

\displaystyle ∫ \left(\frac{∂ℒ}{∂x^k} \:δx^k+\frac{∂ℒ}{∂\dot{x}^k} \:δ\dot{x}^k \right)\:dt=0

. En remarquant que

\displaystyle δ\dot{x}^k=\frac{d\left(δx^k\right)}{dt}

, l'intégration par parties entre deux extrémités fixes donne :

\displaystyle ∫ \left(\frac{∂ℒ}{∂x^k}-\frac{d}{dt} \left(\frac{∂ℒ}{∂\dot{x}^k}\right)\right) \:δx^k \:dt=0

.
• Puisque ceci doit être valable pour toute variation

δx^k

, les équations des géodésiques peuvent alors s'écrire :

\displaystyle \frac{∂ℒ}{∂x^i}=\frac{d}{dt} \left(\frac{∂ℒ}{∂\dot{x}^i}\right)

.
• On obtient ainsi :

\displaystyle \frac{∂ℒ}{∂\dot{x}^i}=\frac{1}{ℒ} \,g_{iμ} \:\dot{x}^μ

;

\displaystyle \frac{∂ℒ}{∂x^i}=\frac{1}{2\,ℒ} \:∂_i g_{μν} \:\dot{x}^μ \,\dot{x}^ν

;

$\displaystyle \frac{d}{dt} \left(\frac{∂ℒ}{∂\dot{x}^i}\right)=-\frac{1}{ℒ^2} \frac{dℒ}{dt} \,g_{iμ} \:\dot{x}^μ+\frac{1}{ℒ} \,∂_ν g_{iμ} \:\dot{x}^ν \,\dot{x}^μ+\frac{1}{ℒ} \,g_{iμ} \:\ddot{x}^μ$ ;
$\displaystyle \frac{1}{ℒ} \,∂_ν g_{iμ} \:\dot{x}^ν \,\dot{x}^μ=\frac{1}{2 \,ℒ} \:\left(∂_ν g_{iμ}+∂_μ g_{iν} \right)\: \dot{x}^μ \,\dot{x}^ν$ ;
$\displaystyle g_{iμ} \:\ddot{x}^μ+\frac{1}{2} \left(∂_ν g_{iμ}+∂_μ g_{iν}-∂_i g_{μν} \right) \:\dot{x}^μ \,\dot{x}^ν=\frac{1}{ℒ} \frac{dℒ}{ds} \:g_{iμ} \:\dot{x}^μ$ .

• Si la métrique n'a pas de termes croisés spatio-temporels :

g^{ki} \:g_{iμ}=δ_μ^k-g^{k0} \:g_{0μ}=δ_μ^k

. En notant

\displaystyle v^μ=\frac{dx^μ}{dt}

, ceci donne finalement :

\displaystyle \frac{dv^i}{dt}+Γ_{\,\,μν}^i \;v^μ \:v^ν =\frac{Dv^i}{dt}=\frac{1}{ℒ} \frac{dℒ}{dt} \:v^i

. Or, cette équation peut aussi s'écrire :

\displaystyle \frac{D}{dt} \left(\frac{v^i}{ℒ}\right)=\frac{Du^i}{dt}=0

, avec

\displaystyle u^i=\frac{dx^i}{ds}

; on retrouve ainsi :

\displaystyle \frac{Du^i}{ds}=0

.
• Par ailleurs :

u_α \,u^α=1

donc

\displaystyle \frac{D}{ds} \left(u_α u^α \right) =2 \:u_α \frac{Du^α}{ds}=2\:u_0 \frac{Du^0}{ds}+2 \:u_i \frac{Du^i}{ds}=0

; finalement ceci impose aussi :

\displaystyle \frac{Du^0}{ds}=0

.
◊ remarque : la description hamiltonienne correspondante est par contre peu évidente.

Géodésiques du genre “lumière”

1.a.	• Pour obtenir une courbe du genre “lumière”, il suffit de considérer une courbe quelconque, puis d'imposer qu'un photon (imaginaire) la décrive à la vitesse de la lumière ; ceci redonne automatiquement $ds=0$ . Il est par contre évident que ceci ne donne généralement pas une géodésique.

1.b.	• Il est assez évident que la lumière, déviée par le champ gravitationnel, ne se propage pas en ligne droite (c'est un des apports importants de la relativité générale). • Par ailleurs, dans un espace courbe, les projections spatiales des géodésiques d'espace-temps ne sont pas forcément des géodésiques d'espace ; la lumière ne suit donc généralement pas des géodésiques d'espace (même s'ils décrivent des effets de déviation, ce ne sont pas forcément les bons). On ne peut donc pas répondre a priori sans préciser les raisonnements.

2.a.	• La quadri-vitesse $\displaystyle u^α=\frac{dx^α}{ds}$ est unitaire : $\left‖dx^α \right‖=ds$ ; $\left‖u^α \right‖=1$ . Mais pour un photon $ds=0$ donc non seulement la norme est indéterminée, mais les composantes sont infinies ; il est donc indispensable d'utiliser un autre paramétrage que $ds$ .

2.b.	• La relation $δ\left(\,∫ ds\right)=0$ peut s'écrire $δ\left(\,{\displaystyle{∫}} \sqrt{g_{μν} \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν\,} \:dσ\right)=0$ . • Les équations des géodésiques peuvent alors s'écrire : $\displaystyle \frac{d}{dσ}\left(\frac{∂\tilde{ℒ}}{∂\dot{\tilde{x}}^α}\right) =\frac{∂\tilde{ℒ}}{∂x^α}$ . • On obtient ainsi : $\displaystyle \frac{∂\tilde{ℒ}}{∂\dot{\tilde{x}}^α}=\frac{1}{\tilde{ℒ}} \,g_{αμ} \:\dot{\tilde{x}}^μ$ ; $\displaystyle \frac{∂\tilde{ℒ}}{∂x^α}=\frac{1}{2 \,\tilde{ℒ}} \:∂_α g_{μν} \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν$ ; $\displaystyle \frac{d}{dσ} \left(\frac{∂\widetilde{ℒ}}{∂\dot{\tilde{x}}^α}\right) =-\frac{1}{\tilde{ℒ}^2} \frac{d\tilde{ℒ}}{dσ} \:g_{αμ} \:\dot{\tilde{x}}^μ+\frac{1}{\tilde{ℒ}} \,∂_ν g_{αμ} \:\dot{\tilde{x}}^ν \,\dot{\tilde{x}}^μ+\frac{1}{\tilde{ℒ}} \,g_{αμ} \:\dot{\tilde{x}}^μ$ ; $\displaystyle \frac{1}{\tilde{ℒ}} \,∂_ν g_{αμ} \:\dot{\tilde{x}}^ν \,\dot{\tilde{x}}^μ=\frac{1}{2 \,\tilde{ℒ}} \:\left(∂_ν g_{αμ}+∂_μ g_{αν} \right) \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν$ ; $\displaystyle g_{αμ} \:\ddot{\tilde{x}}^μ+\frac{1}{2} \,(∂_ν g_{αμ}+∂_μ g_{αν}-∂_α g_{μν} ) \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν=\frac{1}{\tilde{ℒ}} \frac{d\tilde{ℒ}}{dσ} \:g_{αμ}\:\dot{\tilde{x}}^μ$ . • Ceci donne finalement : $\ddot{\tilde{x}}^α+Γ_{\phantom{.}μν}^α \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν=κ(σ) \:\dot{\tilde{x}}^α$ avec $\displaystyle κ(σ)=\frac{1}{\tilde{ℒ}} \frac{d\tilde{ℒ}}{dσ}$ . • Bien sûr, on peut en principe calculer la quantité $κ(σ)$ ; le problème est alors toutefois qu'il subsiste une indétermination : $\displaystyle κ(σ)→\frac{0}{0}$ dans la limite $ds=0$ , donc cette méthode nécessite d'être étudiée plus en détail. ◊ remarque : par contre, ceci n'interdit pas forcément la résolution en pratique : lorsqu'on exprime ces équations dans certains cas particuliers, des simplification opportunes peuvent apparaître et rendre les équations utilisables.

2.c.	• Pour simplifier ainsi, il faudrait un paramètre $σ$ tel que $\displaystyle \frac{d\tilde{ℒ}}{dσ}=\frac{d^2 s}{dσ^2}=0$ et $\displaystyle \tilde{ℒ}=\frac{ds}{dσ}≠0$ , c'est à dire affine en fonction de $s$ (et réciproquement). Or ceci ne peut paramétrer la courbe puisque $ds=0$ pour une géodésique du genre “lumière”.

2.d.	• Si on paramètre par $s$ , alors $\displaystyle ℒ=\frac{ds}{ds}=1$ peut aussi bien être remplacé par $\underline{ℒ}=ℒ^2=1$ dans la mesure où $ℒ^2 \:ds=ℒ \:ds=ds$ (le calcul variationnel est différent mais le résultat est le même) ; l'avantage est que cela fait intervenir l'expression de $ds^2$ qui ne comporte pas de racine carrée. • Si on paramètre par $σ$ , alors $\displaystyle \tilde{ℒ}=\frac{ds}{dσ}≠1$ ne peut pas être remplacé par $\underline{\tilde{ℒ}}=\tilde{ℒ}^2$ dans la mesure où $\tilde{ℒ}^2 \:dσ=\tilde{ℒ} \:ds≠ds$ .

2.e.	• En remarquant que $ds^2=c^2 \,dτ^2=c^2 \,dt_{𝓁oc}^2-d𝓁^2$ , où $dt_{𝓁oc}=\sqrt{g_{00}} \;dt$ décrit le temps local (si on se limite au cas d'une métrique diagonale), on peut écrire $ds=c \,dt_{𝓁oc} \:\sqrt{1-β^2}$ avec $\displaystyle β=\frac{v}{c}$ ; c'est de ce terme que provient l'indétermination dans le cas des photons. • L'action peut s'écrire sous la forme : $𝒮=m\,c \:∫ ds=m\,c\;{\displaystyle{∫}} \sqrt{g_{μν} \:u^μ \,u^ν\,} \;ds={\displaystyle{∫}} \sqrt{g_{μν} \:p^μ \,p^ν\,} \;ds$ avec l'impulsion $\displaystyle p^μ=m\,c \:u^μ=\frac{m}{\sqrt{1-β^2}} \,\frac{dx^μ}{dt_{𝓁oc}}$ . L'indétermination de $u^μ$ provient de la limite $β→1$ quand $m→0$ . • Par analogie avec la relativité restreinte, le passage à la limite pour les photons correspond alors à substituer : $\displaystyle \frac{m}{\sqrt{1-β^2}}←\frac{h\,ν}{c^2}$ .

2.f.	• En relativité générale, la fréquence varie : pour un intervalle de variable $Δt$ délimitant une période, la durée locale de la période peut s'écrire $T=\sqrt{g_{00}} \;Δt$ , donc la fréquence peut s'écrire : $\displaystyle ν=\frac{ν_∞}{\sqrt{g_{00}}}$ en notant $ν_∞$ la fréquence qui serait observée à l'infini (dans la mesure où le champ de gravitation y est nul). On peut donc proposer d'écrire pour un photon : $\displaystyle p^μ=\frac{h\,ν_∞}{c} \,\frac{dx^μ}{dς}$ avec $dς=g_{00} \:c \,dt$ . ◊ remarque : ici $dς=dx_0$ et d'ailleurs plus généralement avec $g_{0i}≠0$ on obtient $dς=g_{0ν} \:dx^ν$ . • Ceci consiste à écrire l'action pour un photon : $\displaystyle 𝒮=\frac{h\,ν_∞}{c} ∫ \frac{ds}{dς} \,ds$ avec un lagrangien $\displaystyle \tilde{ℒ}=\frac{ds}{dς}≠\frac{ds}{ds}$ ; or, ceci peut aussi s'écrire $\displaystyle 𝒮=\frac{h\,ν_∞}{c} \:∫ \tilde{ℒ}^2 dς$ , mais avec un paramètre $ς$ bien particulier (permettant la simplification). Il est clair que ceci évite l'indétermination de $\displaystyle u^μ=\frac{dx^μ}{ds}$ ; il reste toutefois à savoir si cela évite l'intervention d'un terme $\displaystyle κ(ς)=\frac{1}{\underline{\tilde{ℒ}}} \,\frac{d\underline{\tilde{ℒ}}}{dς}$ (qui dans ce cas reste indéterminé). • En notant $\displaystyle \dot{\tilde{x}}^μ=\frac{dx^μ}{dς}$ , on est ramené à étudier la condition : $δ\left(∫ g_{μν} \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν \:dς\right)=0$ correspondant à $\underline{\tilde{ℒ}}=\tilde{ℒ}^2=g_{μν} \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν$ . On obtient ainsi les équations : $\displaystyle \frac{d}{dς} \left(\frac{∂\underline{\tilde{ℒ}}}{∂\dot{\tilde{x}}^α}\right) =\frac{∂\underline{\tilde{ℒ}}}{∂x^α}$ avec : $\displaystyle \frac{∂\underline{\tilde{ℒ}}}{∂x^α}=∂_α g_{μν} \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν$ ; $\displaystyle \frac{∂\underline{\tilde{ℒ}}}{∂\dot{\tilde{x}}^α}=2 \:g_{αμ} \:\dot{\tilde{x}}^μ$ ; $\displaystyle \frac{d}{dς}\left(\frac{∂\underline{\tilde{ℒ}}}{∂\dot{\tilde{x}}^α}\right) =2 \:∂_ν g_{αμ} \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν+2 \:g_{αμ} \:\ddot{\tilde{x}}^μ=\left(∂_ν g_{αμ}+∂_μ g_{αν} \right) \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν+2 \:g_{αμ} \:\ddot{\tilde{x}}^μ$ ; $2\:g_{αμ} \:\ddot{\tilde{x}}^μ+\left(∂_ν g_{αμ}+∂_μ g_{αν} \right) \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν=∂_α g_{μν} \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν$ ; $\ddot{\tilde{x}}^α+Γ_{\phantom{.}μν}^α \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν=0$ . • On constate ainsi que les équations se simplifient de façon analogue à celles des géodésiques qui ne sont pas du genre lumière, mais ici en fonction du paramètre particulier $ς≠s$ . Ceci peut s'écrire sous la forme $\displaystyle \frac{Dυ^α}{dς}=0$ avec $\displaystyle υ^α=\frac{dx^α}{dς}$ telle que $\left‖υ^α \right‖=0$ ; $\tilde{ℒ}=0$ ; $\underline{\tilde{ℒ}}=0$ (donc constantes du mouvement). ◊ remarque : les paramètres pour lesquels les équations se simplifient ainsi sont souvent nommés, parfois à tort, “paramètres affines” ; certes, pour les particules de masse non nulle, la simplification nécessite que la trajectoire soit décrite à l'aide d'un paramètre dont l'expression en fonction de $s$ est affine, mais ici ce n'est pas le cas : la simplification nécessite la description par $ς$ qui n'est pas affine en fonction de $s$ . ◊ remarque : on peut aussi partir de l'hypothèse qu'il existe un paramètre $ς$ permettant une telle simplification, puis résoudre les équations du mouvement correspondant ; si l'hypothèse n'est pas incohérente, on obtient alors en particulier la relation donnant $t\left(ς\right)$ , mais cela ne suffit pas forcément pour justifier une telle hypothèse.

• Le lagrangien

\underline{\tilde{ℒ}}

, paramétré par

ς

, ne donne pas l'expression “classique” des impulsions (le carré donne un facteur 2 ). On peut par contre utiliser

\underline{\tilde{ℒ}}=\frac{1}{2} \,\tilde{ℒ}^2

; ainsi

\displaystyle p_α=\frac{∂\underline{\tilde{ℒ}}}{∂\dot{\tilde{x}}^α} =g_{αμ} \:\dot{\tilde{x}}^μ

et le hamiltonien est :

ℋ=p_α \:\dot{\tilde{x}}^α-\underline{\tilde{ℒ}}=\underline{\tilde{ℒ}}=0

. Toutefois, il faut exprimer en éliminant les

\dot{\tilde{x}}^α

; on considère donc :

ℋ=\frac{1}{2} \,g_{αβ} \:p^α \,p^β

(on dérive formellement sans tenir compte que

ℋ=\underline{\tilde{ℒ}}=0

).
◊ remarque : en toute rigueur

\displaystyle p^α=\frac{h\,ν_∞}{c} \,υ^α

\displaystyle ℋ=\frac{c}{2\,h\,ν_∞} \,g_{αβ} \:p^α \,p^β

sont ici simplifiés.
• Avec ces notations, les équations d'Euler-Lagrange deviennent :

\displaystyle \frac{dp_α}{dς}=-\frac{∂ℋ}{∂x^α}

(redonnant le même résultat) ; en outre, les relations

\displaystyle \frac{dx_α}{dς}=\frac{∂ℋ}{∂p^α}

permettent de retrouver

υ^α=p^α

(plus précisément

\displaystyle \frac{c\,p^α}{h\,ν_∞}

) à partir des notations de Hamilton.

4.a.

• On peut utiliser le lagrangien :

\underline{\tilde{ℒ}}=A\left(r\right) \:c^2 \:\dot{\tilde{t}}^2-C\left(r\right) \:\dot{\tilde{r}}^2-r^2 \:\dot{\tilde{θ}}^2-r^2 \:\sin^2\left(θ\right) \:\dot{\tilde{φ}}^2

avec un paramètre

σ

(à préciser ultérieurement). En choisissant un repérage judicieusement adapté aux conditions initiales, on obtient un mouvement dans le plan

θ=\frac{π}{2}

; ainsi :

\underline{\tilde{ℒ}}=A\left(r\right) \:c^2 \:\dot{\tilde{t}}^2-C\left(r\right) \:\dot{\tilde{r}}^2-r^2 \:\dot{\tilde{φ}}^2

.
• Les équations du mouvement peuvent s'écrire sous la forme d'Euler-Lagrange :

$\displaystyle \frac{d}{dσ} \left(\frac{∂\underline{\tilde{ℒ}}}{∂\dot{\tilde{t}}}\right) =\frac{∂\underline{\tilde{ℒ}}}{∂t}$ ; $\displaystyle \frac{d}{dσ} \left(\frac{∂\underline{\tilde{ℒ}}}{∂\dot{\tilde{r}}}\right) =\frac{∂\underline{\tilde{ℒ}}}{∂r}$ ; $\displaystyle \frac{d}{dσ} \left(\frac{∂\underline{\tilde{ℒ}}}{∂\dot{\tilde{φ}}}\right) =\frac{∂\underline{\tilde{ℒ}}}{∂φ}$ .

• La première équation donne :

A \:c \:\dot{\tilde{t}} =g_{00} \:c \frac{dt}{dσ}=Cste

, donc

σ

est affine en fonction de

ς

; si on choisit de paramétrer par

ς

, on obtient :

A \:c \:\dot{\tilde{t}} =1

.
◊ remarque : ceci revient à dire que, si on suppose qu'il existe un

σ

particulier tel que les équations se simplifient en :

\ddot{\tilde{x}}^α+Γ_{\phantom{.}μν}^α \:\dot{\tilde{x}}^μ \,\dot{\tilde{x}}^ν=0

, alors la résolution redonne automatiquement

σ

affine en fonction de

ς

.
• La troisième équation donne :

r^2 \:\dot{\tilde{φ}}=K=Cste

.
• La seconde équation donne :

-2 \,\dot{\tilde{C}} \:\dot{\tilde{r}}-2 \,C\:\ddot{\tilde{r}}=A' \,c^2 \,\dot{\tilde{t}}^2-C' \,\dot{\tilde{r}}^2-2\,r \,\dot{\tilde{φ}}^2

, mais

C' \,\dot{\tilde{r}}=\dot{\tilde{C}}

donc ceci peut s'écrire :

- \dot{\tilde{C}} \:\dot{\tilde{r}}-2\, C \:\ddot{\tilde{r}} =A' c^2 \,\dot{\tilde{t}}^2-2\,r \,\dot{\tilde{φ}}^2

; on en déduit :

-\dot{\widetilde{C \:\dot{\tilde{r}}^2}}=\frac{\dot{\tilde{A}}}{A^2} -K^2 \:\frac{2 \,\dot{\tilde{r}}}{r^3}

. Compte tenu de

\displaystyle C=\frac{1}{A}

, ceci s'intègre en :

\displaystyle C-C \:\dot{\tilde{r}}^2-\frac{K^2}{r^2} =Cste

.
• Mais on peut y parvenir plus simplement :

ds^2=0

donne ici

A\left(r\right) \:c^2 \,\dot{\tilde{t}}^2-C\left(r\right) \:\dot{\tilde{r}}^2-r^2 \:\dot{\tilde{φ}}^2=0

, dont on peut déduire :

\displaystyle C-C \:\dot{\tilde{r}}^2-\frac{K^2}{r^2} =0

.
• Les équations paramétriques des géodésiques du genre lumière peuvent donc s'écrire :

$\displaystyle \frac{dr}{dς}=\sqrt{1-A \,\frac{K^2}{r^2}}$ ; $\displaystyle \frac{dφ}{dς}=\frac{K}{r^2}$ ; avec par ailleurs : $\displaystyle d𝓁=c \:dt_{𝓁oc}=\sqrt{A} \;c\:dt=\frac{dς}{\sqrt{A}}$ .

4.b.

• Pour les géodésiques qui ne sont pas du genre lumière, le lagrangien devrait conduire à déterminer les variations des

x^i \left(t\right)

. L'usage de notations invariantes relativistes conduit à étudier les

x^α \left(s\right)

qui ne sont pas indépendantes, puisque reliées par l'expression

ds^2

. Toutefois, on ne fait ainsi qu'introduire une équation de plus avec une inconnue de plus : il faut déterminer

∫ ds

.
• Pour les géodésiques du genre lumière, il n'y a pas cette inconnue supplémentaire car

∫ ds=0

, par contre la contrainte supplémentaire impose la variable

ς

en imposant

t\left(ς\right)

Principe d'équivalence et mécanique quantique

• En l'absence d'effets électromagnétiques, le principe d'équivalence conduit à des équations du mouvement dans lesquelles la masse se simplifie. Cela a pour conséquence qu'il est impossible d'utiliser les propriétés du mouvement libre “non quantique” pour déterminer la masse d'une particule.
◊ remarque : cette indépendance de la masse n'est pas totale puisque les photons, particules de masse nulle, ont des mouvements différents.
• Au contraire, l'équation de Schrödinger fait intervenir une masse inerte (dans le terme

\displaystyle \frac{ℏ^2}{2\,m}

provenant de

\displaystyle \frac{p^2}{2\,m}

) et une masse pesante (dans le terme

m\:𝒱

) égales, mais ne se simplifiant pas. Ceci a pour conséquence qu'il est possible d'utiliser les propriétés quantiques du mouvement sous l'effet de la pesanteur pour déterminer la masse d'une particule. Cela a été réalisé pour des neutrons froids.

• L'équation de Schrödinger est une approximation non relativiste, pour les faibles vitesses, mais si la relation relativiste permettait la simplification, alors sa limite non relativiste le permettrait aussi.
• La pesanteur décrit une approximation non relativiste d'un mouvement relativiste libre, mais si la loi relativiste correspondante permettait la simplification, alors sa limite non relativiste le permettrait aussi.

Limite de l'approximation newtonienne

• Le lagrangien newtonien peut s'écrire

L=E_c-E_p=\frac{1}{2} \,m \,v^2-m \,𝒱

, où

𝒱

est le potentiel gravitationnel. Toutefois, pour comparer à la limite du cas relativiste, il est plus pratique d'incorporer l'énergie de masse (constante, donc sans effet sur la limite newtonienne) :

L=-m\,c^2+\frac{1}{2} \,m \,v^2-m \,𝒱

.
• L'action newtonienne peut donc s'écrire :

𝒮=∫ \,L •,dt=-m\,c \,{\displaystyle{∫ \left(c-\frac{v^2}{2\,c}+\frac{𝒱}{c}\right) \:dt}}

; ceci est à comparer avec l'action de la relativité générale :

𝒮=-m\,c\;∫ ds

.
• La correspondance dans le cas limite impose :

\displaystyle ds=\left(c-\frac{v^2}{2\,c}+\frac{𝒱}{c}\right) \:dt

; en élevant au carré et en limitant à l'ordre le plus bas par rapport aux vitesses et au potentiel (les autres termes disparaissent dans la limite

c→∞

), ceci peut s'écrire :

\displaystyle ds^2=\left(1+\frac{2\,𝒱}{c^2} \,\right) \:c^2 \,dt^2-d𝓁^2

(avec

d𝓁=v \:dt

).
• La limite newtonienne correspond donc à :

\displaystyle g_{00}≈1+\frac{2\,𝒱}{c^2}

;

g_{0i}≈0

;

g_{ij}≈η_{ij}

2.a.	• En l'absence de champ de gravitation, la relativité restreinte peut être décrite par un lagrangien de la forme $\displaystyle L=-m\,c^2 \:\sqrt{1-\frac{v^2}{c^2}}$ correspondant à l'action $𝒮=-m\,c\;∫ ds$ (mais où $ds^2=η_{αβ} \:dx^α \,dx^β$ car la métrique n'est pas considérée comme variable). ◊ remarque : la limite pour les faibles vitesses est : $L≈-m\,c^2+\frac{1}{2} \,m \,v^2$ . • Si on veut décrire la gravitation dans l'approximation de la relativité restreinte (vitesses non faibles, mais champ faible), il faut ajouter dans l'action un terme décrivant la gravitation sans passer par la métrique. • Ce terme est forcément un scalaire (invariant par changement de référentiel). S'il dépendait de la vitesse, il ne serait pas de la forme $A_μ \,u^μ$ car cela correspond déjà au cas du champ électromagnétique, ni de forme tensorielle $A_{αβ} \:u^α \,u^β$ car cela aboutirait à une théorie de type relativité générale. C'est donc raisonnablement une fonction de la position seulement (sorte de potentiel de gravitation), correspondant à l'action : $\displaystyle 𝒮=-m\,c \;∫ \left(1+\frac{𝒱}{c^2} \right) \:ds$ et au lagrangien : $\displaystyle L=-m \,.\left(c^2+𝒱\right) \:\sqrt{1-\frac{v^2}{c^2}}$ . ◊ remarque : pour les faibles vitesses, puisqu'on étudie ici le champ faible, on peut négliger le terme de second ordre croisé en $𝒱$ et $v^2$ , ce qui redonne le lagrangien de la question précédente. • Ceci est à comparer avec l'action de la relativité générale : $𝒮=-m\,c\;∫ ds$ (mais dans laquelle $ds^2=g_{αβ} \:dx^α \,dx^β$ car la métrique est considérée comme variable). • La correspondance dans le cas limite impose : $\displaystyle ds=\left(c+\frac{𝒱}{c}\right) \;\sqrt{1-\frac{v^2}{c^2}} \:\,dt$ ; en élevant au carré et en limitant à l'ordre le plus bas par rapport au potentiel (les autres termes disparaissent dans la limite $c→∞$ ), ceci peut s'écrire sous la forme : $\displaystyle ds^2=\left(1+\frac{2\,𝒱}{c^2} \,\right)\:\left(c^2 \,dt^2-d𝓁^2\right)$ . • La limite en relativité restreinte correspondrait donc à : $\displaystyle g_{αβ}≈\left(1+\frac{2\,𝒱}{c^2} \right) \:η_{αβ}$ . ◊ remarque : il s'agit d'une métrique “localement plane” avec seulement un “facteur d'échelle” dépendant du lieu.

2.b.	• La comparaison montre que la limite newtonienne calculée était plausible : l'influence de $g_{ij}$ est d'ordre supérieur pour un champ faible et des faibles vitesses. • Par contre, la tentative de généraliser le traitement du champ gravitationnel faible en relativité restreinte pose problème : même à champ faible, la description des grandes vitesses ne peut se faire que dans le cadre de la relativité générale (par exemple, la relativité restreinte ne prévoit aucune déviation par le champ de gravitation pour des photons passant à proximité d'une étoile).

Charge totale

• La coordonnée temporelle du quadrivecteur densité de courant

\displaystyle j^μ=ρ\: \frac{dx^μ}{dt_{𝓁oc}}

décrit la grandeur physique associée :

\displaystyle \sqrt{g_{00}} \:\,j^0=\sqrt{g_{00}} \:\,ρ \,\frac{dx^0}{dt_{𝓁oc}}=ρ \,c

(comme en relativité restreinte).
• En intégrant cette densité de charge on définit la charge totale :

Q=∫ ρ \;d^3 𝒱={\displaystyle{∫ \:\frac{\sqrt{g_{00}}}{c} \:j^0 \;d^3 𝒱}}

avec le volume élémentaire

d^3 𝒱=\sqrt{ℊ} \:\,d^3 x

.
◊ remarque : bien qu'elle soit souvent négligeable, il faut si nécessaire tenir compte de l'influence de l'énergie du champ électrique sur la géométrie de l'espace-temps.

• On peut calculer

\displaystyle \left‖ \:\overleftrightarrow{j} \:\right‖=\sqrt{g_{μν} \:j^μ \,j^ν\,} =ρ \,c \,\frac{dτ}{dt_{𝓁oc}}=\frac{1}{γ} \,ρ \,c=ρ_0 \,c

. Cette quantité est scalaire car elle tient compte de la contraction associée au mouvement de l'élément de volume considéré : ainsi elle exprime ce que serait

ρ

en mesurant dans son référentiel propre.
• Ceci n'est toutefois pas ce qui nous intéresse si on souhaite déterminer la charge totale contenue dans un volume donné. Lorsqu'on intègre sur ce volume, on utilise ses limites telles qu'elles sont perçues dans le référentiel où on raisonne, donc il faut utiliser

ρ

(pour utiliser

ρ_0

il faudrait se baser sur les limites qu'aurait le volume s'il était au repos, ce qui en général ne fait que compliquer inutilement).
• Par contre, un tel calcul ne correspond pas à une tentative pour ajouter les vecteurs

j^μ

en différents points : on se limite à faire la somme des

j^0

pondérés par

\sqrt{g_{00}}

sans même envisager un transport parallèle de

j^μ

entre les différents points du volume étudié. Un calcul de cette sorte ne peut toutefois être envisagé que si on comprend précisément son interprétation physique (ici la “charge totale”, qui n'est pas un invariant... mais cette quantité est-elle utile ? ).

Tenseur d'énergie-impulsion d'une particule ponctuelle

• En relativité restreinte, le tenseur d'énergie impulsion peut s'écrire :

$\displaystyle T^{αβ}=p^α \:\frac{dX^β}{dt} \:δ^3 \left(x^i-X^i \,\right) =m \:U^α \,U^β \,\frac{dτ}{dt}\, δ^3 \left(x^i-X^i \,\right)$ ;
$T^{αβ}={\displaystyle{∫ m \:U^α \,U^β \,\frac{dτ}{dt} \:δ^4 \left(x^μ-X^μ \right) \:dt}}=∫ \,m \:U^α \,U^β \:δ^4 \left(x^μ-X^μ \right) \:dτ$ .

• En relativité générale, l'invariant d'intégration est

d^4 𝒱=\sqrt{\left|g\right|} \;d^4 x

. Pour définir

\tilde{δ}^4

tel que

∫ ⋯\; \tilde{δ}^4 d^4 𝒱

soit invariant, il faut considérer comme scalaire

\displaystyle \tilde{δ}^4 \left(x^μ-X^μ \right) =\frac{1}{\sqrt{\left|g\right|}} \:δ^4 \left(x^μ-X^μ \right)

; il faut également utiliser

\displaystyle \tilde{δ}^3 \left(x^i-X^i \,\right) =\frac{1}{\sqrt{ℊ}} \:δ^3 \left(x^i-X^i \,\right)

où

ℊ_{ij}

est la métrique spatiale telle que

d^3 𝒱=\sqrt{ℊ} \:\,d^3 x

\sqrt{\left|g\right|}=\sqrt{g_{00}} \:\sqrt{ℊ}

; en outre il faut considérer la durée

dt_{𝓁oc}=\sqrt{g_{00}} \;dt

.
• On obtient ainsi le tenseur :

$\displaystyle T^{αβ}=p^α \:\frac{dX^β}{dt_{𝓁oc}} \:\tilde{δ}^3 \left(x^i-X^i \,\right) =m \:U^α \,U^β \,\frac{dτ}{dt_{𝓁oc}} \,\tilde{δ}^3 \left(x^i-X^i \,\right)$ ;
$T^{αβ}={\displaystyle{∫ m \:U^α \,U^β \,\frac{dτ}{dt_{𝓁oc}} \:\tilde{δ}^4 \left(x^μ-X^μ \right) \:dt_{𝓁oc}}}=∫ \,m \:U^α \,U^β \:\,\tilde{δ}^4 \left(x^μ-X^μ \right) \:dτ$ .

◊ remarque : contrairement à

δ^3 \left(x^i-X^i \left(t\right)\right)

, le “temps”

x^0=c\,t

est une variable “indépendante” dans

δ^4 \left(x^μ-X^μ \right)

2.a.	• Le tenseur énergie-impulsion d'une particule ponctuelle s'écrit : $\displaystyle T^{αβ}=p^α \:\frac{dX^β}{dt_{𝓁oc}} \:\tilde{δ}^3 \left(x^i-X^i \,\right)$ . • Pour retrouver l'énergie-impulsion $\displaystyle p^α=m \:U^α=m \:\frac{dX^β}{dτ}$ , il faut donc considérer : $\displaystyle \frac{dX^0}{dt_{𝓁oc}}=\frac{c \:dt}{dt_{𝓁oc}}=\frac{c}{\sqrt{g_{00}}}$ ; $\displaystyle c \:p^α=∫ \sqrt{g_{00}} \:\,T^{α0} \:d^3 𝒱$ .

2.b.	• Dans la mesure où on retrouve : $\displaystyle c \:p^α=∫ \sqrt{g_{00}} \:\,T^{α0} \:d^3 𝒱$ pour une particule ponctuelle, on pourrait considérer $\sqrt{g_{00}} \:\,T^{α0}$ comme une “3-densité d'énergie-impulsion” généralisée ; l'application à un système quelconque est toutefois délicate. S'il est vrai que (selon la métrique) les coordonnées $T^{i0}$ peuvent décrire les grandeurs associées $\sqrt{g_{00}} \:\,T^{i0}$ (densité d'impulsion) au contraire la coordonnée $T^{00}$ devrait décrire la grandeur associée $g_{00} \:T^{00}$ (densité d'énergie). Tant qu'on étudie une particule, on peut considérer $E=\sqrt{g_{00}} \:\,c \,p^0=\sqrt{g_{00}} \;{\displaystyle{∫}} \sqrt{g_{00}} \:\,T^00 \:d^3𝒱=∫ \,g_{00} \:T^{00} \:d^3 𝒱$ puisque la fonction $δ$ incluse dans l'expression de $T^{00}$ évite toute ambiguïté. Au contraire pour un système quelconque, il faudrait inversement considérer l'énergie totale $E=∫ \,g_{00} \;T^00 \:d^3 𝒱$ puis éventuellement $\displaystyle c \:p^0=\frac{E}{\sqrt{g_{00}}}$ , sauf qu'ici on ne saurait pas où calculer $\sqrt{g_{00}}$ . ☞ remarque : la quantité généralisée est souvent non conservée car les interactions gravitationnelles avec l'espace-temps sont non linéaires.

2.c.	• En plus de la difficulté précédente, le calcul de la quantité $E=∫ \,g_{00} \;T^00 \:d^3 𝒱$ ne donnerait pas l'énergie du système considéré, car l'énergie de la somme n'est pas la somme des énergies. En particulier pour un système immobile, la masse de l'ensemble n'est pas la somme des masses : il faudrait y ajouter l'énergie d'interaction gravitationnelle (c'est lié au caractère non linéaire de la relativité générale).

Tenseur d'énergie-impulsion

• Pour une “densité de force”

ℱ^α

, on obtient en relativité restreinte :

∂_β T^{αβ}=ℱ^α

; la relation devient donc en relativité générale :

D_β T^{αβ}=ℱ^α

.
• Ceci peut s'écrire :

$∂_β T^{αβ}+Γ_{\phantom{.}λβ}^α \,T^{λβ}+Γ_{\phantom{.}λβ}^β \,T^{αλ}=ℱ^α$ ;
$\displaystyle ∂_β T^{αβ}+Γ_{\phantom{.}λβ}^α \,T^{λβ}+\frac{1}{\sqrt{\left|g\right|}} \:∂_λ \left(\sqrt{\left|g\right|}\right) \;T^{αλ}=ℱ^α$ ;
$\displaystyle \frac{1}{\sqrt{\left|g\right|}} \:∂_β \left(\sqrt{\left|g\right|} \;T^{αβ} \right) =ℱ^α-Γ_{\phantom{.}λβ}^α \:T^{λβ}$ .

• L'effet de la gravitation revient alors à ajouter à

ℱ^α

une contribution

-Γ_{\phantom{.}λβ}^α \:T^{λβ}

proportionnelle au tenseur énergie impulsion et au “champ de gravitation” représenté par la connexion affine.
◊ remarque : ceci permet de considérer

\sqrt{\left|g\right|} \:\,T^{αβ}

comme une “4-densité d'énergie-impulsion” généralisée.

Centre d'inertie d'un nageur cosmique

1.a.

• Quand il allonge les bras “presque jusqu'aux pôles”, la symétrie du mouvement est telle que le nageur n'a aucune raison de se déplacer ni selon l'axe droite-gauche, ni selon l'axe avant-arrière.

1.b.

• S'il allonge ensuite les jambes, ses mains ne participent que très peu à l'effet d'inertie puisqu'elles sont près des pôles et que ces derniers sont invariants par rotation selon l'équateur.
• Ainsi tout se passe presque comme si les seules masses étaient la tête et les pieds, ce qui correspondrait à un “centre d'inertie” à mi distance entre les deux. Lors de l'allongement des jambes ce centre d'inertie reste immobile, donc sa tête et ses épaules avancent environ autant que ses pieds reculent.

1.c.

• De même que pour (1.a), le nageur ne se déplace pas quand il raccourcit ses bras.

1.d.

• S'il raccourcit ensuite les jambes, ses mains participent totalement à l'effet d'inertie. Ceci correspond à un “centre d'inertie” environ trois fois plus près de la tête que des pieds. Lors du raccourcissement des jambes ce centre d'inertie reste immobile, donc sa tête et ses épaules reculent environ trois fois moins que ses pieds avancent.

1.e.

• Lors ce cette séquence de mouvements, le nageur a avancé dans la direction et le sens où il est orienté. Or, il est revenu à la même disposition de son corps, donc il peut recommencer et continuer ainsi à avancer (à “nager” dans le cosmos). Il faut toutefois bien comprendre que le procédé (ici grandement exagéré pour faciliter l'explication) est très peu efficace si la courbure de l'espace est faible, c'est à dire si le rayon de courbure est beaucoup plus grand que la dimension du système étudié.

2.a.	• Dans un espace plat, le centre d'inertie du corps n'est pas forcément toujours à même position ; par exemple il se déplace vers le haut quand on lève les bras. Par contre, les contributions des différentes parties du corps à l'inertie sont toujours les mêmes : elles ne dépendent que de leur masse. • Ainsi, quel que soit la séquence de mouvements qu'il voudrait répéter, le “nageur” resterait en moyenne toujours au même endroit. L'effet décrit ici est lié à la courbure de l'espace.

2.b.	• En relativité générale, la courbure de l'espace rend impossible la définition d'une notion “absolue” de centre d'inertie : le pseudo centre d'inertie dépend du mouvement qui est étudié (par contre, on peut tout de même définir un “quasi centre d'inertie” dès lors qu'on raisonne sur de petits objets).