MOUVEMENTS DE PARTICULES - exercices


Transformation de Lorentz

1.     • Dans un espace plat, on raisonne par rapport à un référentiel galiléen ℛ ℛ muni d'un repérage cartésien ( O, x, y, z ) \left(O,x,y,z\right) .  On considère un référentiel ℛ′ ℛ' en translation uniforme par rapport à ℛ ℛ ,  parallèlement à l'axe Ox Ox ,  avec une vitesse v v .
        a) Est-il possible de se repérer par rapport à ℛ′ ℛ' en utilisant les coordonnées suivantes (les notations t′ t' et x′ x' sont réservées pour la suite) :  t″ = t t''=t   ;  x″ = x - vt x''=x-v \:t   ;  y′ = y y'=y   ;  z′ = z z'=z   ?
        b) Quelle est la métrique correspondante (commenter) ?

2.     a) En admettant qu'on sache mesurer t″ t'' dans ℛ′ ℛ' ,   est-il possible de synchroniser les horloges ainsi constituées ?
        b) Quelle est la métrique spatiale correspondante ?

3.     a) Proposer une nouvelle variable t′ t' pour simplifier la synchronisation des horloges (commenter).
        b) Exprimer la métrique spatiale avec cette notation.
        c) Proposer une nouvelle variable x′ x' pour simplifier la métrique spatiale (commenter et conclure).


Métrique associée à un indice optique

        • Dans un espace plat, on considère une cuve remplie d'un fluide d'indice optique n n (pouvant éventuellement dépendre de la position).

1.     a) Si on utilise des horloges fonctionnant de façon identique dans ce milieu ou à l'extérieur, peut-on décrire les phénomènes optiques en raisonnant avec une métrique appropriée (préciser laquelle) ?
        b) Les autres phénomènes peuvent-ils être décrits selon les mêmes raisonnements ?

2.     a) Si on utilise au contraire des horloges fonctionnant par l'intermédiaire de la propagation lumineuse dans le fluide, peut-on décrire les phénomènes optiques en raisonnant avec une métrique appropriée (préciser laquelle) ?
        b) Les autres phénomènes peuvent-ils être décrits selon les mêmes raisonnements ?


Référentiel d'une particule accélérée par une force constante

1.     • Dans un espace plat, on raisonne par rapport à un référentiel galiléen ℛ ℛ muni d'un repérage cartésien ( O, x, y, z ) \left(O,x,y,z\right) .  On considère un référentiel ℛ′ ℛ' associé à une particule, en translation parallèlement à l'axe Ox Ox ,  accélérée par rapport à ℛ ℛ sous l'effet d'une force f→ \overset{→}{f} constante (par exemple électrostatique).
        a) Est-il possible de se repérer, par rapport à ℛ′ ℛ' en utilisant les coordonnées (qu'on peut simplifier en omettant y y et z z dans les raisonnements) :  t′ = t t'=t   ;  x′ = x - m c2 f ( 1 + f2 t2 m2 c2 - 1 ) \displaystyle x'=x-\frac{m\,c^2}{f} \left(\sqrt{1+\frac{f^2 \:t^2}{m^2 \:c^2 }} \:-1\right)   ;  y′ = y y'=y   ;  z′ = z z'=z   ?
        b) Quelle est la métrique correspondante (commenter) ?

2.     a) En admettant qu'on sache mesurer t′ t' dans ℛ′ ℛ' ,  est-il possible de synchroniser les horloges ainsi constituées ?
        b) Quelle est la métrique spatiale correspondante ?


Référentiel en rotation uniforme

1.     • Dans un espace plat, on raisonne par rapport à un référentiel galiléen ℛ ℛ muni d'un repérage cylindrique ( O, r, θ, z ) \left(O,r,θ,z\right) .  On considère un référentiel ℛ′ ℛ' en rotation uniforme par rapport à ℛ ℛ ,  selon l'axe Oz Oz ,  avec une vitesse angulaire ω ω .
        a) Est-il possible de se repérer par rapport à ℛ′ ℛ' en utilisant les coordonnées :  t′ = t t'=t   ;  r′ = r r'=r   ;  θ′ = θ - ωt θ'=θ - ω \:t   ;  z′ = z z'=z   ?
        b) Quelle est la métrique correspondante (commenter) ?

2.     a) En admettant qu'on sache mesurer t′ t' dans ℛ′ ℛ' ,   est-il possible de synchroniser les horloges ainsi constituées ?
        b) Quelle est la métrique spatiale correspondante ?

3.     • Pour  r ≥ rh = cω \displaystyle r≥r_h=\frac{c}{ω}   il se produit un “effet horizon” ; l'espace-temps “existe-t-il” dans cette zone ? Des particules matérielles peuvent-elles y exister ?

4.     • À l'aide d'un jeu de (nombreux) miroirs, on suppose qu'on fait tourner un faisceau lumineux selon une trajectoire fermée.
        a) En considérant le cas particulier d'une trajectoire quasi-circulaire d'équation  r = R < rh r=R < r_h ,  exprimer la célérité apparente c′ c' que calculerait un observateur dans ℛ′ ℛ' omettant le décalage de synchronisation entre le point d'émission et le point de réception (préciser la différence entre le temps propre  dτapp dτ_{app}   de l'observateur fixe et le temps propre  dτ dτ   resynchronisé le long de la trajectoire).
        b) Calculer de même dans le cas d'une trajectoire quelconque en se limitant à l'approximation du premier ordre par rapport à  r ω c \frac{r\:ω}{c} .


Énergie-impulsion

1.     a) On considère le 4-vecteur énergie-impulsion  p↔ = p0 e↔0 + p1 e↔1 + p2 e↔2 + p3 e↔3 \overset{↔}{p}=p^0 \:\overset{↔}{e}_0+p^1 \:\overset{↔}{e}_1 +p^2 \:\overset{↔}{e}_2+p^3 \:\overset{↔}{e}_3   dans un espace-temps dont la métrique n'est pas diagonale :  g0i≠0 g_{0i}≠0   (les hypersurfaces  t=Cste t=Cste   ne sont pas orthogonales à  e↔0 ≘ ∂0M↔ \overset{↔}{e}_0≘∂_0 \overleftrightarrow{M} ).  En faire une représentation graphique à deux dimensions pour  ct c\,t   et  x x .
        b) Un inconvénient du 4-vecteur précédent est qu'il n'est pas simple de savoir à quoi correspond l'énergie. En supposant pour simplifier que la base spatiale est orthogonale, proposer un changement de base tel que e_ ↔ 0 \overset{↔}{\underline{e}}_0 soit orthogonal aux e↔i \overset{↔}{e}_i .

2.     a) Déterminer les coordonnées p_α \underline{p}^α correspondantes.
        b) Préciser la métrique et l'énergie correspondante.
        c) Vérifier qu'on retrouve :  m2 c2 = E2 c2 - p_ → 2 = gαβ pα pβ \displaystyle m^2 \,c^2=\frac{E^2}{c^2} -\overset{→}{\underline{p}}^2=g_{αβ} \:p^α \:p^β .


Énergie-impulsion

1.     a) Préciser les coordonnées du 4-vecteur vitesse  u↔obs \overset{↔}{u}_{obs}   d'un observateur immobile.
        b) Montrer que l'énergie d'une particule peut s'écrire :  E = u↔obs ∙ p↔ E=\overset{↔}{u}_{obs}∙\overset{↔}{p} .

2.     • Justifier que l'expression reste valable pour l'énergie mesurée par un observateur en mouvement.


Étude lagrangienne et hamiltonienne des géodésiques

1.     ☞ remarque : de façon générale, on se limite dans cette étude à des géodésiques qui ne sont pas du genre “lumière”.
        a) Justifier que la condition de déplacement géodésique :  δ ( ∫ds ) =0 δ\left(∫ds\right)=0   peut s'écrire avec un lagrangien ℒ ℒ (à préciser), en paramétrant par  s s   et en utilisant la notation  x˙β = dxβ ds \displaystyle \dot{x}^β=\frac{dx^β}{ds}   (pour privilégier un respect de la covariance relativiste) :  δ ( ∫ ℒ ( xα, x˙β ) ds ) =0 δ\left(∫ ℒ\left(x^α, \dot{x}^β \right) \:ds\right)=0 .
        b) Quelles difficultés risque d'introduire ce choix de paramétrisation ?
        c) En déduire les équations des géodésiques.
        d) Justifier que cette condition de déplacement géodésique est liée à la notion de “transport parallèle”.
        e) Établir comment se transforment les équations des géodésiques en paramétrant par  dσ≠ds dσ≠ds   et en notant  x˜ ˙ β = dxβ dσ \displaystyle \dot{\tilde{x}}^β=\frac{dx^β}{dσ} .

2.     • Certains ouvrages suggèrent de simplifier le calcul des équations en utilisant le lagrangien  ℒ_=ℒ2 \underline{ℒ}=ℒ^2   au lieu de  ℒ ℒ   ; dans quelles conditions cela est-il possible ?

3.     • Que donne la méthode hamiltonienne ?
        ◊ remarque : afin de respecter une correspondance “plus classique” pour les impulsions, il peut être prudent de raisonner ici avec  s s   et  ℒ ℒ   (et non  ℒ_=ℒ2 \underline{ℒ}=ℒ^2 ).


Étude lagrangienne des géodésiques

1.     ☞ remarque : de façon générale, on se limite dans cette étude à des géodésiques qui ne sont pas du genre “lumière”.
        • Justifier que la condition de déplacement géodésique :  δ ( ∫ ds ) =0 δ\left(∫ds\right)=0   peut s'écrire avec un lagrangien ℒ ℒ (à préciser), en paramétrant par la variable temporelle  t t   et en utilisant la notation  x˙β = dxβ dt \displaystyle \dot{x}^β=\frac{dx^β}{dt}   (pour privilégier une comparaison avec la relativité restreinte) :  δ ( ∫ℒ ( xα, x˙β ) dt ) =0 δ\left(∫ ℒ\left(x^α, \dot{x}^β \right) \:dt\right)=0 .

2.     • En déduire les équations des géodésiques, dans le cas où la métrique n'a pas de termes croisés spatio-temporels  ( g0k=0 g_{0k}=0 ).


Géodésiques du genre “lumière”

1.     a) Toute courbe du genre lumière est elle une géodésique du genre lumière ?
        b) Dans un espace plat, la lumière suit des géodésiques d'espace (dans ce cas des droites) ; cela est-il encore vrai dans un espace courbe (avec des géodésiques d'espace courbes) ?

2.     ☞ remarque : cet exercice est plus ou moins une “suite” des précédents : il suppose connues les méthodes de Lagrange et de Hamilton.
        a) Préciser la difficulté d'utiliser  uα = dxα ds \displaystyle u^α=\frac{dx^α}{ds}   dans le cas des photons.
        b) Exprimer les équations des géodésiques par la méthode d'Euler-Lagrange en utilisant le Lagrangien  ℒ˜ ( xα, x˜˙ β ) = gμν x˜˙ μ x˜˙ ν \tilde{ℒ}(x^α, \dot{\tilde{x}}^β ) =\sqrt{g_{μν} \:\dot{\tilde{x}}^μ \:\dot{\tilde{x}}^ν}   avec la notation  x˜˙ β = dxβ dσ \displaystyle \dot{\tilde{x}}^β=\frac{dx^β}{dσ} .
        c) Dans le cas des géodésiques du genre “lumière”, montrer qu'il semble a priori impossible de choisir un paramètre  σ σ   de façon à obtenir des équations simplifiées :  d2xα dσ2 + Γ . μν α dxμ dσ dxν dσ =0 \displaystyle \frac{d^2 x^α}{dσ^2}+Γ_{\phantom{.}μν}^α \frac{dx^μ}{dσ} \frac{dx^ν}{dσ}=0 .
        d) Certains ouvrages suggèrent de simplifier le calcul des équations en utilisant le lagrangien  ℒ_=ℒ2 \underline{ℒ}=ℒ^2   au lieu de  ℒ ℒ   ; dans quelles conditions cela est-il possible ?
        e) Pour contourner des difficultés rencontrées avec le lagrangien  ℒ˜ \tilde{ℒ} paramétré par  σ σ ,  repartir du cas de particules massives et montrer que l'indétermination de uα u^α peut être contournée si on met en évidence le rôle du temps “durée locale” :  dt𝓁oc = g00 dt dt_{𝓁oc}=\sqrt{g_{00}} \;dt   (si on se limite au cas d'une métrique diagonale).
        f) En effectuant un passage à la limite judicieux pour les photons, montrer qu'on peut simplifier l'expression de l'action en utilisant un paramètre  ς ς   particulier (à préciser).

3.     • Que donne dans ce cas la méthode hamiltonienne ?

4.     a) Déterminer les équations différentielles paramétriques des géodésiques du genre “lumière” dans le cas d'une métrique de Schwarzschild sous la forme “classique” : 
ds2 = A(r) c2 dt2 - C(r) dr2 - r2 [ dθ2 + sin2 (θ) dφ2 ] ds^2=A\left(r\right) \:c^2 \,dt^2-C\left(r\right) \:dr^2-r^2 \:\left[dθ^2+\sin^2⁡\left(θ\right) \:dφ^2 \right]    avec   A = 1 - rsr \displaystyle A=1-\frac{r_s}{r}    et   C=1A \displaystyle C=\frac{1}{A} .
        b) La contrainte  ds=0 ds=0   impose ici une inconnue de moins que pour les géodésiques qui ne sont pas du genre lumière ; quelle quantité le système d'équations impose-t-il à la place ?


Principe d'équivalence et mécanique quantique

1.     • En l'absence d'effets électromagnétiques, le principe d'équivalence conduit à des équations du mouvement dans lesquelles la masse se simplifie.
        • Les mouvements quantiques décrits par l'équation de Schrödinger  - ℏ22m d2ψ dx2 + m𝒱 ψ = Eψ \displaystyle -\frac{ℏ^2}{2m} \,\frac{d^2 ψ}{dx^2}+m \,𝒱 \;ψ=E \:ψ   (où  𝒱 𝒱 est le potentiel de gravitation) respectent-ils cette propriété ?

2.     • L'équation de Schrödinger est une approximation non relativiste ; de même la pesanteur décrit une approximation non relativiste d'un mouvement relativiste libre. Ces approximations remettent-elles en question les conclusions précédentes ?


Limite de l'approximation newtonienne

1.     • Établir la limite de l'approximation newtonienne (donc en se limitant aux faibles vitesses) pour un champ gravitationnel faible et statique.

2.     a) Étudier de même la limite d'un champ faible et statique, mais dans le cadre de la relativité restreinte (où la seule limitation sur les vitesses est la célérité de la lumière dans le vide).
        b) On peut montrer (non envisagé ici) que la limite de la relativité générale pour les champs faibles correspond à :  ds2 = ( 1 + 2 𝒱 c2 ) c2 dt2 - ( 1 - 2 𝒱 c2 ) d𝓁2 \displaystyle ds^2=\left(1+\frac{2\,𝒱}{c^2} \right) \:c^2 \,dt^2-\left(1-\frac{2\,𝒱}{c^2} \right) \:d𝓁^2 .  Comparer aux résultats précédents.


Charge totale

1.     • En se basant sur le vecteur densité de courant jμ j^μ ,  semble-t-il possible de calculer la charge totale contenue dans un volume donné ?

2.     • Étant donné qu'en relativité générale il est impossible de définir la somme de deux vecteurs définis en deux points distincts, ne serait-il pas préférable de se baser sur la quantité scalaire   ‖ j ↔ ‖ = gμν jμ jν \left‖ \:\overset{↔}{i}\:\right‖=\sqrt{g_{μν} \:j^μ \,j^ν\,}    ?


Tenseur d'énergie-impulsion d'une particule ponctuelle

1.     • Pour une particule ponctuelle de position X X   { Xα } \{X^α\}   et d'impulsion  pα p^α ,  montrer que le tenseur d'énergie impulsion peut s'écrire sous la forme suivante, où l'intégration est faite selon la trajectoire : 
Tαβ = ∫ m Uα Uβ δ˜4 ( xμ - Xμ ) dτ T^{αβ}=∫m \:U^α \,U^β \:\,\tilde{δ}^4 \left(x^μ-X^μ \,\right) \:dτ    avec   δ˜4 ( xμ - Xμ ) = 1|g| δ4 ( xμ - Xμ ) \displaystyle \tilde{δ}^4 \left(x^μ-X^μ \,\right) =\frac{1}{\sqrt{\left|g\right|}} \:δ^4 \left(x^μ-X^μ \,\right) .

2.     a) En déduire que l'énergie-impulsion correspond à :  c pα = ∫ g00 Tα0 d3𝒱 c \:p^α=∫ \sqrt{g_{00}} \:\,T^{α0} \:d^3 𝒱 .
        b) Cela peut-il se généraliser à un système quelconque ?
        c) Peut-on utiliser ces quantités pour calculer la masse de l'ensemble d'un système ?


Tenseur d'énergie-impulsion

        • Pour un système soumis à une “densité de force”  ℱα ℱ^α ,  mettre en évidence l'influence l'effet de la gravitation sur le tenseur d'énergie-impulsion.


Centre d'inertie d'un nageur cosmique

        • La relativité générale ne permet pas de définir une notion de centre d'inertie. La définition en mécanique newtonienne, qu'on peut étendre à la relativité restreinte, n'est possible que par les approximations dans la description des champs gravitationnels faibles (en négligeant la courbure de l'espace).
        • Plus précisément, si on essaye de définir une sorte de centre d'inertie en relativité générale, on obtient un point qui dépend du mouvement du système étudié. Ceci peut être mis en évidence par l'étude des évolutions d'un “nageur cosmique” imaginaire.

1.     • Considérons un cosmonaute (avec un scaphandre autonome) placé dans l'espace vide, dans une zone où l'espace est courbé par la présence d'astres environnants, mais en supposant que la répartition de matière respecte la symétrie sphérique autour du cosmonaute. Alors ce dernier est dans une position d'équilibre ; comment peut-il, par ses simples mouvements, briser la symétrie et se décaler vers l'un des astres alentour (pour se laisser ensuite entraîner vers cet astre par la gravitation) ?

        • Ne pouvant disposer d'un espace de dimension 5 pour faire un schéma, on dessine une configuration analogue : un nageur d'épaisseur nulle, dans un espace limité à une surface sphérique, dont la courbure est visualisée par une représentation en perspective.
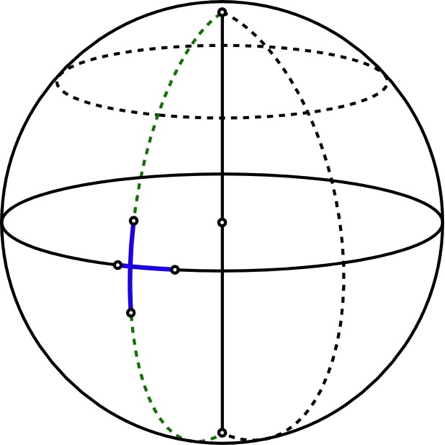
        • Pour simplifier, on suppose que le nageur est orienté selon l'équateur et que sa masse est concentrée en quatre points (sa tête ; ses deux mains écartées de part et d'autre ; ses deux pieds joints).
        • Pour amplifier l'effet étudié afin qu'il soit plus net, on suppose en outre que le nageur peut étendre ses bras et ses jambes “très loin” (ils sont initialement repliés).
mouvement_ex_Im/nageur.png

        a) Justifier que le nageur ne se déplace pas quand il allonge les bras “presque jusqu'aux pôles”.
        b) Justifier que, s'il allonge ensuite les jambes, sa tête et ses épaules avancent environ autant que ses pieds reculent.
        c) Justifier que le nageur ne se déplace pas quand il raccourcit ses bras.
        d) Justifier que, s'il raccourcit ensuite les jambes, sa tête et ses épaules reculent nettement moins que ses pieds avancent.
        e) En conclure qu'en épétant cette séquence de mouvements, il peut avancer dans la direction et le sens où il est orienté.

2.     a) Une telle méthode serait-elle possible dans un espace plat ?
        b) En déduire que la notion de centre d'inertie ne peut pas être définie en relativité générale (ou plus précisément que le pseudo centre d'inertie dépend du mouvement qui est étudié).