RG XVI - EFFETS DE LA ROTATION D'UN ASTRE


Équations du mouvement dans le plan équatorial.

Étude générale

• Tout mouvement initié dans le plan équatorial y subsiste par symétrie. La métrique y est :  ds2=Ac2dt2+2Bcdtdφ−Cdr2−r2dθ2−Edφ2{ds}^2=A \:c^2 \, {dt}^2+2 \,B \:c \,dt \:dφ-C \:{dr}^2-r^2 \:{dθ}^2-E \:{dφ}^2  avec :
A=1−rsr\displaystyle A=1-\frac{r_s}{r}  ;  rs=2𝒢Mc2\displaystyle r_s=\frac{2 \,𝒢 \:M}{c^2}  ;  B=rsαr\displaystyle B=\frac{r_s \: α}{r}  ;  C=r2Δ\displaystyle C=\frac{r^2}{Δ}  ;  Δ=r2−rsr+α2Δ=r^2-r_s \: r+α^2  ;
E=r2+α2.(1+rsr)\displaystyle E=r^2+α^2.\left(1+\frac{r_s}{r}\right) .

En l'absence d'effet électromagnétique, les équations du mouvement (géodésique) d'une particule test peuvent s'écrire  ddσ∂ℒ∂x˙μ−∂ℒ∂xμ=0\displaystyle \frac{d}{dσ} \frac{∂ℒ}{∂\dot{x}^μ}-\frac{∂ℒ}{∂x^μ}=0  avec le lagrangien  ℒ=−12gμνx˙μx˙νℒ=-\frac{1}{2} g_{μν} \: \dot{x}^μ \: \dot{x}^ν  (avec les dérivées par rapport à un paramètre σσ à préciser).

Pour une particule massive, on utilise dans cette partie  σ=sσ=s  (dans la suite plutôt le temps propre ττ ). C'est impossible pour les photons, pour lesquels  ds=0ds=0  ;  on est alors amené à utiliser un paramètre  ςς  imposé par sa relation aux  dxμdx^μ  selon les équations correspondantes (en fait  dς=g0νdxν=dx0dς=g_{0ν} \: dx^ν={dx}_0 ).

• Pour  x0=ctx^0=c \,t  on obtient :  ddσ(−g0νx˙ν)=0\displaystyle \frac{d}{dσ} \left(-g_{0ν} \: \dot{x}^ν \right)=0  donc  Act˙+Bφ˙=𝓀=CsteA \:c \,\dot{t}+B \:\dot{φ}=𝓀 =Cste .

Cette quantité constante est l'impulsion généralisée associée au temps tt ; elle correspond à une généralisation de l'énergie ( e↔0\overset{↔}{e}_0 est un vecteur de Killing).

◊ remarque : pour le cas de Schwarzschild,  B=0B=0  donc on retrouve la constante 𝓀𝓀 correspondante.

• Pour  x3=φx^3=φ  on obtient :  ddσ(−g3νx˙ν)=0\displaystyle \frac{d}{dσ} \left(-g_{3ν} \: \dot{x}^ν \right)=0  donc  −Bct˙+Eφ˙=𝒽c=Cste\displaystyle -B \:c \,\dot{t}+E \:\dot{φ}=\frac{𝒽}{c}=Cste .

Cette quantité constante est l'impulsion généralisée associée à l'angle φφ ; elle correspond à la généralisation du moment cinétique ( e↔3\overset{↔}{e}_3 est un vecteur de Killing).

◊ remarque : pour le cas de Schwarzschild,  B=0B=0  et  E=r2E=r^2  donc on retrouve la constante 𝒽𝒽 correspondante.

• Puisque  AE+B2=ΔA \:E+B^2=Δ ,  le système de deux équations a pour solution :
ct˙=1Δ(𝓀E−𝒽cB)\displaystyle c \,\dot{t}=\frac{1}{Δ} \, \left(𝓀 \:E-\frac{𝒽}{c} \, B\right)   ;   φ˙=1Δ(𝓀B+𝒽cA)\displaystyle \dot{φ}=\frac{1}{Δ} \, \left(𝓀 \:B+\frac{𝒽}{c} \, A\right) .

• Le résultat de l'équation radiale peut être obtenu plus simplement en reportant les expressions de t˙\dot{t} et φ˙\dot{φ} dans la métrique ; ainsi, après simplification :
ds2=−1Δdσ2.(A𝒽2c2+2B𝓀𝒽c−E𝓀2)−Cdr2\displaystyle {ds}^2=-\frac{1}{Δ} \, {dσ}^2.\left(A \,\frac{𝒽^2}{c^2} +2 \,B \:𝓀 \,\frac{𝒽}{c}-E \:𝓀^2 \right)-C \:{dr}^2 .

En posant  R=drdσ\displaystyle R=\frac{dr}{dσ}  on obtient :
◊ pour un photon :  ds2=0{ds}^2=0  ;  R2=−1r2(A𝒽2c2+2B𝓀𝒽c−E𝓀2)\displaystyle R^2= -\frac{1}{r^2} \, \left(A \,\frac{𝒽^2}{c^2} +2 \,B \:𝓀 \,\frac{𝒽}{c}-E \:𝓀^2 \right)  ;
◊ pour une particule matérielle :
ds2=dσ2{ds}^2={dσ}^2  ;  R2=−1r2(Δ+A𝒽2c2+2B𝓀𝒽c−E𝓀2)\displaystyle R^2= -\frac{1}{r^2} \, \left(Δ+A \,\frac{𝒽^2}{c^2} +2 \,B \:𝓀 \,\frac{𝒽}{c}-E \:𝓀^2 \right) .

◊ remarque : avec  α=0α=0  on retrouve le cas de Schwarzschild :
◊ pour un photon :  R2=𝓀2−Ar2𝒽2c2\displaystyle R^2= 𝓀^2-\frac{A}{r^2} \, \frac{𝒽^2}{c^2}  ;
◊ pour une particule matérielle :  R2=𝓀2−Ar2𝒽2c2−A\displaystyle R^2= 𝓀^2-\frac{A}{r^2} \, \frac{𝒽^2}{c^2}-A .

Trajectoires des particules matérielles

• On peut étudier les types de trajectoires en s'aidant de la comparaison avec le cas de Schwarzschild.

La loi radiale peut s'écrire :  12(drdτ)2=12c2.(𝓀2−1)−𝒱r\displaystyle \frac{1}{2} \left(\frac{dr}{dτ}\right)^2=\frac{1}{2} c^2.(𝓀^2-1)-𝒱_r  avec un “potentiel radial” :  𝒱r=−c2rs2r+𝒽22r2(1−rsr)+c2α22r2+crsαr3𝓀𝒽−α22r2(1+rsr)c2𝓀2\displaystyle 𝒱_r=-\frac{c^2 \: r_s}{2 \,r}+\frac{𝒽^2}{2 \,r^2} \,\left(1-\frac{r_s}{r}\right)+\frac{c^2 \: α^2}{2 \,r^2}+\frac{c \:r_s \:α}{r^3} \: 𝓀 \:𝒽-\frac{α^2}{2 \,r^2} \,\left(1+\frac{r_s}{r}\right) \:c^2 \: 𝓀^2 .

Pour  α=0α=0  on retrouve la loi déduite du cas de Schwarzschild, pour laquelle :  𝒱r=−c2rs2r+𝒽22r2(1−rsr)\displaystyle 𝒱_r=-\frac{c^2 \: r_s}{2 \,r}+\frac{𝒽^2}{2 \,r^2} \,\left(1-\frac{r_s}{r}\right) .  Une différence importante est toutefois qu'ici le potentiel radial dépend non seulement de 𝒽𝒽 mais aussi de 𝓀𝓀 .

• Le regroupement par puissances de 1r\displaystyle \frac{1}{r} met alors en évidence une autre formulation :  𝒱r=−c2rs2r+𝒽2−c2α2.(𝓀2−1)2r2−rs.(𝒽−cα𝓀)22r3\displaystyle 𝒱_r=-\frac{c^2 \: r_s}{2 \,r}+\frac{𝒽^2-c^2 \: α^2.(𝓀^2-1)}{2 \,r^2}-\frac{r_s . (𝒽-c \:α \:𝓀)^2}{2 \,r^3} .

On y constate que, pour rechercher les extrémums afin de discriminer les types de trajectoires, un paramètre plus pratique peut être  η=𝒽−cα𝓀η=𝒽-c \:α \:𝓀 :
  𝒱r=−c2rs2r+η.(η+2cα𝓀)+c2α22r2−rsη22r3\displaystyle 𝒱_r=-\frac{c^2 \: r_s}{2 \,r}+\frac{η.(η+2 \,c \:α \:𝓀)+c^2 \: α^2}{2 \,r^2}-\frac{r_s \: η^2}{2 \,r^3}.

Ainsi le terme en  1r2\displaystyle \frac{1}{r^2}  n'est que du premier ordre en 𝓀𝓀 et le terme en  1r3\displaystyle \frac{1}{r^3}  n'en dépend plus.

• Pour  αrs=122\displaystyle \frac{α}{r_s} =\frac{1}{2 \,\sqrt{2}}  fixé, les variations du “potentiel radial” 𝒱r𝒱_r en fonction de ηη sont analogues à celles du cas de Schwarzschild ; les types de trajectoires correspondants le sont donc aussi.

Pour les rotations dans le sens direct (avec  𝓀=0,95𝓀=\text{0,95}  et  ηcrs≈1,0\displaystyle \frac{η}{c \:r_s}≈\text{1,0} ).
rotEffet_Im/Vr_e_d.jpg

Pour le sens rétrograde (avec  𝓀=0,98𝓀=\text{0,98}  et  ηcrs≈−2,5\displaystyle \frac{η}{c \:r_s}≈-\text{2,5} )  les rayons caractéristiques et les niveaux d'énergie sont un peu plus grands.

rotEffet_Im/Vr_e_i.jpg

◊ remarque : il est utile de reporter (en pointillés) la valeur  12(𝓀2−1)\frac{1}{2} \left(𝓀^2-1\right)  jouant ici un rôle équivalent à celui de l'énergie mécanique massique (constante) dans le cas newtonien ; cette quantité doit pouvoir être au niveau des extremums pour pouvoir conclure l'analogie sur les types de trajectoires.

• En particulier il existe des trajectoires bornées entre deux distances rmr_m et rMr_M .

D'autres, pour de plus grandes valeurs de l'énergie ℰℰ (selon la valeur de 𝓀𝓀 pour ηη donné), peuvent ne pas être bornées supérieurement.

D'autres enfin, pour des énergies dépassant le maximum, peuvent ne pas avoir de minimum d'approche et rejoindre forcément la singularité (la rotation doit être suffisante par rapport au mouvement radial) ; qui plus est, l'existence même du maximum suppose que ηη ne soit pas trop petit.

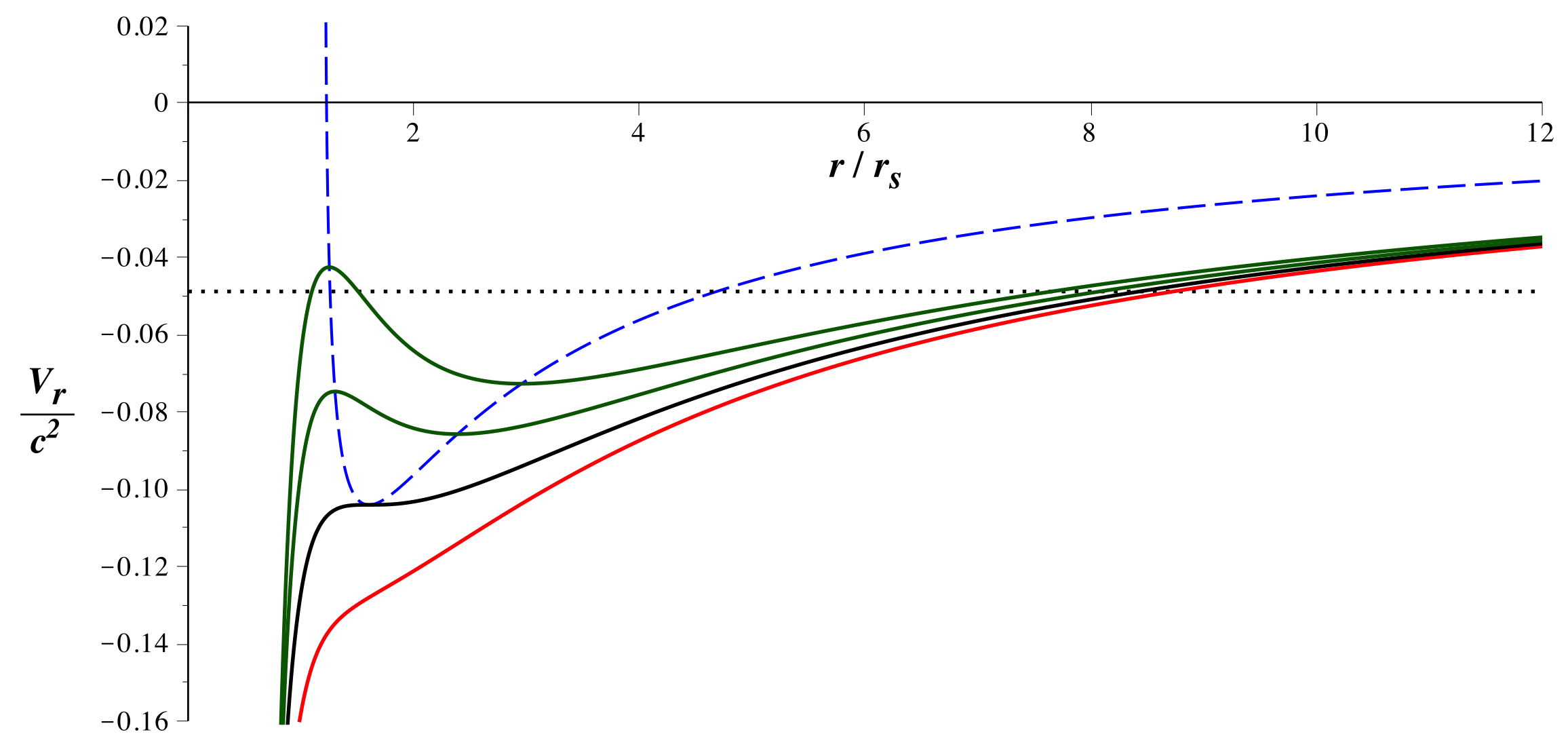
• Une différence importante intervient par contre ici : 𝒱r𝒱_r dépend aussi de 𝓀𝓀 . Ainsi, les courbes correspondant à des plus grandes énergies sont déformées.

Pour  αrs=122\displaystyle \frac{α}{r_s} =\frac{1}{2 \,\sqrt{2}}  et  ηcrs=1,5\displaystyle \frac{η}{c \:r_s}=\text{1,5}  fixés, les variations du “potentiel radial” 𝒱r𝒱_r en fonction de 𝓀𝓀 sont représentées ci-après (en particulier pour  𝓀≈0,95𝓀≈\text{0,95} ).

rotEffet_Im/Vr_k_e_i.jpg

On constate essentiellement que les plus grandes valeurs de 𝓀𝓀 relèvent le maximum et déplacent le minimum vers des plus grandes valeurs de rr .

En pratique il semble que, pour ηη fixé, les particules plus proches du centre tournent plus si elles ont plus d'énergie.

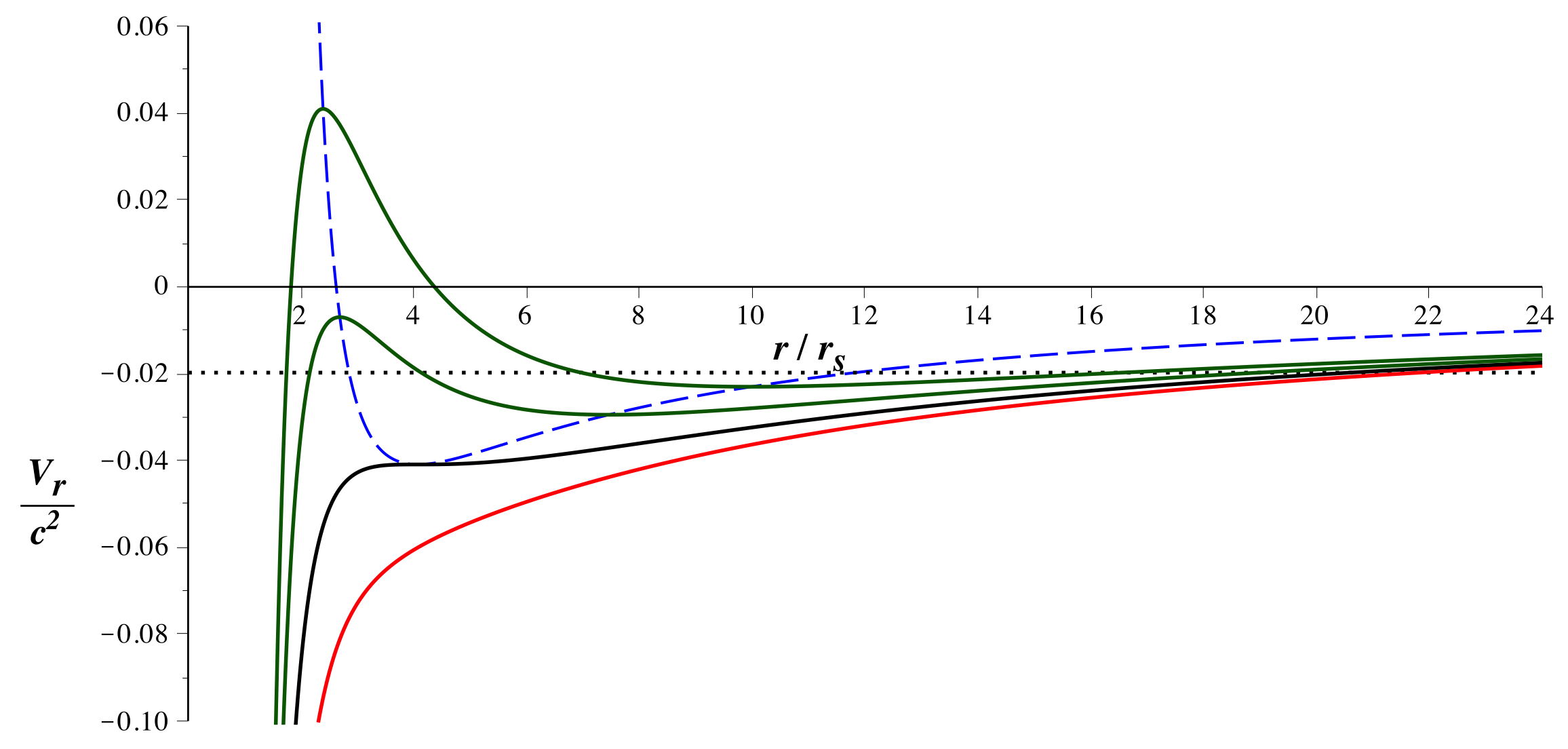
• Au contraire pour  αrs=122\displaystyle \frac{α}{r_s} =\frac{1}{2 \,\sqrt{2}}  et  ηcrs=−2,5\displaystyle \frac{η}{c \:r_s}=-\text{2,5}  fixés, les variations du “potentiel radial” 𝒱r𝒱_r en fonction de 𝓀𝓀 , représentées ci-après (en particulier pour  𝓀≈0,98𝓀≈\text{0,98} ), montrent que les plus grandes valeurs de 𝓀𝓀 abaissent le maximum et déplacent le minimum vers des plus petites valeurs de rr .

rotEffet_Im/Vr_k_e_d.jpg


L'augmentation de rotation évoquée intervient dans le sens direct et les particules plus proches du centre tournent moins dans le sens inverse si elles ont plus d'énergie.

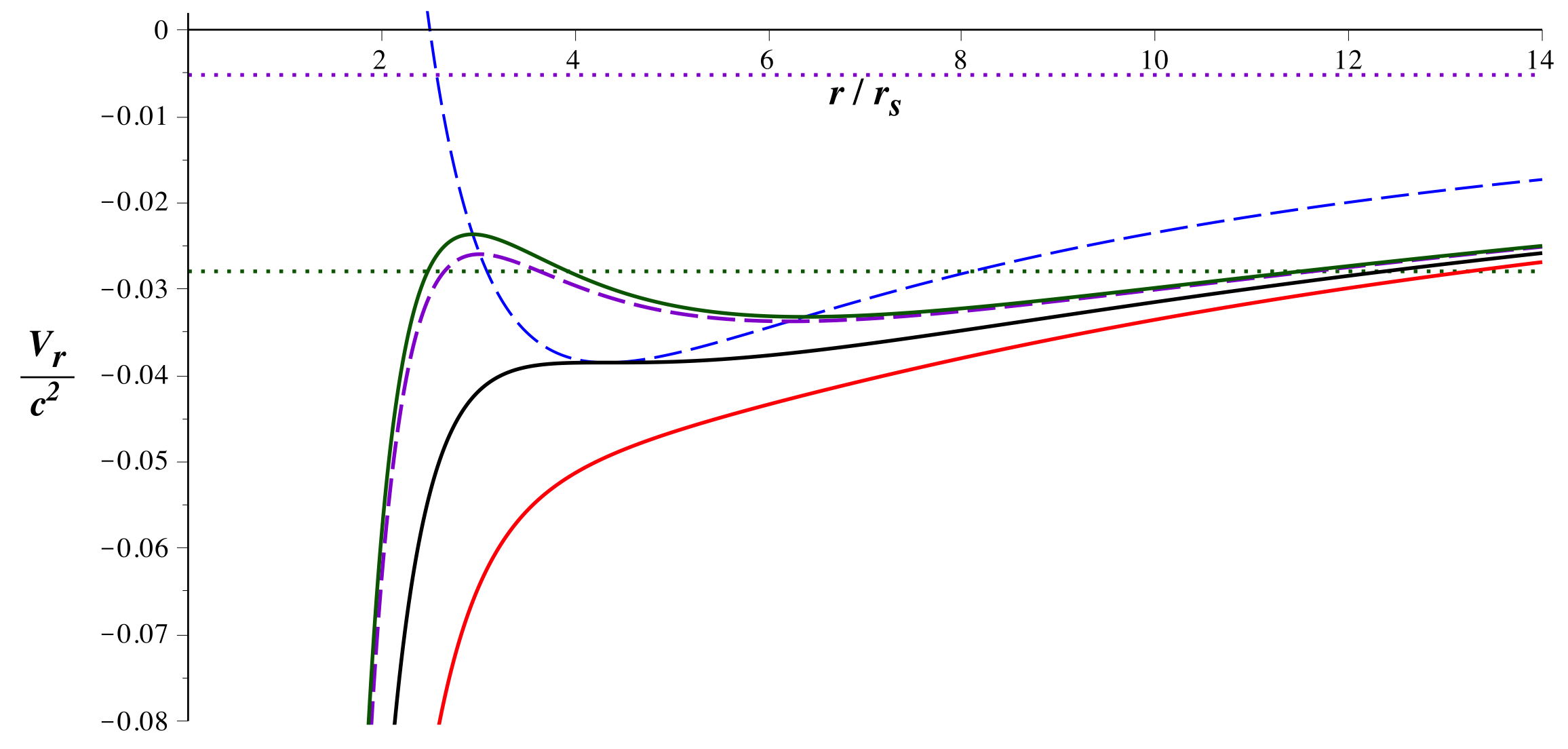
• On peut préciser les courbes en étudiant le lieu des extrémums, caractérisés par :   d𝒱rdr=c2rs2r2−η.(η+2cα𝓀)+c2α2r3+3rsη22r4=0\displaystyle \frac{d𝒱_r}{dr}=\frac{c^2 \: r_s}{2 \,r^2}-\frac{η.(η+2 \,c \:α \:𝓀)+c^2 \: α^2}{r^3} +\frac{3 \,r_s \: η^2}{2 \,r^4}=0 .

Ceci impose :  rers=η.(η+2cα𝓀)+c2α2c2rs2±(η.(η+2cα𝓀)+c2α2c2rs2)2−3η2c2rs2\displaystyle \frac{r_e}{r_s} =\frac{η.(η+2 \,c \:α \:𝓀)+c^2 \: α^2}{c^2 \: r_s^{\:2}}±\sqrt{\left(\frac{η.(η+2 \,c \:α \:𝓀)+c^2 \: α^2}{c^2 \: r_s^{\:2}}\right)^2-\frac{3 \,η^2}{c^2 \: r_s^{\:2}}}  ;  puis en combinant la condition d'extrémum avec l'expression de 𝒱r𝒱_r on obtient :  𝒱r(re)=rs4re3(η2−c2re2)\displaystyle 𝒱_r (r_e )=\frac{r_s}{4 \,r_e^{\:3}} \,\left(η^2-c^2 \: r_e^{\:2} \right)  ;  cela définit paramétriquement (en fonction de ηη ou de 𝓀𝓀 ) les courbes reportées en tirets.

 📖 exercice n° I.

Trajectoires des photons

• On peut de même étudier les types de trajectoires en s'aidant de la comparaison avec le cas de Schwarzschild.

Avec  𝓀=1𝓀=1  la loi radiale peut s'écrire   (drdς)2=1−2𝒱r\displaystyle \left(\frac{dr}{dς}\right)^2=1-2 \,𝒱_r   avec un “potentiel radial” :  𝒱r=𝒽22c2r2(1−rsr)+rsαr3𝒽c−α22r2(1+rsr)\displaystyle 𝒱_r=\frac{𝒽^2}{2 \,c^2 \: r^2} \left(1-\frac{r_s}{r}\right)+\frac{r_s \: α}{r^3} \, \frac{𝒽}{c}-\frac{α^2}{2 \,r^2} \left(1+\frac{r_s}{r}\right) .

Pour  α=0α=0  on retrouve la loi déduite du cas de Schwarzschild, pour laquelle :  𝒱r=𝒽22c2r2(1−rsr)\displaystyle 𝒱_r=\frac{𝒽^2}{2 \,c^2 \: r^2} \left(1-\frac{r_s}{r}\right) .

Le comportement est semblable : les trajectoires passant trop près de l'astre n'ont pas de minimum d'approche (la rotation décrite par 𝒽𝒽 doit être suffisante par rapport au mouvement radial).

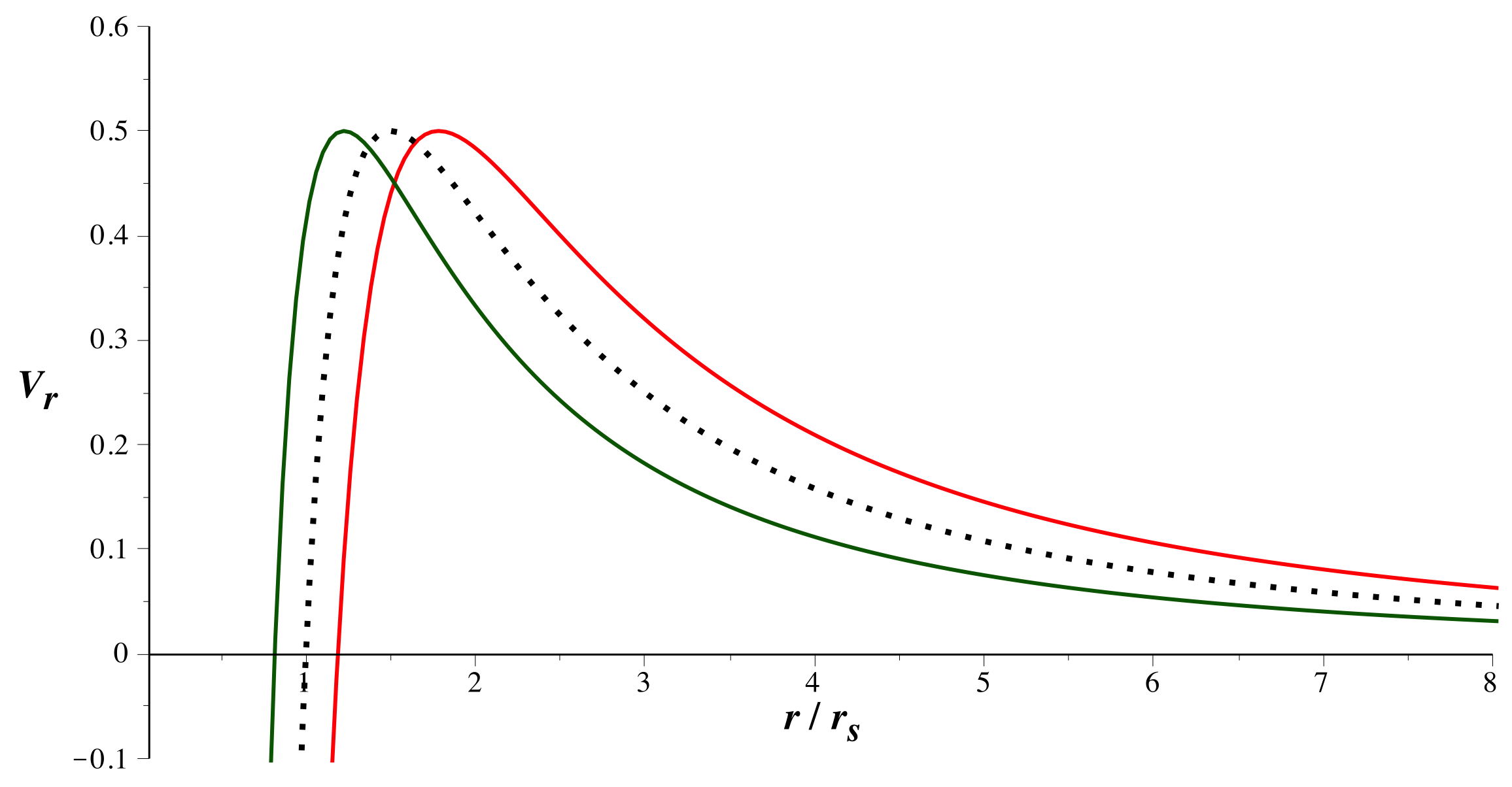
• On peut préciser les courbes en étudiant le maximum, caractérisé par :  d𝒱rdr=𝒽2c2r3(1−3rs2r)+3rsαr3𝒽c+α2r3(1+3rs2r)=0\displaystyle \frac{d𝒱_r}{dr}=\frac{𝒽^2}{c^2 \: r^3} \left(1-\frac{3 \,r_s}{2 \,r}\right)+\frac{3 \,r_s \: α}{r^3} \, \frac{𝒽}{c}+\frac{α^2}{r^3} \left(1+\frac{3 \,r_s}{2 \,r}\right)=0 .

Ainsi :   rers=32𝒽2c2−2α𝒽c+2α2𝒽2c2−2α2\displaystyle \frac{r_e}{r_s} =\frac{3}{2} \, \frac{\frac{𝒽^2}{c^2} -2 \,α \,\frac{𝒽}{c}+2 \,α^2}{\frac{𝒽^2}{c^2} -2 \,α^2}   ;   𝒱r≤𝒱r(re)=227rs2(𝒽2c2−2α2)3(𝒽2c2−2α𝒽c+2α2)2\displaystyle 𝒱_r≤𝒱_r (r_e )=\frac{2}{27 \,r_s^{\:2}} \, \frac{\left(\frac{𝒽^2}{c^2} -2 \,α^2 \right)^3}{\left(\frac{𝒽^2}{c^2} -2 \,α \frac{𝒽}{c}+2 \,α^2 \right)^2}  .

La condition  (drdς)2=1−2𝒱r=0\displaystyle \left(\frac{dr}{dς}\right)^2=1-2 \,𝒱_r=0  nécessite  𝒽≥𝒽min𝒽≥𝒽_{min}  (sinon la trajectoire rejoint forcément la singularité en  r=RH≤rsr=R_H≤r_s ),  où l'expression littérale compliquée de la valeur limite 𝒽min𝒽_{min} est de peu d'intérêt ici (il est plus efficace de tracer les courbes correspondant à ces cas limites).

Pour le sens direct (en vert, avec  αrs=0,25\displaystyle \frac{α}{r_s} =\text{0,25}  et  𝒽crs≈2,15\displaystyle \frac{𝒽}{c \:r_s}≈\text{2,15} )  ;  la distance minimum d'approche est diminuée.

rotEffet_Im/Vrph.jpg

Pour le sens rétrograde (en rouge, avec  αrs=0,25\displaystyle \frac{α}{r_s} =\text{0,25}  et  𝒽crs≈−3,11\displaystyle \frac{𝒽}{c \:r_s}≈-\text{3,11} )  ;  la distance minimum d'approche est augmentée.

Effet Lense-Thirring

• De façon générale, l'effet Lense-Thirring est associé à l'entraînement par la rotation de l'espace autour d'un astre en rotation.

Une particule de moment cinétique nul (qui donc “ne tourne pas” par rapport à l'espace), est telle que :  dφcdt=−g30g33\displaystyle \frac{dφ}{c \,dt}=-\frac{g_{30}}{g_{33}} .

Pour une particule en chute libre, initialement radiale, depuis l'infini, dans le plan  θ=π2θ=\frac{π}{2}  (elle y reste d'après la symétrie), la conservation impose que la trajectoire ne reste pas radiale :  dφcdt=rsαr.(r2+α2.(1+rsr))≈rsαr3\displaystyle \frac{dφ}{c \,dt}=\frac{r_s \: α}{r.\left(r^2+α^2.\left(1+\frac{r_s}{r}\right)\right)}≈\frac{r_s \: α}{r^3} .

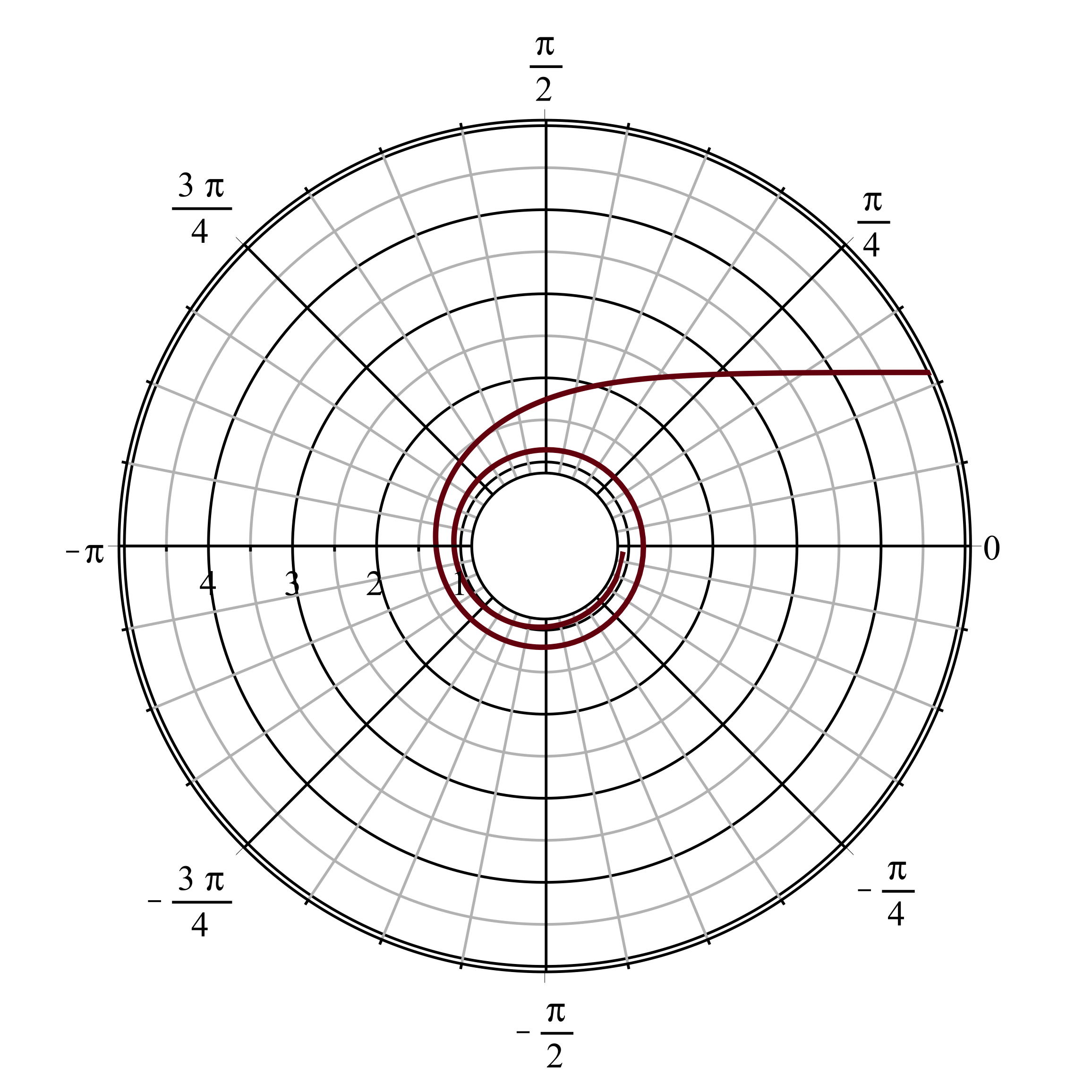
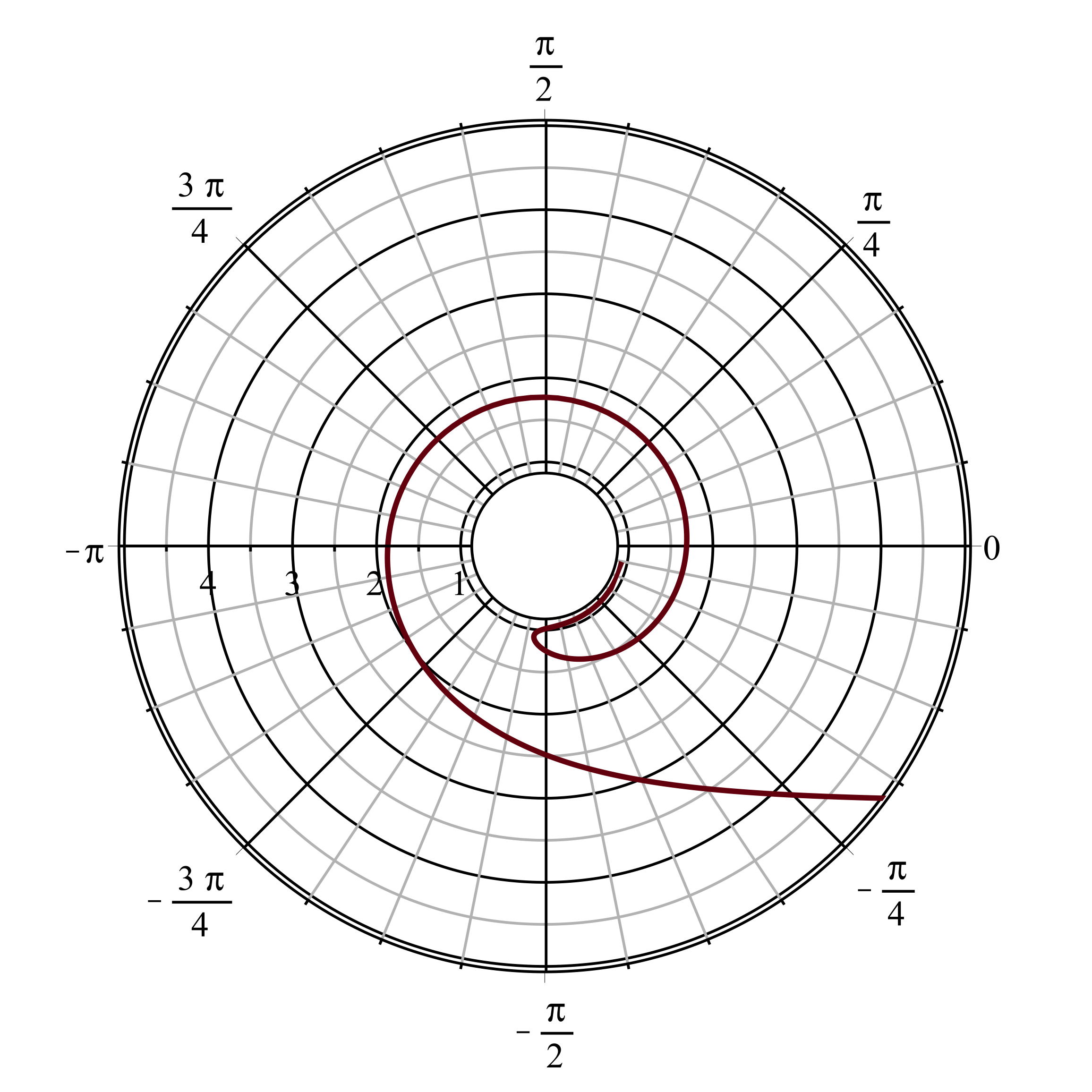
On peut tracer les trajectoires correspondantes des photons, pour  αrs=0,25\displaystyle \frac{α}{r_s} =\text{0,25}  et  𝒽crs=0\displaystyle \frac{𝒽}{c \:r_s}=0 ;  puis pour des cas proches des limites  𝒽crs≈2,1w;,−3,11\displaystyle \frac{𝒽}{c \:r_s}≈\text{2,1} \phantom{w} ; \phantom{,} -\text{3,11} .
 
rotEffet_Im/photon_0.jpg

rotEffet_Im/photon_2.jpg
 rotEffet_Im/photon_-3.jpg

On constate que pour le cas rétrograde la trajectoire est finalement “entraînée” dans le sens direct par la rotation de l'espace-temps autour de l'astre.

◊ remarque : la limite de l'horizon correspond dans ce cas à  RH≈0,933rsR_H≈\text{0,933} \;r_s .

• On décrit toutefois principalement l'effet Lense-Thirring par son effet sur la déviation géodésique d'un gyroscope. La précession est légèrement diminuée pour un gyroscope en orbite circulaire dans le sens direct, ou augmentée dans le sens inverse.

📖 exercices n° II, III, IV et V.