EFFETS DE LA ROTATION D'UN ASTRE - corrigé des exercices

Trajectoires de particules matérielles dans le plan équatorial

• Les variations du “potentiel radial”

𝒱_r (r)

peuvent être tracées numériquement pour différentes valeurs de

𝒽

. Pour

\displaystyle \frac{α}{r_s} =\frac{1}{2 \,\sqrt{2}}

𝓀

fixés, les courbes sont analogues à celles du cas de Schwarzschild ; les types de trajectoires le sont donc aussi.
◊ remarque : il est utile de reporter (en pointillés) la valeur

\frac{1}{2} \,(𝓀^2-1)

jouant ici un rôle équivalent à celui de l'énergie mécanique massique (constante) dans le cas newtonien.

• En particulier :

◊	il existe des trajectoires bornées entre deux distances $r_m$ et $r_M$ ;
◊	d'autres, pour de plus grandes valeurs de l'énergie $ℰ$ (selon la valeur de $𝓀$ pour $𝒽$ donné), peuvent ne pas être bornées supérieurement ;
◊	d'autres enfin, pour des énergies dépassant le maximum, peuvent ne pas avoir de minimum d'approche et rejoindre forcément la singularité (la rotation décrite par $𝒽$ doit être suffisante par rapport au mouvement radial) ; qui plus est, l'existence même du maximum suppose que $𝒽$ ne soit pas trop petit.

• Pour les rotations dans le sens direct (avec

𝓀=\text{0,95}

• Pour le sens rétrograde (avec

𝓀=\text{0,98}

) les rayons caractéristiques et les niveaux d'énergie sont un peu plus grands.

• On peut préciser les courbes en étudiant le lieu des extrémums, caractérisés par :

$\displaystyle \frac{d𝒱_r}{dr}=\frac{c^2 \: r_s}{2 \,r^2}-\frac{h^2-c^2 \: α^2.(𝓀^2-1)}{r^3} +\frac{3 \,r_s .(h-c \:α \:𝓀)^2}{2 \,r^4}=0$ .

• Ceci impose :

\displaystyle \frac{r_e}{r_s} =\frac{𝒽^2-c^2 \: α^2.(𝓀^2-1)}{c^2 \: r_s^{\:2}}±\sqrt{\left(\frac{𝒽^2-c^2 \: α^2.(𝓀^2-1)}{c^2 \: r_s^{\:2}}\right)^2-3 \;\left(\frac{𝒽-c \:α \:𝓀}{c \:r_s}\right)^2}

; puis en combinant la condition d'extrémum avec l'expression de

𝒱_r

on obtient :

\displaystyle 𝒱_r (r_e )=\frac{r_s}{4 \,r_e^{\:3}} \: \left[(𝒽-c \:α \:𝓀)^2-c^2 \: r_e^{\:2} \,\right]

; cela définit paramétriquement (en fonction de

𝒽

, ou ensuite de

𝓀

) les courbes reportées en tirets.

• Une différence importante intervient en fait ici (par rapport au cas de Schwarzschild) :

𝒱_r

dépend aussi de

𝓀

. Ainsi, les courbes correspondant à des plus grandes énergies sont déformées.
• Pour

\displaystyle α=\frac{r_s}{2 \,\sqrt{2}}

𝒽=\text{1,5}

fixés, les variations du “potentiel radial”

𝒱_r (r)

pour différentes valeurs de

𝓀

sont représentées ci-après.

• On constate essentiellement que les plus grandes valeurs de

𝓀

relèvent le maximum et déplacent le minimum vers des plus grandes valeurs de

r

(la partie en tirets gris ne concerne pas le problème physique étudié car elle correspond à

𝓀>1

). En pratique il semble que, pour

𝒽

fixé, les particules plus proches du centre tournent plus si elles ont plus d'énergie.
◊ remarque : ici

𝒽

fixé mesure la rotation par rapport à l'espace, lui même entraîné par la rotation de l'astre ; le pic du maximum correspond à une barrière due à la force centrifuge, elle même plus ou moins liée à la rotation par rapport à la métrique ; l'influence de

𝓀

peut être liée à cette différence.
• On constate en outre (en pointillés) qu'une petite variation de

𝓀

conduit à une grande variation de la valeur

\frac{1}{2} \,(𝓀^2-1)

analogue ici à l'énergie mécanique massique (constante) newtonienne. Or, pour que l'existence des extremums ait une importance physique, il faut que cette constante puisse être entre les deux. L'étude en fonction de

𝓀

(pour

𝒽

fixé) a donc l'intérêt de montrer qu'une variation modérée de l'énergie perturbe peu l'allure de la courbe.

• De façon analogue pour

\displaystyle α=\frac{r_s}{2 \,\sqrt{2}}

𝒽=-\text{2,1}

fixés, les variations du “potentiel radial”

𝒱_r (r)

pour différentes valeurs de

𝓀

, représentées ci-après, montrent que les plus grandes valeurs de

𝓀

abaissent le maximum et déplacent le minimum vers des plus petites valeurs de

r

(la partie en tirets gris est non physique car elle correspond à

𝓀<0

). L'augmentation de rotation évoquée précédemment intervient dans le sens direct et les particules plus proches du centre tournent moins dans le sens inverse si elles ont plus d'énergie.

• L'existence des extremums implique :

\displaystyle \left(\frac{𝒽^2-c^2 \: α^2.(𝓀^2-1)}{c^2 \: r_s^{\:2}}\right)^2-3 \;\left(\frac{𝒽-c \:α \:𝓀}{c \:r_s}\right)^2>0

; on peut simplifier à l'aide de notations réduites :

\displaystyle H=\frac{𝒽}{c \:r_s}

;

\displaystyle 𝒶=\frac{α}{r_s}

.
• Les racines de :

\left[H^2-𝒶^2.(𝓀^2-1)+\sqrt{3} \: (H-𝒶 \:𝓀 )\right].\left[H^2-𝒶^2.(𝓀^2-1)-\sqrt{3} \: (H-𝒶 \:𝓀 )\right]=0

sont :

$H_1=\frac{1}{2}\: \left[\sqrt{3}+\sqrt{(2 \,𝒶 \:𝓀-\sqrt{3})^2-4 \,𝒶^2} \, \right]$ ; $H_2=\frac{1}{2}\: \left[\sqrt{3}-\sqrt{(2 \,𝒶 \:𝓀-\sqrt{3})^2-4 \,𝒶^2} \, \right]$ ;
$H_3=\frac{1}{2}\: \left[-\sqrt{3}+\sqrt{(2 \,𝒶 \:𝓀+\sqrt{3})^2-4 \,𝒶^2} \, \right]$ ; $H_4=\frac{1}{2}\: \left[-\sqrt{3}-\sqrt{(2 \,𝒶 \:𝓀+\sqrt{3})^2-4 \,𝒶^2} \, \right]$ .

• Les graphiques en fonction de

𝓀∈[0\, ;1]

, pour différentes valeurs de

𝒶∈[0 \,;\text{0,5}]

, montrent que les intervalles

[H_1 \, ; H_2 ]

[H_3 \,; H_4 ]

, délimités par deux paraboles symétriques, sont toujours disjoints (ci-dessous pour

𝒶=\text{0,4}

• Les solutions envisageables sont :

H>H_1

dans le sens direct ;

H<H_4

dans le sens rétrograde ;

H_3<H<H_2

principalement dans le sens direct.
• Par ailleurs, le cas limite d'extremum correspond à :

\displaystyle \frac{r_{ei}}{r_s} =H^2-𝒶^2.(𝓀^2-1)

. Or l'existence des extremums n'est utile que si :

r_{ei}>R_H=\frac{1}{2} \left(r_s+\sqrt{r_s^{\:2}-4 \,α^2}\right)

.
• Ceci impose la condition :

H^2>\frac{1}{2} \left(1+\sqrt{1-4 \,𝒶^2} \right)+𝒶^2.(𝓀^2-1)

. Ces limites, représentées en tirets, montrent que le plus souvent l'intervalle

H_3<H<H_2

n'est pas acceptable.

• En outre, pour que l'existence des extremums ait une influence physique, il faut aussi que la quantité

\frac{1}{2} (𝓀^2-1)

décrivant l'énergie puisse être dans l'intervalle entre minimum et maximum. Une recherche (numérique) des paramètres

(H, 𝓀 )

acceptables indique en fait des zones assez restreintes.

• D'un autre point de vue, il existe aussi des cas spéciaux pour les grandes valeurs de

α

. L'existence de

H_1

H_2

nécessite :

(2 \,𝒶 \:𝓀-\sqrt{3})^2-4 \,𝒶^2=(2 \,𝒶 \:𝓀-\sqrt{3}-2 \,𝒶)(2 \,𝒶 \:𝓀-\sqrt{3}+2 \,𝒶)>0

; ceci impose :

𝒶<\frac{\sqrt{3}}{4}≈\text{0,433}

.
• Pour

α

plus grand, pour les grandes valeurs de

𝓀

dans le sens direct (ci-dessous

𝓀>\sqrt{3}-1

pour

𝒶=\text{0,5}

), il n'y a pas de minimum de

𝒽

associé à la forme des courbes ; il subsiste par contre toujours celui associé à la condition

r_{ei}>R_H

• Une recherche (numérique) des paramètres

(H, 𝓀 )

acceptables indique ici encore des zones assez restreintes. On constate en particulier que la région

H>H_1

(quand

H_1

est défini) ne joue aucun rôle. Au contraire, les cas autorisés pour

H_3<H<H_2

(près de la limite) interviennent effectivement.
◊ remarque : les mouvements rétrogrades sont qualitativement peu modifiés.

• On peut s'intéresser au cas avec par exemple :

𝒶=0\text{,}5

;

H=1\text{,}1

(qui correspondrait à

H>H_1

en respectant

r_{ei}>R_H

pour

𝓀≈0\text{,}7

) ; on constate qu'il existe effectivement des extremums, mais que l'énergie n'est dans l'intervalle considéré que pour

𝓀≈0\text{,}9

1\text{,}0

• On peut aussi s'intéresser au cas avec :

𝒶=0\text{,}5

;

𝓀≈0\text{,}7

(avec

H_3<H<H_2

et en respectant

\displaystyle r_{ei}>R_H=\frac{r_s}{2}

) ; on constate qu'il existe effectivement de tels extremums pour

H≈0\text{,}700

0\text{,}715

◊ remarque : dans ce cas, c'est pour

H

décroissant au dessous de la limite (

H<H_2

) qu'apparaissent les extrémums.

Notion de “verticale”

1.a.	• Le mouvement libre correspond à : $\displaystyle \frac{DU^μ}{dτ}=\frac{dU^μ}{dτ}+Γ_{\phantom{.}αβ}^μ \: U^α \: U^β=0$ . • Pour un point soumis à la force de tension du fil, l'évolution peut s'écrire : $\displaystyle \frac{DU^μ}{dτ}=\frac{dU^μ}{dτ}+Γ_{\phantom{.}αβ}^μ \: U^α \: U^β=\frac{f^μ}{m}$ .

1.b.	• La quadri-vitesse du point immobile peut s'écrire : $U^α=(c \,\dot{t} \text{ ; } 0 \text{ ; } 0 \text{ ; } 0)$ , en notant par $\dot{⬚}$ la dérivée par rapport à $τ$ .

2.a.	• La première équation se limite à : $\displaystyle \frac{dU^0}{dτ}=\frac{f^0}{m}$ . • Compte tenu du fait que $\left\|\left\|U\right\|\right\|=c=Cste$ , on peut considérer $\dot{t} =1=Cste$ et $f^0=0$ . ◊ remarque : cette composante de la force est liée à la puissance développée par les composantes spatiales, ici nulle puisqu'il n'y a pas de mouvement.

2.b.	• La seconde équation donne : $\displaystyle \frac{dU^1}{dτ}+Γ_{\phantom{.}00}^1 \: U^0 \: U^0=\frac{f^1}{m}$ . • Avec $\displaystyle \frac{dU^1}{dτ}=0$ , on obtient : $f^1=m \:c^2 \: Γ_{\phantom{.}00}^1$ . • Dans le cas général : $\displaystyle Γ_{\phantom{.}00}^1=\frac{A'}{2 \,C}=\frac{r_s .(r^2-α^2 \: \cos^2(θ))}{2 \,\left[r^2+α^2 \: \cos^2(θ) \right]^3} \; (r^2-r_s\:r+α^2)$ . • Pour $θ=\frac{π}{2}$ : $\displaystyle Γ_{\phantom{.}00}^1=\frac{A'}{2 \,C}=\frac{r_s}{2 \,r^4} \; (r^2-r_s\:r+α^2)$ . ◊ remarque : en développant, le premier terme correspond à la gravitation newtonienne en $\displaystyle \frac{1}{r^2}$ , le second à la correction relativiste en $\displaystyle \frac{1}{r^3}$ ; le troisième ajoute un effet en $\displaystyle \frac{1}{r^4}$ dû à la rotation.

2.c.	• La troisième équation donne : $\displaystyle \frac{dU^2}{dτ}+Γ_{\phantom{.}00}^2 \: U^0 \: U^0=\frac{f^2}{m}$ . • Avec $\displaystyle \frac{dU^2}{dτ}=0$ , on obtient : $f^2=m \:c^2 \: Γ_{\phantom{.}00}^2$ . • Dans le cas général (en notant $⬚°$ les dérivées par rapport à $θ$ ) : $\displaystyle Γ_{\phantom{.}00}^2=\frac{A°}{2 \,D}=\frac{r_s \: r \:α^2 \: \sin(θ) \: \cos(θ)}{\left[r^2+α^2 \: \cos^2(θ) \right]^3}$ . • Pour $θ=\frac{π}{2}$ : $Γ_{\phantom{.}00}^2=0$ .

2.d.	• La quatrième équation se limite à : $\displaystyle \frac{dU^3}{dτ}=\frac{f^3}{m}$ . • Avec $\displaystyle \frac{dU^3}{dτ}=0$ , on obtient : $f^3=0$ .

• Dans le plan équatorial, la seule composante non nulle est

f^1

: la direction “verticale” est radiale.
• Pour

θ≠\frac{π}{2}

la force a une composante

f^2

non nulle : la ”verticale” n'est pas radiale, mais décalée vers l'un des pôles (selon l'hémisphère ; de façon analogue à la force d'inertie d'entraînement en mécanique newtonienne généralisée).
• Il est intéressant de considérer qu'il n'y a pas de composante

f^3

, contrairement à ce qu'aurait pu laisser penser l'effet Lense-Thirring. Cet effet ne s'applique qu'à une particule en mouvement, de façon analogue à la force d'inertie complémentaire de Coriolis en mécanique newtonienne généralisée.

Effet Lense-Thirring

1.a.	• Le mouvement des photons correspond à : $\displaystyle \frac{Dυ^μ}{dς}=\frac{dυ^μ}{dς}+Γ_{\phantom{.}αβ}^μ \: υ^α \: υ^β=0$ avec $\displaystyle υ^μ=\frac{dx^μ}{dς}$ . • Les équations peuvent aussi s'écrire, souvent plus simplement : $\displaystyle \frac{d}{dς}\frac{∂ℒ}{∂\dot{x}^μ}-\frac{∂ℒ}{∂x^μ}=0$ avec le lagrangien quadratique $ℒ=-\frac{1}{2} g_{μν} \: \dot{x}^μ \: \dot{x}^ν$ .

1.b.	• Pour des photons, le mouvement est paramétré par $ς$ tel que $dς={dx}_0=g_{0ν} \: {dx}^ν=A \:c \,dt+B \:dφ$ .

1.c.	• Pour $x^0=c \,t$ on obtient alors : $\displaystyle \frac{d}{dς}\left(-g_{0ν} \: \dot{x}^ν\right)=0$ , donc : $A \:c \,\dot{t}+B \:\dot{φ}=𝓀=1=Cste$ . ◊ remarque : on note par $\dot{⬚}$ les dérivées par rapport à $ς$ .

1.d.	• Pour $x^3=φ$ on obtient : $\displaystyle \frac{d}{dς}\left(-g_{3ν} \: \dot{x}^ν\right)=0$ , donc : $\displaystyle -B \:c \,\dot{t}+E \:\dot{φ}=\frac{𝒽}{c}=Cste$ . ◊ remarque : la constante $𝒽$ est une généralisation de la constante de la “loi des aires” ; pour des photons $\displaystyle \frac{𝒽}{c}$ correspond ainsi au “paramètre d'impact”.

1.e.	• Puisque $A\:E+B^2=Δ$ , le système de deux équations a pour solution : $\displaystyle c \,\dot{t}=\frac{1}{Δ} \, \left(E-\frac{𝒽}{c} \, B\right)$ ; $\displaystyle \dot{φ}=\frac{1}{Δ} \, \left(B+\frac{𝒽}{c} \, A\right)$ .

1.f.	• Pour $x^1=r$ , l'utilisation du lagrangien est moins aisée car il dépend explicitement de $r$ . Dans la mesure où on a déjà déterminé les autres équations, on peut par contre utiliser la relation ${ds}^2=0$ : $\displaystyle {ds}^2=-\frac{1}{Δ} \, {dς}^2 . \left(A \,\frac{𝒽^2}{c^2} +2 \,B \,\frac{𝒽}{c}-E\right)-C \:{dr}^2=0$ ; $\displaystyle \dot{r}^2=\frac{1}{r^2} \, \left(E-2 \,B \,\frac{𝒽}{c}-A \,\frac{𝒽^2}{c^2} \right)$ .

2.a.

• On obtient :

\displaystyle \frac{dφ}{dr}=\frac{\dot{φ}}{\dot{r}} =-\frac{r}{Δ} \, \frac{B+\frac{𝒽}{c} \, A}{\sqrt{E-2 \,B \,\frac{𝒽}{c}-A \,\frac{𝒽^2}{c^2}}}

2.b.

• Si on veut calculer et tracer

\displaystyle φ(r)=∫_∞^r \frac{dφ}{dr'} \, dr'

, l'intégrale numérique doit se faire depuis l'infini avec un nombre important de pas de calcul. Étant donné que

φ

varie peu pour les grandes valeurs de

r

, on peut simplifier le calcul en intégrant en fonction de la variable de Binet

\displaystyle 𝓊=\frac{1}{r}

. On substitue

\displaystyle r=\frac{1}{𝓊}

dans l'expression

\displaystyle \frac{dφ}{dr}

et on utilise :

\displaystyle φ(𝓊)=∫_0^𝓊 \frac{dφ}{d𝓊'} \, d𝓊'

avec

\displaystyle \frac{dφ}{d𝓊}=-\frac{1}{𝓊^2} \, \frac{dφ}{dr}

.
• Tracer le résultat de l'intégrale numérique précédente en fonction de

r

nécessite de recalculer l'intégrale pour chaque point du tracé. Si l'intégrale comporte (selon le point tracé) entre 0 et 1000 pas, un tracé de 1000 points nécessite environ 500000 pas d'intégration.
• Il peut être plus raisonnable de stocker au fur et à mesure les résultats intermédiaires de l'intégrale dans un vecteur : cela ne fait que 1000 pas d'intégration. Si le calcul optimisé dure

≈1 \:\mathrm{s}

, le calcul non simplifié dure

≈8 \:\mathrm{min}

(le gain est non négligeable si on souhaite faire plusieurs essais pour comparer.

2.c.

• On peut tracer les trajectoires des photons, pour

\displaystyle \frac{α}{r_s} =0\text{,}25

\displaystyle \frac{𝒽}{c \:r_s}=0

; puis pour un cas rétrograde

\displaystyle \frac{𝒽}{c \:r_s}≈-3\text{,}1

(proche de la limite au delà de laquelle le photon ne rejoint pas la singularité).

• On constate que pour le cas rétrograde la trajectoire est finalement “entraînée” dans le sens direct par la rotation de l'espace-temps autour de l'astre.
◊ remarque : la limite de l'horizon correspond dans ce cas à

R_H≈0\text{,}933 \;r_s

Précession géodésique

1.	• Les variations du spin correspondent à : $\displaystyle \frac{DS^μ}{dτ}=\frac{dS^μ}{dτ}+Γ_{\phantom{.}αβ}^μ \: S^α \: U^β=0$ .

2.a.

• Le mouvement correspond à :

\displaystyle \frac{DU^μ}{dτ}=\frac{dU^μ}{dτ}+Γ_{\phantom{.}αβ}^μ \: U^α \: U^β=0

2.b.

• L'intégration donne :

\displaystyle A \, \frac{dt}{dτ}+B \, \frac{1}{c} \, \frac{dφ}{dτ}=𝓀=Cste

;

θ=\frac{π}{2}=Cste

;

\displaystyle -B \, \frac{dt}{dτ}+E \, \frac{1}{c} \, \frac{dφ}{dτ}=\frac{𝒽}{c}=Cste

.
• Puisque

A\:E+B^2=Δ

, le système de deux équations a pour solution :

$\displaystyle \frac{dt}{dτ}=\frac{1}{Δ} \, \left(𝓀 \:E-\frac{𝒽}{c} \, B\right)$ ; $\displaystyle \frac{1}{c} \, \frac{dφ}{dτ}=\frac{1}{Δ} \, \left(𝓀 \:B+\frac{𝒽}{c} \, A\right)$ .

2.c.

• L'équation pour

r

est obtenue plus facilement d'après l'expression de la métrique (en notant

\dot{⬚}

la dérivation par rapport à

τ

) :

$\displaystyle c^2 \, {dτ}^2=-\frac{c^2}{Δ} \, {dτ}^2 . \left(A \,\frac{𝒽^2}{c^2} +2 \,B \:𝓀 \,\frac{𝒽}{c}-E \:𝓀^2 \right)-C \:{dr}^2$ ;
$\displaystyle \dot{r}^2=-\frac{c^2}{r^2} \, \left(Δ+A \,\frac{𝒽^2}{c^2} +2 \,B \:𝓀 \,\frac{𝒽}{c}-E \:𝓀^2 \right)$ .

• Ceci peut s'écrire

\displaystyle \frac{1}{2} \dot{r}^2=\frac{1}{2} c^2.(𝓀^2-1)-𝒱_r

avec un “potentiel radial” :

$\displaystyle 𝒱_r=-\frac{c^2 \: r_s}{2 \,r}+\frac{𝒽^2}{2 \,r^2} \, \left(1-\frac{r_s}{r}\right)+\frac{c^2 \: α^2}{2 \,r^2}+\frac{c \:r_s \: α}{r^3} \: 𝓀 \:𝒽-\frac{α^2}{2 \,r^2} \, \left(1+\frac{r_s}{r}\right) \; c^2 \: 𝓀^2$ .

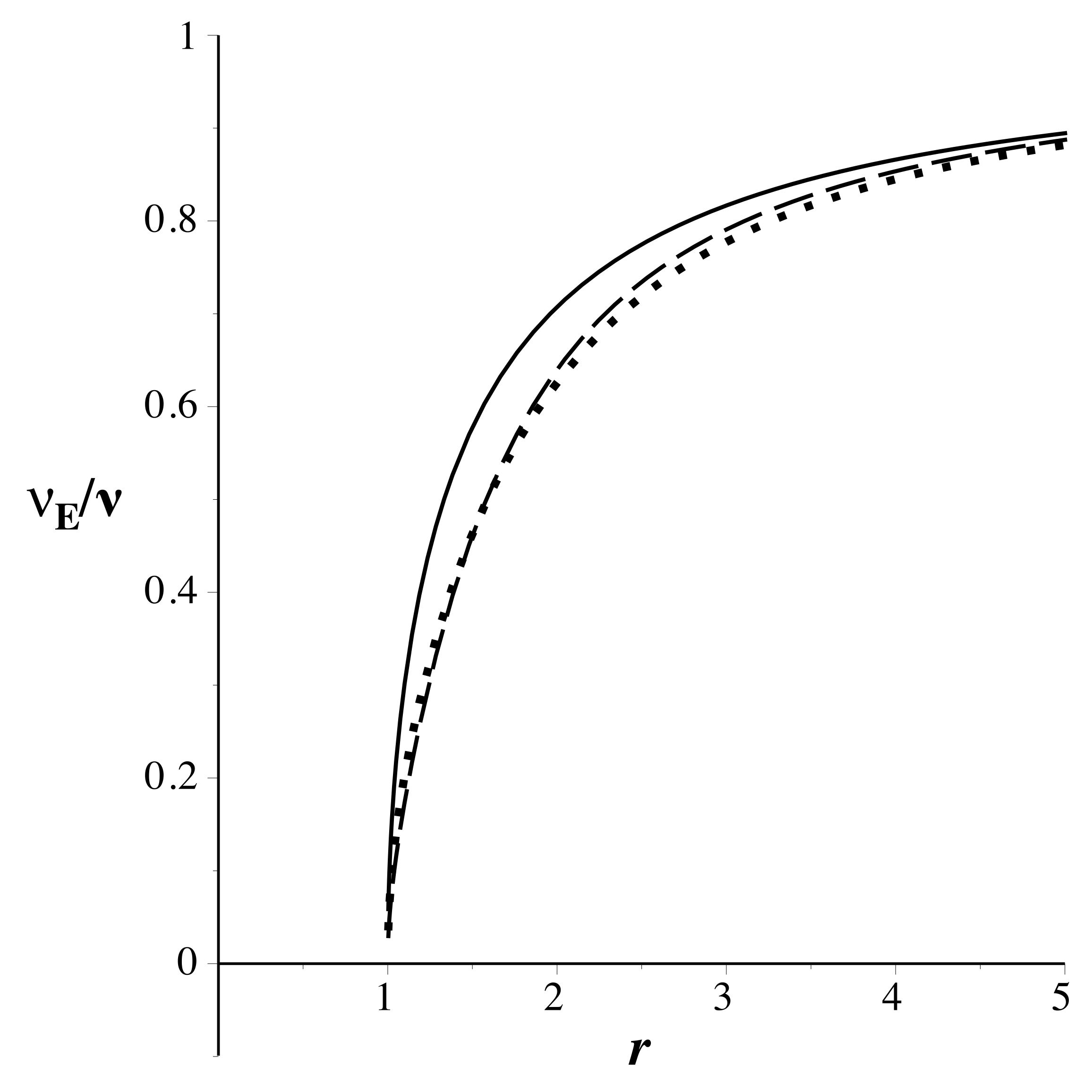
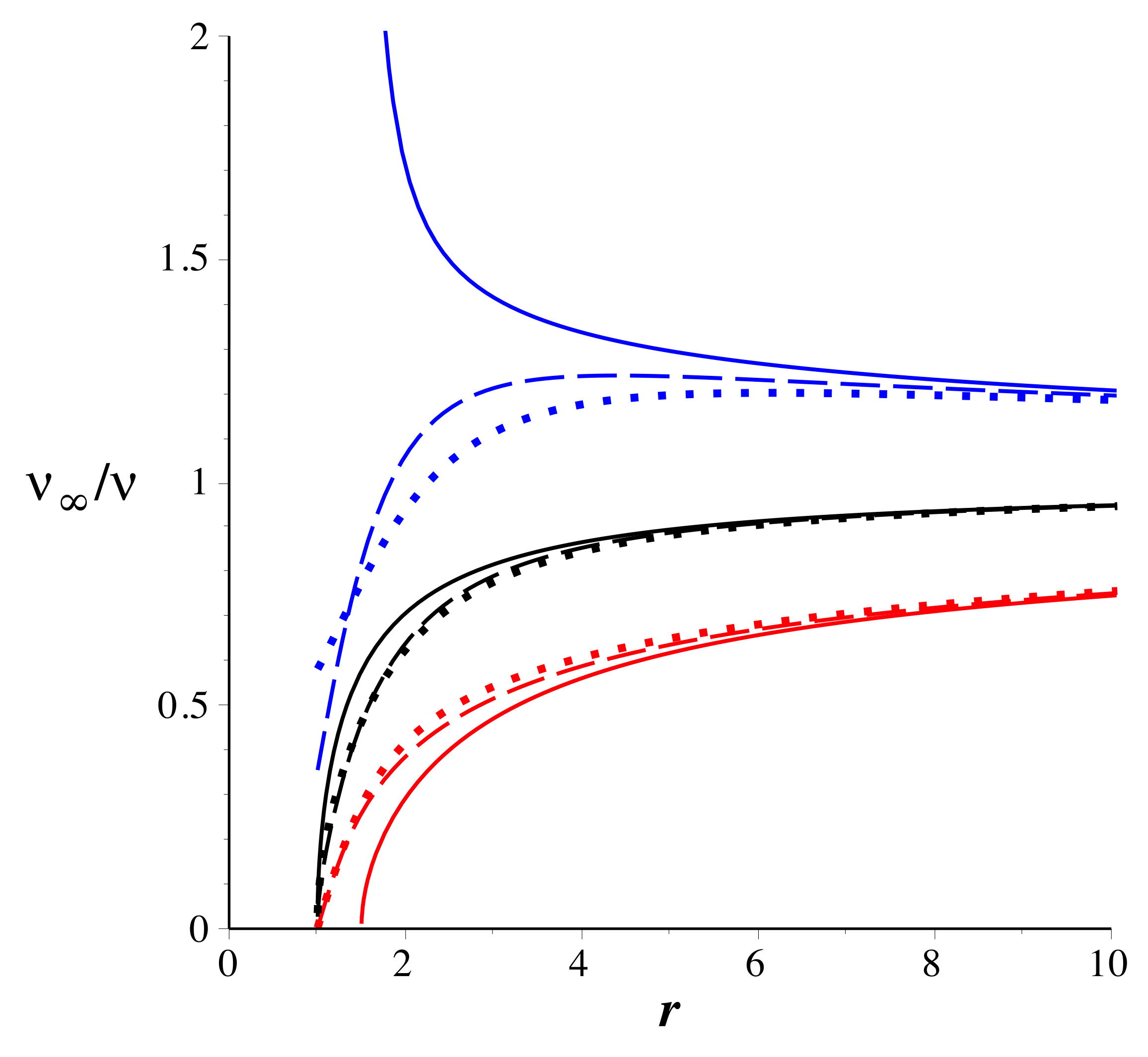
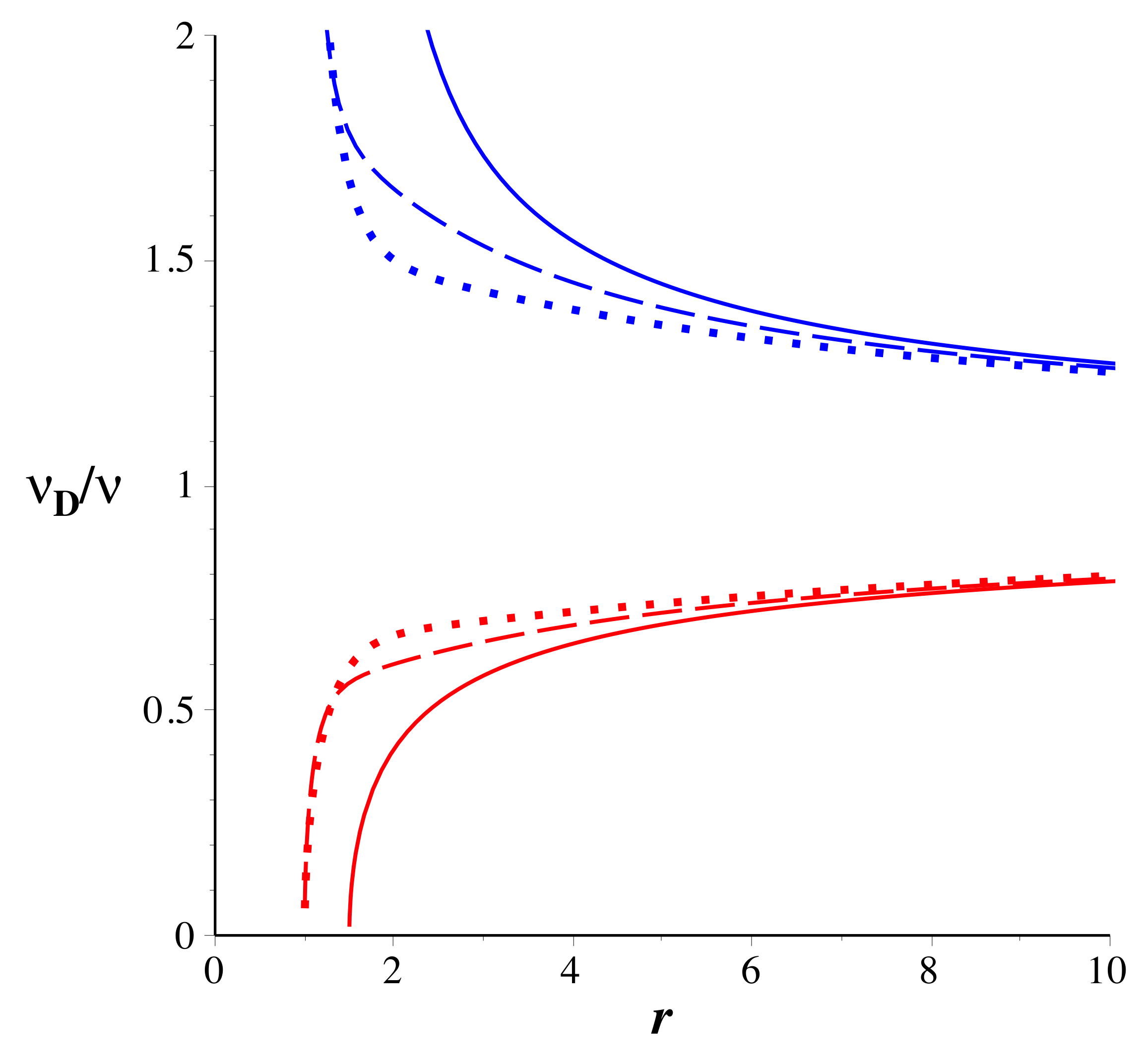
2.d.

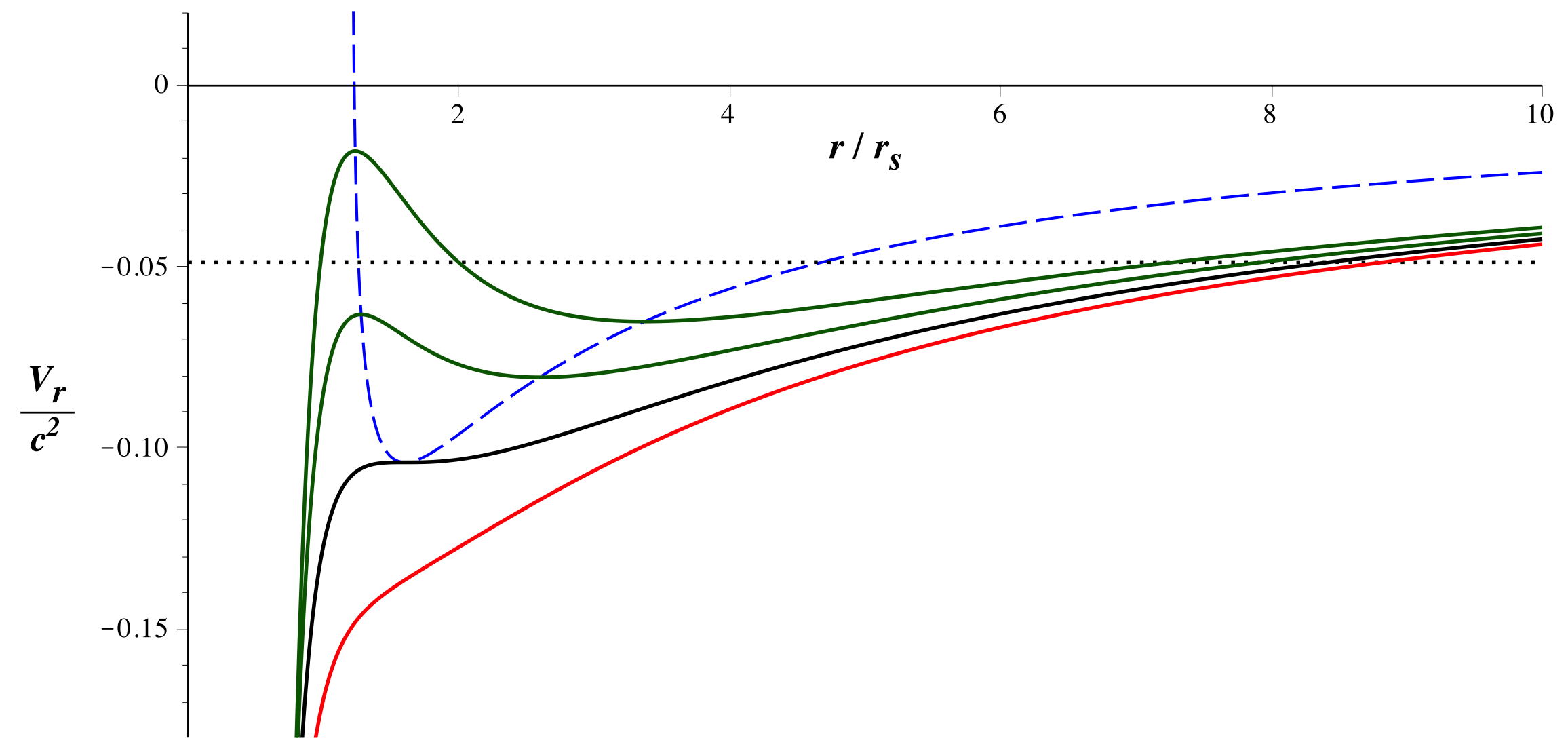
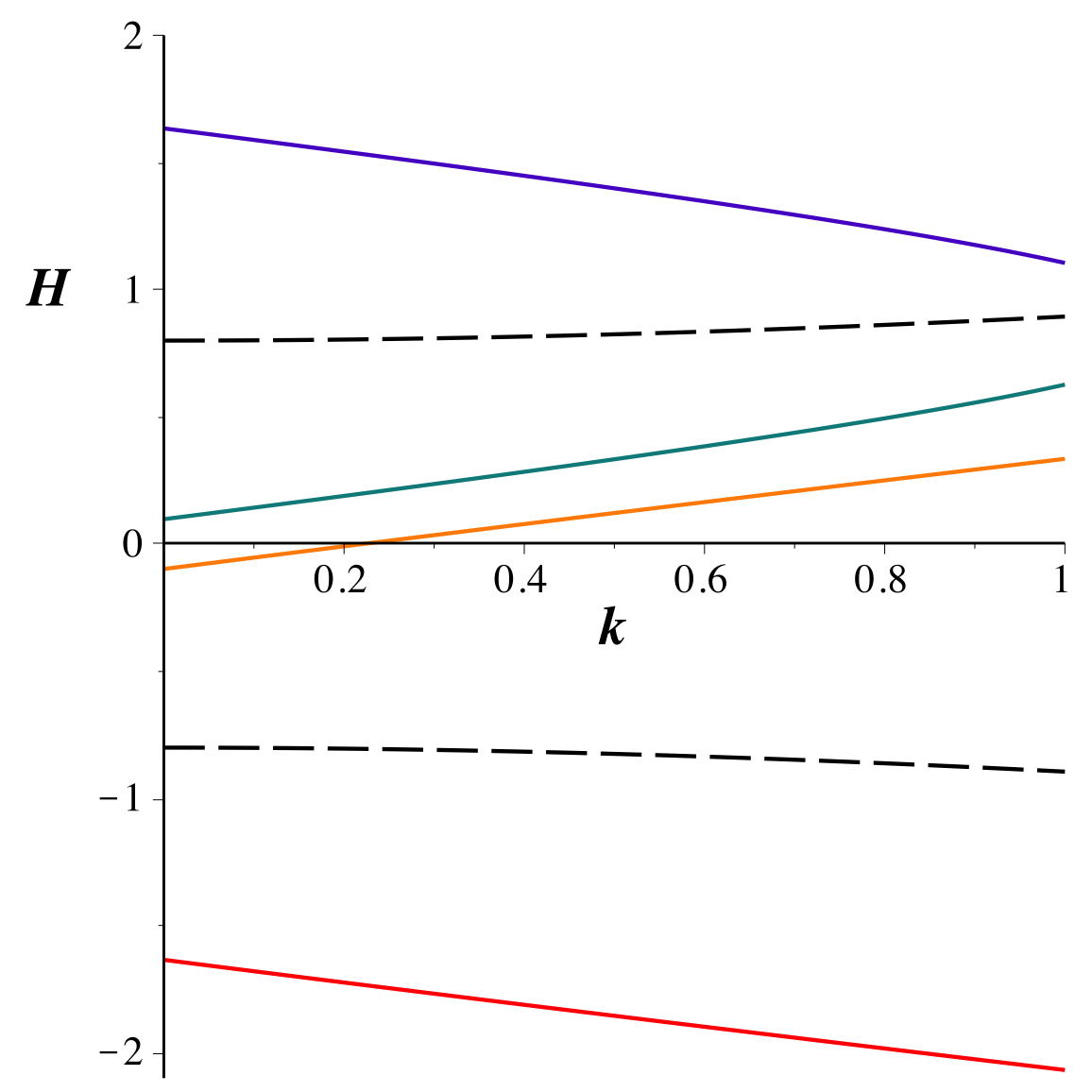
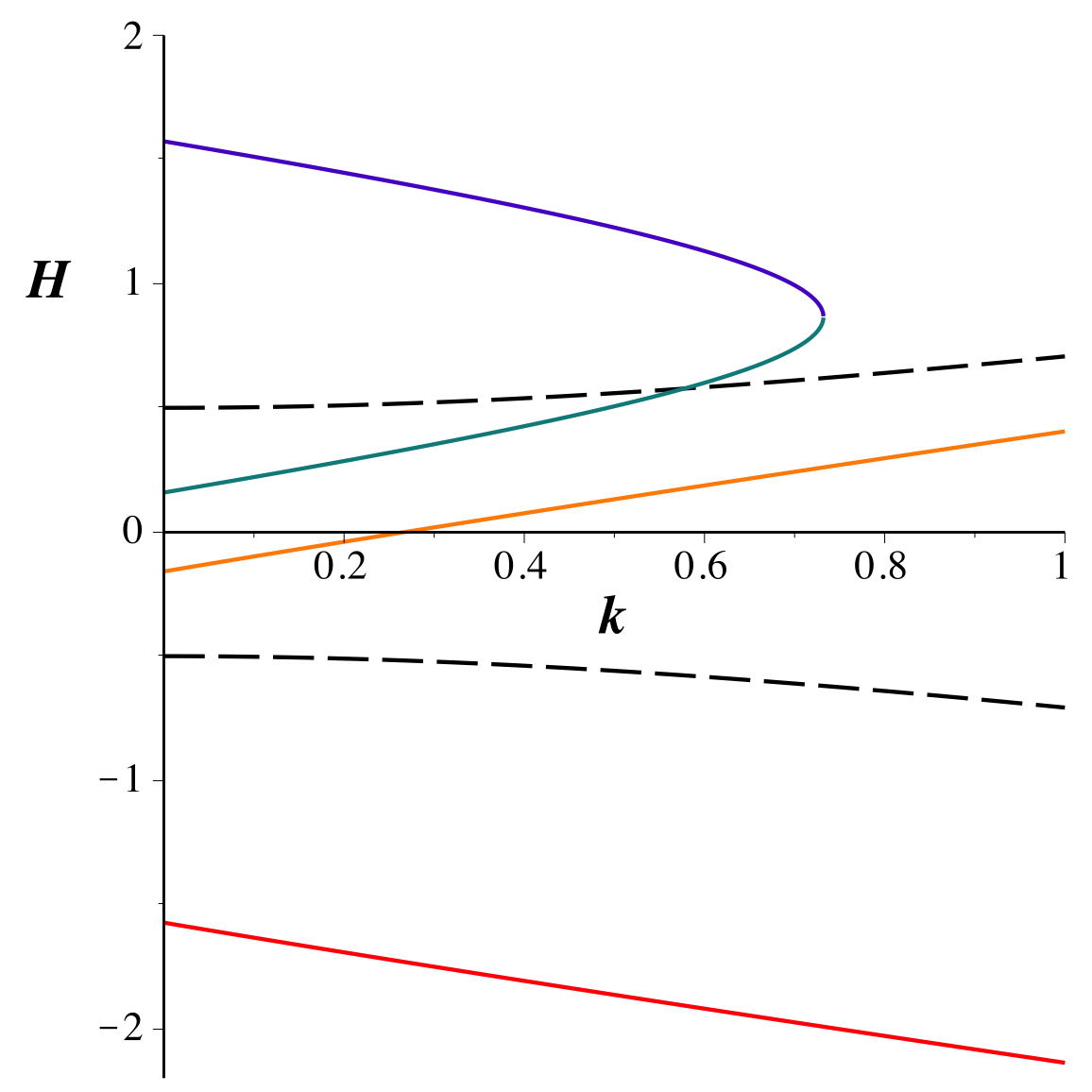
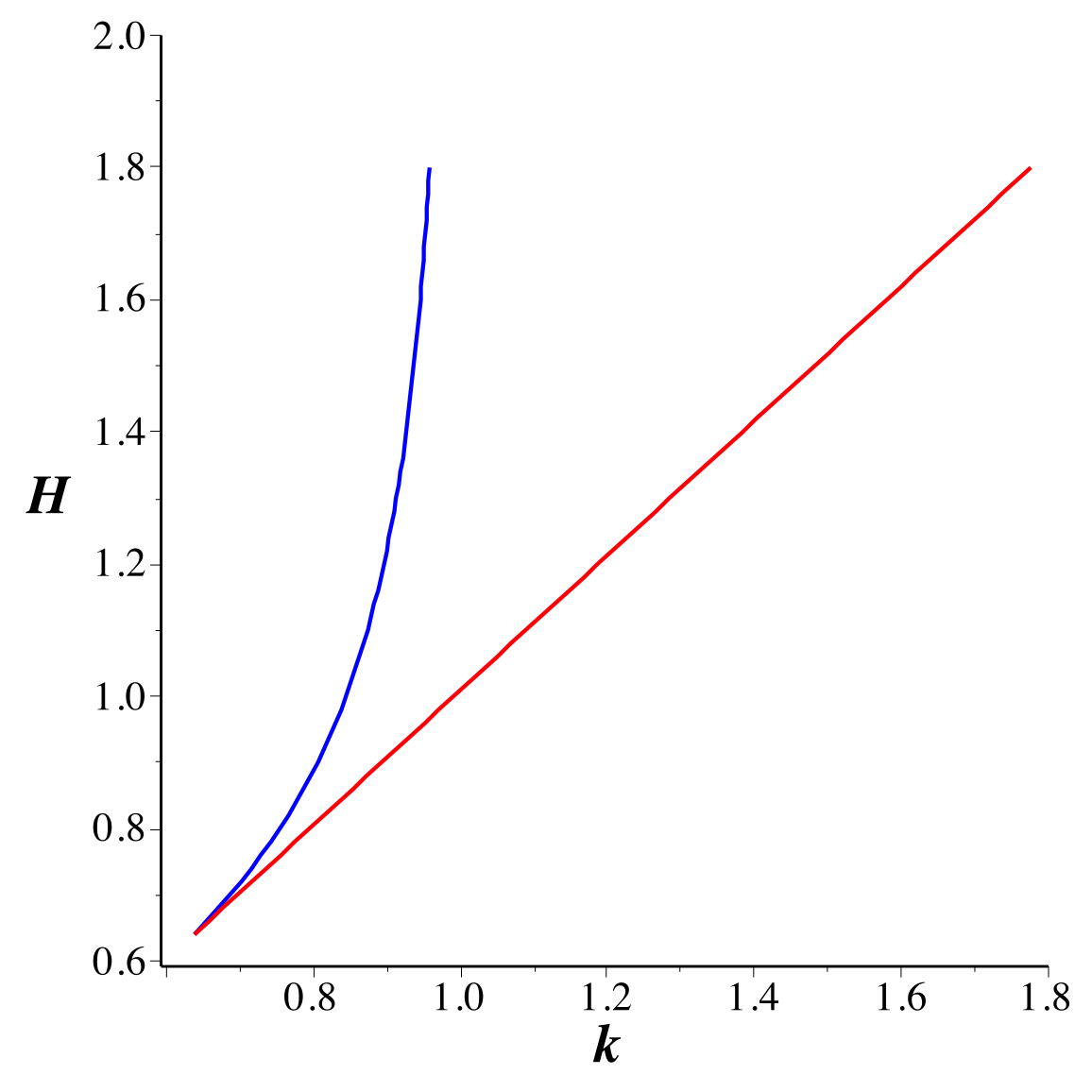
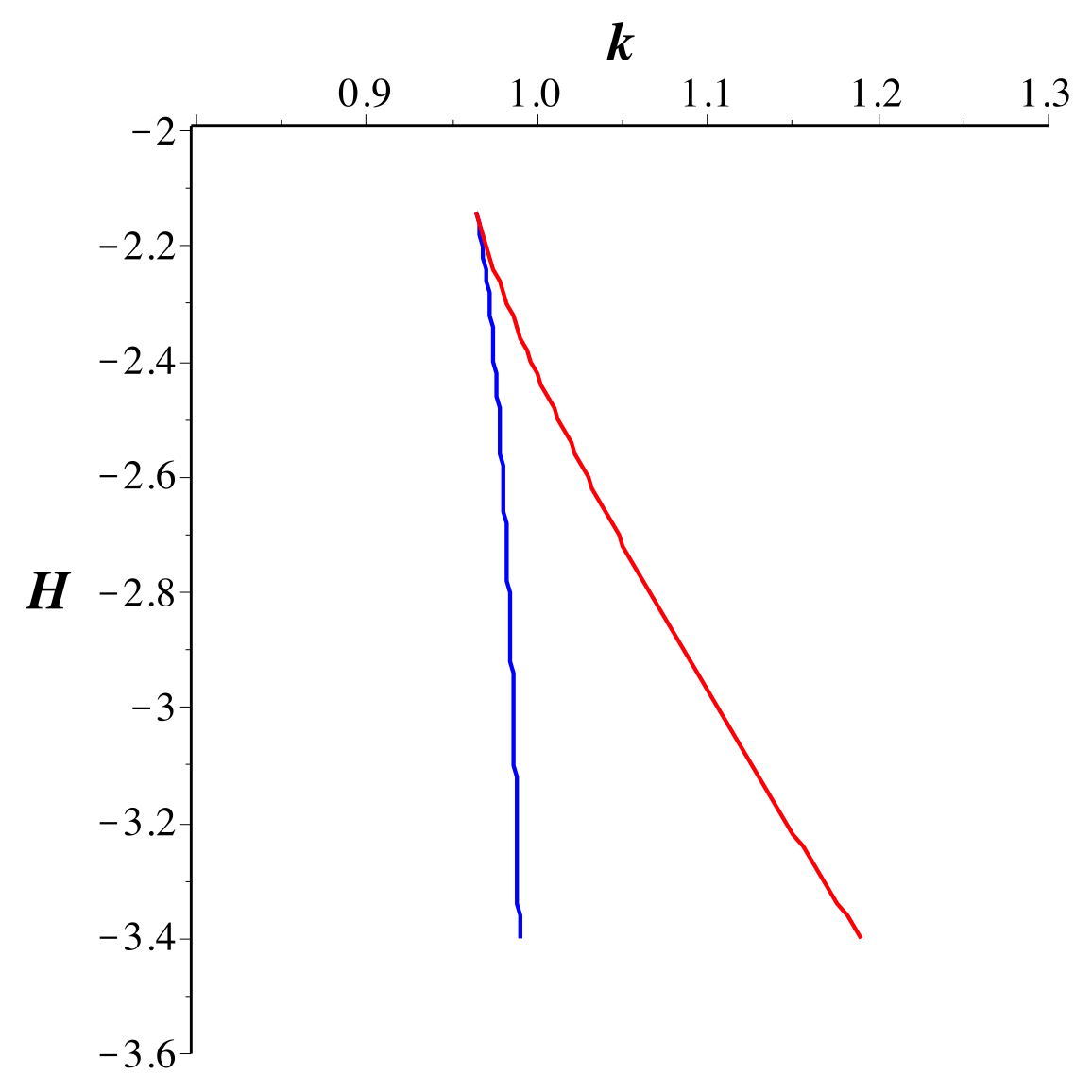
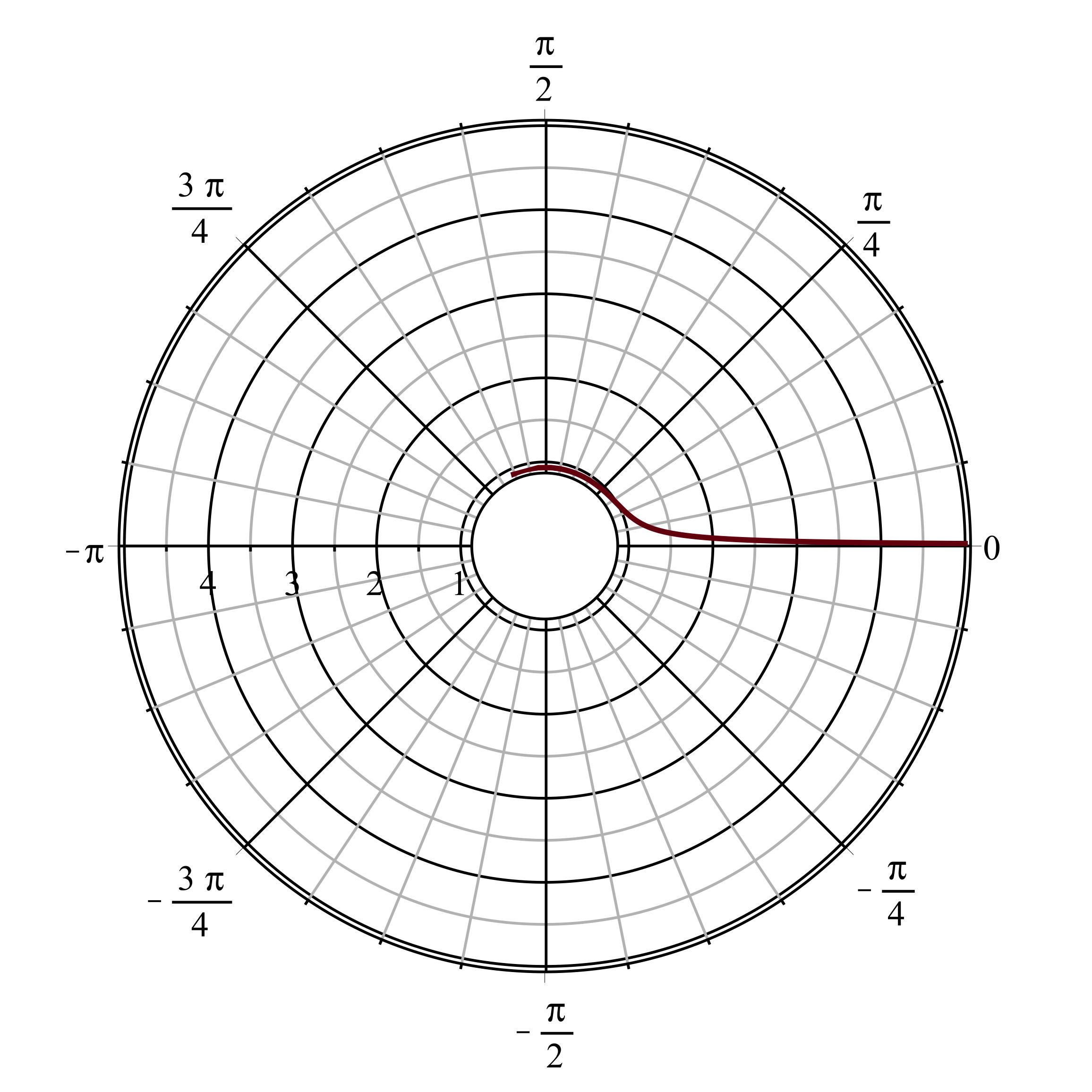
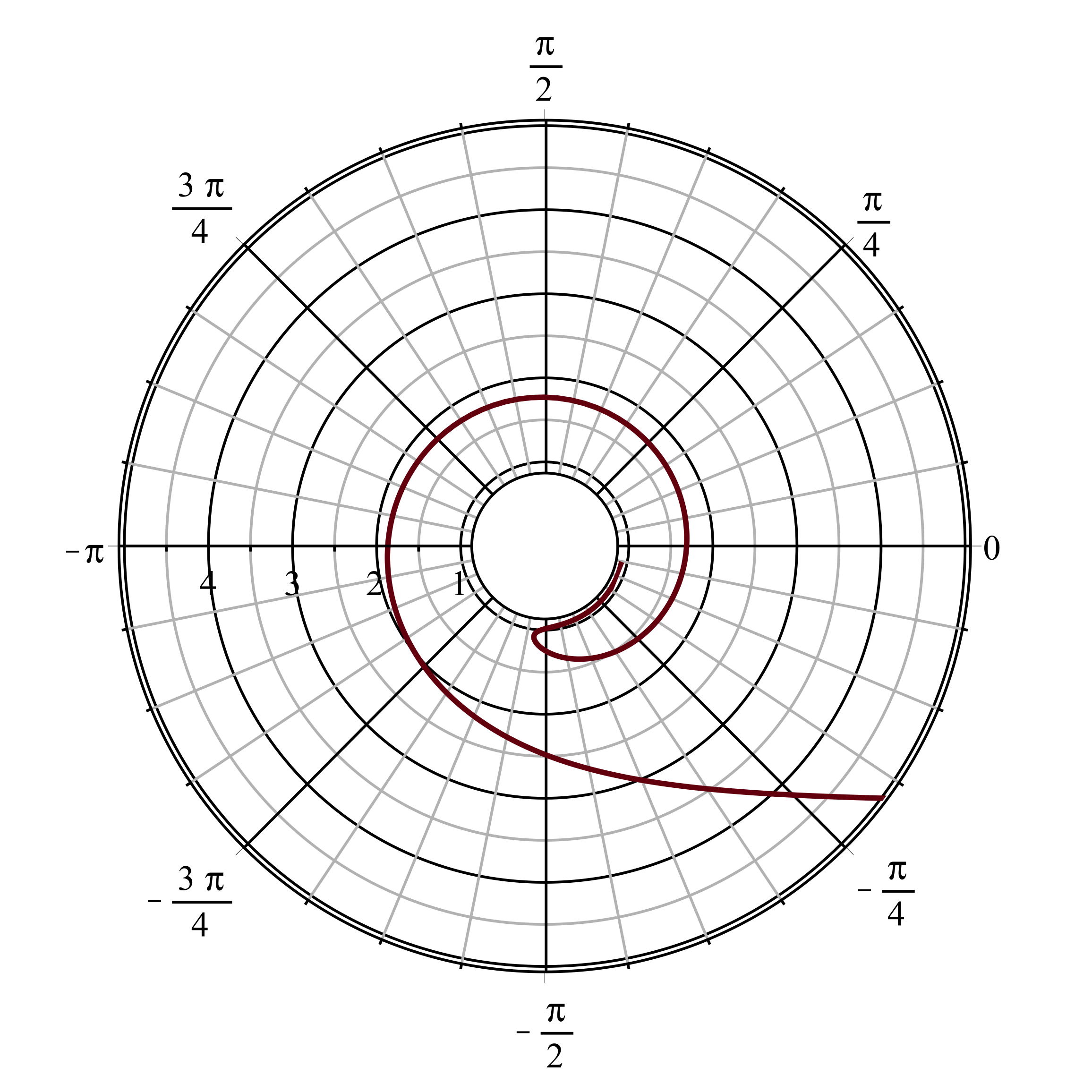
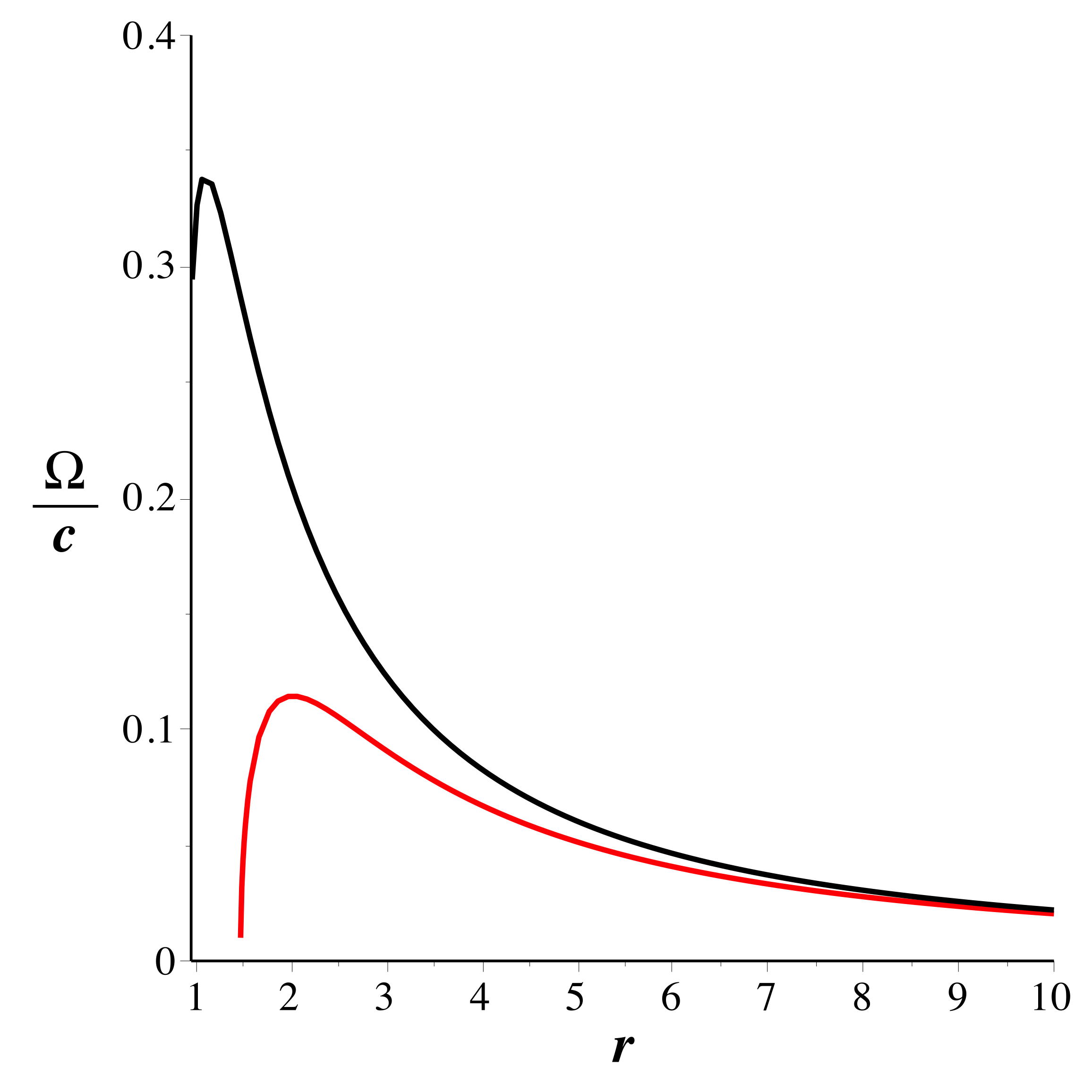
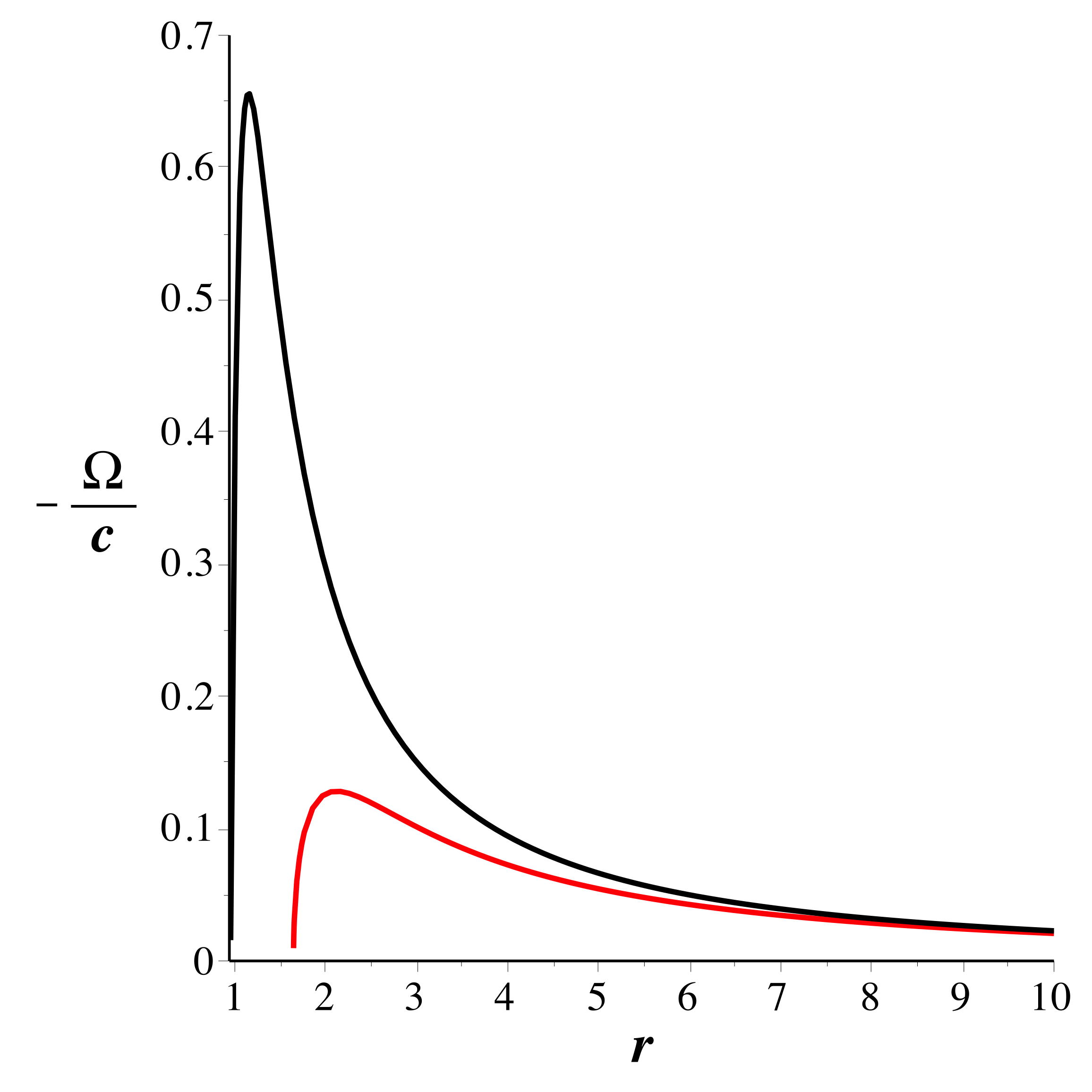
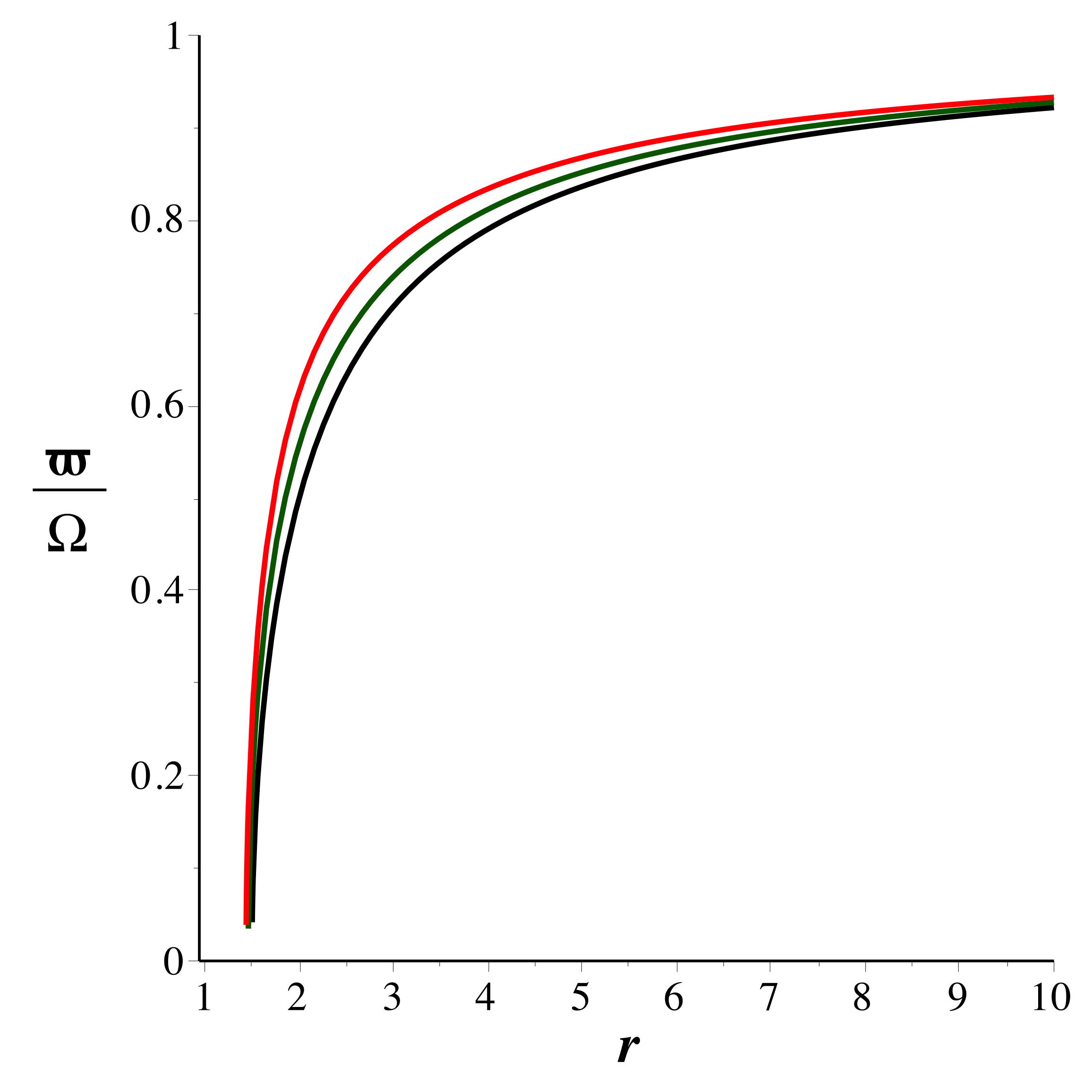
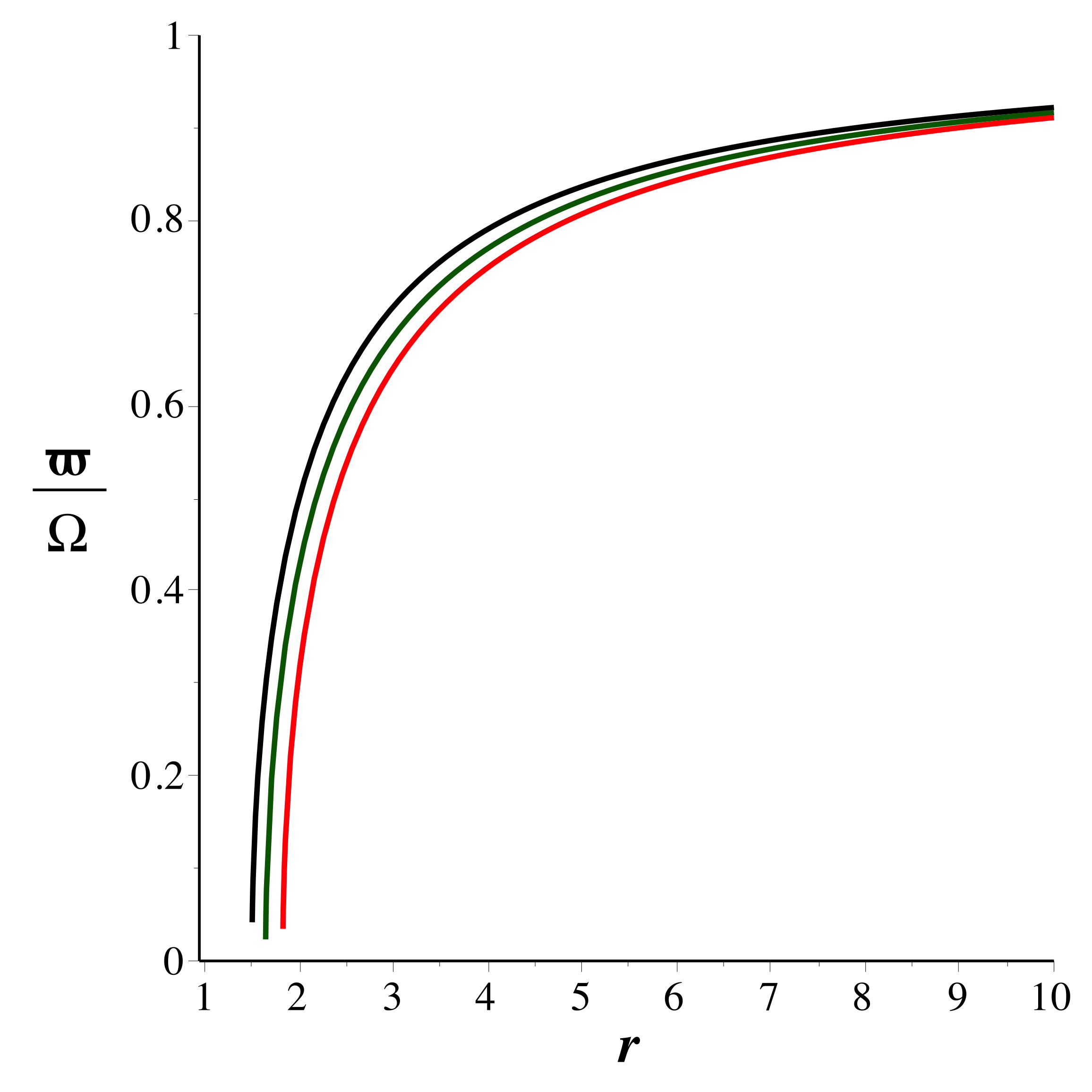
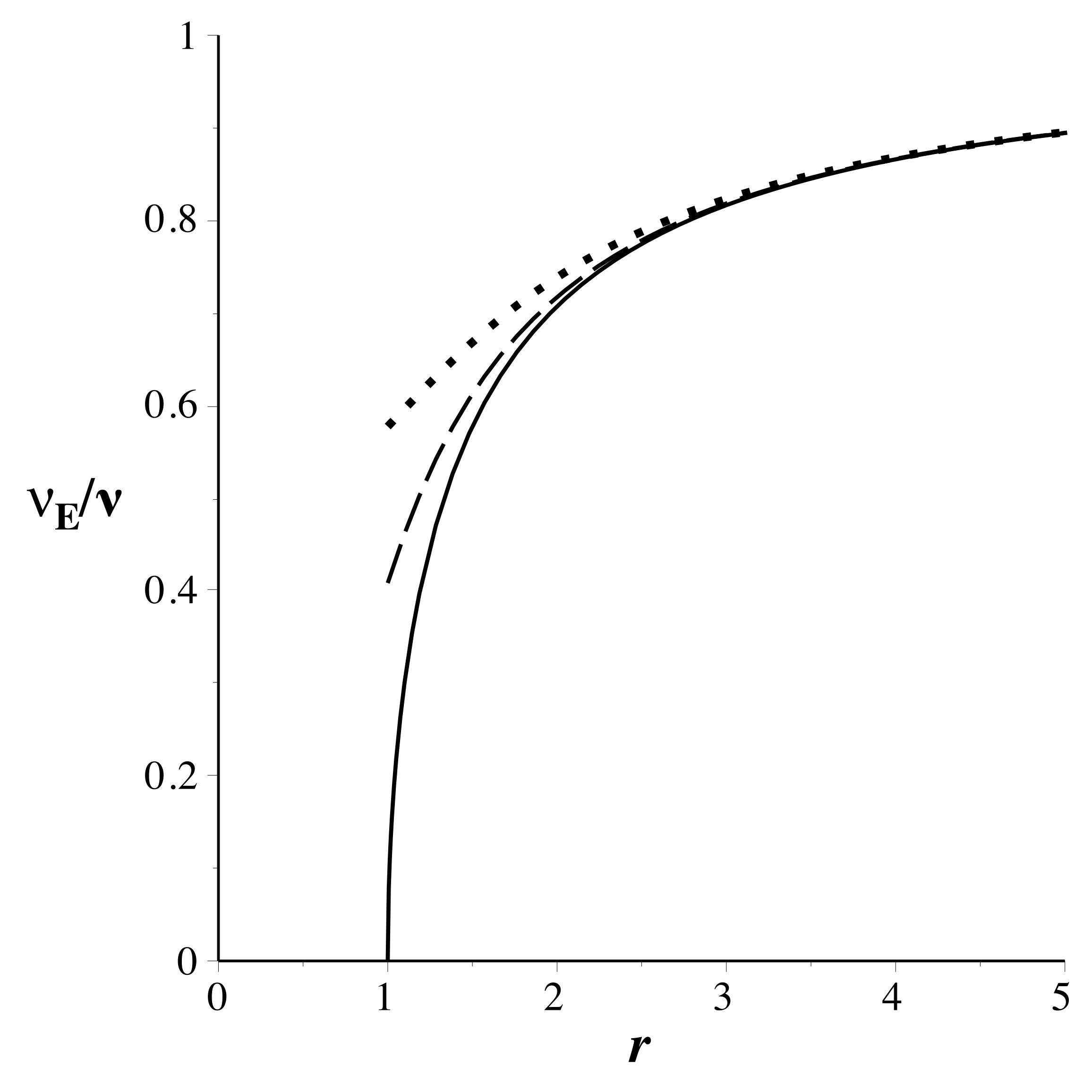
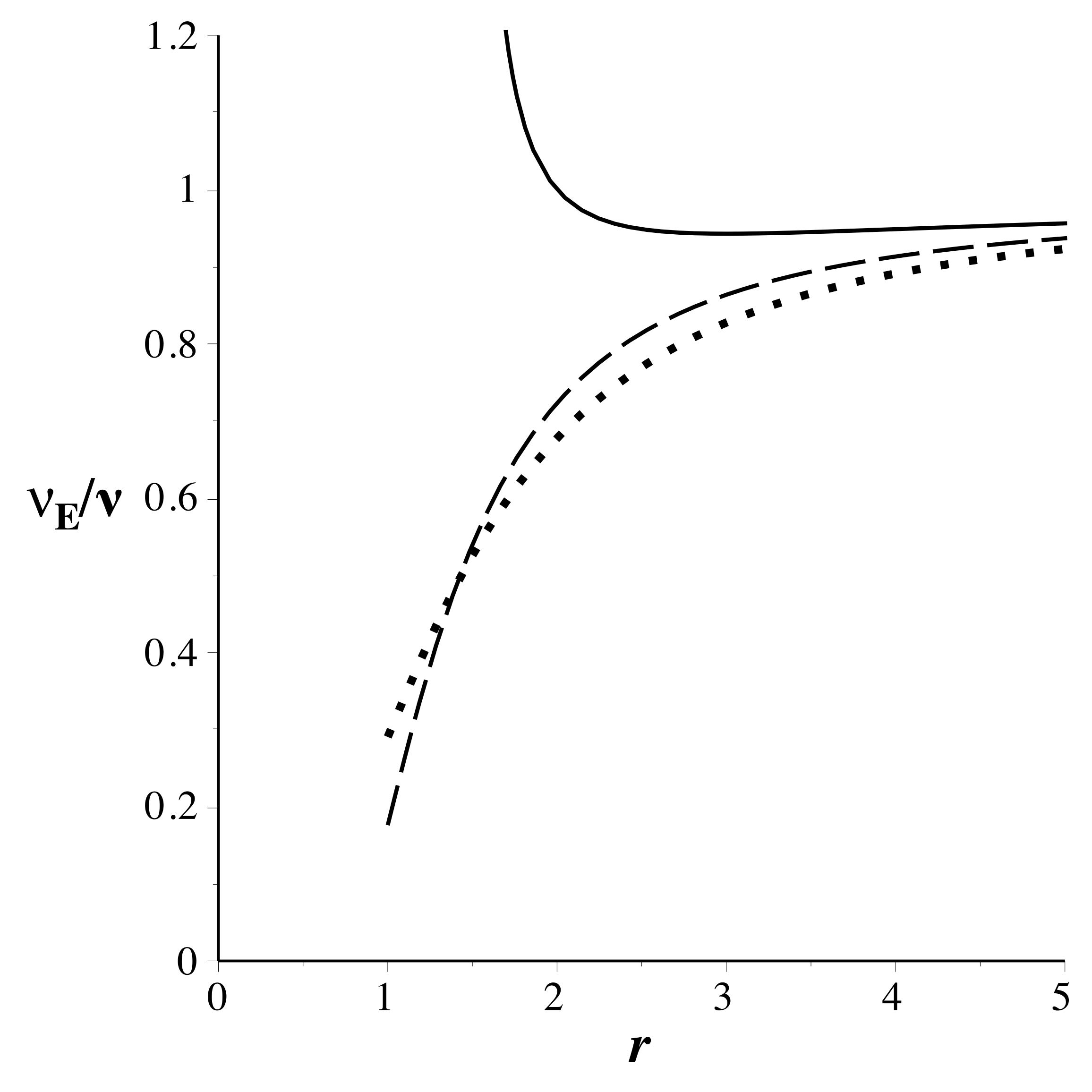
• Les trajectoires circulaires correspondent à

\dot{r}=0

, c'est-à-dire :

\frac{1}{2} c^2.(𝓀^2-1)-𝒱_r=0

.
• En utilisant la variable de Binet

\displaystyle 𝓊=\frac{1}{r}

, la première condition s'écrit :

$-r_s \: c^2 \: 𝓊+\left[h^2-α^2 \: c^2.(𝓀^2-1)\right] \; 𝓊^2-r_s .(𝒽-α \:c \:𝓀)^2 \: 𝓊^3=(𝓀^2-1) \: c^2$ .

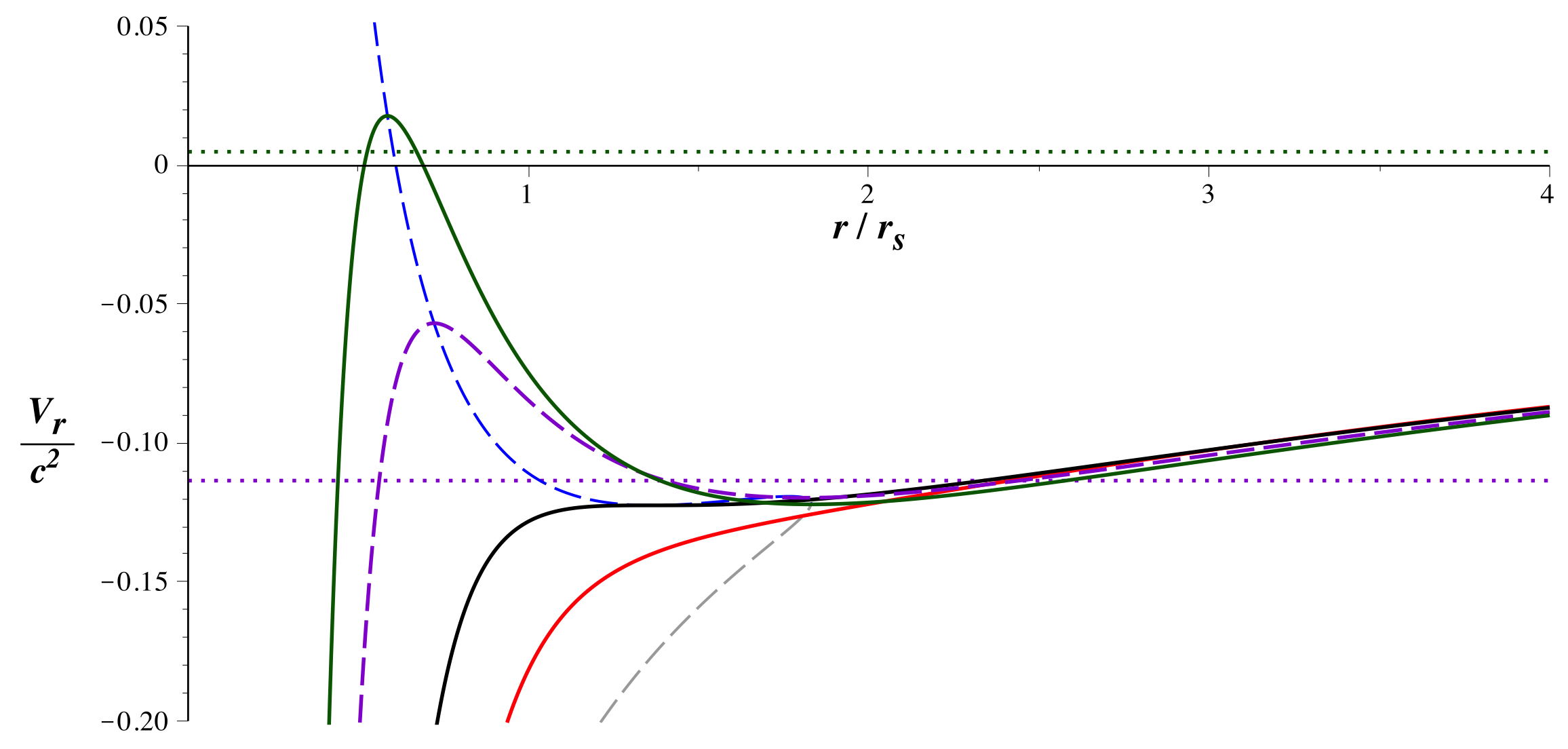
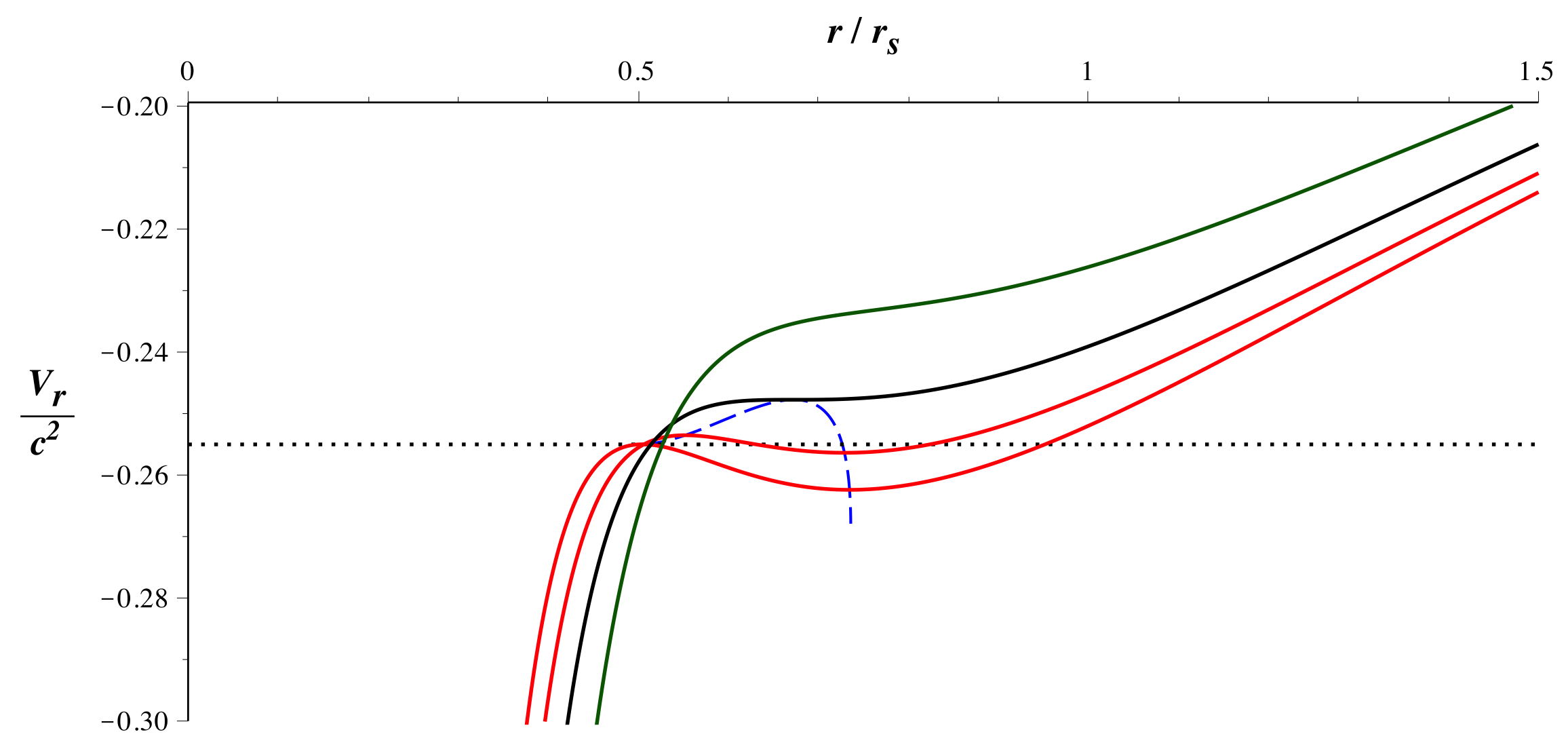
• Les trajectoires circulaires nécessitent de plus :

\ddot{r}=0

, mais cette condition n'est pas simple. Puisqu'elle décrit l'absence de force radiale, il est préférable de considérer la condition d'extremum de

𝒱_r

$\displaystyle \frac{d𝒱_r}{du}= -r_s \: c^2+2 \;\left[𝒽^2-α^2 \: c^2.(𝓀^2-1)\right] \; 𝓊-3 \,r_s .(𝒽-α \:c \:𝓀)^2 \: 𝓊^2=0$ .

• La résolution peut se simplifier en utilisant la variable

η=𝒽-α \:c \:𝓀

	(1)	$-r_s \: c^2 \: 𝓊+\left[η^2+2 \,η \:α \:c \:𝓀+α^2 \: c^2 \right] \; 𝓊^2-r_s \: η^2 \: 𝓊^3=(𝓀^2-1) \: c^2$ ;
	(2)	$-r_s \: c^2+2 \;\left[η^2+2 \,η \:α \:c \:𝓀+α^2 \: c^2 \right] \; 𝓊-3 \,r_s \: η^2 \: 𝓊^2=0$ .

• En éliminant le terme entre crochets entre ces deux équations, on obtient une relation sur

𝓀

		$-r_s \: c^2 \: 𝓊+r_s \: η^2 \: 𝓊^3=2 \;(𝓀^2-1) \: c^2$ ;
	(1a)	$2 \,𝓀^2 \: c^2=(2-r_s \: 𝓊) \: c^2+r_s \: η^2 \: 𝓊^3$ .

• Puis en exprimant le terme entre crochets dans la seconde, on obtient une autre relation sur

𝓀

		$2 \;\left[η^2+2 \,η \:α \:c \:𝓀+α^2 \: c^2 \right] \; 𝓊=r_s \: c^2+3 \,r_s \: η^2 \: 𝓊^2$ ;
	(2a)	$4 \,η \:α \:c \:𝓀 \:𝓊=(3 \,r_s \: 𝓊-2) \: η^2 \: 𝓊-(2 \,α^2 \: 𝓊-r_s ) \: c^2$ .

• En éliminant k entre les deux relations ainsi obtenues, on en déduit une équation sur η :

$𝓊^2 \: η^4 \: \left[(3 \,r_s \: 𝓊-2)^2-8 \,α^2 \: r_s \: 𝓊^3 \right] \: ⋯$

$⋯ \:-2 \,c^2 \: 𝓊 \:η^2 \: \left[(3 \,r_s \: 𝓊-2)(2 \,α^2 \: 𝓊-r_s )-4 \,α^2 \: 𝓊 .(r_s \: 𝓊-2)\right] \: ⋯$

$⋯ \:+c^4 \: (2 \,α^2 \: 𝓊-r_s )^2=0$ .

• Cette équation bicarrée permet de déterminer

η

, mais l'expression peut être très compliquée si on ne simplifie pas ingénieusement. D'abord, l'équation est en fait du second degré pour

\displaystyle \frac{𝓊 \:η^2}{c^2}

. En outre, il est préférable d'obtenir un trinôme du second degré avec un coefficient plus simple du terme quadratique ; on peut ainsi choisir la variable

\displaystyle Y=\frac{c^2}{𝓊 \:η^2}

$(2 \,α^2 \: 𝓊-r_s )^2 \: Y^2-2 \;\left[(3 \,r_s \: 𝓊-2)(2 \:α^2 \: 𝓊-r_s )-4 \,α^2 \: 𝓊 .(r_s \: 𝓊-2)\right] \; Y \:⋯$

$⋯ \:+\left[(3 \,r_s \: 𝓊-2)^2-8 \,α^2 \: r_s \: 𝓊^3 \right]=0$ .

• Le produit et la somme des deux racines sont ainsi :

$\displaystyle 𝒫=\frac{(3 \,r_s \: 𝓊-2)^2-8 \,α^2 \: r_s \: 𝓊^3}{\left(2 \,α^2 \: 𝓊-r_s \right)^2}$ ; $\displaystyle 𝒮=2 \: \frac{(3 \,r_s \: 𝓊-2)(2 \,α^2 \: 𝓊-r_s )-4 \,α^2 \: 𝓊 .(r_s \: 𝓊-2)}{\left(2 \,α^2 \: 𝓊-r_s \right)^2}$ .

• Ensuite, on remarque que les quantités

3 \,r_s \: 𝓊-2

2 \,α^2 \: 𝓊-r_s

intervient à plusieurs endroits. On peut tenter de factoriser le numérateur de

𝒫

$\left(3 \,r_s \: 𝓊-2+2 \,α \:𝓊 \;\sqrt{2 \,r_s \: 𝓊}\,\right)\left(3 \,r_s \: 𝓊-2-2 \,α \:𝓊 \;\sqrt{2 \,r_s \: 𝓊}\,\right)$ .

• Si les deux racines étaient

\displaystyle \frac{3 \,r_s \: 𝓊-2±2 \,α \:𝓊 \;\sqrt{2 \,r_s \: 𝓊}}{2 \,α^2 \: 𝓊-r_s }

, on obtiendrait la somme :

\displaystyle 2 \: \frac{(3 \,r_s \: 𝓊-2)(2 \,α^2 \: 𝓊-r_s )}{\left(2 \,α^2 \: 𝓊-r_s \right)^2}

qui ne convient pas. C'est analogue pour les racines

\displaystyle \frac{-3 \,r_s \: 𝓊+2±2 \,α \:𝓊 \;\sqrt{2 \,r_s \: 𝓊}}{2 \,α^2 \: 𝓊-r_s }

.
• Une idée peut consister à factoriser aussi le dénominateur :

\left(α \:\sqrt{2 \,𝓊}+\sqrt{r_s}\,\right)^2 \:\left(α \:\sqrt{2 \,𝓊}-\sqrt{r_s} \,\right)^2

. On peut alors tester les combinaisons

\displaystyle \frac{3 \,r_s \: 𝓊-2±2 \,α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊})}{\left(α \:\sqrt{2 \,𝓊}±\sqrt{r_s}\right)^2}

\displaystyle \frac{3 \,r_s \: 𝓊-2±2 \,α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊})}{\left(α \:\sqrt{2 \,𝓊}∓\sqrt{r_s}\right)^2}

. Elles donnent hélas aussi une somme qui ne convient pas :

\displaystyle 2 \: \frac{(3 \,r_s \: 𝓊-2)(2 \:α^2 \: 𝓊+r_s )∓8 \,α^2 \: r_s \: 𝓊^2}{\left(2 \,α^2 \: 𝓊-r_s \right)^2}

.
• On peut enfin encore tester les combinaisons

\displaystyle \frac{-3 \,r_s \: 𝓊+2±2 \,α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊})}{\left(α \:\sqrt{2 \,𝓊}±\sqrt{r_s}\right)^2}

\displaystyle \frac{-3 \,r_s \: 𝓊+2±2 \,α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊})}{\left(α \:\sqrt{2 \,𝓊}∓\sqrt{r_s}\right)^2}

.
• La première possibilité donne une somme qui ne convient pas :

\displaystyle 2 \: \frac{(-3 \,r_s \: 𝓊+2)(2 \:α^2 \: 𝓊+r_s )-8 \,α^2 \: r_s \: 𝓊^2}{\left(2 \,α^2 \: 𝓊-r_s \right)^2}

.
• La seconde possibilité donne (enfin) la somme qui convient :

$\displaystyle 2 \: \frac{(-3 \,r_s \: 𝓊+2)(2 \:α^2 \: 𝓊+r_s )+8 \,α^2 \: r_s \: 𝓊^2}{\left(2 \,α^2 \: 𝓊-r_s \right)^2}= 2 \: \frac{(3 \,r_s \: 𝓊-2)(2 \:α^2 \: 𝓊-r_s )-4 \,α^2 \: 𝓊 .(r_s \: 𝓊-2)}{\left(2 \,α^2 \: 𝓊-r_s \right)^2}$ .

• Les racines sont donc :

\displaystyle Y=\frac{2-3 \,r_s \: 𝓊±2 \,α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}}{\left(α \:\sqrt{2 \,𝓊}∓\sqrt{r_s}\, \right)^2 }

, donnant :

\displaystyle η^2=\frac{c^2}{𝓊 \:Y}=\frac{c^2}{𝓊} \, \frac{\left(α \:\sqrt{2 \,𝓊}∓\sqrt{r_s}\, \right)^2}{2-3 \,r_s \: 𝓊±2 \,α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}}

.
◊ remarque : ce type de démarche nécessite de l'intuition (pour voir que les ressemblances des termes peuvent donner une bonne combinaison), de l'opiniâtreté (pour tester toutes les possibilités, après avoir tout de même estimé que leur nombre n'est pas trop grand) et de la chance (ça pourrait y ressembler mais qu'il n'y ait pas de bonne combinaison).
• Les deux solutions pour

η^2

correspondent à quatre solutions pour

η

; non seulement il y a les deux sens de rotation (ici différents), mais pour chacun il y a l'extrémum stable de

𝒱_r

et l'extremum instable. On pourrait tester le signe de

\displaystyle \frac{d^2𝒱_r}{{du}^2}

, mais ici encore les calculs ne se simplifient pas et une autre méthode est préférable.
• En reportant dans l'équation (1a), on obtient :

$\displaystyle 2 \,𝓀^2 \: c^2=(2-r_s \: 𝓊) \: c^2+r_s \: η^2 \: 𝓊^3=c^2 \: \frac{\left(2-2 \,r_s \: 𝓊±α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}\, \right)^2}{2-3 \,r_s \: 𝓊±2 \,α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}}$ ; $\displaystyle 𝓀=\frac{2-2 \,r_s \: 𝓊±α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}}{\sqrt{2 \:\left(2-3 \,r_s \: 𝓊±2 \,α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}\, \right)}}$ .

• Le signe de

𝓀

n'est pas ambigu car on doit retrouver

\displaystyle 𝓀=\frac{ℰ}{m \:c^2}≈1

pour

𝓊≈0

(à l'infini). Les cas instables correspondent seulement au signe inapproprié de

η

, ce qui n'intervient pas ici. Par ailleurs, on retrouve ainsi pour

α=0

l'expression obtenue avec la métrique de Schwarzschild :

\displaystyle 𝓀=\frac{1-r_s \: 𝓊}{\sqrt{1-\frac{3}{2} r_s \: 𝓊}}

.
• Faute de connaître le signe pour exprimer

η

, on peut ici noter :

\displaystyle η={(\text{±})}_η \: \frac{c}{\sqrt{𝓊}} \, \frac{α \:\sqrt{2 \,𝓊}∓\sqrt{r_s}}{\sqrt{2-3 \,r_s \: 𝓊±2 \,α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}}}

. En reportant ensuite dans l'équation (2a), on en déduit

𝓀 \:η

; or, le signe de

𝓀

est connu, donc on en déduit le signe pour

η

{(\text{±})}_η=-1

;

\displaystyle η=- \frac{c}{\sqrt{𝓊}} \, \frac{α \:\sqrt{2 \,𝓊}∓\sqrt{r_s}}{\sqrt{2-3 \,r_s \: 𝓊±2 \,α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}}}

.
• On peut ensuite reporter dans

𝒽=η+α \:c \:𝓀

\displaystyle \frac{𝒽}{c}=±\frac{\sqrt{r_s}}{\sqrt{𝓊}} \: \frac{1∓2 \,α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}+α^2 \: 𝓊^2}{\sqrt{2-3 \,r_s \: 𝓊±2 \,α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}}}

.
• On retrouve ainsi pour

α=0

l'expression obtenue avec la métrique de Schwarzschild (où les deux sens distincts ne diffèrent plus que par le signe) :

\displaystyle \frac{𝒽}{c}=±\frac{\sqrt{r_s}}{\sqrt{𝓊.(2-3 \,r_s \: 𝓊)}}

2.e.

• On peut calculer :

\displaystyle Ω=\frac{dφ}{dt}=\frac{\dot{φ}}{\dot{t}} =c \: \frac{B+\frac{𝒽}{c \:𝓀} \: A}{E-\frac{𝒽}{c \:𝓀} \: B}

avec

\displaystyle \frac{𝒽}{c \:𝓀}=±\frac{\sqrt{2 \,r_s}}{\sqrt{𝓊}} \: \frac{1∓2 \,α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}+α^2 \: 𝓊^2}{2-2 \,r_s \: 𝓊±α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}}

et (pour

θ=\frac{π}{2}

) :

$\displaystyle A=1-\frac{r_s}{r}$ ; $\displaystyle B=\frac{r_s \: α}{r}$ ; $\displaystyle E=r^2+α^2+\frac{r_s \: α^2}{r}$ .

◊ remarque : pour

α=0

on retrouve l'expression obtenue avec la métrique de Schwarzschild.

2.f.

• La 4-vitesse correspond à :

U^β=(c \,\dot{t} \text{ , }0 \text{ , }0 \text{ , }\dot{φ})=\dot{t} .(c \text{ , }0 \text{ , }0 \text{ , }Ω)

avec :

$\displaystyle \dot{t}=\frac{1}{Δ} \: \left(𝓀 \:E-\frac{𝒽}{c} \, B\right)$ ; $Δ=r^2-r_s \: r+α^2$ .

3.a.

• Les variations du spin correspondent à :

\displaystyle \frac{DS^μ}{dτ}=\dot{S^μ}+Γ_{\phantom{.}αβ}^μ \: S^α \: U^β=0

; ainsi pour

θ=\frac{π}{2}

$\dot{S^{0}} + Γ_{10}^{0} S^{1} U^{0} + Γ_{13}^{0} S^{1} U^{3} = 0

;$

$A \:E+B^2=Δ=r^2-r_s \: r+α^2$ ;
$\displaystyle Γ_{\phantom{.}10}^0= \frac{E\:A'}{2\,Δ}+ \frac{B\:B'}{2\,Δ}=\frac{r_s}{2 \,r^2} \, \frac{r^2+α^2}{r^2-r_s \: r+α^2}$ ;
$\displaystyle Γ_{\phantom{.}13}^0= \frac{E\:B'}{2\,Δ}- \frac{B\:E'}{2\,Δ}=-\frac{r_s \: α}{2 \,r^2} \, \frac{3 \,r^2+α^2}{r^2-r_s \: r+α^2}$ ;

$\dot{S^1}+Γ_{\phantom{.}00}^1 \: S^0 \: U^0+Γ_{\phantom{.}30}^1 \: S^3 \: U^0+Γ_{\phantom{.}03}^1 \: S^0 \: U^3+Γ_{\phantom{.}33}^1 \: S^3 \: U^3=0$ ;

$\displaystyle Γ_{\phantom{.}00}^1=\frac{A'}{2 \,C}=\frac{r_s}{2 \,r^4} \, (r^2-r_s \: r+α^2 )$ ;
$\displaystyle Γ_{\phantom{.}30}^1=\frac{B'}{2 \,C}=-\frac{r_s \: α}{2 \,r^4} \: (r^2-r_s \: r+α^2 )$ ;
$\displaystyle Γ_{\phantom{.}33}^1=-\frac{E'}{2 \,C}=-\frac{2 \,r^3-r_s \: α^2}{2 \,r^4} \: (r^2-r_s \: r+α^2 )$ ;

$\dot{S^2}+Γ_{\phantom{.}00}^2 \: S^0 \: U^0+Γ_{\phantom{.}30}^2 \: S^3 \: U^0+Γ_{\phantom{.}03}^2 \: S^0 \: U^3+Γ_{\phantom{.}33}^2 \: S^3 \: U^3=\dot{S^2}=0$ ;

la composante $S^2$ parallèle à l'axe de l'orbite reste constante ;

$\dot{S^3}+Γ_{\phantom{.}10}^3 \: S^1 \: U^0+Γ_{\phantom{.}13}^3 \: S^1 \: U^3=0$ ;

$\displaystyle Γ_{\phantom{.}10}^3=\frac{B\:A'}{2 \,Δ}- \frac{A \:B'}{2 \,Δ}=\frac{r_s}{2 \,r^2} \, \frac{α}{r^2-r_s \: r+α^2}$ ;
$\displaystyle Γ_{\phantom{.}13}^3=\frac{A\:E'}{2\:Δ}+\frac{B\:B'}{2\:Δ}=\frac{1}{2 \,r^2} \frac{2 \,r^3-2 \,r_s \: r^2-r_s \: α^2}{r^2-r_s \: r+α^2}$ .

3.b.

• On peut utiliser le système des trois équations sur

S^0

S^1

S^3

$\displaystyle \frac{d}{dt} S^0+\left(Γ_{\phantom{.}10}^0 \: c+Γ_{\phantom{.}13}^0 \: Ω\right) \: S^1=\frac{d}{dt} S^0+λ_0 \: S^1=0$
$\displaystyle \frac{d}{dt} S^1+\left(Γ_{\phantom{.}00}^1 \: c+Γ_{\phantom{.}03}^1 \: Ω\right) \: S^0+\left(Γ_{\phantom{.}30}^1 \: c+Γ_{\phantom{.}33}^1 \: Ω\right) \: S^3=\frac{d}{dt} S^1-κ_0 \: S^0-κ_3 \: S^3=0$ ;
$\displaystyle \frac{d}{dt} S^3+\left(Γ_{\phantom{.}10}^3 \: c+Γ_{\phantom{.}13}^3 \: Ω\right) \: S^1=\frac{d}{dt} S^3+λ_3 \: S^1=0$ .

3.c.

• Pour résoudre, on peut substituer :

\displaystyle \frac{d^2}{{dt}^2} S^1+(κ_0 \: λ_0+κ_3 \: λ_3 ) \: S^1=0

. En notant

ϖ=\sqrt{κ_0 \: λ_0+κ_3 \: λ_3}

et en choisissant l'origine du temps à l'instant où

S^1

est maximum, on obtient :

S^1 (t)=S^1 (0) \; \cos(ϖ \:t)

.
◊ remarque : d'après ce qui suit et compte tenu de la parité du cosinus on peut alors aussi écrire :

S^1 (t)=S^1 (0) \; \cos(-ϖ \:t)

.
• On en déduit (le spin est ainsi initialement orienté dans la direction radiale) :

$\displaystyle S^0=\frac{λ_0}{ϖ} \: S^1 (0) \; \sin(-ϖ \:t)$ ; $\displaystyle S^3=\frac{λ_3}{ϖ} \: S^1 (0) \; \sin(-ϖ \:t)$ ;
$\displaystyle \frac{d}{dt} S^1=ϖ \:S^1 (0) \; \sin(-ϖ \:t)=κ_0 \: S^0+κ_3 \: S^3$ .

3.d.

• La relation

\displaystyle \frac{DS^μ}{dτ}=0

implique

\displaystyle \frac{D}{dτ} (S^μ \:S_μ )=0

.
• En notant ici pour simplifier :

\displaystyle Ξ=A \: \frac{λ_0^{\:2}}{ϖ^2} +2 \,B \: \frac{λ_0}{ϖ} \, \frac{λ_3}{ϖ}-E \: \frac{λ_3^{\:2}}{ϖ^2}

, on obtient :

$\left|\left|S\right|\right|^2=S^μ \:S_μ=[S^1 (0)]^2 \: \left[Ξ \;\sin^2(-ϖ \:t)-C \;\cos^2(-ϖ \:t) \right]=-C .[S^1 (0)]^2=Cste$ .

• Compte tenu de l'allure très différente des expressions, il n'est pas évident de vérifier que les coefficients se simplifient et donnent

Ξ=-C

(ce qui correspond au résultat analogue à celui obtenu avec la métrique de Schwarzschild), mais la simplification est facile avec un logiciel de calcul formel.

3.e.

• On obtient plus précisément :

$\displaystyle \frac{ϖ^2}{c^2} =\frac{1}{4 \,r^4} \left[\frac{Ω^2}{c^2} \: [4 \,r^3.(r-r_s )-r_s \: α^2.(4 \,r+r_s )]+\frac{Ω}{c} \: 2 \,r_s \: α.(2 \,r+r_s )-r_s^{\:2} \right]$ .

◊ remarque : pour

α=0

on retrouve l'expression obtenue avec la métrique de Schwarzschild

\displaystyle ϖ=\sqrt{κ_0 \: λ_0+κ_3 \: λ_3}=Ω \:\sqrt{1-\frac{3 \,r_s}{2 \,r}}

.
• Il n'est pas simple de comparer littéralement

ϖ

Ω

, mais on peut le faire numériquement (en fonction de

r

) pour

r_s=1

( pris comme unité) et

α=\frac{1}{4}

, dans le sens direct et dans le sens inverse ; on vérifie que

ϖ<Ω

• Le gyroscope est en orbite à la vitesse angulaire

Ω

; par rapport à la direction radiale locale (tournant comme le mouvement orbital), le spin précesse à la vitesse angulaire

-ϖ

avec

ϖ<Ω

. Si l'effet était négligeable (

ϖ≈Ω

), la direction du gyroscope resterait fixe par rapport à un observateur “à l'infini”. Plus la correction est importante, plus le gyroscope prend de retard dans la “compensation” de

Ω

par rapport à l'infini, donc il précesse légèrement dans le sens de

Ω

3.f.

• Dans le référentiel de repos

S^0=0

; dans le référentiel où le gyroscope est en mouvement, on peut considérer l'orthogonalité :

g_{αβ} \: S^α \: U^β=A \:S^0 \: U^0+B \:S^3 \: U^0+B \:S^0 \: U^3-E \:S^3 \: U^3=0

.
• On en déduit :

(A \:U^0+B \:U^3) \:S^0+(B \:U^0-E \:U^3) \:S^3=0

; ainsi :

$(A \:U^0+B \:U^3) \:λ_0+(B \:U^0-E \:U^3) \:λ_3=0$ .

• La résolution de cette équation donne :

\displaystyle \frac{Ω}{c}=\frac{r \:\sqrt{2 \,r_s \: r}±α \:r_s}{α^2 \: r_s-2 \,r^3}

, qui pour

α=0

redonne effectivement l'expression obtenue avec la métrique de Schwarzschild.

⚠︎ Il n'est pas évident de savoir si l'expression qu'on avait trouvée avant pour

\displaystyle \frac{Ω}{c}

(vérifiée) peut se simplifier et être égale à celle trouvée ici, mais on peut facilement tester numériquement en traçant la variation en fonction de

r

, pour

r_s=1

( pris comme unité) et

α=\frac{1}{4}

; les courbes obtenues sont analogues mais différentes, donc il est clair que

S^μ

U^μ

semblent ici ne pas être orthogonaux !... Ceci peut remettre plus ou moins en question la validité des résultats obtenus dans cette partie

4.a.

• Pour un tour complet, le décalage angulaire est :

\displaystyle ψ=2π .\left(1-\frac{ϖ}{Ω} \, \right)

(il est généralement faible car

r≫r_s

). La vitesse de précession est :

\displaystyle ω=Ω-ϖ= Ω .\left(1-\frac{ϖ}{Ω} \, \right)

4.b.

• Il est important de raisonner avec

\displaystyle \frac{ϖ}{Ω}

car

ϖ

varie avec

α

, mais

Ω

aussi.
• Il n'est pas simple de comparer littéralement

\displaystyle \frac{ϖ}{Ω}

à la valeur correspondant à

α=0

, mais on peut le faire numériquement (en fonction de

r

) pour

r_s=1

α=0

(en noir) ;

\frac{1}{4}

(en vert) ;

\frac{1}{2}

(en rouge).
• Dans le sens direct, on constate que l'augmentation de

α

tend à augmenter légèrement

\displaystyle \frac{ϖ}{Ω}

, donc à diminuer l'effet de précession. Dans le sens inverse, l'augmentation de

α

tend à diminuer légèrement

\displaystyle \frac{ϖ}{Ω}

, donc à augmenter l'effet de précession.

4.c.

• Les relations précédentes ont été établies avec la métrique d'un “trou-noir” ; or, pour le cas d'un astre en rotation, la métrique dépend de la répartition de masse intérieure. On peut toutefois supposer que l'ordre de grandeur obtenu est correct.
• On considère généralement que

\displaystyle α=\frac{J}{c \:M}

avec un moment cinétique

J=\frac{2}{5} M \:R^2 \: ω_T

pour un astre sphérique homogène ; ceci donne :

α≈4 \:\mathrm{m}

.
• Le rayon de Schwarzschild de la Terre est

r_s≈8\text{,}9 \:\mathrm{mm}

et l'étude de la métrique de Kerr montre qu'on doit généralement se limiter à

\displaystyle α≲\frac{r_s}{2}

. Au delà de cette limite, l'astre en rotation ne présente plus d'horizon des événements (seulement une “singularité nue”), donc ne se comporte pas en trou-noir. Dans le cas de la Terre (qui n'est pas un trou-noir), le problème vient du fait que

R_T≫r_s

. On peut espérer que l'ordre de grandeur du résultat obtenu reste ici encore correct.
• Sur une orbite terrestre de faible altitude (

h≈640 \:\mathrm{km}

;

r≈7000 \:\mathrm{km}

) on obtient dans le sens direct :

ω≈(1,0\underline{15}).{10}^{-12} \: \mathrm{rad.s^{-1}}

, en comparaison de

ω≈(1,0\underline{30}).{10}^{-12} \: \mathrm{rad.s^{-1}}

avec la métrique de Schwarzschild.
• Pour l'expérience du satellite “gravity probe B”, dont la trajectoire n'est pas équatoriale mais polaire, une autre méthode de calcul (approximation au premier ordre) a donné dans ce cas un terme correctif environ deux fois plus faible

≈(0\text{,}0\underline{06}).{10}^{-12} \: \mathrm{rad.s^{-1}}

. Bien que les incertitudes de mesure dues aux blindages électrostatique et magnétique soient importantes (

≈20 \:%

), cet écart a été raisonnablement confirmé.
◊ remarque : l'intérêt d'une trajectoire polaire est que l'effet Lense-Thirring agit alors perpendiculairement à l'effet Einstein-De Sitter, ce qui permet de tester les deux.

Effet Doppler et vitesse des étoiles dans une galaxie

1.a.	• Le mouvement des photons correspond à : $\displaystyle \frac{Dυ^μ}{dς}=\frac{dυ^μ}{dς}+Γ_{\phantom{.}αβ}^μ \: υ^α \: υ^β=0$ avec $\displaystyle υ^μ=\frac{dx^μ}{dς}$ . • Les équations peuvent aussi s'écrire, souvent plus simplement : $\displaystyle \frac{d}{dς} \frac{∂ℒ}{∂\dot{x}^μ}-\frac{∂ℒ}{∂x^μ}=0$ avec le lagrangien quadratique $ℒ=-\frac{1}{2} g_{μν} \: \dot{x}^μ \: \dot{x}^ν$ .

1.b.	• Pour des photons, le mouvement est paramétré par $ς$ tel que $dς={dx}_0=g_{0ν} \: {dx}^ν=A \:c \,dt+B \:dφ$ .

1.c.	• Pour $x^0=c \,t$ on obtient alors : $\displaystyle \frac{d}{dς}\left(-g_{0ν} \: \dot{x}^ν\right)=0$ , donc : $A \:c \,\dot{t}+B \:\dot{φ}=\underline{𝓀}=1=Cste$ . ◊ remarque : on note par $\dot{⬚}$ les dérivées par rapport à $ς$ .

1.d.	• Pour $x^3=φ$ on obtient : $\displaystyle \frac{d}{dς}\left(-g_{3ν} \: \dot{x}^ν\right)=0$ , donc : $\displaystyle -B \:c \,\dot{t}+E \:\dot{φ}=\frac{\underline{𝒽}}{c}=Cste$ . ◊ remarque : la constante $\underline{𝒽}$ est une généralisation de la constante de la “loi des aires” ; pour des photons $\displaystyle \frac{\underline{𝒽}}{c}$ correspond ainsi au “paramètre d'impact”.

1.e.	• Puisque $A\:E+B^2=Δ$ , le système de deux équations a pour solution : $\displaystyle c \,\dot{t}=\frac{1}{Δ} \, \left(E-\frac{\underline{𝒽}}{c} \, B\right)$ ; $\displaystyle \dot{φ}=\frac{1}{Δ} \, \left(B+\frac{\underline{𝒽}}{c} \, A\right)$ .

1.f.	• Pour $x^1=r$ , l'utilisation du lagrangien est moins aisée car il dépend explicitement de $r$ . Dans la mesure où on a déjà déterminé les autres équations, on peut par contre utiliser la relation ${ds}^2=0$ : $\displaystyle {ds}^2=-\frac{1}{Δ} \, {dς}^2 \: \left(A \:\frac{\underline{𝒽}^2}{c^2} +2 \:B \:\frac{\underline{𝒽}}{c}-E\right)-C \:{dr}^2=0$ ; $\displaystyle \dot{r}^2=\frac{1}{r^2} \, \left(E-2 \,B \,\frac{\underline{𝒽}}{c}-A \,\frac{\underline{𝒽}^2}{c^2} \right)$ .

1.g.	• Le minimum d'approche correspond à $\dot{r}=0$ d'où on déduit : $\displaystyle \frac{\underline{𝒽}}{c}=\frac{-B±\sqrt{Δ}}{A}$ ; le signe négatif correspond à des photons émis dans le sens rétrograde. ◊ remarque : en l'absence de rotation ( $α=0$ ) on retrouve deux valeurs opposées de $\displaystyle \frac{\underline{𝒽}}{c}$ .

1.h.	• En reportant on obtient : $\displaystyle c \,\dot{t}=\frac{1}{A} \, \left(1∓\frac{B}{\sqrt{Δ}}\right)$ ; $\displaystyle φ ̇=±\frac{1}{\sqrt{Δ}}$ . • Pour un photon, on peut considérer : $\displaystyle P^μ=h \:ν_∞ \: \frac{dx^μ}{dς}$ .

2.a.	• Afin de séparer l'effet Doppler de l'effet Einstein, on peut calculer les résultats observés pour un émetteur fixe, de quadri-vitesse : $u^β=(c \,\dot{t} \text{ , }0 \text{ , }0 \text{ , }0)$ avec ${ds}^2=A \:c^2 \, {dt}^2$ ; $\displaystyle c \,\dot{t}=\frac{1}{\sqrt{A}}$ . • Dans le référentiel de l'émetteur, l'énergie d'émission est la même dans les deux sens (sans effet Doppler) et indépendante de la rotation du centre galactique : $\displaystyle h \:ν=g_{αβ} \: u^α \: P^β=h \:ν_∞ \: c \,\dot{t}=h \:ν_E \, \frac{1}{\sqrt{A}}$ . Cela correspond à l'effet Einstein “classique” : $h \:ν_E=h \:ν \:\sqrt{A}$ .

2.b.	• Pour tester le comportement de l'effet Doppler (pouvant dépendre de $α$ ), on peut calculer les résultats observés pour un émetteur de moment cinétique nul (fixe par rapport à l'espace entraîné en rotation), c'est à dire avec une rotation $\displaystyle \frac{ω}{c}=\frac{B}{E}$ correspondant à $\displaystyle \frac{\underline{𝒽}}{c}=0$ . • Dans ce cas la quadri-vitesse peut s'écrire : $u^β=(c \,\dot{t} \text{ , }0 \text{ , }0 \text{ , }\dot{φ})=c \,\dot{t} .\left(1 \text{ , }0 \text{ , }0 \text{ , }\frac{ω}{c}\right)$ correspondant à : $\displaystyle {ds}^2=\frac{Δ}{E} \: c^2 \, {dt}^2$ ; $\displaystyle c \,\dot{t}=\sqrt{\frac{E}{Δ}}$ . • L'énergie d'émission, dans le référentiel de l'émetteur, correspond à : $\displaystyle h \:ν=g_{αβ} \: u^α \: P^β=h \:ν_∞ \: c \,\dot{t} \, \frac{Δ}{E \:A} \,\left(1∓\frac{B}{\sqrt{Δ}}\right)=h \:ν_∞ \: c \,\dot{t} .\left[1-\frac{ω}{c} \, \frac{\underline{𝒽}}{c} \right]=h \:ν_∞ \, \frac{1}{\sqrt{A}} \, \frac{\sqrt{Δ}∓B}{\sqrt{E \:A}}$ .

2.c.	• Si on suppose que l'effet Doppler dans les deux sens est ici décrit par le terme changeant de signe, on est conduit à considérer que l'effet Einstein correspond à la moyenne arithmétique des signaux observés à l'infini et combinant l'effet Einstein et l'effet Doppler : $\displaystyle h \:ν_E=h \:ν \:\sqrt{A} \: \frac{\sqrt{Δ}}{\sqrt{E \:A}}≠h \:ν \:\sqrt{A}$ . ◊ remarque : une telle estimation est importante car il est nécessaire de disposer d'une méthode pour évaluer les contributions respectives des deux effets à partir des mesures à l'infini. ◊ remarque : pour les photons émis dans le sens rétrograde, le décalage Doppler vers le rouge s'ajoute à l'effet Einstein ; au contraire, pour les photons émis dans le sens direct, le décalage vers le bleu dû à l'effet Doppler est en sens contraire de celui causé par l'effet Einstein. • Le facteur correctif $\displaystyle \frac{\sqrt{Δ}}{\sqrt{E \:A}}=\sqrt{1+\frac{B^2}{E \:A}}$ (qui peut raisonnablement être attribué à l'effet Lense-Thirring) a une influence modérée et serait souvent négligeable, mais il peut aussi être intéressant de considérer de façon analogue la moyenne géométrique des effets dans les deux sens : $\displaystyle \frac{\sqrt{E \:A}}{(\sqrt{Δ}-B)(\sqrt{Δ}+B)} =1$ , c'est à dire qu'on retrouve ainsi l'effet Einstein en l'absence de rotation (est-ce une coïncidence fortuite pour ce cas particulier ?).

3.a.	• Pour un astre en rotation autour du centre, dans un bras galactique, le mouvement correspond à : $\displaystyle \frac{Du^μ}{ds}=\frac{du^μ}{ds}+Γ_{\phantom{.}αβ}^μ \: u^α \: u^β=0$ ; $θ=\frac{π}{2}=Cste$ . • L'intégration donne : $\displaystyle A \: \frac{dt}{dτ}+B \: \frac{1}{c} \, \frac{dφ}{dτ}=𝓀=Cste$ ; $\displaystyle -B \: \frac{dt}{dτ}+E \: \frac{1}{c} \, \frac{dφ}{dτ}=\frac{𝒽}{c}=Cste$ .

3.b.	• Puisque $A\:E+B^2=Δ$ , le système de deux équations a pour solution : $\displaystyle c \,\dot{t}=\frac{c}{Δ} \, \left(𝓀 \:E-\frac{𝒽}{c} \, B\right)$ ; $\displaystyle \dot{φ}=\frac{c}{Δ} \, \left(𝓀 \:B+\frac{𝒽}{c} \, A\right)$ . ◊ remarque : on note ici par $\dot{⬚}$ les dérivées par rapport à $τ$ .

3.c.	• L'équation pour $r$ est obtenue plus facilement d'après l'expression de la métrique : $\displaystyle c^2 \, {dτ}^2=-\frac{c^2}{Δ} \, {dτ}^2 \, \left(A \:\frac{𝒽^2}{c^2} +2 \,B \:𝓀 \:\frac{𝒽}{c}-E \:𝓀^2 \right)-C \:{dr}^2$ ; $\displaystyle \dot{r}^2=-\frac{c^2}{r^2} \: \left(Δ+A \:\frac{𝒽^2}{c^2} +2 \,B \:𝓀 \:\frac{𝒽}{c}-E \:𝓀^2 \right)$ .

3.d.	• Les orbites circulaires correspondent à $\dot{r}=0$ , ce qui impose une relation entre $𝓀$ et $\displaystyle \frac{𝒽}{c}$ , mais aussi à $\ddot{r}=0$ , ce qui impose une seconde relation. • La résolution de ce système de deux équations est compliquée ; le résultat peut être obtenu moins difficilement par une autre méthode. En utilisant la variable de Binet $\displaystyle 𝓊=\frac{1}{r}$ , on obtient : $\displaystyle 𝓀=\frac{2-2 \,r_s \: 𝓊±α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}}{\sqrt{2 \:\left(2-3 \,r_s \: 𝓊±2 \,α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}\, \right)}}$ ; $\displaystyle \frac{𝒽}{c}=±\frac{\sqrt{r_s}}{\sqrt{𝓊}} \, \frac{1∓2 \,α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}+α^2 \: 𝓊^2}{\sqrt{2-3 \,r_s \: 𝓊±2 \,α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}}}$ . ◊ remarque : le signe inférieur correspond au sens rétrograde, non utilisé ici.

3.e.	• On peut calculer : $\displaystyle Ω=\frac{dφ}{dt}=\frac{\dot{φ}}{\dot{t}} =c \; \frac{B+\frac{𝒽}{c \:𝓀} \, A}{E-\frac{𝒽}{c \:𝓀} \, B}$ avec $\displaystyle \frac{𝒽}{c \:𝓀}=±\frac{\sqrt{2 \,r_s}}{\sqrt{𝓊}} \, \frac{1∓2 \,α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}+α^2 \: 𝓊^2}{2-2 \,r_s \: 𝓊±α \:𝓊 \:\sqrt{2 \,r_s \: 𝓊}}$ et (pour $θ=\frac{π}{2}$ ) : $\displaystyle A=1-\frac{r_s}{r}$ ; $\displaystyle B=\frac{r_s \: α}{r}$ ; $\displaystyle E=r^2+α^2+\frac{r_s \: α^2}{r}$ .

3.f.	• La 4-vitesse correspond à : $u^β=\frac{1}{c} \: (c \,\dot{t} \text{ , }0 \text{ , }0 \text{ , }\dot{φ})=\dot{t} .\left(1 \text{ , }0 \text{ , }0 \text{ , }\frac{Ω}{c} \right)$ avec : $\displaystyle \dot{t}=\frac{1}{Δ} \, \left(𝓀 \:E-\frac{𝒽}{c} \, B\right)$ ; $Δ=r^2-r_s \: r+α^2$ .

4.a.

• On considère l'énergie des photons émis par les atomes d'un astre satellite en trajectoire circulaire dans le sens direct. Pour les photons, il faut considérer les deux sens.
• Cette énergie d'émission, dans le référentiel de l'émetteur, correspond à :

$\displaystyle h \:ν=g_{αβ} \: u^α \: P^β=h \:ν_∞ \: \dot{t} .\left(1+\frac{Ω}{c} \,\frac{B∓\sqrt{Δ}}{A} \,\right)=h \:ν_∞ \: \dot{t} .\left[1-\frac{Ω}{c} \, \frac{\underline{𝒽}}{c} \right]$ .

4.b.

• L'effet Einstein peut être estimé par la moyenne arithmétique :

\displaystyle h \:ν_E=\frac{h \:ν}{\dot{t}} \, \frac{1+\frac{Ω}{c} \, \frac{B}{A}}{\left(1+\frac{Ω}{c} \, \frac{B}{A}\,\right)^2-\frac{Δ}{A^2} }≠h \:ν \:\sqrt{A}

. Cette méthode semble peu cohérente, car pour

α=0

(à gauche, trait plein) on doit logiquement retrouver l'effet Einstein non perturbé par l'effet Lense-Thirring.

• On peut aussi utiliser la moyenne géométrique :

\displaystyle h \:ν_E=\frac{h \:ν}{\dot{t}}\, \frac{1}{\sqrt{\left(1+\frac{Ω}{c} \, \frac{B}{A}\right)^2-\frac{Δ}{A^2}}}≠h \:ν \:\sqrt{A}

. Cette seconde méthode (à droite) semble cohérente de ce point de vue ; c'est celle qu'on choisit pour la suite.

4.c.

• Pour l'estimation géométrique, on évalue chaque effet Doppler (dans les deux sens) par quotient avec l'effet Einstein :

\displaystyle h \:ν_D=h \:ν \, \frac{\sqrt{\left(1+\frac{Ω}{c} \, \frac{B}{A}\right)^2-\frac{Δ}{A^2}}}{1+\frac{Ω}{c} \, \frac{B∓\sqrt{Δ} }{A}}

.
◊ remarque : en l'absence de rotation du centre galactique, la limite aux courtes distances pour les données brutes (à gauche) montre que l'effet Doppler prédomine ; par contre, pour un centre en rotation, l'effet Einstein est prépondérant aux courtes distances.
• On constate (à droite) que l'effet Doppler est plutôt diminué par la rotation du centre galactique (tirets, pointillés) en comparaison d'un centre statique (trait plein).

• L'étude de l'effet Doppler, depuis l'infini, permet d'estimer la vitesse de rotation des astres autour du centre galactique, mais il faut pour cela bien séparer les contributions des effets Einstein et Doppler. Aux faibles distances, les décalages observés semblent indiquer des vitesses de rotation plus faibles que celles attendues pour un centre galactique statique.