RG XV - ASTRES EN ROTATION


Étude du cas statique extérieur

• Un astre en rotation n'est pas “statique” au sens strict, mais en supposant une symétrie axiale, on est ramené à une étude de type statique (indépendance par rapport au temps).

◊ remarque : une telle situation est souvent qualifiée de “stationnaire”, mais ce n'est pas au sens d'une variation périodique ; l'astre à symétrie cylindrique tourne mais semble toujours “pareil” ; il s'agit donc d'une “stationnarité” forte, très proche d'une situation statique.

• Pour un astre tournant selon un axe associé à l'angle φφ ,  on peut utiliser des coordonnées cylindriques, mais la comparaison avec le cas sans rotation conduit à préférer les coordonnées sphériques d'axe polaire correspondant.

Dans le vide, on peut chercher la métrique statique sous la forme suivante :
ds2=A(r,θ)c2dt2+2B(r,θ)cdtdφ−C(r,θ)dr2⋯{ds}^2=A(r,θ) \:c^2 \, {dt}^2+2 \,B(r,θ) \:c \,dt \:dφ-C(r,θ) \:{dr}^2\,⋯
⋯−D(r,θ)dθ2−E(r,θ)dφ2⋯\,-D(r,θ) \:{dθ}^2-E(r,θ) \:{dφ}^2 .

◊ remarque : au sens strict, la situation est statique quand les hypersurfaces  t=Cstet=Cste  sont orthogonales au vecteur de Killing e↔0\overset{↔}{e}_0 ; ici ce n'est pas le cas à cause des termes mixtes gtφg_{tφ} .

• On obtient alors (en notant ici les dérivées ∂θ∂_θ par ° ) :
g00=Ag_{00}=A  ;  g03=Bg_{03}=B  ;  g11=−Cg_{11}=-C  ;  g22=−Dg_{22}=-D  ;  g33=−Eg_{33}=-E  ;

g00=EAE+B2\displaystyle g^{00}=\frac{E}{A \:E+B^2}  ;  g03=BAE+B2\displaystyle g^{03}=\frac{B}{A \:E+B^2}  ;  g11=−1C\displaystyle g^{11}=-\frac{1}{C}  ;  g22=−1D\displaystyle g^{22}=-\frac{1}{D}  ;  g33=−AAE+B2\displaystyle g^{33}=-\frac{A}{A \:E+B^2}  ;

Γ001=−Γ100=A′2\displaystyle Γ_{001}=-Γ_{100}=\frac{A'}{2}  ;  Γ002=−Γ200=A°2\displaystyle Γ_{002}=-Γ_{200}=\frac{A°}{2}  ;
Γ111=−C′2\displaystyle Γ_{111}=-\frac{C'}{2}  ;  Γ112=−Γ211=−C°2\displaystyle Γ_{112}=-Γ_{211}=-\frac{C°}{2}  ;  Γ221=−Γ122=−D′2\displaystyle Γ_{221}=-Γ_{122}=-\frac{D'}{2}  ;  Γ222=−D°2\displaystyle Γ_{222}=-\frac{D°}{2}  ;
Γ331=−Γ133=−E′2\displaystyle Γ_{331}=-Γ_{133}=-\frac{E'}{2}  ;  Γ332=−Γ233=−E°2\displaystyle Γ_{332}=-Γ_{233}=-\frac{E°}{2}  ;
Γ301=Γ031=−Γ103=B′2\displaystyle Γ_{301}=Γ_{031}=-Γ_{103}=\frac{B'}{2}  ;  Γ320=Γ032=−Γ203=B°2\displaystyle Γ_{320}=Γ_{032}=-Γ_{203}=\frac{B°}{2}  ;

Γ.010=g00Γ001+g03Γ301=EAE+B2A′2+BAE+B2B′2\displaystyle Γ_{\phantom{.}01}^0=g^{00} \: Γ_{001}+g^{03} \: Γ_{301}=\frac{E}{A \:E+B^2} \, \frac{A'}{2}+\frac{B}{A \:E+B^2} \, \frac{B'}{2}  ;  Γ.001=A′2C\displaystyle Γ_{\phantom{.}00}^1=\frac{A'}{2 \,C}  ;
Γ.020=EAE+B2A°2+BAE+B2B°2\displaystyle Γ_{\phantom{.}02}^0=\frac{E}{A \:E+B^2} \, \frac{A°}{2}+\frac{B}{A \:E+B^2} \, \frac{B°}{2}  ;  Γ.002=A°2D\displaystyle Γ_{\phantom{.}00}^2=\frac{A°}{2 \,D}  ;
Γ.111=C′2C\displaystyle Γ_{\phantom{.}11}^1=\frac{C'}{2 \,C}  ;  Γ.121=C°2C\displaystyle Γ_{\phantom{.}12}^1=\frac{C°}{2 \,C}  ;  Γ.112=−C°2D\displaystyle Γ_{\phantom{.}11}^2=-\frac{C°}{2 \,D}  ;
Γ.221=−D′2C\displaystyle Γ_{\phantom{.}22}^1=-\frac{D'}{2 \,C}  ;  Γ.122=D′2D\displaystyle Γ_{\phantom{.}12}^2=\frac{D'}{2 \,D}  ;  Γ.222=D°2D\displaystyle Γ_{\phantom{.}22}^2=\frac{D°}{2 \,D}  ;
Γ.331=−E′2C\displaystyle Γ_{\phantom{.}33}^1=-\frac{E'}{2 \,C}  ;  Γ.133=AAE+B2E′2+BAE+B2B′2\displaystyle Γ_{\phantom{.}13}^3=\frac{A}{A \:E+B^2} \, \frac{E'}{2}+\frac{B}{A \:E+B^2} \, \frac{B'}{2}  ;
Γ.332=−E°2D\displaystyle Γ_{\phantom{.}33}^2=-\frac{E°}{2 \,D}  ;  Γ.233=AAE+B2E°2+BAE+B2B°2\displaystyle Γ_{\phantom{.}23}^3=\frac{A}{A \:E+B^2} \, \frac{E°}{2}+\frac{B}{A \:E+B^2} \, \frac{B°}{2}  ;
Γ.130=EAE+B2B′2−BAE+B2E′2\displaystyle Γ_{\phantom{.}13}^0=\frac{E}{A \:E+B^2} \, \frac{B'}{2}-\frac{B}{A \:E+B^2} \, \frac{E'}{2}  ;  Γ.031=B′2C\displaystyle Γ_{\phantom{.}03}^1=\frac{B'}{2 \,C}  ;  Γ.013=BAE+B2A′2−AAE+B2B′2\displaystyle Γ_{\phantom{.}01}^3=\frac{B}{A \:E+B^2} \, \frac{A'}{2}-\frac{A}{A \:E+B^2} \, \frac{B'}{2}  ;
Γ.230=EAE+B2B°2−BAE+B2E°2\displaystyle Γ_{\phantom{.}23}^0=\frac{E}{A \:E+B^2} \, \frac{B°}{2}-\frac{B}{A \:E+B^2} \, \frac{E°}{2}  ;  Γ.032=B°2D\displaystyle Γ_{\phantom{.}03}^2=\frac{B°}{2 \,D}  ;  Γ.023=BAE+B2A°2−AAE+B2B°2\displaystyle Γ_{\phantom{.}02}^3=\frac{B}{A \:E+B^2} \, \frac{A°}{2}-\frac{A}{A \:E+B^2} \, \frac{B°}{2} .

• Dans le vide entourant un astre en rotation, les équations du champ (correspondant à  Rμν=0R_{μν}=0 )  donnent en simplifiant des équations peu simples :
A″2C+A°°2D+AAE+B2(B′22C+B°22D)⋯\displaystyle \frac{A''}{2 \,C}+\frac{A°°}{2 \,D}+\frac{A}{A \:E+B^2} \: \left(\frac{{B'}^2}{2 \,C}+\frac{{B°}^2}{2 \,D}\right) \,⋯
⋯+A′2C(−EAE+B2A′2−BAE+B2B′−C′2C+D′2D+AAE+B2E′2)⋯\displaystyle ⋯ \,+\frac{A'}{2 \,C} \: \left(-\frac{E}{A \:E+B^2} \, \frac{A'}{2}-\frac{B}{A \:E+B^2} \, B'-\frac{C'}{2 \,C}+\frac{D'}{2 \,D}+\frac{A}{A \,E+B^2} \, \frac{E'}{2}\right) \,⋯
⋯+A°2C(−EAE+B2A°2−BAE+B2B°+C°2C−D°2D+AAE+B2E°2)=0\displaystyle ⋯\, +\frac{A°}{2 \,C} \, \left(-\frac{E}{A \:E+B^2} \, \frac{A°}{2}-\frac{B}{A \:E+B^2} \, B°+\frac{C°}{2 \,C}-\frac{D°}{2 \,D}+\frac{A}{A \:E+B^2} \, \frac{E°}{2}\right)=0  (R00R_{00})  ;

et les autres  (R03R_{03} ; R11R_{11} ; R12R_{12} ; R22R_{22} et R33R_{33})  sont encore moins simples.

• La résolution est impossible ainsi : d'éventuelles combinaisons permettant de simplifier sont trop peu décelables. Cela a été étudié par R. Kerr avec des méthodes abstraites sur les géodésiques. Il a obtenu une solution particulière qui, avec les coordonnées de R. Boyer et R. Lindquist, correspond à :
A=1−rsrρ2\displaystyle A=1-\frac{r_s \: r}{ρ^2}   avec  rs=2𝒢Mc2\displaystyle r_s=\frac{2 \,𝒢 \:M}{c^2}   et   ρ2=r2+α2cos2(θ)ρ^2=r^2+α^2 \; \cos^2(θ) ,
où  αα  décrit le moment cinétique de l'astre  ( J=MαcJ=M \:α \:c ) ;
B=rsαrρ2sin2(θ)\displaystyle B=\frac{r_s \: α \:r}{ρ^2} \: \sin^2(θ)  ;  C=ρ2Δ\displaystyle C=\frac{ρ^2}{Δ}   avec  Δ=r2−rsr+α2Δ=r^2-r_s \: r+α^2  ;
D=ρ2D=ρ^2  ;  E=(r2+α2+rsα2rρ2sin2(θ))sin2(θ)\displaystyle E=\left(r^2+α^2+\frac{r_s \: α^2 \: r}{ρ^2} \: \sin^2(θ) \right) \; \sin^2(θ) .

Pour  α≠0α≠0  la métrique de Kerr est asymptotiquement “plate” (comme celle de Schwarzschild).

Pour  α=0α=0  on retrouve  ρ=rρ=r  et la métrique de Kerr se simplifie en celle de Schwarzschild (avec les coordonnées classiques).

• Cette solution, dépendant uniquement d'une masse totale et d'un moment cinétique total, est généralement considérée comme décrivant un “trou noir” en rotation (astre censé être effondré au delà d'un “horizon”, de même que pour la solution de Schwarzschild).

Même si cela peut y ressembler à distance “suffisante”, ce n'est pas la solution générale pour l'extérieur d'un astre en rotation, dont la métrique dépend de façon plus complexe de la répartition de masse et d'énergie-impulsion.

Synchronisation des horloges

• La métrique de Kerr n'étant pas diagonale, elle exprime les durées mais il est impossible de synchroniser les horloges dans l'ensemble de l'espace : le décalage peut s'écrire :  cdtd=−g0ig00dxi=−BAdφ\displaystyle c \,{dt}_d=-\frac{g_{0i}}{g_{00}} \: {dx}^i=-\frac{B}{A} \, dφ .

L'intégrale dépendant du chemin suivi, la synchronisation est seulement possible le long d'une ligne, ou dans un voisinage infinitésimal d'un point donné.

Pour décrire les durées associées au mouvement d'une particule, on peut tout au plus préférer écrire la métrique sous la forme :
ds2=A.[cdt+BAdφ]2−Cdr2−Ddθ2−AE+B2Adφ2\displaystyle {ds}^2=A .\left[c \,dt+\frac{B}{A} \, dφ\right]^2-C \:{dr}^2-D \:{dθ}^2-\frac{A \:E+B^2}{A} \, {dφ}^2 .

La durée locale correspond alors à :  cdtloc=A.[cdt+BAdφ]\displaystyle c \,{dt}_{loc}=\sqrt{A} .\left[c \,dt+\frac{B}{A} \, dφ\right]  et la distance parcourue est :  d𝓁2=ℊijdxidxj=Cdr2+Ddθ2+AE+B2Adφ2\displaystyle {d𝓁}^2=ℊ_{ij} \: {dx}^i \: {dx}^j=C \:{dr}^2+D \:{dθ}^2+\frac{A \:E+B^2}{A} \, {dφ}^2  ; la métrique spatiale  ℊij=g0ig0jg00−gij\displaystyle ℊ_{ij}=\frac{g_{0i} \: g_{0j}}{g_{00}} -g_{ij}  est l'inverse de  ℊij=gijℊ^{ij}=g^{ij} .

Horizon

• Dans le cas sphérique de Schwarzschild, la limite  r=rsr=r_s  correspond à une singularité de la coordonnée radiale “classique”, mais aussi à un comportement singulier de la coordonnée temporelle. Ce dernier rend ce qui se produit au delà inobservable par tout observateur extérieur ; effet nommé “horizon” (ou “horizon des événements”). Mais cette hypothèse supposant l'existence de valeurs  r<rsr<r_s  pour décrire l'intérieur conduit à des anomalies théoriques.

• La situation est ici un peu analogue mais différente : la singularité radiale intervient pour  Δ=0Δ=0 ,  ce qui ne correspond pas à  A=0A=0 .

On peut dans ce cas nommer “horizon” la limite  r=RHr=R_H  pour laquelle  Δ=0Δ=0  ;  ceci correspond à deux solutions :  r=12(rs±rs2−4α2)r=\frac{1}{2} \left(r_s±\sqrt{r_s^{\:2}-4 \,α^2}\, \right) .

On considère généralement surtout l'horizon “extérieur” (expression à préciser dans ce qui suit) :  RH=12(rs+rs2−4α2)R_H=\frac{1}{2} \left(r_s+\sqrt{r_s^{\:2}-4 \,α^2}\, \right) .

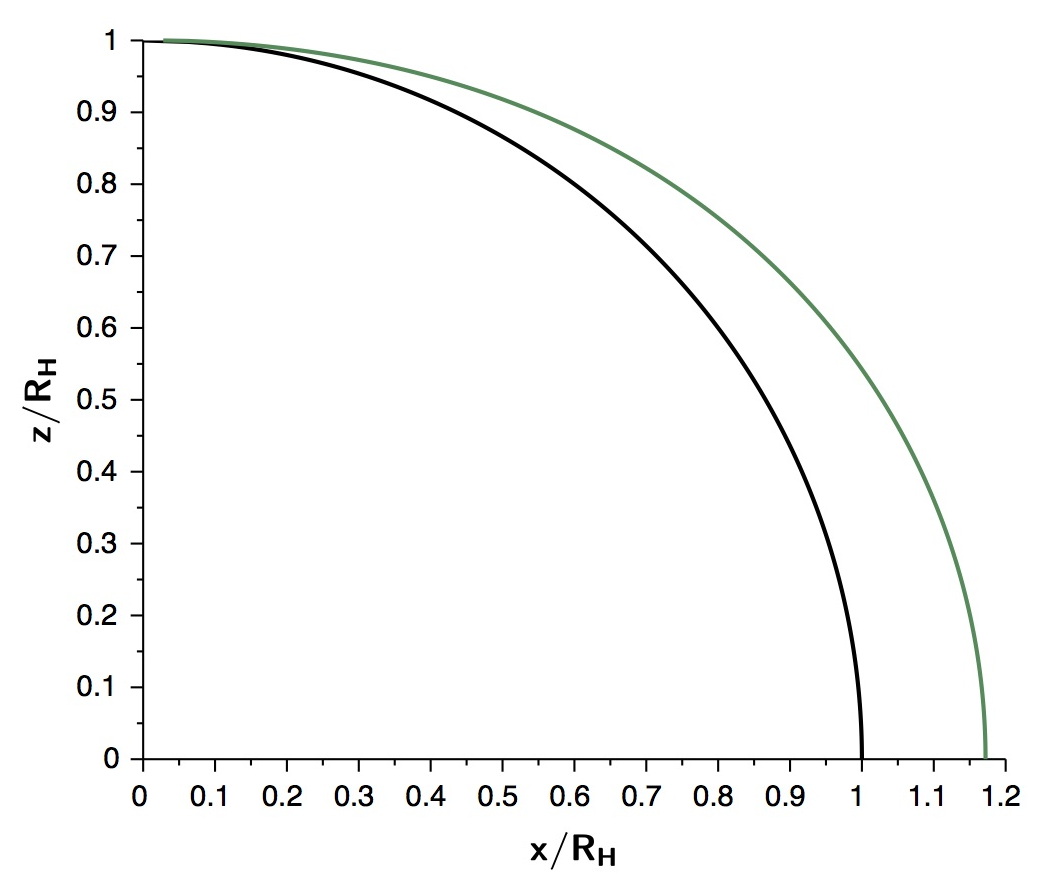
◊ remarque : d'après la métrique, la géométrie des surfaces avec  r=Cster=Cste  (donc en particulier l'horizon) n'est pas sphérique, mais ressemble plutôt à celle d'un ellipsoïde de révolution (de demi-petit-axe rr et de demi-grands-axes r2+α2\sqrt{r^2+α^2} )  ;  cette propriété n'intervient pas ici.

• Le déplacement radial correspond par ailleurs à :  d𝓁2=Cdr2=ρ2Δdr2\displaystyle {d𝓁}^2=C \:{dr}^2=\frac{ρ^2}{Δ} \, {dr}^2 .  De façon analogue au cas de Schwarzschild, la variable rr peut tout aussi bien présenter un minimum pour  r=RHr=R_H  puisque  drd𝓁=0\displaystyle \frac{dr}{d𝓁}=0 .  Les valeurs  r<RHr<R_H  dans le vide ont donc la même ambiguïté que suggèrent les coordonnées “isotropes” dans le cas sans rotation.

📖 exercices n° I, II et III.

Ergosphère

• Pour  r<RHr<R_H  (si cela est possible), on obtiendrait  Δ<0Δ<0  ;  donc la variable rr deviendrait du genre temps (comme pour l'horizon de Schwarzschild).

• Pour  r=RHr=R_H  on obtient  A=−α2ρ2sin2(θ)<0\displaystyle A=-\frac{α^2}{ρ^2} \: \sin^2(θ)<0 ,  donc la variable tt est “déjà” devenue une variable de genre espace (est-ce bien cohérent ?).

L'ergosphère correspond à la limite où  A=1−rsrρ2=0\displaystyle A=1-\frac{r_s \: r}{ρ^2} =0 .  On obtient deux solutions :  r=12(rs±rs2−4α2cos2(θ))r=\frac{1}{2} \left(r_s±\sqrt{r_s^{\:2}-4 \,α^2 \: \cos^2(θ)} \, \right) .

Compte tenu de ce qui précède, on considère uniquement l'ergosphère “extérieure” :  RE=12(rs+rs2−4α2cos2(θ))R_E=\frac{1}{2} \left(r_s+\sqrt{r_s^{\:2}-4 \,α^2 \: \cos^2(θ)} \, \right) .

◊ remarque : l'appellation “ergo-sphère” est ici ambiguë puisque cette surface ressemble plutôt à un ellipsoïde de révolution (sans en être un), tangent aux pôles à l'horizon.

rotation_Im/ergosphere.jpg

◊ remarque : dans le cas limite sans rotation, l'ergosphère est confondue avec l'horizon de Schwarzschild.

• La zone comprise entre l'horizon et l'ergosphère est nommée ergorégion. Sa principale caractéristique est qu'il ne peut y exister de point matériel statique “par rapport à l'infini” (selon les coordonnées de Boyer-Lindquist).

En effet, sa 4-vitesse serait de la forme  (u0,0,0,0)(u^0, \,0, \,0, \,0)  ;  or dans cette zone la variable  tt  est du genre espace, alors que pour un point matériel statique il faudrait une 4-vitesse du genre temps.

Puisqu'un référentiel doit pouvoir être associé à un repérage par rapport à des points matériels, cela suggère que l'espace est “entrainé” par le mouvement de rotation du “trou noir”.

• Ceci peut être précisé en considérant un photon émis (depuis une position quelconque) avec une vitesse tangentielle selon φφ . Ce photon suit une géodésique du genre lumière :  ds2=g00c2dt2+2g03cdtdφ+g33dφ2=0{ds}^2=g_{00} \: c^2 \, {dt}^2+2 \,g_{03} \: c \,dt \:dφ+g_{33} \: {dφ}^2=0 .

Pour un observateur lointain, avec le temps tt , la vitesse du photon se déduit de  dφcdt=−g03±(g03)2−g00g33g33\displaystyle \frac{dφ}{c \,dt}=\frac{-g_{03}±\sqrt{(g_{03})^2-g_{00} \: g_{33}}}{g_{33}} ,  où le signe indique le sens d'émission.

Ainsi (avec  g33<0g_{33}<0 ),  non seulement le mouvement semble plus rapide dans le sens de rotation du trou noir, mais de plus s'il est sur l'ergosphère (où  g00=0g_{00}=0 )  le photon rétrograde semble immobile, ce qui est impossible. Ceci signifie qu'à ce niveau l'espace est entrainé par la rotation.

• Une autre approche consiste à décrire le mouvement d'une particule à l'aide d'un lagrangien (ici choisi quadratique et simplifié) :  ℒ=−12gμνx˙μx˙νℒ=-\frac{1}{2} g_{μν} \: \dot{x}^μ \: \dot{x}^ν ,  où les dérivées sont prises par rapport à un paramètre σσ .

Cela donne les équations du mouvement :  ddσ∂ℒ∂x˙μ−∂ℒ∂xμ=0\displaystyle \frac{d}{dσ} \frac{∂ℒ}{∂\dot{x}^μ}-\frac{∂ℒ}{∂x^μ}=0 .  En particulier pour  x3=φx^3=φ  on obtient :  ddσ(−g3νx˙ν)=0\displaystyle \frac{d}{dσ} \left(-g_{3ν} \: \dot{x}^ν \right)=0 ,  donc  −g30ct˙−g33φ˙=Cste-g_{30} \: c \,\dot{t}-g_{33} \: \dot{φ}=Cste .

Cette quantité constante est l'impulsion généralisée associée à l'angle φφ ; elle correspond à la généralisation du moment cinétique.

Une particule de moment cinétique nul (qui donc “ne tourne pas” par rapport à l'espace), est donc telle que :  dφcdt=−g30g33\displaystyle \frac{dφ}{c \,dt}=-\frac{g_{30}}{g_{33}}  .  On peut donc considérer que l'espace tourne localement à la vitesse angulaire :  ω(r,θ)=−cg30g33\displaystyle ω(r,\,θ)=-c \, \frac{g_{30}}{g_{33}} .

◊ remarque : dans ce cas, le paramètre σσ se simplifie et n'intervient pas.

◊ remarque : en relativité restreinte, il n'y a pas d'hypothétique “éther” par rapport auquel la lumière se propagerait ; en relativité générale, les propriétés de l'espace se déduisent de la répartition de matière et d'énergie (en accord avec le principe de Mach), donc il n'y a pas contradiction à considérer que cet espace “tourne” sous l'effet de la rotation de l'astre central ; la dépendance  ω=ω(r,θ)ω=ω(r,\,θ)  fait que la métrique n'est pas statique, mais stationnaire.

◊ remarque : les mouvements des photons sont simplement limités par la vitesse de la lumière de part et d'autre du mouvement de l'espace.

📖 exercices n° IV, V, VI, VII et VIII.

Autre formulation de la métrique

• Pour tenir compte de la rotation de l'espace, on peut juger préférable de repérer par l'intermédiaire d'un angle  dϕ=dφ−ωdtdϕ=dφ-ω \:dt  ;  on ne peut par contre pas définir d'angle ϕϕ car la rotation ωω dépend de rr .

On peut écrire :  E=(r2+α2+rsα2rρ2sin2(θ))sin2(θ)=Σ2ρ2sin2(θ)\displaystyle E=\left(r^2+α^2+\frac{r_s \: α^2 \: r}{ρ^2} \: \sin^2(θ) \right) \; \sin^2(θ)=\frac{Σ^2}{ρ^2} \: \sin^2(θ)  en posant :  Σ2=(r2+α2)2−α2Δsin2(θ)Σ^2=(r^2+α^2 )^2-α^2 \: Δ \; \sin^2(θ) .

Compte tenu de  ω=cBE=crsαrΣ2\displaystyle ω=c \, \frac{B}{E}=\frac{c \:r_s \: α \:r}{Σ^2} ,  on peut noter la métrique sous la forme simplifiée :  ds2=𝒜c2dt2−Cdr2−Ddθ2−Edϕ2{ds}^2=𝒜 \:c^2 \, {dt}^2-C \:{dr}^2-D \:{dθ}^2-E \:{dϕ}^2  avec :
𝒜=A+Eω2c2=AE+B2E=1g00=Δρ2Σ2\displaystyle 𝒜=A+E \: \frac{ω^2}{c^2} =\frac{A \:E+B^2}{E}=\frac{1}{g^{00}} =\frac{Δ \:ρ^2}{Σ^2}  .

• Ainsi, en se repérant par rapport à l'espace en rotation, le coefficient 𝒜𝒜 de la métrique s'annule (comme ΔΔ ) au niveau de l'horizon (pour  r=RHr=R_H ).  L'ergorégion a donc pour seule propriété l'inévitable mouvement par rapport à l'infini.

• On constate par ailleurs qu'avec ce repérage il n'y a plus de désynchronisation des horloges : celle-ci est due au “mouvement” par rapport à l'espace du repérage “immobile” par rapport à l'infini.

📖 exercices n° IX et X.

Choix de la variable radiale

Position du problème

• La variable radiale r de R. Boyer et R. Lindquist a été choisie “au plus simple” pour adapter la métrique de R. Kerr, assez compliquée car obtenue par des considérations mathématiques très abstraites.

Cette coordonnée présente toutefois des caractéristiques semblables à celles qui sont reprochées à la coordonnée “isotrope” r_\underline{r} pour la métrique de Schwarzschild : une “duplication” de certains objets associés.

La cause en est que  r(r_)r(\underline{r})  passe par un minimum  r=rsr=r_s  pour  r_=r_s=rs4\displaystyle \underline{r}=\underline{r}_s=\frac{r_s}{4} .  Ainsi dès lors qu'un trou noir a un disque d'accrétion pour  r_>r_s\underline{r}>\underline{r}_s  il en a un autre pour  r_<r_s\underline{r}<\underline{r}_s  correspondant à la même valeur de rr ; en fait la gravitation y est répulsive et cela conduit à des difficultés d'interprétation physique.

• La situation est en fait analogue pour la variable rr de Boyer-Lindquist : il y a ainsi un “horizon interne” et une “ergosphère interne”. En outre J. Fric signale également un effet de gravitation répulsive “de l'autre côté”. Pour tout physicien dénigrant la variable r_\underline{r} “isotrope”, cela doit alerter sur la pertinence du choix utilisé ici.

Le cas n'est toutefois pas identique : le “dédoublement” correspond à  r=rs2\displaystyle r=\frac{r_s}{2}  et n'est pas au niveau de l'horizon (qui est lui même dupliqué).

Amélioration éventuelle

• Dans la mesure où les conséquences de la rotation sur la métrique sont plutôt associées à une généralisation des forces d'inertie classiques (“centrifuge” et “complémentaire”), il semble souhaitable de se référer (au moins initialement) aux conditions aux pôles où ces effets sont en principe absents.

◊ remarque : toutes les difficultés constatées pour la métrique “classique” de Schwarzschild subsistent par contre de même avec rotation, puisqu'elles s'appliquent aux mouvements selon l'axe polaire.

◊ remarque : la variable rr de Boyer-Lindquist semble un peu illogique en ce sens qu'elle prend comme référence l'équateur pour  ρ2=r2+α2cos2(θ)ρ^2=r^2+α^2 \; \cos^2(θ)  ;  il pourrait sembler plus logique d'utiliser une référence polaire :  𝓇=r2+α2𝓇=\sqrt{r^2+α^2}  et  ρ2=𝓇2−α2sin2(θ)ρ^2=𝓇^2-α^2 \; \sin^2(θ)  ;  ceci amène un problème pour  α>𝓇α>𝓇  mais de toute façon une limitation sur αα apparaît inévitablement à d'autres endroits.

• Avec les coordonnées “classiques” de Schwarzschild, l'horizon des événements est associé à l'annulation de  1C=1−rsr\displaystyle \frac{1}{C}=1-\frac{r_s}{r} .  Pour les notations de Boyer-Lindquist cela correspond aux pôles à :  1C=Δρ2=1−rsrr2+α2\displaystyle \frac{1}{C}=\frac{Δ}{ρ^2} =1-\frac{r_s \: r}{r^2+α^2} .

Une idée peut être alors de considérer la variable  r˜=r2+α2r=r+α2r\displaystyle \tilde{r}=\frac{r^2+α^2}{r}=r+\frac{α^2}{r}  pour retrouver la même expression :  1C=1−rsr˜\displaystyle \frac{1}{C}=1-\frac{r_s}{\tilde{r}} .

Sur l'axe polaire, on obtient alors en outre :  A=1−rsr˜\displaystyle A=1-\frac{r_s}{\tilde{r}}  ;  B=0B=0  ;  E=0E=0 .  Mais cela ne signifie pas que l'axe polaire est totalement “insensible” à la rotation.

Dans la métrique, cela correspond en effet à :
1C˜=(1−rsr˜)(dr˜dr)2=(1−rsr˜)(1−α2[r(r˜)]2)2\displaystyle \frac{1}{\tilde{C}}=\left(1-\frac{r_s}{\tilde{r}}\right) \: \left(\frac{d\tilde{r}}{dr}\right)^2=\left(1-\frac{r_s}{\tilde{r}}\right) \: \left(1-\frac{α^2}{\left[r(\tilde{r})\right]^2} \right)^2.

Outre l'horizon “classique”, il apparait ainsi un autre horizon associé à la rotation. La condition  r(r˜)=αr(\tilde{r})=α  correspond à une unique valeur  r˜=2α\tilde{r}=2 \,α  (qui est le minimum de  r˜(r)\tilde{r} (r)  donc associé à une seule valeur de rr ).

rotation_Im/rotation.jpg

• Avec cette variable, tant que  α<rs2\displaystyle α<\frac{r_s}{2}  l'horizon “de rotation” est masqué par l'horizon “classique”, mais la description n'en est pas pour autant totalement simplifiée : les valeurs  r˜<2α\tilde{r}<2 α  sont associées à des notations complexes.

◊ remarque : les notations complexes sont déjà nécessaires dans certaines descriptions sans rotation, avec les variables “classiques” de Schwarzschild ou des repérages généralisés de Lemaître, donc elles ne sont pas rédhibitoires, mais tout de même souvent moins pratiques.

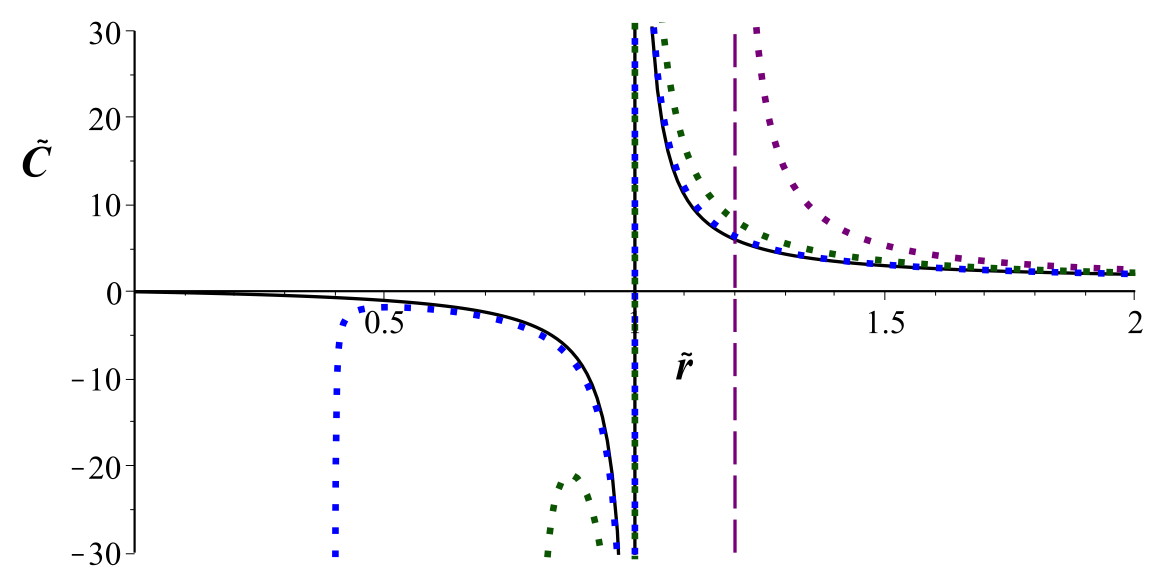
• On constate que, bien qu'invariant, l'axe polaire est un peu influencé par la rotation de l'astre du point de vue de la géométrie spatiale décrite par C˜\tilde{C} (pointillés en bleu et en vert).

• Pour  α>rs2\displaystyle α>\frac{r_s}{2}  (pointillés en rouge) c'est au contraire l'horizon “classique” qui est masqué par l'horizon “de rotation” (il existe “en principe” tout de même dans ce cas, mais des notations complexes seraient nécessaires dans la région de l'espace correspondante, dans la mesure où r˜(r)\tilde{r}(r) passe par un minimum et ne peut pas l'atteindre).

• Plus facile à interpréter physiquement, cette description n'est par contre pas généralisable hors de l'axe.

📖 exercice n° XI.

Amélioration impossible

• On peut aussi considérer le cas équatorial, référence des coordonnées de Boyer-Lindquist.

Ceci correspond à  ρ2=r2ρ^2=r^2   et   1C=Δρ2=1−rsr+α2r2\displaystyle \frac{1}{C}=\frac{Δ}{ρ^2} =1-\frac{r_s}{r}+\frac{α^2}{r^2}   ;  on constate que la variable rr est tout-à-fait adaptée dans ce cas : on retrouve l'effet gravitationnel en  −rsr\displaystyle -\frac{r_s}{r}  modifié par un effet “centrifuge” en  +α2r2\displaystyle +\frac{α^2}{r^2}  .

La rotation a pour effet de décaler l'horizon en  r=RHr=R_H  et même de le faire disparaitre si  α>rs2\displaystyle α>\frac{r_s}{2}  (le trinôme est alors toujours positif).

◊ remarque : selon l'axe polaire  r˜=rs\tilde{r}=r_s  correspond de même à  r=RHr=R_H  mais l'intérêt de r˜\tilde{r} est de bien montrer que l'effet gravitationnel y est pratiquement le même que pour la métrique de Schwarzschild.

• L'impossibilité d'amélioration vient du fait que pour les cas intermédiaires on ne peut pas adapter  1C=Δρ2=1−rsrρ2+α2sin2⁡(θ)ρ2\displaystyle \frac{1}{C}=\frac{Δ}{ρ^2} =1-\frac{r_s \: r}{ρ^2} +\frac{α^2 \: \sin^2⁡(θ)}{ρ^2}  avec un  r˜(r,θ)\tilde{r}(r,θ)  qui ajouterait dans la métrique un terme en  dr˜dθd\tilde{r} \: dθ .  L'énorme avantage mathématique de la variable rr est de parvenir à découpler les coordonnées radiale et angulaires, ce qui a permis de trouver la solution de Kerr.