ASTRES EN ROTATION - corrigé des exercices

Horizon des événements

1.	• On peut écrire : $\displaystyle A=\frac{ρ^2-r_s \: r}{ρ^2} =\frac{r^2+α^2 \; \cos^2(θ)-r_s \: r}{ρ^2} =\frac{Δ-α^2 \; \sin^2(θ)}{ρ^2}$ . • La surface horizon est déterminée par $Δ=0$ , donc correspond à : $\displaystyle A=-\frac{α^2}{ρ^2} \: \sin^2(θ)$ .

2.a.	• L'hypersurface horizon correspond à $Δ=0$ pour tout $t$ . Le quadrivecteur “normal” $n_μ$ est donc orienté selon le “gradient” ; la seule composante non nulle est : $n_1=∂_1 Δ=2 \,R_H -r_s=\sqrt{r_s^{\:2}-4 \,α^2}$ . • La norme du quadrivecteur normal est alors : $\displaystyle g^{μν} \: n_μ \: n_ν=g^{11} \: n_1 \: n_1=-\frac{Δ}{ρ^2} \:\left(r_s^{\:2}-4 \,α^2\right)=0$ ; il s'agit donc d'un quadrivecteur du genre lumière.

2.b.	• Pour comparer, il faut calculer l'unique composante contravariante : $n^1=g^{11} \: n_1=0$ ; ceci correspond à un quadrivecteur nul, sans en être un, donc l'interprétation est pour le moins délicate. ◊ remarque : pour retrouver la composante covariante, il faut repasser à la limite pour $r→r_s$ . • Les quadrivecteurs tangents ont des composantes contravariantes de la forme $(c \,dt\,,0\,,dθ\,,dφ)$ . Il est vrai que, d'une certaine façon, le quadrivecteur nul obtenu précédemment “en fait partie”, mais ceux tangents ont “par nature” une seconde composante covariante nulle.

2.c.	• Avec $A≠0$ presque partout (sauf aux pôles), les quadrivecteurs tangents non nuls ont pour norme : ${ds}^2=A \:c^2 \,{dt}^2+2 \,B \:c \,dt \:dφ-D \:dθ^2-E \:dφ^2$ . • Rien n'interdit de considérer des valeurs de composantes angulaires telles que ${ds}^2≠0$ (elles peuvent être quelconques puisqu'elles sont orthoradiales). Ces quadrivecteurs ne sont donc en général pas du genre lumière.

• Pour éviter la divergence de

\displaystyle C(r)=\frac{ρ^2}{Δ}

r=R_H

, liée au fait que la variable

r

semble présenter en ce point un minimum, on peut appliquer une méthode analogue à celle utilisée pour la métrique de Schwarzschild.
• Puisque

Δ=(r-R_H)(r-r_H)

avec

R_H=\frac{1}{2} \,\left(r_s+\sqrt{r_s^{\:2}-4 \,α^2}\right)

r_H=\frac{1}{2} \,\left(r_s-\sqrt{r_s^{\:2}-4 \,α^2}\right)

, on peut utiliser une variable

\underline{r}

telle que

\displaystyle r=\underline{r} \, .\left(1+\frac{\underline{R}_H^{\:2}}{\underline{r}^2} \right)=\frac{\underline{r}^2+\underline{R}_H^{\:2}}{\underline{r}}

.
• Ceci donne :

\displaystyle \frac{dr}{d\underline{r}}=1-\frac{\underline{R}_H^{\:2}}{\underline{r}^2}=\frac{(\underline{r}+\underline{R}_H)(\underline{r}-\underline{R}_H)}{\underline{r}^2}

; le minimum correspond à

\underline{r}=\underline{R}_H

donc

R_H=2 \,\underline{R}_H

.
• Puisque

\underline{C} \: {d\underline{r}}^2=C \:{dr}^2

on obtient :

\displaystyle \underline{C}=\frac{\left(\underline{r}^2+\underline{R}_H^{\:2} \right)^2+\underline{r}^2 \: α^2 \; \cos^2(θ)}{\left(\underline{r}^2+\underline{R}_H^{\:2}-\underline{r} \; R_H \right)\left(\underline{r}^2+\underline{R}_H^{\:2}-\underline{r} \; r_H \right)} \: \left(\frac{dr}{d\underline{r}}\right)^2

.
• Avec

\underline{r}^2+\underline{R}_H^{\:2}-\underline{r} \; R_H=\left(\underline{r}-\underline{R}_H\right)^2

, ceci donne :

\displaystyle \underline{C}=\frac{\left(\underline{r}^2+\underline{R}_H^{\:2} \right)^2+\underline{r}^2 \: α^2 \; \cos^2(θ)}{\underline{r}^2+\underline{R}_H^{\:2}-\underline{r} \; r_H } \: \frac{\left(\underline{r}+\underline{R}_H\right)^2}{\underline{r}^4}

.
• On peut alors vérifier que le polynôme

\underline{r}^2+\underline{R}_H^{\:2}-\underline{r} \; r_H

n'a pas de racine réelle puisque son discriminant

-\frac{1}{16} \:\left(3 \,r_s+\sqrt{r_s^{\:2}-4 \,α^2}\right)\left(r_s+3 \:\sqrt{r_s^{\:2}-4 \,α^2}\right)

est négatif. Ainsi la divergence est effectivement évitée, ce qui peut suggérer qu'un tel horizon n'a pas forcément de signification physique ; on retombe toutefois dans les mêmes difficultés qu'avec les coordonnées isotropes.
◊ remarque : comme pour la métrique de Schwarzschild, puisque la métrique utilisant

\underline{r}

est moins simple, on peut conserver les notations classiques tant qu'on le fait avec les précautions requises.

Géométrie ellipsoïdale

1.a.	• La métrique de Kerr simplifiée peut s'écrire sous la forme : $\displaystyle -{ds}^2=ρ^2 \: {dθ}^2+\left(r^2+α^2+\frac{r_s \: α^2 \: r}{ρ^2} \: \sin^2(θ) \right) \; \sin^2(θ) \: {dφ}^2$ . • On peut penser que cela correspond à la longueur spatiale. Toutefois, pour une métrique non diagonale, la notion locale de distance est décrite par ${d𝓁}^2=ℊ_{ij} \: {dx}^i \: {dx}^j$ avec un tenseur métrique tridimensionnel $\displaystyle ℊ_{ij}=\frac{g_{0i} \: g_{0j}}{g_{00}} -g_{ij}$ (cette métrique spatiale est l'inverse de la partie spatiale $ℊ^{ij}=g^{ij}$ ). • On obtient ainsi : $\displaystyle ℊ_{33}=\frac{B^2}{A}+E=\frac{Δ}{A} \: \sin^2(θ)$ ; cela ne change rien dans les deux questions suivantes puisqu'on se ramène au cas $φ=Cste$ .

1.b.	• Il s'agit d'une surface de révolution invariante par rotation d'angle $φ$ ; il suffit donc de l'étudier en coupe dans un plan $φ=Cste$ .

1.c.	• La métrique simplifiée peut s'écrire : ${d𝓁}^2=[r^2+α^2 \; \cos^2(θ) ] \: {dθ}^2$ (ici $r$ est une constante). Cela peut aussi s'écrire sous la forme : ${d𝓁}^2=[r^2 \; \sin^2(θ)+(r^2+α^2 ) \; \cos^2(θ) ] \; {dθ}^2$ . • En géométrie euclidienne dans le plan $(Oxz)$ on peut considérer une ellipse centrée à l'origine, avec un demi-grand-axe $𝒶=\sqrt{r^2+α^2}$ selon $(Ox)$ et un demi-petit-axe $𝒷=r$ selon $(Oz)$ . En considérant : $x=𝒶 \; \sin(θ)$ et $z=𝒷 \; \cos(θ)$ l'équation de l'ellipse peut s'écrire : $\displaystyle \frac{x^2}{𝒶^2} +\frac{z^2}{𝒷^2} =1$ . La métrique correspondante est alors : ${d𝓁}^2={dx}^2+{dz}^2=[𝒷^2 \; \sin^2(θ)+𝒶^2 \; \cos^2(θ) ] \; {dθ}^2$ . ◊ remarque : pour l'ellipse en géométrie euclidienne, $r$ varie en même temps que $θ$ ; pour pouvoir comparer, il faut pour trouver une écriture de la métrique en fonction de $θ$ seulement. • Lorsqu'on obtient une métrique en résolvant les équations d'Einstein, le fait que les coordonnées ressemblent à celles utilisées dans un espace plat ne signifie pas que leur interprétation doit être la même. La coordonnée $r$ de la métrique de Kerr ne représente pas une “distance radiale” à l'origine comme en géométrie euclidienne ; il en découle que les surfaces déterminées par $r=Cste$ ne correspondent pas à des sphères au sens usuel.

1.d.	• La métrique spatiale sur un parallèle correspond à : $\displaystyle {d𝓁}^2=\frac{Δ}{A} \: \sin^2(θ) \; {dφ}^2$ . On peut tout de suite noter qu'au niveau de l'horizon $Δ=0$ donc la variation de $φ$ ne contribue pas à l'élément de longueur, ce qui est tout-à-fait incompatible avec un ellipsoïde. • Pour comparer avec un ellipsoïde (pour lequel $r$ dépend de $θ$ ) on peut utiliser $z=𝒷 \; \cos(θ)$ , ou bien $\displaystyle ζ=\frac{z}{𝒷}$ pour simplifier. Le périmètre correspond à $Q=2π \:x$ avec $x=𝒶 \; \sin(θ)$ , donc : $Q=2π \:𝒶 \:\sqrt{1-ζ^2}$ . • Pour la métrique de Kerr avec $r=Cste>R_H$ , on peut étudier le périmètre $\displaystyle P=2π \:\sqrt{\frac{Δ}{A}} \:\, \sin(θ)$ en fonction de $z=r \; \cos(θ)$ . • En considérant $r=𝒷$ pour comparer, on peut écrire : $\displaystyle \frac{Δ}{A}=(𝒶^2-r_s \: 𝒷) \: \frac{𝒷^2+α^2 \: ζ^2}{𝒷^2+α^2 \: ζ^2-r_s \: 𝒷}$ . • La condition $r=𝒷=R_H$ donne $𝒶^2=r_s \: 𝒷$ , d'où le périmètre nul noté précédemment, mais la condition $r=𝒷>R_H$ n'est en fait pas suffisante. Pour que le périmètre soit défini, il faut que le dénominateur (issu de $A$ ) soit défini pour tout $ζ$ . En particulier pour $ζ=0$ il faut $𝒷^2-r_s \: 𝒷>0$ donc $𝒷>r_s>R_H$ . Cette contrainte supplémentaire est liée au fait qu'en deçà il ne peut exister aucun observateur (ni “périmètre”) immobile ; il y a un effet d'entrainement par la rotation de l'espace (voir l'étude de l'ergosphère). 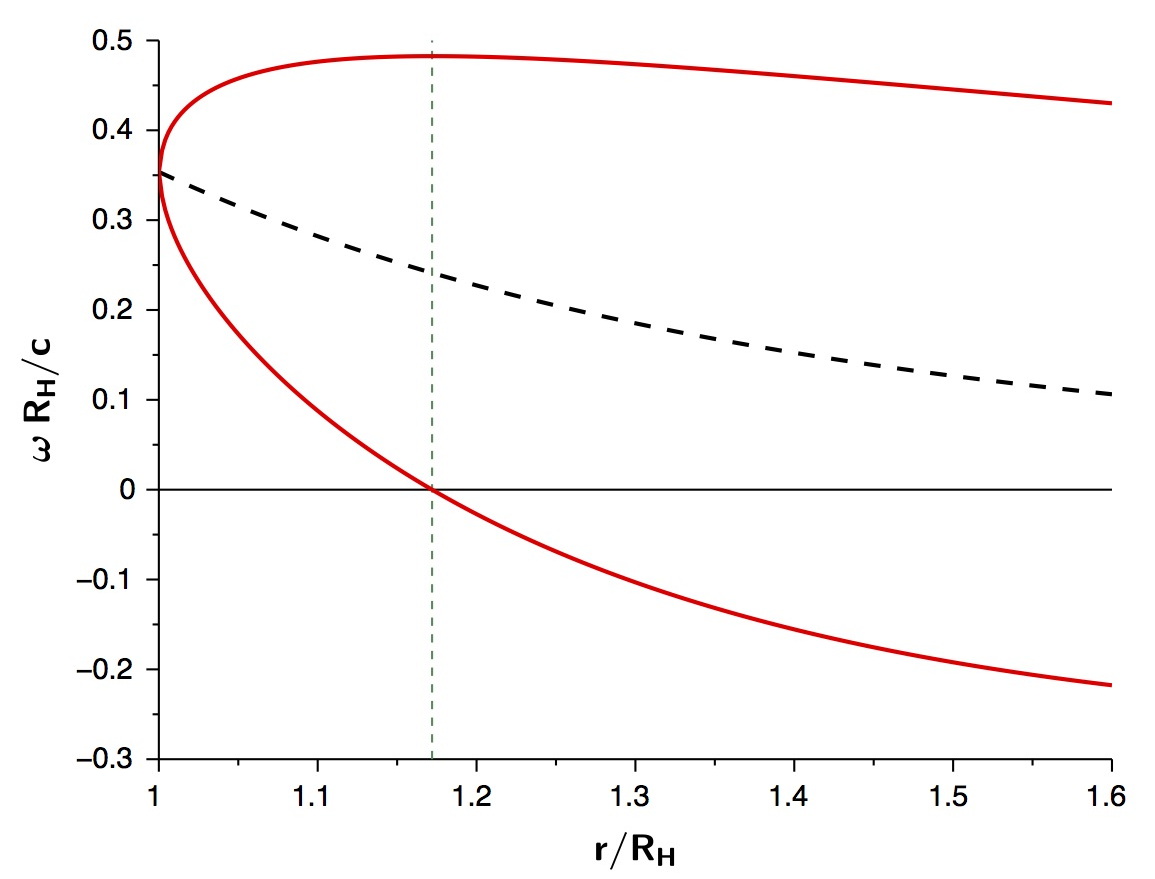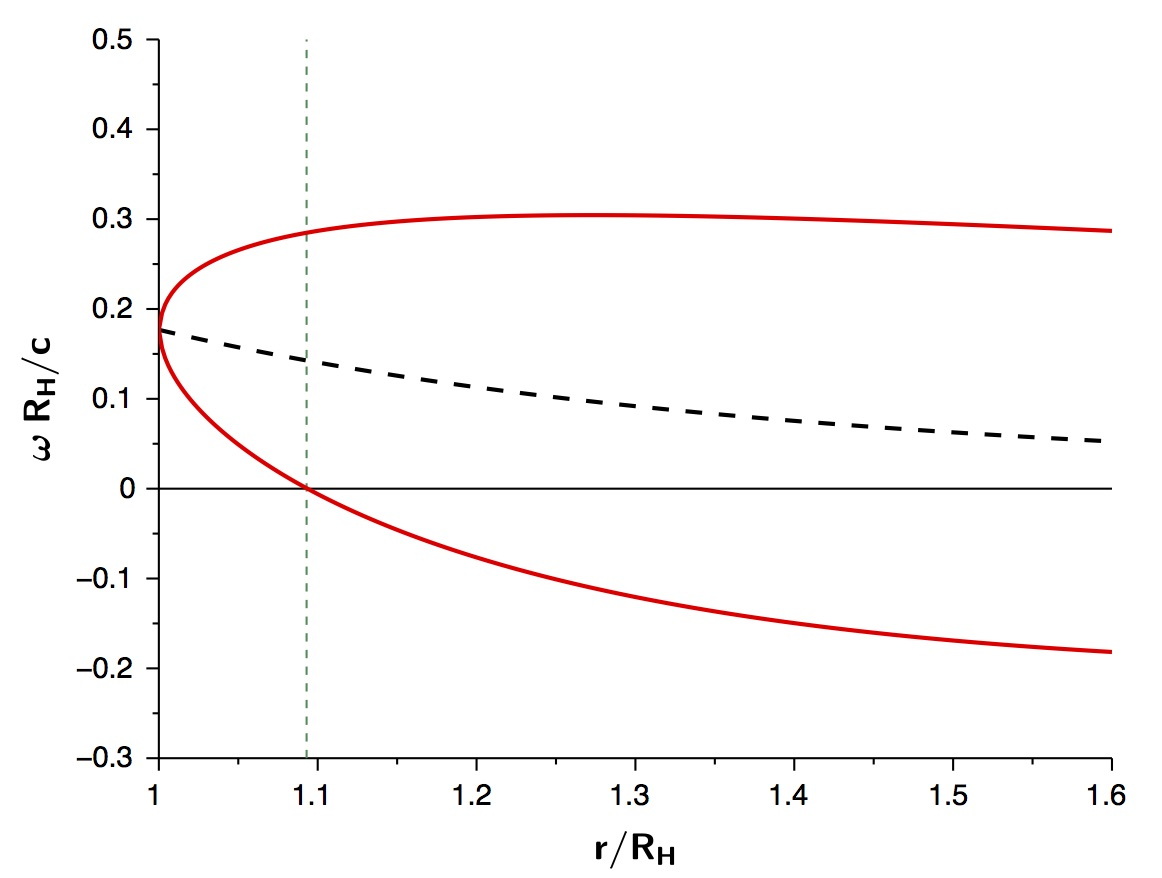• L'expression n'étant pas simple, on peut en préciser numériquement le comportement à l'aide d'un cas particulier, par exemple pour $4 \,α^2=\frac{1}{2} r_s^{\:2}$ (l'expression de $R_H$ nécessite $4 \,α^2<r_s^{\:2}$ ) . Ceci donne : $\displaystyle α=\frac{r_s}{2 \,\sqrt{2}}$ ; $\displaystyle R_H=\frac{r_s}{2} \, \frac{\sqrt{2}+1}{\sqrt{2}}$ ; $\displaystyle r=𝒷=\sqrt{2} \; R_H=r_s \: \frac{\sqrt{2}+1}{2}>r_s>R_H$ ; $\displaystyle 𝒶=\sqrt{𝒷^2+α^2}=\frac{r_s}{2} \: \frac{\sqrt{2 \,\left(\sqrt{2}+1\right)^2+1}}{\sqrt{2}}$ . • Pour simplifier l'étude, on peut choisir $R_H$ comme unité de longueur ; ceci donne : $R_H=1$ ; $r_s=\frac{2 \:\sqrt{2}}{\sqrt{2}+1}≈\text{1,172}$ ; $α=\frac{1}{\sqrt{2}+1}≈\text{0,4142}$ ; $𝒷=\sqrt{2}≈1,414$ ; $𝒶=\sqrt{𝒷^2+α^2}≈\text{1,474}$ . ◊ remarque : l'ellipticité est faible dès qu'on s'éloigne de l'horizon. 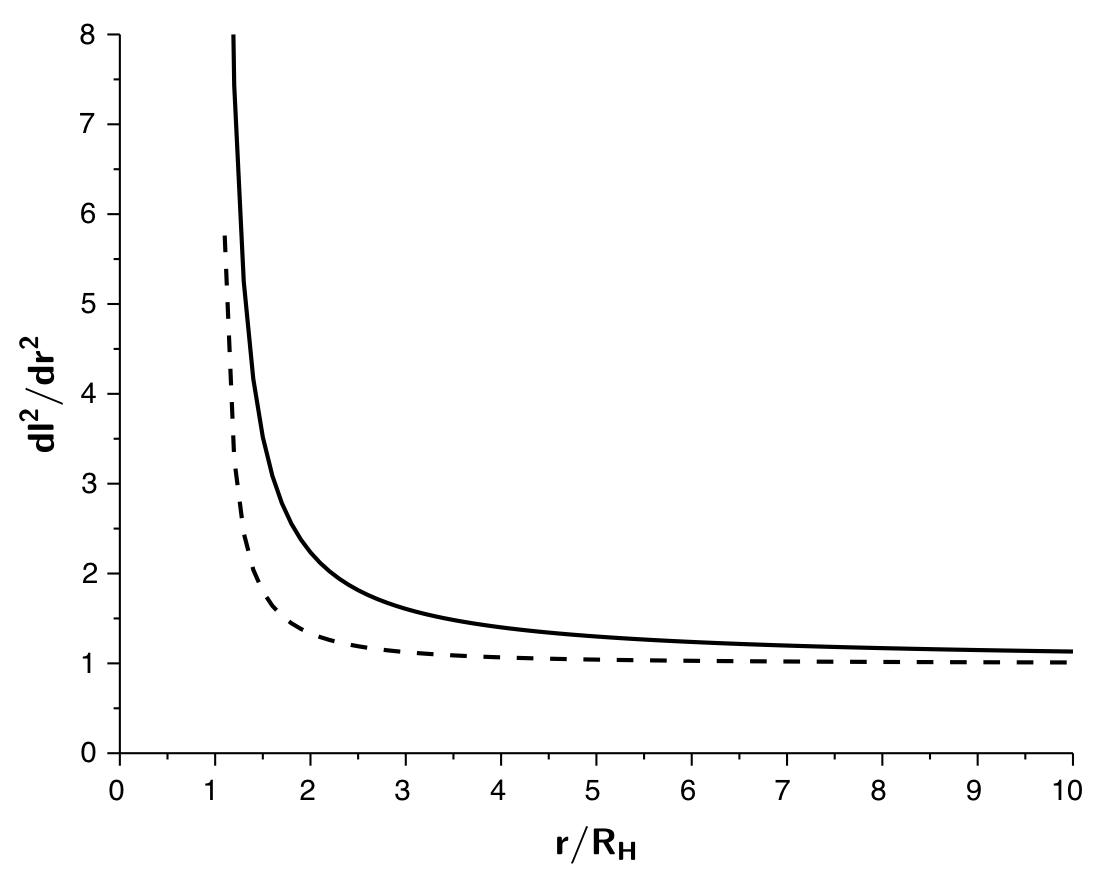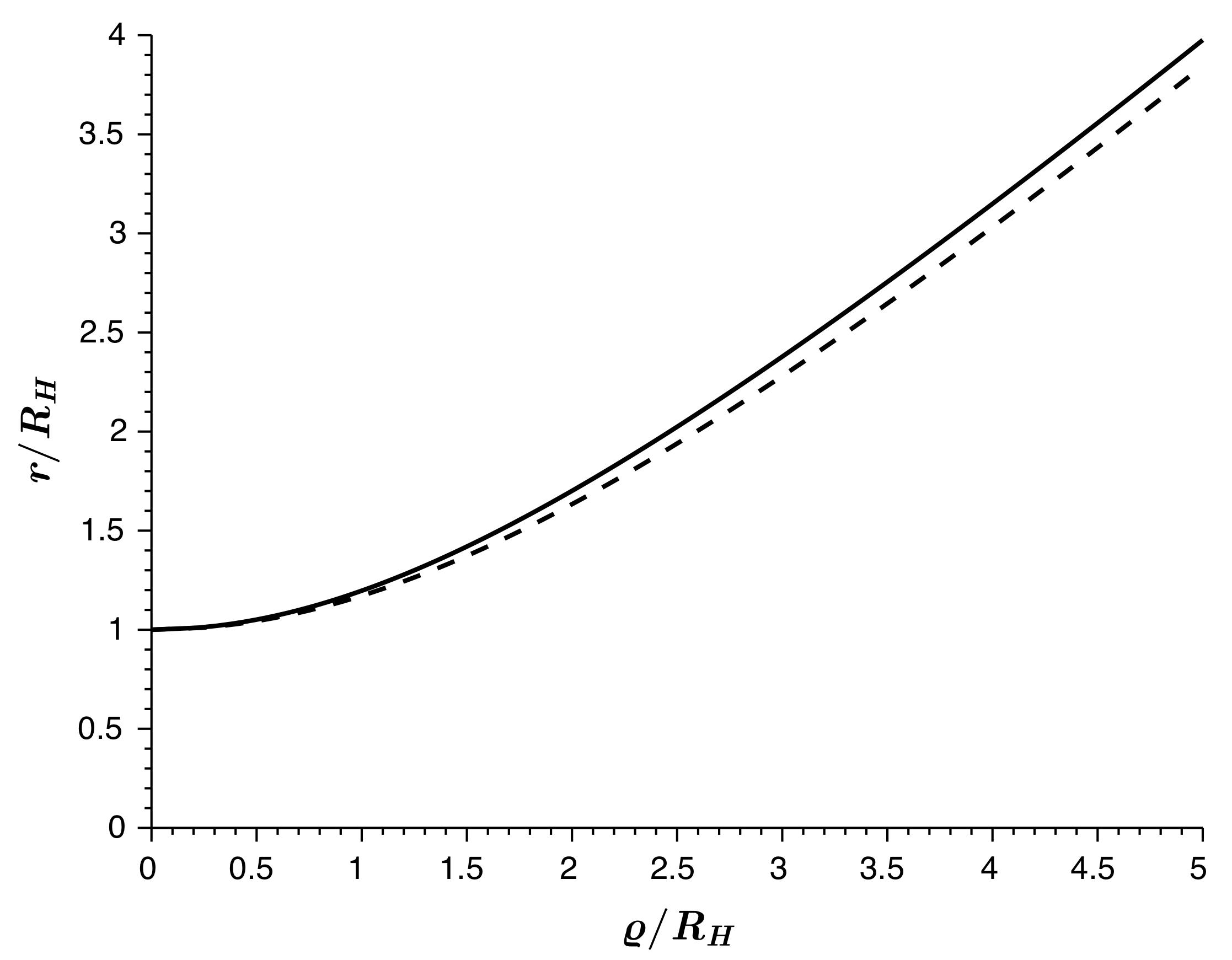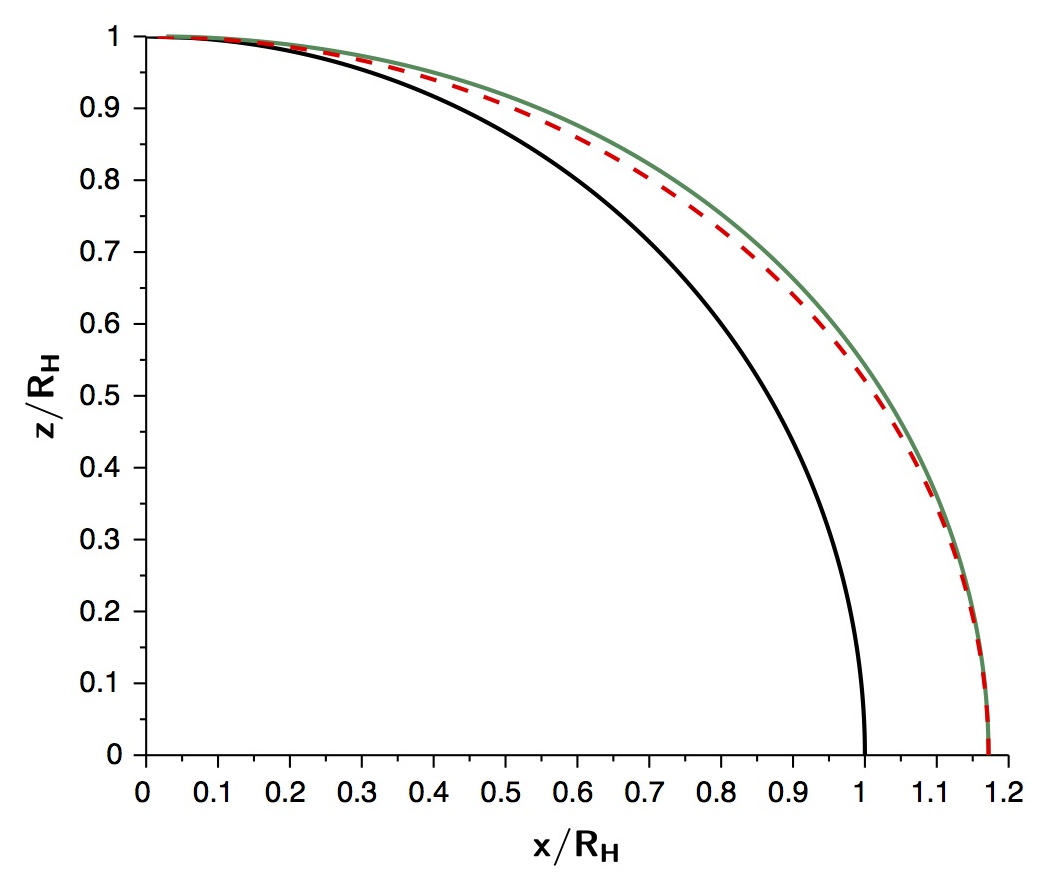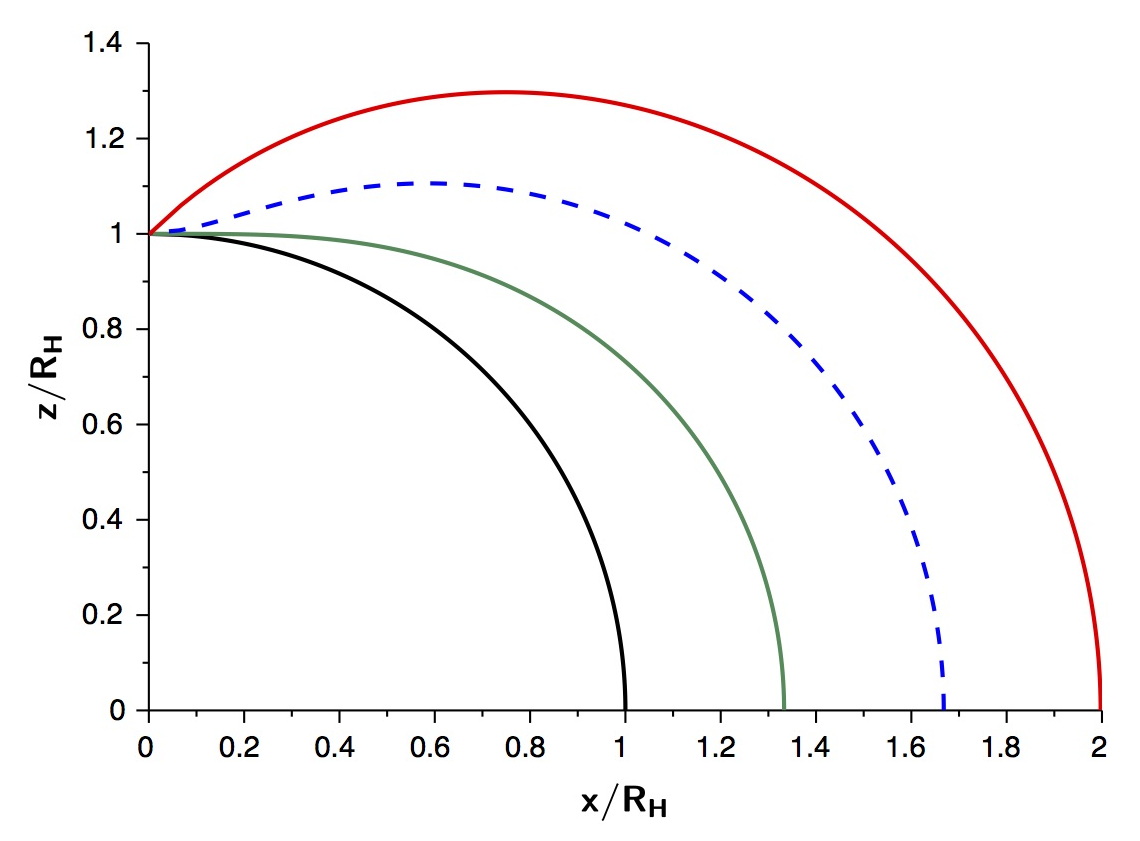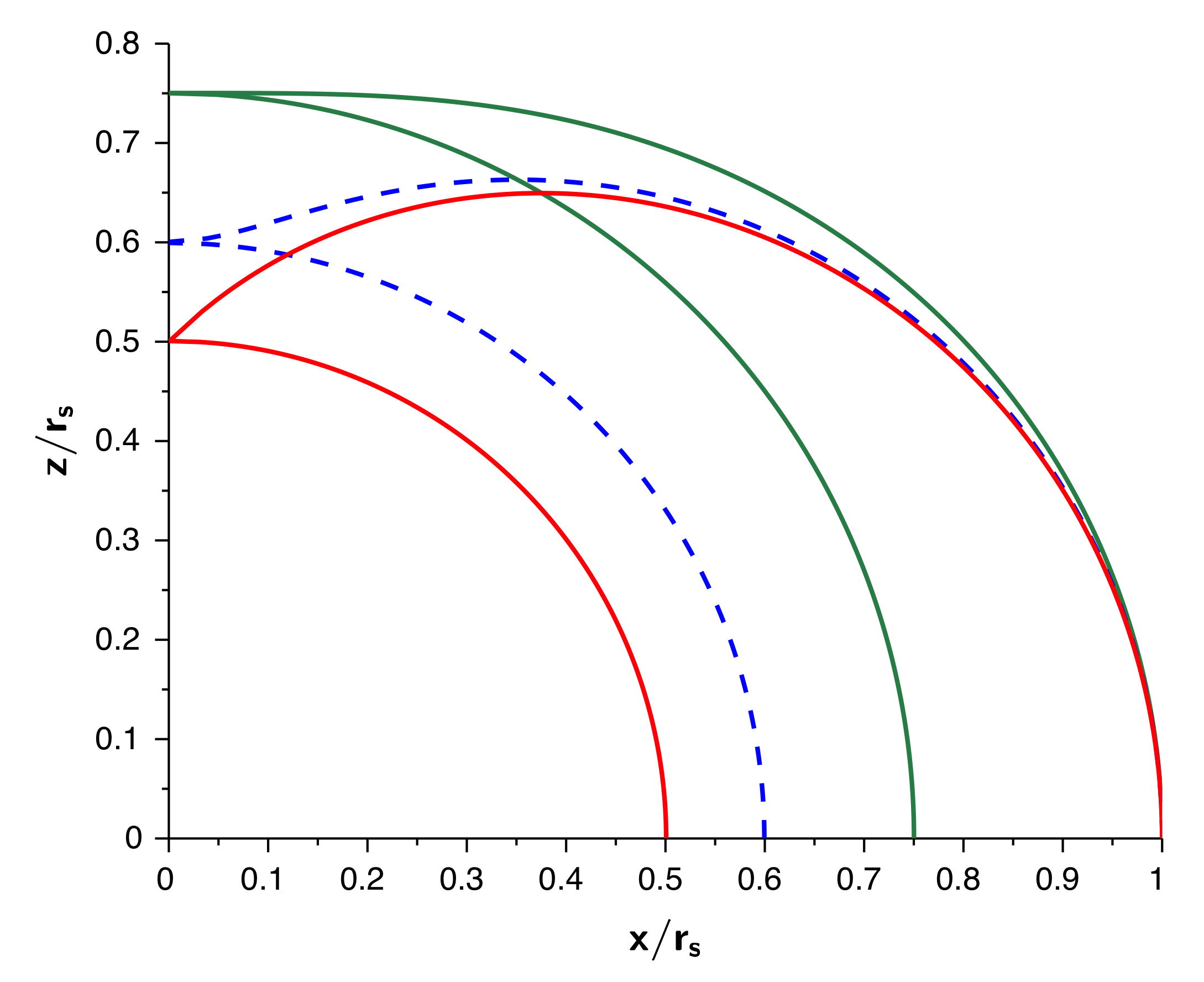• On peut alors tracer (avec q en pointillé) : $\displaystyle q=\sqrt{\frac{Q}{2π \:𝒶}}=\sqrt{1-ζ^2}$ et $\displaystyle p=\sqrt{\frac{P}{2π \:𝒶}}=\sqrt{1-\frac{r_s \: 𝒷}{𝒶^2}} \:\: \sqrt{\frac{𝒷^2+α^2 \: ζ^2}{𝒷^2+α^2 \: ζ^2-r_s \: 𝒷}} \;\: \sqrt{1-ζ^2}$ . • On constate alors que la métrique à la surface d'une ellipse n'est pas totalement représentative de la métrique de Kerr pour $r=Cste$ . 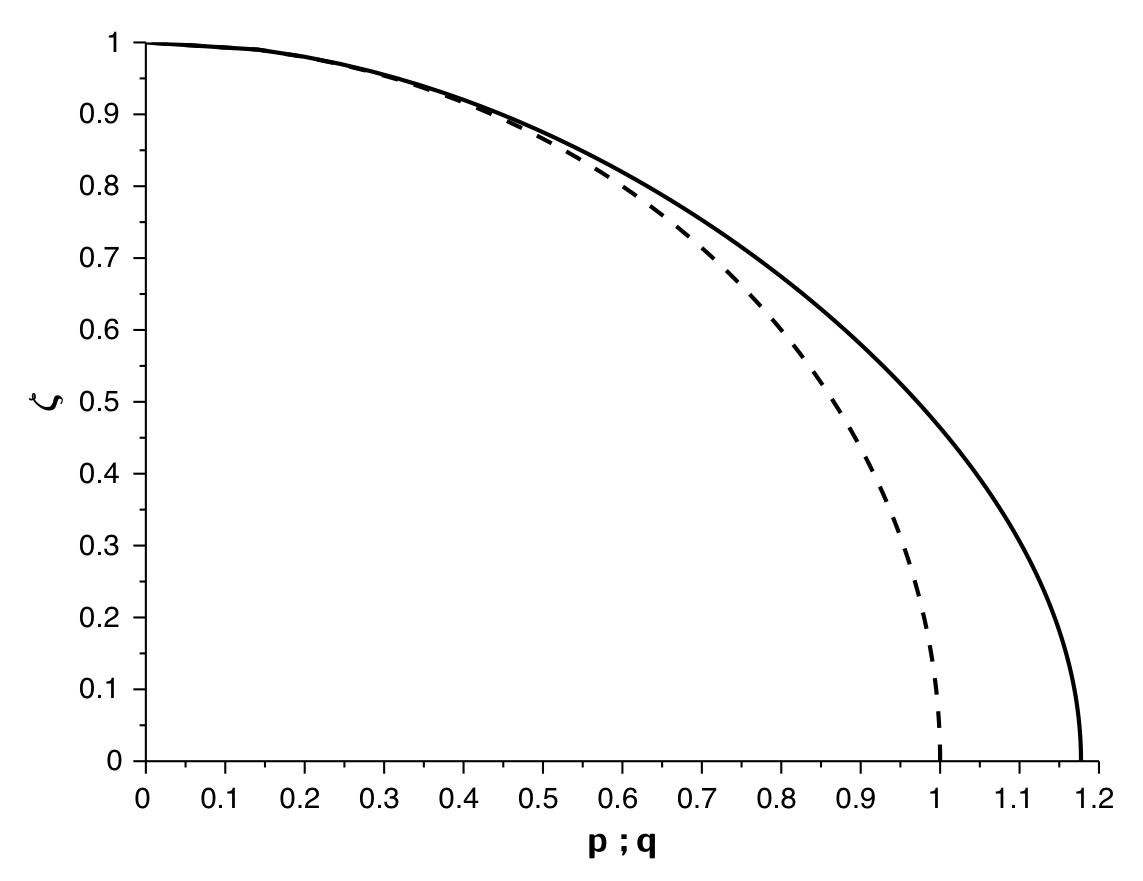◊ remarque : contrairement à ce que pourrait suggérer le cas $r=𝒷=R_H$ , on constate qu'au voisinage de l'équateur $p→∞$ (et non vers zéro) quand $r=𝒷→r_s$ ; ceci est lié au fait que $p$ n'est pas défini pour $R_H<𝒷≤r_s$ (de ce fait, sa signification pour $𝒷=R_H$ est forcément douteuse).

1.e.	• Pour une surface euclidienne possédant la symétrie axiale de révolution, l'équation est de la forme $r=R(θ)$ . La métrique est alors : ${d𝓁}^2={dR}^2+R^2 \: {dθ}^2+R^2 \: \sin^2(θ) \: {dφ}^2$ avec $\displaystyle dR=\frac{∂R}{∂θ} \: dθ$ : ${d𝓁}^2=\left[R^2+{R'}^2 \,\right] \: {dθ}^2+R^2 \; \sin^2(θ) \: {dφ}^2$ . • Pour que cela soit représentatif de la métrique de Kerr avec $r=Cste$ , il faudrait : $\displaystyle R^2=\frac{Δ}{A}=(𝒶^2-r_s \: 𝒷) \: \frac{𝒷^2+α^2 \: ζ^2}{𝒷^2+α^2 \: ζ^2-r_s \: 𝒷}$ ; $R^2+{R'}^2=ρ^2=𝒷^2+α^2 \: ζ^2$ . • La comparaison impose : $\displaystyle {R'}^2=α^2.(ζ^2-1) \: \frac{𝒷^2+α^2 \: ζ^2}{𝒷^2+α^2 \: ζ^2-r_s \: 𝒷}$ . Or ceci est impossible pour $R'$ réel avec $ζ^2≤1$ . Non seulement l'ellipsoïde n'est pas complètement représentatif, mais il n'existe pas de surface qui le soit.

• La métrique de Kerr simplifiée peut s'écrire sous la forme :

$\displaystyle -{ds}^2=\frac{ρ^2}{Δ} \: {dr}^2+\left(r^2+α^2+\frac{r_s \: α^2 \: r}{ρ^2} \: \sin^2(θ) \right) \; \sin^2(θ) \: {dφ}^2$ .

• La notion locale de distance est décrite par

{d𝓁}^2=ℊ_{ij} \: {dx}^i \: {dx}^j

avec

\displaystyle ℊ_{ij}=\frac{g_{0i} \: g_{0j}}{g_{00}} -g_{ij}

. On obtient ainsi :

\displaystyle ℊ_{33}=\frac{B^2}{A}+E=\frac{Δ}{A} \: \sin^2⁡(θ)

, mais cela ne change rien dans la suite puisqu'on se ramène au cas

φ=Cste

.
• La métrique simplifiée peut s'écrire :

\displaystyle {d𝓁}^2=\frac{r^2+α^2 \; \cos^2(θ)}{r^2-r_s \: r+α^2} \: {dr}^2

. Pour

θ=Cste

cela peut aussi s'écrire sous la forme :

\displaystyle {d𝓁}^2=\frac{r^2+λ}{(r-R_H)(r-r_H)} \: {dr}^2

en posant

λ=α^2 \: \cos^2(θ)

.
◊ remarque : on retrouve que

d𝓁≈dr

quand

r→∞

, mais aussi que

dr→0

quand

r→R_H

(comme pour la variable “classique” de Schwarzschild, la variable

r

semble présenter un minimum au niveau de l'horizon).
• Il est parfois indiqué (sans démonstration) que, “de la même façon” que pour

θ

, cela correspond à la métrique sur une hyperbole. Certes, pour une métrique plane, les droites

θ=Cste

sont les courbes orthogonales aux cercles

r=Cste

. Ceci suggère qu'on obtient ici des courbes orthogonales aux ellipses vues précédemment, donc des hyperboles. Une étude plus précise est toutefois utile.
• En géométrie euclidienne dans le plan

(Oxz)

on peut considérer une hyperbole centrée à l'origine, avec un demi-grand-axe noté

𝒶

selon

(Ox)

et un demi-petit-axe noté

𝒷

selon

(Oz)

. L'équation de l'hyperbole peut s'écrire :

\displaystyle \frac{x^2}{𝒶^2} -\frac{z^2}{𝒷^2} =1

. La métrique correspondante est alors :

{d𝓁}^2={dx}^2+{dz}^2

; on souhaite l'exprimer en fonction de

r

dr

seulement.
• D'après l'équation, on peut écrire :

\displaystyle \frac{x}{𝒶^2} \: dx-\frac{z}{𝒷^2} \: dz=0

. Mais par ailleurs :

r^2=x^2+z^2

, par suite :

r \:dr=x \:dx+z \:dz

. En combinant on obtient :

\displaystyle r \:dr=\frac{𝒶^2+𝒷^2}{𝒶^2} \: x \:dx=\frac{𝒶^2+𝒷^2}{𝒷^2} \: z \:dz

. Ainsi :

$\displaystyle {d𝓁}^2=\frac{r^2}{x^2} \: \left(\frac{𝒶^2}{𝒶^2+𝒷^2}\right)^2{dr}^2+\frac{r^2}{z^2} \: \left(\frac{𝒷^2}{𝒶^2+𝒷^2}\right)^2 {dr}^2$ .

• D'autre part :

\displaystyle r^2=x^2+z^2=x^2+𝒷^2 \: \frac{x^2-𝒶^2}{𝒶^2} =𝒶^2 \: \frac{z^2+𝒷^2}{𝒷^2} +z^2

. Ainsi :

$\displaystyle x^2=\frac{𝒶^2}{𝒶^2+𝒷^2} \: (r^2+𝒷^2 )$ ; $\displaystyle z^2=\frac{𝒷^2}{𝒶^2+𝒷^2} \: (r^2-𝒶^2 )$ ;
$\displaystyle {d𝓁}^2=\frac{r^2}{r^2+𝒷^2} \, \frac{𝒶^2}{𝒶^2+𝒷^2} \: {dr}^2+\frac{r^2}{r^2-𝒶^2} \, \frac{𝒷^2}{𝒶^2+𝒷^2} \: {dr}^2=\frac{r^2.(r^2-𝒶^2+𝒷^2 )}{(r^2+𝒷^2 )(r^2-𝒶^2 )} \: {dr}^2$ .

• S'il est vrai que cette expression ressemble un peu à celle issue de la métrique de Kerr (en choisissant au moins

𝒶=R_H

) on peut toutefois montrer qu'elle est n'est pas compatible (cela semble clair pour

r=0

, mais il n'est pas évident que la partie pour

r<R_H

soit pertinente).
• Pour préciser, on peut étudier numériquement un cas particulier, par exemple pour

θ=\frac{π}{4}

4 \,α^2=\frac{1}{2} r_s^{\:2}

(l'expression de

R_H

nécessite

4 \,α^2≤r_s^{\:2}

). Ceci donne :

$\cos^2(θ)=\frac{1}{2}$ ; $\displaystyle α=\frac{r_s}{2 \,\sqrt{2}}$ ; $\displaystyle 𝒶=R_H=\frac{r_s}{2} \, \frac{\sqrt{2}+1}{\sqrt{2}}$ ; $\displaystyle r_H=\frac{r_s}{2} \, \frac{\sqrt{2}-1}{\sqrt{2}}$ .

• Pour simplifier l'étude, on peut choisir

R_H

comme unité de longueur ; ceci donne :

$𝒶=R_H=1$ ; $r_s=\frac{2 \,\sqrt{2}}{\sqrt{2}+1}≈\text{1,172}$ ; $α=\frac{1}{\sqrt{2}+1}≈\text{0,4142}$ ;
$r_H=\frac{\sqrt{2}-1}{\sqrt{2}+1}≈\text{0,1716}$ ; $λ=\frac{\left(\sqrt{2}-1\right)^2}{2}≈\text{0,0858}$ .

• On peut traçer

\displaystyle \frac{{d𝓁}^2}{{dr}^2}

pour les deux cas en notant :

H=\frac{r^2+λ}{(r-R_H)(r-r_H)}

à comparer à

\displaystyle G_𝒷=\frac{r^2.(r^2-𝒶^2+𝒷^2 )}{(r^2+𝒷^2 )(r^2-𝒶^2 )}

pour diverses valeurs de

𝒷

.
• Quelques essais rapides montrent toutefois que

G_𝒷<H

dans tous les cas. La visualisation peut alors utiliser

\displaystyle \frac{r^2-𝒶^2+𝒷^2}{r^2+𝒷^2}<1

(limite pour

𝒷→∞

) ; il suffit ainsi de comparer à

\displaystyle G_∞=\frac{r^2}{r^2-𝒶^2}

.
• Le tracé montre (en tirets) que

G_∞<H

(en trait plein). Contrairement à ce qui est parfois trop vite affirmé, ces deux expressions ont vaguement la même allure mais sont incompatibles.

Distance radiale

• Pour

θ

fixé, la distance radiale

ϱ

peut être décrite par :

$\displaystyle dϱ=d𝓁=\frac{\sqrt{r^2+α^2 \: \cos^2(θ)}}{\sqrt{r^2-r_s \: r+α^2}} \: dr=\frac{\sqrt{r^2+λ}}{\sqrt{(r-R_H)(r-r_H)}} \: dr$ .

• Pour représenter les variations de

r

en fonction de

ϱ

, l'intégration numérique peut être faite avec par exemple

4 \,α^2=\frac{1}{2} r_s^{\:2}

(l'expression de

R_H

nécessite

4 \,α^2≤r_s^{\:2}

).
• Pour simplifier, on peut en outre choisir

R_H

comme unité de longueur ; ceci donne :

$R_H=1$ ; $r_s=\frac{2 \,\sqrt{2}}{\sqrt{2}+1}≈\text{1,172}$ ; $α=\frac{1}{\sqrt{2}+1}≈\text{0,4142}$ ;
$r_H=\frac{\sqrt{2}-1}{\sqrt{2}+1}≈\text{0,1716}$ ; $λ=\left(\sqrt{2}-1\right)^2 \, \cos^2(θ)≈\text{0,1716} \:\, \cos^2(θ)$ .

• Le calcul peut être fait pour quelques valeurs de

θ

; les valeurs extrêmes suffisent car la différence est faible : polaire (

θ=0

;

λ≈\text{0,1716}

; tirets) ; équatorial : (

θ=\frac{π}{2}

;

λ=0

• La situation est semblable à celle constatée avec la métrique de Schwarzschild : la variable radiale

r

semble présenter un minimum, ici pour

r=R_H

.
◊ remarque : l'intégration est faite ici en partant arbitrairement de

ϱ=0

pour

r=R_H

Ergosphère

• Pour représenter les variations de

r

en fonction de

θ

on peut choisir par exemple

4 \,α^2=\frac{1}{2} r_s^{\:2}

(l'expression de

R_H

nécessite

4 \,α^2≤r_s^{\:2}

).
• Pour simplifier, on peut en outre choisir

R_H

comme unité de longueur ; ceci donne :

$R_H=1$ ; $r_s=\frac{2 \,\sqrt{2}}{\sqrt{2}+1}≈\text{1,172}$ ; $α=\frac{1}{\sqrt{2}+1}≈\text{0,4142}$ .

• La représentation obtenue montre pour l'ergosphère (en vert) une allure elliptique.

• Pour l'ergosphère, on obtient

r=R_H

sur l'axe polaire et

r=r_s

dans le plan équatorial. Pour un ellipsoïde, ceci correspondrait à un demi-grand-axe

𝒶=r_s

et un demi-petit-axe

𝒷=R_H

.
• Pour l'ellipse, avec

z=r \; \cos(θ)

, l'équation

\displaystyle \frac{x^2}{𝒶^2} +\frac{z^2}{𝒷^2} =1

donne :

$\displaystyle r^2=x^2+z^2=r_s^{\:2}+r^2 \; \cos^2(θ) \: \frac{𝒷^2-𝒶^2}{𝒷^2}$ .

• On peut alors représenter l'ellipse avec

\displaystyle r=\frac{𝒶 \:𝒷}{\sqrt{𝒷^2+(𝒶^2-𝒷^2 ) \: \cos^2(θ)}}

. On constate (en tirets rouges) que l'ergosphère n'est pas exactement elliptique.

• Constatant que la forme est plutôt “au dessus” d'une ellipse, il est en outre possible de préciser en étudiant les extremums de

z(θ)=R_E (θ) \; \cos(θ)

. En posant

ζ=\cos(θ)

on obtient

\displaystyle \frac{dz}{dθ}=-\sin(θ) \: \frac{dz}{dζ}

. Cela donne en particulier un extrémum au pôle nord, mais pas forcément un maximum.
• Avec

\displaystyle \underline{α}=\frac{2 \,α}{r_s}

on peut écrire

\displaystyle z(ζ)=\frac{ζ \:r_s}{2} \: \left(1+\sqrt{1-\underline{α}^2 \: ζ^2} \right)

puis :

$\displaystyle \frac{dz}{dζ}=\frac{r_s}{2} \: \left(1+\sqrt{1-\underline{α}^2 \: ζ^2}-\frac{\underline{α}^2 \: ζ^2}{\sqrt{1-\underline{α}^2 \: ζ^2}}\right)=\frac{r_s}{2\; \sqrt{1-\underline{α}^2 \: ζ^2}} \: \left(\sqrt{1-\underline{α}^2 \: ζ^2}+1-2 \,\underline{α}^2 \:ζ^2 \right)$ .

• Les extrémums correspondent à :

$\sqrt{1-\underline{α}^2 \: ζ^2}=2 \,\underline{α}^2 \: ζ^2-1>0$ ;
$1-\underline{α}^2 \: ζ^2=\left(2 \,\underline{α}^2 \: ζ^2-1\right)^2$    avec    $\underline{α}^2 \: ζ^2>\frac{1}{2}$ ;
$\underline{α}^2 \: ζ^2.(4 \,\underline{α}^2 \: ζ^2-3)=0$    avec    $\underline{α}^2 \: ζ^2>\frac{1}{2}$ ;
$\underline{α}^2 \: ζ^2=\frac{3}{4}$ ;   $\displaystyle \cos(θ)=ζ=\frac{\sqrt{3}}{2 \,\underline{α}}$ .

• Dans l'exemple étudié précédemment :

\underline{α}=\frac{1}{\sqrt{2}}≈\text{0,71}

;

\displaystyle \frac{\sqrt{3}}{2 \,\underline{α}}≈\text{1,22}>1

; l'extrémum au pôle nord est le seul du graphique et c'est un maximum.
• Un autre extrémum peut exister, pour un angle

θ_0

, à condition que

\cos(θ_0 )≤1

. Ceci correspond à :

\underline{α}≥\frac{\sqrt{3}}{2}≈\text{0,866}

. Dans ce cas, l'extrémum au pôle nord est un minimum et celui pour

θ_0

est un maximum. En outre, puisque l'existence de

R_H

impose

\underline{α}<1

, l'angle est tel que :

\cos(θ_0 )>\frac{\sqrt{3}}{2}

;

θ_0<\frac{π}{6}≘30°

.
• On peut préciser en représentant, pour

R_H=1

fixé (pris comme unité), trois cas caractéristiques :

◊ la limite pour   $\underline{α}≈\text{0,866}$ (en vert) ;
◊ la limite pour   $\underline{α}≈1-{10}^{-6}$ (en rouge), respectant   $\underline{α}<1$ ;
◊ un cas intermédiaire pour   $\underline{α}≈\text{0,98}$ (en tirets bleus).

• On peut aussi juger préférable de choisir

r_s=1

(pris comme unité), associé à une masse fixée, puis d'adapter

R_H

pour trois valeurs de

\underline{α}

associées à des rotations différentes :

◊ la limite pour   $\underline{α}≈\text{0,866}$ ;   $R_H=\text{0,75}$ ;
◊ la limite pour   $\underline{α}≈1-{10}^{-6}$ ;   $R_H=\text{0,50071}$ ;
◊ un cas intermédiaire pour   $\underline{α}≈\text{0,98}$ ;   $R_H=\text{0,5995}$ .

• À cette occasion, on peut se demander si la variable radiale

r

de Boyer-Lindquist est la plus pertinente : pour

α≠0

elle ne correspond pas à

R_H=r_s

aux pôles, où la rotation pourrait sembler sans effet (bien qu'elle redonne

R_H=r_s

pour

α=0

).
• Or, il est possible de changer pour

\underline{r}=r+Cste

sans modifier la forme de la métrique, afin d'obtenir

\underline{R}_H=r_s

; il suffit pour ça d'imposer :

\displaystyle \underline{r}=r-R_H+r_s=r+\frac{r_s}{2} \: \left(1+\sqrt{1-\underline{α}^2} \right)

. Cela redonne un comportement qualitatif correspondant à la première des deux représentations, où

\underline{R}_H

est constant (pour une masse donnée) et où l'écart de l'ergosphère augmente vers l'extérieur (l'effet de la rotation s'ajoutant à celui de la gravitation).
• Dans ces conditions, ne serait-il pas préférable de choisir

\underline{r}

comme variable radiale ? En pratique non car cela complique la plupart des calculs. Il faut simplement garder en mémoire que (contrairement à la géométrie euclidienne) la variable

r

n'est pas ici la distance radiale, mais seulement un paramètre permettant de repérer la position radiale. Il faut dans chaque cas prendre garde à son interprétation.

Espace euclidien en rotation

• On peut dans ce cas utiliser la variable

θ'=θ-ω \:t

. Pour une vitesse

ω

constante, ceci correspond à :

dθ'=dθ-ω \:dt

. On obtient ainsi :

{dθ}^2={dθ'}^2+ω^2 \:{dt}^2+2 \,ω \:dt \:dθ'

; d'où la métrique :

$\displaystyle {ds}^2=\left(1-\frac{ω^2 \: r^2}{c^2} \right) \: c^2 \, {dt}^2-2 \,ω \:r^2 \: dt \:dθ'-{dr}^2-r^2 \: {dθ'}^2-{dz}^2$ .

◊ remarque : pour simplifier, on peut poser

\displaystyle λ=\frac{ω \:r}{c}

2.	• Le coefficient temporel $g_{00}=1-λ^2$ est négatif pour : $\displaystyle r>r_L=\frac{c}{ω}$ .

• Un photon émis tangentiellement selon

θ

se propage en vérifiant la relation :

${ds}^2=0=(1-λ^2 ) \: c^2 \,{dt}^2-2 \,λ \:r \:c \,dt \:dθ'-r^2 \: {dθ'}^2$ .

• Pour un observateur situé à l'origine, la durée est mesurée par

dt

. Cela correspond pour le photon à une rotation décrite par :

\displaystyle \frac{dθ'}{dt}=-ω±\frac{c}{r}=(±1-λ) \: \frac{c}{r}

, où le signe

±

décrit le sens d'émission.
• On constate une dissymétrie : les photons semblent ne pas se propager à la même vitesse dans les deux sens.
• La distance parcourue correspond à :

{d𝓁}^2=ℊ_{ij} \: {dx}^i \: {dx}^j

avec un tenseur métrique tridimensionnel

\displaystyle ℊ_{ij}=\frac{g_{0i} \: g_{0j}}{g_{00}} -g_{ij}

(cette métrique spatiale est l'inverse de la partie spatiale

ℊ^{ij}=g^{ij}

). Ainsi :

$\displaystyle {d𝓁}^2=ℊ_{22} \: {dθ'}^2=\frac{1}{1-λ^2} \: r^2 \: {dθ'}^2$ .

• La durée locale (en un point) étant telle que :

c^2 \, {dt}_{𝓁oc}^{\:2}=(1-λ^2) \:c^2 \, {dt}^2

, on obtient apparemment :

$\displaystyle c'=\frac{\widebar{d𝓁}}{{dt}_{𝓁oc}} =±c \: \frac{1}{1±λ}$ .

• Mais avec une telle métrique (non diagonale), il est impossible de synchroniser les horloges dans l'ensemble de l'espace (seulement le long d'une ligne, ou dans un voisinage infinitésimal d'un point donné). Dans la mesure où on a conservé la variable

t

décrivant le temps dans la métrique initiale (sans rotation), les horloges suivant le repérage en rotation sont décalées de :

\displaystyle c \,{dt}_d=-\frac{g_{0i}}{g_{00}} \: {dx}^i

.
• La durée nécessaire pour parcourir

d𝓁

entre deux points voisins (décalés de

dθ'

) est donc (en retranchant le décalage des horloges pour le compenser) :

$\displaystyle c \,{dt}_{𝓁oc}=\sqrt{1-λ^2} \; \left[c \,dt+\frac{g_{02}}{g_{00}} \: dθ'\right]=\sqrt{1-λ^2} \; \left[c \,dt-\frac{λ}{1-λ^2} \:r \:dθ'\right]$ ;
$\displaystyle c \,{dt}_{𝓁oc}=\frac{1-λ^2}{\sqrt{1-λ^2}} \: c \,dt-\frac{±λ-λ^2}{\sqrt{1-λ^2}} \: c \,dt=\frac{1∓λ}{\sqrt{1-λ^2}} \: c \,dt$ .

◊ remarque : à cause de la périodicité de

θ'

, une telle correction locale ne peut évidemment pas être généralisée à tout l'espace en redéfinissant la variable temporelle (et de toute façon elle serait nettement moins simple si on ne raisonnait pas pour

r

fixé).
• On retrouve ainsi que le photon se propage à la vitesse de la lumière :

\displaystyle \frac{\widebar{d𝓁}}{{dt}_{𝓁oc}} =\frac{r}{1∓λ} \, \frac{dθ'}{dt}=±c

• Pour

r=r_L

(donc

λ=1

) on constate que, depuis l'origine, le mouvement des photons dans le sens direct semble nul :

\displaystyle \frac{dθ'}{dt}=c \:\frac{1-λ}{r}=0

. Ceci caractérise le fait que le repérage spatial est en mouvement. C'est une “limite de stationnarité” pour les particules matérielles, puisque leur immobilité par rapport au repérage imposerait qu'elles se déplacent à la vitesse de la lumière.
• Pour

r>r_L

(donc

λ>1

) la difficulté est que

g_{00}<0

; la variable

t

n'est plus du genre temps. Sans l'interdire complètement, cela complique nettement la description des particules pouvant exister dans cette région (pourvu que leur mouvement soit compatible avec l'intervalle obtenu pour les deux sens des photons précédents).
◊ remarque : en particulier, dans cette région, on ne peut pas définir de temps local (qui serait associé à un point matériel immobile).

• Puisqu'il apparait que le repérage est en mouvement, on peut changer de repérage pour supprimer (ou au moins diminuer) la difficulté précédente. Soit par exemple un repérage en rotation à la vitesse

-ω'

par rapport au précédent, avec

ω'<ω

. En notant

ω''=ω-ω'

\displaystyle λ''=\frac{ω'' \:r}{c}<λ

, on obtient dans ce référentiel une métrique :

{ds}^2=(1-{λ''}^2 ) \: c^2 \, {dt}^2-2 \,λ'' \:r \:c \,dt \:dθ''-{dr}^2-r^2 \: {dθ''}^2-{dz}^2

. Cela agrandit la zone “utile” puisque

λ''<1

à la limite où

λ=1

.
• La “limite d'immobilité” est donc d'une certaine façon un “horizon cinétique” :

◊ il s'agit d'une limite cinétique (sur le mouvement) ;
◊ des particules peuvent exister au delà, mais on les “voit” mal (description “indirecte”) ;
◊ lorsqu'on se rapproche (cinétiquement) de la condition fixant l'horizon, celui-ci “recule”.

• La situation est un peu analogue pour la métrique “classique” de Schwarzschild, car la limite

g_{00}=0

pour

r=r_s

impose aux particules de ne pouvoir l'atteindre qu'à la vitesse de la lumière. Mais ce cas est par ailleurs nettement différent. Indépendamment du fait que le cas observé ici est directement lié à l'existence d'un terme non diagonal

g_{02}≠0

, qui n'a pas d'équivalent dans la métrique de Schwarzschild, l'horizon de ce dernier ne “recule” pas si on l'observe dans un référentiel en mouvement radial centripète.

Espace euclidien en expansion

• On peut dans ce cas utiliser la variable

\displaystyle r'=\frac{r}{ω \:t}

. Pour une coefficient

ω

constant, ceci correspond à :

dr=ω \:t \:dr'+ω \:r' \:dt

. On obtient ainsi :

{dr}^2=ω^2 \: t^2 \: {dr'}^2+ω^2 \: {r'}^2 \: {dt}^2+2 \,ω^2 \: t \:r' \:dt \:dr'

; d'où la métrique :

\displaystyle {ds}^2=\left(1-\frac{ω^2 \: {r'}^2}{c^2} \right) \; c^2 \, {dt}^2-2 \,ω^2 \: t \:r' \:dt \:dr'-ω^2 \: t^2 \: {dr'}^2-ω^2 \: t^2 \: {r'}^2 \: {dΩ}^2

.
◊ remarque :

{dΩ}^2={dθ}^2+\sin^2(θ) \;{dφ}^2

; pour simplifier, on peut poser :

\displaystyle λ=\frac{ω \:r'}{c}

2.	• Le coefficient temporel $g_{00}=1-λ^2$ est négatif pour : $\displaystyle r'>r_L=\frac{c}{ω}$ .

• Un photon émis radialement se propage en vérifiant la relation :

${ds}^2=0=(1-λ^2 ) \: c^2 \, {dt}^2-2 \,λ \:ω \:t \:c \,dt \:dr'-ω^2 \: t^2 \: {dr'}^2$ .

• Pour un observateur situé à l'origine, la durée est mesurée par

dt

. Cela correspond pour le photon à un mouvement décrit par :

\displaystyle \frac{dr'}{dt}=(±1-λ) \: \frac{c}{ω \:t}

, où le signe

±

décrit le sens d'émission.
• On constate une dissymétrie : les photons semblent ne pas se propager à la même vitesse dans les deux sens.
• La distance parcourue correspond à :

{d𝓁}^2=ℊ_{ij} \: {dx}^i \: {dx}^j

avec un tenseur métrique tridimensionnel

\displaystyle ℊ_{ij}=\frac{g_{0i} \: g_{0j}}{g_{00}} -g_{ij}

(cette métrique spatiale est l'inverse de la partie spatiale

ℊ^{ij}=g^{ij}

). Ainsi :

$\displaystyle {d𝓁}^2=ℊ_{11} \: {dr'}^2=\frac{1}{1-λ^2} \: ω^2 \: t^2 \: {dr'}^2$ .

◊ remarque : puisque la métrique dépend du temps, il faut interpréter avec beaucoup de précaution les longueurs calculées en intégrant cet élément de longueur.
• La durée locale (en un point) étant telle que :

c^2 \, {dt}_{𝓁oc}^{\:2}=(1-λ^2) \:c^2 \, {dt}^2

, on obtient apparemment :

$\displaystyle c'=\frac{\widebar{d𝓁}}{{dt}_{𝓁oc}} =±c \: \frac{1}{1±λ}$ .

t

décrivant le temps dans la métrique initiale (sans expansion), les horloges suivant le repérage en rotation sont décalées de :

\displaystyle c \,{dt}_d=-\frac{g_{0i}}{g_{00}} \: {dx}^i

.
• La durée nécessaire pour parcourir

d𝓁

entre deux points voisins (décalés de

dr'

) est donc (en retranchant le décalage des horloges pour le compenser) :

$\displaystyle c \,{dt}_{𝓁oc}=\sqrt{1-λ^2} \; \left[c \,dt+\frac{g_{01}}{g_{00}} \: {dr'}\right]=\sqrt{1-λ^2} \; \left[c \,dt-\frac{λ}{1-λ^2} \: ω \:t \:dr'\right]$ ;
$\displaystyle c \,{dt}_{𝓁oc}=\frac{1-λ^2}{\sqrt{1-λ^2}} \: c \,dt-\frac{±λ-λ^2}{\sqrt{1-λ^2}} \: c\, dt=\frac{1∓λ}{\sqrt{1-λ^2}} \: c \,dt$ .

• On retrouve ainsi que le photon se propage à la vitesse de la lumière :

\displaystyle \frac{\widebar{d𝓁}}{{dt}_{𝓁oc}} =\frac{ω \:t}{1∓λ} \, \frac{dr'}{dt}=±c

.

◊ remarque : l'intégration du terme de décalage

\displaystyle -\frac{λ}{1-λ^2} \: ω \:t \:dr'

dépend du chemin suivi ; on peut donc resynchroniser le long d'une ligne (par exemple la trajectoire d'un point), ou dans tout un voisinage infinitésimal d'un point donné, mais non dans tout l'espace ; on peut par contre utiliser la forme :

$\displaystyle {ds}^2=(1-λ^2 ) \: \left[c \,dt-\frac{λ}{1-λ^2} \: ω \:t \:dr'\right]^2-\frac{ω^2 \: t^2}{1-λ^2} \: {dr'}^2-ω^2 \: t^2 \: {r'}^2 \: {dΩ}^2$ .

• Pour

r'=r_L

(donc

λ=1

) on constate que, depuis l'origine, le mouvement des photons dans le sens direct semble nul :

\displaystyle \frac{dr'}{dt}=c \: \frac{1-λ}{ω \:t}=0

r'>r_L

(donc

λ>1

) la difficulté est que

g_{00}<0

; la variable

t

\displaystyle \frac{dr'}{dt}=-v

constante par rapport au précédent :

r''=r'+v \:t

;

dr'=dr''-v \:dt

.
• On obtient dans ce référentiel :

${ds}^2=(1-λ^2 ) \: c^2 \, {dt}^2-2 \,ω^2 \: t \:r' \:dt .(dr''-v \:dt)-ω^2 \: t^2.(dr''-v \:dt)^2-ω^2 \: t^2 \: {r'}^2 \: {dΩ}^2$ ;
$\displaystyle {ds}^2=\left[(1-λ^2 )+2 \,\frac{ω^2}{c^2} \: v \:t .(r'-\frac{1}{2} v \:t)\right] \: c^2 \, {dt}^2 \; ⋯$

$⋯ \;-2 \,ω^2 \: t .(r'-v \:t) \: dt \:dr''-ω^2 \: t^2.{dr''}^2-ω^2 \: t^2 \: {r'}^2 \: {dΩ}^2$ ;

◊ remarque : afin de comparer simplement, les coefficients sont ici exprimés en fonction de

r'

.
• Pour

λ=1

on obtient :

\displaystyle g_{00}=2 \, \frac{ω^2}{c^2} \: v \:t .(r'-\frac{1}{2} v \:t)>0

tant que

\displaystyle t<\frac{2 \,r_L}{v}

, c'est à dire que la limite est “reculée” au moins pendant une certaine durée (ensuite l'expansion “rattrape” le référentiel utilisé).

• La “limite d'immobilité” est donc d'une certaine façon un “horizon cinétique” :

◊ il s'agit d'une limite cinétique (sur le mouvement) ;
◊ des particules peuvent exister au delà, mais on les “voit” mal (description “indirecte”) ;
◊ lorsqu'on se rapproche (cinétiquement) de la condition fixant l'horizon, celui-ci “recule”.

• La situation semble un peu analogue pour la métrique “classique” de Schwarzschild, car la limite

g_{00}=0

pour

r=r_s

impose aux particules de ne pouvoir l'atteindre qu'à la vitesse de la lumière. Mais ce cas est en fait différent (indépendamment du fait que le cas observé ici est directement lié à l'existence d'un terme non diagonal

g_{01}≠0

, qui n'a pas d'équivalent dans la métrique de Schwarzschild).
• En notant

\displaystyle κ=\frac{r_s}{r}

la métrique s'écrit :

\displaystyle {ds}^2=(1-κ) \: c^2 \, {dt}^2-\frac{1}{1-κ} \: {dr}^2-r^2 \: {dΩ}^2

. L'horizon pour

κ=1

ne pouvant être franchi par les particules matérielles qu'à la vitesse de la lumière, on peut changer de repérage pour voir si cela modifie cette propriété.
• Soit par exemple un repérage en effondrement décrit par la “vitesse” radiale

\displaystyle \frac{dr}{dt}=-v

constante par rapport au précédent :

r'=r+v \:t

;

dr=dr'-v \:dt

. Avec

\displaystyle β=\frac{v}{c}

on obtient dans ce référentiel :

$\displaystyle {ds}^2=(1-κ) \: c^2 \, {dt}^2-\frac{1}{1-κ} \: (dr'-v \:dt)^2-r^2 \: {dΩ}^2$ ;
$\displaystyle {ds}^2=\frac{1}{1-κ} \: \left[(1-κ)^2-β^2 \right] \: c^2 \, {dt}^2+\frac{2 \,v}{1-κ} \: dt \:dr'-\frac{1}{1-κ} \: {dr'}^2-r^2 \: {dΩ}^2$ .

◊ remarque : afin de comparer simplement, les coefficients sont ici exprimés en fonction de

r

.
• On obtient ainsi :

\displaystyle g_{00}=\frac{1}{1-κ} \: (1-κ+β)(1-κ-β)=0

en premier pour :

\displaystyle r=\frac{r_s}{1-β}>r_s

, c'est à dire que non seulement la limite n'est pas “reculée”, mais qu'elle est au contraire avancée. La “singularité” de Schwarzschild n'est pas un simple “horizon cinétique”.
◊ remarque : on peut éliminer le terme non diagonal en utilisant

\displaystyle c \,t'=c \,t+\frac{β}{(1-κ)^2-β^2} \: dr'

; cela ne modifie pas

g_{00}

Espace euclidien en expansion

• On peut dans ce cas utiliser la variable

\displaystyle r'=\frac{r}{ω \:t}

. Pour une coefficient

ω

constant, ceci correspond à :

dr=ω \:t \:dr'+ω \:r' \:dt

. On obtient ainsi :

{dr}^2=ω^2 \: t^2 \: {dr'}^2+ω^2 \: {r'}^2 \: {dt}^2+2 \,ω^2 \: t \:r' \:dt \:dr'

, d'où la métrique :

\displaystyle {ds}^2=\left(1-\frac{ω^2 \: {r'}^2}{c^2} \right) \; c^2 \, {dt}^2-2 \,ω^2 \: t \:r' \:dt \:dr'-ω^2 \: t^2 \: {dr'}^2-ω^2 \: t^2 \: {r'}^2 \: {dΩ}^2

2.	• En notant $\displaystyle λ=\frac{ω \:r'}{c}$ , le coefficient temporel $g_{00}=1-λ^2$ est négatif pour : $\displaystyle r'>r_L=\frac{c}{ω}$ .

3.a.	• On obtient alors, en se limitant à une étude radiale : $g_{00}=1-λ^2$ ; $g_{01}=-λ \:ω \:t$ ; $g_{11}=-ω^2 \: t^2$ ; $g^{00}=1$ ; $\displaystyle g^{01}=-\frac{λ}{ω \:t}$ ; $\displaystyle g^{11}=-\frac{1-λ^2}{ω^2 \: t^2}$ ; $\displaystyle Γ_{001}=-\frac{ω^2 \: r'}{c^2}$ ; $\displaystyle Γ_{101}=-\frac{ω^2 \: t}{c}$ ; $\displaystyle Γ_{\phantom{.}01}^0=\frac{1}{c \:t}$ . • Les équations du mouvement radial peuvent s'écrire : $\displaystyle \frac{d^2 t}{{dτ}^2} =0$ ; $\displaystyle \frac{d^2 r'}{{dτ}^2} +\frac{2}{t} \, \frac{dt}{dτ}\, \frac{dr'}{dτ}=0$ . • La première donne : $\displaystyle \frac{dt}{dτ}=Cste$ , donc on peut simplifier la seconde : $\displaystyle \frac{d^2 r'}{{dt}^2} +\frac{2}{t} \, \frac{dr'}{dt}=0$ . ◊ remarque : puisque $t$ correspond au temps dans $ℛ$ , où une particule libre se déplace à vitesse constante, alors on obtient logiquement $dτ∝dt$ ; or $dτ$ est invariant lors du passage de $ℛ$ à $ℛ'$ . • En notant $\displaystyle R=\frac{dr'}{dt}$ , ceci donne : $t^2 \: R=υ=Cste$ . • Une seconde intégration donne : $\displaystyle r'=-\frac{υ}{t}+Cste=-\frac{υ}{t}+\left(r'_0+\frac{υ}{t_0}\right)$ . • On peut obtenir ce résultat à partir de la métrique : $\displaystyle \left(\frac{dτ}{dt}\right)^2=(1-λ^2 )-2 \, \frac{ω^2 \: r' \:t}{c^2} \, R-\frac{ω^2 \: t^2}{c^2} \, R^2=1-\frac{ω^2}{c^2} \: ({r'}^2+2 \,r' \:t \:R+t^2 \: R^2 )=1-\frac{ω^2}{c^2} \, (r'+t \:R)^2$ . • Avec $\displaystyle \frac{dt}{dτ}=Cste$ on en déduit : $\displaystyle r'+t \:R=υ'=Cste=\frac{d(t \:r')}{dt}$ . • Ceci donne : $t \:r'=υ' \:t+Cste=υ' \:t-υ$ ; $\displaystyle r'=υ'-\frac{υ}{t}=-\frac{υ}{t}+\left(r'_0+\frac{υ}{t_0} \right)$ .

3.b.	• La distance parcourue correspond à : ${d𝓁}^2=ℊ_{ij} \: {dx}^i \: {dx}^j$ avec un tenseur métrique tridimensionnel $\displaystyle ℊ_{ij}=\frac{g_{0i} \: g_{0j}}{g_{00}} -g_{ij}$ (cette métrique spatiale est l'inverse de la partie spatiale $ℊ^{ij}=g^{ij}$ ). Ainsi : $\displaystyle {d𝓁}^2=ℊ_{11} \: {dr'}^2=\frac{ω^2 \: t^2}{1-λ^2} \: {dr'}^2$ . ◊ remarque : puisque la métrique dépend du temps, il faut interpréter avec beaucoup de précaution les longueurs calculées en intégrant cet élément de longueur. • La durée locale (en un point) étant telle que : $c^2 \, {dt}_{𝓁oc}^{\:2}=(1-λ^2) \:c^2 \, {dt}^2$ . Mais avec cette métrique non diagonale les horloges suivant le repérage en expansion sont décalées de : $\displaystyle c \,{dt}_d=-\frac{g_{0i}}{g_{00}} \: {dx}^i$ . • La durée nécessaire pour parcourir $d𝓁$ entre deux points voisins (décalés de $dr'$ ) est donc (en retranchant le décalage des horloges pour le compenser) : $\displaystyle c \,{dt}_{𝓁oc}=\sqrt{1-λ^2} \; \left[c \,dt+\frac{g_{01}}{g_{00}} \: {dr'}\right]=\sqrt{1-λ^2} \; \left[c \,dt-\frac{λ}{1-λ^2} \: ω \:t \:dr'\right]$ . • La vitesse dans $ℛ'$ est : $\displaystyle v'=\frac{d𝓁}{{dt}_{𝓁oc}}$ ; $\displaystyle \frac{1}{v'}=\frac{{dt}_{𝓁oc}}{d𝓁}=\frac{1-λ^2}{ω \:t} \: \left[\frac{1}{R}-\frac{λ}{1-λ^2} \: \frac{ω \:t}{c}\right]=\frac{1-λ^2}{ω} \: \frac{t}{υ}-\frac{λ}{c}$ . • On voit que $υ$ est déterminé par les conditions initiales $r'_0$ et $v'_0$ à l'instant $t_0$ (mais de façon compliquée) : $\displaystyle \frac{1}{v'_0}=\frac{1-λ_0^{\:2}}{ω} \: \frac{t_0}{υ}-\frac{λ_0}{c}$ .

3.c.	• La vitesse dans $ℛ$ est : $\displaystyle v=\frac{dr}{dt}=v_0=Cste$ . • Avec $\displaystyle r'=\frac{r}{ω \:t}$ la transformation n'est définie que pour $t>0$ . On peut par exemple choisir de noter : $r'_0=r'(t_0)=r(t_0)=r_0$ pour $t=t_0$ ; ceci correspond à $\displaystyle ω=\frac{1}{t_0}$ . • On est alors amené à considérer : $r=r_0+v .(t-t_0)$ . • Ceci correspond à : $\displaystyle r'=\frac{r_0-v \:t_0}{ω t}+\frac{v}{ω}$ ; ainsi : $\displaystyle υ=\frac{v \:t_0-r_0}{ω}$ et $\displaystyle r'_0+\frac{υ}{t_0} =r'_0+v \:t_0-r_0 =\frac{v}{ω}$ . • On obtient : $\displaystyle λ_0=\frac{ω \:r'_0}{c}$ puis $\displaystyle v'_0=\frac{v-ω \:r_0}{1-\frac{ω \:r_0 \: v}{c^2}}$ ; ceci correspond à ce qu'on attend de la composition relativiste pour une vitesse d'entrainement initiale $v'_e=-ω \:r_0$ (pour $ℛ$ par rapport à $ℛ'$ ).

3.d.	• On peut considérer $\displaystyle v=v_e⊕v'=\frac{v'+v_e}{1+\frac{v' \:v_e}{c^2}}$ , où $v_e$ (vitesse d'entraînement) est la vitesse dans $ℛ$ d'un point fixe “coïncident” de $ℛ'$ . • Avec $r=ω \:t \:r'$ où $r'=Cste$ , on obtient $v_e=ω \:r'$ . • On peut alors inverser la relation précédente : $\displaystyle v'=\frac{v-v_e}{1-\frac{v \:v_e}{c^2}}$ ; ceci donne la composition inverse avec une vitesse d'entraînement (logique) : $v'_e=-v_e=-ω \:r'$ . ◊ remarque : le fait de passer par un calcul dans $ℛ$ a l'intérêt d'éviter un raisonnement dans un repérage accéléré. • Ceci confirme la cohérence du calcul précédent de $v'_0$ mais donne par ailleurs une autre expression générale de $v'$ ; l'équivalence entre les deux est loin d'être évidente.

3.e.	• On peut considérer $\displaystyle v'=v'_e⊕v=\frac{v+v'_e}{1+\frac{v \:v'_e}{c^2}}$ où $v'_e$ (vitesse d'entraînement) est la vitesse dans $ℛ'$ d'un point fixe “coïncident” de $ℛ$ . Ce raisonnement n'est toutefois pas évident, dans la mesure où il n'est pas démontré qu'on peut l'appliquer dans un repérage en expansion. • Avec $\displaystyle r'=\frac{r}{ω \:t}$ où $r=Cste$ , on obtient $\displaystyle dr'=-\frac{r}{ω \:t^2} \: dt$ , mais ici la vitesse ne s'en déduit pas aussi simplement. • La distance parcourue correspondante est : $\displaystyle d𝓁=\frac{ω \:t}{\sqrt{1-λ^2}} \: dr'=-\frac{r}{\sqrt{1-λ^2}} \, \frac{dt}{t}$ . • La durée de ce parcours est : $\displaystyle {dt}_{𝓁oc}=\sqrt{1-λ^2} \; \left[dt-\frac{λ}{1-λ^2} \, \frac{ω \:t}{c} \: dr'\right]=\frac{dt}{\sqrt{1-λ^2}}$ . • La vitesse d'entraînement est ainsi : $\displaystyle v'_e=\frac{d𝓁}{{dt}_{𝓁oc}} =-\frac{r}{t}=-ω \:r'$ . • Ceci redonne effectivement le même résultat que celui obtenu en raisonnant dans $ℛ$ , tendant ainsi à suggérer que la méthode se généralise aux repérages accélérés.

3.f.	• La relation $\displaystyle r'=-\frac{υ}{t}+\left(r'_0+\frac{υ}{t_0}\right )$ avec $\displaystyle υ=\frac{v \:t_0-r_0}{ω}$ indique que $r'$ est croissant si et seulement si $υ>0$ donc $\displaystyle v>\frac{r_0}{t_0} =ω \:r_0$ , c'est-à-dire $v'_0>0$ . Dans ce cas la valeur limite théoriquement atteinte est : $r'_{max}=v \:t_0$ , correspondant à : $\displaystyle λ_{max}=\frac{v}{c}≤1$ . Si le référentiel $ℛ$ existe (associé à des objets matériels), alors toute particule libre ne peut atteindre la limite qu'asymptotiquement. En outre il en est de même pour une particule accélérée, puisque dans $ℛ$ cette dernière ne peut atteindre la vitesse de la lumière qu'asymptotiquement. ◊ remarque : puisque $\displaystyle \frac{dt}{dτ}=Cste$ pour une particule libre, elle ne peut de même atteindre la limite qu'après une durée propre infinie. • Inversement, $\displaystyle v'_0=c^2 \: \frac{v-ξ}{c^2-v \:ξ}$ est une expression décroissante de $ξ=ω \:r'_0=ω \:r_0$ . Sa dérivée est $\displaystyle \frac{dv'_0}{dξ}=\frac{c^2}{(c^2-v \:ξ)^2} \: (v^2-c^2 )<0$ quelle que soit $v<c$ dans $ℛ$ (supposé référentiel). Par conséquent pour $\displaystyle r'_0>r_L=\frac{c}{ω}$ on obtient : $v'_0<-c$ ; donc toute particule doit s'y déplacer vers l'origine à une vitesse supérieure à $c$ par rapport à $ℛ'$ ; de ce fait il ne peut pas y avoir de référentiel $ℛ'$ associé au repérage dans cette zone (l'espace se déplace par rapport à ce repérage). ◊ remarque : inversement, si on supposait que $ℛ'$ y est un référentiel, alors $ℛ$ ne le serait pas. • Ceci est cohérent avec le fait que $r'>r_L$ correspond à $r>c \,t$ . Par rapport à $ℛ$ , si une particule est en deçà de la limite, elle ne peut l'atteindre sans dépasser la vitesse de la lumière (et elle ne “l'approche” asymptotiquement que pour $t→∞$ ).

• Pour mettre en évidence le décalage des horloges, on peut utiliser la métrique sous la forme :

$\displaystyle {ds}^2=(1-λ^2 ) \: \left[c \,dt-\frac{λ}{1-λ^2} \: ω \:t \:dr'\right]^2-\frac{ω^2 \: t^2}{1-λ^2} \: {dr'}^2-ω^2 \: t^2 \: {r'}^2 \: {dΩ}^2$ .

• Avec

ω \:dr'=c \:dλ

on peut écrire :

\displaystyle \sqrt{1-λ^2} \: c \,dt-\frac{λ}{\sqrt{1-λ^2}} \: c \,t \:dλ=c \,dt'

où

t'=t \:\sqrt{1-λ^2}

.
• Ceci semble pouvoir simplifier la métrique :

\displaystyle {ds}^2=c^2 \, {dt'}^2-\frac{ω^2 \: {t'}^2}{\left(1-λ^2 \right)^2} \: {dr'}^2-\frac{ω^2 \: {t'}^2}{1-λ^2} \: {r'}^2 \: {dΩ}^2

.
• Il est intéressant de constater que l'annulation de

g_{00}

pour

r'=r_L

a disparu (la divergence de la partie spatiale est par contre toujours présente). Les propriétés caractéristiques du mouvement ne peuvent toutefois pas avoir changé.

5.a.	• Avec la variable $t'$ et la métrique radiale : $\displaystyle {ds}^2=c^2 \, {dt'}^2-\frac{ω^2 \: {t'}^2}{\left(1-λ^2 \right)^2} \: {dr'}^2$ , on obtient : $g_{00}=1$ ; $\displaystyle g_{11}=-\frac{ω^2 \: {t'}^2}{\left(1-λ^2 \right)^2}$ ; $g^{00}=1$ ; $\displaystyle g^{11}=-\frac{\left(1-λ^2 \right)^2}{ω^2 \: {t'}^2}$ ; $\displaystyle Γ_{011}=-Γ_{101}=\frac{ω^2 \: t'}{c.\left(1-λ^2 \right)^2}$ ; $\displaystyle Γ_{111}=-2 \,λ \: \frac{ω^3 \: {t'}^2}{c.\left(1-λ^2 \right)^3}$ ; $\displaystyle Γ_{\phantom{.}11}^0=\frac{ω^2 \: t'}{c.\left(1-λ^2 \right)^2}$ ; $\displaystyle Γ_{\phantom{.}01}^1=\frac{1}{c \,t'}$ ; $\displaystyle Γ_{\phantom{.}11}^1=2 \,λ \: \frac{ω}{c.\left(1-λ^2 \right)}$ . • Les équations du mouvement radial peuvent s'écrire : $\displaystyle \frac{d^2 t'}{{dτ}^2} +\frac{ω^2 \: t'}{c^2.\left(1-λ^2 \right)^2} \: \left(\frac{dr'}{dτ}\right)^2=0$ ; $\displaystyle \frac{d^2 r'}{{dτ}^2} +\frac{2}{t'} \: \frac{dt'}{dτ} \, \frac{dr'}{dτ}+2 \,λ \: \frac{ω}{c.\left(1-λ^2 \right)} \: \left(\frac{dr'}{dτ}\right)^2=0$ . • La caractéristique principale est que, si la métrique peut sembler de forme plus simple, les équations qui s'en déduisent le sont nettement moins.

5.b.	• On peut obtenir une autre équation non indépendante à partir de la métrique : $\displaystyle 1=\left(\frac{dt'}{dτ}\right)^2-\frac{ω^2 \: {t'}^2}{c^2.\left(1-λ^2 \right)^2} \, \left(\frac{dr'}{dτ}\right)^2$ . • Avec $\displaystyle λ=\frac{ω \:r'}{c}$ et en notant $\dot{⬚}$ les dérivées par rapport à $τ$ , on peut écrire : $\displaystyle 1=\dot{t'}^2- \frac{{t'}^2}{\left(1-λ^2 \right)^2} \: \dot{λ}^2$ . Les équations du mouvement peuvent être déduites du lagrangien quadratique : $\displaystyle ℒ=\frac{1}{2} \,\left(\dot{t'}^2-\frac{{t'}^2}{\left(1-λ^2 \right)^2} \: \dot{λ}^2 \right)$ . On obtient ainsi : $\displaystyle \ddot{t'}+\frac{t'}{\left(1-λ^2 \right)^2} \: \dot{λ}^2=0$ ; $\displaystyle \ddot{λ}+\frac{2}{t'} \:\dot{t'} \: \dot{λ}+\frac{2 \,λ}{1-λ^2} \: \dot{λ}^2=0$ .

5.c.	• Avec $\displaystyle t=\frac{t'}{\sqrt{1-λ^2}}$ la relation déduite de l'expression $r'(t)$ obtenue d'après $r(t)$ dans $ℛ$ peut s'écrire : $\displaystyle λ=\frac{ω \:r'}{c}=\frac{r_0-v \:t_0}{c \,t'} \: \sqrt{1-λ^2}+\frac{v}{c}$ . • Il est clair que les expressions qui s'en déduisent pour $λ(t')$ puis $r'(t')$ sont difficilement utilisables. • On y retrouve toutefois que $λ$ croissant implique $r_0-v \:t_0<0$ . Le maximum $λ=1$ peut être atteint seulement pour $v=c$ ; on obtient alors : $\displaystyle \frac{r_0-v \:t_0}{c \,t'}=-\sqrt{\frac{1-λ}{1+λ}}$ montrant que cela implique $t'→∞$ .

5.d.	• La métrique peut s'écrire : $\displaystyle {ds}^2=c^2 \, {dt'}^2-c^2 \, {t'}^2.\left[\frac{1}{\left(1-λ^2 \right)^2} \: {dλ}^2+\frac{λ^2}{1-λ^2} \: {dΩ}^2 \right]$ . • Le changement de variable $λ'=\mathrm{artanh}(λ)$ correspond à : $\displaystyle dλ'=\frac{dλ}{1-λ^2}$ ; $\displaystyle \sinh(λ')=\frac{λ}{\sqrt{1-λ^2}}$ . La métrique peut ainsi s'écrire : ${ds}^2=c^2 \, {dt'}^2-c^2 \, {t'}^2.\left[ {dλ'}^2+\sinh^2(λ') \: {dΩ}^2 \right]$ . • Ceci décrit une partie spatiale en expansion proportionnellement à $t'$ , avec (même pour $t'$ fixé) une distance radiale infinie pour rejoindre $λ'=∞$ , correspondant à $λ=1$ . Ceci confirme qu'il est vain de chercher à prolonger au delà de la limite $λ=1$ . ◊ remarque : cette limite équivalant à $r'=r_L$ ne peut être atteinte que pour $t→∞$ , donc ne correspond à aucune limitation sur $r$ .

5.e.	• La métrique limitée au mouvement radial peut s'écrire : ${ds}^2=c^2 \, {dt'}^2-c^2 \, {t'}^2 \: {dλ'}^2$ . • On obtient ainsi : $1=\dot{t'}^2-{t'}^2 \: \dot{λ'}^2$ . Le lagrangien quadratique : $ℒ=\frac{1}{2}\, \left(\dot{t'}^2-{t'}^2 \: \dot{λ'}^2 \right)$ donne les équations du mouvement : $\ddot{t'}=-{t'}^2 \: \dot{λ'}^2$ ; $\dot{\overbrace{\left({t'}^2 \: \dot{λ'}\right)}}=0$ . • La seconde équation donne $\displaystyle \dot{λ'}=\frac{k\:}{{t'}^2}$ (où $k=Cte$ ). • Le report dans la première donne : $\displaystyle \ddot{t'}=-\frac{k^2}{{t'}^3}$ . En multipliant par $2 \,\dot{t'}$ on en déduit : $\displaystyle \dot{t'}^2=\frac{k^2}{{t'}^2} +α$ (où $α$ est une constante dépendant des conditions aux limites). En multipliant la racine par $2 \,t'$ on en déduit : $\dot{\overbrace{\left({t'}^2 \right)}}=2 \:\sqrt{k^2+α \:{t'}^2}$ . Ceci donne enfin : $\displaystyle \frac{k^2}{{t'}^2} +α \:{t'}^2+k^2=(α \:τ+β)^2$ (où $β$ est une constante dépendant des conditions aux limites). • Il n'est pas nécessaire de terminer la résolution des équations du mouvement, puisque ceci montre que $t'→∞$ implique $τ→∞$ .

Particule dans l'ergorégion

1.	• Au voisinage du point de lancement, la métrique simplifiée tangentiellement à la trajectoire peut s'écrire : ${ds}^2=A \:c^2 \, {dt}^2+2 \,B \:c \,dt \:dφ-E \:{dφ}^2$ .

• En notant

\displaystyle ϖ=\frac{ω_a}{c}=\frac{dφ}{c \,dt}

, cette métrique peut s'écrire :

{ds}^2=(A+2 \,B \:ϖ-E \:ϖ^2 ) \: c^2 \, {dt}^2

.
• Pour un photon, le polynôme

P(ϖ)=-E \:ϖ^2+2 \,B \:ϖ+A

doit être nul ; pour une particule massive, il doit être positif. Puisque le coefficient d'ordre

2

est

-E>0

, la quantité

ϖ

doit être comprise entre les deux racines, qui correspondent aux solutions pour un photon. Ceci vient du fait que la vitesse de la particule ne peut pas dépasser celle de la lumière.
• Le discriminant réduit (simplifié par 4) est :

$\displaystyle Д=B^2+A \:E=\frac{r_s^{\:2} \: α^2 \: r^2}{ρ^4} \: \sin^4(θ)+\frac{ρ^2-r_s \: r}{ρ^2} \: \frac{Σ^2}{ρ^2} \: \sin^2(θ)$ ;
$\displaystyle Д=\frac{\sin^2(θ)}{ρ^4} \: \left\{r_s^{\:2} \: α^2 \: r^2 \: \sin^2(θ)+(ρ^2-r_s \: r)\left[(r^2+α^2 ) \: ρ^2+α^2 \: r_s \: r \:\sin^2(θ) \right]\right\}$ ;
$\displaystyle Д=\frac{\sin^2(θ)}{ρ^4} \: \left \{ρ^2.\left[(r^2+α^2 ) \: ρ^2+α^2 \: r_s \: r \:\sin^2(θ) \right]-r_s \: r.(r^2+α^2 ) \: ρ^2 \right\}$ ;
$\displaystyle Д=\frac{\sin^2(θ)}{ρ^2} \: \left \{(r^2+α^2 ) \: ρ^2-r_s \: r.(r^2+α^2-α^2 \: \sin^2(θ) )\right\}$ ;
$\displaystyle Д=\frac{\sin^2(θ)}{ρ^2} \: \left \{(r^2+α^2 ) \: ρ^2-r_s \: r \:ρ^2 \right\}=Δ \: \sin^2(θ)$ .

• On constate ainsi que ce discriminant est positif, comme

Δ

, pour

r>R_H

.
• Avec une rotation de l'espace

ω=c \: \frac{B}{E}

les racines donnent les limites :

\displaystyle ω_a=ω±c \: \frac{\sqrt{Д}}{E}

.

• Pour représenter

ω

et l'intervalle de

ω_a

en fonction de

r

; on peut choisir par exemple

4 \,α^2=\frac{1}{2} r_s^{\:2}

(l'expression de

R_H

nécessite

4 \,α^2≤r_s^{\:2}

).
• Pour simplifier, on peut en outre choisir

R_H

comme unité de longueur ; ceci donne :

$R_H=1$ ; $r_s=\frac{2 \,\sqrt{2}}{\sqrt{2}+1}≈\text{1,172}$ ; $α=\frac{1}{\sqrt{2}+1}≈\text{0,4142}$ .

• On peut choisir comme exemple

θ=\frac{π}{2}

; ainsi :

$R_E=r_s≈\text{1,172}$ ; $Д=Δ=r^2+α^2-r_s \: r$ ; $ρ^2=r^2$ ; $\displaystyle B=\frac{r_s \: α}{r}$ ; $\displaystyle E=r^2+α^2+\frac{r_s \: α^2}{r}$ .

• On constate la dissymétrie apparente entre les rotations de part et d'autre (en fait symétriques par rapport à

ω

) ; on vérifie qu'il n'y a pas d'immobilité possible pour

r<R_E

.
• On constate en outre que, pour

r=R_H

, il ne peut y avoir rotation par rapport à l'espace (l'intervalle se réduit à la valeur

ω

• Pour comparer avec un autre cas, on peut choisir

θ=\frac{π}{4}

; ainsi :

$R_E=r_s \, \frac{\sqrt{3}+2}{4}=\frac{\sqrt{3}+2}{\sqrt{2}+2}≈\text{1,093}$ ; $\displaystyle Д=\frac{Δ}{2}=\frac{r^2+α^2-r_s \: r}{2}$ ;
$\displaystyle ρ^2=r^2+\frac{α^2}{2}$ ; $\displaystyle B=\frac{r_s \: α \:r}{2 \,ρ^2}$ ; $\displaystyle E=\frac{1}{2} \,\left(r^2+α^2+\frac{r_s \: α^2 \: r}{2 \,ρ^2}\right)$ .

• On vérifie que

ω

R_E

sont plus petits que précédemment, mais le comportement est qualitativement le même.

Métrique d'un espace en rotation

• On obtient :

E \:{dϕ}^2=E.({dφ}^2-2 \,ω \:dt \:dφ+ ω^2 \: {dt}^2)=E \:{dφ}^2-2 \,B \:c \,dt \:dφ+E \:ω^2 \: {dt}^2

.
• Ainsi en substituant :

{ds}^2=𝒜 \:c^2 \, {dt}^2-C \:{dr}^2-D \:{dθ}^2-E \:{dϕ}^2

avec

\displaystyle 𝒜=A+E \: \frac{ω^2}{c^2} =\frac{A \:E+B^2}{E}

.
• On peut écrire :

\displaystyle 𝒜=A+\frac{B^2}{E}=\frac{ρ^2-r_s \: r}{ρ^2} +\frac{r_s^{\:2} \: α^2 \: r^2}{ρ^2 \: Σ^2} \: \sin^2(θ)

.
• En réécrivant :

Σ^2=(r^2+α^2 )^2-α^2 \: Δ \; \sin^2(θ)=(r^2+α^2 ) \: ρ^2+α^2 \: r_s \: r \; \sin^2(θ)

, on obtient :

$\displaystyle 𝒜=\frac{1}{ρ^2 \: Σ^2}\, \left\{(ρ^2-r_s \: r)\left[(r^2+α^2 ) \: ρ^2+α^2 \: r_s \: r \;\sin^2(θ) \right]+r_s^{\:2} \: α^2 \: r^2 \; \sin^2(θ) \right\}$ ;
$\displaystyle 𝒜=\frac{1}{ρ^2 \: Σ^2} \: \left\{ρ^2.\left[(r^2+α^2 ) \: ρ^2+α^2 \: r_s \: r \;\sin^2(θ) \right]-r_s \: r.(r^2+α^2 ) \: ρ^2 \right\}$ ;
$\displaystyle 𝒜=\frac{1}{Σ^2} \, \left\{(r^2+α^2 ) \: ρ^2-r_s \: r.(r^2+α^2-α^2 \; \sin^2(θ) )\right\}=\frac{1}{Σ^2} \, \left\{(r^2+α^2 ) \: ρ^2-r_s \: r \:ρ^2 \right\}=\frac{Δ \:ρ^2}{Σ^2}$ .

Métrique d'un espace en rotation

1.a.	• Une approche consiste à décrire le mouvement d'une particule à l'aide d'un lagrangien (ici choisi quadratique et simplifié) : $ℒ=-\frac{1}{2} g_{μν} \: \dot{x}^μ \: \dot{x}^ν$ , où les dérivées sont par rapport à un paramètre $σ$ . • Cela donne les équations du mouvement : $\displaystyle \frac{d}{dσ} \frac{∂ℒ}{∂\dot{x}^μ}-\frac{∂ℒ}{∂x^μ}=0$ . En particulier pour $x^3=φ$ on obtient : $\displaystyle \frac{d}{dσ} \left(-g_{3ν} \: \dot{x}^ν \right)=0$ , donc : $-B \:c \,\dot{t}+E \:\dot{φ}=Cste$ . ◊ remarque : cette quantité constante est l'impulsion généralisée associée à l'angle $φ$ ; elle correspond à la généralisation du moment cinétique.

1.b.	• La même approche en utilisant $x^3=ϕ$ donne : $\displaystyle \frac{d}{dσ} \left(-g_{3ν} \: \dot{x}^ν \right)=0$ , donc : $E \:\dot{ϕ}=Cste$ . • Puisque $dϕ=dφ-ω \:dt$ avec $\displaystyle ω=c \, \frac{B}{E}$ , ceci correspond à : $E.(\dot{φ}-ω \:\dot{t})=E \:\dot{φ}-B \:c \,\dot{t}=Cste$ . On obtient donc dans ce cas la même équation (la constante se déduit des conditions initiales).

2.a.	• Pour la variable $x^0=c \,t$ associée à $φ$ on obtient : $\displaystyle \frac{d}{dσ} \left(-g_{0ν} \: \dot{x}^ν \right)=0$ , donc : $-A \:c \,\dot{t}-B \:\dot{φ}=Cste$ .

2.b.	• Pour la variable $x^0=c \,t$ associée à $ϕ$ on obtient : $\displaystyle \frac{d}{dσ} \left(-g_{0ν} \: \dot{x}^ν \right)=0$ , donc : $-𝒜 \:c \,\dot{t}=Cte$ . • Pour comparer, on peut mettre cette équation sous la forme : $\displaystyle -A \:c \,\dot{t}-\frac{B^2}{E} \, c \,\dot{t}=Cte$ , puis exprimer le second terme en fonction de $\dot{φ}$ . Ceci peut s'écrire : $\displaystyle -A \:c \,\dot{t}-\frac{B}{E} \, B \:c \,\dot{t}=-A \:c \,\dot{t}-\frac{B}{E} \; (E \:\dot{φ}-Cste)=-A \:c \,\dot{t}-B \: \dot{φ}+\frac{B}{E} \: Cste=Cte$ . • On est alors amené à se demander si les équations pour $r$ et $θ$ sont (ou non) telles que $\displaystyle \frac{B}{E}=\frac{ω}{c}$ reste constant. Par symétrie, il est clair qu'un mouvement initié dans le plan $θ=\frac{π}{2}$ s'y poursuit. A priori, la variation radiale fait alors inévitablement changer $ω$ . • On obtient donc généralement une équation différente : la formulation avec $ϕ$ aide à comprendre la rotation de l'espace, mais on ne peut pas l'utiliser sans risque pour résoudre les équations du mouvement. La raison en est qu'en général il n'existe pas de variable $ϕ$ ; tant qu'on fait intervenir seulement $\displaystyle \dot{ϕ}=\frac{dϕ}{dσ}$ , le fait que $dϕ$ ne soit pas une différentielle totale importe peu, mais on ne peut faire intervenir une variable $ϕ$ que dans les cas particuliers où $dϕ$ est intégrable : pour $ω(r)$ constant.

Coordonnée radiale pour la métrique de Kerr

1.a.	• On peut écrire : $\displaystyle Δ=\left(r-\frac{r_s}{2}\right)^2+α^2-\left(\frac{r_s}{2}\right)^2$ ; le minimum pour $\displaystyle r=\frac{r_s}{2}$ est négatif tant que $\displaystyle α<\frac{r_s}{2}$ .

1.b.	• La variable $\displaystyle \tilde{r}=\frac{Δ}{r}=\frac{r^2+α^2}{r}-r_s=r+\frac{α^2}{r}-r_s$ s'annule comme $Δ$ et est bien équivalente à $r$ à l'infini, mais elle a un minimum $\tilde{r}=2 \,α-r_s$ pour $r=α$ ; elle ne convient pas de ce point de vue.

1.c.	• La variable $\tilde{r}=\sqrt{Δ}$ s'annule comme $Δ$ et est bien équivalente à $r$ à l'infini, en outre elle a bien un minimum pour $\displaystyle r=\frac{r_s}{2}$ tant que ce minimum est positif, mais elle pose problème dans le cas le plus utile où le minimum est négatif (condition nécessaire pour l'annulation). • On peut considérer $\tilde{r}=\sqrt{\|Δ\|}$ mais alors le sens de variation dépend du signe. • La variable $\displaystyle \tilde{r}=\frac{Δ}{\sqrt{\|Δ\|}}$ donne une variation monotone, mais n'évite pas le problème du dédoublement.

• On obtient

\displaystyle C=\frac{ρ(\tilde{r} )^2}{\tilde{r}^2}

avec

ρ^2=\tilde{r}^2+r_s \: r

\displaystyle r=\frac{r_s}{2}±\sqrt{\tilde{r}^2+\left(\frac{r_s}{2}\right)^2-α^2}

, ce qui ne se simplifie pas.
• Par ailleurs

\displaystyle \tilde{C}=C .\left(\frac{dr}{d\tilde{r}}\right)^2=C \: \frac{\tilde{r}^2}{\left(r-\frac{r_s}{2}\right)^2} =\frac{ρ(\tilde{r} )^2}{\left(r-\frac{r_s}{2}\right)^2}

; cela n'apporte pas d'amélioration.
• Au total, il semble que même si c'est l'annulation de

Δ

qui détermine l'horizon, c'est plutôt le comportement global du coefficient

C

, y compris l'effet de

ρ

, qu'il est intéressant de simplifier.