Espace-temps thermodynamique
• En l'absence d'interaction, le temps ne s'écoule probablement
pas car il ny a rien par rapport à quoi le repérer
(conformément à certaines idées d'Ernst Mach [1]).
Si le temps est lié aux interactions, alors on peut envisager
une analogie avec la thermodynamique statistique (est-ce la
thermodynamique cachée envisagée par Louis de Broglie ?)
et proposer une définition du
genre : 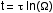 où
où 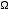 est
un nombre associé à la complexité du diagramme de
Feynman décrivant le système étudié, et
où
est
un nombre associé à la complexité du diagramme de
Feynman décrivant le système étudié, et
où  est une constante de normalisation (arbitraire ?).
est une constante de normalisation (arbitraire ?).
Le sens de l'écoulement du temps [2] serait alors
“évident”
: pour qu'un événement se produise “après” un
autre,
il faut et il suffit qu'il intervienne dans un diagramme de l'Univers
ayant
un plus grand nombre de “branches”. En particulier, pour qu'un
événement soit perçu avant un autre, il faut que
les diagrammes décrivant le second contiennent plus de branches
que les diagrammes contenant des branches décrivant
l'interaction qui permet de détecter (de “mémoriser” ?)
le premier.
Ceci redonne en particulier 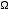 = 1 et t = 0 pour
un propagateur (nu) isolé, ce qui est conforme à
l'instantanéité relativiste envisagée ici.
= 1 et t = 0 pour
un propagateur (nu) isolé, ce qui est conforme à
l'instantanéité relativiste envisagée ici.
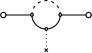
De même, les diagrammes suivants correspondraient respectivement
à 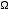 = 4,
= 4, 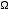 = 3 et
= 3 et 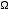 = 6.
= 6.
L'analyse dimensionnelle permet par ailleurs de proposer comme
durée élémentaire quantifiée la valeur
 =
= 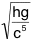 = 1,34.10-43
s (parfois appelée “temps de Planck”, mais ce n'est pas
forcément cette valeur qui convient).
= 1,34.10-43
s (parfois appelée “temps de Planck”, mais ce n'est pas
forcément cette valeur qui convient).
• Le “temps” ainsi défini correspond a priori à celui
valable pour l'Univers en entier. On peut ensuite envisager de
définir un temps “local” en limitant l'étude des
diagrammes associés
à une (petite) partie de l'Univers. Resterait alors à
résoudre le problème relativiste pour deux points
“classiquement” reliés par un intervalle “du genre espace” (dont
l'ordre temporel dépend du
référentiel en relativité restreinte). Mais pour
cela,
il faudrait d'abord préciser la notion de mouvement, et avant
même
préciser la notion de distance.
• Dans cette approche, le temps s'écoulerait plus vite (?) dans les zones de l'espace (?)
où il y a plus d'interactions, c'est-à-dire peut
être bien dans les zones où il y a plus d'énergie
pour interagir, ce qui conduit à une propriété
rappelant qualitativement la théorie relativiste de la
gravitation.
Mais d'autres aspects appellent à la réflexion : en
particulier la durée “diminuée” de traversée
intervenant dans l'effet tunnel [3]. Certaines des particules sont
réfléchies en interagissant avec la “zone interdite”.
Celles (peu nombreuses) qui traversent par effet tunnel semblent passer
directement en “ignorant” la
“zone interdite”, comme si (faute d'y interagir) cette distance
n'existait pas pour elles, ce
qui (bien que peu probable) réduit logiquement en
conséquence la durée de transit (dans les rares cas
où cela se produit). Cela peut il ainsi être
considéré comme une éventuelle conséquence
de l'interprétation précédente du temps ? D'une
part il faudrait préciser l'interprétation, d'autre part
il
faudrait trouver confirmation dans des comportements analogues pour
d'autres situations
: dans un dispositif d'interférences tel que les fentes d'Young,
les particules qui traversent une “frange sombre” sans y interagir ont
elles pour cela une durée de transit diminuée ?
• D'un autre point de vue, si on se base sur l'analogie entre d'une
part : dU = T dS - p
dV avec :
U l'énergie interne, T la température, S
l'entropie, p la pression et V le volume
et d'autre part : dA = E dt - p dx avec :
A l'action, E l'énergie, t le temps, p
l'impulsion et x la position
alors la mise en correspondance de (T,p) et (E,p) suggère
que l'énergie-impulsion d'une particule quantique isolée
n'existe pas ; ce serait une propriété moyenne
statistique des interactions (en supposant qu'il y a
“quasi-équilibre”, ce qui correspond peut-être à la
couche de masse ?).
• Dans une situation de quasi-équilibre, l'énergie et
l'impulsion sont liées par une équation d'état ;
celle-ci n'est pas
vérifiée si on s'éloigne de l'équilibre.
Les
incertitudes de Heisenberg pour les particules “hors de leur couche de
masse”
ne sont peut être que la description statistique des fluctuations
autour
de l'équilibre (d'autant plus grandes que l'écart
à l'équilibre
est violent).
• Peut-on prolonger l'analogie et considérer une quantité
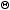 ,
analogue du transfert thermique (chaleur), telle que d
,
analogue du transfert thermique (chaleur), telle que d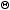 ≤ E
dt de façon analogue à dQ ≤ T dS (avec
égalité dans les cas voisins d'une situation
d'équilibre ?).
≤ E
dt de façon analogue à dQ ≤ T dS (avec
égalité dans les cas voisins d'une situation
d'équilibre ?).
Puisqu'en thermodynamique la création locale d'entropie est
proportionnelle à 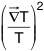 ou
ou 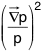 , on peut
envisager ici une création locale de temps qui serait
proportionnelle à un terme du type
, on peut
envisager ici une création locale de temps qui serait
proportionnelle à un terme du type 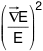 où il faudrait
encore transformer le “gradient” puisque cela décrit une
dérivée par rapport à la position dans l'espace (quel “espace” ?). Peut-on
envisager pour ceci le quotient de la variation d'énergie par la
“longueur de la chaîne d'interaction” locale ?
où il faudrait
encore transformer le “gradient” puisque cela décrit une
dérivée par rapport à la position dans l'espace (quel “espace” ?). Peut-on
envisager pour ceci le quotient de la variation d'énergie par la
“longueur de la chaîne d'interaction” locale ?
• Au “voisinage” d'un équilibre, l'analogue de la conservation
de l'énergie d'un système thermodynamique serait une
action quasi-constante (?). L'analogue d'une entropie maximum serait un
temps extrémum (?).
L'analogue du facteur de Boltzmann e-E/kT
devrait être du type 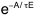 (resterait à voir, du point de vue quantique, s'il y a des
variantes pour les fermions et les bosons). Les actions les plus
probables seraient alors les plus faibles, et d'autant plus à
faible énergie. Il est en outre possible que l'action soit
quantifiée (de quantum h).
(resterait à voir, du point de vue quantique, s'il y a des
variantes pour les fermions et les bosons). Les actions les plus
probables seraient alors les plus faibles, et d'autant plus à
faible énergie. Il est en outre possible que l'action soit
quantifiée (de quantum h).
• Enfin, une autre analogie serait envisageable pour expliquer la
différence d'abondance entre matière et
antimatière. Partant du constat que l'intégration sur
l'énergie-impulsion des particules virtuelles (dans les
diagrammes de Feynman) se fait y compris hors de la couche de masse, et
que les mêmes diagrammes peuvent par “retournement”
décrire des interactions d'électrons ou de positons, on
est amené à considérer ces derniers comme des
électrons “remontant le temps” [4]. L'analogue d'une particule
remontant le temps est une diminution de l'entropie d'un système
isolé : bien que l'entropie d'un tel système ait
statistiquement tendance à augmenter, des fluctuations locales
peuvent se produire. Les apparentes “inversions du temps” que
constituent les observations d'antiparticules seraient des fluctuations
peu probables, réservées à des situations
particulières où nous détectons l'effet de la
quantification de l'espace-temps.
__________________
Références :
1. “La Mécanique”, E. Mach, éd. J. Gabay (traduction
française).
2. On peut distinguer plusieurs notions comme le “cours du temps” qui
précise le sens (apparemment inéluctable)
de
variation du temps et la
“flèche
du temps” qui précise le sens d'évolution de
phénomènes irréversibles ; tout en étant
d'accord sur la
nécessité de clarification suggérée par
divers auteurs, je pense qu'il serait déraisonnable d'essayer de
construire la notion de temps à partir d'autre chose que son
contenu événementiel (le temps ne s'écoule
probablement pas s'il ne se passe “rien”, mais reste à savoir
précisément quel “rien”... quand on considère
usuellement qu'un verre est “vide” dès lors qu'il ne contient
pas de liquide) ; c'est pourquoi je désigne aussi par
“flèche du temps” l'irréversibilité du “cours du
temps” ; voir par exemple :
“Le temps est différent
des
propriétés qu'on lui attribue”, E. Klein, Science &
Vie,
janvier 2003 ;
“Faut-il distinguer cours du temps et flèche
du temps ?”, E. Klein, Bulletin de l'Union des Professeurs de
Spéciales
n° 890, janvier 2007.
.
3. voir par exemple (pour une interprétation intéressante
des durées, montrant en particulier l'absence de
dépassement de la vitesse de la lumière) : “Effet tunnel
: plus vite que la lumière ?”, La Recherche, n° 281,
novembre 1995.
4. voir en particulier :
“les intégrales de chemin”, Pour
la Science - les génies de la science, n° 19 (“Feynman,
génie magicien”), mai 2004 ;
“la médiation de Dyson”, Pour la
Science - les génies de la science, n° 19 (“Feynman,
génie magicien”), mai 2004.
Retour au début

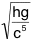 = 1,34.10-43
s (parfois appelée “temps de Planck”, mais ce n'est pas
forcément cette valeur qui convient).
= 1,34.10-43
s (parfois appelée “temps de Planck”, mais ce n'est pas
forcément cette valeur qui convient).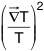 ou
ou 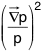 , on peut
envisager ici une création locale de temps qui serait
proportionnelle à un terme du type
, on peut
envisager ici une création locale de temps qui serait
proportionnelle à un terme du type 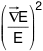 où il faudrait
encore transformer le “gradient” puisque cela décrit une
dérivée par rapport à la position dans l'espace (quel “espace” ?). Peut-on
envisager pour ceci le quotient de la variation d'énergie par la
“longueur de la chaîne d'interaction” locale ?
où il faudrait
encore transformer le “gradient” puisque cela décrit une
dérivée par rapport à la position dans l'espace (quel “espace” ?). Peut-on
envisager pour ceci le quotient de la variation d'énergie par la
“longueur de la chaîne d'interaction” locale ?