Expansion de l'Univers ; “big bang” ou “petit plop” ?
• Si la notion “intrinsèque” de distance doit se déduire
de la structure de diagrammes en permanente complexification, et si
le
référentiel local “naturel” (celui où l'expression
des calculs est plus simple) correspond à l'échelle
élémentaire, alors le référentiel
que nous utilisons est par rapport à cela en expansion.
Cette expansion étant raisonnablement proportionnelle au contenu
de la structure considérée, elle serait exponentielle.
Ceci
n'est peut-être pas sans rapport avec les observations
cosmologiques
récentes [1], mais le rapprochement doit être
envisagé
avec prudence : si nos mesures de distances doivent être
envisagées
comme “renormalisées”, alors il faut préalablement
soigneusement comparer les renormalisations respectives du
phénomène étudié et du mécanisme de
mesure utilisé (si les deux diffèrent, leur
différence s'ajoute à ce qu'on croit observer).
Une telle expansion accélérée peut être
assez naturellement associée à l'effet d'inertie que
constitue la force de gravitation. Il est alors normal que la
masse inerte soit égale à la masse pesante, et
qu'Einstein ait pû représenter
ceci par une formulation en géométrie riemannienne, sauf
que
cela est souvent fait en considérant une métrique
statique
; est-ce le bon choix (en particulier vis a vis de la description
des
trous
noirs) ?
Mais ce qui est intéressant dans cette approche, c'est que
l'expansion en question apparaît comme universelle :
serait
en expansion non seulement toute région de l'espace (?)
contenant de la masse, mais toute région de l'espace contenant
de l'énergie (des diagrammes d'interaction, et il me semble
probable que “l'espace” n'existe que par les interactions qui le
constituent).
Par ailleurs, le mécanisme envisagé décrit une
expansion “sans expansion”, en ce sens que la distance entre les
galaxies
grandit,
mais nous aussi, et d'une façon comparable. Le décalage
vers
le rouge de la lumière venant de loin est simplement dû au
fait
que l'échelle de référence au moment de
l'émission
n'était pas la même que celle qui est la nôtre au
moment
de la réception. De ce fait, l'Univers ne se “dilue” pas ; c'est
simplement
son échelle “naturelle” de référence qui diminue.
Cette
échelle de référence serait en quelque sorte
l'équivalent,
par rapport à la loi d'invariance d'échelle, de ce que
représentent
les référentiels galiléens par rapport à
l'invariance
par translation.
Une façon de présenter ceci peut être de considerer
que si le degré de ramification “local” des diagrammes augmente
avec le temps, les propagateurs intervenant dans un diagramme plus
tardif portent chacun moins d'énergie (par répartition de
celle-ci) compte tenu de l'expantion par ailleurs associée
à ce mécanisme, donc les photons (entre autres)
reçus maintenant en provenance du “passé” sont
statistiquement d'autant plus basse énergie qu'ils proviennent
de plus loin. Ceci est qualitativement cohérent avec l'autre
interprétation, associée à l'utilisation d'un
référentiel en expansion, mais on ne peut pas conclure
plus précisément sans comprendre en détail le
mécanisme de renormalisation associé aux distances et
peut-être aussi aux énergies.
Je serais pour ma part enclin à chercher une équation
ressemblant plus ou moins à (en améliorant pour respecter
les lois d'invariance qui s'imposent) : dX/X = K E dt
; où X serait une grandeur caractéristique de
l'espace (le tenseur métrique, ou la partie spatiale du tenseur
métrique, pourraient correspondre) ; où E serait une
grandeur comme une densité d'énergie associée aux
diagrammes de Feynmann “passant par là” (une quantité
plus ou moins comme la composante temporelle g00 du
tenseur
métrique ne me semblerait pas absurde) et où K serait une
constante (qui pourrait bien être liée à la fois
à la constante de Planck et à celle de Hubble).
Précision indispensable : il ne s'agirait pas d'une
équation prétendant remplacer les équations
d'Einstein associées à la relativité
générale (dont la validité est maintenant
avérée, au moins en ce qui concerne la description
“après renormalisation” de l'éventuelle structure
quantique de l'espace-temps), mais d'utiliser le
degré de
liberté qui y subsiste pour examiner plus en détails les
solutions, et en particulier les “singularités”
associées, avec ce point de vue particulier. Certains
s'empresseront de commenter : “inutile puisque tous les systèmes
de coordonnées solution sont équivalents”... certes, mais
notre façon de les interpréter ne l'est pas
forcément et il ne me semble pas impossible que nous puissions
avoir un intérêt à chercher dans cette voie.
• Un inconvénient de cette démarche tient à la
vitesse d'une telle expansion accélérée :
même considéré comme une sorte de “moyenne”
(restant à préciser) d'interactions avec le “voisinage”,
un champ de pesanteur g = 9,8 m.s-2
à la
surface terrestre ne tarderait pas à correspondre à une
vitesse d'expansion rédhibitoire, surtout si cette expansion
perdure depuis le début (?) de l'Univers.
Un autre point délicat tient à la comparaison avec les
observations cosmiques : il semble plutôt au contraire que les
zones soient en expansion d'autant moins importante que la
densité d'énergie (matière et/ou interactions) y
est grande [2, 3]. Certes, on peut rétorquer qu'une
renormalisation
locale, selon des mécanismes non encore imaginés,
pourrait modifier notre perception du phénomène, mais
encore faudrait-il trouver comment...
• Quel que soit le mécanisme envisagé pour décrire
l'expansion, il faut en outre considérer que, par
l'intermédiaire de l'instantanéité relativiste, la
répartition statistique des photons émis sur le
cône futur d'une source peut aussi dépendre de la
densité de répartition des récepteurs potentiels
sur ce cône futur. Ceci peut non seulement conduire à une
variation de l'expansion au cours du temps, mais aussi à des
effets plus complexes comme des oscillations.
• D'un autre point de vue, si on envisage un espace de bipoints,
correspondant plus ou moins aux propagateurs, on peut envisager de
définir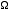 
d'après un temps commençant lors
d'une
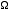interaction initiale : = 1 et t = 0
à l'apparition du premier propagateur ; le début de
l'Univers serait alors un “petit plop” plutôt qu'un “big bang”.
On peut aussi envisager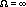 
(dénombrable ?),
correspondant au contraire (après une indispensable
renormalisation) à un Univers fractal [4], sans
début mais en complexification continuelle.
• Si le nombre total de branches est infini, on peut raisonnablement
envisager une invariance par retournement du temps ; au contraire,
s'il
est fini, il est fort probable que seule une quasi-invariance [5]
est
envisageable, d'autant plus proche de l'invariance que le nombre
total
de branches augmente quand on s'éloigne de l'instant initial.
Ainsi la brisure de symétrie ne serait pas constante mais
décroissante, elle aurait été plus grande au
début de l'Univers.
D'un autre point de vue, la description envisagée ici
étant associée à des “fluctuations quantiques” de
l'espace-temps, ces dernières pouvaient être en proportion
plus importantes au début de l'Univers, si on envisage que le
diagramme global correspondant était alors plus simple.
L'interprétation de l'antimatière comme de la
matière “remontant le temps” lors de fluctuations conduit alors
à considérer que les proportions
matière-antimatière pouvaient être comparables au
tout début de l'Univers, mais qu'elles ont de toute façon
très rapidement évolué pour laisser presque
uniquement de la matière.
__________________
Références :
1. voir par exemple :
“Accélération
confirmée”, Pour la Science n° 313, p. 14, novembre 2003 ;
“Que cache la constante cosmologique”, J. P. Uzan, Pour la Science
n° 326, décembre 2004 ;
“Pourquoi l'Univers accélère-t-il ?”, J.O. Baruch et S.
Fay, La Recherche n° 384, mars 2005.
2. voir par exemple : “Les paradoxes du Big Bang”, Pour la Science
n° 330, avril 2005.
3. la géométrie de l'espace à l'échelle
cosmique est toutefois encore un sujet de tests approfondis et des
écarts par rapport à la théorie subsistent ; voir
par exemple :
“Les amas bousculent l'énergie
du vide”, Pour la Science n° 315, p. 20, janvier 2004 ;
“La gravitation sous surveillance”, S. Reynaud, Pour la
Science n° 326, décembre 2004 ;
“L'étrange trajectoire des sondes Pioneer”, J.O. Baruch, La
Recherche n° 390, octobre 2005 ;
“Big Bang ; des origines de l'Univers aux origines de la vie”, S.
Katsanevas et coll.,
dossiers
du
CNRS, décembre 2005.
4. ceci est peut-être à considérer en relation
avec d'autres approches ; entre autres :
• “The stochastic interpretation of quantum mechanics :
a
critical review”, G.C. Ghirardi, C. Omero, A. Rimini and T. Weber,
Rivista del nuovo cimento, vol 1, n° 3, 1978 ;
• “Physical foundations of quantum theory : stochastic formulation
and
proposed experimental test”, V.J. Lee, Foundations of physics, vol
10,
n°
1/2, 1980 ;
• “L'espace-temps fractal”, L. Nottale, Pour la Science n° 215,
septembre 1995 ;
• “La relativité d'échelle l'épreuve des faits”,
L.
Nottale, Pour la Science n° 309, juillet 2003.
5. voir par exemple :
“Le miroir brisé de
l'antimatière”,
I. Mannelli, Pour la Science n° 303, janvier 2003 ;
“L'antimatière questionne toujours le Big Bang”, La Recherche
n° 382, janvier 2005.
Retour au début
