Distances et topologie
• Quand on envisage de définir une notion de distance en
“comptant les nœuds intermédiaires des diagrammes”, il est
évident que quelques précisions s'imposent.
En procédant simplement ainsi, pour décrire un photon (de
masse nulle) arrivant sur Terre en provenant d'une galaxie “lointaine”,
on
aboutirait à un photon ayant parcouru une distance nulle (en une
durée nulle), ce qui n'est pas ce à quoi on se
réfère usuellement.
• On peut proposer de réfléchir par analogie avec la
mesure d'un objet usuel constitué d'atomes : sa longueur peut
nous paraître bien définie à notre échelle
macroscopique, mais sembler plutôt “fractale” quand on regarde
à une échelle plus petite. Il est donc nécessaire
de définir comment on “passe à la limite microscopique”.
En particulier, la définition des dérivées
“physiques” s'obtient pour des petites variations tendant vers
zéro... sans tendre vers zéro : il faut préciser
jusqu'à où on considère la “limite”.
• Revenant aux décomptes sur les diagrammes, il faut
peut-être prendre de même une sorte de moyenne (peut
être une “limite inférieure”) dans l'ensemble des
diagrammes possibles reliant deux événements, mais il
faut probablement pour cela définir une “pondération”
dans la moyenne (ou une façon de considérer la limite),
ce qui
constitue plus ou moins la définition d'un filtre de
voisinages, c'est-à-dire une topologie.
La pondération envisagée pourrait être basée
sur
une mesure comme celle de Levin, utilisant la complexité de
Kolmogorov
[1], ou bien sur les méthodes servant à décrire
les flux dans les chaînes de production [2] ou les interactions
dans les
réseaux [3].
La métrique découle alors éventuellement de la
topologie, mais peu probablement l'inverse [4, 5, 6]. Ce que je crains
alors,
c'est que la complexité du problème mathématique
soit un obstacle à toute résolution prochaine. En effet,
bien que de formation mathématique
plutôt relativement renforcée pour un physicien (lorsque
j'envisageais
de trouver un emploi de recherche en physique théorique, j'avais
en prévision approfondi ma formation mathématique de
base), il me semble que l'approche de ce problème est tellement
différente de ce qui a été utilisé
précédemment qu'elle risque de nécessiter ou bien
un fantastique coup de hasard (un physicien qui rencontre fortuitement
les outils mathématiques nécessaires), ou bien une
résolution par un mathématicien de haut niveau
(connaissant une large panoplie d'outils et curieux de
s'intéresser à l'application en physique de
théories plus “abstraites”). Dommage, c'est un peu tard pour
Grothendieck [7]. On pourait aussi penser à quelqu'un comme
Gregori Perelman, capable de s'inverstir dans un projet complexe sans
trop s'attacher aux espoirs de récompenses [8], mais ce genre de
personnes est par nature peu accessible (si vous le rencontrez, dites
lui de regarder si mes divagations l'intéressent).
• Ainsi, on peut envisager que les “voisinages” d'une particule en
mouvement ne soient pas les mêmes que ceux définis pour le
“milieu de propagation” (ce par rapport à quoi on
considère que la particule se déplace) et que cette sorte
“d'effet Doppler topologique” apparaisse globalement sous la forme de
la transformation de Lorentz (ou sa généralisation pour
un mouvement accéléré).
• Qui plus est, les différentes sortes de particules
n'intéragissant pas de la même façon, elles ne
“voient” probablement pas l'espace avec la même
topologie/métrique : seule une théorie unifiée des
interactions conduirait à une métrique unique.
En particulier, j'ai plutôt tendance à penser que la
gravitation n'est que ce qui reste, vu de loin, quand on
considère l'ensemble des
autres interactions se compensant en moyenne. Je suis ici conduit
à envisager la relativité générale, en fin
de compte, comme
une théorie macroscopique approchée dont la
métrique n'est pas du tout appropriée pour décrire
le niveau microscopique.
• Que ce soit pour la relativité générale ou pour
les théories quantiques décrivant des interactions dans
un
“vide” renormalisé, certaines approches semblent en fait
indiquer que l'intégrabilité des équations
découlant des théories macroscopiques ne serait pas
indépendante de l'invariance conforme des
phénomènes microscopiques sous-jacents [9].
• Finalement, il serait peut être intéressant de chercher
une approche du problème à partir de la méthode
des intégrales de chemin [10]. En se basant sur l'action A,
l'intégration K(xfin, tfin | xin,
tin) = 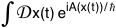 sur tous les
chemins possibles conduit à une difficulté si on
considère ces chemins dans un espace supposé
préalablement existant. Il faudrait résoudre le
problème inverse : trouver un espace (réseau
d'interactions ?) où “intégrer”, tel que disparaissent
les divergences associées aux théories quantiques.
Peut-être aurions nous alors la surprise d'être conduits
à un espace inattendu, par exemple d'une nature
intermédiaire entre l'infini dénombrable et le continu
[11].
sur tous les
chemins possibles conduit à une difficulté si on
considère ces chemins dans un espace supposé
préalablement existant. Il faudrait résoudre le
problème inverse : trouver un espace (réseau
d'interactions ?) où “intégrer”, tel que disparaissent
les divergences associées aux théories quantiques.
Peut-être aurions nous alors la surprise d'être conduits
à un espace inattendu, par exemple d'une nature
intermédiaire entre l'infini dénombrable et le continu
[11].
__________________
Références :
1. voir par exemple : “La complexité mesurée...”,
J.P. Delahaye, Pour la Science n° 314, décembre 2003.
2. voir par exemple : “L'algèbre des sandwichs”, G. Cohen,
S. Gaubert et J.P. Quadrat, Pour la Science n° 328, février
2005.
3. voir par exemple :
“Étude des réseaux par la
physique statistique”, A. Barrat, M. Barthétémy et A.
Vespignani, Bulletin de l'UPS n° 212, octobre 2005 ;
“Vivre serein dans un monde cruel”, J.P. Delahaye et
R. Dorat, Pour la Science n° 346, août 2006.
4. si, à partir de la théorie des ensembles, on essaye de
construire une géométrie au niveau
“élémentaire”, on est amené à associer une
notion de “droite” à un propagateur reliant deux vertex ;
l'essentiel du raisonnement s'arrête dès qu'on aborde les
axiomes d'ordre sur une “droite” : il n'y a aucun autre point que les
deux vertex et la “géométrie” qui en résulte est
trop rudimentaire pour être vraiment utile ; il semble donc qu'il
faudrait plutôt construire la géométrie au niveau
macroscopique sur la base d'une nouvelle interprétation au
niveau élémentaire ; des difficultés semblables
avaient d'ailleurs été évoquées dès
Euclide, au sujet des a priori que pouvaient sous-entendre certains de
ses axiomes ; voir par exemple :
“Foundations of
geometry for university students and high-school students”, R.
Sharipov, fr.arxiv.org/abs/math/0702029, février 2007 ;
“Les avatars de la rigueur mathématique”, É. Barbin, Pour
la Science n° 356, juin 2007.
5. cela peut aussi impliquer des structures moins usuelles comme les
prétopologies, voire même un couple de structures
prétopologiques associées respectivement aux dispositifs
émetteurs et récepteurs ; voir par exemple : “Les
mathématiques des frontières floues”, S. Dugowson, Pour
la Science n° 350, décembre 2006.
6. cela peut d'ailleurs poser d'autant plus de questions
délicates que les mathématiciens sont déjà
circonspects au sujet de problèmes comme ceux liés
à l'axiome du choix (indépendemment de l'utilisation
physique des mathématiques) ; en ce qui concerne les
applications, il me semble que la simple existence du paradoxe de
Banach-Tarski implique le caractère rédhibitoire de la
forme forte de l'axiome du choix pour décrire l'espace physique
aux échelles usuelles, d'autant plus que la forme faible
associée à la mesurabilité de Lebesgue conduit
à des propriétés mathématiques suffisantes
pour cela (et qu'on peut en outre envisager d'y ajouter d'autres
axiomes) ; par contre, il n'est pas évident que le jeu d'axiomes
judicieux doive être le même pour la description à
l'échelle microscopique “élémentaire”
envisagée ici (d'où l'intérêt à ce
que les mathématiciens continuent à travailler sans
préjugé sur les différentes possibilités) ;
voir par exemple : “Coloriages irréels”, J.P. Delahaye,
Pour la Science n° 328, décembre 2005.
7. voir par exemple : “Grothendieck : au fond des choses”, A.
Hobeika, Pour la Science n° 334, août 2005.
8. voir par exemple : “Un mystérieux mathématicien
pour une complexe conjecture”, C. Dumas,
sciences.nouvelobs.com/sci_20060818.OBS8690.html, août 2006.
9. voir par exemple : “Les mille et une facettes de
l'intégrabilité”, D. Bernard et P. di Francesco, Pour la
Science n° 336, octobre 2005.
10. voir par exemple :
wikipedia,
http://fr.wikipedia.org/wiki/Intégrale_de_chemin ;
cours de C.
Cohen Tannoudji,
http://www.phys.ens.fr/cours/notes-de-cours/cct-dea/index.html.
11. voir par exemple : “Imaginer l'infini, ou le découvrir
?”, J.P. Delahaye, Pour la Science n° 370, août 2008.
Retour au début
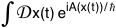 sur tous les
chemins possibles conduit à une difficulté si on
considère ces chemins dans un espace supposé
préalablement existant. Il faudrait résoudre le
problème inverse : trouver un espace (réseau
d'interactions ?) où “intégrer”, tel que disparaissent
les divergences associées aux théories quantiques.
Peut-être aurions nous alors la surprise d'être conduits
à un espace inattendu, par exemple d'une nature
intermédiaire entre l'infini dénombrable et le continu
[11].
sur tous les
chemins possibles conduit à une difficulté si on
considère ces chemins dans un espace supposé
préalablement existant. Il faudrait résoudre le
problème inverse : trouver un espace (réseau
d'interactions ?) où “intégrer”, tel que disparaissent
les divergences associées aux théories quantiques.
Peut-être aurions nous alors la surprise d'être conduits
à un espace inattendu, par exemple d'une nature
intermédiaire entre l'infini dénombrable et le continu
[11].