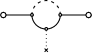
Distances and renormalization
• As for durations, the notion of distance between two “points of
space” risks to have no meaning in the absence of interaction.
If one tries to found upon the Feynman's style diagrams,
one may propound to count the number N of
intermediate nodes, and consider a distance of the form
d =
n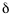 where
where 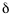 is an elementary (arbitrary ?) distance.
is an elementary (arbitrary ?) distance.
This gives back in particular N = 0 and d = 0
for an isolated (naked) propagator, what is consistent with the
relativistic instantaneousness here considered ; but within such a
model, is the distance independent of the kind of interaction
considered to foreseen it (the
question arises as soon as one considers more complex
diagrams) ?
Thus the following diagrams (with respect to the two outmost points)
would correspond respectively to N = 2,
N = 1 and N = 2 or 3 (?).
Dimensionnal analysis furthermore allows to propound as elementary
quantified distance the value 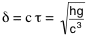 = 4,0.10-35 m (sometimes called “Planck
distance”, but this is not necessarily the appropriate value).
= 4,0.10-35 m (sometimes called “Planck
distance”, but this is not necessarily the appropriate value).
• Among the difficulties issued from the model, an important point is
the necessary reinterpretation of the renormalization.
Within usual quantum theories, some diagrams with more branches occur
as higher order corrections with respect to simpler diagrams describing
the same
interaction. In the argumentation considered here, these diagrams would
occur in the description of the same
phenomenon, but later (as with more
branches).
This aspect which may look as troublesome is not necessarily
“negative”, since if one consider that as the time proceeds, the
“dressed up” propagator describing an interaction complexifies itself,
and that this is connected to an increase of distances, thus this may
lead to a “natural” effect of Universe
expansion.
• Inversely, in order to describe a “constant distance” between two
points which interact “always likewise” (the two ends of a length
standard ?), it might be necessary to introduce a
renormalization of distances (the length standard is submitted to
expansion in a similar way as the distances that it is supposed to
measure).
The renormalization would thus be different : the mass would issue from
“lateral” branches of diagrams
(associated with undetected interactions), and not from “loops”, which
on the contrary would intervene in a renormalization of distances.
• After that, it would be elsewere necessary to think to
define clearly some notions as mouvement, and so on...
Return to the beginning