Distances et renormalisation


• De même que pour les durées, la notion de distance entre deux “points de l'espace” risque de n'avoir aucune signification en l'absence d'interaction.

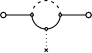
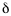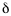Si on cherche à se baser sur les diagrammes à la Feynman, on peut proposer de compter le nombre N de nœuds intermédiaires, et envisager une distance de la forme  d = n  où  est une distance élémentaire (arbitraire ?).

Ceci redonne en particulier  N = 0  et  d = 0  pour un propagateur (nu) isolé, ce qui est conforme à l'instantanéité relativiste envisagée ici ; mais dans une telle modélisation, la distance ne dépend-elle pas du type d'interaction envisagé pour la considérer (la question se pose dès qu'on envisage des diagrammes plus complexes) ?

Ainsi les diagrammes suivants (vis à vis des deux points extrèmes) correspondraient respectivement à  N = 2,  N = 1  et  N = 2 ou 3 (?).


L'analyse dimensionnelle permet par ailleurs de proposer comme distance élémentaire quantifiée la valeur 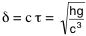  = 4,0.10^-35 m  (parfois appelée “distance de Planck”, mais ce n'est pas forcément cette valeur qui convient).

• Parmi les difficultés découlant du modèle, un point important est la réinterprétation nécessaire de la renormalisation.

Dans les théories quantiques usuelles, certains diagrammes avec plus de branches interviennent comme corrections d'ordre supérieur par rapport à des diagrammes plus simples décrivant la même interaction. Dans le raisonnement envisagé ici, ces diagrammes interviendraient dans la description du même phénomène, mais plus tard (puisqu'avec plus de branches).

Cet aspect qui peut sembler gênant n'est pas forcément “négatif”, puisque si on considère qu'au fur et à mesure que le temps s'écoule, le propagateur “habillé” décrivant une interaction se complexifie, et que cela est associé à une augmentation des distances, alors on peut aboutir à un effet “naturel” d'expansion de l'Univers.

• Inversement, pour décrire une “distance constante” entre deux points qui interagissent “toujours pareil” (les deux extrémités d'un étalon de longueur ?), il serait peut être nécessaire de faire intervenir une renormalisation des distances (l'étalon de longueur subit l'expansion de façon analogue aux distances qu'il est censé mesurer).

La renormalisation serait  donc différente : la masse découlerait des branches “latérales” des diagrammes (associées à des interactions non détectées), et non des “boucles”, qui au contraire interviendraient dans une renormalisation des distances.

• Ensuite, encore faudrait-il réfléchir à définir clairement des notions comme le mouvement, etc...



Retour au début