Gravitation quantique


• Une théorie relativement prometteuse (et qui, sur certains aspects, utilise le même genre de concepts que ceux que je défends ici), est celle appelée “gravitation quantique à boucles” [1]. Cette théorie comporte toutefois (à mon humble avis) un certain nombre de “défauts” dont il n'est pas évident qu'ils soient contournables.

• Cette théorie “persiste” à considérer que l'espace-temps quantifié existe a priori ; elle y ajoute ensuite des interactions (sous la forme équivalant à des diagrammes de Feynman) en pondérant certains nœuds des graphes ; ces interactions influencent l'espace-temps qui les contient, mais ce dernier peut exister en leur absence.

Je pense qu'il faut au contraire envisager une théorie où l'espace-temps n'est qu'une des propriétés découlant des interactions (diagrammes de Feynman) et rien d'autre : sans interactions il n'y a pas d'espace-temps.



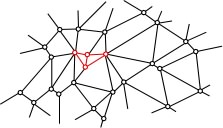
• Quand la gravitation quantique à boucles envisage (par exemple) un photon se propageant dans l'espace-temps quantifié, elle le décrit comme une modification locale des graphes représentant l'espace-temps (ce qui peut être visualisé, de façon très simplifiée, à l'aide du premier des diagrammes ci-dessus).

Je pense au contraire que les graphes de l'espace-temps sont beaucoup plus enchevêtrés (et ce d'une façon fondamentale, qui n'est pas seulement due à la simplification inévitable pour la visualisation) : ce que nous considérons “voisin” à l'échelle macroscopique (et donc ce qui est à “faible distance” d'après la métrique de l'espace-temps) n'est pas forcément “voisin” au niveau “microscopique”, et réciproquement.

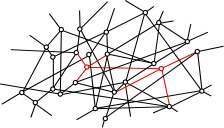
Deux points, distants de millions d'année-lumière au sens de notre métrique macroscopique, mais reliés par un photon (ou n'importe quelle particule de masse nulle), sont à une distance nulle au sens des interactions élémentaires. L'espace lui-même découle d'une multitude d'interactions dont un bon nombre sont entre points “très éloignés” (plutôt selon le second des diagrammes ci-dessus) et dont les corrélations à “grande distance” (dont des effets de type E.P.R.) causent les phénomènes tels que l'inertie.

Il ne me semble pas indispensable d'ajouter quoi que ce soit d'autre pour faire intervenir un effet d'inertie... et de ce fait je suis convaincu qu'il n'y a rien à ajouter : les seuls diagrammes à considérer seraient ceux des interactions qui ont lieu dans l'espace-temps (diagrammes de Feynman) et la gravitation ne serait qu'un effet de leurs corrélations multiples à longue distance.

• Une autre approche, qui tombe dans les mêmes défauts, est celle évoquée sous le nom de “gravitation quantique euclidienne” [2] : pour chercher une structure limite décrivant l'espace-temps, il faut ne pas partir de polyèdres d'espace-temps préexistants.

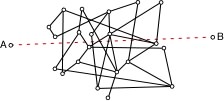
• L'interprétation peut en outre être compliquée par des a priori associés aux concepts usuels. Considérons par exemple le déplacement d'une particule, depuis un point A jusqu'à un point B, en passant au voisinage d'une zone de “forte densité d'interaction” (dans les schémas symboliques suivants, le détail des interactions de la particule lors du trajet n'est pas précisé) [3].


Si on envisage un raisonnement “local”, on peut conclure qu'un trajet contournant la zone soit causé par une attraction : le mouvement commence de côté (sans intention préalable d'atteindre B), puis l'attraction le dévie et lui fait finalement atteindre B. Si on envisage un raisonnement “global”, on peut conclure à une sorte de répulsion : parmi les trajets allant globalement de A à B, les plus probables sont ceux qui ne traversent pas la zone d'interaction et sont en quelque sorte “repoussés” (comme les lignes de champ magnétique sont “repoussées” par les supraconducteurs).

• Bien entendu, dans la mesure où il n'est pas évident de trouver quelle topologie associer à un écheveau aussi enchevêtré, on peut essayer de le représenter (par une sorte de renormalisation) à l'aide d'une théorie “duale”, dont chaque graphe représente localement l'effet global des corrélations à grande distance dans la théorie initiale. Ce serait alors plus où moins à la gravitation quantique à boucles que ressemblerait probablement une telle théorie duale. Mais dans ce cas, s'il est probable qu'elle permettrait une meilleure “liaison” avec notre description macroscopique, elle ne serait au contraire pas représentative des diagrammes élémentaires microscopiques.

Il faut par ailleurs noter que, malgré l'analogie de “l'absence de gravitation”, le point de vue envisagé ici me semble sans rapport direct avec le type de théorie “duale” qui a été proposé avec extrapolation au ”bord” de dimensions supplémentaires [4] (mais peut-être mon incrédulité n'est elle pas indépendante des doutes que m'inspirent les théories des cordes).

__________________
Références :

1. voir par exemple :  “Des atomes d'espace et de temps”, L. Smolin, Pour la Science n° 316, février 2004.

2. voir par exemple : “L'univers quantique auto-organisé”, J. Ambjorn, J. Jurkiewicz et R. Loll, Pour la Science n° 371, septembre 2008.

3. bien que les concepts étudiés soient en bonne partie différents, certaines recherches sur les communications dans les réseaux apporteront peut être des idées importantes en ce sens ; voir par exemple :  “Double clustering and graph navigability”, O. Sandberg, <http://fr.arxiv.org/abs/0709.0511>, septembre 2007.

4. voir par exemple :  “La gravité est-elle illusion ?”, J. Maldacena, Pour la Science n° 339, janvier 2006.




Retour au début