Masse et interactions
• Un objet isolé ne peut pas avoir de masse inerte car le
principe de l'inertie suppose que l'objet est sensible à la
notion de mouvement ; or in n'y a aucune notion de mouvement s'il
n'y a rien pour se repérer (conformément aux
idées de Mach), et s'il y a quelque chose, l'objet
considéré ne peut s'en servir de repère qu'en
interagissant avec.
Pour une particule massive, la durée propre entre le
départ et l'arrivée est non nulle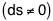 
. Ceci
peut suggérer que la particule massive “interagit” pendant
son trajet, même si on ne décèle pas ces
interactions, un peu à la façon d'un photon qui se
propage dans un guide d'ondes (ou dans un matériau
transparent), ou d'une particule élémentaire laissant
une trace dans une chambre à bulles. Il s'agirait alors
probablement d'un très grand nombre d'interactions
infinitésimales (avec ce qu'on appelle à tort “le
vide”), et la masse serait une traduction de l'énergie
moyenne d'interaction.
On retrouve ainsi les idées utilisées par les
théories renormalisées : les particules “nues” ont une
masse nulle et la masse, associée à une brisure
spontanée de symétrie, se déduit (en relation
avec la renormalisation) de l'habillage des particules par les
interactions. Inversement, pour les particules virtuelles (non
détectées) intervenant dans les diagrammes de Feynman,
il faut intégrer sur toutes les possibilités de
mouvement y compris en dehors de la “couche de masse” [1].
Ceci introduit d'ailleurs des divergences car il existe une
équivalence entre la description énergie-impulsion et
la description espace-temps, dans laquelle les grandes
énergies correspondent aux petites distances. Dès lors
des infinis apparaissent lorsqu'on intègre sur les grandes
énergies, puisque les petites “distances” n'existent pas en
tant que telles : faute de savoir comment corriger cela (par quoi
remplacer l'intégration en question ?), la renormalisation
actuellement utilisée consiste à “bricoler” des
combinaisons de diagrammes telles que les divergences ainsi
introduites se compensent [2].
• Toutefois, contrairement à ce qu'envisagent
généralement les théories renormalisées,
les interactions en question peuvent-elles se limiter à des
interactions virtuelles “isolées” ?
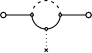
En effet, dans l'état d'esprit de la démarche
précédente, les diagrammes non connectés
à une portion significative de l'Univers (comme le premier
des trois représentés ci-dessus) peuvent sembler ne
pas donner d'effet d'inertie : quand une particule se scinde en une
paire de particules virtuelles, si cette paire n'a d'interaction
avec rien d'autre, elle n'a aucun repérage pouvant donner
lieu à un phénomène d'inertie.
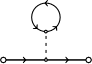
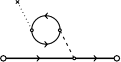
Il faudrait alors envisager une multitude de petites interactions
(“virtuelles” ?) avec le reste de l'Univers (comme dans les deux
derniers des trois diagrammes ci-dessus, où le propagateur
terminé par x désigne une
interaction “extérieure” non précisée). Par
“virtuelles”, on entend ici “non décelées” et non
directement décelables, dans la mesure où tout
dispositif permettant de les déceler en modifierait le mode
d'interaction.
Ainsi, en quelque sorte, il n'existerait pas de système
isolé au sens strict (en ce sens que ce que les
théories quantiques usuelles appellent le “vide” est toujours
présent et actif). Il me semble que le rayonnement d'un
électron accéléré montre le lien entre
l'inertie et l'interaction
(électro-magnéto-faible-forte ; je pense qu'il n'y en
a qu'une) de la même façon que le comportement de la
force de Lorentz lors d'un changement de vitesse montre le lien
entre électricité et magnétisme. La masse et
l'inertie sont l'une des propriétés des interactions
(et ne sont que cela).
• Cela n'est pas indépendant de l'interprétation que
Feynman avait proposée pour tenter d'éliminer de
certains calculs les divergences causées par
l'autointeraction des électrons [3]. Ces diagrammes
d'autointeraction, avec des boucles du type du premier des
diagrammes suivants, Lifchitz et Pitayevski les écartent en
considérant “qu'une telle boucle correspond simplement
à la valeur moyenne du courant dans le vide... donc doit
forcément être nulle après renormalisation” [4].
Il me semble qu'il y a une raison plus fondamentale :
l'électron de la boucle devrait revenir en arrière
dans le temps pour faire cela, donc se comporter comme un positon ;
sans le dire clairement, il ne s'agit pas tout à fait d'une
autointeraction : ce diagramme comporte donc au moins une
création de paire à partir de rien (“énergie du
vide”) et/ou annihilation de paire ne donnant rien (“disparition
d'énergie dans le vide”), comme ceci peut être
décrit par le second des diagrammes suivants
(incorporé, après renormalisation, dans l'effet
décrit par le second des diagrammes
précédents).
Par ailleurs, si un électron interagissait avec
lui-même, il “le saurait” (par l'instantanéité
relativiste, dont Feynman n'est pas loin, même s'il ne la cite
pas comme telle, lorsqu'il considère une interaction
“à distance”), or je pense que l'électron “en tant
qu'émetteur” ne peut pas interagir avec lui même “en
tant que récepteur” (il ne peut y avoir d'intersection entre
son cône passé et son cône futur que s'il subit au
moins une autre interaction entre les deux).
Mais de toute façon, quoi qu'il en soit, cela ne pourrait pas
participer à son inertie (seules les interactions avec les
autres électrons peuvent y contribuer) ; donc non seulement
cela ne peut pas constituer l'origine de sa masse (énergie
d'autointeraction), mais cela ne peut même pas y contribuer.
• Il est à noter qu'on peut aller plus loin dans la sorte de
questionnement précédente : un électron peut-il
émettre un photon virtuel puis l'absorber, sans que ni l'un
ni l'autre n'ait interagi entretemps ? Si on envisage aussi de tels
diagrammes comme non-physiques, cela modifie beaucoup le
développement perturbatif et sa renormalisation. Certaines
divergences ne proviennent-elles pas de boucles représentant
mal (physiquement) des interactions avec un “vide” imaginaire, qui
n'est que l'ensemble de ce qu'on “ne voit pas” participer à
l'interaction ?
• D'un autre point de vue, on peut se demander si les interactions
“élémentaires” (non décelées), pouvant
correspondre à l'habillage d'un propagateur, ne sont pas
associées à une sorte de “vibration” (dans une
dimension non visible à notre échelle) comme celles
envisagées dans les théories des cordes [5].
Pour la recherche d'une telle interprétation, il faudrait
toutefois revoir à la base la notion de “dimensions”
cachées puisque, dans les raisonnements envisagés ici,
la notion de dimension ne préexiste pas mais devrait se
déduire des interactions.
• On peut enfin envisager qu'il y ait une relation entre de telles
interactions et la masse importante de “matière noire” qui
semble manquer pour interpréter les mouvements des
étoiles et des galaxies [6].
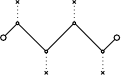
• L'interprétation doit toutefois être prudente, car on
peut aussi penser qu'en modifiant le nombre d'interactions
élémentaires, donc en modifiant la notion de temps,
les diagrammes tel que le second ci-dessous interviennent dans
l'inertie décrite par le premier.
__________________
Références :
1. ceci peut éventuellement être décrit par
l'interaction avec le boson de Higgs ; voir par exemple (le
phénomène est cité dans de nombreux articles) :
“Qui attrapera le Higgs”, La Recherche n° 364, mai 2003.
2. voir par exemple : “Les séries divergentes”, J.P. Ramis,
Pour la Science n° 350, décembre 2006.
3. voir par exemple (tout en notant que l'interaction “à
distance” n'est pas vraiment ce que son nom semble indiquer si la
notion de “distance” n'existe pas à l'échelle d'une
interaction élémentaire) : “vous voulez rire”,
Pour la Science - les génies de la science, n° 19
(“Feynman, génie magicien”), mai 2004.
4. “Théorie quantique relativiste (2)”, E. Lifchitz et L.
Pitayevski, Physique théorique tome IV, éd. Mir, 1973.
5. voir par exemple :
“Le monde
des cordes est-il le nôtre ?”, P. Ramond, Pour la Science
n° 300, octobre 2002 ;
“Le paysage
de la théorie des cordes”, R. Bousso et J. Polchinski, Pour
la Science n° 326, décembre 2004 ;
en notant toutefois l'existence de
difficultés liées aux théories de ce type
(variations non observées de certaines constantes physiques
avec le temps) :
“L'Univers avant le Big
Bang”, G. Veneziano, Pour la Science n° 320, juin 2004 ;
“Les constantes... le sont”, C. Pichon, Pour la Science
n° 320, juin 2004.
6. voir par exemple (le phénomène est cité dans
de nombreux articles) : “La face cachée des galaxies”, G.
Lagache et B. Guiderdoni, Pour la Science n° 296, juin 2002.
Retour au début
