Temps de vie du photon ; instantanéité et
“localéité” relativistes des interactions
• L'un des tests de la relativité est lié à la
durée de vie des particules. Si on considère un muon
provenant des rayons cosmiques et arrivant sur la Terre à une
vitesse proche de celle de la lumière, on constate que sa
durée de vie est plus grande que celle d'un muon au repos. Ceci
tient au fait que la durée qui importe physiquement pour le muon
est celle qui correspond à son référentiel propre
; il faut donc se baser sur l'intervalle de temps propre 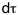 (ou sur l'élément de métrique invariant
relativiste ds = c
(ou sur l'élément de métrique invariant
relativiste ds = c 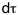 ) plutôt que sur
l'intervalle de durée dt mesuré dans notre
référentiel.
) plutôt que sur
l'intervalle de durée dt mesuré dans notre
référentiel.
Si on s'intéresse au cas analogue pour un photon, dont la masse
est nulle, on peut considérer une particule de masse non nulle,
puis faire tendre la masse vers zéro à quantité de
mouvement constante. Pour un muon qui se déplace à la
vitesse v entre un point A et un point B
séparés par une distance D, la durée du trajet
est T = D/v. Dans le référentiel où le
muon est au repos, la durée du trajet est T’ = T . 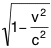 , durée
pendant laquelle les points A et B (qui se
déplacent à la vitesse -v) parcourent une distance
D’ = D .
, durée
pendant laquelle les points A et B (qui se
déplacent à la vitesse -v) parcourent une distance
D’ = D . 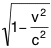 .
.
Quand on fait tendre la masse vers zéro à quantité
de mouvement constante, la vitesse v tend vers c et donc T’ et D’
tendent vers zéro. Ceci consiste à dire que, par rapport
à son “référentiel propre”, le photon parcourt une
distance nulle en une durée nulle.
On en arrive ainsi à une notion de photon qui “arrive en
même temps qu'il part” (non pas par rapport à notre vision
des choses, mais par rapport à l'interaction à laquelle
il est en train de participer), ce qui n'empêche pas de
distinguer entre le point de départ et le point d'arrivée
puisqu'il y a transport d'énergie de l'un vers l'autre.
• Cette sorte de jaillissement “instantané” rejoint
l'idée, déjà utilisée par Newton, de
particules interagissant instantanément à distance. Bien
qu'il soit certain que la lumière “part de la source” et “se
dirige vers le récepteur”, la propagation qui
découle de l'image newtonienne des interactions est en quelque
sorte instantanée (ce qui est un abus de langage car le terme
“propagation” évoque un décalage spatial mais aussi un
décalage temporel). Or, si on remplace (conformément
à l'introduction par Einstein de la propagation relativiste de
la lumière) l'instantanéité correspondant
à dt = 0 par son analogue correspondant
à 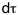 = 0, on constate que la
propagation à la vitesse de la lumière peut très
bien être considérée comme
l'instantanéité relativiste de l'interaction lumineuse.
= 0, on constate que la
propagation à la vitesse de la lumière peut très
bien être considérée comme
l'instantanéité relativiste de l'interaction lumineuse.
Tout ceci conduit à un modèle non
local, ou
possédant plutôt une “localéité” relativiste
liée à la propriété ds = 0,
où la trajectoire d'un paquet d'ondes décrivant une
particule doit être considérée globalement (je
préfère utiliser le néologisme
“localéité” plutôt que le terme “localité”,
qui a plusieurs acceptions, pour faire ressortir la même
différence qu'entre les mots “instant” et
“instantanéité”).
Cette interprétation des phénomènes possède
des aspects fortement déterministes en ce sens que, étant
considérée comme un tout, l'onde présente des
corrélations avec les informations sur son point
d'arrivée dès le moment où elle part. Cette
façon globale de considérer les interactions peut
contrarier l'intuition, surtout dans certains cas de
corrélations à distance
où il devient difficile de
séparer les causes et les effets sans contredire la
mécanique quantique. Toutefois, lorsqu'on étudie un champ
électromagnétique dans la jauge de Coulomb, on est
amené à utiliser le potentiel scalaire non retardé
de l'électrostatique, qui semble ne rien avoir de relativiste ;
on aboutit pourtant au même résultat que dans la jauge de
Lorentz où on utilise le potentiel retardé. Ceci est en
fait cohérent avec le principe déterministe qui dit que
le présent peut se déduire du passé et lui est
donc en partie équivalent du point de vue de l'information
contenue ; ceci montre par ailleurs que les corrélations
spatio-temporelles du monde physique peuvent paraître
étranges quand on ne les exprime pas dans le
référentiel ou la jauge appropriés.
• En outre, cela n'est pas indépendant de
l'interprétation que Feynman avait proposée pour tenter
d'éliminer de certains calculs les divergences causées
par l'autointeraction des électrons : avec Wheeler, il
envisageait une interaction à distance associée à
une superposition d'égales contributions d'ondes
retardées et avancées [1]. Un reproche souvent fait
à ce travail était de remplacer la difficulté
d'une divergence par la difficulté d'un non respect du principe
de causalité. Or, ce type d'argument n'est pas approprié
dans l'approche de l'instantanéité relativiste : non
seulement un électron peut interagir par potentiels
avancés en tant qu'émetteur, mais (dans la mesure
où est respectée la symétrie entre les deux sens
du temps) il le fait logiquement autant qu'il interagit par potentiels
retardés en tant que récepteur.
• Une complication peut sembler apparaître si on revient au cas
du muon pour
traiter, dans l'ordre d'idées évoqué au
début, le cas des particules massives,
qui se déplacent à une vitesse inférieure à
celle de la lumière. On n'a plus en effet ds = 0 le
long de la trajectoire et on ne peut donc pas utiliser directement
l'instantanéité relativiste.
Plusieurs hypothèses peuvent être envisagées pour
généraliser cette notion. Mais la
généralisation est directe si on considère que les
particules “nues” ont une masse nulle et que la masse des particules
“habillées” par les interactions découle d'une
renormalisation.
__________________
Références :
1. voir par exemple : “vous voulez rire”, Pour la Science -
les génies de la science, n° 19 (“Feynman, génie
magicien”), mai 2004.
Retour au début
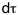 (ou sur l'élément de métrique invariant
relativiste ds = c
(ou sur l'élément de métrique invariant
relativiste ds = c 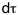 ) plutôt que sur
l'intervalle de durée dt mesuré dans notre
référentiel.
) plutôt que sur
l'intervalle de durée dt mesuré dans notre
référentiel.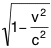 , durée
pendant laquelle les points A et B (qui se
déplacent à la vitesse -v) parcourent une distance
D’ = D .
, durée
pendant laquelle les points A et B (qui se
déplacent à la vitesse -v) parcourent une distance
D’ = D . 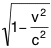 .
.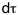 = 0, on constate que la
propagation à la vitesse de la lumière peut très
bien être considérée comme
l'instantanéité relativiste de l'interaction lumineuse.
= 0, on constate que la
propagation à la vitesse de la lumière peut très
bien être considérée comme
l'instantanéité relativiste de l'interaction lumineuse.